Abstract
The ability to attend to a particular sound in a noisy environment is an essential aspect of hearing. To accomplish this feat, the auditory system must segregate sounds that overlap in frequency and time. Many natural sounds, such as human voices, consist of harmonics of a common fundamental frequency (F0). Such harmonic complex tones (HCTs) evoke a pitch corresponding to their F0. A difference in pitch between simultaneous HCTs provides a powerful cue for their segregation. The neural mechanisms underlying concurrent sound segregation based on pitch differences are poorly understood. Here, we examined neural responses in monkey primary auditory cortex (A1) to two concurrent HCTs that differed in F0 such that they are heard as two separate “auditory objects” with distinct pitches. We found that A1 can resolve, via a rate-place code, the lower harmonics of both HCTs, a prerequisite for deriving their pitches and for their perceptual segregation. Onset asynchrony between the HCTs enhanced the neural representation of their harmonics, paralleling their improved perceptual segregation in humans. Pitches of the concurrent HCTs could also be temporally represented by neuronal phase-locking at their respective F0s. Furthermore, a model of A1 responses using harmonic templates could qualitatively reproduce psychophysical data on concurrent sound segregation in humans. Finally, we identified a possible intracortical homolog of the “object-related negativity” recorded noninvasively in humans, which correlates with the perceptual segregation of concurrent sounds. Findings indicate that A1 contains sufficient spectral and temporal information for segregating concurrent sounds based on differences in pitch.
Keywords: multiunit activity, current source density, auditory evoked potentials, ORN, concurrent sound segregation, pitch perception
Introduction
The ability to perceptually segregate concurrent sounds is crucial for successful hearing in complex acoustic environments (Bregman, 1990). Sound segregation is a computationally challenging task for the auditory system given that sounds tend to overlap in frequency and time when multiple sound sources are active. Natural sounds, such as human voices and animal vocalizations, are often temporally periodic and consist of frequencies (harmonics) that are integer multiples of a common fundamental frequency (F0). Such harmonic complex tones (HCTs) are typically heard as having a unitary pitch at their F0 (Plack et al., 2005). When two spectrally overlapping HCTs differing in F0 are presented concurrently, they are usually perceived as two separate “auditory objects” with pitches at their respective F0s. Thus, a difference in F0 between simultaneous HCTs provides a powerful cue for their segregation (Darwin and Carlyon, 1995; Micheyl and Oxenham, 2010).
Neural mechanisms underlying concurrent sound segregation are poorly understood. Several lines of evidence support a role for auditory cortex in concurrent sound segregation (Alain et al., 2005; Alain, 2007; Bidet-Caulet et al., 2007, 2008) and in selective attention to particular streams of concurrent speech (Ding and Simon, 2012; Mesgarani and Chang, 2012; Zion-Golumbic et al., 2013). However, the ability to attend to one speech stream in the midst of other competing streams critically depends on how well they are perceptually segregated from one another (Shinn-Cunningham and Best, 2008). The key question of how the auditory system segregates concurrent, spectrally overlapping, sounds before their attentional selection remains unanswered.
Perceptual segregation of simultaneous HCTs is generally facilitated when their harmonics are spectrally “resolved” by the auditory system (Micheyl and Oxenham, 2010). In a previous study (Fishman et al., 2013), we found that neural populations in monkey primary auditory cortex (A1) can resolve the lower harmonics of single HCTs via a “rate-place” code. Furthermore, the F0 of single HCTs can be temporally represented by neural phase-locking to the periodicity in the stimulus waveform. Correspondingly, humans and nonhuman primates use both spectral and temporal cues in pitch perception (Plack et al., 2005; Bendor et al., 2012). Theoretically, the pitch of an HCT can be extracted from these rate-place and temporal representations via “harmonic templates” (Goldstein, 1973) and “periodicity detectors” (Licklider 1951; Meddis and Hewitt, 1992), respectively.
Accordingly, if F0-based sound segregation relies critically on A1, then neural representations of concurrent HCTs in A1 must convey sufficient spectral and temporal information to enable accurate perceptual segregation of the sounds. Here, we test this hypothesis by examining neural representations of double HCTs in macaque A1. F0s of the HCTs differed by 4 semitones, an amount sufficient for the sounds to be perceptually segregated by human listeners (Assmann and Paschall, 1998). Our findings demonstrate that A1 can indeed represent the harmonic spectra and waveform periodicities of concurrent HCTs with a resolution necessary and sufficient for extracting their pitches and for their perceptual segregation. Furthermore, a model of A1 responses using harmonic templates was able to qualitatively reproduce psychophysical data on concurrent sound segregation in humans.
Materials and Methods
Neurophysiological data were obtained from two adult male macaque monkeys (Macaca fascicularis) using previously described methods (Steinschneider et al., 2003; Fishman and Steinschneider, 2010). All experimental procedures were reviewed and approved by the Association for Assessment and Accreditation of Laboratory Animal Care-accredited Animal Institute of Albert Einstein College of Medicine and were conducted in accordance with institutional and federal guidelines governing the experimental use of nonhuman primates. Animals were housed in our Association for Assessment and Accreditation of Laboratory Animal Care-accredited Animal Institute under daily supervision of laboratory and veterinary staff. Before surgery, monkeys were acclimated to the recording environment and were trained to perform a simple auditory discrimination task (see below) while sitting in custom-fitted primate chairs.
Surgical procedure.
Under pentobarbital anesthesia and using aseptic techniques, rectangular holes were drilled bilaterally into the dorsal skull to accommodate epidurally placed matrices composed of 18-gauge stainless steel tubes glued together in parallel. Tubes served to guide electrodes toward A1 for repeated intracortical recordings. Matrices were stereotaxically positioned to target A1 and were oriented to direct electrode penetrations perpendicular to the superior surface of the superior temporal gyrus, thereby satisfying one of the major technical requirements of one-dimensional current source density (CSD) analysis (Müller-Preuss and Mitzdorf, 1984; Steinschneider et al., 1992). Matrices and Plexiglas bars, used for painless head fixation during the recordings, were embedded in a pedestal of dental acrylic secured to the skull with inverted bone screws. Perioperative and postoperative antibiotic and anti-inflammatory medications were always administered. Recordings began after at least 2 weeks of postoperative recovery.
Stimuli.
Stimuli were generated and delivered at a sample rate of 48.8 kHz by a PC-based system using an RX8 module (Tucker Davis Technologies). Frequency response functions (FRFs) derived from responses to pure tones characterized the spectral tuning of the cortical sites. Pure tones used to generate the FRFs ranged from 0.15 to 18.0 kHz, were 200 ms in duration (including 10 ms linear rise/fall ramps), and were randomly presented at 60 dB SPL with a stimulus onset-to-onset interval of 658 ms. Resolution of FRFs was 0.25 octaves or finer across the 0.15–18.0 kHz frequency range tested.
All stimuli were presented via a free-field speaker (Microsatellite; Gallo) located 60 degrees off the midline in the field contralateral to the recorded hemisphere and ∼1 m away from the animal's head (Crist Instruments). Sound intensity was measured with a sound level meter (type 2236; Bruel and Kjaer) positioned at the location of the animal's ear. The frequency response of the speaker was flat (within ±5 dB SPL) over the frequency range tested.
Rate-place and temporal representations of double HCTs were evaluated using a stimulus design used in auditory-nerve studies of pitch encoding (Cedolin and Delgutte, 2005; Larsen et al., 2008) and in studies of neural responses to single HCTs in macaque auditory cortex (Fishman et al., 2013). At each recording site, 89 double HCTs with variable F0s were presented in random order. Individual HCTs comprising the double HCTs were composed of 12 equal-amplitude harmonics, each presented at 60 dB SPL (the same intensity as that of pure tone stimuli), added together in sine phase. Thus, double HCTs consisted of 24 harmonics, 12 from each of the two HCTs. When all harmonics fell within the flat frequency range of the speakers (0.15–18.0 kHz), the overall level of each HCT was ∼71 dB SPL. The F0s of the HCTs comprising the double HCTs were separated by 4 semitones (a ratio of 1.26), an amount sufficient for them to be reliably heard by human listeners as separate “auditory objects” with distinct pitches at their respective F0s (Assmann and Paschall, 1998; Snyder and Alain, 2005). Henceforth, HCTs with the lower and higher F0 are referred to as HCT1 and HCT2, respectively. The particular F0s of the 89 double HCTs presented were selected according to the best frequency (BF) of the recording site, as defined below. The F0 of the lower HCT (HCT1) was systematically varied, such that the BF of the recording site occupied harmonic number positions 1 through 12 in 1/8 harmonic-number increments (where harmonic number = BF/F0). The relationship between the frequency tuning of the site and spectral components of the double HCT stimuli is schematically illustrated in Figure 1A. HCT stimuli were 225 ms in duration, including 10 ms linear rise/fall ramps. Of the 89 sounds comprising a stimulus set, the HCT1 with the highest F0 was configured such that its F0 (first harmonic) matched the BF of the site, whereas that with the lowest F0 was configured such that its highest component (12th harmonic) matched the BF. Effects of stimulus onset asynchrony (SOA) on the neural representation of the harmonics of individual HCTs comprising the double HCT stimuli were examined by delaying the onset of one of the HCTs by 80 ms relative to that of the other HCT (with the total duration of the double HCT stimulus remaining fixed at 225 ms).
Figure 1.
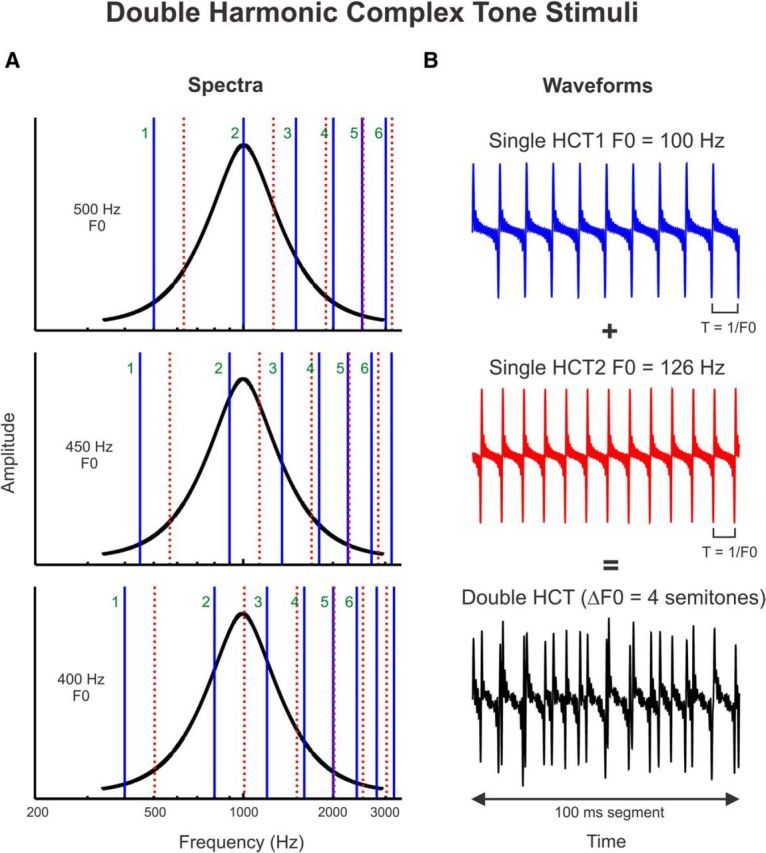
Schematic representation of the double HCT stimuli presented in the study. A, Spectra of double HCT stimuli. Stimulus amplitude and frequency are represented along the vertical and horizontal axes, respectively. Stimuli consisted of a series of two simultaneously presented HCTs with a fixed F0 difference between them of 4 semitones. Harmonics of the HCT with the lower F0 and higher F0 (referred to in the text as HCT1 and HCT2, respectively) are represented by the solid blue lines and broken red lines, respectively. The F0 of the lower HCT is varied such that harmonics of the double HCTs fall progressively either on the peak (at the BF, here equal to 1000 Hz) or on the sides of the neuronal FRF (black). The F0 of HCT1 is indicated on the left of each plot; the first 6 harmonics of HCT1 are labeled. If individual harmonics of the double HCT stimuli can be resolved by frequency-selective neurons in A1, then response amplitude as a function of F0 (or harmonic number: BF/F0) should display peaks when a given harmonic of HCT1 or HCT2 overlaps the BF (top and bottom plots) and troughs when the BF falls in between two adjacent harmonics of the concurrent sounds (middle panel). B, Temporal waveforms (100 ms segment) of single (blue and red curves, corresponding to HCT1 and HCT2, respectively) and double HCT stimuli (black curve). Note that waveforms correspond to stimuli with F0s different from those represented in A. Waveforms of single HCTs display a periodicity at T = 1/F0.
Completing the above-described stimulus protocol typically required 3–4 h of recording time. Hence, it was generally not possible to test more than one F0 separation and more than two SOA conditions (0 and 80 ms) in a given electrode penetration, as doing so would have required prohibitively long neurophysiological recording sessions in awake monkeys. Although testing additional stimulus conditions would have been optimal, the use of a 4 semitone F0 separation at least allowed us to determine whether A1 can resolve harmonics of concurrent HCTs at the minimum F0 separation required to reliably hear the concurrent HCTs as two separate sounds with distinct pitches at their respective F0s, according to human psychophysical studies (Assmann and Paschall, 1998). Similarly, the use of an 80 ms SOA at least allowed us to determine whether resolvability of harmonics in A1 is improved for delays, which are known to markedly facilitate the perceptual segregation of double HCTs in human listeners (Lentz and Marsh, 2006; Hedrick and Madix, 2009; Shen and Richards, 2012).
Neurophysiological recordings.
Responses to double HCTs were recorded at the same sites in the same animals as those examined in a parallel study of responses to single HCTs (Fishman et al., 2013). Recordings were conducted in an electrically shielded, sound-attenuated chamber. Monkeys were monitored via video camera throughout each recording session. To promote attention to the sounds during the recordings, animals performed a simple auditory discrimination task (detection of a randomly presented noise burst interspersed among test stimuli) to obtain liquid rewards. An investigator entered the recording chamber and delivered preferred treats to the animals before the beginning of each stimulus block to further maintain alertness of the subjects.
Local field potentials (LFPs) and multiunit activity (MUA) were recorded using linear-array multicontact electrodes comprised of 16 contacts, evenly spaced at 150 μm intervals (U-Probe; Plexon). Individual contacts were maintained at an impedance of ∼200 kΩ. An epidural stainless-steel screw placed over the occipital cortex served as the reference electrode. Neural signals were bandpass filtered from 3 Hz to 3 kHz (roll-off 48 dB/octave) and digitized at 12.2 kHz using an RA16 PA Medusa 16-channel preamplifier connected via fiber-optic cables to an RX5 data acquisition system (Tucker-Davis Technologies). LFPs time-locked to the onset of the sounds were averaged on-line by computer to yield auditory evoked potentials (AEPs). CSD analyses of the AEPs characterized the laminar distribution of net current sources and sinks within A1 and were used to identify the laminar location of concurrently recorded AEPs and MUA (Steinschneider et al., 1992, 1994). CSD was calculated using a 3 point algorithm that approximates the second spatial derivative of voltage recorded at each recording contact (Freeman and Nicholson, 1975; Nicholson and Freeman, 1975).
MUA was derived from the spiking activity of neural ensembles recorded within lower lamina 3, as identified by the presence of a large amplitude initial current sink that is balanced by concurrent superficial sources in mid-upper lamina 3 (Steinschneider et al., 1992; Fishman et al., 2001). This current dipole configuration is consistent with the synchronous activation of pyramidal neurons with cell bodies and basal dendrites in lower lamina 3. Previous studies have localized the initial sink to the thalamorecipient zone layers of A1 (Müller-Preuss and Mitzdorf, 1984; Steinschneider et al., 1992; Sukov and Barth, 1998; Metherate and Cruikshank, 1999). To derive MUA, neural signals (3 Hz to 3 kHz pass-band) were high-pass filtered at 500 Hz (roll-off 48 dB/octave), full-wave rectified, and then low-pass filtered at 520 Hz (roll-off 48 dB/octave) before averaging of single-trial responses (for a methodological review, see Supèr and Roelfsema, 2005). MUA is a measure of the envelope of summed (synchronized) action potential activity of local neuronal ensembles (Brosch et al., 1997; Schroeder et al., 1998; Vaughan and Arezzo, 1988; Supèr and Roelfsema, 2005; O'Connell et al., 2011). Thus, whereas firing rate measures are typically based on threshold crossings of neural spikes, MUA, as derived here, is an analog measure of spiking activity in units of response amplitude (e.g., see Kayser et al., 2007). MUA and single-unit activity, recorded using electrodes with an impedance similar to that in the present study, display similar orientation and frequency tuning in primary visual and auditory cortex, respectively (Supèr and Roelfsema, 2005; Kayser et al., 2007). Adjacent neurons in A1 (i.e., within the sphere of recording for MUA) display synchronized responses with similar spectral tuning, a fundamental feature of local processing that may promote high-fidelity transmission of stimulus information to subsequent cortical areas (Atencio and Schreiner, 2013). Thus, MUA measures are appropriate for examining the neural representation of spectral and temporal cues in A1, which may be used by neurons in downstream cortical areas for pitch extraction and concurrent sound segregation.
Positioning of electrodes was guided by online examination of click-evoked AEPs. Pure tone stimuli were delivered when the electrode channels bracketed the inversion of early AEP components and when the largest MUA and initial current sink were situated in middle channels. Evoked responses to 40 presentations of each pure tone or HCT stimulus were averaged with an analysis time of 500 ms that included a 100 ms prestimulus baseline interval. The BF of each cortical site was defined as the pure tone frequency eliciting the maximal MUA within a time window of 0–75 ms after stimulus onset. This response time window includes the transient “On” response elicited by sound onset and the decay to a plateau of sustained activity in A1 (e.g., see Fishman and Steinschneider, 2009). After determination of the BF, HCT stimuli were presented.
At the end of the recording period, monkeys were deeply anesthetized with sodium pentobarbital and transcardially perfused with 10% buffered formalin. Tissue was sectioned in the coronal plane (80 μm thickness) and stained for Nissl substance to reconstruct the electrode tracks and to identify A1 according to previously published physiological and histological criteria (Merzenich and Brugge, 1973; Morel et al., 1993; Kaas and Hackett, 1998). Based upon these criteria, all electrode penetrations considered in this report were localized to A1, although the possibility that some sites situated near the low-frequency border of A1 were located in field R cannot be excluded.
Analysis and interpretation of responses to double HCTs.
Responses to double HCTs were analyzed with the aim of determining whether A1 contains sufficient spectral and temporal information to reliably extract the F0s of each of the HCTs via spectral harmonic templates or temporal periodicity detectors, respectively. The former require sufficient neuronal resolution of individual harmonics of the HCTs (Plack et al., 2005), whereas the latter require accurate neural phase-locking at the F0 (Cariani and Delgutte, 1996). Published data (Fishman et al., 2013) obtained from the same recording sites based on responses to individual (single) HCTs comprising the double HCT stimuli are presented in this report for comparison purposes. The extensive analyses required to adequately characterize responses to single HCTs precluded concurrent presentation of results based on responses to both single and double HCTs in the previously cited work.
At each recording site, the F0 of the lower HCT of the double HCT stimuli was varied in small increments (as described earlier), such that harmonics fell either on the peak or, in a progressive manner, on the sides of the neuronal pure-tone tuning functions (Fig. 1A). As the F0 of the higher-pitched HCT of the double HCT stimuli was always fixed at 4 semitones (a major third) above the F0 of the lower-pitched HCT, the F0 of the higher-pitched HCT varied correspondingly. The resulting neuronal firing-rate-versus-harmonic-number functions are referred to as “rate-place profiles.” If harmonics of the lower HCT (HCT1) in double HCT stimuli (i.e., its spectral fine-structure) can be resolved by patterns of firing rate across frequency-selective neurons in A1, then rate-place profiles should display a periodicity with peaks occurring at integer values of harmonic number. Similarly, if A1 neurons can resolve harmonics of the higher HCT (HCT2), then rate-place profiles should display a periodicity with peaks occurring at integer multiples of 1.26 (corresponding to a ratio of F0s differing by 4 semitones). Neural representation of the harmonic spectra of the double HCTs, as reflected by periodicity in the rate-place profile, was evaluated by computing the discrete Fourier transform (DFT) of the rate-place profile. The salience of the periodicity is quantified by the amplitude of the peak in the DFT at a frequency of 1.0 cycle/harmonic number (for harmonics of HCT1) and of 1/1.26 = 0.79 cycle/harmonic number (for harmonics of HCT2). Statistical significance of peaks in the DFTs was assessed using a nonparametric permutation test (Ptitsyn et al., 2006; Womelsdorf et al., 2007; Fishman et al., 2013), which entails randomly shuffling the data points in the rate-place profile, computing the DFT of the shuffled data, and measuring the spectral magnitude at 1.0 cycle/harmonic number and at 0.79 cycle/harmonic number. This method of quantification is illustrated in Figure 2C. Repeating this process 1000 times yields a “null” distribution of spectral magnitudes. The probability of obtaining a spectral magnitude equal to or greater than the value observed, given the null, can be estimated by computing the proportion of the total area under the distribution at values equal to and greater than the observed value (Fishman et al., 2013). Spectral magnitude values yielding p values <0.05 were considered statistically significant and interpreted as indicating neural representation of the HCT harmonics via a rate-place code.
Figure 2.
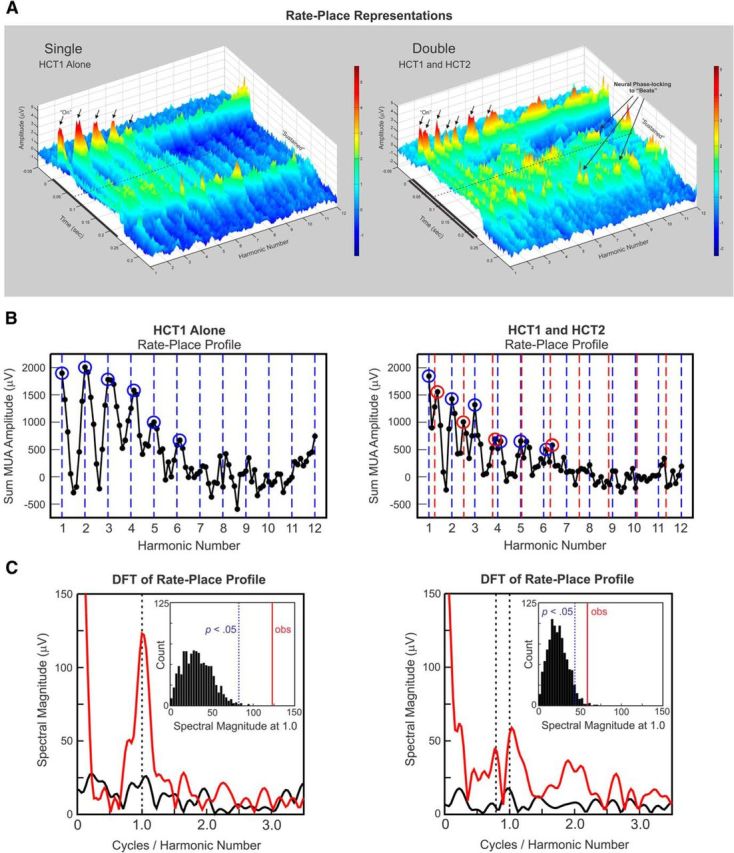
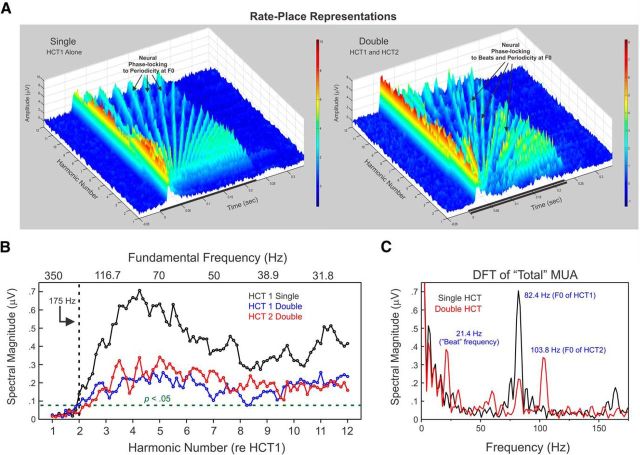
Example rate-place representations of responses evoked by single and double HCTs. A, Rate-place representations of responses to single (left) and double (right) HCTs at a site with a BF of 1550 Hz. Axes represent harmonic number (BF/F0 of HCT1), time, and response amplitude in μV (also color coded), as indicated. Black bars represent the duration of the stimuli (225 ms). In rate-place representations of responses to single HCTs (HCT1 alone), amplitude of “On” and “Sustained” activity displays a periodicity with prominent peaks (indicated by black arrows) occurring at or near integer values of harmonic number. In rate-place representations of responses to double HCTs (HCT1 and HCT2), “On” responses (indicated by black arrows) occur at or near values of harmonic number corresponding to components of each of the HCTs. Neuronal phase-locking to “beat” frequencies is also evident in rate-place profiles of responses to double HCTs. B, Corresponding rate-place profiles of responses to single (left) and double (right) HCTs based on the area under the MUA waveform within the “On” time window. Values of harmonic number corresponding to the frequency components of HCT1 and HCT2 are indicated by the blue and red dashed lines, respectively. Peaks in neural activity occurring at or near these values are enclosed by the blue and red circles. C, Corresponding DFTs of the rate-place profiles shown in B (red curve: harmonic numbers 1–6; black curve: harmonic numbers 7–12). Periodicity in the rate-place profile based on responses to single HCTs for harmonic numbers 1–6 is reflected by the peak in the DFT at 1.0 cycle/harmonic number. The magnitude of this peak is statistically significant (p < 0.001), as evaluated via a nonparametric permutation test. Significant periodicity in rate-place profiles of responses to double HCTs corresponding to components of HCT1 and HCT2 is reflected by peaks in the DFT at 1.0 and 0.79 cycle/harmonic number, respectively. Insets, Histograms of spectral magnitudes at 1.0 cycle/harmonic number in the DFTs of randomly shuffled rate-place data. Histograms, included here for illustrative purposes, represent an empirical “null” distribution relative to which the probability of obtaining a spectral magnitude equal to or greater than the value observed in the DFT of the unshuffled rate-place data can be estimated. The observed spectral magnitude at 1.0 cycle/harmonic number is indicated by the vertical red line in the insets; the spectral magnitude corresponding to an estimated probability of 0.05, given the “null” distribution, is indicated by the dashed vertical blue line (see Materials and Methods). The distribution for the spectral magnitude at the expected periodicity corresponding to harmonics of HCT2 is omitted for clarity.
Three response time windows were analyzed: “On” (0–75 ms), “Sustained” (75–225 ms), and “Total” (0–225) ms (for analyses of pure tone responses in A1 based on similar time windows, see Fishman and Steinschneider, 2009). The rationale for examining the responses to HCTs in different time windows is based on the observation that “On” and “Sustained” responses display a differential capacity to represent the spectral fine-structure of single HCTs (Fishman et al., 2013). Furthermore, recent studies in auditory cortex indicate that specific sound attributes are differentially represented by neural responses occurring within specific time windows (Walker et al., 2011). In addition, given that pitch may be reliably conveyed by sounds as brief as 75 ms (Plack et al., 2005), if spectral information represented in A1 is sufficient for extracting the pitch of HCTs, one would predict that “On” responses contain sufficient information for deriving the F0s of the HCTs. The rationale for analyzing the “Total” response window is motivated by the possibility that auditory areas involved in pitch extraction which receive input from A1 integrate activity occurring over the entire duration of the HCT stimuli. An additional 75 ms time window (80–155 ms; referred to as “Sustained B”) was analyzed to compare the “On” response elicited by a given HCT when it was presented synchronously with the other HCT with the “On” response elicited when it was delayed by 80 ms relative to the other HCT.
If the F0s of HCT1 and HCT2 in double HCT stimuli are temporally represented in A1 by neuronal discharges phase-locked to the periodic waveform of the sounds (Fig. 1B), then there should be significant periodicity in neural responses at the F0s of the HCTs. Phase-locking at the F0s of HCT1 and HCT2 was quantified by computing the DFT of the “Total” response (0–225 ms) and measuring the spectral magnitude at frequencies corresponding to the F0s of the HCTs. Statistical significance of phase-locking at the F0s was evaluated via the same nonparametric permutation test used to evaluate significance of periodicity in rate-place profiles, except that it was based on random shuffling of time points in the MUA waveforms. Permutation test results yielding p values <0.05 were considered to indicate statistically significant neuronal phase-locking at the F0.
“Harmonic Number” versus “Adjusted Harmonic Number.”
The BF derived from pure tone responses may differ from that reflected in responses to the double HCTs. Reasons for this include nonlinear interactions between responses to components of the complex sounds, inadequate sampling of the FRF leading to misidentification of the BF, or differences in frequency tuning between onset responses and later sustained responses in A1 (Fishman and Steinschneider, 2009; Fishman et al., 2013). This discrepancy would lead to misalignment in neuronal rate-place profiles such that periodic peaks occur at noninteger values of harmonic number. For instance, the rate-place profile based on “Sustained” responses to HCT stimuli may be misaligned if their frequency tuning differs from that of “On” responses used to derive the BF of the site and accordingly to determine the F0s of the HCTs presented. Potential misalignment was corrected offline by a process that varied the “assumed” BF in small increments and measured the resulting amplitude in the DFT of the rate-place profiles at 1.0 cycle/harmonic number (the expected periodicity corresponding to harmonics of HCT1). The “adjusted” BF was that which maximized the DFT amplitude. The x-axis of the rate-place profile was modified accordingly, such that the harmonic number = adjusted BF/F0 and is labeled throughout as “Adjusted Harmonic Number” (see also Fishman et al., 2013).
Model-based analyses of responses to concurrent HCTs.
We used an analysis-by-synthesis modeling approach (Larsen et al., 2008) to (1) demonstrate the feasibility of estimating the F0s of concurrent HCTs based on A1 rate-place profiles and (2) facilitate comparison between the present neurophysiological data and psychophysical data on concurrent sound segregation in humans. In this approach, rate-place profiles were synthesized by computing the output of a cortical receptive-field model based on the spectra of single or double HCTs for different values of F0 (for HCT1), as in the neurophysiological experiments. The receptive-field model was formed by combining an excitatory response curve with an inhibitory response curve. These response curves were each defined by a rounded-exponential (roex) function, which was introduced into the auditory-research literature to model auditory filters (Patterson et al., 1982) and was found in previous studies to model frequency-response curves in A1 (Fishman and Steinschneider, 2006; Fishman et al., 2013; Micheyl et al., 2013). The roex function is defined as follows:
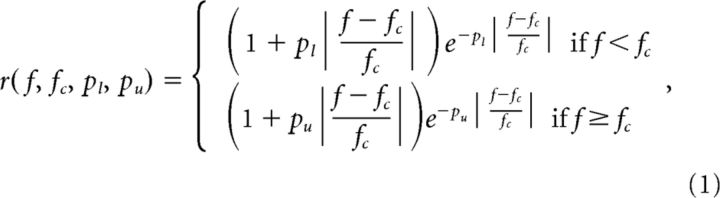 |
where r is the response magnitude at frequency f, fc is the center frequency of the frequency-response curve, and the parameters, pl and pu, determine the steepness of the lower and upper slopes of the frequency-response curve, respectively.
To produce a model of cortical receptive fields, two roex functions were nonlinearly combined as follows:
where the parameter β, controls the magnitude of the inhibitory response component (the second term) relative to the excitatory response component (the first term), and the exponents αe, and αi control the compression (α < 1) or expansion (α >1) of the excitatory and inhibitory response components.
Neural rate-place profiles were then modeled as follows:
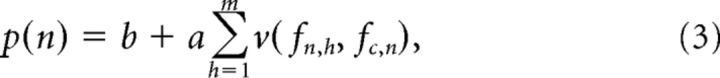 |
where b and a are linear intercept and scaling parameters, respectively, n is the harmonic number (a number varying from 0 to 12 in 1/eighth steps), m is the number of spectral components in the stimulus (m = 12 for a single HCT and m = 24 for a double HCT), and fn,h is the frequency of the hth harmonic in the HCT stimulus corresponding to harmonic number, n. Recall that, in the neurophysiological experiments, the harmonic number with respect to the BF determined the stimulus F0 so that F0= fc/n; accordingly, fn,h is given by mfc/n. The model parameters b, a, ple, pue, pli, pui, β, αe, αi, and fc, were estimated by minimizing the mean-square error between the actual rate-place profile elicited by a single HCT and the simulated rate-place profile. These parameters were then used to “predict” responses to double HCTs.
To demonstrate the possibility of estimating the F0s of concurrent HCTs based on neural rate-place profiles in A1, we extended the model with a harmonic template-matching mechanism. F0s were estimated by computing the correlations between simulated rate-place profiles and a series of harmonic templates, which were generated by adding Gaussian functions centered on harmonics of an F0 (for a single HCT), or of a pair of F0s (for concurrent HCTs with a given F0 separation). This template-matching procedure is illustrated in Results.
Results
Data presented here were obtained from the same recording sites as those examined in a previous study investigating the neural representation of single HCTs in A1 (Fishman et al., 2013). Results are based on MUA, AEP, and CSD profiles recorded in 29 multicontact electrode penetrations into A1 of two monkeys (15 and 14 sites in Monkey A and Monkey L, respectively; 12 and 17 sites in the right and left hemispheres, respectively). MUA data presented in this report were recorded in lower lamina 3. Seven additional sites were excluded from analysis because they did not respond to any of the HCTs presented, were characterized by “Off”-dominant responses, had aberrant CSD profiles that precluded adequate assessment of laminar structure, or displayed FRFs that were too broad to accurately determine a BF. Sites that showed no responses to the HCTs had BFs <300 Hz and were clustered near the border between A1 and field R. Sites that showed broad frequency tuning were situated along the lateral border of A1. For all sites examined, responses occurring within the “On” response time window (0–75 ms after stimulus onset) displayed sharp frequency tuning characteristic of small neural populations in A1 (Fishman and Steinschneider, 2009). Mean onset latency and mean 6-dB bandwidths of FRFs of MUA recorded in lower lamina 3 were ∼14 ms and ∼0.6 octaves, respectively. These values are comparable with those reported for single neurons in A1 of awake monkeys (Recanzone et al., 2000). Although this onset latency is more consistent with activation of cortical neuron populations than with thalamocortical fiber activity (e.g., Steinschneider et al., 1992, 1998; Y. I. Fishman and M. Steinschneider, unpublished observations), the possibility that spikes from thalamocortical afferents contributed to our response measures cannot be excluded. BFs of recording sites ranged from 240 to 16,500 Hz (median 1550 Hz).
Rate-place representation of concurrent HCTs in A1
Neural population responses in A1 can resolve individual harmonics of both HCT1 and HCT2 when presented concurrently. This capacity is illustrated in Figure 2A (right), which shows rate-place representations of double HCTs (HCT1 and HCT2) based on MUA recorded at a representative site whose BF (1550 Hz) was also at the median BF of our sample. The rate-place representation of single HCTs (HCT1 alone) is included for comparison (Fig. 2A, left). Each rate-place representation is a composite of individual averaged responses to 89 single or double HCTs depicted as a 3D plot, with axes representing harmonic number (BF/F0) with respect to the F0 of HCT1, time, and response amplitude (also color coded). Periodicity with respect to harmonic number is evident in the rate-place representation based upon “On” and “Sustained” responses elicited by HCT1 when presented alone. Specifically, peaks in response amplitude occur at integer values of harmonic number- values at which a spectral component of HCT1 matches the BF of the site. The rate-place representation of double HCTs also shows prominent peaks in response amplitude occurring at harmonic number values corresponding to the spectral components of both HCT1 and HCT2 (indicated by the black arrows). Moreover, neuronal phase-locking to “beats” (corresponding to amplitude modulations in the stimulus waveform in addition to those at the F0s) is also evident in rate-place profiles of responses to double HCTs. These beats occur at rates equal to the difference in frequency between harmonics of the two concurrent HCTs.
Associated rate-place profiles based on the area under the MUA waveform within the “On” time window are shown in Figure 2B. Periodic peaks in rate-place profiles corresponding to harmonics of HCT1 and HCT2 are enclosed by blue and red circles, respectively. Consistent with previous findings relating to the neural representation of single HCTs in A1 (Fishman et al., 2013), periodicity in the rate-place profiles for responses to double HCTs is more prominent at lower harmonic numbers (1–6) than at higher harmonic numbers (7–12), thus indicating a greater capacity of neural responses to resolve lower harmonics of the HCTs. A similar periodicity is observed in the rate-place profile for “Sustained” responses (data not shown).
Periodicity at 1.0 cycle/harmonic number in the rate-place profile for “On” responses elicited by single HCTs is statistically significant, as evaluated via a nonparametric permutation test based on the DFT of the rate-place profile (Fig. 2C, left; p < 0.001; see Materials and Methods). Significant periodicity at 1.0 and 0.79 cycle/harmonic number (p < 0.01 and p < 0.05, respectively) is also observed in the rate-place profile for responses to double HCTs (Fig. 2C, right), thus demonstrating the ability of this site to resolve lower harmonics of each of the concurrently presented HCTs.
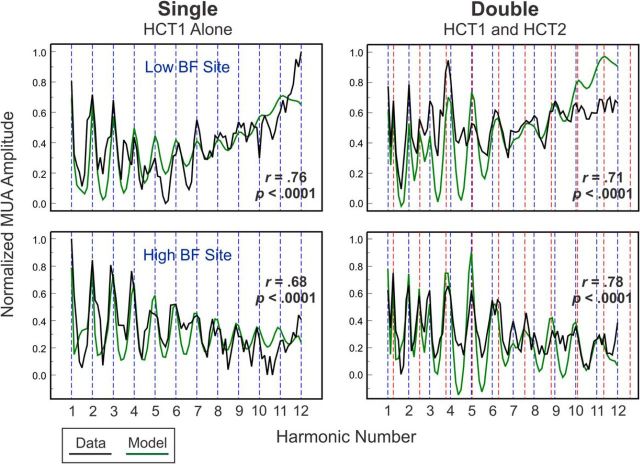
To illustrate the generality of findings illustrated in Figure 2 across recording sites in A1, Figure 3 (right column) depicts adjusted rate-place profiles based on “Total” MUA elicited by double HCTs from four representative sites with different BFs. Corresponding rate-place profiles based on MUA elicited by single HCTs are included for comparison (left column). For all four sites, peaks in rate-place profiles occur at or near harmonics of HCT1 and HCT2, indicated by dashed blue and red vertical lines, respectively. Thus, frequency-selective neural populations in A1 are capable of resolving, via a rate-place code, individual harmonics of each of the concurrently presented HCTs.
Figure 3.
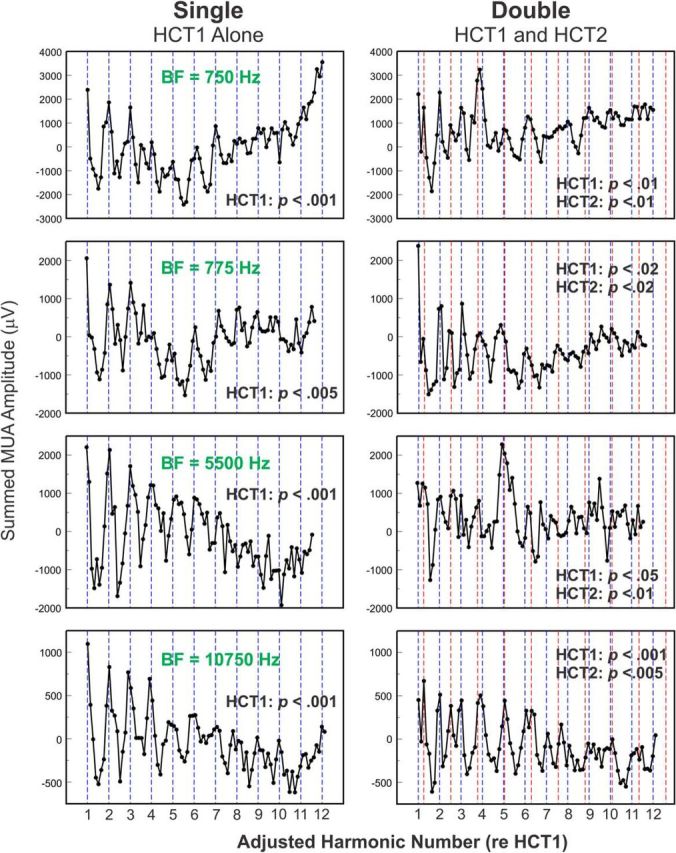
Representative rate-place profiles of responses to single and double HCTs. Rate-place profiles of responses (“Total” MUA) recorded at four sites with different BFs to single and double HCTs (left and right column, respectively). BFs of the sites are indicated in green. The x-axis of the rate-place profiles has been changed to “Adjusted Harmonic Number,” as described in Materials and Methods. Note peaks in rate-place profiles occurring at or near values of harmonic number corresponding to components of HCT1 and HCT2 (blue and red dashed lines, respectively). p values derived from permutation tests used to evaluate periodicities in rate-place profiles corresponding to harmonics of HCT1 and HCT2 are indicated in the plots (see Materials and Methods).
To evaluate this capacity across all sites sampled, the estimated probability of the observed periodicity in rate-place profiles based on the area under the MUA waveform is plotted as a function of BF in Figure 4. As results for double HCT harmonics 7–12 were not statistically significant, only those for harmonics 1–6 are shown. Data for “On” and “Sustained” MUA are plotted in Figure 4A and Figure 4B, respectively. Results corresponding to the rate-place representation of harmonics of single HCTs (Fishman et al., 2013) and of harmonics of HCT1 and HCT2 in double HCTs are presented in the left, middle, and right columns, respectively, as indicated. Lower probability values indicate greater periodicity in rate-place profiles at harmonics of HCT1 and HCT2 (1.0 and 0.79 cycle/Adjusted Harmonic Number, respectively) and a correspondingly greater capacity of neural responses to resolve individual components of the HCTs. Numbers in the ovals indicate the percentage of sites displaying statistically significant (p < 0.05) periodicity in rate-place profiles for the different response time windows. Whereas harmonics of single HCTs were better resolved than those of double HCTs, neural populations in A1 are still able to resolve individual lower harmonics of double HCTs. Consistent with findings in the cat auditory nerve (Larsen et al., 2008), sites with higher BFs generally resolved lower harmonics (1–6) of both single and double HCTs better than sites with lower BFs. Nonetheless, harmonics of at least one of the HCTs in the double HCT stimuli could still be clearly resolved at sites with BFs as low as 400 Hz.
Figure 4.
Evaluation of periodicity in rate-place profiles of responses to single and double HCTs across all recording sites. Estimated probabilities of the observed periodicity in rate-place profiles of responses to single and double HCTs, given the null distribution derived from random shuffling of points in rate-place profiles, are plotted as a function of BF. Results for single HCTs and for double HCTs (separately for HCT1 and HCT2) are shown in separate columns, as indicated. Results for “On” and “Sustained” area under the MUA waveform are plotted in A and B, respectively. Only results based on rate-place data corresponding to harmonic numbers 1–6 are shown. Lower probability values indicate greater periodicity at 1.0 cycle/(adjusted) harmonic number (corresponding to harmonics of HCT1) and at 0.79 cycle/(adjusted) harmonic number (corresponding to harmonics of HCT2), and a correspondingly greater capacity of neural responses to resolve individual harmonics of the HCTs. As probability values >0.05 are considered nonsignificant, for display purposes, values ≥0.05 are plotted along the same row, as marked by the upper horizontal dashed line at 0.05 along the ordinate. As permutation tests were based on 1000 shuffles of rate-place data, probability values <0.001 could not be evaluated. Therefore, probability values ≤0.001 are plotted along the same row, as marked by the lower horizontal dashed line at 0.001 along the ordinate. Numbers in ovals indicate the percentage of sites displaying statistically significant (p < 0.05) periodicity in rate-place profiles corresponding to harmonics of the HCTs.
Temporal representation of the F0s of concurrent HCTs in A1
Previous studies in A1 of awake nonhuman primates have shown that the F0 of sounds with harmonic structure may be temporally represented by neural phase-locking to the periodic waveform envelope of the stimuli (e.g., De Ribaupierre et al., 1972; Bieser and Müller-Preuss, 1996; Steinschneider et al., 1998; Bendor and Wang, 2007; Fishman et al., 2013) (Fig. 1B). Here, we sought to determine whether the F0s of two concurrent HCTs could be simultaneously represented in the temporal firing patterns of neural populations in A1 and thereby enable concurrent sound segregation based on pitch differences. This capacity is illustrated in rate-place data from a representative site with a BF of 350 Hz (Fig. 5). The rate-place representation of single HCTs (HCT1 alone) obtained at the same recording site is included for comparison (Fig. 5A, left; adapted from Fishman et al., 2013). Periodicity at the F0 of single HCTs is evident in the waveform of the responses (Fig. 5A, black arrows). In contrast, periodicity is lacking with respect to the harmonic number axis in the rate-place representation. Thus, although neural responses at this site are unable to resolve individual harmonics of the HCTs via a rate-place code, they are able to represent the F0 of single HCTs by a temporal code. Remarkably, neural responses at this site are able to temporally represent the F0s of both HCT1 and HCT2 when they are presented concurrently (Fig. 5A, right). Specifically, neural responses are phase-locked to the waveform periodicity at the F0s of both HCTs. Phase-locking to lower “beat” frequencies, corresponding to the difference in frequency between the harmonics of HCT1 and HCT2, is also evident in the rate-place representation of double HCT stimuli.
Figure 5.
Temporal representation of the F0s of single and double HCTs. A, Rate-place representations from a site (BF = 350 Hz) exhibiting phase-locking of MUA at the F0s of single (left; HCT1 alone) and double (right; HCT1 and HCT2) HCT stimuli. Note the absence of periodicity in response amplitude with respect to harmonic number, thus indicating the inability of this site to resolve individual harmonics of the HCTs. Same conventions as in Figure 2. Graph axes have been rotated relative to those in Figure 2 to facilitate visualization of phase-locked responses. Phase-locking at “beat” frequencies is evident in the rate-place representation of responses to the double HCTs. B, Spectral magnitude at the F0 in the DFT of “Total” MUA as a function of harmonic number (lower x-axis) and stimulus F0 (upper x-axis); values of harmonic number and F0 are with respect to HCT1. Spectral magnitudes at the F0 for responses to HCT1 alone are plotted in black, whereas spectral magnitudes at the F0 of HCT1 and HCT2 for responses to double HCT stimuli are plotted in blue and red, respectively. Data points lying above and to the right of the dashed lines represent statistically significant (p < 0.05) phase-locking at the F0, as evaluated via a nonparametric permutation test. At this site, significant phase-locking at the F0 is observed for stimulus F0s up to 175 Hz, with maximal phase-locking observed at an F0 value of 82.4 Hz. C, DFTs of “Total” MUA elicited by single (black line) and double (red line) HCT stimuli wherein the F0 of HCT1 was 82.4 Hz. The DFT of the response to the double HCT stimulus exhibits a peak at the F0 of HCT2 (103.8 Hz). Moreover, the peak at 82.4 Hz (seen in the DFT of the response to HCT1 when presented alone) is still present in the DFT of the response elicited by the double HCT stimuli. Thus, this site can simultaneously represent, via a temporal code, the F0s of both concurrently presented HCTs.
At this site, significant neural phase-locking at the F0s of single and double HCT stimuli is observed for F0s up to 175 Hz (Fig. 5B). The DFT of the response to the single HCT eliciting the maximal degree of phase-locking at the F0 (i.e., 82.4 Hz) is depicted in Figure 5C (black curve). The DFT of the response to the double HCT stimulus wherein HCT1 had an F0 of 82.4 Hz and HCT2 had an F0 of 103.8 Hz is shown superimposed (red curve). The F0s of both HCTs are represented in the DFTs of the MUA, although the magnitude of phase-locking at the F0 of HCT1 is diminished (but still significant) when HCT1 is presented concurrently with HCT2.
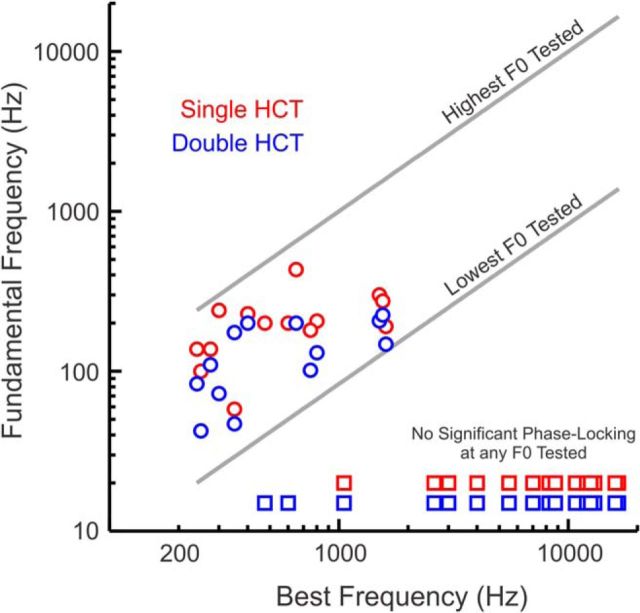
Results pertaining to the temporal representation of the F0s of double HCTs are summarized in Figure 6. The highest F0s at which statistically significant phase-locking was observed at the F0 of HCT1 or HCT2 in double HCT stimuli is plotted as a function of BF (blue symbols). Corresponding values for phase-locking at the F0 of single HCTs (HCT1 alone) at the same sites is included for comparison (red symbols; data reproduced from Fishman et al., 2013). The gray lines indicate the highest and lowest F0s tested at each site, as constrained by the experimental design of the stimulus sets. Sites showing no significant phase-locking at any of the F0s tested are represented by the square symbols at the bottom of the plot. Whereas for responses to single HCTs, the highest F0 at which significant phase-locking at the F0 was observed was 433 Hz, the corresponding value for responses to double HCTs was 200 Hz, with upper limits falling in the 40–200 Hz range. Thus, the salience of neural phase-locking at the F0 is greater when an HCT is presented alone than when it is presented concurrently with another spectrally and temporally overlapping HCT.
Figure 6.
Temporal representation of the F0s of single and double HCTs in A1: summary of results. Highest F0s at which statistically significant phase-locking at the F0 was observed are plotted as a function of BF. Values for single HCTs and double HCTs are represented by red and blue symbols, respectively. Gray lines indicate the highest and lowest F0s tested at each site, as constrained by the design of the stimulus sets. Square symbols (red: single HCTs; blue: double HCTs) represent sites showing no significant phase-locking at any of the F0s tested.
Onset asynchrony enhances rate-place representations of double HCT spectra in A1
An important stimulus cue that greatly facilitates the perceptual segregation of concurrent sounds is a difference in their onset time (Micheyl and Oxenham, 2010). Accordingly, if neural representations of harmonic spectra in A1 are potentially relevant for pitch perception and concurrent sound segregation based on differences in F0, then one would predict that these neural representations will be enhanced when there is an onset asynchrony between the two HCTs compared with when they are presented synchronously. To test this prediction, we compared rate-place profiles obtained for responses to double HCTs when the two HCTs were presented synchronously with those obtained when the onset of one of the HCTs was delayed relative to that of the other by 80 ms, an asynchrony that is sufficient to markedly facilitate the perceptual segregation of spectrally and temporally overlapping HCT (Lentz and Marsh, 2006; Hedrick and Madix, 2009; Shen and Richards, 2012).
Effects of onset asynchrony on rate-place representations of double HCTs at an example site are illustrated in Figure 7. As predicted, rate-place representations of harmonics of both HCT1 and HCT2 are more salient when there is an onset asynchrony between the two HCTs. Specifically, peaks corresponding to low-numbered harmonics of both HCTs (arrows) are more prominent when HCT2 is delayed relative to HCT1 (Fig. 7A, right) compared with when HCT1 and HCT2 are presented synchronously (Fig. 7A, left). These observations are quantified in the remaining panels of Figure 7. For comparison, the rate-place profile based upon “On” responses evoked by HCT2 presented alone is shown in Figure 7B and displays peaks near integer multiples of 1.26 (as indicated by the dashed lines), which correspond to harmonics of an F0 that is 4 semitones above that of HCT1. Figure 7C shows rate-place profiles based upon “On” (0–75 ms) responses evoked by HCT1 and HCT2 when presented synchronously (black curve) and “Sustained B” (80–155 ms) responses evoked when HCT2 is delayed by 80 ms (red curve). The “On” and “Sustained B” response windows capture the “On” response evoked by HCT1 and the delayed “On” response evoked by HCT2, respectively. The rate-place representation of HCT2 harmonics is more salient when HCT2 is delayed compared with when the HCTs are presented synchronously. DFT magnitudes of F0-related periodicities in rate-place profiles evoked by HCT1 and HCT2 presented synchronously and asynchronously are plotted in Figure 7D and Figure 7E, respectively. In the synchronous condition, statistically significant F0-related periodicity was observed only for HCT2 (asterisk). However, in the asynchronous condition, significant F0-related periodicities were observed for both HCT1 and HCT2 in the “On” and “Sustained B” response windows.
Figure 7.
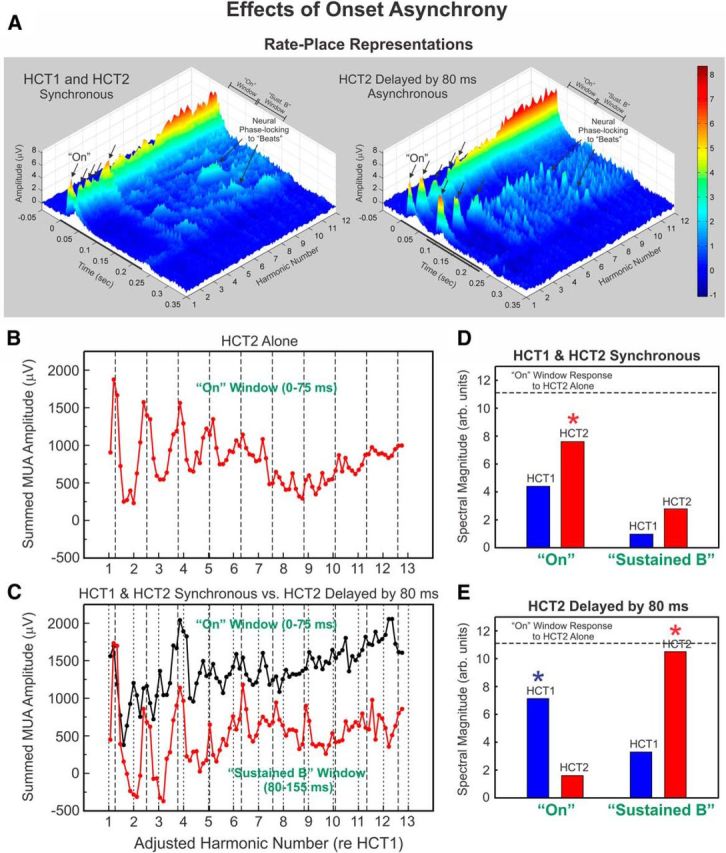
Effects of onset asynchrony on rate-place representations at a representative site. A, Rate-place profiles at a 1.65 kHz-BF site based on responses elicited by two synchronous (left) or asynchronous (right) HCTs (in this example, the onset of HCT2 is delayed by 80 ms relative to that of HCT1). Same conventions as in Figure 2. Shorter black bar in the rate-place representation under the asynchronous condition represents the time during which HCT2 was presented. “On” responses occurring at values corresponding to low-numbered harmonics of both HCTs (arrows) are more prominent when HCTs are presented asynchronously, compared with when they are concurrent. B, Rate-place profile based upon “On” responses (0–75 ms) to HCT2 alone displays peaks at integer multiples of 1.26 (= 4 semitones above F0 of HCT1), as indicated by dashed lines. C, Rate-place profiles based upon “On” (0–75 ms) and “Sustained B” (80–155 ms) responses (as indicated) evoked by double HCTs when presented synchronously (black line) and when HCT2 is delayed by 80 ms (red line). Spectral magnitude of F0-related periodicities in rate-place profile based on responses to HCT1 and HCT2 when they are presented synchronously (D) and asynchronously (E). In the synchronous condition, significant F0-related periodicity was observed only for HCT2 (asterisk). In the asynchronous condition, significant F0-related periodicities were observed for both HCT1 and HCT2 in the “On” and “Sustained B” response windows, which capture the “On” response evoked by HCT1 and the delayed “On” response evoked by HCT2, respectively. The dashed horizontal line represents the corresponding spectral magnitude observed when HCT2 was presented alone.
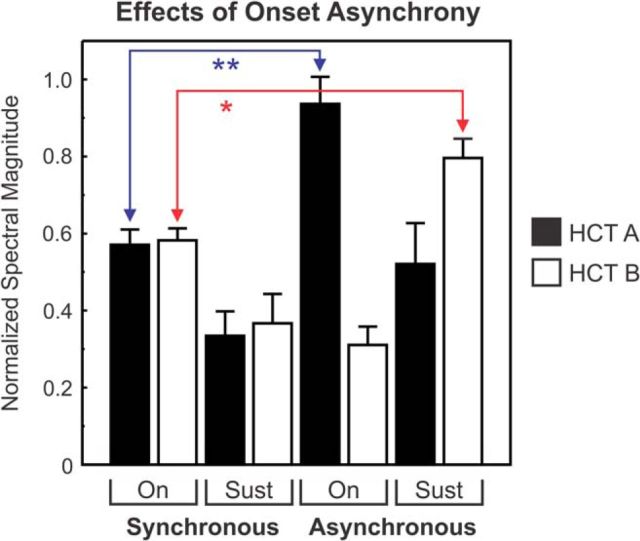
Figure 8 shows effects of onset asynchrony on rate-place representations averaged across all recording sites at which effects of SOA were tested (N = 18). Before averaging across sites, DFT magnitudes of F0-related periodicities in rate-place profiles under synchronous and asynchronous conditions were normalized to magnitudes obtained when HCT1 or HCT2 were presented alone. As either HCT1 or HCT2 could be delayed at a given recording site, here the nondelayed and delayed HCTs are generically referred to as HCTA and HCTB, respectively. Normalized mean DFT magnitudes of F0-related periodicities corresponding to harmonics of HCTA and HCTB are represented by the black and white bars, respectively. Values for responses occurring in the “On” and “Sustained B” time windows under the synchronous and asynchronous conditions are plotted separately, as indicated. On average, for responses occurring in the “On” time window, introducing an onset asynchrony between the HCTs leads to enhanced rate-place representations of the harmonics of the nondelayed HCT (p < 0.0001; one-tailed t test comparing responses to HCTA under the synchronous and asynchronous conditions in the “On” time window; Fig. 8, blue line). Moreover, onset asynchrony yields enhanced rate-place representations of the harmonics of the delayed HCT (p < 0.01; one-tailed t test comparing responses to HCTB under the synchronous condition in the “On” time window and those under the asynchronous condition in the “Sustained B” time window; Fig. 8, red line). These findings thus parallel the enhanced perceptual segregation of spectrally and temporally overlapping sounds that have asynchronous onsets in humans (e.g., Hukin and Darwin, 1995; Lentz and Marsh, 2006; Hedrick and Madix, 2009; Lipp et al., 2010; Lee and Humes, 2012; Shen and Richards, 2012).
Figure 8.
Effects of onset asynchrony on rate-place profiles in A1: summary of results. Mean DFT magnitudes quantifying F0-related periodicities in rate-place profiles under synchronous and asynchronous conditions are shown (N = 18 sites). Before averaging across sites, DFT magnitudes were normalized to magnitudes obtained when HCT1 or HCT2 were presented alone. As either HCT1 or HCT2 could be delayed at a given recording site, here the nondelayed and delayed HCTs are generically referred to as HCTA and HCTB, respectively. Normalized mean DFT magnitudes of F0-related periodicities corresponding to harmonics of HCTA and HCTB are represented by the black and white bars, respectively. Values for responses occurring in the “On” and “Sustained B” time windows under the synchronous and asynchronous conditions are plotted separately, as indicated. Error bars indicate SEM. Double blue asterisk and single red asterisk indicate p values of <0.0001 and <0.01, respectively, obtained from one-tailed t tests comparing the means indicated by the red and blue lines. For discussion, see Results.
Potential intracortical homologs of the human object-related negativity (ORN) in Monkey A1
Human scalp recordings of event-related potentials have led to the identification of a response component called the ORN whose appearance, even under passive listening conditions, correlates with the perceptual segregation of spectrally overlapping concurrent sounds (Alain et al., 2001, 2002; Snyder and Alain, 2005; Alain, 2007; Lipp et al., 2010). The ORN has been attributed to neural generators along the superior temporal gyrus, including primary and nonprimary auditory cortex (Alain et al., 2001, 2005; Alain and McDonald, 2007; Arnott et al., 2011).
We investigated whether a potential homolog of the human ORN could be found in macaque A1 by comparing AEPs elicited by single HCTs with those elicited by the two simultaneous HCTs with an F0 difference between them of 4 semitones. The rationale for this comparison derives from the observation that only one sound “object” is heard when listening to a single HCT, whereas two sound “objects” can be heard when listening to two simultaneous HCTs that differ in F0 (as is the case for the double HCT stimuli used in the present study). AEPs were analyzed at four cortical depths corresponding to the locations of four stereotypical CSD components commonly observed in multilaminar recordings of sound-evoked responses in macaque A1 (e.g., see Lakatos et al., 2007; Steinschneider et al., 2008; Fishman and Steinschneider, 2012) (supragranular source, supragranular sink, lower lamina 3 sink, and infragranular source). AEPs at each of these cortical depths were separately averaged across all the single HCT and double HCT F0s presented at each electrode penetration into A1. The justification for averaging responses across all F0s (i.e., regardless of whether an HCT with a given F0 elicits a large or small response) is based on the assumption that the scalp-recorded ORN reflects, in part, the summed volume-conducted extracellular currents associated with the synaptic activity of widespread neural populations within the superior temporal gyrus that may be optimally or suboptimally tuned to different frequency components of the complex sounds (Alain, 2007). To extract potential homologs of the ORN, we computed grand mean difference waveforms by subtracting the averaged responses to the single HCTs from the averaged responses to the double HCTs at each site and then averaging these differences across sites.
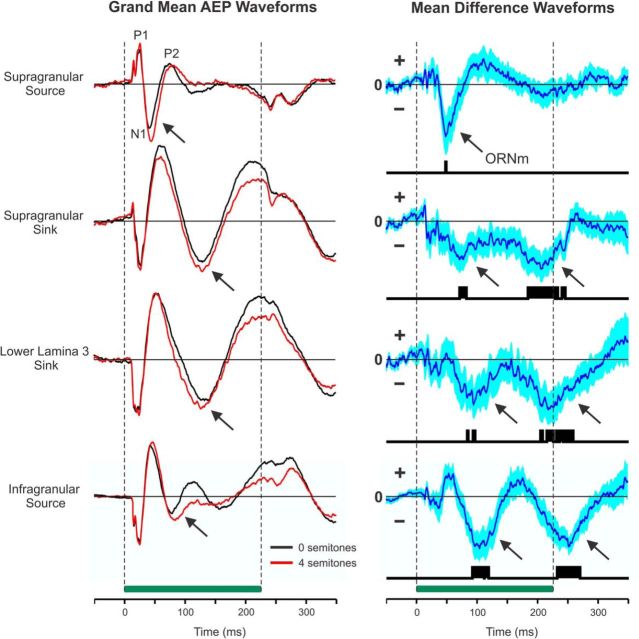
Comparison between grand mean AEPs elicited by single and double HCTs reveals greater negativities (indicated by arrows) at all the cortical depths examined in response to the double HCTs (Fig. 9, left column). Grand mean difference waveforms (Fig. 9, right column) yield corresponding negativities (indicated by arrows) which are statistically significant (p < 0.01) at time points occurring later than the initial “On” response in A1 (>40 ms poststimulus onset; vertical black bars indicate time points at which p < 0.01, uncorrected). Similar trends were found for CSD components and MUA recorded at the same cortical depths, with sustained MUA elicited by double HCTs being slightly larger than that elicited by single HCTs (data not shown). However, difference waveforms for CSD and MUA response measures were not statistically significant (at an α level of 0.05).
Figure 9.
Potential intracortical homologs of the human ORN in Monkey A1. Grand mean AEP waveforms elicited by single and double HCTs (left column). AEPs at four cortical depths (corresponding to the location of the supragranular source, supragranular sink, lower lamina 3 sink, and infragranular source identified in CSD profiles) were separately averaged across all the single HCT and double HCT F0s presented at each electrode penetration into A1. Mean responses to single HCTs (which, by definition, had a difference in F0 of 0 semitones) and to double HCTs (which had a difference in F0 of 4 semitones) are plotted in black and red, respectively. Stimulus duration is represented by the horizontal green bar. AEPs recorded at the different cortical depths are scaled proportionately (arbitrary units). Major components of the AEP (P1, N1, P2) recorded in superficial layers of A1 are labeled. Corresponding grand mean difference waveforms (right column) were obtained by subtracting the averaged responses to the single HCTs from the averaged responses to the double HCTs at each site and then averaging the resultant differences across sites. The extent of blue shading above and below the mean difference waveforms represents SEM. Time points at which difference waveforms are significantly different from zero (t test: p < 0.01, uncorrected) are indicated by the vertical black bars beneath the difference waveforms. Arrows indicate potential intracortical homologs of the human ORN.
The earliest significant negativity in the grand mean difference waveforms of AEPs peaks at ∼50 ms after stimulus onset and is most prominently observed in superficial laminae. This early negativity inverts in polarity across the cortical layers, manifesting as a positivity in infragranular layers. Interestingly, this early negativity immediately follows the N1 component of the AEP (labeled in Fig. 9), similar to the time course of the ORN noninvasively recorded in humans (Snyder and Alain, 2005; Alain, 2007). These findings suggest that a potential intracortical homolog of the human ORN (labeled in Fig. 9 as “ORNm”), which correlates with the perception of more than one auditory object in humans, can indeed be identified in macaque A1.
Computational modeling of responses to concurrent HCTs and comparisons with psychophysical data
Model of cortical responses
To allow further comparisons between A1 responses to double HCTs and psychophysical data in humans relating to the perceptual segregation of concurrent HCTs based on F0 differences, we used a computational modeling approach (see Materials and Methods). Figure 10 shows examples of actual and model rate-place profiles for two A1 sites: one with a low BF (750 Hz) and the other with a high BF (10,750 Hz), which correspond to two of the sites illustrated in Figure 3. Model parameters were estimated by fitting the model to the rate-place profile elicited by a single HCT (left column). These parameters were then used to “predict” responses to the double-HCT stimuli (right column). As can be seen, despite its simplicity, the model is able to reproduce most of the features apparent in the rate-place profiles, including slow modulations (e.g., decrease, increase, or decrease followed by increase) in the magnitude of responses to harmonics as a function of harmonic number, an effect of lateral suppression, which is captured by the inhibitory response component of the model.
Figure 10.
Modeling of A1 responses to single and double HCTs. Rate-place profiles based on MUA elicited by single and double HCTs at representative low BF (750 Hz) and high BF (10,750 Hz) sites are plotted in black in the top and bottom rows, respectively. For illustration purposes, MUA amplitudes are normalized to the maximum response at each site. Corresponding rate-place profiles derived from the generative model of A1 responses (as described in Materials and Methods) are plotted in green. Vertical dashed lines indicate values of harmonic number corresponding to components of HCT1 (blue) and HCT2 (red). Pearson correlations (r) between data- and model-derived rate-place profiles and associated p values are included in each plot.
Using the generative model of rate-place profiles described above, we were able to compute (or “predict”) rate-place profiles for stimuli other than those tested in the neurophysiological experiments. For example, and as described below, we predicted rate-place profiles for double HCTs with F0s differing by 0, 0.25, 0.5, 1, 2, 3, 4, 5, or 6 semitones. These predicted rate-place profiles were then used to investigate the possibility of using A1 responses to estimate the F0s of concurrent HCTs, and to evaluate relationships with psychophysical data relating to F0-based concurrent sound segregation in human listeners.
Model-based F0 estimation
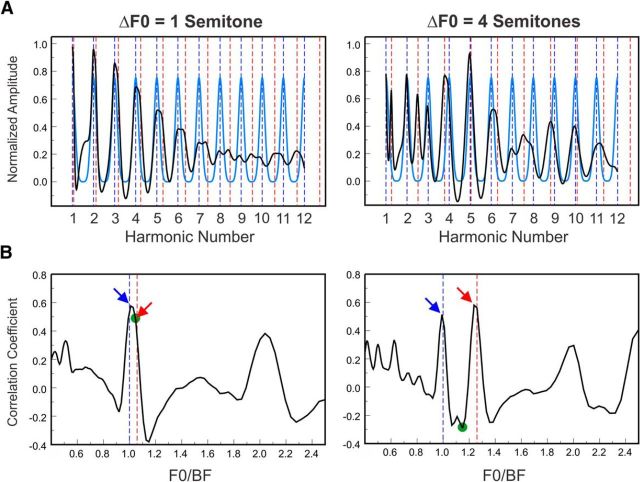
To demonstrate the possibility of estimating the F0s of single and concurrent HCTs based on neural rate-place profiles, we extended the model with a harmonic template-matching mechanism. Specifically, to estimate the F0s, we computed correlations between simulated rate-place profiles and a series of harmonic templates, which were generated by adding Gaussian functions centered on harmonics of an F0 (for single HCTs) or of a pair of F0s (for double HCTs with a given F0 separation). An example of this template-matching procedure is illustrated in Figure 11A, wherein simulated rate-place profiles (top, black curves) elicited by double HCTs with F0 separations of 1 and 4 semitones (left and right panels, respectively) are overlaid on a harmonic template (blue curves) whose F0 is equal to the lower F0 of the double HCT stimuli (HCT1).
Figure 11.
Matching of modeled rate-place profiles to harmonic templates. A, Modeled rate-place profiles elicited by double HCTs with an F0 separation of 1 and 4 semitones (black curves) are superimposed upon harmonic templates (blue curves) with an F0 equal to that of the lower HCT (HCT1). Vertical dashed lines indicate harmonics of HCT1 (blue) and HCT2 (red). B, Correlation between modeled rate-place profiles and harmonic templates as a function of the BF-normalized F0 (F0/BF) of the harmonic template. Vertical blue and red dashed lines indicate the two BF-normalized F0s of HCT1 and HCT2, respectively. The downward-pointing arrows indicate the correlation-function values corresponding to the two estimated F0s. The green dots represent the “troughs” (minimum intervening points) between these two values. Whereas the correlation function for the response to the double HCT with an F0 separation of 1 semitone displays a single peak near the (BF-normalized) F0 of HCT1, two prominent and well-separated peaks occurring near the F0s of the two HCTs are observed for the response to the double HCT with an F0 separation of 4 semitones. Additional peaks in the correlation functions are seen at harmonics and subharmonics of the primary peaks.
Figure 11B shows the correlations between the model rate-place profiles and harmonic templates corresponding to different BF-normalized F0s (F0/BF). In this example (based on data from the high BF site shown in Fig. 10), the correlation function shows a single peak for the response to the double HCT with an F0 separation of 1 semitone, which occurs near the (BF-normalized) F0 of HCT1 (blue dashed line). In contrast, two well-separated peaks in the correlation function are seen for the response to the double HCT with an F0 separation of 4 semitones, which occur near the F0s of the two HCTs (blue and red dashed lines). The F0s corresponding to these two peaks differed slightly from the two actually presented F0s, an effect that can be explained by a small mis-estimation of the BF of the cortical site during the neurophysiological experiments (see Materials and Methods).
Pitch-separability predictions
To quantify the capacity of neural responses to separate the pitches of the concurrent HCTs based on predicted rate-place profiles elicited by double HCT stimuli, we computed the mean amplitude of F0-related peaks in the correlation function (Fig. 11B, arrows), relative to the trough between these peaks (Fig. 11B, green dot). Intuitively, when the correlation function contains two well-separated peaks corresponding to the two F0s presented, the peak-to-trough amplitude difference will be large; when the double HCTs produce either a single, or two largely overlapping peaks, the peak-to-trough amplitude difference will be small. This computation was performed for simulated rate-place profiles corresponding to F0 separations of 0, 0.25, 0.5, 1, 2, 3, 4, 5, and 6 semitones. These separations were chosen based on previous psychophysical studies in humans, the results of which indicate that pitch separability increases as a function of F0 separation over this range (Assmann and Paschall, 1998).
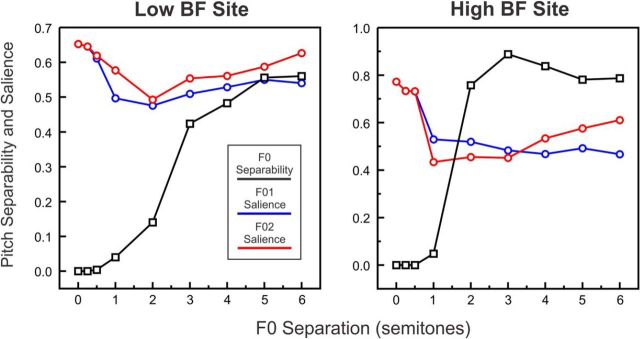
Paralleling these psychophysical data, pitch separability estimated from simulated A1 rate-place profiles increases with F0 separation. Figure 12 illustrates this increase for the low and high BF sites considered in Figure 10. For both sites, the peak-to-trough amplitude difference (black curves) was equal, or close to, zero for F0 separations of 1 semitone or less, and increased as F0 separation increased between 0.5 and 3 semitones; for the low BF site, estimated pitch separability continued to increase up to the 5 semitone separation. Similar results were observed for other cortical sites. These results are qualitatively consistent with psychophysical data in humans (Assmann and Paschall, 1998), which show unimodal distributions of pitch-matches for two concurrent harmonic sounds (vowels) with F0s separated by 1 semitone, suggesting that listeners heard a single pitch; and bimodal distributions for concurrent harmonic sounds with F0s separated by 4 semitones, suggesting that listeners heard two separate pitches.
Figure 12.
Pitch separability and salience estimated from modeled rate-place profiles elicited by double HCTs. Estimated pitch separability (black curves) and pitch salience (blue and red curves; F0 of HCT1 and HCT2, respectively) are plotted as a function of F0 separation for two example low BF (750 Hz) and high BF (10,750 Hz) A1 sites.
Pitch-salience predictions
To quantify pitch salience based on predicted rate-place profiles elicited by double HCTs, we computed the difference between the amplitude of the correlation-function peak (obtained in the harmonic template-matching procedure) corresponding to one of the two stimulus F0s, and a baseline correlation, which was defined as the mean correlation across the range of candidate F0s from 2.5 octaves below to 2.5 octaves above the lower F0 of the double HCT stimulus, excluding a 5-bin-wide interval centered on the stimulus F0-related peak, or on each F0-related peak, when two peaks were present, to avoid including peaks in the computation of the baseline. This approach to estimate pitch salience is similar to that used by Cariani and Delgutte (1996), who applied it successfully to pooled interspike-interval histograms based on auditory-nerve responses. Pitch salience was estimated for each of the two F0s of the double HCT stimuli. In cases where the correlation function contained a single peak for both F0s, the computation was applied twice to the same peak and yielded the same result.
Figure 12 (blue and red curves) shows the estimated pitch salience for the lower and higher F0s of the double HCT stimuli as a function of F0 separation, for the same two example A1 sites. Estimated pitch salience was usually highest at the 0 and 0.25 semitone separations, conditions in which double HCTs yielded a single peak in the correlation function. As F0 separation increased beyond 0.25 semitones, estimated pitch salience first decreased until the F0 separation reached 2 or 3 semitones, after which it either remained flat or increased as F0 separation increased toward 6 semitones. Interestingly, for the 4 and 6 semitone F0 separations, estimated pitch salience was greater for the higher F0 than for the lower F0. These results are qualitatively consistent with psychophysical findings in human listeners (Assmann and Paschall, 1998), suggesting the following: (1) pitch salience is greatest at the smallest F0 separations (for which only a single pitch is heard); and (2) when two separate pitches are heard (at the largest F0 separations), the dominant pitch generally corresponds to the higher F0.
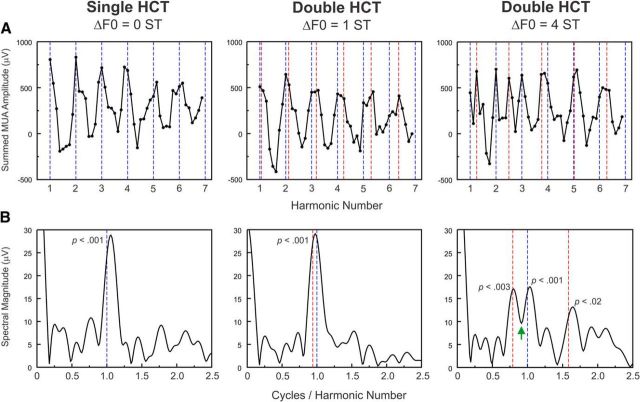
To provide further experimental validation of the modeling results, at one A1 site (BF = 8750 Hz), we presented an abbreviated set of double HCT stimuli with F0 separations of 0, 1, and 4 semitones. Figure 13A compares rate-place profiles (restricted here to harmonic numbers 1–6.875) elicited by a single HCT (ΔF0 = 0, by definition) and by double HCTs with 1 and 4 semitone F0 separations. Whereas DFTs of rate-place profiles elicited by the single HCT and the double HCT with a 1 semitone F0 separation display a single prominent peak occurring near the periodicity corresponding to the F0 of HCT1, the DFT of the rate-place profile of responses to the double HCT with a 4 semitone F0 separation displays two distinct peaks occurring near the periodicities corresponding to the F0s of the two HCTs (Fig. 13B). Thus, in qualitative agreement with both psychophysical data relating to F0-based concurrent sound segregation in humans (Micheyl and Oxenham, 2010) and the modeling results described above, neural resolvability of harmonics of both HCT1 and HCT2 in A1 is improved when the F0s of concurrent HCTs are separated by 4 semitones compared with when they are separated by 1 semitone.
Figure 13.
Neural resolvability of harmonics of double HCTs in A1 is enhanced at larger F0 separations. A, Rate-place profiles (restricted here to harmonic numbers 1–6.875) elicited by a single HCT (ΔF0 = 0, by definition) and by double HCTs with 1- and 4-semitone F0 separations. Vertical dashed lines indicate values of harmonic number corresponding to components of HCT1 (blue) and HCT2 (red). B, DFTs of rate-place profiles shown in A. DFTs of rate-place profiles elicited by the single HCT and the double HCT with a 1-semitone F0 separation display a single prominent peak occurring near the periodicity corresponding to the F0 of HCT1. In contrast, the DFT of the rate-place profile of responses to the double HCT with a 4-semitone F0 separation displays two distinct peaks occurring near the periodicities corresponding to the F0 of HCT1 and HCT2 (vertical blue and left-most red dashed lines at 1.0 and 0.79, respectively). A peak is also seen near 1.6 cycles/harmonic number, the second harmonic of the periodicity at 0.79. p values corresponding to these DFT peaks (permutation test; see Materials and Methods) are included in the plots. The DFT amplitude at the trough separating the two main peaks (indicated by the green arrow) is not statistically significant (p > 0.05).
Discussion
Using a stimulus design employed in auditory nerve studies of pitch encoding (Cedolin and Delgutte, 2005; Larsen et al., 2008), the present study examined whether spectral and temporal information sufficient for extracting the F0s of two simultaneously presented HCTs, a prerequisite for their perceptual segregation, is available at the level of A1. F0s of the concurrent HCTs differed by 4 semitones, an amount sufficient for them to be reliably heard as two separate auditory objects with distinct pitches in human listeners (Assmann and Paschall, 1998; Micheyl and Oxenham, 2010). We found that neural populations in A1 are able to resolve, via a rate-place code, lower harmonics (1–6) of each of the HCTs comprising double HCT stimuli. Importantly, evidence strongly suggests that resolvability of these lower harmonics is critical for pitch perception and for the ability to perceptually segregate complex sounds based on F0 differences in humans (Micheyl and Oxenham, 2010; Micheyl et al., 2010).
Furthermore, neural populations in A1 were capable of temporally representing the F0s of both of the concurrently presented HCTs (<200 Hz) by neuronal phase-locking to their respective periodic waveform envelopes. Previous studies have reported phase-locked responses at the F0 of harmonic sounds in auditory cortex of unanesthetized animals (De Ribaupierre et al., 1972; Steinschneider et al., 1998; Bendor and Wang, 2007; Fishman et al., 2013) and humans (Nourski and Brugge, 2011; Steinschneider et al., 2013). To our knowledge, this is the first study to demonstrate neuronal phase-locking at the F0s of two simultaneous HCTs in A1. Theoretically, the pitches of the two HCTs could be extracted from this spectral and temporal information by neurons that receive the output of A1 and implement the functional equivalent of harmonic templates (Goldstein, 1973) (e.g., see Results) or temporal periodicity detectors (Licklider 1951; Meddis and Hewitt, 1992).
Accordingly, neurons have been identified in nonprimary auditory cortex of marmosets, which respond to the pitch but not to the individual harmonics of HCTs (Bendor and Wang, 2005, 2006). These “pitch-selective” neurons are found in an area located immediately anterior and lateral to A1. This putative “pitch center” may be homologous to a comparable region of auditory cortex identified via noninvasive techniques in humans (Bendor and Wang, 2006; Griffiths and Hall, 2012). Although A1 may not be necessary for pitch extraction by pitch-selective neurons, it seems likely that such neurons would integrate spectral and temporal information from A1 given its connections to more anterior and lateral auditory cortical fields (Morel et al., 1993; Hackett et al., 1998; de la Mothe et al., 2006). In principle, the entire range of F0s typical of human pitch perception (30–5000 Hz) (Plack et al., 2005) can be extracted, without gaps, by combining the spectral and temporal information available in A1. For instance, although the harmonic spectrum of an HCT with an F0 of 50 Hz would not generally be resolved by neurons in A1, its F0 could still be represented by phase-locked responses at 50 Hz. On the other hand, because of phase-locking limitations, an HCT with an F0 of 500 Hz would not be represented by a temporal code in A1, but its lower, resolved harmonics could be reliably represented by a rate-place code. Our results are therefore consistent with a dual-pitch processing mechanism, whereby pitch is ultimately derived from temporal envelope cues for lower pitch sounds composed of higher-order harmonics and from spectral fine-structure cues for higher pitch sounds with lower-order harmonics (Carlyon and Shackleton, 1994; see also Steinschneider et al., 1998; Bendor et al., 2012).
In addition, we demonstrate that introducing an onset asynchrony between the two (otherwise temporally overlapping) HCTs increases the salience of the rate-place representation of their harmonics in A1, paralleling the enhanced ability to perceptually segregate sounds with asynchronous onsets in humans (Hukin and Darwin, 1995; Lentz and Marsh, 2006; Hedrick, and Madix, 2009; Lipp et al., 2010; Lee and Humes, 2012). Interestingly, these findings may provide a cortical neurophysiological explanation for why onset asynchrony improves sound segregation. Specifically, the enhanced rate-place representation of the harmonic spectrum of the delayed HCT may be attributed to the fact that responses to sounds in A1 are typically characterized by a large initial “On” component, which is followed by a quasi-exponential decay to a lower-amplitude plateau of activity over the course of ∼75 ms (Steinschneider et al., 2005; Fishman and Steinschneider, 2009) (Fig. 7). When the two HCTs are presented simultaneously, their harmonics elicit “On” responses that overlap in both tonotopic place and time, thus limiting their neural discriminability (signal-to-noise ratio). However, when one of the HCTs is delayed by >75 ms (as in the present study), larger “On” responses elicited by harmonics of the delayed HCT are superimposed upon the lower-amplitude plateau of activity elicited by the preceding HCT, thereby enhancing their salience relative to the background activity in A1. Although only two SOAs (0 and 80 ms) were tested at each recording site (for reasons described in Materials and Methods), based on the present data, it is reasonable to expect that harmonic resolvability in A1 would remain the same or even improve with a further increase in SOA.
Surprisingly, neural resolvability of double HCT harmonics in A1 is comparable with or greater than that observed in the auditory nerve of the anesthetized cat, where responses to HCTs tend to saturate at moderate to high stimulus levels (Cedolin and Delgutte, 2010). Despite their relatively high level in the present study (60 dB SPL per component), many of the lower harmonics of the double HCTs were well resolved in rate-place profiles. Thus, spectral information is preserved, and perhaps even enhanced, as it ascends from periphery to cortex. Enhancement of spectral contrast could occur via lateral suppression in A1 and in subcortical auditory nuclei (Shamma and Symmes, 1985; Ehret and Merzenich, 1988; Fishman and Steinschneider, 2006; Sadagopan and Wang, 2010). Alternatively, the high fidelity of spectral fine-structure encoding in A1 may reflect a transformation of temporal representations of individual HCT components in peripheral structures into a rate code at higher levels of the auditory pathway (Buonomano and Merzenich, 1995; Wang et al., 2008). It is important to note that the F0s of the HCT stimuli used in the present study were varied at each site such that the BF occupied different values of harmonic number with respect to the F0 of the sounds. Thus, the present results provide only an indirect measure of neural resolvability in A1. However, by invoking the principle of “scaling invariance” (Larsen et al., 2008), whereby the ratio of frequency tuning bandwidth to BF at each site is constant across sites, the present data can be used to infer the response to an arbitrary double HCT across sites in A1. Given that scaling invariance holds to a good approximation in A1 (Fishman et al., 2013), measures of neural resolvability obtained at individual sites are generally representative of the resolvability of double HCT harmonics across sites in A1.
Finally, we have identified a potential intracortical homolog of the ORN recorded noninvasively in humans, which correlates with the perceptual segregation of concurrent HCTs (Snyder and Alain, 2005; Alain, 2007). Similar potential homologs of the ORN associated with the perceptual “pop out” of mistuned harmonics in humans (Alain et al., 2001, 2002; Alain, 2007; Lipp et al., 2010) have been previously reported in macaque A1 (Fishman and Steinschneider, 2010). However, the possibility that the putative ORN homolog described here primarily reflects stimulus differences between the single and double HCTs, rather than the perception of one-versus-two auditory objects per se, cannot be excluded, a caveat that applies also to the ORN recorded in humans (however, see Sanders et al., 2008). Furthermore, although evidence suggests that macaques can perceive single HCTs as having a unitary pitch at their F0 (Tomlinson and Schwarz, 1988), it remains undetermined whether they, like humans, can perceive two concurrent HCTs differing in F0 as two auditory objects with distinct pitches. Nonetheless, insofar as the macaque monkey represents a translationally valid animal model for elucidating the neural bases of human event-related potentials (e.g., Eggermont and Ponton, 2002), the present results suggest that the ORN recorded in humans originates, at least in part, from neural generators within primary auditory cortex.
Together, the present results indicate that A1 contains sufficient spectral and temporal information for extracting the pitches of concurrent HCTs (e.g., via harmonic templates and temporal periodicity detectors), and for their perceptual segregation based on differences in F0. Although compatible also with non-“labeled-line” schemes of pitch encoding at the cortical level (e.g., Bizley et al., 2010), findings match predictions of a hierarchical model of pitch extraction whereby A1 supplies pitch-related spectral and temporal information to neurons in nonprimary auditory cortex (Lewis et al., 2009; Kumar et al., 2011; Kumar and Schönwiesner, 2012). Furthermore, they support models of auditory scene analysis which postulate a close connection between processes involved in deriving the pitch of complex sounds and those contributing to auditory grouping and segregation (Bregman, 1990; Hartmann, 1996; Micheyl and Oxenham, 2010).
Footnotes
This work was supported by National Institutes of Health Grant DC00657. We thank Jeannie Hutagalung for invaluable assistance with animal training, surgery, and data collection; and Dr. Steven Walkley for providing histological facilities.
The authors declare no competing financial interests.
References
- Alain C. Breaking the wave: effects of attention and learning on concurrent sound perception. Hear Res. 2007;229:225–236. doi: 10.1016/j.heares.2007.01.011. [DOI] [PubMed] [Google Scholar]
- Alain C, McDonald KL. Age-related differences in neuromagnetic brain activity underlying concurrent sound perception. J Neurosci. 2007;27:1308–1314. doi: 10.1523/JNEUROSCI.5433-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alain C, Arnott SR, Picton TW. Bottom-up and top-down influences on auditory scene analysis: evidence from event-related brain potentials. J Exp Psychol Hum Percept Perform. 2001;27:1072–1089. doi: 10.1037/0096-1523.27.5.1072. [DOI] [PubMed] [Google Scholar]
- Alain C, Schuler BM, McDonald KL. Neural activity associated with distinguishing concurrent auditory objects. J Acoust Soc Am. 2002;111:990–995. doi: 10.1121/1.1434942. [DOI] [PubMed] [Google Scholar]
- Alain C, Reinke K, McDonald KL, Chau W, Tam F, Pacurar A, Graham S. Left thalamo-cortical network implicated in successful speech separation and identification. Neuroimage. 2005;26:592–599. doi: 10.1016/j.neuroimage.2005.02.006. [DOI] [PubMed] [Google Scholar]
- Arnott SR, Bardouille T, Ross B, Alain C. Neural generators underlying concurrent sound segregation. Brain Res. 2011;1387:116–124. doi: 10.1016/j.brainres.2011.02.062. [DOI] [PubMed] [Google Scholar]
- Assmann PF, Paschall DD. Pitches of concurrent vowels. J Acoust Soc Am. 1998;103:1150–1160. doi: 10.1121/1.421249. [DOI] [PubMed] [Google Scholar]
- Atencio CA, Schreiner CE. Auditory cortical local subnetworks are characterized by sharply synchronous activity. J Neurosci. 2013;33:18503–18514. doi: 10.1523/JNEUROSCI.2014-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendor D, Wang X. The neuronal representation of pitch in primate auditory cortex. Nature. 2005;436:1161–1165. doi: 10.1038/nature03867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendor D, Wang X. Cortical representations of pitch in monkeys and humans. Curr Opin Neurobiol. 2006;16:391–399. doi: 10.1016/j.conb.2006.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bendor D, Wang X. Differential neural coding of acoustic flutter within primate auditory cortex. Nat Neurosci. 2007;10:763–771. doi: 10.1038/nn1888. [DOI] [PubMed] [Google Scholar]
- Bendor D, Osmanski MS, Wang X. Dual-pitch processing mechanisms in primate auditory cortex. J Neurosci. 2012;32:16149–16161. doi: 10.1523/JNEUROSCI.2563-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bidet-Caulet A, Fischer C, Besle J, Aguera PE, Giard MH, Bertrand O. Effects of selective attention on the electrophysiological representation of concurrent sounds in the human auditory cortex. J Neurosci. 2007;27:9252–9261. doi: 10.1523/JNEUROSCI.1402-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bidet-Caulet A, Fischer C, Bauchet F, Aguera PE, Bertrand O. Neural substrate of concurrent sound perception: direct electrophysiological recordings from human auditory cortex. Front Hum Neurosci. 2008;1:5. doi: 10.3389/neuro.09.005.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bieser A, Müller-Preuss P. Auditory responsive cortex in the squirrel monkey: neural responses to amplitude-modulated sounds. Exp Brain Res. 1996;108:273–284. doi: 10.1016/S0079-6123(08)62546-7. [DOI] [PubMed] [Google Scholar]
- Bizley JK, Walker KM, King AJ, Schnupp JW. Neural ensemble codes for stimulus periodicity in auditory cortex. J Neurosci. 2010;30:5078–5091. doi: 10.1523/JNEUROSCI.5475-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bregman AS. Auditory scene analysis: the perceptual organization of sound. Cambridge, MA: MIT; 1990. [Google Scholar]
- Brosch M, Bauer R, Eckhorn R. Stimulus-dependent modulations of correlated high-frequency oscillations in cat visual cortex. Cereb Cortex. 1997;7:70–76. doi: 10.1093/cercor/7.1.70. [DOI] [PubMed] [Google Scholar]
- Buonomano DV, Merzenich MM. Temporal information transformed into a spatial code by a neural network with realistic properties. Science. 1995;267:1028–1030. doi: 10.1126/science.7863330. [DOI] [PubMed] [Google Scholar]
- Cariani PA, Delgutte B. Neural correlates of the pitch of complex tones: I. Pitch and pitch salience. J Neurophysiol. 1996;76:1698–1716. doi: 10.1152/jn.1996.76.3.1698. [DOI] [PubMed] [Google Scholar]
- Carlyon RP, Shackleton TM. Comparing the fundamental frequencies of resolved and unresolved harmonics: evidence for two pitch mechanisms? J Acoust Soc Am. 1994;95:3541–3554. doi: 10.1121/1.409971. [DOI] [PubMed] [Google Scholar]
- Cedolin L, Delgutte B. Pitch of complex tones: rate-place and interspike interval representations in the auditory nerve. J Neurophysiol. 2005;94:347–362. doi: 10.1152/jn.01114.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cedolin L, Delgutte B. Spatiotemporal representation of the pitch of harmonic complex tones in the auditory nerve. J Neurosci. 2010;30:12712–12724. doi: 10.1523/JNEUROSCI.6365-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darwin CJ, Carlyon RP. Auditory grouping. In: Moore BCJ, editor. The handbook of perception and cognition, Ed 2, Vol 6: Hearing. London: Academic; 1995. [Google Scholar]
- de la Mothe LA, Blumell S, Kajikawa Y, Hackett TA. Cortical connections of the auditory cortex in marmoset monkeys: core and medial belt regions. J Comp Neurol. 2006;496:27–71. doi: 10.1002/cne.20923. [DOI] [PubMed] [Google Scholar]
- De Ribaupierre F, Goldstein MH, Jr, Yeni-Komshian G. Intracellular study of the cat's primary auditory cortex. Brain Res. 1972;48:185–204. doi: 10.1016/0006-8993(72)90178-3. [DOI] [PubMed] [Google Scholar]
- Ding N, Simon JZ. Emergence of neural encoding of auditory objects while listening to competing speakers. Proc Natl Acad Sci U S A. 2012;109:11854–11859. doi: 10.1073/pnas.1205381109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggermont JJ, Ponton CW. The neurophysiology of auditory perception: from single units to evoked potentials. Audiol Neurootol. 2002;7:71–99. doi: 10.1159/000057656. [DOI] [PubMed] [Google Scholar]
- Ehret G, Merzenich MM. Complex sound analysis (frequency resolution, filtering and spectral integration) by single units of the inferior colliculus of the cat. Brain Res. 1988;472:139–163. doi: 10.1016/0165-0173(88)90018-5. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Steinschneider M. Spectral resolution of monkey primary auditory cortex (A1) revealed with two-noise masking. J Neurophysiol. 2006;96:1105–1115. doi: 10.1152/jn.00124.2006. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Steinschneider M. Temporally dynamic frequency tuning of population responses in monkey primary auditory cortex. Hear Res. 2009;254:64–76. doi: 10.1016/j.heares.2009.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman YI, Steinschneider M. Neural correlates of auditory scene analysis based on inharmonicity in monkey primary auditory cortex. J Neurosci. 2010;30:12480–12494. doi: 10.1523/JNEUROSCI.1780-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman YI, Steinschneider M. Searching for the mismatch negativity in primary auditory cortex of the awake monkey: deviance detection or stimulus specific adaptation? J Neurosci. 2012;32:15747–15758. doi: 10.1523/JNEUROSCI.2835-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fishman YI, Volkov IO, Noh MD, Garell PC, Bakken H, Arezzo JC, Howard MA, Steinschneider M. Consonance and dissonance of musical chords: neural correlates in auditory cortex of monkeys and humans. J Neurophysiol. 2001;86:2761–2788. doi: 10.1152/jn.2001.86.6.2761. [DOI] [PubMed] [Google Scholar]
- Fishman YI, Micheyl C, Steinschneider M. Neural representation of harmonic complex tones in primary auditory cortex of the awake monkey. J Neurosci. 2013;33:10312–10323. doi: 10.1523/JNEUROSCI.0020-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman JA, Nicholson C. Experimental optimization of current source-density technique for anuran cerebellum. J Neurophysiol. 1975;38:369–382. doi: 10.1152/jn.1975.38.2.369. [DOI] [PubMed] [Google Scholar]
- Goldstein JL. An optimum processor theory for the central formation of the pitch of complex tones. J Acoust Soc Am. 1973;54:1496–1516. doi: 10.1121/1.1914448. [DOI] [PubMed] [Google Scholar]
- Griffiths TD, Hall DA. Mapping pitch representation in neural ensembles with fMRI. J Neurosci. 2012;32:13343–13347. doi: 10.1523/JNEUROSCI.3813-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hackett TA, Stepniewska I, Kaas JH. Subdivisions of auditory cortex and ipsilateral cortical connections of the parabelt auditory cortex in macaque monkeys. J Comp Neurol. 1998;394:475–495. doi: 10.1002/(SICI)1096-9861(19980518)394:4<475::AID-CNE6>3.0.CO%3B2-Z. [DOI] [PubMed] [Google Scholar]
- Hartmann WM. Pitch, periodicity, and auditory organization. J Acoust Soc Am. 1996;100:3491–3502. doi: 10.1121/1.417248. [DOI] [PubMed] [Google Scholar]
- Hedrick MS, Madix SG. Effect of vowel identity and onset asynchrony on concurrent vowel identification. J Speech Lang Hear Res. 2009;52:696–705. doi: 10.1044/1092-4388(2008/07-0094). [DOI] [PubMed] [Google Scholar]
- Hukin RW, Darwin CJ. Comparison of the effect of onset asynchrony on auditory grouping in pitch matching and vowel identification. Percept Psychophys. 1995;57:191–196. doi: 10.3758/BF03206505. [DOI] [PubMed] [Google Scholar]
- Kaas JH, Hackett TA. Subdivisions of auditory cortex and levels of processing in primates. Audiol Neurootol. 1998;3:73–85. doi: 10.1159/000013783. [DOI] [PubMed] [Google Scholar]
- Kayser C, Petkov CI, Logothetis NK. Tuning to sound frequency in auditory field potentials. J Neurophysiol. 2007;98:1806–1809. doi: 10.1152/jn.00358.2007. [DOI] [PubMed] [Google Scholar]
- Kumar S, Schönwiesner M. Mapping human pitch representation in a distributed system using depth-electrode recordings and modeling. J Neurosci. 2012;32:13348–13351. doi: 10.1523/JNEUROSCI.3812-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar S, Sedley W, Nourski KV, Kawasaki H, Oya H, Patterson RD, Howard MA, 3rd, Friston KJ, Griffiths TD. Predictive coding and pitch processing in the auditory cortex. J Cogn Neurosci. 2011;23:3084–3094. doi: 10.1162/jocn_a_00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Chen CM, O'Connell MN, Mills A, Schroeder CE. Neuronal oscillations and multisensory interaction in primary auditory cortex. Neuron. 2007;53:279–292. doi: 10.1016/j.neuron.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen E, Cedolin L, Delgutte B. Pitch representations in the auditory nerve: two concurrent complex tones. J Neurophysiol. 2008;100:1301–1319. doi: 10.1152/jn.01361.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee JH, Humes LE. Effect of fundamental-frequency and sentence-onset differences on speech-identification performance of young and older adults in a competing-talker background. J Acoust Soc Am. 2012;132:1700–1717. doi: 10.1121/1.4740482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lentz JJ, Marsh SL. The effect of hearing loss on identification of asynchronous double vowels. J Speech Lang Hear Res. 2006;49:1354–1367. doi: 10.1044/1092-4388(2006/097). [DOI] [PubMed] [Google Scholar]
- Lewis JW, Talkington WJ, Walker NA, Spirou GA, Jajosky A, Frum C, Brefczynski-Lewis JA. Human cortical organization for processing vocalizations indicates representation of harmonic structure as a signal attribute. J Neurosci. 2009;29:2283–2296. doi: 10.1523/JNEUROSCI.4145-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Licklider JC. A duplex theory of pitch perception. Experientia. 1951;7:128–134. doi: 10.1007/BF02156143. [DOI] [PubMed] [Google Scholar]
- Lipp R, Kitterick P, Summerfield Q, Bailey PJ, Paul-Jordanov I. Concurrent sound segregation based on inharmonicity and onset asynchrony. Neuropsychologia. 2010;48:1417–1425. doi: 10.1016/j.neuropsychologia.2010.01.009. [DOI] [PubMed] [Google Scholar]
- Meddis R, Hewitt MJ. Modeling the identification of concurrent vowels with different fundamental frequencies. J Acoust Soc Am. 1992;91:233–245. doi: 10.1121/1.402767. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Brugge JF. Representation of the cochlear partition of the superior temporal plane of the macaque monkey. Brain Res. 1973;50:275–296. doi: 10.1016/0006-8993(73)90731-2. [DOI] [PubMed] [Google Scholar]
- Mesgarani N, Chang EF. Selective cortical representation of attended speaker in multi-talker speech perception. Nature. 2012;485:233–236. doi: 10.1038/nature11020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metherate R, Cruikshank SJ. Thalamocortical inputs trigger a propagating envelope of gamma-band activity in auditory cortex in vitro. Exp Brain Res. 1999;126:160–174. doi: 10.1007/s002210050726. [DOI] [PubMed] [Google Scholar]
- Micheyl C, Oxenham AJ. Pitch, harmonicity and concurrent sound segregation: psychoacoustical and neurophysiological findings. Hear Res. 2010;266:36–51. doi: 10.1016/j.heares.2009.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Keebler MV, Oxenham AJ. Pitch perception for mixtures of spectrally overlapping harmonic complex tones. J Acoust Soc Am. 2010;128:257–269. doi: 10.1121/1.3372751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Schrater PR, Oxenham AJ. Auditory frequency and intensity discrimination explained using a cortical population rate code. PLoS Comput Biol. 2013;9:e1003336. doi: 10.1371/journal.pcbi.1003336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morel A, Garraghty PE, Kaas JH. Tonotopic organization, architectonic fields, and connections of auditory cortex in macaque monkeys. J Comp Neurol. 1993;335:437–459. doi: 10.1002/cne.903350312. [DOI] [PubMed] [Google Scholar]
- Müller-Preuss P, Mitzdorf U. Functional anatomy of the inferior colliculus and the auditory cortex: current source density analyses of click-evoked potentials. Hear Res. 1984;16:133–142. doi: 10.1016/0378-5955(84)90003-0. [DOI] [PubMed] [Google Scholar]
- Nicholson C, Freeman JA. Theory of current source-density analysis and determination of conductivity tensor for anuran cerebellum. J Neurophysiol. 1975;38:356–368. doi: 10.1152/jn.1975.38.2.356. [DOI] [PubMed] [Google Scholar]
- Nourski KV, Brugge JF. Representation of temporal sound features in the human auditory cortex. Rev Neurosci. 2011;22:187–203. doi: 10.1515/RNS.2011.016. [DOI] [PubMed] [Google Scholar]
- O'Connell MN, Falchier A, McGinnis T, Schroeder CE, Lakatos P. Dual mechanism of neuronal ensemble inhibition in primary auditory cortex. Neuron. 2011;69:805–817. doi: 10.1016/j.neuron.2011.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson RD, Nimmo-Smith I, Weber DL, Milroy R. The deterioration of hearing with age: frequency selectivity, the critical ratio, the audiogram, and speech threshold. J Acoust Soc Am. 1982;72:1788–1803. doi: 10.1121/1.388652. [DOI] [PubMed] [Google Scholar]
- Plack CJ, Oxenham AJ, Popper AN, Fay RR, editors. Pitch: neural coding and perception. New York: Springer; 2005. [Google Scholar]
- Ptitsyn AA, Zvonic S, Gimble JM. Permutation test for periodicity in short time series data. BMC Bioinformatics. 2006;7(Suppl 2):S10. doi: 10.1186/1471-2105-7-S2-S10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Recanzone GH, Guard DC, Phan ML. Frequency and intensity response properties of single neurons in the auditory cortex of the behaving macaque monkey. J Neurophysiol. 2000;83:2315–2331. doi: 10.1152/jn.2000.83.4.2315. [DOI] [PubMed] [Google Scholar]
- Sadagopan S, Wang X. Contribution of inhibition to stimulus selectivity in primary auditory cortex of awake primates. J Neurosci. 2010;30:7314–7325. doi: 10.1523/JNEUROSCI.5072-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders LD, Joh AS, Keen RE, Freyman RL. One sound or two? Object-related negativity indexes echo perception. Percept Psychophys. 2008;70:1558–1570. doi: 10.3758/PP.70.8.1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder CE, Mehta AD, Givre SJ. A spatiotemporal profile of visual system activation revealed by current source density analysis in the awake macaque. Cereb Cortex. 1998;8:575–592. doi: 10.1093/cercor/8.7.575. [DOI] [PubMed] [Google Scholar]
- Shamma SA, Symmes D. Patterns of inhibition in auditory cortical cells in awake squirrel monkeys. Hear Res. 1985;19:1–13. doi: 10.1016/0378-5955(85)90094-2. [DOI] [PubMed] [Google Scholar]
- Shen Y, Richards VM. Spectral processing of two concurrent harmonic complexes. J Acoust Soc Am. 2012;131:386–397. doi: 10.1121/1.3664081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinn-Cunningham BG, Best V. Selective attention in normal and impaired hearing. Trends Amplif. 2008;12:283–299. doi: 10.1177/1084713808325306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder JS, Alain C. Age-related changes in neural activity associated with concurrent vowel segregation. Brain Res Cogn Brain Res. 2005;24:492–499. doi: 10.1016/j.cogbrainres.2005.03.002. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Tenke CE, Schroeder CE, Javitt DC, Simpson GV, Arezzo JC, Vaughan HG., Jr Cellular generators of the cortical auditory evoked potential initial component. Electroencephalogr Clin Neurophysiol. 1992;84:196–200. doi: 10.1016/0168-5597(92)90026-8. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Schroeder CE, Arezzo JC, Vaughan HG., Jr Speech-evoked activity in primary auditory cortex: effects of voice onset time. Electroencephalogr Clin Neurophysiol. 1994;92:30–43. doi: 10.1016/0168-5597(94)90005-1. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Reser DH, Fishman YI, Schroeder CE, Arezzo JC. Click train encoding in primary auditory cortex of the awake monkey: evidence for two mechanisms subserving pitch perception. J Acoust Soc Am. 1998;104:2935–2955. doi: 10.1121/1.423877. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Fishman YI, Arezzo JC. Representation of the voice onset time (VOT) speech parameter in population responses within primary auditory cortex of the awake monkey. J Acoust Soc Am. 2003;114:307–321. doi: 10.1121/1.1582449. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Volkov IO, Fishman YI, Oya H, Arezzo JC, Howard MA., 3rd Intracortical responses in human and monkey primary auditory cortex support a temporal processing mechanism for encoding of the voice onset time phonetic parameter. Cereb Cortex. 2005;15:170–186. doi: 10.1093/cercor/bhh120. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Fishman YI, Arezzo JC. Spectrotemporal analysis of evoked and induced electroencephalographic responses in primary auditory cortex (A1) of the awake monkey. Cereb Cortex. 2008;18:610–625. doi: 10.1093/cercor/bhm094. [DOI] [PubMed] [Google Scholar]
- Steinschneider M, Nourski KV, Fishman YI. Representation of speech in human auditory cortex: is it special? Hear Res. 2013;305:57–73. doi: 10.1016/j.heares.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukov W, Barth DS. Three-dimensional analysis of spontaneous and thalamically evoked gamma oscillations in auditory cortex. J Neurophysiol. 1998;79:2875–2884. doi: 10.1152/jn.1998.79.6.2875. [DOI] [PubMed] [Google Scholar]
- Supèr H, Roelfsema PR. Chronic multiunit recordings in behaving animals: advantages and limitations. Prog Brain Res. 2005;147:263–282. doi: 10.1016/S0079-6123(04)47020-4. [DOI] [PubMed] [Google Scholar]
- Tomlinson RW, Schwarz DW. Perception of the missing fundamental in nonhuman primates. J Acoust Soc Am. 1988;84:560–565. doi: 10.1121/1.396833. [DOI] [PubMed] [Google Scholar]
- Vaughan HG, Jr, Arezzo JC. The neural basis of event-related potentials. In: Picton TW, editor. Human event-related potentials, EEG handbook, revised series. Vol 3. New York: Elsevier; 1988. pp. 45–96. [Google Scholar]
- Walker KM, Bizley JK, King AJ, Schnupp JW. Multiplexed and robust representations of sound features in auditory cortex. J Neurosci. 2011;31:14565–14576. doi: 10.1523/JNEUROSCI.2074-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Lu T, Bendor D, Bartlett E. Neural coding of temporal information in auditory thalamus and cortex. Neuroscience. 2008;157:484–494. doi: 10.1016/j.neuroscience.2008.07.050. [DOI] [PubMed] [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–1612. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Zion-Golumbic EM, Ding N, Bickel S, Lakatos P, Schevon CA, McKhann GM, Goodman RR, Emerson R, Mehta AD, Simon JZ, Poeppel D, Schroeder CE. Mechanisms underlying selective neuronal tracking of attended speech at a “cocktail party.”. Neuron. 2013;77:980–991. doi: 10.1016/j.neuron.2012.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]