Sampling bigslides
- 1. Sampling
- 2. Why Sample? • Why not study everyone? • Debate about Census vs. sampling
- 3. Problems in Sampling? • What problems do you know about? • What issues are you aware of? • What questions do you have?
- 4. Key Sampling Concepts Copyright ©2002, William M.K. Trochim, All Rights Reserved
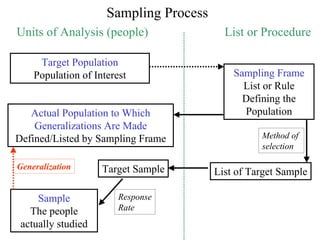
- 5. Sampling Process Units of Analysis (people) List or Procedure Target Population Population of Interest Sampling Frame List or Rule Defining the Actual Population to Which Population Generalizations Are Made Defined/Listed by Sampling Frame Method of selection Generalization Target Sample List of Target Sample Sample Response The people Rate actually studied
- 6. Key Ideas • Distinction between the population of interest and the actual population defined by the sampling frame • Generalizations can be made only to the actual population • Understand crucial role of the sampling frame
- 7. Sampling Frame • The list or procedure defining the POPULATION. (From which the sample will be drawn.) • Distinguish sampling frame from sample. • Examples: – Telephone book – Voter list – Random digit dialing • Essential for probability sampling, but can be defined for nonprobability sampling
- 8. Types of Samples Probability Simple Random Systematic Random Stratified Random Random Cluster Stratified Cluster Complex Multi-stage Random (various kinds) Non-Probability Quota Convenience Purposive
- 9. Probability Samples • A probability sample is one in which each element of the population has a known non-zero probability of selection. • Not a probability sample of some elements of population cannot be selected (have zero probability) • Not a probability sample if probabilities of selection are not known.
- 10. Probability Sampling • Cannot guarantee “representativeness” on all traits of interest • A sampling plan with known statistical properties • Permits statements like: “The probability is .99 that the true population correlation falls between .46 and .56.”
- 11. Sampling Frame is Crucial in Probability Sampling • If the sampling frame is a poor fit to the population of interest, random sampling from that frame cannot fix the problem • The sampling frame is non-randomly chosen. Elements not in the sampling frame have zero probability of selection. • Generalizations can be made ONLY to the actual population defined by the sampling frame
- 12. Types of Probability Samples Simple Random Systematic Random Stratified Random Random Cluster Stratified Cluster Complex Multi-stage Random (various kinds)
- 13. Simple Random Sampling • Each element in the population has an equal probability of selection AND each combination of elements has an equal probability of selection • Names drawn out of a hat • Random numbers to select elements from an ordered list
- 14. Stratified Random Sampling-1 • Divide population into groups that differ in important ways • Basis for grouping must be known before sampling • Select random sample from within each group
- 15. Stratified Random Sampling-2 • For a given sample size, reduces error compared to simple random sampling IF the groups are different from each other • Tradeoff between the cost of doing the stratification and smaller sample size needed for same error • Probabilities of selection may be different for different groups, as long as they are known • Oversampling small groups improves inter- group comparisons
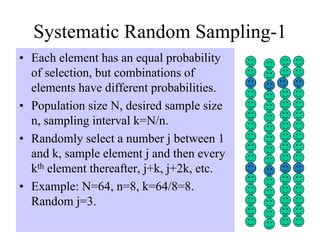
- 16. Systematic Random Sampling-1 • Each element has an equal probability of selection, but combinations of elements have different probabilities. • Population size N, desired sample size n, sampling interval k=N/n. • Randomly select a number j between 1 and k, sample element j and then every kth element thereafter, j+k, j+2k, etc. • Example: N=64, n=8, k=64/8=8. Random j=3.
- 17. Systematic Random Sampling-2 • Has same error rate as simple random sample if the list is in random or haphazard order • Provides the benefits of implicit stratification if the list is grouped
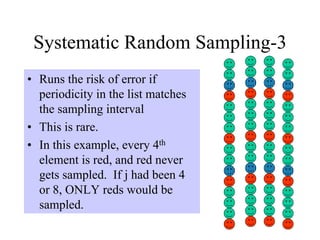
- 18. Systematic Random Sampling-3 • Runs the risk of error if periodicity in the list matches the sampling interval • This is rare. • In this example, every 4th element is red, and red never gets sampled. If j had been 4 or 8, ONLY reds would be sampled.
- 19. Random Cluster Sampling - 1 • Done correctly, this is a form of random sampling • Population is divided into groups, usually geographic or organizational • Some of the groups are randomly chosen • In pure cluster sampling, whole cluster is sampled. • In simple multistage cluster, there is random sampling within each randomly chosen cluster
- 20. Random Cluster Sampling - 2 • Population is divided into groups • Some of the groups are randomly selected • For given sample size, a cluster sample has more error than a simple random sample • Cost savings of clustering may permit larger sample • Error is smaller if the clusters are similar to each other
- 21. Random Cluster Samplng - 3 • Cluster sampling has very high error if the clusters are different from each other • Cluster sampling is NOT desirable if the clusters are different • It IS random sampling: you randomly choose the clusters • But you will tend to omit some kinds of subjects
- 22. Stratified Cluster Sampling • Reduce the error in cluster Strata sampling by creating strata of clusters • Sample one cluster from each stratum • The cost-savings of clustering with the error reduction of stratification
- 23. Stratification vs. Clustering Stratification Clustering • Divide population into • Divide population into groups different from each comparable groups: other: sexes, races, ages schools, cities • Sample randomly from • Randomly sample some of each group the groups • Less error compared to • More error compared to simple random simple random • More expensive to obtain • Reduces costs to sample stratification information only some areas or before sampling organizations
- 24. Stratified Cluster Sampling • Combines elements of stratification and clustering • First you define the clusters • Then you group the clusters into strata of clusters, putting similar clusters together in a stratum • Then you randomly pick one (or more) cluster from each of the strata of clusters • Then you sample the subjects within the sampled clusters (either all the subjects, or a simple random sample of them)
- 25. Multi-stage Probability Samples –1 • Large national probability samples involve several stages of stratified cluster sampling • The whole country is divided into geographic clusters, metropolitan and rural • Some large metropolitan areas are selected with certainty (certainty is a non-zero probability!) • Other areas are formed into strata of areas (e.g. middle-sized cities, rural counties); clusters are selected randomly from these strata
- 26. Multi-stage Probability Samples –2 • Within each sampled area, the clusters are defined, and the process is repeated, perhaps several times, until blocks or telephone exchanges are selected • At the last step, households and individuals within household are randomly selected • Random samples make multiple call-backs to people not at home.
- 27. The Problem of Non-Response - 1 • You can randomly pick elements from sampling frame and use them to randomly select people • But you cannot make people respond • Non-response destroys the generalizeability of the sample. You are generalizing to people who are willing to respond to surveys • If response is 90% or so, not so bad. But if it is 50%, this is a serious problem
- 28. The Problem of Non-Response - 2 • Multiple call-backs are essential for trying to reduce non-response bias • Samples without call-backs have high bias: cannot really be considered random samples • Response rates have been falling • It is very difficult to get above a 60% response rate • You do the best you can, and try to estimate the effect of the error by getting as much information as possible about the predictors of non-response.
- 29. Non-probability Samples • Convenience • Purposive • Quota
- 30. Convenience Sample • Subjects selected because it is easy to access them. • No reason tied to purposes of research. • Students in your class, people on State Street, friends
- 31. Purposive Samples • Subjects selected for a good reason tied to purposes of research • Small samples < 30, not large enough for power of probability sampling. – Nature of research requires small sample – Choose subjects with appropriate variability in what you are studying • Hard-to-get populations that cannot be found through screening general population
- 32. Quota Sampling • Pre-plan number of subjects in specified categories (e.g. 100 men, 100 women) • In uncontrolled quota sampling, the subjects chosen for those categories are a convenience sample, selected any way the interviewer chooses • In controlled quota sampling, restrictions are imposed to limit interviewer’s choice • No call-backs or other features to eliminate convenience factors in sample selection
- 33. Quota Vs Stratified Sampling • In Stratified Sampling, • In Quota Sampling, selection of subject is interviewer selects random. Call-backs first available subject are used to get that who meets criteria: is particular subject. a convenience sample. • Stratified sampling • Highly controlled quota without call-backs may sampling uses probability not, in practice, be much sampling down to the last different from quota block or telephone sampling. exchange But you should know the difference for the test!!
- 34. Sample Size • Heterogeneity: need larger sample to study more diverse population • Desired precision: need larger sample to get smaller error • Sampling design: smaller if stratified, larger if cluster • Nature of analysis: complex multivariate statistics need larger samples • Accuracy of sample depends upon sample size, not ratio of sample to population
- 35. Sampling in Practice • Often a non-random selection of basic sampling frame (city, organization etc.) • Fit between sampling frame and research goals must be evaluated • Sampling frame as a concept is relevant to all kinds of research (including nonprobability) • Nonprobability sampling means you cannot generalize beyond the sample • Probability sampling means you can generalize to the population defined by the sampling frame