While most graphs are represented with equations involving variables x and y, there are some curves that are best handled with a third variable t called a parameter.
Parametric Equations of a curve express the coordinates of the points of the curve as functions of a third variable.
Typically, this parameter is designated t, for time, but as stated by Wikipedia, the parameter may represent some other physical quantity such as a geometric variable, or may merely be selected arbitrarily for convenience.
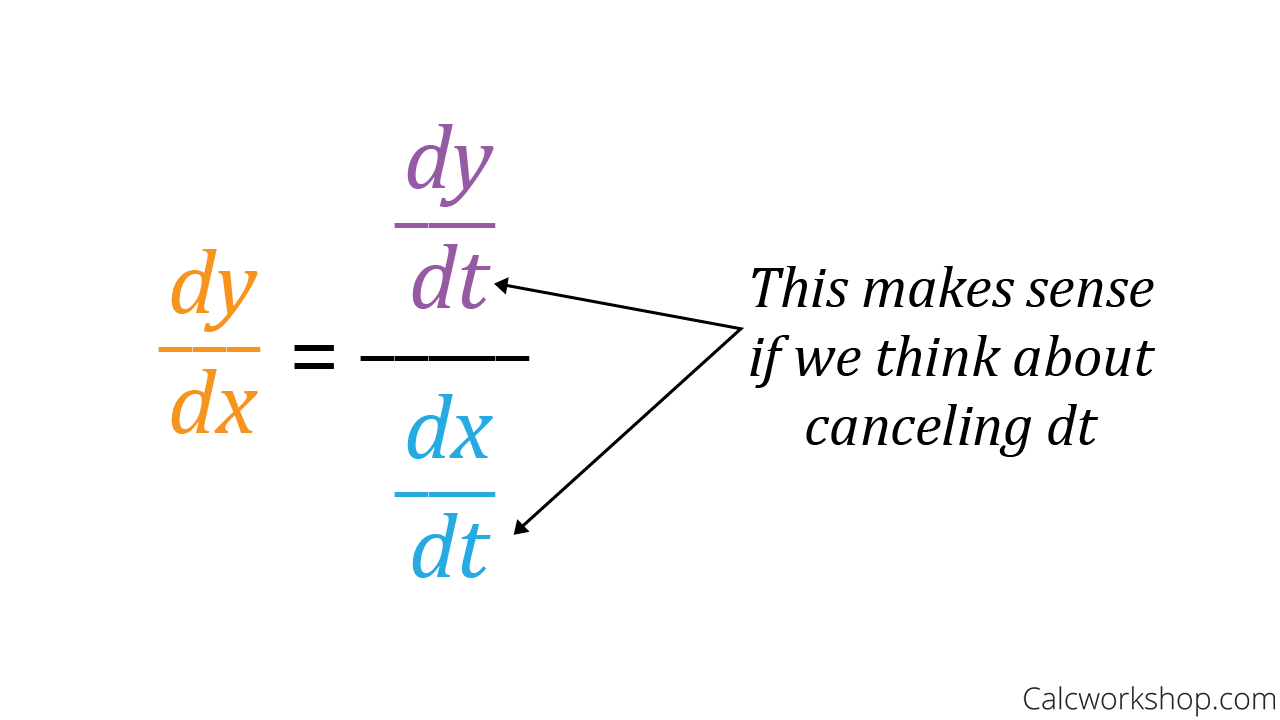
Slope of Tangent Line of Parametric Equations
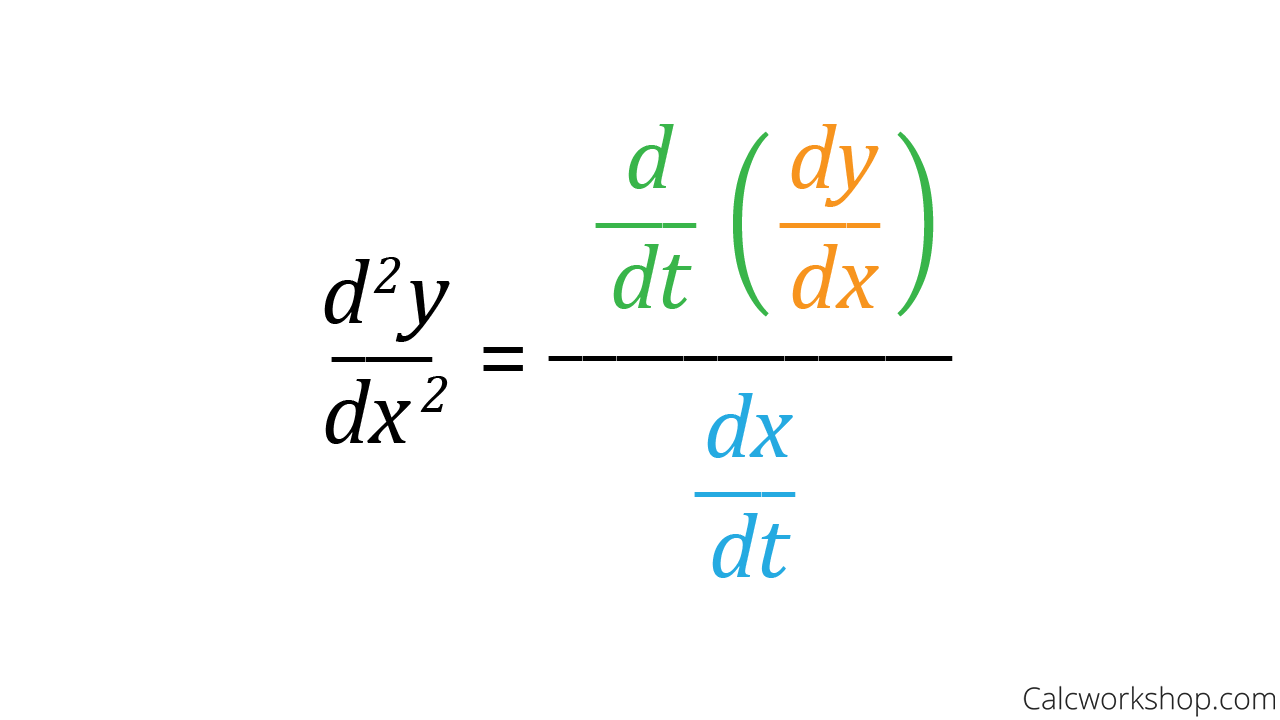
Formula for Finding the Second Derivative in Parametric
For the purposes of this video lesson we will allow our parameter to denote time.
We begin our lesson with a quick review of Vectors, and see how a Vector can be transformed (rewritten) in Parametric Form.

Finding Area of Parametric Equations
Next we will look at the graph of a Parametric Equation, and learn how to find the Slope and Concavity of a Parameterized Curve.
Then, we will use our formula for finding the slope of a Parametric Function to help us find where a Parametric Curve has Horizontal and Vertical Tangent Lines.
And lastly, we will calculate the Area enclosed by a Parametric Curve, as well as finding the Length (distance) of a curve in Parametric Form.
Parametric Lesson Video

Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.