Knowing the properties of quadrilaterals are essential to doing well in geometry.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
In today’s geometry lesson, you’ll learn how to identify, name, and work with all different types of these quadrilaterals.
How do we make sense of special quadrilaterals? What makes them similar and different?
Quadrilateral Hierarchy
First, this diagram helps us to recognize seven different types of quadrilaterals.

Quadrilateral Flow Chart
Secondly, we can see that trapezoids and kites are special quadrilaterals and that rectangles, rhombi, and squares maintain all the properties of a parallelogram, as Math is Fun accurately states.
But what about side lengths, angles, and diagonals?
The chart below shows in much greater detail the distinctive characteristics of each quadrilateral so that we can differentiate similarities and differences.

Properties of Quadrilaterals
Types Of Quadrilaterals
1. Parallelogram
Properties
- Opposite Side Parallel
- Opposite Sides Congruent
- Opposite Angles Congruent
- Diagonals Bisect Each Other

6 Properties of Parallelograms Defined
Formulas
- Perimeter = a + b + c + d ; where a, b, c, and d are the lengths of the sides of the parallelogram
- Area = bh ; where b = length of the base, and h = length of the altitude of the parallelogram

Area of a Parallelogram Formula
2. Rectangle
Properties
- Opposite Side Parallel
- Opposite Sides Congruent
- Opposite Angles Congruent
- Diagonals Bisect Each Other
- Diagonals Congruent
- Four Right Angles

Properties of a Rectangle
Formulas
- Perimeter = 2l + 2w , where l = length and w = width
- Area = lw , where l = length and w = width

Area of a Rectangle
3. Rhombus
Properties
- Opposite Side Parallel
- Opposite Sides Congruent
- Opposite Angles Congruent
- Diagonals Bisect Each Other
- Diagonals Are Perpendicular
- Four Congruent Sides
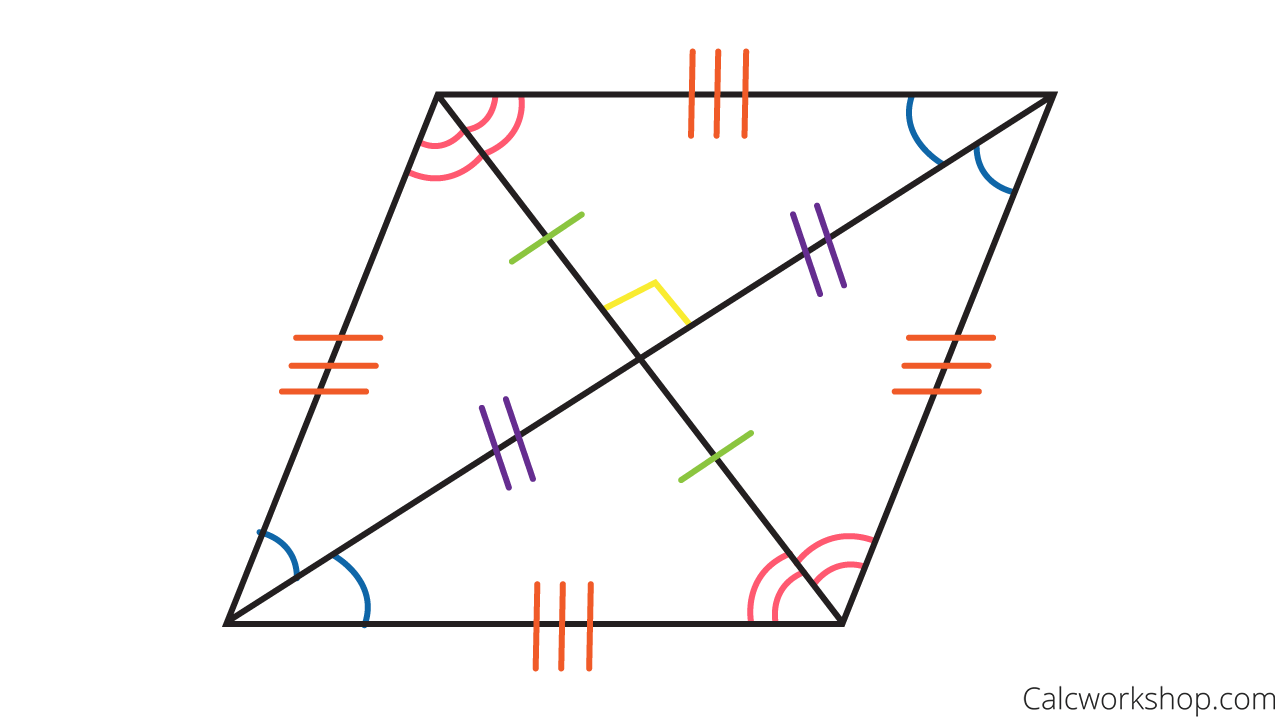
Properties of a Rhombus
Formulas
- Perimeter = a + b + c + d , where a, b, c, and d are the lengths of the sides of the rhombus
- Area = (1/2)d1*d2 , where d1 = length of first diagonal, and d2 = length of second diagonal
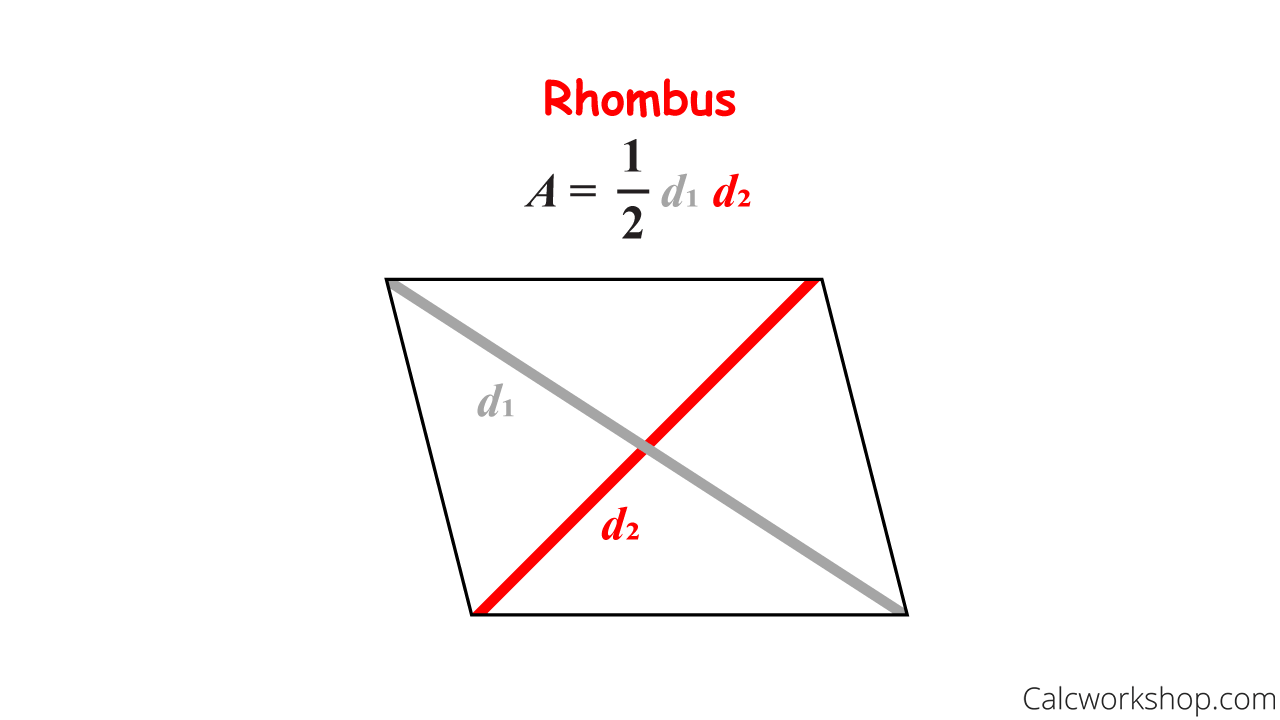
Rhombus Area Formula
4. Square
Properties
- Opposite Side Parallel
- Opposite Sides Congruent
- Opposite Angles Congruent
- Diagonals Bisect Each Other
- Diagonals Congruent
- Diagonals Are Perpendicular
- Four Right Angles
- Four Congruent Sides

Properties of a Square
Formulas
- Perimeter = 4x , where x is the length of one side of the square
- Area = x^2 , where x is the length of one side of the square

Area of a Square
5. Trapezoid
Properties
- 1 Pair Opposite Sides Parallel
- 1 Pair Opposite Sides Congruent

Midsegment of a Trapezoid
Formulas
- Perimeter = a + b + c + d , where a, b, c, and d are the lengths of the sides of the trapezoid
- Area = (1/2)*h*(b1 + b2) , where b1 = length of base one, and b2 = length of base two
- Midsegment = (1/2)(b1 + b2) , where b1 = length of base one, and b2 = length of base two
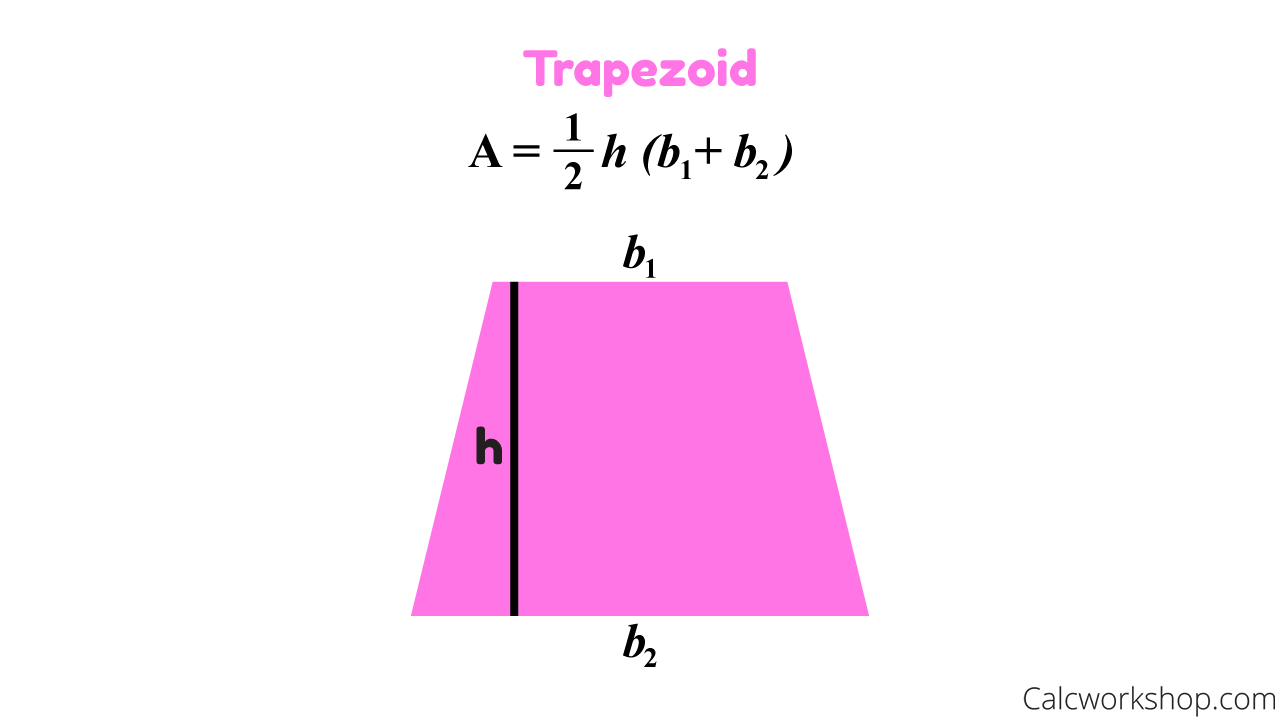
Trapezoid Area Formula
6. Isosceles Trapezoid
Properties
- 1 Pair Opposite Sides Parallel
- 1 Pair Opposite Sides Congruent
- Diagonals Congruent

Properties of an Isosceles Trapezoid
Formulas
- Perimeter = a + b + c + d , where a, b, c, and d are the lengths of the sides of the trapezoid
- Area = (1/2)*h*(b1 + b2) , where b1 = length of base one, and b2 = length of base two
- Midsegment = (1/2)(b1 + b2) , where b1 = length of base one, and b2 = length of base two

Trapezoid Area Formula
7. Kite
Properties
- Diagonals Are Perpendicular
- Non vertex angles are congruent

Perpendicular Diagonals of a Kite
Formulas
- Perimeter = a + b + c + d , where a,b,c, and d are the lengths of the sides of the kite
- Area = (1/2) d1 * d2 , where d1 = length of first diagonal, and d2 = length of second diagonal
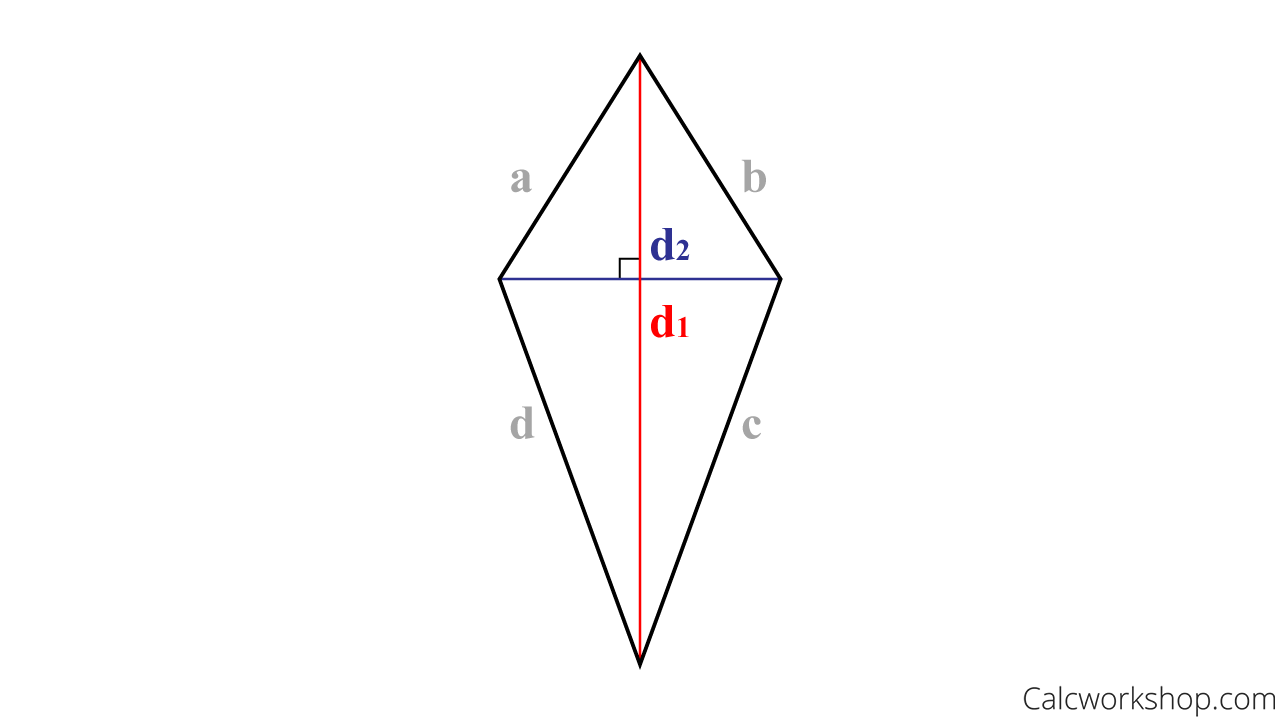
Area of a Kite
Together we are going to use our properties of special quadrilaterals to state all possible names for each polygon, the most specific name for each polygon, as well as determine a polygon by finding distinguishing characteristics.
Quadrilateral Properties – Lesson & Examples (Video)
37 min
- Introduction to quadrilaterals
- 00:00:28 – Characteristics of a quadrilateral (Examples #1-3)
- Exclusive Content for Member’s Only
- 00:11:45 – Write as many names as possible for each quadrilateral (Examples #4-6)
- 00:16:03 – Give the most specific name for the quadrilateral (Examples #7-12)
- 00:22:41 – Determine the name of the polygon given four ordered pairs (Example #13)
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.