Abstract
The extraordinary responsiveness and large diversity of self-assembled structures of liquid crystals are well documented and they have been extensively used in devices like displays. For long, this application route strongly influenced academic research, which frequently focused on the performance of liquid crystals in display-like geometries, typically between flat, rigid substrates of glass or similar solids. Today a new trend is clearly visible, where liquid crystals confined within curved, often soft and flexible, interfaces are in focus. Innovation in microfluidic technology has opened for high-throughput production of liquid crystal droplets or shells with exquisite monodispersity, and modern characterization methods allow detailed analysis of complex director arrangements. The introduction of electrospinning in liquid crystal research has enabled encapsulation in optically transparent polymeric cylinders with very small radius, allowing studies of confinement effects that were not easily accessible before. It also opened the prospect of functionalizing textile fibers with liquid crystals in the core, triggering activities that target wearable devices with true textile form factor for seamless integration in clothing. Together, these developments have brought issues center stage that might previously have been considered esoteric, like the interaction of topological defects on spherical surfaces, saddle-splay curvature-induced spontaneous chiral symmetry breaking, or the non-trivial shape changes of curved liquid crystal elastomers with non-uniform director fields that undergo a phase transition to an isotropic state. The new research thrusts are motivated equally by the intriguing soft matter physics showcased by liquid crystals in these unconventional geometries, and by the many novel application opportunities that arise when we can reproducibly manufacture these systems on a commercial scale. This review attempts to summarize the current understanding of liquid crystals in spherical and cylindrical geometry, the state of the art of producing such samples, as well as the perspectives for innovative applications that have been put forward.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Liquid crystals present phenomena that no other materials can reproduce. They uniquely combine the long-range order that we know from solid crystals with the mobility and flexibility of fluid phases. The fact that they are liquid allows them to easily change shape, accommodating very different boundaries from the standard flat and rigid confining substrates typically used when studying or applying liquid crystals (LCs) in display-like geometries. Curved confinement can trigger fascinating effects, since curvature of the sample boundary, in case of sufficiently strong anchoring of the LC alignment direction at the boundary, is transmitted into the bulk in form of deformation of the orientational field. In many cases topological defects and sometimes also dislocations form, often with beautiful as well as informative consequences. In fact, the nanoscopic response of a smectic LC to the macroscopic curvature of a droplet (the droplet becomes 'stepped') was instrumental to Grandjean's experiments leading up to the identification of the molecular organization in smectics, and Mauguin's experiments of liquid crystal flow through capillary tubes demonstrated the surprising result that the viscosity could be lower in the nematic than in the isotropic phase [1].
As these classic experiments took place at the dawn of the 20th century, one might think that the mysteries of droplets, cylinders and other curved geometries for studying LCs would by now be elucidated and the research field exhausted. This is very far from the case. With the considerable advances in understanding of LCs that have developed during their first 128 years in human awareness (the first report of liquid crystals, by Reinitzer, dates from 1888 [2]) the enormous complexity and beauty of these states of matter has become apparent, continuously leading to new stimulating mysteries and providing many good reasons to revisit the classic experiments. Modern theoretical knowledge allow a deeper analysis of the behavior of LCs with curved boundaries, and the experimental equipment has developed to such an extent that today investigations that Mauguin and Grandjean could not dream of are possible.
Beyond superior imaging equipment, we now also have methods for producing LC samples with curved geometries with unprecedented control. The key development in this respect is the advent of microfluidics, which not only allows rapid production of thousands of identical LC droplets with extraordinary monodispersity, but even the 'excavation' of the droplet, by including a droplet of isotropic liquid inside it, thus creating a thin shell of LC. With shells we have obtained a truly fascinating new configuration for studying LCs, with two closely spaced curved interfaces, with positive curvature on one side and negative on the other. Another powerful technique is electrospinning, which allows us to prepare LC samples in a geometry that fundamentally is cylindrical with very small radius (on the order of a micron), but which can also be modulated into a beads-on-a-string type morphology, if desired.
This review is motivated by the many new opportunities that are now available for studying LCs in the shape of drops, shells or fibers, and the intriguing behavior that different LC phases grant us with when subjected to these sample geometries. These new configurations are intriguing not only from a fundamental science point of view, but they can be very interesting also in an applied perspective. Recent research has demonstrated application potential in sensors, actuators, photonics and even security. We believe that such cross-fertilization opportunities render the systems that we discuss interesting also outside the LC community. Even without a focus on applications, researchers working with microfluidics of isotropic liquids may find the new opportunities arising by incorporating LCs stimulating. The electrospinning and fiber technology research community will find that the responsiveness that LCs can add to textile and other fibers open many new opportunities.
Therefore, we begin the review with a brief introduction to the liquid crystalline states of matter and the terminology used to describe them in section 2, directed at researchers curious in the topic but without the LC background. Section 3 is devoted to shells and droplets of LCs, where we also provide a brief introduction to microfluidics in section 3.1, limiting ourselves to the key issues relevant for LC work. In the rest of section 3 we discuss the technicalities of producing and tuning LC droplets and shells in section 3.2, moving to the intriguing physics related to the topological defects that arise when preparing droplets or shells of LC in section 3.3, and then to two application opportunities, in LC elastomer actuators (section 3.4) and in photonics (section 3.5), respectively. The section ends with a brief discussion in section 3.6 of the very recent addition of LC droplet swimmers and active LCs in shell geometry.
Cylindrical confinement of LCs is the topic of section 4. We first give a general overview, summarizing seminal work on LCs filled into glass capillaries or in narrow Anopore or Nucleopore membranes. We then give a general introduction to the electrospinning technique in section 4.2, focusing on the specific challenge of incorporating LCs within polymer fibers in section 4.3. Finally, we move on to application opportunities of LC fibers in section 4.4. We end the article with an outlook in section 5.
2. The liquid crystalline states of matter
The long-range order in arrangement of molecules, molecule aggregates or particles that make up the LC phase gives it anisotropic macroscopic properties, like birefringence, direction-dependent viscosity and the ability to rearrange its internal structure in response to electromagnetic fields. Reflecting the unique combination of anisotropy with fluidity, LCs are sometimes referred to as anisotropic liquids. Many LCs are colloids, the phase building blocks then being nanoparticles or aggregates of amphiphilic molecules in an isotropic solvent (frequently water). This group constitutes the broad class of lyotropic LCs. The phase diagram of lyotropic LCs depends primarily on the volume fraction of the disperse phase.
Because the vast majority of studies of LC drops, shells and fibers were not done with lyotropics but rather with thermotropic LCs, we will focus mainly on the latter class in this review. Here no solvent is needed, and the phase is homogeneous down to the molecular scale, rather than colloidal. The molecules making up a thermotropic LC are called mesogens, as they generate mesophases (from Greek  = intermediate), an alternative name for liquid crystal phase. An LC-forming compound is sometimes called mesogenic, but most often it is simply referred to as a liquid crystal. This somewhat careless terminology can be confusing for the newcomer, who may have difficulties to tell LC phases apart from LC materials, in particular since the latter exhibit crystalline solid states at low temperatures and isotropic liquid states at high temperatures.
= intermediate), an alternative name for liquid crystal phase. An LC-forming compound is sometimes called mesogenic, but most often it is simply referred to as a liquid crystal. This somewhat careless terminology can be confusing for the newcomer, who may have difficulties to tell LC phases apart from LC materials, in particular since the latter exhibit crystalline solid states at low temperatures and isotropic liquid states at high temperatures.
Indeed, the phase diagram of thermotropics depends primarily on temperature (pressure is also relevant, but for practical reasons most experiments are done at atmospheric pressure), a fact that is reflected in the name of this LC class. While ordinary materials melt directly from the crystalline solid into the isotropic liquid state, LCs exhibit at least two transitions separating these states: first the crystal melts into a liquid crystalline state, then there may be transitions between different LC phases, before the highest-temperature LC phase is replaced by the isotropic liquid state at the clearing point. The latter name reflects the fact that a bulk LC without control of its alignment scatters light, in contrast to the behavior in the isotropic phase of the same material, where it becomes transparent and clear. In case of mixtures between multiple mesogens (sometimes also involving non-mesogenic constituents), also the mixture composition becomes a key parameter in determining the phase diagram.
A large number of thermotropic LC phases have been identified over the years. In this review we will only deal with a small selection that we consider the most important for the field that we cover: the nematic, in its non-chiral and chiral versions (the latter often called cholesteric), and the smectic phases SmA and SmC. In the following subsections each phase is introduced in some detail, and thereafter we will say a few words about the peculiar behavior of LC rubbers, or elastomers (LCEs).
2.1. Thermotropic nematics
The least ordered thermotropic LC phase is called nematic (abbreviated N), and it is characterized by long-range order in orientation of the molecules (which evidently must be anisometric, e.g. rod- or disc-shaped) but no long-range positional order, see figure 1. In terms of positional order the N phase is similar to an ordinary liquid, with only short-range positional order and no periodic lattice, no grains and no grain boundaries. Indeed, nematics typically flow easily, making them an ideal candidate for exploring liquid crystalline drops, shells or fibers. To describe the long-range orientational order and analyze how it gives rise to the anisotropic physical properties, one introduces the director, abbreviated  . It indicates the direction along which the molecules tend to align, thus the principal symmetry axis of the phase. Because there are equally many molecules 'pointing upwards' as are 'pointing downwards' in an averaging ensemble, +
. It indicates the direction along which the molecules tend to align, thus the principal symmetry axis of the phase. Because there are equally many molecules 'pointing upwards' as are 'pointing downwards' in an averaging ensemble, + and -
and - are indistinguishable. This is often expressed by the director sign invariance, formalized as
are indistinguishable. This is often expressed by the director sign invariance, formalized as  . More specifically, the director can be said to be a signless pseudovector.
. More specifically, the director can be said to be a signless pseudovector.
Figure 1. Cartoon of the order in a nematic phase of rod-like mesogens (left), aligning on the average along the director  , without any long-range positional order. The right drawing illustrates the parameters required for calculating the orientational order parameter according to (1). The polar angle β expresses the deviation of a certain molecule from
, without any long-range positional order. The right drawing illustrates the parameters required for calculating the orientational order parameter according to (1). The polar angle β expresses the deviation of a certain molecule from  and the azimuthal angle φ defines the deviation direction. The variable φ does not appear explicitly in (1) but it is implicit in the pointed brackets, which express averaging over all three space dimensions.
and the azimuthal angle φ defines the deviation direction. The variable φ does not appear explicitly in (1) but it is implicit in the pointed brackets, which express averaging over all three space dimensions.
Download figure:
Standard image High-resolution image2.1.1. The nematic order parameter.
The long-range orientational order of LCs is quantified by an orientational order parameter (also called nematic order parameter) that in 3D takes the form:

The angle β describes the deviation in orientation away from  of a particular molecule in the averaging ensemble, see figure 1. The pointed brackets here express averaging over 3D space, thus integrating over the angles β and φ, defined in figure 1.
of a particular molecule in the averaging ensemble, see figure 1. The pointed brackets here express averaging over 3D space, thus integrating over the angles β and φ, defined in figure 1.
In 3D, the order parameter (1) is zero for total disorder, whereas for complete orientational order, S = 1. The isotropic-nematic transition in thermotropics is first-order, i.e. S jumps discretely at the phase transition from zero to a non-zero value, typically around S = 0.4. On further cooling, S increases, initially fast but rapidly approaching saturation around S = 0.6–0.7.
2.1.2. Optical anisotropy and the terminology for describing LC orientation.
The mesogen anisometry together with the long-range orientational order generally render LCs optically anisotropic, i.e. their refractive index  parallel to
parallel to  is different from that perpendicular to the director,
is different from that perpendicular to the director,  . The director defines the optic axis. The magnitude of optical anisotropy, the birefringence, is defined as
. The director defines the optic axis. The magnitude of optical anisotropy, the birefringence, is defined as  . Consequently, if
. Consequently, if  is the maximum refractive index,
is the maximum refractive index,  and we call the LC positive uniaxial (normal case for rod-shaped mesogens). Light passing through the sample will experience
and we call the LC positive uniaxial (normal case for rod-shaped mesogens). Light passing through the sample will experience  as the ordinary refractive index no, while the extraordinary index ne varies depending on the direction of light propagation,
as the ordinary refractive index no, while the extraordinary index ne varies depending on the direction of light propagation,  being the limiting value.
being the limiting value.
Like any birefringent material, LCs can affect the polarization  of light, changing it continuously between linear, elliptical and circular as well as changing the main oscillation direction or reversing rotation handedness. The effect disappears, however, if the light propagates along
of light, changing it continuously between linear, elliptical and circular as well as changing the main oscillation direction or reversing rotation handedness. The effect disappears, however, if the light propagates along  , because a birefringent material appears isotropic to light traveling along the optic axis: since light is a transverse wave,
, because a birefringent material appears isotropic to light traveling along the optic axis: since light is a transverse wave,  is then by necessity perpendicular to the optic axis, hence the light experiences only no. An LC sample that is prepared such that the director is perpendicular to its boundary is called homeotropic, a name that reflects the 'isotropic-like' appearance for light entering the sample at normal incidence, along the director. If a flat homeotropic LC sample is placed between crossed polarizers during observation and if the alignment persists throughout the sample (also the other boundary must thus be homeotropic), it appears black. When working with curved samples, like those considered in this review, the meaning of the term 'homeotropic' as director perpendicular to the boundary is carried over. Note, however, that the curvature then means that light will generally not enter the sample along the director, and the curved sample will thus not (except in certain points) appear black.
is then by necessity perpendicular to the optic axis, hence the light experiences only no. An LC sample that is prepared such that the director is perpendicular to its boundary is called homeotropic, a name that reflects the 'isotropic-like' appearance for light entering the sample at normal incidence, along the director. If a flat homeotropic LC sample is placed between crossed polarizers during observation and if the alignment persists throughout the sample (also the other boundary must thus be homeotropic), it appears black. When working with curved samples, like those considered in this review, the meaning of the term 'homeotropic' as director perpendicular to the boundary is carried over. Note, however, that the curvature then means that light will generally not enter the sample along the director, and the curved sample will thus not (except in certain points) appear black.
The geometry orthogonal to homeotropic, where  is in the plane of the sample boundary, is called planar. If the sample is flat and if also the opposite boundary promotes the same planar alignment, such that
is in the plane of the sample boundary, is called planar. If the sample is flat and if also the opposite boundary promotes the same planar alignment, such that  is uniform throughout the sample, the full birefringence
is uniform throughout the sample, the full birefringence  is experienced by light entering at normal incidence. Inside the LC the light is split up into two eigenmodes with polarization perpendicular and parallel to
is experienced by light entering at normal incidence. Inside the LC the light is split up into two eigenmodes with polarization perpendicular and parallel to  , respectively, experiencing the refractive indices
, respectively, experiencing the refractive indices  and
and  . Homeotropic and planar anchoring are the two limiting cases of anchoring, but the anchoring conditions can often promote an arbitrary tilt of
. Homeotropic and planar anchoring are the two limiting cases of anchoring, but the anchoring conditions can often promote an arbitrary tilt of  out of the interfacial plane. A tilt of 0° corresponds to planar alignment, a tilt of 90° is homeotropic, whereas we here refer to anchoring with any other inclination simply as tilted.
out of the interfacial plane. A tilt of 0° corresponds to planar alignment, a tilt of 90° is homeotropic, whereas we here refer to anchoring with any other inclination simply as tilted.
For curved samples the situation is again more complex. As for the term 'homeotropic', the terms 'planar' and 'tilted' are carried over in the sense of how  is oriented with respect to the sample boundary. A planar interface thus has the director in the boundary plane, regardless of how this curves. This means that, across the surface of a planar-aligned curved sample,
is oriented with respect to the sample boundary. A planar interface thus has the director in the boundary plane, regardless of how this curves. This means that, across the surface of a planar-aligned curved sample,  and thus the optic axis change direction with respect to the light propagation. The resulting optical behavior is very different compared to a planar flat sample. We refer the reader to an optics textbook for a deeper analysis, here settling by pointing out that the effective birefringence in most points is lower than for a flat planar sample, the difference depending on the inclination of
and thus the optic axis change direction with respect to the light propagation. The resulting optical behavior is very different compared to a planar flat sample. We refer the reader to an optics textbook for a deeper analysis, here settling by pointing out that the effective birefringence in most points is lower than for a flat planar sample, the difference depending on the inclination of  in each point. The reduction in
in each point. The reduction in  is partially compensated by an increased length of light passage through the curving LC. For a shell, moreover, we frequently have top and bottom surfaces and—as discussed in section 3.3—both contribute to the birefringence, even if only one of them is in focus.
is partially compensated by an increased length of light passage through the curving LC. For a shell, moreover, we frequently have top and bottom surfaces and—as discussed in section 3.3—both contribute to the birefringence, even if only one of them is in focus.
If light propagates perpendicular to a uniformly planar-aligned LC, the orientation that  has within the sample plane—which is then equal to the light's polarization plane—is also very important for the optical effect of the LC. For tilted alignment the same holds for the orientation of the projection of
has within the sample plane—which is then equal to the light's polarization plane—is also very important for the optical effect of the LC. For tilted alignment the same holds for the orientation of the projection of  onto this plane, which we here call
onto this plane, which we here call  . Whenever the light polarization
. Whenever the light polarization  is along or perpendicular to
is along or perpendicular to  (or
(or  ), one of the two eigenmodes has zero amplitude, and the effect of the birefringence is lost. Therefore, when a sample is observed between crossed polarizers and
), one of the two eigenmodes has zero amplitude, and the effect of the birefringence is lost. Therefore, when a sample is observed between crossed polarizers and  or
or  (or
(or  or
or  ), it appears black. For all other polarizations both components exist, the birefringence changes the polarization state, and the sample typically appears bright between crossed polarizers, see figure 2.
), it appears black. For all other polarizations both components exist, the birefringence changes the polarization state, and the sample typically appears bright between crossed polarizers, see figure 2.
Figure 2. The schlieren texture of a flat nematic sample with degenerate planar alignment prevailing uniformly from one substrate to the other, observed between crossed polarizers. The dashed lines are sketches of the director field variations within the sample. Two topological defects are highlighted with grey spots, the upper one with strength s = 1 and the lower with strength s = 1/2. The texture photo was previously shown in [3]. Reproduced with permission from [3].
Download figure:
Standard image High-resolution imagePlanar alignment means that the director is in the sample boundary plane, and tilted alignment that it has a component  in that plane, but the terms say nothing about which orientation in this plane
in that plane, but the terms say nothing about which orientation in this plane  or
or  should adopt. With a solid substrate a preferred orientation can often be induced, for instance by rubbing the substrate in a specific direction, but many planar- or tilted-aligning interfaces induce what is called 'degenerate planar/tilted alignment', giving no preference for any particular direction within the interface plane. In a nematic LC subject to such boundary conditions, the direction of
should adopt. With a solid substrate a preferred orientation can often be induced, for instance by rubbing the substrate in a specific direction, but many planar- or tilted-aligning interfaces induce what is called 'degenerate planar/tilted alignment', giving no preference for any particular direction within the interface plane. In a nematic LC subject to such boundary conditions, the direction of  /
/ in the interface plane can vary smoothly as a function of location. Since
in the interface plane can vary smoothly as a function of location. Since  defines the optic axis, this means that such a spatially varying director field
defines the optic axis, this means that such a spatially varying director field  is recognized in the polarizing microscope through a characteristic schlieren texture, named after the German word for streak. An example is shown in figure 2. Softly curving black 'brushes' appear, often emanating from crosses or cusps that are defects in the director field (see section 3.3). Along a black brush,
is recognized in the polarizing microscope through a characteristic schlieren texture, named after the German word for streak. An example is shown in figure 2. Softly curving black 'brushes' appear, often emanating from crosses or cusps that are defects in the director field (see section 3.3). Along a black brush,  is parallel to one of the polarizers.
is parallel to one of the polarizers.
2.1.3. The viscous flow properties of nematics.
While nematics normally can flow easily, it makes a great difference if the flow is along or perpendicular to  , and, for the latter case, it also makes a difference if the flow velocity gradient is along or perpendicular to
, and, for the latter case, it also makes a difference if the flow velocity gradient is along or perpendicular to  . These three situations, depicted by three orthogonal director orientations
. These three situations, depicted by three orthogonal director orientations  ,
,  and
and  in figure 3, were investigated by the Polish physicist Marian Mięsowicz [4], after whom the three corresponding viscosities,
in figure 3, were investigated by the Polish physicist Marian Mięsowicz [4], after whom the three corresponding viscosities,  ,
,  and
and  are now called the Mięsowicz viscosities. The lowest viscosity is
are now called the Mięsowicz viscosities. The lowest viscosity is  , when the flow is along the director, whereas the highest is
, when the flow is along the director, whereas the highest is  , measured when the director is perpendicular to the flow but parallel to the flow velocity gradient. The third director orientation,
, measured when the director is perpendicular to the flow but parallel to the flow velocity gradient. The third director orientation,  , perpendicular to both flow and gradient, results in an intermediate viscosity
, perpendicular to both flow and gradient, results in an intermediate viscosity  , generally much closer to
, generally much closer to  than to
than to  . The Mięsowicz viscosities are typically on the order of a Poise, or 1kg m−1 s−1 in SI units.
. The Mięsowicz viscosities are typically on the order of a Poise, or 1kg m−1 s−1 in SI units.
Figure 3. To define the three Mięsowicz viscosities,  ,
,  and
and  , one considers an experiment of flow of nematic liquid crystal through, e.g. a tube; the dashed arrows on the left indicate the flow velocity along the tube, as a function of location. The director
, one considers an experiment of flow of nematic liquid crystal through, e.g. a tube; the dashed arrows on the left indicate the flow velocity along the tube, as a function of location. The director  is blocked by an external magnetic field, giving three possible orthogonal director orientations,
is blocked by an external magnetic field, giving three possible orthogonal director orientations,  ,
,  and
and  , with respect to the flow direction, each giving rise to the respective Mięsowicz viscosity.
, with respect to the flow direction, each giving rise to the respective Mięsowicz viscosity.
Download figure:
Standard image High-resolution imageThe Mięsowicz viscosities constitute the first approximation for understanding the viscous flow of LCs. If we make no effort to control the director orientation during flow,  will align nearly parallel to the flow to minimize viscous losses. The minimum viscosity is actually obtained for a slight offset, as a more rigorous treatment shows [5]. Flow alignment can be important in the study of drops, shells and fibers of LCs, as the sample preparation always involves flow. If the samples are prepared with the material in its nematic phase, the viscosity anisotropy will lead to a relatively uniform alignment during the process. Note, however, that for smectics (see section 2.2) the minimum dissipation is not along
will align nearly parallel to the flow to minimize viscous losses. The minimum viscosity is actually obtained for a slight offset, as a more rigorous treatment shows [5]. Flow alignment can be important in the study of drops, shells and fibers of LCs, as the sample preparation always involves flow. If the samples are prepared with the material in its nematic phase, the viscosity anisotropy will lead to a relatively uniform alignment during the process. Note, however, that for smectics (see section 2.2) the minimum dissipation is not along  but along the smectic layers. Moreover, in many cases the LC is brought into an isotropic state during sample preparation, by heating or by adding a solvent.
but along the smectic layers. Moreover, in many cases the LC is brought into an isotropic state during sample preparation, by heating or by adding a solvent.
2.1.4. Liquid crystal elasticity and deformations in the director field.
Liquid crystals, with nematics forming the clearest example, exhibit a type of elasticity that is unique to this materials class. This 'nematic elasticity' is fundamentally different from solid or rubber elasticity, since in this case there is no restoring force arising in response to deformation of the sample shape, but instead a restoring torque that builds up in response to deformation of the director field  .
.
In the elastic ground state of an achiral nematic (ignoring thermally activated fluctuations [1]) the director field is uniform, i.e.  is a constant, independent of location. A deviation from the uniform field costs energy, and this is what gives rise to nematic elasticity. This energy is quantified in the Oseen–Frank theory, based on Oseen's groundwork in the 1920s and the refinement, and introduction of modern terminology, by Frank in 1958 [2]. In the bulk of a nematic, any generic deformation from uniform
is a constant, independent of location. A deviation from the uniform field costs energy, and this is what gives rise to nematic elasticity. This energy is quantified in the Oseen–Frank theory, based on Oseen's groundwork in the 1920s and the refinement, and introduction of modern terminology, by Frank in 1958 [2]. In the bulk of a nematic, any generic deformation from uniform  can be described as a linear combination of three elementary elastic deformations: splay, twist and bend. These three fundamental distortions, defined graphically in figure 4, are independent of each other, such that no combination of twist and/or splay can compensate for a bend etc. The total free energy Fb related to bulk elastic deformations of the director field can thus be calculated by integrating a bulk energy density fb, containing one term each for splay, twist and bend, over the volume of the sample (if S is not uniform within the volume considered, a fourth term, saddle-splay, to be discussed in a moment, must be included as well):
can be described as a linear combination of three elementary elastic deformations: splay, twist and bend. These three fundamental distortions, defined graphically in figure 4, are independent of each other, such that no combination of twist and/or splay can compensate for a bend etc. The total free energy Fb related to bulk elastic deformations of the director field can thus be calculated by integrating a bulk energy density fb, containing one term each for splay, twist and bend, over the volume of the sample (if S is not uniform within the volume considered, a fourth term, saddle-splay, to be discussed in a moment, must be included as well):


Figure 4. Graphical definitions of the three elementary director field deformations splay, twist and bend, together with their corresponding terms in the elastic free energy density and their respective elastic constants K1, K2 and K3.
Download figure:
Standard image High-resolution imageReflecting its character as a source, the splay term in (2b) contains the divergence of the director field ( ), whereas the terms representing the two rotational distortions twist and bend contain the curl (
), whereas the terms representing the two rotational distortions twist and bend contain the curl ( ). Because each term is squared, the bulk elastic constants, K1 for splay, K2 for twist and K3 for bend, must all be positive, otherwise there would be no finite energy minimum.
). Because each term is squared, the bulk elastic constants, K1 for splay, K2 for twist and K3 for bend, must all be positive, otherwise there would be no finite energy minimum.
When considering strongly confined LC samples such as drops, shells and fibers, one must also consider the influence from the bounding interfaces. There are two contributions to the interfacial energy. First, as with any interface, there is an energy term given by the product of interfacial tension and the bounding area. However, since this is an LC the interfacial tension may depend on how  is aligned with respect to the boundary. We say that
is aligned with respect to the boundary. We say that  is anchored in a certain preferred orientation at the interface. This terminology should not be interpreted too literally, however, as we may have anything from very strong to very weak anchoring. The balance between surface anchoring and bulk elasticity will be discussed for the case of droplets in section 3.3.1. The anchoring energy is quantified by a parameter W. A common expression for this contribution to the interfacial energy is the Rapini–Papoular energy density (an area density, thus J/m2) [6, 7]:
is anchored in a certain preferred orientation at the interface. This terminology should not be interpreted too literally, however, as we may have anything from very strong to very weak anchoring. The balance between surface anchoring and bulk elasticity will be discussed for the case of droplets in section 3.3.1. The anchoring energy is quantified by a parameter W. A common expression for this contribution to the interfacial energy is the Rapini–Papoular energy density (an area density, thus J/m2) [6, 7]:

where the unit vector  denotes the preferred orientation of the director at the interface, and we let the index 'a' stand for 'anchoring'.
denotes the preferred orientation of the director at the interface, and we let the index 'a' stand for 'anchoring'.
The second interfacial energy contribution is the just mentioned saddle-splay term, which actually is an elastic energy related to director field distortion in the Oseen–Frank theory. As the name suggests, the term, quantified by the saddle-splay constant K24, relates to a deformation of the director field such that  is normal to a saddle (or potato chip) surface [8]. Such surfaces have negative Gaussian curvature, i.e. their two principal curvatures have opposites signs; a saddle curves upwards along the horse but downwards across the horse. The corresponding energy density is a pure divergence (
is normal to a saddle (or potato chip) surface [8]. Such surfaces have negative Gaussian curvature, i.e. their two principal curvatures have opposites signs; a saddle curves upwards along the horse but downwards across the horse. The corresponding energy density is a pure divergence ( ) term:
) term:

This means that its volume integral, required to calculate the corresponding energy, can be converted into a surface integral via the divergence theorem (Gauss' theorem), provided that K24 is constant within the integration volume:

Note that the integrand in the last term in (5) is not f24, as defined in (4), which is a volume energy density, J/m3. Compiling the above, we can obtain the total free energy (in the absence of fields and for constant K24 within the sample volume) as [7]:

A key difference between the F24 term and the other contributions to the free energy is that F24 enters with negative sign. In other words, while any deformation described by Fb raises the free energy, as does any increase in interfacial area, captured by  , a saddle-splay deformation of the bounding interface actually decreases the energy if K24 > 0. This seems to be the case for all materials that have been experimentally studied so far with respect to saddle-splay deformation.
, a saddle-splay deformation of the bounding interface actually decreases the energy if K24 > 0. This seems to be the case for all materials that have been experimentally studied so far with respect to saddle-splay deformation.
Because the saddle-splay term in case of constant K24 does not influence the bulk energy far from boundaries it has often been ignored, as the sample size was reasonably large in many studies. Moreover, when the sample boundaries are flat, as in standard display-like devices, the F24 contribution vanishes entirely. In contrast, in our focus on small samples with strongly curved boundaries, where the interface influence can be considerable, the F24 contribution can play an important role. If K24 varies within the sample volume, which should be the case if the order parameter S is non-uniform, Gauss' theorem cannot be applied and the saddle-splay contribution must be treated as a bulk elastic energy. Such a situation is not as exotic as one might at first think; at temperatures near the clearing point a temperature gradient within the sample would lead to varying S and thus varying K24, but even at uniform temperature, S decreases in the close vicinity of a topological defect or an impurity. As droplets, shells and fibers frequently comprise topological defects, the saddle-splay term may need to be treated with its full bulk character2.
The four elastic constants are significant material parameters, with key relevance for understanding the behavior of strongly confined LCs. When the boundaries are strongly curved, as in the cases considered in this review, the boundary conditions often impose elastic distortions within the LC, thereby raising the free energy. The elastic constants have the dimension J/m = N, i.e. a force, with a magnitude typically in the pN range. Note that the saddle-splay energy density (4) contains no squared terms, hence the saddle-splay constant K24 can, in principle, take negative as well as positive signs, in contrast to the bulk elastic constants. For thermotropics, K1 and K2 often have about the same value whereas K3 is about twice that value. A commonly applied convenient approximation is  and K24 = 0, a simplification referred to as the 'one-constant approximation'.
and K24 = 0, a simplification referred to as the 'one-constant approximation'.
Since a spatial derivative yields an inverse length, each term in (2b) is proportional to 1/R2, where R is the characteristic length of the respective deformation. This is the pitch in case of a twist, the radius of curvature of a bend, and the distance to the 'source' of a splay deformation. Note that R is independent of location for a twist of constant magnitude, while, in contrast, the characteristic length of bend and splay is only defined once we have chosen a certain location. A bend or splay gets less apparent the further away from the center of curvature or 'source' that we are.
The 1/R2 dependence and the small magnitude of the elastic constants means that elastic deformations with large characteristic length cost very little energy, so little in fact that large-scale deformations are thermally generated in a bulk nematic LC in its ground state. This means that large-scale non-uniformities arise spontaneously in bulk LC samples, giving them a characteristic turbid character. A uniform  actually has higher free energy, which we may provide, e.g. by applying a magnetic field that aligns the LC [1].
actually has higher free energy, which we may provide, e.g. by applying a magnetic field that aligns the LC [1].
2.2. Thermotropic smectics
The defining characteristic of smectic LCs is a layered structure, see figure 5. The layering should not be understood too literally, however. While we often speak of 'layer boundaries' for practical purposes, these are mainly help concepts: there are no sharp layer boundaries in smectics, but rather a quasi-long-range electron density modulation along one direction [9]. In the smectic-A phase, abbreviated SmA, the density modulation is along the director, i.e.  is identical to the smectic layer normal
is identical to the smectic layer normal  . The modulation can, however, also develop along an arbitrary angle with respect to
. The modulation can, however, also develop along an arbitrary angle with respect to  , which means that the director tilts in the layers. The most imported tilted smectic is the smectic-C phase, SmC.
, which means that the director tilts in the layers. The most imported tilted smectic is the smectic-C phase, SmC.
Figure 5. Schematic 2D drawings of the two most important smectic phases. Mesogens are drawn as ellipses, layer boundaries with dashed lines. Due to the tilt in the SmC phase of  with respect to the layer normal
with respect to the layer normal  , by an angle θ, the layer thickness dC is smaller than the layer thickness dA in the SmA phase.
, by an angle θ, the layer thickness dC is smaller than the layer thickness dA in the SmA phase.
Download figure:
Standard image High-resolution imageThe SmC tilt angle, normally given the symbol θ, is generally temperature dependent, often approaching zero on heating towards a SmA phase, while it at lower temperatures may saturate in the range 20–30°. The exception is if the SmC phase follows on cooling directly from an N phase or from the isotropic liquid state; then θ is often large (around 45°) and close to temperature-independent. The same holds in case of a transition from a SmA phase with strong first-order character. There are several versions of the basic smectic-C-type structure, distinguished by different interlayer tilting direction correlation schemes (see e.g. [10]). In the fundamental SmC phase the tilt in adjacent layers is in the same direction.
The magnitude of tilt θ critically influences the free energy of a SmC phase, but the tilting direction has no impact on the energy. Any direction is thus equally good, yielding a range of degenerate SmC states that define a cone (the SmC tilt cone), with opening angle  and symmetry axis along
and symmetry axis along  . Basically, the smectic layer thickness is the projection of the average mesogen length on
. Basically, the smectic layer thickness is the projection of the average mesogen length on  (taking conformational disorder into account [10]), see figure 5(b).
(taking conformational disorder into account [10]), see figure 5(b).
The Oseen–Frank elasticity theory was developed for nematics but it can be extended to phases with partial positional order. One must then take into account the special restrictions imposed on  by the symmetry of each phase. Twist and bend are incompatible with the constant layer thickness in the SmA phase. In contrast, the phase is compatible with director splay, and rolling-up of SmA layers into a splayed director configuration frequently occurs.
by the symmetry of each phase. Twist and bend are incompatible with the constant layer thickness in the SmA phase. In contrast, the phase is compatible with director splay, and rolling-up of SmA layers into a splayed director configuration frequently occurs.
Although SmC is less symmetric than SmA it allows more fluctuations in  . Tilting gives a new freedom (tilt direction) that enables deformations which do not interfere with the layered structure. In fact, the projection of
. Tilting gives a new freedom (tilt direction) that enables deformations which do not interfere with the layered structure. In fact, the projection of  onto the layer plane (this projection is often called the C-director,
onto the layer plane (this projection is often called the C-director,  ) behaves similar to the ordinary director in the nematic. The characteristic texture of a quasi-homeotropic SmC sample therefore reminds of the schlieren texture of a planar-aligned nematic, the changing curvature of the schlieren reflecting variations in
) behaves similar to the ordinary director in the nematic. The characteristic texture of a quasi-homeotropic SmC sample therefore reminds of the schlieren texture of a planar-aligned nematic, the changing curvature of the schlieren reflecting variations in  . There are some important differences in terms of which topological defects (see section 3.3) can develop, however, because the sign invariance of the director,
. There are some important differences in terms of which topological defects (see section 3.3) can develop, however, because the sign invariance of the director,  , does not apply to the C-director (
, does not apply to the C-director (
 -
- ). The director tilting directions for
). The director tilting directions for  and -
and - are opposite, hence they correspond to different physical states.
are opposite, hence they correspond to different physical states.
2.3. Cholesterics (chiral nematics)
In recognition of the first chiral nematic-forming compounds being cholesterol derivatives, we often use the term cholesteric as an alternative name for chiral nematic. The phase can consequently be abbreviated either Ch or N*, where the star signifies chirality. The key expression of chirality is a helical modulation of  in the N* ground state, see the schematic illustration in figure 6. The helix axis, often chosen as
in the N* ground state, see the schematic illustration in figure 6. The helix axis, often chosen as  , is perpendicular to
, is perpendicular to  . The period, generally referred to as pitch p, is defined as the distance over which
. The period, generally referred to as pitch p, is defined as the distance over which  makes a 2π rotation. Due to the director sign invariance the physical properties repeat along
makes a 2π rotation. Due to the director sign invariance the physical properties repeat along  with a period p/2.
with a period p/2.
Figure 6. In chiral nematics the director is modulated helically, with a pitch p, along an axis  that is everywhere perpendicular to
that is everywhere perpendicular to  . Reproduced from [11]. CC BY 3.0.
. Reproduced from [11]. CC BY 3.0.
Download figure:
Standard image High-resolution imageIn the ground state the pitch has a well-defined value p0, sometimes called the natural pitch. This helical ground state is incompatible with (2b), which models a non-chiral nematic and thus indicates that any twist would raise the free energy. But for a cholesteric phase a non-helical state raises the free energy, as would any helix pitch different from p0. The free energy density expression must therefore be modified, extending the achiral twist term slightly to express the spontaneous twist:

The added term  is the wave vector of the spontaneous cholesteric helix. If the tendency to twist is weak, q0 is small and the term in (7) does not significantly affect the elastic energy density. For strong spontaneous twist, however, typically with the pitch on the same order as the wavelength of visible light or smaller, the added term in (7) can have a considerable impact.
is the wave vector of the spontaneous cholesteric helix. If the tendency to twist is weak, q0 is small and the term in (7) does not significantly affect the elastic energy density. For strong spontaneous twist, however, typically with the pitch on the same order as the wavelength of visible light or smaller, the added term in (7) can have a considerable impact.
Chirality has several important consequences for the physical properties of LC phases, sometimes related to the helical modulation, sometimes in general to the loss of mirror symmetry [12, 13]. Here we will restrict ourselves to discuss the effect of the helix on the optical properties of cholesterics, which is probably the most striking chirality expression. For more detailed information on chiral LCs, see, e.g. the book by Kitzerow and Bahr [13]. A good derivation of the optical properties of cholesterics can be found in a text by Priestly [14].
If p0 is short, on the order of 300 nm,  of the phase changes sign compared to the non-helical analog, and the helix axis
of the phase changes sign compared to the non-helical analog, and the helix axis  becomes the optic axis. Moreover, such a short-pitch cholesteric typically shows selective reflection of visible light incident along
becomes the optic axis. Moreover, such a short-pitch cholesteric typically shows selective reflection of visible light incident along  , turning the sample iridescently colored, the color depending on the viewing angle as well as on p0. In modern terminology, the cholesteric LC intrinsically exhibits a photonic band gap. The reflected light is circularly polarized with the same handedness as the helix, whereas the opposite handedness of circularly polarized light is transmitted.
, turning the sample iridescently colored, the color depending on the viewing angle as well as on p0. In modern terminology, the cholesteric LC intrinsically exhibits a photonic band gap. The reflected light is circularly polarized with the same handedness as the helix, whereas the opposite handedness of circularly polarized light is transmitted.
The helical modulation of  leads to a periodic modulation along the direction of light propagation of the refractive index, as long as the light does not enter perpendicular to
leads to a periodic modulation along the direction of light propagation of the refractive index, as long as the light does not enter perpendicular to  . Although the helix periodicity is p0 the optical periodicity along the helix axis is half of this, since already a 180° turn of
. Although the helix periodicity is p0 the optical periodicity along the helix axis is half of this, since already a 180° turn of  takes us back to an optically equivalent situation. We can apply Bragg's geometrical method (figure 7), well known from x-ray diffraction, to obtain an expression for the relation between the selectively reflected wavelength
takes us back to an optically equivalent situation. We can apply Bragg's geometrical method (figure 7), well known from x-ray diffraction, to obtain an expression for the relation between the selectively reflected wavelength  (as measured within the N* phase) and the viewing angle:
(as measured within the N* phase) and the viewing angle:

where m is an integer. For normal incidence (along  ) we can set m = 1 because only the fundamental reflection is present. Higher-order reflections would be the result of higher harmonics of the periodic structure but a sinusoidal modulation has no harmonics, only the fundamental. For oblique incidence the modulation is no longer perfectly sinusoidal since we are not following the helix, hence we then get weak higher-order reflections.
) we can set m = 1 because only the fundamental reflection is present. Higher-order reflections would be the result of higher harmonics of the periodic structure but a sinusoidal modulation has no harmonics, only the fundamental. For oblique incidence the modulation is no longer perfectly sinusoidal since we are not following the helix, hence we then get weak higher-order reflections.
Figure 7. The viewing angle dependence of the color of a cholesteric liquid crystal, summarized in the bottom cartoon, can be understood following a simple graphical procedure analogous to Bragg's law for x-ray diffraction, sketched at the top. Reproduced with permission from [3].
Download figure:
Standard image High-resolution imageSelective reflection occurs within a band of wavelengths that for normal incidence has the width  , where
, where  is the birefringence the sample would have had if the helix were unwound. The light wavelength in the N* phase is shortened with respect to the wavelength in vacuum by a factor equal to the average refractive index. For typical LCs this is about 1.5. Thus, if an N* phase appears green (∼550 nm wavelength in air) at normal incidence, the helix pitch must be around 370 nm.
is the birefringence the sample would have had if the helix were unwound. The light wavelength in the N* phase is shortened with respect to the wavelength in vacuum by a factor equal to the average refractive index. For typical LCs this is about 1.5. Thus, if an N* phase appears green (∼550 nm wavelength in air) at normal incidence, the helix pitch must be around 370 nm.
A decrease in the angle of incidence α of the light leads, according to (8), to a reduced wavelength of the selectively reflected light. This explains the observation that the color changes towards shorter wavelengths (from red to blue) if we tilt a cholesteric sample away from us, as schematically summarized in the lower part of figure 7. If the pitch is slightly too long to give selective reflection at normal incidence, we might start seeing colors under oblique incidence.
2.4. Liquid crystal elastomers
Liquid crystal elastomers (LCEs) comprise a unique class of materials due to their remarkable feature of dramatic shape change induced by a phase transition (usually the clearing transition). Experimental studies have reported up to ∼400% strain and stress of ∼10–100 kPa [15–17]. They are sometimes portrayed as artificial muscles although soft actuator is perhaps more appropriate; in his plenary talk at the ILCC 2002 (Edinburgh, UK) Pierre-Gilles de Gennes pointed out that LCEs are unlikely to match the force and speed of real biological muscles. Nevertheless, there are many interesting application scenarios, e.g. in soft robotics or other areas where shape change is required but ordinary rigid mechanics are not an option.
When you stretch a piece of rubber (the layman's term for elastomer) you are working against entropy. The polymer chains in the rubber, which cannot flow due to a limited amount of crosslinks, yet still have considerable conformational freedom, will adopt an isotropic random coil conformation in the ground state. As you stretch the rubber you reduce the number of accessible conformations, imposing the much reduced set in which the polymer is extended along the stretching direction. It is the entropic cost of this reduced conformational freedom that provides the restoring force that brings the rubber back to its original shape when you release it.
In an LCE the polymer chains are stretched out into the extended subset of conformations even without any external force applied. The extension is along  ; the long-range orientational order of the LC state, with the resulting macroscopic anisotropic physical properties, restricts the conformational freedom of the polymer chains to fluctuate perpendicular to
; the long-range orientational order of the LC state, with the resulting macroscopic anisotropic physical properties, restricts the conformational freedom of the polymer chains to fluctuate perpendicular to  , and promotes alignment along
, and promotes alignment along  . But just like when you release a stretched piece of ordinary rubber, the polymer chains will rearrange into their preferred set of isotropic conformations if the stretching force disappears. With an LCE this corresponds to heating above the clearing point of the LC phase, or otherwise inducing the transition into an isotropic state. The interesting thing is that, because the system is lightly crosslinked, this change of conformation brings with it a change in macroscopic sample shape, as schematically illustrated in figure 8. The process is fully reversible, so when the sample is brought back into the LC state, the shape reverts as well. There are a number of excellent reviews of LCEs and their actuation behavior [17–23]. As we here can only give a very brief introduction to the basic concept we refer the interested reader to these texts for more details.
. But just like when you release a stretched piece of ordinary rubber, the polymer chains will rearrange into their preferred set of isotropic conformations if the stretching force disappears. With an LCE this corresponds to heating above the clearing point of the LC phase, or otherwise inducing the transition into an isotropic state. The interesting thing is that, because the system is lightly crosslinked, this change of conformation brings with it a change in macroscopic sample shape, as schematically illustrated in figure 8. The process is fully reversible, so when the sample is brought back into the LC state, the shape reverts as well. There are a number of excellent reviews of LCEs and their actuation behavior [17–23]. As we here can only give a very brief introduction to the basic concept we refer the interested reader to these texts for more details.
Figure 8. The working principle of actuation of a nematic liquid crystal elastomer (LCE). In the nematic ground state (left) the polymer chains are stretched out along  in an entropically unfavored reduced set of conformations. Upon inducing the phase transition into the isotropic phase (right), the anisotropic environment disappears and the polymer chains adapt the preferred isotropic random coil average conformation. The crosslinks couple this conformational change to a macroscopic sample shape change, with compression along the original
in an entropically unfavored reduced set of conformations. Upon inducing the phase transition into the isotropic phase (right), the anisotropic environment disappears and the polymer chains adapt the preferred isotropic random coil average conformation. The crosslinks couple this conformational change to a macroscopic sample shape change, with compression along the original  and expansion in both orthogonal dimensions. Reproduced from [21] John Wiley & Sons. Copyright © 2010 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
and expansion in both orthogonal dimensions. Reproduced from [21] John Wiley & Sons. Copyright © 2010 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Download figure:
Standard image High-resolution imageLCEs may be subdivided into three main classes [17, 21, 24], differing in the generic chemical structure, see figure 9. In main chain LCEs, the mesogens are part of the polymer chain, whereas they are attached as pendants to the polymer chain in side chain LCEs. The latter are further subdivided into side-on and end-on versions, referring to the attachment point within the mesogen to the polymer chain.
Figure 9. Schematic drawings of the three main types of LCEs, together with example mesogenic monomers for each case; main chain LCE (the example structure is studied in Ahir et al [25]), side-on side chain LCE (example structure studied in Naciri et al [26]) and end-on side chain LCE (example structure studied in Finkelmann et al [27]).
Download figure:
Standard image High-resolution imageA prerequisite for the operation of LCEs is that  is uniform in the ground state. Often this is achieved by starting with a liquid crystalline but non-polymeric mixture of low molar mass precursors. This mixture can be aligned by placing it in contact with substrates coated with an aligning layer [28–30], applying a magnetic[31–33] or electric field [34], or subjecting it to shear flow [35–37]. The precursor mixture typically consists of reactive mesogens, such as the acrylate mesogens exemplified in Figure 9, a small amount of diacrylate crosslinkers, and often a suitable photoinitiator. Then polymerization and crosslinking can be initiated by UV illumination after the desired uniform alignment has been ensured (in case of alignment by shear flow, photopolymerization must be initiated during shearing). Using photosensitive mesogenic components in the mixture, also the alignment can be achieved by UV illumination, in that case using linearly polarized UV light [23, 38, 39].
is uniform in the ground state. Often this is achieved by starting with a liquid crystalline but non-polymeric mixture of low molar mass precursors. This mixture can be aligned by placing it in contact with substrates coated with an aligning layer [28–30], applying a magnetic[31–33] or electric field [34], or subjecting it to shear flow [35–37]. The precursor mixture typically consists of reactive mesogens, such as the acrylate mesogens exemplified in Figure 9, a small amount of diacrylate crosslinkers, and often a suitable photoinitiator. Then polymerization and crosslinking can be initiated by UV illumination after the desired uniform alignment has been ensured (in case of alignment by shear flow, photopolymerization must be initiated during shearing). Using photosensitive mesogenic components in the mixture, also the alignment can be achieved by UV illumination, in that case using linearly polarized UV light [23, 38, 39].
Another solution is the two-step polymerization introduced by the Finkelmann group, [40, 41] producing the very first LCEs after they had been predicted by de Gennes [42]. An intermediate main-chain polymer is produced in a first step of incomplete polymerization. Because the sample is now polymeric, uniaxial stretching can align  throughout the sample. Then, under the influence of the aligning mechanical field, the second polymerization and crosslinking step is triggered, which fixes the ground state orientation and produces the LCE film. This approach has the limitation that the resulting elastomer still remains somewhat mechanically constrained due to the presence of sharp domain boundaries, and it is difficult to remove excessive random crosslinks which persist [43].
throughout the sample. Then, under the influence of the aligning mechanical field, the second polymerization and crosslinking step is triggered, which fixes the ground state orientation and produces the LCE film. This approach has the limitation that the resulting elastomer still remains somewhat mechanically constrained due to the presence of sharp domain boundaries, and it is difficult to remove excessive random crosslinks which persist [43].
Following the Finkelmann group principle, Yakacki and co-workers recently introduced a convenient approach to prepare LCE actuators that uses solely commercially available components [44]. The LCE formation here follows a two-stage thiol-acrylate Michael addition and photopolymerization reaction. The approach is attractive as it opens for low-cost and large-scale LCE synthesis without requiring in-house synthetic chemistry facilities.
When producing LCEs in shape of droplets, shells or fibers, the requirement on uniform alignment may be fulfilled in alternative ways, since the production method and/or the sample geometry impose a specific director field. External alignment fields or substrates may not be necessary (in fact, it may even be impossible to apply them) and some rather interesting curved LCE actuators can be realized with relative ease. This will be further discussed in section 3.4.
Heating is not the only means of inducing the phase transition that triggers actuation. A powerful method is to incorporate dyes that change shape between rod- and kink-shaped upon illumination with light of adequate wavelength. [19, 45] The most common choice is azo dyes, which switch from a rod-shaped trans-isomer in the dark state to a kinked cis-isomer upon illumination by UV-light. Visible light illumination speeds up the reverse isomerization, back to the trans state, allowing switching in both directions using light with different wavelengths [46]. Because the cis-isomer disturbs the liquid crystalline ordering, all LC-related phase transitions, including the clearing point, are brought down to lower temperatures by the presence of cis-isomer azo dye, compared to when the dye is in its rod-shaped trans-isomer. The latter isomer is fully compatible with the long-range order. With the right amount of azo dye one can thus modulate the clearing point between above room temperature without UV illumination and below room temperature during UV illumination. This means that light can trigger the LCE actuation, not by heating, but by dynamically changing the phase diagram.
3. Liquid crystal shells and droplets
We now have the required basic knowledge about LCs and LCEs to discuss the effects of varying types of confinement. This section is devoted to spherical confinement, in droplets and shells, whereas section 4 covers cylindrical confinement. In section 3.1 we introduce the microfluidic production technique, which has revolutionized our capability of producing droplets and shells with high precision and reproducibility. This is followed by a survey of options for making LC spheres, including but not limited to microfluidics, how to stabilize them and at the same time control the alignment (section 3.2.1), and how to tune the size and thickness of shells via osmosis (section 3.2.2).
Section 3.3 deals with topological defects in LC spheres. After defining the key concepts for describing and quantifying topological defects we continue with surveying the experimental and simulation data on nematic, cholesteric and SmA/SmC droplets and shells. We discuss actuators made by polymerizing LC droplets and shells into LCEs, followed by an overview of application opportunities of short-pitch N* spheres in security, ending the section with a quick look at the role of droplets and shells in the emerging field of active LCs.
3.1. Microfluidics in a nutshell
The emergence of microfluidics started around the 1980's from the miniaturisation of flow geometries through micro- and nano-fabrication technologies [47–49]. Microfluidics is a rapidly growing multidisciplinary field, where physical, biological, chemical and engineering sciences converge into a single platform. It deals with the process and manipulation of fluids in channels with dimensions of tens of microns [48, 50–52]. Consequently, the surface to volume ratio increases in microfluidic systems, thus inertial forces are often negligible in comparison to viscous, electrostatic/electrodynamic, or surface tension forces. Especially, the surface forces are crucial for regulating the fluid flow in microfluidic devices [53]. Typical values of the Reynolds number, Re, which is a dimensionless number that relates the inertial to the viscous forces, are less than 10 for microfluidic flows [54, 55].
The revolutionary growth of the microfluidics field was triggered by the advancement of a lithography technique originated from the Whitesides group, known as soft lithography. The term soft refers to the design of channels using a soft elastomer, typically polydimethylsiloxane, or PDMS. The PDMS based soft lithography system has several advantages. It is easy to design and fabricate various flow patterns, from simple to complex and multiphase. PDMS is inexpensive, optically transparent for microscopy and permeable to gases, the latter aspect crucial for microbiological culture [52]. Thus, soft lithography is rapidly spreading in various research fields like diagnostics and biological research [56], fluid physics [57–60], chemical synthesis [61], the study of infectious diseases and preventive medicine [62, 63] and many other interdisciplinary research fields [52].
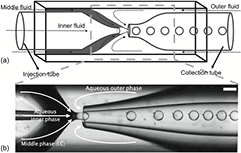
When chemical and thermal stability is required, alternative materials to PDMS are needed, such as glass, steel or silica [52]. A completely different design for microfluidics, based on nested glass capillaries with circular and square cross sections, respectively, was developed in the Weitz group. The basic principle for this method, which allows easy production of multiple emulsions with excellent control, is shown in figure 10. Since the outer diameter of the tapered cylindrical capillaries matches the inner side length of the square one, all capillaries are easily aligned in a concentric fashion. An inner (often aqueous) phase, which is immiscible with the middle phase, is injected through the left cylindrical capillary. The middle phase is flown in the same direction, through the corner spaces between cylindrical and square capillaries. While the two phases are co-flowing, they meet a counter-flowing outer phase, also immiscible with the middle phase (also the outer phase is often aqueous), introduced from the opposite side, again via the corner spaces between cylindrical and square capillaries. The pressure of the outer fluid flow-focuses the co-flowing liquids as a narrow jet [64, 65]. The interfacial tension between the middle and outer fluids causes breaking of the stream into shells via the Rayleigh–Plateau instability. Several modifications of the basic device are possible, the one depicted in figure 10 yielding a double emulsion. If a simple emulsion of droplets is preferred, the same device can be used with the flow rate of the inner fluid reduced to zero.
Figure 10. (a) Schematic illustration of the nested glass capillary microfluidic device for generating double emulsions from coaxial jets. Two tapered cylindrical glass capillaries are inserted into a square capillary, its inner side length identical to the outer diameter (∼1 mm) of the cylindrical capillaries. Injection and collection tubes are tapered using a micropipette puller, in order to ensure the desired constriction size, and a micro forge is then used to cut off the tips and establish the orifices. The middle fluid must be immiscible with the inner as well as the outer fluid, and interface stabilisers are added to prevent coalescence of the dispersed phase. (b) Liquid crystal shell production. The shells in this example are about 130 μm in diameter and below 3 μm in thickness and there are small satellite droplets next to each individual shell. The scale bar is 200 μm.
Download figure:
Standard image High-resolution imageCompared to the PDMS-based microfludic set-up, a glass micro capillary device has the advantage of reusability, thanks to its chemical resistance, and it does not suffer from swelling problems when working with organic solvents. A disadvantage is the difficulty in designing curved flow patterns. So far, the nested glass capillary technique dominates over PDMS-based microfluidics when the target is to prepare LC droplets and shells. Irrespective of the type of microfluidic device, the fluids are generally injected into the different channels by syringe pumps or pneumatic control units specially designed for microfluidics. The manipulation of multiphase flows in both systems enables generation of mono disperse bubbles [66], droplets [67], shells [68, 69], micro reactors for biology and medicine and various chemical reactions [56, 61–63, 70, 71].
To make LC droplets or shells, the LC is the disperse phase while the continuous phase is isotropic. It is worth mentioning that fascinating effects can also be seen when flowing LC as a continuous phase in microchannels. This brings novel flow profiles generated from the combination of surface anchoring and topological flow constraints within the channel, which are not observed with an isotropic continuous phase. As with conventional flat glass substrates, the alignment of an LC in a PDMS flow channel can be controlled by treating the channel walls chemically for either homeotropic or planar alignment, and even combinations of opposing alignment on different walls can be obtained by combining chemical alignment agents and plasma treatment and/or leave one side open to air [72, 73].
The different possibilities for surface anchoring combinations and the freedom to vary the channel aspect ratio (width/depth) open a playground for the creation of various topological constraints. In this way one can trigger the formation of topological point or line defects in nematics, which in turn are useful for guided transportation of micro-scale objects and tunable flow shaping [73–75]. Further interesting possibilities arise with SmA liquid crystals in rectangular channels, as reported by several research groups [76–78]. Here, the main focus is on inducing arrays of focal conic defects with controlled size and locations, again using different anchoring conditions and channel geometries to tune the final defect arrangements. Besides the channel-confined focal conic defect structures, Shojaei et al reported the formation of a two-dimensional network of the same defect structures in a thin film of the SmA-forming LC 8CB using cracked PDMS films [77]. Here, the crack pattern is controlled by stretching the plasma treated PDMS film.
3.2. How to make liquid crystal shells and droplets using microfluidics
A typical way of producing LC droplets is preparing emulsions by dispersing liquid crystals in an immiscible liquid. Among numerous methods for the emulsion preparation, stirring or vortexing constitute quick and low-cost approaches. The drawback of these methods, crudely breaking the bulk liquid crystal into small droplets by mechanical agitation, is the difficulty in controlling the size and obtaining uniformity. A common alternative is ultrasonication, in which a strong oscillating shear flow is induced by pressure waves at ultrasonic frequencies. This technique can provide a somewhat narrower size distribution with smaller droplets, even below the micron scale, in form of a miniemulsion [79]. Yet, also with ultrasonication one is far from achieving monodispersity, and the non-uniform size further leads to Ostwald ripening, which reduces emulsion stability. The high interface curvature of a small droplet raises the solubility of the disperse phase, triggering molecular diffusion from small to large droplets.
With the coaxial microfluidic technology developed in the Weitz group, a new alternative appeared that enables the production of highly controlled monodisperse simple as well as multiple emulsions [68], the liquid crystal taking the role of the middle phase. Now, not only LC droplets of selectable size could be produced, but even thin shells of LC, where a few microns thick spherical layer of the desired liquid crystal material is surrounded by isotropic immiscible phases (typically aqueous) on both sides. The shell/droplet dimensions, i.e. diameter and thickness (in case of shells), can be adjusted by tuning the production parameters: capillary/orifice size, flow rates, interfacial tension and viscosities of the fluids involved. The orifice sizes of the tapered cylindrical capillaries have a direct impact on the shell/droplet sizes. At low flow rate the resulting droplet/shell diameter can be estimated to be close to the orifice diameter [80].
However, the relative flow rates also play a critical role in controlling the shell/droplet sizes, even determining whether or not emulsion formation is at all possible. Utada et al distinguished between two different droplet-forming mechanisms in co-flowing Newtonian fluids, namely dripping and jetting modes [81]. Which of the two modes is active depends on the interplay between interfacial tension and viscous drag force, acting on the interface between middle and outer fluids. If the flow rates of the inner and middle phases are fixed, a high flow rate of the outer fluid increases viscous stress at the interface, eventually dominating over the interfacial tension such that a long stream of inner+middle phase is stabilized (jetting mode). In contrast, at lower flow rate of the outer fluid the inner complex stream is rapidly broken up into shells (dripping mode), because now the interfacial tension dominates. Even if liquid crystals are (weakly) non-Newtonian fluids, the basic drop-forming process is expected to be similar to that of Newtonian fluids [81]. On the other hand, the LC is most often brought to the isotropic state, for instance by heating, during production, turning it into a Newtonian fluid at this stage. Further tuning of shell/droplet size is possible via variations of interfacial tension (e.g. using surfactants) and viscosity [80, 82].
3.2.1. The connected problems of interface stabilization and liquid crystal alignment control.
The stabilization of liquid crystal shells/droplets can be ensured by adding interface stabilizers, also called emulsifiers, most often to the aqueous phases. Compared to water a thermotropic LC can be considered an oil phase, immiscible with water, thus the stabilizers are needed to reduce the interfacial tension between the phases. Without stabilizers, droplets would coalesce and shells would collapse into droplets. Importantly, the stabilizers may also play another key role, namely to determine the liquid crystal alignment.
The common choice for emulsifier/stabilizer is either an ionic surfactant, e.g. sodium dodecyl sulfate (SDS), or a water soluble polymer, e.g. polyvinylalcohol (PVA). At the water–LC interface, a surfactant adsorbs with its apolar aliphatic chain penetrating into the LC, promoting homeotropic alignment (see section 2.1.2) and thus a radial orientation of the director field in the shell/droplet. In contrast, a dissolved polymer like PVA in aqueous solution has a disordered random coil configuration which cannot be expected to promote a particular type of ordering in the LC. The polymer thus most likely acts solely as a stabilizer, leaving the LC-water interaction to determine  at the interface, which ends up being planar or possibly tilted. This is because the mesogens typically contain an aromatic core, and often also a cyano group, which can participate in hydrogen bonding with the surrounding water, whereas the aliphatic chains at the mesogen end are avoided by the water. In case of the shells, we can additionally achieve hybrid director alignment [83, 84] by imposing asymmetric boundary conditions at the interfaces to the LC. In this case we may use a surfactant in the inner phase and PVA in the outer, or vice versa.
at the interface, which ends up being planar or possibly tilted. This is because the mesogens typically contain an aromatic core, and often also a cyano group, which can participate in hydrogen bonding with the surrounding water, whereas the aliphatic chains at the mesogen end are avoided by the water. In case of the shells, we can additionally achieve hybrid director alignment [83, 84] by imposing asymmetric boundary conditions at the interfaces to the LC. In this case we may use a surfactant in the inner phase and PVA in the outer, or vice versa.
As a first approximation, we can consider stabilizers to be localized to the LC–water interface and the immiscible phases to be truly immiscible, i.e. the LC is in its pure state within the actual shell. Because the phase sequence of LCs is so sensitive to contaminants, however, it is easy to find evidence that this simplified picture is not quite true in practice. We recently reported that the clearing point of nematic shells of the commonly used mesogen 5CB is distinctly lower than that of the bulk LC [85]. Interestingly, the study revealed that all constituents of the surrounding aqueous phases can enter the shell to some extent, water, surfactant and glycerol, which is often added to the aqueous phases for density and viscosity tuning. Moreover, an alignment change was detected in a long-term experiment with shells that were initially hybrid-aligned thanks to preparation with surfactant in one aqueous phase and PVA in the other. Over the course of a few days, the alignment was transformed into fully homeotropic, demonstrating that the surfactant can pass through the LC shell and adsorb on the opposite side.
3.2.2. Osmotic control of shell thickness and diameter.
By varying the orifice sizes of capillaries, interfacial tensions, viscosities, flow rates etc during the microfluidic production, we can tune the diameter and thickness of LC shells over a considerable range. However, it is challenging to produce the shells with a diameter smaller than about a 100 μm or a thickness below a few μm. If a thinner and larger or smaller and thicker shell is desired, an elegant trick can be applied for post processing, introduced by Lopez-Leon and co-workers [87], involving osmosis. Because the LC is not impenetrable to water, the LC shell can act like a semipermeable membrane separating the inner and outer phases, and if these have non-equal compositions, an osmotic pressure will develop that drives water into or out of the shell's inner isotropic droplet.
Although it was not properly elucidated until the mid 19th century, osmosis is a very common phenomenon on Earth, playing an important role in many vital and central processes in biological systems [88]. Originally osmosis is used to describe the movement of a solvent across a semipermeable membrane towards a higher concentration of solute, which is driven by the chemical potential difference between the two sides of the membrane [88, 89]. The membrane can be solid or liquid and it can be formed by layers of cells, particles and molecules [88]. The permeability of the membrane depends not only on the size of holes in the membrane, compared to the size of the solvent molecules, but also on the polarity of the solvent molecules and their miscibility with the material making up the membrane.
Lopez-Leon and co-workers introduced osmosis into LC shell studies as a method to reduce the shell thickness by increasing the size of the inner droplets [87]. Water based solutions were used as the inner and outer phase with different salt concentrations. Compared with the salt, water is more miscible with the liquid crystal, so the water can flow from low salt concentration side to the side with high concentration by passing through the LC shell. The shell thickness change can happen in both directions: by giving the outer phase a higher salt concentration than the inner phase, water would flow from inside the LC to the outside, making the shell thicker and the diameter smaller. By tuning the thickness of the nematic LC layer, the elastic free energy related to the defect arrangement is changed, allowing the authors to control which defects are formed and how they are distributed across the shell, see section 3.3.4.
Osmosis was also used in our recent studies to help remove the oily streak defects in cholesteric shells with planar anchoring on both sides of the LC layer [86]. Instead of using salt content difference to establish an osmotic pressure, we used higher concentration of PVA in the inner droplets (15wt.%) than in the outer continuous phase (10wt.%). As a result, the shells were expanded and became thinner over the course of several hours, with a consequent rapid disappearance of oily streak defects (figure 11). Already after 12 h the shells are free of visible defects, which should be compared to about a week without osmosis. In the process of osmotic expansion, the shell diameter increased from about 180 μm–240 μm, and the shell thickness decreased from 27 μm to 11 μm.
Figure 11. Removal of oily streak defects in short-pitch cholesteric shells by osmotic thinning. Optical microscopy textures in transmission without analyser (a, focus on top of shell) and in reflection between crossed polarisers (b) of a cholesteric shell subjected to expansion and thinning by osmosis. The patterns are explained in section 3.5. Scale bar 100 μm. Image adapted from [86]. CC BY 4.0.
Download figure:
Standard image High-resolution image3.3. Topological defects in liquid crystal shells and droplets
Liquid crystal shells and droplets exhibit a large variety of director field configurations with intriguing textures and defect structures. Numerous experimental, theoretical and simulation studies have focused on the origin of this structural diversity and established a detailed picture of what director configurations can occur in nematic, cholesteric or smectic droplets and shells. While the respective equilibrium director field results from a sensitive interplay between interfacial and bulk properties (e.g. spatial dimension of the spherical confinement, surface curvature, anchoring conditions at the confining interfaces, bulk and surface elasticity or density mismatch of the constituting fluids), the principle reason for the formation of topological defects is the sperical confinement itself. When a liquid crystal volume is confined by a spherical boundary, the anchoring conditions at this interface impose topological constraints on the director field which unavoidably force topological defects to be formed [90, 91].
A topological defect constitutes a singularity in the local orientational order of the LC, which is depicted by the director field  . In the close vicinity of this singularity the liquid crystalline order is reduced and the scalar order parameter S decreases. In the core of the defect the order breaks down completely and the LC is isotropic. A topological defect cannot decay and the director field in its surrounding cannot be continuously transformed into a uniform director field with no singularities.
. In the close vicinity of this singularity the liquid crystalline order is reduced and the scalar order parameter S decreases. In the core of the defect the order breaks down completely and the LC is isotropic. A topological defect cannot decay and the director field in its surrounding cannot be continuously transformed into a uniform director field with no singularities.
An important distinction has to be made between topological defects confined to surfaces and topological bulk defects, see figure 12. Defects in the bulk are called hedgehogs and carry an integer topological charge of Q (see figures 12(a) and (b)) [91]. The magnitude of the bulk charge  is given by the fraction of all possible director orientations occuring within an imaginary sphere around the defect core. A detailed analytical description for the determination of the hedgehog charge can be found in references [91–93]. Since the nematic director is a sign-less pseudovector
is given by the fraction of all possible director orientations occuring within an imaginary sphere around the defect core. A detailed analytical description for the determination of the hedgehog charge can be found in references [91–93]. Since the nematic director is a sign-less pseudovector  , the sign of the hedgehog charge is degenerate in three-dimensional space, i.e. a positive defect can be continously transformed into a negative defect [94]. In this review we adopt the common practice that a radial hedgehog is given the topological charge Q = +1 whereas a hyperbolic hedgehog is designated with Q = −1 [95].
, the sign of the hedgehog charge is degenerate in three-dimensional space, i.e. a positive defect can be continously transformed into a negative defect [94]. In this review we adopt the common practice that a radial hedgehog is given the topological charge Q = +1 whereas a hyperbolic hedgehog is designated with Q = −1 [95].
Figure 12. Schematic representations of topological bulk defects (a) + (b), singular points confined to interfaces (c)–(g) and a disclination (h) in a nematic director field. Bulk defects (hedgehogs) are characterized by the bulk charge Q. We distinguish between (a) radial hedgehog defects with Q = +1 and (b) hyperbolic hedgehogs with Q = −1. Defects confined to surfaces carry a topological charge s, which can be integer (c)–(e) or half-integer (f)–(g). Half-integer surface defects induce defect lines (disclinations) in the bulk which connect two surface defects of similar sign (h). A misunderstanding commonly arises since for half-integer defects (f) + (g) the director representation in the confining interfaces (shown as grey planes in (h)) appears identical to the director representation in an arbitrary plane cutting through the line defect (dashed plane in (h)). However, for integer charge defects (c)–(e) the point singularity only exists in the confining interface; these defects do not induce the formation of line defects in the bulk. One should therefore be aware that the sketches (c)–(g) represent the director orientation as it appears in the 2D confining interface of a bounded nematic.
Download figure:
Standard image High-resolution imageIn contrast to hedgehogs, topological surface defects are confined to interfaces and cannot exist freely in the bulk (see figures 12(c)–(g)). This type of defect is characterized by a surface charge s, which is defined by the index of the director field projection onto the confining interface (see [91] or [93] for more details). The strict distinction between bulk charge Q and surface charge s is important: While hedgehogs with Q = 1 can exist both in the bulk and at the surface, their surface analogs with s = 1 cannot move inside the nematic bulk and are restricted to the interface [95]. Such surface defects with unity charge s are called boojums, inspired by the imaginary creature 'boojum' in Lewis Carroll's poem The hunting of the Snark [91]. Unlike bulk defects, surface defects can appear not only with integer but also with half-integer strength s. The strength of a surface defect is given by the ratio  with γ being the angle by which the director in the surface projection rotates along a path encircling the singularity [93].
with γ being the angle by which the director in the surface projection rotates along a path encircling the singularity [93].
Following this definition, the strength s of a topological surface defect in LCs can easily be determined by analyzing the polarizing microscopy texture surrounding the defect, see e.g. figure 2. The relationship between  and the number b of brushes pinned to the center of the singularity is given by
and the number b of brushes pinned to the center of the singularity is given by  . Consequently, defects in the center of four brushes hold a strength
. Consequently, defects in the center of four brushes hold a strength  and defects with only two brushes hold a strength of
and defects with only two brushes hold a strength of  [93]. The sign of the defect strength can be determined by rotating the crossed polarizers: if the brushes rotate in the same sense the defect is positive, if it rotates in the opposite, it is negative. It should be mentioned that the sign of a surface defect can only be derived by following the Volterra process and is not part of the topological stability theory [96].
[93]. The sign of the defect strength can be determined by rotating the crossed polarizers: if the brushes rotate in the same sense the defect is positive, if it rotates in the opposite, it is negative. It should be mentioned that the sign of a surface defect can only be derived by following the Volterra process and is not part of the topological stability theory [96].
Despite being pinned to an interface, surface defects also cause director distortions in the bulk. In the case of a radial defect with s = 1, which is shown in figure 12(c), these distortions resemble one half of the director field around a hedgehog defect [91]. Beyond the surface charge s, this defect can therefore also be characterized by a bulk charge Q. Upon changing the boundary conditions from planar to homeotropic, a surface defect continously disappears and, when carrying a bulk charge of Q = +1, is transformed into a hedgehog defect [97], as illustrated in figure 13. Other types of surface defects with integer strength are shown in figures 12(d) and (e). The bulk distortions caused by (d) and (e) induce virtual lines of strong director deformation along which the director field escapes into the third dimension [98]. Although often referred to as 'defect lines', these lines lack a defect core in their center, hence they are not 'defects' in a strict sense. They typically connect two integer surface defects through the bulk.
Figure 13. Schematic drawing of the two distinct boojum transformations under changing boundary conditions from planar to homeotropic (adapted with permission from [97]). If the boojum carries the topological charges  , the defect dissolves from the interface and forms a hedgehog defect in the bulk. (a) In case the bulk charge Q of the boojum is zero
, the defect dissolves from the interface and forms a hedgehog defect in the bulk. (a) In case the bulk charge Q of the boojum is zero  , the defect gradually disappears upon reducing the tangential director field component at the interface (b).
, the defect gradually disappears upon reducing the tangential director field component at the interface (b).
Download figure:
Standard image High-resolution imageHalf-integer surface defects (f)–(h) play a special role among the configurations shown in figure 12: they induce stable line defects in the bulk of the liquid crystal, so called disclinations. Integer defect lines are not stable and the formation of a defect core is avoided by a director escape into the third dimension [98]. Disclinations can be subdivided into wedge and twist types [5], of which we will only consider the former in this review. The 'wedge' reflects the defect construction by insertion or removal of a wedge of matter following the Volterra process [96, 99]. Line defects occur in the bulk of the liquid crystal, but they typically end at a surface. While open-ended disclinations do not exist, defect lines can also close up into a loop, then existing separated from the surface. Such closed loops can be considered as hedgehogs with an extended core, an issue described in more detail in references [95, 100, 101] or with respect to defects in fibers in section 4.1. The determination of their topological charge then works accordingly to the determination of surface charges s in a virtual plane perpendicular to the disclinaton, while the bulk charge Q of the closed ring is unity [93].
The sum of all topological charges s and Q in a confined liquid crystal obey conservation laws, which are connected to the Euler characteristic of the confining surface [91]. For spherical confinement and planar or tilted alignment, the Poincaré-Hopf theorem requires a total topological charge of s = +2 on the surface, which corresponds to the Euler characteristic of a sphere [84, 102]. For homeotropic anchoring, having no director component in the interface, a total topological bulk charge of Q = +1 (half of the respective Euler characteristic) must be contained inside the spherical volume according to the Gauss-Bonnet theorem, while the total topological surface charge is zero [84].
Even without full knowledge of the bulk and interfacial properties of a liquid crystal shell or droplet, the thermodynamic ground state of the director configuration can be derived by energetic considerations. Any deformation in a uniform director field increases the elastic free energy as characterized by the Oseen-Frank free energy density (see (2b)). The director field is therefore driven towards a state that minimizes the total free energy given by (6) while still complying with the topological constraints imposed by the boundary of the spherical confinement [84, 103].
An important aspect of studying topological defects in LC shells and droplets by optical polarising microscopy has been emphasized by Liang et al [104]: while the optical setup can only be focused to a topological defect on one side of the shell or droplet, the birefringence of the other side, although being blurred, also contributes to the observed polarizing microscopy texture. This can render an analysis of the director field within the shell or droplet rather difficult. An ideal situation is given when the director field on the side currently out of focus is rather uniform, such that either the polarizer or the analyzer can be oriented in the same direction and the influence of birefringence from this side is minimized.
3.3.1. Nematic droplets.
Observable textures in nematic droplets differ for various droplet sizes and anchoring conditions and the respective equilibrium director field configuration strongly depends on bulk and surface energy contributions. The bulk elastic energy Fb scales linearly with the droplet radius R [91], while the surface energy Fs scales as  [105], where the coefficent W is the amplitude of the angular dependent anchoring energy from (3). Consequently, the energetic contribution of the interface dominates for large droplet radii. This relation might seem counterintuitive, since the ratio of surface area to bulk volume increases upon decreasing droplet radius and one might expect a dominating surface contribution for small droplets. The reason is the 1/R2 dependence of the bulk elastic energy density, and experimental observations confirm that influence of the topological constraints imposed by the interface vanishes for small droplet sizes. The director configuration is then determined solely by the bulk elasticity of the liquid crystal [105]. A critical radius Rc = K/W (in the one-constant approximation) with a transition from small droplet to large droplet behavior is, depending on the anchoring energy W and bulk elasticity K, in the order of 1 μm [91].
[105], where the coefficent W is the amplitude of the angular dependent anchoring energy from (3). Consequently, the energetic contribution of the interface dominates for large droplet radii. This relation might seem counterintuitive, since the ratio of surface area to bulk volume increases upon decreasing droplet radius and one might expect a dominating surface contribution for small droplets. The reason is the 1/R2 dependence of the bulk elastic energy density, and experimental observations confirm that influence of the topological constraints imposed by the interface vanishes for small droplet sizes. The director configuration is then determined solely by the bulk elasticity of the liquid crystal [105]. A critical radius Rc = K/W (in the one-constant approximation) with a transition from small droplet to large droplet behavior is, depending on the anchoring energy W and bulk elasticity K, in the order of 1 μm [91].
In small droplets (R < K/W) with homeotropic anchoring the bulk elastic energy enforces a defect and deformation-free uniaxial director configuration, which disregards the homeotropic boundary condition and the topological constraints related to it [105, 106]. A schematic representation of such a director configuration is shown on the top left side of figure 14. Upon increasing the droplet size, the surface contribution also increases and for R > Rc the homeotropic anchoring conditions impose a bulk charge Q of unity within the droplet [107]. The topological constraints imposed by the Gauss-Bonnet theorem are fullfilled by forming a radial director field with a hedgehog defect in the center of the droplet (see figure 14 top-right) [84, 107]. This centrosymmetric director field then typically relaxes away from the symmetric radial configuration to a lower energy twisted state, which appears as a spiraling cross between crossed polarizers [5, 107].
Figure 14. Schematic representation of the director configuration in nematic droplets. For homeotropic boundary conditions (top), decreasing the drop radius R below a critical value  induces a transition from a radial to a uniform director field. For such small droplet size, the energy penalty for disregarding the anchoring conditions is smaller than the energy gain from decreasing the elastic energy density in the bulk. For planar boundary conditions (bottom), a decrease of droplet size induces a transition from a bipolar configuration to a radial configuration. Reproduced from [105] with permission of The Royal Society of Chemistry.
induces a transition from a radial to a uniform director field. For such small droplet size, the energy penalty for disregarding the anchoring conditions is smaller than the energy gain from decreasing the elastic energy density in the bulk. For planar boundary conditions (bottom), a decrease of droplet size induces a transition from a bipolar configuration to a radial configuration. Reproduced from [105] with permission of The Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageNanometer-sized droplets with planar or tilted anchoring conditions exhibit a radial director configuration in equilibrium [108, 109], while a bipolar configuration is frequently observed in larger droplets (see figure 14, bottom). Tomar et al showed by numerical simulations that this transition from bipolar to radial upon decreasing droplet dimension is connected to the saddle-splay term (see (4) in section 2.1) in the elastic free energy [105]. For large nematic droplets (R > K/W) with planar or tilted anchoring the topological constraints expressed by the Poincaré-Hopf theorem require a total topological surface charge of s = +2 at the droplet interface. The liquid crystal typically meets these constraints by forming bipolar drops, which are characterized by two boojums with topological charge s = +1 separated by the maximum distance of a drop diameter [84]. The director field within the droplet is then aligned parallel between these two radial half hedgehogs, corresponding to pure splay deformation close to the defects and bend in the droplet bulk [103].
A second possible director configuration that fullfills the topological constraints, the concentric configuration with two bend disclinations of surface charge s = +1, is only observed for unusually low splay elastic constant, in comparison to the twist and bend constants [103]. The surface is here decorated by line rather than point defects, but—as stated in section 3.3—integer line defects are not stable. The line defect 'escapes in the third dimension' via a twisted configuration, yielding a virtual line defect connecting the two surface defects. There is no defect core, but the bulk is still much more distorted than in the usual bipolar configuration [110]. As shown by Fernández-Nieves and coworkers, this unstable concentric configuration is easily transformed into the stable bipolar configuration by applying external electric fields to align the director field [103]. The authors also show that a retransformation from bipolar to escaped concentric does not occur and contribute this observation to a significant energy barrier [111] between the two configurations and an overall lower energy for the bipolar configuration. According to their findings, only the large forces occuring during circular flow inside an LC droplet allow a transition from bipolar back to the escaped concentric configuration.
A continous transition between the bipolar and the radial director field configuration can be observed upon changing the anchoring conditions from planar to homeotropic or vice versa, as demonstrated by Volovik and Lavrentovich for large drops [91, 97]. The transformation may take place via a so-called axial configuration, in which the surface is already homeotropic but an equatorial defect ring allows a non-radial internal director field [91].
3.3.2. Cholesteric droplets.
The first description of cholesteric droplets dates back to Lehmann and Friedel [112] at the beginning of the 20th century, but only from the 1980s onwards a systematic study of the complex configurations in higher ordered liquid crystal droplets began [113]. In contrast to the nematic phase, the equilibrium director configuration in cholesteric droplets depends not only on the boundary conditions at the interface and the bulk elasticity, but it is also influenced by a factor qR, the product of the cholesteric helix wave vector (see section 2.3) and the droplet radius [113, 114]. The continuous twist allows for new types of disclinations in cholesteric liquid crystals, which can be categorized into the three classes  ,
,  and
and  [93, 115]. Half-integer and integer values for m characterize the winding number of the respective defect type, schematic representations of which are shown in figure 15.
[93, 115]. Half-integer and integer values for m characterize the winding number of the respective defect type, schematic representations of which are shown in figure 15.
Figure 15. Schematic representation of  ,
,  and
and  disclination lines in cholesteric liquid crystals. Half-integer and integer values for m characterize the winding number of the defect. The director orientation is represented by blue cylinders while the defect locations are indicated by red spheres. The core of the χ disclinations is depicted as a black line. Reproduced from [115] with permission of The Royal Society of Chemistry.
disclination lines in cholesteric liquid crystals. Half-integer and integer values for m characterize the winding number of the defect. The director orientation is represented by blue cylinders while the defect locations are indicated by red spheres. The core of the χ disclinations is depicted as a black line. Reproduced from [115] with permission of The Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageSince a smooth unwinding of the cholesteric helix yields the uniaxial order of the nematic phase, a continuous transition from the director field configuration of a cholesteric droplet towards that of a nematic droplet can be expected. For cholesterics with a long pitch that are confined to small droplets (qR < 1) with planar or tilted boundary conditions, Bezić and Žumer predicted an unwinding of the cholesteric helix and the formation of a bipolar structure as frequently observed for nematics [114]. Their model yielded that the director lies solely in the meridional planes of the droplet, which could not be confirmed by later experimental studies [116]. Instead, Xu and Crooker established a twisted bipolar model for cholesteric droplets, which differs from the bipolar model for nematics by higher twist within the droplet (see figure 16(a)). While in nematic bipolar droplets the twist is not intrinsic and decays exponentially from the surface towards the bulk, the model introduced by Xu and Crooker assumes a linear decay of twist [116].
Figure 16. Polarising optical micrographs of cholesteric droplets with planar boundary conditions. The value of qR, the helix wave vector multiplied by the droplet radius, continously increases from (a)–(e). For low qR (a), a twisted bipolar texture is observed. As qR increases ((b)–(f)), the configuration evolves towards the Frank-Pryce structure (e). This structure is characterized by a central hedgehog with an attached s = +2 disclination line. Reproduced from [113] (© Springer-Verlag 2011). With permission of Springer.
Download figure:
Standard image High-resolution imageFor larger cholesteric droplets with planar/tilted anchoring and/or short helix pitch (qR > 1) the Frank-Pryce structure is the most commonly observed configuration. This structure is shown in figure 16(e) and consists of an s = +2 disclination line of length R that connects a hedgehog in the center of the droplet with its surface [114, 117]. The configuration is also referred to as radial spherical structure or spherulitic texture [115]. This structure also attracted attention beyond liquid crystal research, as it represents an intriguing analogy to an elementary magnetic charge known as Dirac monopole [91, 118]. Several studies report that the regular Frank-Pryce structure structure can relax into the so-called escaped Frank-Pryce structure, in which the director escapes along the direction of the disclination line [116, 119]. Bouligand and Livolant found that the Frank-Pryce structure with concentric layers can sometimes also occur with the defect line covering the whole diameter of the droplet [120]. Droplets with such structure show cylindrical symmetry as the disclination line connects two diametrical surface defects of topological charge s = +1 [114]. Frank-Pryce structures with a curved defect line connecting two non-antipodal s = +1 surface defects have only rarely been reported [120]. When a cholesteric droplet with Frank-Pryce structure is observed along the disclination line, one sees either a double spiral texture (usually for a defect line of length R) or concentric circles (typically for defect lines of length 2R or curved singular defect lines) [120].
Besides these experimentally observed structures in cholesteric droplets with planar or tilted anchoring, a more recent numerical simulation study by Seć and coworkers suggested that the s = +2 disclination line of the Frank-Pryce structure is actually unstable and can decompose into two s = +1 defect lines [115]. Based on their simulation results, the authors introduced two new director field configurations in cholesteric droplets: the Lyre-structure, which resembles the shape of a lyre instrument, symmetric around the vertical axis, and the Yeti structure, with two diametrically positioned boojums and higher symmetry than the Lyre structure [115].
For cholesteric droplets with homeotropic boundary conditions and high values qR > 10, the conditions on the surface do not affect the packing of the helix. The textures in the droplets indicate that the Frank-Pryce structure prevails [113, 117]. For qR < 5 the appearance of an equatorial disclination ring is observed [117]. For smaller qR values, this ring relaxes to a surface point defect, which then for even smaller qR < 1 relocates to the center of the droplet, yielding the radial structure frequently observed in nematic droplets [117].
3.3.3. Smectic droplets.
Director field configurations of smectic phases (SmA, SmC) in spherical confinement have been less intensively studied than for nematic or cholesteric phases. One reason for this is that smectic textures are typically highly complex with numerous macroscopic defects called focal conic domains [121, 122]. It is generally assumed that the smectic texture represents a packing of curved and equally spaced surfaces [123], as long as the dimension of confinement (typically in the μm range) is much larger than the spacing of smectic layers (typically < 10 nm). Although Kleman and Lavrentovich showed that the filling of space by smectic layers is far from complete [124], this simplifying assumption still allows a reasonable description of smectic textures in spherical confinement [122].
For spherical confinement and planar boundary conditions, a bipolar configuration represents the simplest SmA texture [122]. As in the bipolar configuration for nematic droplets, two boojums (s = +1) at the surface are separated by the diameter and  connects the two defects along the shortest possible path throughout the sphere. The smectic layers are perpendicular to the director field and consequently run along the parallels of the sphere [125]. A topologically equivalent configuration is obtained by dividing the two boojums into four surface defects with topological charge
connects the two defects along the shortest possible path throughout the sphere. The smectic layers are perpendicular to the director field and consequently run along the parallels of the sphere [125]. A topologically equivalent configuration is obtained by dividing the two boojums into four surface defects with topological charge  , positioned along a great circle on the sphere [122]. Both configurations exhibit the same free energy [126] and can by principle be transformed one into another by cutting the bipolar configuration in two halves, through a plane containing both boojums, and subsequently rotating one half with respect to the other by an angle of
, positioned along a great circle on the sphere [122]. Both configurations exhibit the same free energy [126] and can by principle be transformed one into another by cutting the bipolar configuration in two halves, through a plane containing both boojums, and subsequently rotating one half with respect to the other by an angle of  [125]. A schematic representation of both configurations is shown in figure 17.
[125]. A schematic representation of both configurations is shown in figure 17.
Figure 17. (a) Schematic representation of the smectic layer configuration in planar SmA droplets with two boojums s = +1 at the poles. While the surface director follows the meridians of the sphere, the smectic layers run perpendicular to  , along the parallels of the sphere. (b) Schematic drawing of an equivalent configuration with four
, along the parallels of the sphere. (b) Schematic drawing of an equivalent configuration with four  defects. The two configurations shown in (a) and (b) are equal in energy. Adapted with permission of Springer from [122] (2001) © EDP Sciences, Springer-Verlag, Società Italiana di Fisica 2001.
defects. The two configurations shown in (a) and (b) are equal in energy. Adapted with permission of Springer from [122] (2001) © EDP Sciences, Springer-Verlag, Società Italiana di Fisica 2001.
Download figure:
Standard image High-resolution image3.3.4. Nematic shells.
Liquid crystal shells exhibit an even larger variety of equilibrium director field configurations than full droplets, as the presence of the inner interface imposes additional topological constraints to the director field. Beyond the classification of shells into homeotropic or planar/tilted shells, this second interface allows the formation of hybrid shells, i.e. shells with one interface imposing homeotropic alignment while the other interface imposes planar or tilted anchoring.
Early studies on the formation of topological defects in liquid crystal shells date back to the work by Lubensky et al [107] and Poulin et al [90] on multiple emulsions (i.e. water droplets dispersed in larger nematic droplets that in turn are dispersed in a continous aqueous phase). Due to a lack of a proper method for precise control over the shell dimensions during these early works, these studies derive information on  from topological constraints only and do not study the formation of defects in detail. The introduction of a microfluidic-based method by Fernández-Nieves and coworkers [127], as described in detail in section 3.2, allowed the preparation of droplet-in-droplet double emulsions with well- controlled radii of outer (LC) and inner droplet (e.g. water) in an immiscible continuous phase. This setup also allowed studying the effects of the frequently observed thickness heterogeneity of shells in more detail: Depending on elastic forces in the nematic shell and density differences between the LC and the fluid of the inner droplet, the latter is not located in the center of the shell but shifted along one direction, in case of a density mismatch along the direction of gravity. More advanced topological studies on the formation of defects in nematic shells then focused on the effect of shell thickness [87, 104], heterogeneity in thickness [128] or variations of elastic constants [87, 128]. As discussed in more detail in section 3.2.2, dynamic tuning of shell thickness and diameter was achieved by utilizing osmosis [87, 104].
from topological constraints only and do not study the formation of defects in detail. The introduction of a microfluidic-based method by Fernández-Nieves and coworkers [127], as described in detail in section 3.2, allowed the preparation of droplet-in-droplet double emulsions with well- controlled radii of outer (LC) and inner droplet (e.g. water) in an immiscible continuous phase. This setup also allowed studying the effects of the frequently observed thickness heterogeneity of shells in more detail: Depending on elastic forces in the nematic shell and density differences between the LC and the fluid of the inner droplet, the latter is not located in the center of the shell but shifted along one direction, in case of a density mismatch along the direction of gravity. More advanced topological studies on the formation of defects in nematic shells then focused on the effect of shell thickness [87, 104], heterogeneity in thickness [128] or variations of elastic constants [87, 128]. As discussed in more detail in section 3.2.2, dynamic tuning of shell thickness and diameter was achieved by utilizing osmosis [87, 104].
Homeotropic-aligned nematic shells.
In shells with homeotropic boundary conditions at both interface,  adopts a radial configuration throughout the shell [107]. The inner droplet is thereby equivalent to a virtual radial hedgehog defect with unity charge and matches the topological requirements of the outer droplet [90]. The equilibrium director configuration in a simple shell with only one inner droplet therefore does not require additional topological defects. In multiple emulsions with homeotropic anchoring containing more than one inclusion, there must always be one hedgehog defect less than the number of inclusions, as was demonstrated by Poulin and Weitz [90]. When observed between crossed polarizers, the radial director configuration of a homeotropic shell appears as a rigid unrotated cross [107]. The regular orthoscopy texture resembles a conoscopy image of a flat slab of a uniaxial liquid crystal with homeotropic boundary conditions. The similarity arises from the analogy of image aquisition: While conoscopy probes all light directions through a flat sample, orthoscopy of a homeotropic shell probes a single light direction through all possible sample film orientations [104].
adopts a radial configuration throughout the shell [107]. The inner droplet is thereby equivalent to a virtual radial hedgehog defect with unity charge and matches the topological requirements of the outer droplet [90]. The equilibrium director configuration in a simple shell with only one inner droplet therefore does not require additional topological defects. In multiple emulsions with homeotropic anchoring containing more than one inclusion, there must always be one hedgehog defect less than the number of inclusions, as was demonstrated by Poulin and Weitz [90]. When observed between crossed polarizers, the radial director configuration of a homeotropic shell appears as a rigid unrotated cross [107]. The regular orthoscopy texture resembles a conoscopy image of a flat slab of a uniaxial liquid crystal with homeotropic boundary conditions. The similarity arises from the analogy of image aquisition: While conoscopy probes all light directions through a flat sample, orthoscopy of a homeotropic shell probes a single light direction through all possible sample film orientations [104].
Planar-aligned nematic shells.
Nematic shells with planar anchoring at outer and inner interfaces show a larger variety of defect structures. For thick shells with small inner droplet a bipolar defect configuration with two pairs of opposing surface defects at the outer and inner shell surfaces is expected [129]. Experimental observations show that for such shells the defect pairs are either located along a shell diameter [87, 127], resembling the boojum structure of bipolar nematic droplets (see figure 18(i)), or situated close to each other at one side of the shell [84, 128], see figures 18(g) + (h). The latter defect configuration is observed for shells with high thickness heterogeneity, i.e. a large offset of the inner droplet from the center of the shell, and the defects are located at the thinnest part of the LC [84]. The equilibrium distance between the defects is given by the balance between elastic director field distortions in the bulk of the nematic and the repulsion between defects of same topological charge [130]. Within the shell, the bulk director deformation around each boojum core represents half hyperbolic hedgehogs on the inner surface, while the distortion close to the outer surface resembles half radial hedgehogs [84]. Each defect carries a topological surface charge of s = +1 and can be identified by four black brushes when observed between crossed polarizers [84].
Figure 18. Polarizing optical microscopy images of planar shells with different thickness and thickness heterogeneity showing various defect configurations with four defects ((a)–(c)), three defects ((d)–(f)) or only two defects ((g)–(i)). The shell thickness and thickness heterogeneity increase along the rows from left to right, leading to different spatial arrangements of the defects. Reprinted by permission from Macmillan Publishers Ltd: Nature Physics [87], copyright 2011.
Download figure:
Standard image High-resolution imageFor thin planar shells a defect configuration with four surface defects constitutes the ground state [128, 131]. In the limit of infinitely thin shells the LC is confined to a two-dimensional surface and the disclinations reduce to points with no extension to the bulk. Each of the four defects carries a topological surface charge of s = +1/2, which reflects the π rotation of  along a path encircling each defect. The sum of topological charges is then +2, as required by the Poincaré-Hopf theorem for the coinciding outer and inner interfaces [128]. Depending on the elastic anisotropy and the heterogeneity in thickness, the ground state with four defects can occur as tetrahedral arrangement of defects [131] (see figure 18(a)), as clustering of defects at the thinnest part of the shell [132] (figures 18(b) + (c)), or as arrangement of defects along a great circle [132, 133].
along a path encircling each defect. The sum of topological charges is then +2, as required by the Poincaré-Hopf theorem for the coinciding outer and inner interfaces [128]. Depending on the elastic anisotropy and the heterogeneity in thickness, the ground state with four defects can occur as tetrahedral arrangement of defects [131] (see figure 18(a)), as clustering of defects at the thinnest part of the shell [132] (figures 18(b) + (c)), or as arrangement of defects along a great circle [132, 133].
Fernández-Nieves et al [127] and Lopez-Leon et al [87] showed that the local defect clustering occurs in asymmetric shells only, as long as the average shell thickness is high enough that the reduction of the length of the defect cores can minimize the total free energy [132]. Later experimental studies showed that the four defects are then typically not symmetrically arranged around the thinnest part of the shell, but they adopt a skewed configuration of two pairs, where the defects in one pair are separated by a larger distance compared to the defects in the other pair [132, 133] (see figure 18(b)). By performing a basic polarization optics analysis, Liang et al noted that  between the short pair of defects mainly exhibits bend deformation, while
between the short pair of defects mainly exhibits bend deformation, while  around the longer pair is mainly splay. Because bend defomations typically have greater energy densities than splay deformations (
around the longer pair is mainly splay. Because bend defomations typically have greater energy densities than splay deformations ( ) the total elastic free energy is minimized by contracting the length of the bend disclinations at expense of the splay disclinations [132]. The difference in the free energy cost of director bend and splay thereby causes the frequently observed skewed distribution of surface defects.
) the total elastic free energy is minimized by contracting the length of the bend disclinations at expense of the splay disclinations [132]. The difference in the free energy cost of director bend and splay thereby causes the frequently observed skewed distribution of surface defects.
Seč and coworkers later confirmed these observations by computer simulations [128]: The two closest defects are connected by a director field that runs along the shortest arc, whereas the other two defects are connected by the longest arc spanning a large fraction of a great circle (see figure 19). Increasing the anisotropy of elasticity further enhances the asymmetry between the two defect pairs. The simulations also showed that for larger ratios  the defects connected by splay deformations move towards opposite sides of the sphere until they stabilize in the equatorial plane. Only after this first step, upon further increasing the elastic anisotropy, the defects of the bend pair progressively migrate towards the equatorial plane. This large ring configuration is expected to occur when the elastic splay deformation is strongly energetically favoured over bend deformation, as also confirmed by Monte Carlo simulations [126, 134]. Seč et al also showed that upon reducing the thickness heterogeneity of the shell, the defects increase their separation in a roughly symmetrical way and the ratio of separation between the two pairs of defects remains roughly constant [128].
the defects connected by splay deformations move towards opposite sides of the sphere until they stabilize in the equatorial plane. Only after this first step, upon further increasing the elastic anisotropy, the defects of the bend pair progressively migrate towards the equatorial plane. This large ring configuration is expected to occur when the elastic splay deformation is strongly energetically favoured over bend deformation, as also confirmed by Monte Carlo simulations [126, 134]. Seč et al also showed that upon reducing the thickness heterogeneity of the shell, the defects increase their separation in a roughly symmetrical way and the ratio of separation between the two pairs of defects remains roughly constant [128].
Figure 19. Schematic summary of the numerical simulation study by Seč et al [128]. (a) Metastable and (b) stable inhomogeneous shell states with equal defect positions and nonequal director: The director links defects over the long and over the short arc as indicated by the black lines in the schematics. (c) Free energy difference between the states shown in (a) and (b). (d) Scheme of transformation trajectories between director and defect shell states that can be controlled by varying the displacement  of the inner droplet from the center of the outer droplet and elastic constant anisotropy
of the inner droplet from the center of the outer droplet and elastic constant anisotropy  . The metastable state becomes unstable at
. The metastable state becomes unstable at  that depends substantially on the shell radius R and thickness h. Reprinted with permission from [128], Copyright 2012 by the American Physical Society.
that depends substantially on the shell radius R and thickness h. Reprinted with permission from [128], Copyright 2012 by the American Physical Society.
Download figure:
Standard image High-resolution imageExperimental observations near the N-SmA transition, see figure 20, confirm this relationship between the defect configuration and the relative elastic constant values [128, 132, 133], as the ratio between K3 and K1 increases rapidly on approaching a second-order transition to the SmA phase. Moreover, we recently demonstrated that this relationship can be used to tune the defect location by moving closer to or further away from the N-SmA transition and then making the configuration permanent by polymer-stabilization [135]. However, it turns out that polymerization of the reactive component very close to the transition actually triggers the phase transition, even though the temperature rises due to the heat released during polymerization, an effect of the smectic-promoting character of acrylate reactive mesogens. In addition to defect configurations with two or four surface defects per interface, a third possible configuration is found for intermediate shell thickness which contains three topological defects forming an isosceles triangle [87], see figures 18(d)–(f).
Figure 20. N-SmA transition in a planar-aligned shell  m, thickness ≈4 μm). In (a)–(h) the focus is on the thin shell side, where the defects are concentrated, thus the initial signs of the transition (c)–(g)—starting on the thick side—are blurry. In (i) the focus is on the thick side. Drawings (b) and (c) sketch
m, thickness ≈4 μm). In (a)–(h) the focus is on the thin shell side, where the defects are concentrated, thus the initial signs of the transition (c)–(g)—starting on the thick side—are blurry. In (i) the focus is on the thick side. Drawings (b) and (c) sketch  corresponding to (a) on the thin and thick sides, respectively. Reprinted with permission from [132]. Copyright (2011) by the American Physical Society.
corresponding to (a) on the thin and thick sides, respectively. Reprinted with permission from [132]. Copyright (2011) by the American Physical Society.
Download figure:
Standard image High-resolution imageBuoyancy enhances the tendency for thickness heterogeneity in shells and favours vertical shifts along the field of gravity, so that only two scenarios (inner droplet shifted up or down) are experimentally observed. Seč and coworkers showed by numerical simulations that even in the absence of gravity heterogeneous shells are lower in energy compared to concentric shells [128]. These simulations also indicate that the total free energy would reach its minimum for a maximum displacement of the inner droplet. However, inner and outer surfaces of experimental shells have not been observed to coalesce [128]. The authors assume the existence of a disjoining pressure between outer and inner interface. This pressure is probably caused by the presence of PVA as a stabilizer. The PVA concentration increases as the nematic film gets thinner and this effect tends to homogenize the thickness [128]. In conclusion, buoyancy effects initiate and liquid crystal elasticity enhances a thickness heterogeneity of nematic shells by displacing the inner droplet from the center of the outer droplet. This symmetry breaking is irrespective of the elastic anisotropy [128].
Hybrid-aligned nematic shells.
Hybrid shells feature one interface with homeotropic anchoring conditions and one interface with planar boundary conditions. Consequently, there are two types of hybrid shells, shells with planar anchoring at the outer interface and shells with planar anchoring at the inner interface. Since the Poincaré-Hopf theorem only requests a topological surface charge of s = +2 at a planar or tilted interface, hybrid shells in equilibrium do not show topological defects at the homeotropic interface, but have two boojums of charge s = +1 at the planar interface [84]. The appearance of half-integer surface defects in hybrid shells is ruled out by the symmetry-breaking bend deformation through the bulk of the shell [104]. As discussed already for planar droplets, two possible director configurations at the planar interface of hybrid shells exist which fullfill these topological requirements: The bipolar configuration with two splay-type boojums and the concentric configuration with two bend-type defects [83, 113]. The two configurations are topologically distinct by considering the director field within the shell, but give rise to identical textures between crossed polarizers. Liang et al showed that a clear distinction between the two configurations can be made by using a polarising microscope with compensator plate and confirmed that, as for droplets, the bipolar configuration is typically observed [83]. The two defects in the bipolar configuration cannot both be half-hyperbolic hedgehogs, since the hybrid alignment at the interfaces could then not be commensurate [84]. Instead, one of the boojums must be a half-radial hedgehog [84]. A continuous transition from a planar shell into a hybrid shell was reported by Lopez-Leon and Fernandez-Nieves by changing the additive in the outer aqueous continous phase to induce homeotropic alignment [84].
Noh et al recently reported a two-step clearing transition for hybrid shells with surfactant-induced homeotropic anchoring at the outer shell interface and PVA-induced planar or tilted anchoring at the inner interface, or vice versa. The bipolar hybrid texture at first changes into the centrosymmetric homeotropic texture upon heating, before the nematic shell enters the isotropic phase. The authors argued that this behavior might be explained by a local stabilization of the nematic order caused by an adsorbed oriented monolayer of surfactant on one side [85].
3.3.5. Cholesteric shells.
In a recent experimental study on cholesteric shells with planar anchoring, Darmon and coworkers discussed bipolar and radial director field configurations with a higher complexity than director fields in cholesteric droplets [118]. A bivalent configuration with two topological defects of surface charge s = +1 at the outer and inner shell interface is observed for cholesteric liquid crystals with long pitch p0. The pairs of boojums on one interface appear close to each other and the defects on the outer and inner interface are linked to a stack of disclination rings through the shell.
Liquid crystals with shorter p0 lead to monovalent shells with a radial defect. This structure is reminiscent of the Frank-Pryce structure described above for cholesteric droplets. Darmon et al showed by polarising optical microscopy that the disclination line in this structure actually consists of two  interwinded disclination lines forming a double helix [118]. The authors thereby provide an experimental confirmation for numerical simulations on cholesteric droplets by Seč et al, who were the first to suggest that the disclination line of the Frank-Pryce structure is not a
interwinded disclination lines forming a double helix [118]. The authors thereby provide an experimental confirmation for numerical simulations on cholesteric droplets by Seč et al, who were the first to suggest that the disclination line of the Frank-Pryce structure is not a  disclination, but is built from two
disclination, but is built from two  disclinations, whose ends form a pair of close s = +1 defects at the outer surface while they form a monopole at the center of the droplet [115, 118]. A transition between the two possible configurations was shown to be of first-order. In a shell of thickness h the angular distance between the boojums is governed by the ratio h/R, while the transition itself depends on h/p0 [118]. The optical behavior of cholesteric shells with sub-micron p0 values will be discussed in section 3.5.
disclinations, whose ends form a pair of close s = +1 defects at the outer surface while they form a monopole at the center of the droplet [115, 118]. A transition between the two possible configurations was shown to be of first-order. In a shell of thickness h the angular distance between the boojums is governed by the ratio h/R, while the transition itself depends on h/p0 [118]. The optical behavior of cholesteric shells with sub-micron p0 values will be discussed in section 3.5.
3.3.6. Smectic shells.
Experimental textures of planar SmA shells can be quite complex [104, 125, 132, 133], see figure 20. The equilibrium texture exhibits four topological defects of charge s = +1/2, located within the equatorial great circle, together with a set of additional lines which connect the defects by pairs [125]. The additional lines represent curvature walls that divide the sphere in crescent domains (spherical lunes) within which the smectic layers are undulated in a wavy fashion. Liang et al proposed that the undulation arises from a layer strain that is caused by the radially increasing spherical cross section area, coupled with the fact that the SmA phase is incompatible with director bend (see section 2.2) [132]. Dislocations would be needed to obtain a larger number of smectic layers at the outer interface compared to the inner interface, but the high free energy cost of such a solution renders it unfavoured.
Instead, the layers buckle increasingly on approaching the outer interface, increasing the effective smectic layer distance a1 along the original director orientation compared to the true layer spacing a0 (see figure 21). This reconciles the radially increasing surface area with the requirement for constant a0. Lopez-Leon et al rather emphasized the possibility of a tilted instead of planar anchoring at the shell interfaces in order to release the layer strain [133]. In a subsequent theoretical treatment of SmA shells of varying thickness, Manyuhina and Bowick confirmed that both scenarios are possible [136]. In our recent study of polymer stabilization of LC shells [135] we demonstrated that the regular buckled geometry can be imprinted on the polymer network, rendering the instability-generated structure stable over a large temperature range, even after heating to the isotropic range of the host LC.
Figure 21. (a) Smectic layering in a curved shell poses problems for retaining the smectic layer thickness, which can be solved by dislocations (upper path) or layer buckling (lower path). (b) Sketch of how the effective layer distance along a cut can increase from a0 at the inside to  at the outside through a gradually increasing layer undulation. Reprinted figure with permission from [132]. Copyright (2011) by the American Physical Society.
at the outside through a gradually increasing layer undulation. Reprinted figure with permission from [132]. Copyright (2011) by the American Physical Society.
Download figure:
Standard image High-resolution imageIn SmA shells with homeotropic anchoring at the inner and outer interfaces the characteristic cross-like texture as for nematic shells is observed, the only difference between nematic and SmA shells being a reduction of thermal fluctuations in SmA [104]. Liang et al also proposed that, compared to nematics, smectic LCs reduce the shell thickness heterogeneity and moves the inner droplet towards the shell centre [137]. In a homeotropic shell with high thickness heterogeneity, many smectic layers in the thicker part of the shell cannot be closed since fewer layers fit in the thinner part of the shell.
Smectic-A shells with hybrid alignment show focal conic domains as equilibrium director field configuration, mediating between planar/tilted alignment at the outer interface and homeotropic alignment at the inner interface, or vice versa. After the phase transition from the nematic phase, an unstable pattern of stripes, connecting the two poles of the shell, appears [104]. These stripes represent the boundaries of a folding membrane of remaining nematic order, which connects the smectic regimes with opposite alignment that grow from the two interface regions of the shell [83, 104]. Torza and Cladis observed the same type of texture much earlier for hybrid alignment in flat smectic samples, explaining it as a result of director bend being expelled from SmA [138]. The stripes are unstable since they come with an interfacial energy between two fluid phases. Hence they undergo a Rayleigh instability and break up into toric focal conic domains within which the layers bend, the SmA phase now spanning the full sample. In this configuration the SmA phase can accommodate the hybrid boundary conditions by only showing splay deformations of the director field [83].
A pecularity occurs for homeotropic SmC shells, as despite homeotropic anchoring the tilt in the smectic layers provides a tangential director field component at the interfaces and therefore requires the formation of topological defects [104]. Half-integer defects are ruled out because the C-director field is not sign invariant (see section 2.2), so a bipolar defect configuration with two opposing boojums at the outer and inner interface constitutes the ground state. Upon further cooling the SmC biaxiality becomes apparent and the texture distorts such that it does not allow to identify the number and charge of topological defects [104]. Liang et al propose that at low temperatures the SmC phase avoids the formation of defects by locally reducing the tilt to zero and shifting the system to a SmA state [104].
3.4. Droplet- and shell-shaped liquid crystal elastomer actuators
The above drops and shells were all made from low molar mass LCs, with limited lifetime and stability. By polymerizing the liquid crystal or a reactive component mixed into it, robust and durable particles can be produced, templated from the LC. Apart from providing robustness and enable long-term storage, the polymerization can lead to new properties, in particular if the polymerization is done such as to obtain an LCE (see section 2.4). In this section, we review the existing experimental methods for creating micron-scale droplet-/shell-shaped LCEs and their actuation mechanism.
In order to allow the production of droplets/shells with good control of diameter and thickness (in case of shells) one must start with low molar mass precursors and carry out the polymerization and cross-linking after the microfluidic production process. Thus, the first step in designing an experiment is to select the appropriate initial mesogenic monomers along with cross-linkers, keeping in mind that they must be miscible with each other, but not with any of the isotropic phases that form the external continuous phase and (in case of shells) the internal phase. The two-stage Finkelmann approach [41] may be feasible, provided that also the first step of polymerization is done after droplet/shell production and that an appropriate means of aligning the intermediate polymer state can be found.
The microfluidic platform is well established for the synthesis of monodisperse non-LC polymer beads [139, 140]. Zentel and later on others transferred this approach to the case of side-on side chain LCE micro droplet synthesis [21, 37, 141, 142]. A complication is that all starting materials for the LCE synthesis are in solid phase at room temperature, hence they used fused silica capillaries assembled in a form of T-junction immersed in a hot bath of silicone oil as shown in figure 22. Syringe pumps were used to flow both the LC monomer mixture (dispersed phase) and a silicone oil stream, which was used as continuous phase, through the hot bath. The LC monomer mixture stream breaks up into droplets after the T-junction due to the Rayleigh instability, driven by the interfacial tension between the two fluids. The shear flow within the droplet as it flows downstream ensures director alignment, although—as discussed in section 3.3.1—one should expect a continuous transformation between bipolar and concentric configuration [103].
Figure 22. Schematic drawing of microfluidic setup for LCE particle synthesis:(1) shows the structure of the LC-monomer used and (2) the structure of the crosslinker. Image adapted, with permission, from [37] John Wiley & Sons. Copyright © 2009 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Download figure:
Standard image High-resolution imageThe size of the droplets could be controlled by varying the flow rates of the disperse and the continuous phases. With optimized flow ratio between the phases, they achieved monodisperse droplets, with a coefficient of variation in size that was less than 0.7%. It is important to keep the monomer mixture in the nematic phase during the polymerization and crosslinking stage. This was achieved by maintaining the nematic phase temperature downstream from the point of droplet break-up using a separate hot plate as shown in figure 22.
The actuation of the LCE particles produced in this way involved a sphere–ellipsoid shape transformation upon heating to the isotropic phase and back. A similar approach was used to produce planar-aligned LCE particles by Kim et al [143], and in the production of LCE particles using thiol-ene 'click' chemistry by Fleischmann et al [144]. Recently, Marshall et al demonstrated an alternative approach for the production of this type of LCE particles, separating in time the droplet production from the UV crosslinking step [145]. Here, a PDMS based microfluidic device was used rather than the capillary device. Contrary to the Zentel group approach, Marshall et al used mechanical stretching as a tool for aligning the droplet of LCE precursor mixture into a mono-domain. This was possible by collecting the spherical droplets of precursor mixture in a high-concentrated aqueous PVA solution, from which the water was then evaporated. The thermoplastic matrix that thus developed was then stretched, resulting in elongation of the encapsulated precursor droplets with consequent uniform alignment of the director, and at that stage the sample was polymerized and cross-linked by UV illumination. Afterwards, the produced LCE ellipsoids were separated from the PVA film by dissolving PVA in water. This approach too is rather straightforward and useful for bulk production of LCE particles in micron scale. The authors reported a reversible shape change with 30% strain and 30 kPa stress upon heating from nematic to isotropic and back, see figure 23 [145].
Figure 23. Anisotropic shape change of LCE particle in glycerol upon heating and cooling. The top row shows the texture between crossed polarizers; the LCE gradually looses birefringence and eventually turns dark at the far right, which indicates that the particle is now optically isotropic, although its shape has not fully relaxed to spherical. The latter aspect is clear from the second-row images, taken without crossed polarizers. The scale bar represents 15 μm. Reprinted with permission from [145]. Copyright (2014) American Chemical Society.
Download figure:
Standard image High-resolution imageA very interesting new avenue for applying LCE microspheres, opening an entirely new direction of research, was recently introduced by the group of Elda Hegmann [146]. Here a network of polydisperse LCE microspheres produced by emulsion polymerization was investigated as a scaffold for muscle cell growth. Rather than using microfluidic production, the authors dispersed the LC monomer mixture in toluene along with a small quantity of aqueous surfactant solution, leading to formation of droplets under vigorous agitation. The same approach was used by the Zentel group to produce nanosized shape-changing LCE particles [147]. Once the desired emulsion is produced, polymerization and crosslinking of the precursor mixture into LCE droplets is triggered by UV illumination. In the Hegmann study a 3D network of LCE particles formed after removing the solvent and surfactant.
In a joint study by the Lagerwall and Zentel groups, a modified nested capillary microfluidic device was used to produce LCE shells, which upon actuation functioned as one-piece micropumps [35]. Again the inconveniently high LC temperature range of the precursor mixture called for some modifications of the shell production set-up. Rather than aqueous surrounding phases, the authors used silicone oil for the outer phase and glycerol for the inner phase, and no stabilizers of any kind were included. In order to allow stable production of the triple emulsion, with glycerol inside the LCE precursor mixture inside the silicone oil, a three-fold coaxial capillary geometry was chosen, allowing unidirectional flow of all liquids. The microfluidic device comprised three capillaries; a tapered square glass capillary carried the LC monomer mixture, and into this was nested a tapered cylindrical capillary, carrying the inner phase. Finally, an outer teflon tubing was used as collection tube as well as for carrying the outer phase as shown in figure 24(a).
Figure 24. Nested capillary setup for LCE shell production. (a) A triple microfluidic co-flow geometry allows fabrication of LCE shells with glycerol core. (b) Shell formation at the capillary tip. (c) Demonstration of micropump: when heated to 130 °C (isotropic), the force exerted by the actuating shell pushes the glycerol core upwards into an inserted capillary. The glycerol sinks to its original level when the shell resumes its former shape on cooling to 90 °C (nematic). Scale bars, 100 μm. Reprinted by permission from Macmillan Publishers Ltd: Nature Communications [35], Copyright (2012).
Download figure:
Standard image High-resolution imageThe precursor mixture was heated to its isotropic phase at 90 °C and the temperature of the silicone oil flowing through the collection tube was adjusted to the nematic range at 65 °C, using different hot plates. Note that this set-up for shell production involves two consecutive Rayleigh instabilities, first the glycerol stream breaking up into droplets within the LCE precursor stream, then this compound stream breaking up into shells within the silicone oil stream. The second of these instabilities is shown in figure 24(b). UV illumination was then used to induce polymerization and cross-linking, effectively freezing the flow induced planar director orientation within the nematic shell. This was confirmed by wide angle x-ray scattering [35].
Probably due to the dynamic production procedure, the shells were biaxial ellipsoidal in shape. Upon actuation by heating them above the clearing point of the LCE, the ellipsoid changed the relation between its three axes, the shortest axis becoming the longest, extending by a factor of about 2. The most interesting effect was obtained by punching a hole in the shell after heating it above the LCE glass transition temperature and inserting a pointed capillary, until it reached the glycerol core. Actuating the punctured shell by heating above TNI now yielded a micropump action, as the shell pushed out the glycerol core into the capillary (against gravity) on heating, sucking it back in when cooled back into the nematic phase, see figure 24(c). Approximately 65% of the inner fluid can be actively pumped out and sucked back in, in a total of ≈0.4 s time.
In summary, micro/nano LCE droplets and shells have been generated using various designs of microfluidic systems as well as by regular emulsion polymerization. The LCE network alignment was generally achieved by the shear induced flow fields during the production, and the alignment was fixed by UV illumination before the director field could relax. Considering the excellent control of  achieved with low molar mass LC shells where no conversion into an LCE was attempted, it is a promising direction for future research to move away from flow-induced alignment. Instead one may rely on the control of topological defects to control
achieved with low molar mass LC shells where no conversion into an LCE was attempted, it is a promising direction for future research to move away from flow-induced alignment. Instead one may rely on the control of topological defects to control  throughout the shell. The actuation behavior of LCE droplets/shells was so far demonstrated only with external heating as a stimuli. Also here there are many openings for future improvements, e.g. by tuning the shell composition such that light can be used as a trigger.
throughout the shell. The actuation behavior of LCE droplets/shells was so far demonstrated only with external heating as a stimuli. Also here there are many openings for future improvements, e.g. by tuning the shell composition such that light can be used as a trigger.
3.5. Tunable photonic crystal microspheres made from cholesteric shells and droplets
As introduced in section 2.3, cholesteric LCs are recognized as extraordinary photonic materials, providing UV, visible or IR selective (Bragg) reflection due to the spontaneously formed helical structure with a pitch p0 that is equal to the reflected light wavelength within the LC. This turns cholesterics into dynamically tunable, self-assembled photonic crystals [2]. When confining a short-pitch cholesteric LC within a small spherical shape, like a droplet or a shell, the combination of periodic internal structure and spherical geometry can lead to many intriguing and useful phenomena. Humar and Musevic [148] succeeded in turning cholesteric droplets into omnidirectional lasers, and later Uchida et al [149] and Chen et al [150] achieved the same with cholesteric shells. Cipparrone and co-workers demonstrated chiral optomechanics involving the interaction of cholesteric droplets and optical tweezers [151].
We recently showed that the selective reflection in combination with the spherical geometry of cholesteric droplets [152, 153] or shells [86] gives rise to a very interesting new behaviour when many such cholesteric spheres are brought close to each other: a photonic cross communication takes place between adjacent spheres, along specific channels defined by Bragg's law and the directions of communication. This generates intricate multicolored patterns that can be dynamically tuned by varying the illuminated area (see figure 25). Panel (b) in the figure schematically illustrates the cross communication for the case of a normally red-reflecting cholesteric. A red spot seen at the center of each sphere corresponds to normal incidence selective reflection. A first set of peripheral blue cross communication spots appears when the illumination beam meets the cholesteric neighbor sphere at an angle of 45° with the helical axis. The light is reflected horizontally until it reaches the central sphere, which reflects the light back up to the observer. This constitutes the most basic type of cross communication, which we refer to as direct communication.
Figure 25. (a) The selective reflection from N* spheres with planar anchoring. Because of the radial arrangement of the helix the usual dependence of the color on the viewing angle does not appear: in any direction that you view a planar-aligned N* droplet you see reflected light only from the center, and here you are looking along the helix. In an isolated sphere, you thus see only a central spot with the normal selective reflection color. (b) Schematic of direct (D) photonic cross communication between nearest neighbor (nn) droplets (same pitch) and of the communication path mediated via total internal reflection (TIR) against the surface of the continuous phase. (c) Hexagonally close-packed array of droplets of a normally red-reflecting cholesteric. The sample is uncovered, thus with air following the continuous phase, and it is observed in reflection between crossed polarizers. The scale bar is 100 μm.
Download figure:
Standard image High-resolution imageA second category of cross communication arises in uncovered samples, where the continuous phase is followed by air, with lower refractive index. This boundary condition allows for total internal reflection (TIR) at the continuous phase–air interface, enabling an indirect cross communication that is recognized through green-yellow spots. They have the same hexagonal symmetry as the main green spots, a bit further towards the centre of each sphere. Several additional series of spots can arise from cross communication with cholesteric spheres situated further away, in particular in uncovered samples and with rather large spheres [86, 152].
In our first paper on the topic [152], we discussed a number of potential applications of cholesteric spheres based on their peculiar reflection properties, including photonic couplers, all-optical switches/distributors, or autonomous sensors. Currently, we believe that the most interesting application opportunity is in creating secure authentication tokens, relying on the uniqueness and unclonability of the patterns [86]. The helical N* self-assembly provides an intrinsic protection from cloning, as the colored patterns arise from reflection, changing dynamically depending on how large area is illuminated and where this area is located. As the light additionally is circularly polarized, it would be exceptionally difficult to reproduce the pattern in a copy. While an adversary with the same microfluidic N* sphere production technique would be able to produce a new token that is qualitatively similar, it would be extremely difficult to reproduce a particular random arrangement, and thus the particular pattern. This makes each token unique to the point that even the authorized manufacturer could not make an identical copy.
Further opportunities for introducing a unique character into the cholesteric spheres and their resulting patterns were demonstrated by the Li and Katsonis groups, by incorporating light-sensitive chiral dopants [150, 154–156]. By illuminating their spheres with UV light they could dynamically and locally tune the pitch of the cholesteric helix and consequently the reflection wavelength and the resulting colored patterns. With the molecular motors used as chiral dopants in the Katsonis group work, they could even dynamically change the handedness of the helix [156]. The Li group added additional detail to the pattern by producing dual layers of cholesteric droplets [155].
Before one can realistically exploit any novel applications of cholesteric spheres, however, the optical quality needs to be improved and long-term stability and durability needs to be ensured. The durability issue is best addressed by polymerization and several groups have explored this approach. The Kim group produced cholesteric droplets inside a shell of polymerizable immiscible liquid, thereby protecting the LC either by a hydrogel shell [157] or an elastomer shell [158]. The latter technique is particularly attractive, since the same elastomer precursor as was used to produce the sheath protecting the droplets after production can be used as a new continuous phase, which can then in turn be polymerized. In this way the authors could tune the communication color by changing the refractive index of the continuous phase, and a flexible photonic film functionalized by N* droplets could be realized [158]. Moreover, the droplets sustained substantial mechanical deformation without loss of selective reflection. The Katsonis group attempted polymerization of a reactive component mixed into the LC [156]. While this helped to stabilize the droplets, the polymerization reaction negatively affected the optical quality. In transmission the optical appearance was severely degraded while the reflection pattern was still visible, but with a substantial quality decrease even with only 5% of reactive component.
In our recent work we moved from droplets to shells, thereby solving the optical quality as well as the stability problems [86]. With droplets of  μm the influence of the single aligning interface is too weak to prevent thermal fluctuation of the helix axis. This renders the cholesteric rich in so-called oily streak defects [159], giving the droplets poor optical quality. In several reports on N* droplets the reflection is non-uniform [152, 153, 157]. By using shells instead of droplets we could greatly improve the optical quality since the inner interface provides a second aligning influence, that together with the alignment imposed by the outer interface reduces the helix thermal fluctuations. Moreover, because the shell contains a much smaller volume of LC, with the two boundaries supporting the planar alignment, we were also able to polymerize as much as 20% of reactive mesogen within the shells without loss of optical quality. The stabilizing action was enough to ensure that the shells sustained substantial mechanical deformation without rupture, perfectly retaining their selective reflection properties throughout the process [86].
μm the influence of the single aligning interface is too weak to prevent thermal fluctuation of the helix axis. This renders the cholesteric rich in so-called oily streak defects [159], giving the droplets poor optical quality. In several reports on N* droplets the reflection is non-uniform [152, 153, 157]. By using shells instead of droplets we could greatly improve the optical quality since the inner interface provides a second aligning influence, that together with the alignment imposed by the outer interface reduces the helix thermal fluctuations. Moreover, because the shell contains a much smaller volume of LC, with the two boundaries supporting the planar alignment, we were also able to polymerize as much as 20% of reactive mesogen within the shells without loss of optical quality. The stabilizing action was enough to ensure that the shells sustained substantial mechanical deformation without rupture, perfectly retaining their selective reflection properties throughout the process [86].
While the shells can be considered thin in comparison to the diameter, they are still thick enough to ensure effective selective reflection. In fact, as was first demonstrated by Fan et al [155], a set of well-aligned cholesteric droplets exhibit photonic cross communication at different depths, leading to defocused lines rather than sharp spots in the generated pattern. By moving step by step from a full droplet to increasingly thin shells, we gradually removed the unfocused communication spots, enhancing the optical quality and sharpening the reflection pattern [86]. An additional benefit of working with shells is that we can use the osmotic process discussed in section 3.2.2 to thin the shells [87]. As demonstrated in figure 11 the thinning of the shell greatly reduced the time required to remove oily streak defects, as compared to the week-long annealing required without osmosis.
Based on the simplest level of analysis presented in our original work, shells with different pitch should not communicate, and one would thus expect missing spots in the communication patterns. In reality, cross communication does occur, as shown in figure 26. The communication between shells with different p0 is possible because the asymmetry in N* pitch can be compensated by an asymmetry in ray directions and reflection planes [86]. The microscope used for illuminating and imaging the sample integrates light over a certain range of propagation directions, depending on the aperture diaphragm and numerical aperture of the objective used.
Figure 26. Several cholesteric microspheres with different pitch length p0 and varying sizes arranged randomly, showing photonic cross communication with different wavelengths in different directions. The scale bar is 100 μm. Reproduced from [86]. CC BY 4.0.
Download figure:
Standard image High-resolution imageAs figure 26 demonstrates, the photonic cross communication between shells with different p0 values means that one and the same shell can exhibit many different colors of communication spots along its perimeter. The possibility to randomly combine shells with different photonic band gaps in a single token, with bi- as well as uni-directional communication at intermediate wavelengths, thus vastly extends the possibilities of creating unique and highly distinct patterns using these shells, with great potential in the field of secure authentication.
While most of the attention concerning N*spheres has been focused on their appearance in reflection, we recently analyzed their optical properties also in transmission [160]. The combination of optical activity, birefringence and selective reflection (in this case having a subtractive effect) gives rise to a quite peculiar and complex appearance of planar-aligned short-pitch cholesteric shells also when they are viewed in transmission between crossed polarizers. Pitch, shell thickness and diameter all influence the texture, but in contrast to the reflection behavior, there is no apparent cross communication seen in transmission. An isolated shell looks essentially similar to shells in an assembly.
3.6. Active liquid crystal droplets and shells
A recent strong trend in LC research is to study active liquid crystals, i.e. non-equilibrium fluid systems with long-range orientational order that continuously dissipate energy. Droplets and shells appear also in this field, hence we end this section by briefly discussing this development. In nature, we come across several 'active LC' systems like flocks, fish swarms and bacterial colonies, in which the 'particles' actively interact with each other during their collective motion, leading to the emergeance of complex patterns [161]. In order to understand such real-life systems one has to deal with the complex collective behavior, mutual interactions, and pattern formation [162–165]. Bacterial colonies are convenient as they constitute a live system that can be studied experimentally in the lab, rendering an elucidation of the origin of their collective behavior viable. On the other hand, there are several inanimate but energy dissipating systems that also develop collective behavior, making them suitable for lab experiments.
In this view, autonomously swimming LC droplets, recently introduced as model units from the Bahr and Herminghaus groups, have opened a new avenue for investigating life-like non-equilibrium systems [166]. Considering the size of the droplets in the order of micrometers and average speed about one diameter per second, this leads to typical Reynolds numbers smaller than unity. This means that viscous forces are dominant over inertial forces. Herminghaus et al used LC droplets in comparatively high-concentrated aqueous surfactant solutions [167] and demonstrated that the swimming originated from the generation of non-uniform interfacial tension around the droplet interface. In detail, nematic 5CB droplets were placed in a continuous phase of water-dissolved tetradecyl-trimethyl-ammonium bromide (TTAB). The surfactant concentration is maintained well above the critical micellar concentration (CMC). The dissolution of mesogens into the surfactant solution, and conversely the inflow of water into the LC droplets, creates a gradient in interfacial tension. This leads to Marangoni stresses which propel the 5CB droplets. Interestingly, the phenomenon lasts for hours to days depending on the reserve concentration of LC and surfactant micelles in the continuous water phase.
The mechanism of self-propulsion is explained by two possible dissolution scenarios for the 5CB phase into the aqueous surfactant phase: either by micellar pathway or by molecular pathway. The solubilization of mesogens at the interface is captured by micelles in the micellar pathway, whereas in the molecular pathway mesogens freely diffuse away from the interface and are then captured by micelles. In both cases, the 5CB solubilization creates a gradient in surfactant concentration at the interface, with consequent spatial variation of interfacial tension. The Marangoni stress at the interface in turn creates a convective flow inside the LC droplet. The collective motion of several convective LC droplets arranged into a two dimensional colloidal-crystalline raft in a shallow well is shown in figure 27(a) and a colloidal crystal deformed into the third dimension against buoyancy during swimming in a deep well is shown in figure 27(b).
Figure 27. Snapshots of collective motion of swimming LC droplets. (a) Crystalline raft formation of nematic droplets during collective motion. (b) A part of a crystalline raft of swimming droplets is out of focus, which shows that it propagates in three dimensions as an integral structure. Reproduced from [167]. CC BY 3.0.
Download figure:
Standard image High-resolution imageThe surfactant layer at the surface of each droplet results in a homeotropic alignment at the interface, thus a radial director field, hence a topological point defect at the center of each drop appears. Since LCs are birefringent, it is easy to visualize the convection profile inside the droplet using a polarizing microscope [166, 167]. The coupling between the swimming behavior, internal convection and nematic director profile leads to continuous rotation of the droplet during swimming [168]. The detailed theoretical analysis on LC droplet swimmers is beyond the scope of this paper. The interested reader is referred to the review of Maass et al [166].
The chiral version of LC droplet swimmers was also reported recently [169]. Here, the authors extended the above mentioned Marangoni flow induced self-propulsion concept to cholesteric LC droplets. The authors observed the time evolution of director profile in 2D and 3D swimming droplets with different handedness of the chiral dopant. The swimming trajectories of the droplets exhibit a helical path which is opposite to the handedness of the chiral dopant. The theoretical description was formulated based on translational velocity from Marangoni flows, an angular velocity from the rotation of the droplet and the internal helical director field [169].
While the above examples constitute active systems of LC droplets developing collective behavior, it is also possible to incorporate an active liquid crystal system, with very different composition from that of thermotropic nematics, within a shell. In a large-scale collaboration between the Giomi, Bowick, Marchetti, Dogic and Bausch groups, Keber et al succeeded in preparing a vesicle (a shell consisting of a bilayer of phospholipids) containing an active nematic phase of motile microtubules driven by kinesin motors [170]. As for the case of shells of passive nematic, the spherical topology implies that defects are formed on the surface, but the fact that the phase is active leads to entirely different dynamics. The defects move spontaneously and the authors observed, on the one hand, oscillations of defect configurations and, on the other hand, changes in shape of the entire vesicle driven by the motility of the microtubules.
4. Core-sheath fibers with encapsulated LC
The focus now shifts to LCs inside fibers, where they are subject to strong cylindrical confinement. We first review the classic works—as well as some recent additions—on LCs in containers like glass capillaries or porous inorganic membranes. Thus, sections 4.1.1–4.1.4 will be of more fundamental physics character, describing how nematics, smectics and cholesterics respond to cylindrical containment. In section 4.2 we survey the relevant literature regarding electrospinning, beginning with how the process fundamentally works, what experimentalists should generally expect to observe during the process, and the key components of the setup. This discussion is primarily for physicists and chemists who are unfamiliar with the experimental technique. This section will also further elucidate important solution specific parameters such as polymer concentration, molecular weight, and viscosity (section 4.2.3–4.2.4). Section 4.2.5 focuses on some aspects of coaxial electrospinning, useful for introducing low molar mass LCs into the fiber cores.
In section 4.3.1 we survey the reports so far of successful incorporation of LCs into fibers. We cover fibers from liquid crystalline polymers (LCPs) as well as low molar mass LCs incorporated in the core of non-liquid crystalline polymer sheaths. The latter topic is, in fact, the main focus throughout section 4. Finally, in section 4.4 we also relate to the application areas which we feel that LC core fibers and textile could help to advance in today's world. In this context we cover fields ranging from visibly responsive volatile gas sensors (section 4.4.1) to smart flexible actuators (section 4.4.2).
4.1. Nematics, cholesterics and smectics in cylinders
While containment inside fibers is a relatively recent addition to LC research, being easily accessible since the introduction of LC core electrospinning (section 4.2.1), the confinement of LCs inside cylindrical cavities has been studied since long, theoretically, in simulation as well as experimentally. In reviewing the key outcomes of these studies, we limit ourselves to the N, N* and SmA phases, in cylinders with planar and homeotropic surface anchoring, respectively. We do not consider spontaneously forming LC filaments [171–174], typically occurring in certain smectics and discotics subjected to tensile strain, although this is indeed a fascinating phenomenon.
Unfortunately the study of cylindrical confinement presents a case of confusing terminology mix-up. In section 2 we introduced the terms homeotropic and planar as referring to the orientation of  with respect to the sample interface, the former referring to orthogonal alignment whereas the latter means that
with respect to the sample interface, the former referring to orthogonal alignment whereas the latter means that  is in the plane of the interface. This is the modern definition of the terms and they are widely used as such in current literature. However, in the early studies of LCs in cylinders, the term 'planar' was often used to indicate that
is in the plane of the interface. This is the modern definition of the terms and they are widely used as such in current literature. However, in the early studies of LCs in cylinders, the term 'planar' was often used to indicate that  lies in the cross section plane perpendicular to the fiber axis. In order to avoid a self-contradicting terminology, we thus adjust the notation for cylindrical
lies in the cross section plane perpendicular to the fiber axis. In order to avoid a self-contradicting terminology, we thus adjust the notation for cylindrical  slightly, replacing the problematic old-style 'planar' with perpendicular, referring to the fact that the director lies fully within the perpendicular cross section plane. This choice has the advantage that we are able to stick to the original abbreviation P in our text. When comparing with the problematic original articles, the reader needs to keep in mind that 'planar' in those texts may correspond to 'perpendicular' in ours.
slightly, replacing the problematic old-style 'planar' with perpendicular, referring to the fact that the director lies fully within the perpendicular cross section plane. This choice has the advantage that we are able to stick to the original abbreviation P in our text. When comparing with the problematic original articles, the reader needs to keep in mind that 'planar' in those texts may correspond to 'perpendicular' in ours.
4.1.1. Nematics in cylinders with homeotropic surface anchoring.
The attention early on focused on the interesting frustration caused when a nematic is confined in a narrow cylindrical space with homeotropic anchoring to the surface. The intuitive idea that an s = +1 wedge disclination line would form along the core, with a uniformly splayed, or Radial (R), director field within the Perpendicular (P) cross section (PR, see figure 28a) was early on recognized to be incorrect; the LC can in most cases reduce the elastic distortion energy by the escape into the third dimension (see section 3.3). In the cylinder this means that  (
( ) bends into the cylinder axis as one moves from the periphery to the center. Indeed, this Escaped Radial (ER) configuration was confirmed by optical microscopy in 1972 by Williams, Pieranski and Cladis [110] and by Meyer [98]. Both studies used the nematic compound MBBA in glass capillaries where the inner wall was coated with a surfactant for homeotropic alignment. The capillary radius in these studies varied from 20 μm to 200 μm. Since the direction of escape ('up' or 'down' the cylinder axis) is arbitrary, Williams et al also found a regular set of
) bends into the cylinder axis as one moves from the periphery to the center. Indeed, this Escaped Radial (ER) configuration was confirmed by optical microscopy in 1972 by Williams, Pieranski and Cladis [110] and by Meyer [98]. Both studies used the nematic compound MBBA in glass capillaries where the inner wall was coated with a surfactant for homeotropic alignment. The capillary radius in these studies varied from 20 μm to 200 μm. Since the direction of escape ('up' or 'down' the cylinder axis) is arbitrary, Williams et al also found a regular set of  point defects where an upward escape encountered a downward escape and vice versa. Considering a certain length of the cylinder we may call this configuration Escaped Radial with Point Defects (ERPD, figure 28(b)).
point defects where an upward escape encountered a downward escape and vice versa. Considering a certain length of the cylinder we may call this configuration Escaped Radial with Point Defects (ERPD, figure 28(b)).
Figure 28. Schematic illustrations of the four different director configurations considered for cylindrical confinement with homeotropic surface anchoring. The top drawings show a circular cross section perpendicular to the cylinder and the bottom drawings show a cross section through the middle of the cylinder, along the cylinder axis. Nail heads point down below the paper plane. PR = perpendicular cross section radial; ERPD = escaped radial with point defects; PP = perpendicular cross section polar; PPLD = perpendicular cross section polar with line defects.
Download figure:
Standard image High-resolution imageSome 20 years later the focus shifted to cylindrical cavities of radically smaller diameter. LCs were now filled into the pores of Nucleopore (polycarbonate) or Anopore (alumina) membranes, where the radius is frequently below 1 μm. Classic optical microscopy does not provide a resolution high enough to interrogate  (
( in such thin channels, thus most studies were done using nuclear magnetic resonance (NMR). Crawford, Allender and Doane [175] filled selectively deuterated 5CB into a series of Nucleopore membranes, varying the pore radius from 0.05 μm to 0.5 μm. In some cases they left the pristine polycarbonate in contact with the LC, in others they coated the pore walls with lecithin, a classic agent for promoting homeotropic alignment. The key question was whether the ERPD configuration would still be energetically favorable in these narrow cylindrical cavities, as the required bend deformation would now take place over such a small range that the elastic distortion cost would be substantial.
in such thin channels, thus most studies were done using nuclear magnetic resonance (NMR). Crawford, Allender and Doane [175] filled selectively deuterated 5CB into a series of Nucleopore membranes, varying the pore radius from 0.05 μm to 0.5 μm. In some cases they left the pristine polycarbonate in contact with the LC, in others they coated the pore walls with lecithin, a classic agent for promoting homeotropic alignment. The key question was whether the ERPD configuration would still be energetically favorable in these narrow cylindrical cavities, as the required bend deformation would now take place over such a small range that the elastic distortion cost would be substantial.
The result depends on the anchoring strength: for strong homeotropic anchoring—surprisingly given by the naked polycarbonate—the ERPD configuration developed down to 0.05 μm pore radius. Lecithin actually gave weaker homeotropic anchoring, such that ERPD was found only at 0.5 μm radius. For thinner cavities another configuration developed, which we here refer to as Perpendicular cross section Polar (PP, figure 28(c))3. The homeotropic anchoring breaks down at two antipodes on the cylinder periphery. This allows a defect-free  , entirely within the cross section perpendicular to the cylinder axis, with only moderate splay-bend deformation. Interestingly, the authors also succeeded in establishing the saddle-splay constant K24 of 5CB, finding that it is comparable to the bulk elastic constants. Kralj and Zumer later proposed [176], based on numerical simulation, that a modification of the PP configuration may arise for strong homeotropic alignment. In this case two
, entirely within the cross section perpendicular to the cylinder axis, with only moderate splay-bend deformation. Interestingly, the authors also succeeded in establishing the saddle-splay constant K24 of 5CB, finding that it is comparable to the bulk elastic constants. Kralj and Zumer later proposed [176], based on numerical simulation, that a modification of the PP configuration may arise for strong homeotropic alignment. In this case two  disclination lines, developing along the cylinder axis, allows the homeotropic anchoring to be retained everywhere on the surface, while the deformations in the perpendicular circular cross section are moderate. We refer to this configuration as perpendicular cross section polar with line defects, PPLD (figure 28(d)).
disclination lines, developing along the cylinder axis, allows the homeotropic anchoring to be retained everywhere on the surface, while the deformations in the perpendicular circular cross section are moderate. We refer to this configuration as perpendicular cross section polar with line defects, PPLD (figure 28(d)).
In a complementary experimental study, Crawford et al studied Anopore membranes with 0.2 μm diameter pores, in which the alumina surface was coated with fatty acids of varying chain length, acting as surfactant [177]. The naked alumina promotes planar alignment whereas the fatty acid increasingly promotes homeotropic alignment the longer the chain. This allowed them to detect an alignment transition from the PP configuration for long fatty acids, to fully planar alignment for chain lengths of 6–7 carbon atoms. The LC thus adopts a uniform axial (UA) configuration, where  points along the cylinder axis everywhere (figure 30(a)).
points along the cylinder axis everywhere (figure 30(a)).
Crawford, Stannarius and Doane conducted an interesting study where the high surface-to-volume ratio of Anopore membranes was used to induce nematic order at temperatures high above the bulk clearing point  [178]. Depending on the surface treatment slightly different results were obtained, but in all cases nematic order was detected close to the solid surfaces at least 15 K above
[178]. Depending on the surface treatment slightly different results were obtained, but in all cases nematic order was detected close to the solid surfaces at least 15 K above  . The same phenomenon was later detected by Lagerwall et al using Raman spectroscopy on a nematic mixture contained within electrospun fibers with a PVP-titania composite sheath [179]. Here anisotropic order was detected even 20 K above
. The same phenomenon was later detected by Lagerwall et al using Raman spectroscopy on a nematic mixture contained within electrospun fibers with a PVP-titania composite sheath [179]. Here anisotropic order was detected even 20 K above  .
.
While the majority of experiments have been conducted on uniform confining cylinders, i.e. with constant radius (and the corresponding theory was developed for the same situation), Matthias and Kitzerow conducted a combined experimental-simulation study of the behavior of a nematic inside channels of sinusoidally varying diameter [180]. The channels were electrochemically etched out of a silicon substrate, and the walls were then coated with surfactant to ensure strong homeotropic alignment, hence the ERPD configuration was expected. The pore diameter was about an order of magnitude larger than in Anopore/Nucleopore membranes, varying between 2.2 μm at the necks and 3.3 μm at the bellies.
A smart choice was to work with a glass forming LC polymer. This allowed the researchers to fill the pores at high temperature, anneal the sample in the N phase until an equilibrium configuration is stable, and then quench-cool the sample into the glassy state. The silicon substrate was removed chemically, allowing a confocal microscopy characterization of the nematic glass. While the basic ER configuration was indeed confirmed, the hedgehog point defects split into disclination rings, the cross section of which is illustrated on the right in figure 29. Because of the sinusoidal diameter modulation the ring defects were regularly spaced, the positive-signed disclination rings appearing at the bellies and the negative-signed ones at the necks. These observations of LC behavior in cylinders with modulated diameter are highly relevant for the understanding of LCs in fibers, formed e.g. by electrospinning, since a certain modulation of fiber diameter is not uncommon, see section 4.2.
Figure 29. Escaped Radial with Defect Rings (ERDR) configuration (right) detected when a glass-forming nematic LCP was filled into homeotropic-aligning pores with sinusoidally varying diameter (left). Compilation of two images, reprinted from [180], with the permission of AIP Publishing.
Download figure:
Standard image High-resolution imageThis appears to be the first experimental report of hedgehog point defects splitting into disclination rings in cylinders, but it turns out that the modulated pore diameter is not necessary for this to occur. In fact, a number of theoretical papers predicted that point defects are unstable and should always be replaced by nanometer-sized disclination rings [95, 100, 105, 181–183]. In an elegant recent experimental study [184], the Abbott group verified that this is in fact the case for Q = +1 radial hedgehogs, replaced by an  line disclination bent into a nano-sized loop, but not for Q = −1 hyperbolic hedgehogs.
line disclination bent into a nano-sized loop, but not for Q = −1 hyperbolic hedgehogs.
They filled a 400 μm diameter capillary, prepared with homeotropic-inducing aligning agent, with 5CB to which was added fluorescently labeled and photopolymerizable phospholipids, respectively. These lipids spontaneously aggregate within defect lines above a critical concentration [185], allowing the researchers to localize defects and even form solid objects templated by them. When studying the capillary using fluorescence microscopy the authors found lipid aggregation in the radial Q = +1 hedgehog but not in the hyperbolic Q = −1. Moreover, imaging the solids formed by polymerizing the aggregated lipids in transmission electron microscopy (TEM), they found the objects to be not spheres, but tori (rings). A calculation of the free energies of  point defects and
point defects and  disclination rings confirmed that the positive-signed hedgehog was unstable with respect to the disclination ring, but not the negative-signed hedgehog. A question that may be interesting to investigate in the future is why these defect rings were orders of magnitude smaller than those found by Matthias et al [180].
disclination rings confirmed that the positive-signed hedgehog was unstable with respect to the disclination ring, but not the negative-signed hedgehog. A question that may be interesting to investigate in the future is why these defect rings were orders of magnitude smaller than those found by Matthias et al [180].
4.1.2. Nematics in cylinders with planar surface anchoring.
With planar surface anchoring, the intuitive expectation is that the director aligns without deformation along the cylinder axis, in a so-called uniform axial (UA) configuration (figure 30(a)), at least for thin cylinders. Interestingly, Ondris-Crawford et al succeeded in preparing a sample where planar anchoring was promoted, yet with the preferred direction in the interface being azimuthal [186]. They coated the polycarbonate surface of Nucleopore membranes with polyimide, benefiting from a production-induced inner corrugated topography of the pores to create a preference for circumferential rather than axial alignment. Having achieved this unusual boundary condition for nematics in cylindrical confinement, they contemplated three possible configurations (figures 30(b)–(d)): perpendicular cross section concentric (PC), perpendicular cross section bipolar (PB) and escaped twisted (ET). Unsurprisingly, the PC configuration, with its extremely strong bend deformation at the core, was never observed. For small cavity sizes, with radii of 0.2–0.3 μm, the PB configuration was detected, whereas for radius greater than 0.3 μm a transition to the ET configuration was found.
Figure 30. Schematics of the four director configurations considered for cylindrical confinement with planar surface anchoring. The top drawings show a circular cross section perpendicular to the cylinder and the bottom drawings shows a cross section through the middle, along the cylinder axis. Nail heads point down below the paper plane. UA = uniform axial; PC = perpendicular cross section concentric; PB = perpendicular cross section bipolar; ET = escaped twisted; rh = right-handed; lh = left-handed; PD = point defect.
Download figure:
Standard image High-resolution imageThe ET configuration is intriguing, as it means that an achiral LC spontaneously develops a twist. As in any such case of spontaneous chiral symmetry breaking, the twisting sense can be left- or right-handed, each occurring with equal probability, hence interesting phenomena happen where left- and right-handed regimes meet [187]. The twist can either be unwound at the meeting point, resulting in a wall that locally violates the boundary condition, or a hedgehog point defect can form at the center. This costs much energy locally but it respects the boundary condition, hence it may be preferable in case of strong anchoring at the cylinder interface. Considering the results discussed above, suggesting that a Q = +1 point defect is unstable with respect to a nanoscopic ring-shaped + defect line, it may be that—in practice—the point defect (PD) connection sketched towards the bottom of figure 30(d) should rather be a defect ring.
defect line, it may be that—in practice—the point defect (PD) connection sketched towards the bottom of figure 30(d) should rather be a defect ring.
The saddle-splay term F24 of the elastic energy, (5), was important for explaining the transition to the escaped twisted state in the study by Ondris-Crawford et al. Recently, in three separate studies [187–189], F24 was found to generate twist also in planar-aligning cylinders of much greater thickness, and without any tangential symmetry breaking promoting concentric to axial alignment of  . In the first case [188] the cylinder was bent into a torus, following an ingenious preparation procedure where 5CB nematic is injected into a yield-stress material subjected to continuous rotation. Because a torus has a topological Euler characteristic
. In the first case [188] the cylinder was bent into a torus, following an ingenious preparation procedure where 5CB nematic is injected into a yield-stress material subjected to continuous rotation. Because a torus has a topological Euler characteristic  (see section 3.3) the total topological defect charge on the surface of a planar-aligned nematic torus must be zero. Hence no surface defect formation is expected, in contrast to the case of a planar-aligned shell or droplet. Indeed, no defects were formed on a simple torus, but the surprising observation was that
(see section 3.3) the total topological defect charge on the surface of a planar-aligned nematic torus must be zero. Hence no surface defect formation is expected, in contrast to the case of a planar-aligned shell or droplet. Indeed, no defects were formed on a simple torus, but the surprising observation was that  was always twisted, although no chiral dopant had been added.
was always twisted, although no chiral dopant had been added.
It is perhaps less surprising that F24 generates twist in a torus than in a cylinder, since the inside of a torus is indeed saddle-shaped. Importantly,  only experiences this saddle shape if the surface director is neither parallel nor perpendicular to the local symmetry axis of the torus. In these two special cases it would experience pure bend, but for any other orientation, i.e. in a twisted configuration, it will experience the saddle-splay on the inside. If this is difficult to visualize, it becomes clear by simply drawing lines in different directions on a donut. Thus, if K24 > 0, making F24 negative and thereby promoting saddle-splay, a twisted ground state seems plausible for a torus. Pairam et al complemented their experimental study with numerical simulations, finding that, indeed, the tighter the torus, the more a twist will reduce the free energy. However, even as the torus gets larger and larger, eventually to an infinite major radius, corresponding to a straight cylinder, they found that a twist can be promoted if
only experiences this saddle shape if the surface director is neither parallel nor perpendicular to the local symmetry axis of the torus. In these two special cases it would experience pure bend, but for any other orientation, i.e. in a twisted configuration, it will experience the saddle-splay on the inside. If this is difficult to visualize, it becomes clear by simply drawing lines in different directions on a donut. Thus, if K24 > 0, making F24 negative and thereby promoting saddle-splay, a twisted ground state seems plausible for a torus. Pairam et al complemented their experimental study with numerical simulations, finding that, indeed, the tighter the torus, the more a twist will reduce the free energy. However, even as the torus gets larger and larger, eventually to an infinite major radius, corresponding to a straight cylinder, they found that a twist can be promoted if  [188].
[188].
The twist in straight cylinders with degenerate planar boundary conditions was found last year in two independent studies [187, 189]. In these cases, the thermotropic 5CB was replaced by lyotropic chromonic nematics, formed by aqueous solutions of the dyes sunset yellow (SSY) [187] and disodium chromoglycate (DSCG) [189], respectively. Chromonics are convenient because they have exceptionally low twist constant K2. Thus,  , ensuring a twisted ground state in the cylinder although both chromonic nematics are non-chiral. The theoretical analysis of the effect of F24 on
, ensuring a twisted ground state in the cylinder although both chromonic nematics are non-chiral. The theoretical analysis of the effect of F24 on  is quite involved and the two papers follow slightly different approaches, coming to qualitatively identical conclusions but a quantitative offset: while Nayani et al [189] reproduce the
is quite involved and the two papers follow slightly different approaches, coming to qualitatively identical conclusions but a quantitative offset: while Nayani et al [189] reproduce the  condition found in the study of tori by Pairam et al [188], Davidson et al [187] require
condition found in the study of tori by Pairam et al [188], Davidson et al [187] require  to stabilize a twisted
to stabilize a twisted  .
.
Both author teams conclude that most thermotropics such as 5CB will generally not have a sufficiently large K24 compared to K2 to generate a twisted configuration in degenerate planar-aligning cylinders. However, very recently such twisted states appear to have been detected in electrospun fibers containing 5CB, without any chiral dopant present [190]. These fibers are substantially smaller (diameter on the order of a μm) than the glass capillaries used in the chromonics studies (100 and 400 μm, respectively) but both theoretical analyses predict that the effect should be scale invariant. While the results on the electrospun fibers are preliminary, and further investigations both of  (
( and of possible deviations from a degenerate planar-aligning cylindrical cavity are required, the observations may indicate that K24 is still slightly larger than K2 in 5CB, and that this difference is sufficient to stabilize a twisted ground state.
and of possible deviations from a degenerate planar-aligning cylindrical cavity are required, the observations may indicate that K24 is still slightly larger than K2 in 5CB, and that this difference is sufficient to stabilize a twisted ground state.
4.1.3. Chiral nematics in cylinders.
While twisted structures arising in non-chiral nematics are surprising at first sight, this is what we expect when a chiral LC is used, whether by using chiral mesogens or by adding a chiral dopant. The non-trivial question is in what way  will twist within the cylinder, and again it depends sensitively on the boundary conditions. One of the first studies, by Cladis et al, focused on an N* phase formed on heating from SmA*, contained in a cylindrical capillary imposing radial boundary conditions [191]. The authors also studied the effect of an applied magnetic field. Because neither twist nor bend is compatible with the SmA/SmA* geometry, the authors considered PR (figure 28(a)) as starting configuration (later theoretical studies, discussed below, indicate that this may not have been quite appropriate). As mentioned above, the PR configuration is unstable in N/N* and consequently the authors detected a splitting directly after the phase transition into two
will twist within the cylinder, and again it depends sensitively on the boundary conditions. One of the first studies, by Cladis et al, focused on an N* phase formed on heating from SmA*, contained in a cylindrical capillary imposing radial boundary conditions [191]. The authors also studied the effect of an applied magnetic field. Because neither twist nor bend is compatible with the SmA/SmA* geometry, the authors considered PR (figure 28(a)) as starting configuration (later theoretical studies, discussed below, indicate that this may not have been quite appropriate). As mentioned above, the PR configuration is unstable in N/N* and consequently the authors detected a splitting directly after the phase transition into two  line defects, essentially developing the PPLD configuration of figure 28(d), with the modification that the disclinations spiral due to the chirality. Moreover, they found an additional helically modulated line, which they postulated to be an s = +2 non-singular line [191].
line defects, essentially developing the PPLD configuration of figure 28(d), with the modification that the disclinations spiral due to the chirality. Moreover, they found an additional helically modulated line, which they postulated to be an s = +2 non-singular line [191].
Close to the N*-SmA* phase transition, heating/cooling yields strong simultaneous variations in elastic constants and helix pitch p0 (on cooling towards a second order N*-SmA* transition p0 must diverge and become infinite), rendering this study rather complex. Moreover, kinetic aspects are important, hence the speed of heating influenced the behavior strongly. An elegant way to systematically study  (
( as a function of p0 in the long-pitch regime without the complication of simultaneous changes in the elastic constants was presented by Kitzerow and co-workers [192]. They used a chiral dopant known to exhibit a helical twisting power inversion at a specific temperature, such that it induces helices with opposite handedness above and below this temperature. At the inversion point p0 is infinite, thus there is no difference in
as a function of p0 in the long-pitch regime without the complication of simultaneous changes in the elastic constants was presented by Kitzerow and co-workers [192]. They used a chiral dopant known to exhibit a helical twisting power inversion at a specific temperature, such that it induces helices with opposite handedness above and below this temperature. At the inversion point p0 is infinite, thus there is no difference in  (
( from a non-chiral nematic at exactly this temperature.
from a non-chiral nematic at exactly this temperature.
The authors prepared capillaries with diameters ranging from 25 to 200 μm with agents for hometropic and planar boundary conditions, respectively, in the latter case also imposing (weak) director anchoring along the cylinder by means of photoalignment. In homeotropic-aligning cylinders at the helix inversion temperature they reproduced the ERPD configuration (figure 28(b)) well known from studies of achiral nematics under the same type of confinement. A peculiar observation was the behavior of the hedgehog point defects as the temperature was slightly raised or lowered from the helix inversion point: while p0 was still too long for any sign of helix formation to be detected in the capillary, the radial hedgehog defects moved towards one capillary wall whereas the hyperbolic defects stayed in the middle of the capillary, see figure 31. At the time of publication, the authors explained the difference by the inability of the hyperbolic defect to satisfy the homeotropic boundary conditions. In light of the recent experimental results of Wang et al [184] mentioned above, demonstrating that the radial hedgehog defects are in fact no point defects but nanoscopic defect rings, it would be worthwhile to revisit this difference between radial and hyperbolic hedgehog in weakly chiral systems.
Figure 31. Polarizing microscopy textures in a homeotropic-aligning cylindrical capillary filled with an N* mixture exhibiting a helix inversion at 38°C, as a function of temperature T and ratio between the capillary radius R and the pitch (consistently denoted p0 in the main text but labelled P in this figure). Reprinted figure with permission from [192], Copyright (1996) by the American Physical Society.
Download figure:
Standard image High-resolution imageAs p0 decreased further on heating or cooling from the inversion point, the defect pattern gradually increased in complexity, first with a sinusoidal periodicity remaining visible, finally succeeded by a chaotic pattern. Representative snapshots for different p0 are shown in figure 31. The pitch in this study was never very short, its minimum value being several tens of micrometers. Within the cylinder diameter range investigated, it appears that only the ratio of pitch and capillary diameter was important, hence one may anticipate a similar behavior for short-pitch cholesterics in very thin cylinders, such as those formed by electrospinning (see below), if strong homeotropic anchoring can be ensured.
In the planar-aligning cylinders a perfect UA configuration was found at the inversion point, without any sign of twist, see figure 32. While this may be interpreted as a sign of F24 playing a less important role here than in the cylinder-enclosed chromonics discussed above [187, 189], we note that in this case the boundary conditions were not degenerate planar, but with anchoring for axial director alignment. It would be interesting to revisit also this experiment with degenerate planar anchoring conditions.
Figure 32. Polarizing microscopy textures in a planar-aligning cylindrical capillary filled with a cholesteric mixture exhibiting a helix inversion at 55.6°C, as a function of temperature T and inverse pitch p−1. Reprinted figure with permission from [192], Copyright (1996) by the American Physical Society.
Download figure:
Standard image High-resolution imageFar away from the inversion point, where p0 is much smaller than the capillary diameter, a periodically striped 'fingerprint' texture was observed (figure 32). The lines ran along the capillary, indicating that  adopted a radially twisted arrangement, as known from the so-called double-twist (DT) cylinders (figure 33(c)) characteristic of blue phases. The director must be aligned along the capillary axis at the boundaries and at the center, to comply with the boundary conditions, hence an integer number of helix pitches must fit within the diameter. As the temperature was shifted towards the inversion point the fingerprint lines therefore did not move away from each other continuously, but the pitch quantization imposed by the boundary conditions forced them to do so in discrete steps, each time with a pair of lines disappearing. The confinement locks the pitch into non-equilibrium values
adopted a radially twisted arrangement, as known from the so-called double-twist (DT) cylinders (figure 33(c)) characteristic of blue phases. The director must be aligned along the capillary axis at the boundaries and at the center, to comply with the boundary conditions, hence an integer number of helix pitches must fit within the diameter. As the temperature was shifted towards the inversion point the fingerprint lines therefore did not move away from each other continuously, but the pitch quantization imposed by the boundary conditions forced them to do so in discrete steps, each time with a pair of lines disappearing. The confinement locks the pitch into non-equilibrium values  . The same effect was later described by Enz et al [193] for selectively reflecting short-pitch cholesterics, confined inside the much thinner cylindrical cavity provided by electrospun fibers, as discussed in section 4.3.1.
. The same effect was later described by Enz et al [193] for selectively reflecting short-pitch cholesterics, confined inside the much thinner cylindrical cavity provided by electrospun fibers, as discussed in section 4.3.1.
Figure 33. Drawings of possible director fields of cholesterics in cylindrical capillaries with planar-aligning boundary conditions. ATPB = axially twisted Perpendicular cross section Bipolar; ED = eccentric double-twist; DT = double-twist. Adapted with permission from (a) [194] and (b−c) [192], Copyright (1994) and (1996), respectively, by the American Physical Society.
Download figure:
Standard image High-resolution imageSurprisingly, when p0 tightened again after having passed the inversion point, the fingerprint texture reflecting a double-twist cylinder configuration did not reappear. Instead, the texture transitioned into a complex but regular spiral pattern, see the right side of figure 32. Supported by computer- simulated polarizing microscopy textures the authors conjectured that this pattern was due to an Eccentric Double-twisted (ED) cylinder configuration (figure 33(b)). As p0 decreased further, instabilities in the helical arrangement were detected once p0 was below the radius of the cylinder. These helical instabilities, as well as the double-twist configurations at slightly longer p0, were also detected in an earlier study by Lequeux and Kleman [195].
The first study of cholesterics in smaller cylindrical confinement than what glass capillaries offer was reported by Ondris-Crawford et al in 1994 [194]. NMR was again used to characterize the configurations in the cylindrical pores of alumina anopore membranes, with diameter of 0.1 μm. As mentioned above, the uncoated Anopore membrane induces planar alignment, and the anchoring is not degenerate but concentric, perpendicular to the cylinder axis. In these very thin cylinders the authors found an alignment transition for p0 < 1 μm from the DT configuration to a configuration in which the helix develops along the cylinder. The Perpendicular cross section is of the Bipolar type, with the bipolar axis direction being helically modulated (figure 33(a)); we may call this configuration the axially twisted perpendicular cross section bipolar (ATPB) configuration.
This alignment transition was not seen by Kitzerow et al in their study of much thicker planar-aligning cylinders, for corresponding pitch-to-diameter ratios [192]. It has also not been detected in the first optical studies of cholesterics in very thin cylinders, conducted on coaxially electrospun fibers [193, 196, 197]. In these cases cholesterics with pitch short enough to yield selective reflection were confined inside channels as narrow as 0.5 μm [196], and selective reflection was always detected, suggesting a (possibly distorted) DT configuration rather than an ATPB configuration, which should not be reflective when studied in a direction orthogonal to the fiber axis.
Matthias et al studied also cholesterics in the cylinders with modulated diameter [198]. As with the study of non-chiral nematics they chose a glass-forming LC, which they could then investigate by fluorescence polarizing microscopy in the glassy state after the template had been removed. The experimental study was complemented with a thorough theoretical treatment. For very long pitch they again found disclination rings rather than point defects in an escaped radial structure, positioned regularly along the channel thanks to the sinusoidally modulated diameter. For pitch comparable to the pore size, a twisted escaped radial structure was found.
4.1.4. The SmA phase in cylinders.
A variety of director fields might be expected when different smectics are confined in a cylindrical space. Here we will discuss only the response of SmA/SmA*, with planar as well as homeotropic boundary conditions. While the chiral SmA* phase has reduced symmetry and thus a different response to electric fields than non-chiral SmA [12], the structures of the chiral and non-chiral versions are identical. Some studies of other smectics exist and it may be a stimulating topic for future work to investigate different smectic phases within cylinders with varying boundary conditions.
The fact that SmA/SmA* cannot sustain twist or bend means that no other deformations than splay should appear in an equilibrium director field configuration for pure SmA/SmA*. Specifically, this would mean that the director escape in the third dimension that favors the ERPD over the PR configuration (figure 28) is no longer expected. As a consequence, the PR configuration was early on thought to be seen in homeotropic-aligned SmA/SmA* in cylinders [191], as mentioned above.
Ondris-Crawford et al did a corresponding study with achiral 8CB in the thin pores of a Nucleopore polycarbonate membrane to follow the effect of diverging K3 on cooling the N phase towards the second-order transition to SmA, potentially extracting information also about surface anchoring W and the saddle-splay constant K24 [199]. Their theoretical analysis of the elastic deformations in these very narrow cylinders suggested that a direct transition from ERPD to PR should be found in case of strong anchoring, and that the temperature of the transition can be used to establish K24. However, the homeotropic anchoring in their nucleopore membranes was too weak, bringing the system into a regime where also the PP configuration is stable. They were not able to give an absolute numerical value of the saddle-splay constant but they could conclude that  in 8CB.
in 8CB.
A more elaborate theoretical study of possible smectic arrangements inside narrow cylinders with homeotropic surface anchoring was carried out a few years later by Kralj and Zumer [200]. They expanded the viewpoint first by considering that the confinement-induced frustration may lead to an extremely thin prevailing nematic core that releases the elastic stress by letting  escape in the third dimension through a centrally localized ERPD configuration, although the temperature is below
escape in the third dimension through a centrally localized ERPD configuration, although the temperature is below  of a bulk sample. This is similar to the model of Cladis and Torza discussed in section 3.3.4, for explaining the striped patterns forming during a N-SmA transition of a sample subject to hybrid boundary conditions, with homeotropic and planar anchoring on the two surfaces [138].
of a bulk sample. This is similar to the model of Cladis and Torza discussed in section 3.3.4, for explaining the striped patterns forming during a N-SmA transition of a sample subject to hybrid boundary conditions, with homeotropic and planar anchoring on the two surfaces [138].
Second, Kralj and Zumer contemplated that, at least for weak homeotropic anchoring, the core may adopt layers perpendicular to the fiber or tilted in a chevron geometry. Their analysis revealed that the PR configuration is in fact extremely unlikely, and that rather a supercooled nematic ERPD core exists in case of strong homeotropic anchoring, whereas weak anchoring yields chevron or perpendicular smectic layers. This would suggest that the core of any smectic arrangement with concentric layers, for instance in the Dupin cyclides that often form spontaneously in bulk samples with little control of alignment [5], should be nematic in an ERPD configuration. Considering today's possibilities to confirm such structures on the nanoscale, as demonstrated by Wang et al [184], this motivates new studies of smectics in frustrated geometries.
Using calorimetry, Iannacchione and Finotello studied the N-SmA transition of 8CB in the 0.2 μm pores of Anopore membrane (alumina), prepared for planar and homeotropic surface anchoring, respectively [201]. They found a profound influence on the N-SmA as well as N-isotropic transitions, both broadening considerably and reducing in transition enthalpy as an effect of the confinement, for either alignment geometry. Moreover, the clearing point was always reduced in confinement, whereas the N-SmA transition was shifted to lower temperatures with planar alignment but to higher temperatures with radial alignment. Unfortunately no information was given on sample history during the experiments, in particular concerning whether the measurements were done on cooling or heating, and the time for which the sample had stayed in the preceding phase prior to the experiment.
These aspects can be very important for the behavior of LCs in strong cylindrical confinement, as shown in a later calorimetry study by Enz et al of 8CB inside electrospun fibers with PVP sheath [202]. While this study was restricted to planar alignment (as confirmed by x-ray scattering on the fibers), increase as well as decrease of the N-SmA transition could be found, depending on the sample history. On heating, the SmA-N transition was considerably increased compared to the bulk value of  , up to some 5K for the thinnest fibers studied (outer fiber diameter less than 2 μm; inner core diameter was not assessed). However, when cooling back from the isotropic phase, through the nematic, the N-SmA transition was absent throughout the experiment. The N-SmA transition thus exhibits extreme supercooling inside the planar-aligning fibers. The encapsulated LC stayed in the N state well below room temperature, as confirmed by a subsequent heating experiment where only the clearing transition was detected. However, if the fibers were annealed at room temperature for several weeks, the smectic phase reformed and the SmA-N transition peak was recovered in the calorimetry curves, shifted to higher temperatures compared to the bulk value.
, up to some 5K for the thinnest fibers studied (outer fiber diameter less than 2 μm; inner core diameter was not assessed). However, when cooling back from the isotropic phase, through the nematic, the N-SmA transition was absent throughout the experiment. The N-SmA transition thus exhibits extreme supercooling inside the planar-aligning fibers. The encapsulated LC stayed in the N state well below room temperature, as confirmed by a subsequent heating experiment where only the clearing transition was detected. However, if the fibers were annealed at room temperature for several weeks, the smectic phase reformed and the SmA-N transition peak was recovered in the calorimetry curves, shifted to higher temperatures compared to the bulk value.
The authors explained these surprising observations as a result of the mesogens at the interface to the polymer sheath being strongly anchored at that interface, in an arrangement reflecting the history. After long annealing at room temperature, allowing the SmA phase to develop, the sheath-anchored mesogens are in a smectic arrangement, promoting the layering and thereby raising  . However, if the positional order is lost by heating into the nematic or isotropic state, then the mesogens close to the polymer sheath are anchored without a layered arrangement, promoting the N state in a narrow cylinder where the influence of surface molecules can penetrate throughout the volume of the sample. The broadening and weakening of transition peaks seen by Iannacchione and Finotello was reproduced in this study, but the clearing point on heating was always raised (the shift was much smaller than for
. However, if the positional order is lost by heating into the nematic or isotropic state, then the mesogens close to the polymer sheath are anchored without a layered arrangement, promoting the N state in a narrow cylinder where the influence of surface molecules can penetrate throughout the volume of the sample. The broadening and weakening of transition peaks seen by Iannacchione and Finotello was reproduced in this study, but the clearing point on heating was always raised (the shift was much smaller than for  ) in the fibers.
) in the fibers.
4.2. Electrospinning basics
4.2.1. A brief note on the development & popularity of electrospinning.
Electrospinning is the process by which solidified filaments are drawn from a viscous, continuously flowing polymer solution by the action of an electric field. While the modern term 'electrospinning' was popularized by Doshi, Reneker, and many other researchers in the latter end of the 20th century [203–207], the process had in fact already appeared in many patents filed during the period 1900–1940 by John Francis Cooley, and Anton Formhals. It was then referred to as 'electrostatic' or 'electrical spinning' [208–210].
During the mid-1900s, much of the world moved towards a fast paced industrially and commercially developing economy, and many were attempting to exploit the electrospinning process for commercial gains. This explains the appearance mainly of patents rather than fundamental research articles on the topic during this time [211–214]. It wouldn't be until the 1960s, and then again, in the 1990s, when the rigorous theoretical and experimental frameworks for truly understanding the process would be developed. Sir Geoffrey Ingram Taylor contributed to the former by first accurately proposing a model for the characteristic shape of the prolate polymer solution droplet (now referred to as the Taylor cone) known to emerge from the charged spinneret proceeding the fiber forming process [215, 216].
Since then, a large number of theoretical and experimental works for comprehensively explaining the intricate level of instabilities observed during electrospinning, such as the onset of jet formation and the final bending trajectories of the fiber formed from the jet, have been published [217–222]. At the forefront, Reneker and Yarin were the leaders in revitalizing modern 21st century interest in the process by not only further characterizing the bending instabilities of the fluid jet, but also systematically studying the parameters affecting various types of fiber formation [217, 223, 224]. Ultimately, while these parameters have succumbed to countless debates and scrutiny by both experimentalists and theoreticians over the years, it has all culminated into the identification of a select handful of both processing parameters (set-up and apparatus related), and solution specific parameters (such as concentration, polymer type, polymer molar mass M, and solvent type) which influence fiber production the most. These parameters will be discussed in section 4.2.2.
The 2000s saw an exponential increase in the research devoted to electrospinning [208]. The technique has proved to be extremely useful for the development of advanced materials, as well as the advanced functioning of other processes in many fields, from air filtration [225, 226] and biotechnology [227] to sensors [228] and waste remediation [229]. The introduction of LCs to the field of electrospinning is rather recent. Interestingly, the two discoveries—the electrospinning method and the liquid crystalline state of matter—were formally first reported by C.V. Boys, and Friedrich Reinitzer, respectively, within only one year of each other in 1887, and 1888. And yet, the first study on combining LCs with electrospinning was published only just nine years ago. Since then, though, it has been steadily growing in popularity.
The first electrospun LCE fibers were presented by Wendorff and Finkelmann et al [230]. About one year later Godinho and co-workers demonstrated electrospun fibers from lyotropic LCP solutions [231], and within the same year Lagerwall, Xia and co-workers demonstrated the incorporation of low molar mass LCs inside the core of coaxially electrospun fibers [179]. Our group continuously developed the coaxial approach [190, 193, 202, 232, 233], while two years later West and co-workers [234] demonstrated that LC core fibers could be spun from mixing LC and polymer in a common solvent, without separating them into two channels. This single-phase electrospinning relies on in situ phase separation during solvent evaporation for acquiring the final coaxial LC-polymer fiber morphology.
Ultimately, the realization that LC functionalized fibers may prove to be useful in the future for the development of highly functional, environmentally responsive textile fabrics is steadily moving toward the forefront. In the sections following the discussion of how the electrospinning process works, and the parameter considerations that should be considered during the fiber development process, we discuss how electrospun LC-fibers, and LC-elastomeric fibers are already showing high potential for becoming the next non-electronic functional gas sensors.
4.2.2. How does the electrospinning process work?
Despite the many complex and interdependent variables that must be accounted for in order to properly analyze an electrospinning experiment, it is extensively used by researchers in many independent scientific, and even design-related [235], fields. The simple reason is that the process provides immense flexibility for experimenting with fiber production more quickly than other fiber spinning processes and that the set-up (see figure 34) is small-scale, not very complex and comparatively inexpensive. An experiment starts with dissolving a chosen polymer with appropriate molar mass in a compatible solvent until it is homogenously dispersed. This solution is mechanically pumped via an external device (often a syringe pump) through a metal spinneret which is connected to a high voltage power supply. In case of coaxial electrospinning a thin second capillary runs at the center of the main spinneret, allowing ejection of a core fluid inside the polymer solution, see figure 35.
Figure 34. A schematic of the generalized electrospinning process showing the most basic components needed, and the connections necessary, to create nano- and micro- fibers.
Download figure:
Standard image High-resolution imageFigure 35. Schematic illustration of coaxial electrospinning with LC core. Reproduced from [202]. CC BY 2.0.
Download figure:
Standard image High-resolution imageA strong electric field (∼kV m−1) is then established between spinneret and a grounded counter electrode some 10–20 cm away. As the solution in the spinneret becomes charged, the droplet protruding from the tip undergoes distortion into a conical shape (the Taylor cone) as a result of the conflict between surface tension—promoting a spherical droplet shape—and the electrostatic attraction to the grounded counter electrode acting on the high density of charges in the droplet. Once the voltage passes a threshold, usually 10–30 kV (depending on solution viscosity, type of polymer and solvent, and the ionic content), the combined action of attraction to the ground electrode and self-repulsion between the concentrated like-charged ions overpowers the surface tension and a thin jet is expelled from the tip of the Taylor Cone.
The polymer solution carried by the jet undergoes a series of helical whipping and bending instabilities as solvent evaporates. The initial jet formation and the subsequent instabilities (figure 36) are triggered, in part, by the fluid jet attempting to lower the charge density by extending [236], in part by the electrostatic self-repulsion between like-charged ions along the jet [217]. The equations describing the initial stage of the process have been derived by Bugarski et al [237, 238], Loeb et al [239] and Yarin et al [240], respectively. The final result is a solidified, continuous fiber collected as a non-woven mat on the grounded electrode or on another collector inserted between spinneret and counter electrode [217, 236].
Figure 36. Key features of the Taylor cone and polymer solution jet development. An electrified polymer solution droplet is shown in (a) (reproduced from [241]. © IOP Publishing Ltd. All rights reserved). Two high-speed camera images of the polymer jet undergoing helical whipping at the early stages of spinning are shown in (b) and (c), at 16 and 32 milliseconds after jet ejection, respectively (reprinted from [221] with the permission of AIP Publishing).
Download figure:
Standard image High-resolution imageAll components required to devise a basic electrospinning setup are shown in figure 34. Typically, the dissolved polymer solution is placed into a syringe, with an appropriately sized needle, hereafter referred to as the spinneret (often blunt ended needles between 22 gauge and 18 gauge are employed). The solution is pumped (via a syringe pump or similar device) to the needle orifice at constant rate on the order of 0.1– 1 ml h−1. The viscosity of the polymer solution is often near that of corn syrup or molasses, about 30–100 Ps (or, 3–10 Ns m−2).
If the dissolved polymer has insufficient molar mass and/or concentration, the stretching within the jet is so large that polymer coils are disconnected (there are too few entanglements) and then nothing prevents the Rayleigh–Plateau instability (already mentioned in section 3.1) to break the jet up into droplets. Such an experiment results in the electrospraying phenomenon. Electrospray involves further interesting phenomena as the solvent evaporates, leading to break-up of the initial droplets into much smaller ones, but a deeper discussion of electrospray is outside the scope of this review.
However, if the polymer solution employed contains enough molecular chain entanglements, then electrospraying will not occur. The Rayleigh–Plateau instability is now counteracted by a continuous chain of stretched-out but entangled polymer molecules along the jet. To ensure continuous spinning, polymers of  –100 kg mol−1 are used, with concentrations varying from 5% (for high M polymers) up to 30% (for low M) [242, 243].
–100 kg mol−1 are used, with concentrations varying from 5% (for high M polymers) up to 30% (for low M) [242, 243].
As the jet is stretched considerably due to the whipping instability, it will get considerably thinner before enough solvent has evaporated to solidify the polymer, and the diameter of electrospun fibers can thus reach values as low as tens of nanometers. In the case of electrospinning PAN (poly(acrylonitrile)) fibers from a DMF (N,N-dimethylformamide) solution, according to Wu et al [244], a jet emanating from a Taylor cone that is 50 μm in diameter, can be reduced during solvent evaporation to about 100 nm diameter in only a few seconds. For jets that start at sub-micron diameters, their reduction to the nanometer scale can occur within milliseconds.
While fibers collected onto the grounded collector have a landing speed of about 10 m s−1, the initial acceleration of the straight part of the jet from the Taylor cone can be up to 600 m s−2 [242]. The fact that this value is about two orders of magnitude larger than the acceleration due to the gravitational force plainly indicates that the effects gravity acting on the electrospinning jet are nearly negligible—it is also the reason why we have the flexibility of creating setups which can function horizontally or vertically without the jet being perturbed in the electrospinning process. However, in case of coaxial electrospinning, where the Taylor cone is comprised of two different fluids, generally with different density, gravity may have an influence on the symmetry of the Taylor cone. One may speculate that this could influence the structure of the produced fibers, but this is hardly investigated.
Viscoelastic shearing in the jet is largely absent as well since the speed at which fluid flows inside of the launching jet can be up to 5 m s−1 at a 2 cm distance from the Taylor cone, much lower than the speed with which the whole jet is moved due to the stretching. Once the whipping jet impacts the collector it should by this point be a solidified fiber. Depending on the type of polymer and the solvent used, the fiber can have varying morphologies, but typically, continuous and bead free fibers with circular cross-section are desired [236, 242, 245, 246].
4.2.3. The right polymer, with the right solvent, gives the right electrospun fiber.
There are many polymers which, when dissolved in the right solvent and electrospun under certain conditions, can form a very large variety of fiber morphologies, from the standard cylindrical to fibers with internal pores and cavities [247, 248] to barbed fibers [249]. Although the processing related parameters, such as the spinneret—ground electrode distance, the polymer solution flow rate and the applied voltage all can have significant effects on the final fiber quality, they come secondary to the choices of polymer and solvent. These two components dictate the solution properties, determining whether or not fibers can be spun.
When we wish to incorporate a low molar mass LC in the fiber core, whether by using a coaxial spinneret or by relying on in situ phase separation, choosing the polymer for the sheath can be non-trivial. If we use a crystallizing polymer, for instance, the elongational forces acting on the solidifying jet during spinning will cause the polymer molecules to be much better aligned than if we used an amorphous polymer. While beneficial for fiber strength, this gives the sheath strong birefringence, competing with the birefringence of the incorporated LC. In case of coaxial electrospinning, also the polymer solvent can be a tricky decision to make: if the solvent is miscible with the LC it may significantly diffuse into the core during spinning, a loss of control that may have considerable impact on the end result.
In applied research, the choice of polymer is largely limited by the intended use of the fibers. Biodegradable polymers such as poly(ethylene glycol) (PEG), and poly(l-lactide) (PLLA) may be better suited for producing tissue scaffolds due to their lack of toxicity effects [227, 250], than polystyrene (PS) or polyurethane (PU). If high tensile strength is critical, then crystallizing polymers like Nylon-6 may be useful, although we then get problems with sheath birefringence. Moreover, electrospun nylon fibers tend to be very thin, most likely a consequence of the rather low maximum values of M that are commercially available. A large number of literature reviews, books and book chapters exist, discussing how choice of polymer and solvent influence the final fiber performance [217, 242, 251].
As far as the solvents go, polar aprotic or nonpolar solvents are often recommended. While it is possible to electrospin polymers dissolved in polar protic solvents, which tend to have lower vapor pressure (e.g. water: 17.5 hPa; aqueous acetic acid: 15.3 hPa), special care needs to be taken when working with such solvents [252]. Their strong tendency for hydrogen bonding increases ionic dissociation, thus raising the conductivity of the polymer solution, with the possible consequence of rapidly fluctuating charge densities during electrospinning. This can destabilize the Taylor cone, which may dissociate into multiple, small side cones and result in the formation of branched fibers [253]. Moreover, the limited rate of solvent evaporation can lead to swollen or wet fibers landing on the collector.
Even if no water is in the original polymer solution, the hydrophilic character of non-aqueous polar protic solvents can lead to accumulation of water from the vapor in the atmosphere [254], hence high humidity should generally be avoided. Usually, electrospinning at 20–40% relative humidity works well for most polymer solutions. Higher humidity can influence electrospinning dramatically, both for water-soluble and water-insoluble polymers. For instance, at 50% relative humidity PS, being hydrophobic, will tend to form porous fibers [248, 255, 256], whereas PEG and PLLA, when spun together, will create hydrophilic fibers that can easily bead or mesh together [227, 254].
Solvents with higher vapor pressures such as 1,1-dichloroethane (240 hPA), acetone (240 hPA), tetrahydrofuran (THF) (200 hPA), and ethyl acetate (97 hPA), are commonly used, often yielding smooth cylindrical fibers [236]. Many researchers use guides such as the Hildebrand solubility parameter for solvents [257], and the more comprehensive Teas Plots, first developed by Jean Teas [258] and made popular by John Burke [259]. A Teas plot is particularly useful if one is attempting to find multiple solvents for a particular polymer, as the graph is able to more specifically show the fractional contributions of dispersive, hydrogen, and polar bonding that make up the total Hildebrand solubility parameter [236, 259].
4.2.4. The critical roles of polymer molar mass and polymer concentration.
As already mentioned, the molar mass of the polymer is critical for successful electrospinning. The molecules must be large enough, and present at sufficient concentration, to ensure that a continuous chain of entangled molecules persist throughout spinning, otherwise the Rayleigh–Plateau instability will disrupt the jet and no fibers are produced. We thus have two critical values that must be considered for the polymer: the molar mass M and the concentration, which must both be greater than a respective minimum value [236, 260]. Raising the polymer concentration beyond the minimum will not necessarily have an increased positive effect in the spinning process. In fact, very high concentration could lead to premature drying at the spinneret tip, and a solidified Taylor cone before fibers can even be ejected [241, 261].
Typical M values range from 10 to 104 kg mol−1. To give a few reference values, the isoprene compound (commonly called Latex) that naturally pours out from rubber trees as a thick white syrup generally has M > 100 kg mol−1 [262], while Nylon ranges between 3 to 20 kg mol−1 [263]. While molar mass and concentration are clearly related, no increase in concentration can compensate for too low molar mass. This precludes spinning of certain polymers, which may be impossible to obtain at the high molar mass required for electrospinning.
The viscosity of a polymer solution can provide a first indication of whether or not sufficient entanglements are present to allow stable fiber spinning [243, 264–266]. However, it can be misleading, since also the solvent can strongly influence the viscosity. According to Agarwal et al, for a certain polymer type and molar mass, low vapor pressure solvents tend to raise the viscosity of the solution, whereas high vapor pressure solvents yield lower viscosity [261].
Close to the critical values of molar mass and concentration, fibers may be produced but the Rayleigh–Plateau instability is not entirely hindered. Some polymer molecules disentangle from the overall chain, coiling up more or less spherically as they are no longer subject to the stretching force. This results in periodic bulging-out of the fibers, a phenomenon often referred to as 'beading', since the final fiber morphology may resemble beads on a string. Koski and co-workers found that electrospinning a solution of PVA with  kg mol−1 yielded beaded fibers, while raising M to 30–50 kg mol−1 produced non-beaded smooth long fibers, with all other parameters kept constant, and an equal concentration of 25% PVA in solvent for both situations [267].
kg mol−1 yielded beaded fibers, while raising M to 30–50 kg mol−1 produced non-beaded smooth long fibers, with all other parameters kept constant, and an equal concentration of 25% PVA in solvent for both situations [267].
4.2.5. A note regarding multi-core & coaxial electrospinning.
Even though many aspects of the coaxial electrospinning process are insufficiently understood, this process for making core-shell nano- and micro-fibers has gained popularity as it can allow low viscosity fluids to be incorporated within polymer fibers. Numerical simulations of coaxial electrospinning suggest that charges rapidly escape to the outer surface of the compound flow, meaning that it is fundamentally the sheath that is acted upon by the electric field, and the extension of the core flow into the jet thus relies on traction between sheath and core flows during spinning [268–270].
As the sheath solution is forming the Taylor cone and the jet is ejected from it, the core fluid, flowing at a similar rate as that of the sheath solution, is being 'carried' inside. Processing parameters, such as applied voltage and spinneret design, influence coaxial fiber formation strongly. Too high applied voltage will result in jet splitting whereby both the core fluid and sheath fluid separate and spin as two Taylor cones side by side [271]. Experiments have shown that core incorporation into the jet is favored by having the inner capillary of the coaxial spinneret protruding slightly from the outer sheath fluid nozzle [268].
4.3. LCs in polymer fibers
4.3.1. Low molar mass LCs in fibers.
Coaxial electrospinning is a very convenient and adaptable technique for introducing LCs into micro- and nanosized fibers. The spinning components can be easily assembled, most of the materials are readily available, and small amounts are sufficient to produce macroscale non-woven fiber mats which can be easily handled. Moreover, by replacing syringe pumps with a pneumatic microfluidic control system [137, 193, 202], very small vials can be used, the dead volume minimized, and temperature control is greatly simplified. These aspects makes the coaxial electrospinning approach for incorporating LCs into fibers very attractive, as LCs can be very expensive. The set-ups used in our group offers a simple, low-cost and versatile solution for coaxially introducing nematic [179, 190, 202, 272], smectic [202] and cholesteric [193, 197, 232, 233, 272] LCs into polymer fiber cores for obtaining fibers with varying functionalities.
Since a non-crystallizing polymer is preferred when spinning together with LCs, to avoid competition in birefringence when they are characterized via polarized light microscopy, many experiments were done with polyvinylpyrrolidone (PVP) as sheath. This amorphous polymer is available at very high molar mass. The polymer sheath serves the double function of encapsulation and alignment layer, because it appears that the stretching during spinning gives a slight preferential axial alignment of the polymer chains (not so strong as to induce significant birefringence) that orients  along the fiber [196]. As the polymer sheath often becomes quite thin during the spinning, and as the core is filled with the LC component, responsive core-sheath fibers can be readily obtained, the macroscopic properties being governed by the type of LC used.
along the fiber [196]. As the polymer sheath often becomes quite thin during the spinning, and as the core is filled with the LC component, responsive core-sheath fibers can be readily obtained, the macroscopic properties being governed by the type of LC used.
In the very first report by Lagerwall et al [179] core-sheath fibers were obtained by coaxially spinning a room temperature nematic LC mixture inside a solution of PVP in ethanol containing dissolved Ti(O iPr)4, a sol-gel precursor for TiO2. The diameters of the non-woven and aligned fibers were on the order 0.1-1 μm, see figure 37. Because the large amount of TiO2 in the sheath precluded polarizing microscopy characterization, Raman spectroscopy was used to establish that LC was present in the fiber core, with  aligned along the fiber axis. As discussed in section 4.1.1 a considerable increase in LC clearing point as a result of encapsulation was detected.
aligned along the fiber axis. As discussed in section 4.1.1 a considerable increase in LC clearing point as a result of encapsulation was detected.
Figure 37. Fibres consisting of LC core and TiO2-PVP sheath observed by SEM, (a) non-woven sample, (b) aligned sample, and by differential interference optical microscopy (c). The sheath solution flow rate was 0.4 ml h−1 and the LC flow rate 0.2 ml h−1 ((a), (b)) and 0.3 ml h−1 (c). Reproduced from [179] by permission of The Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageIn a subsequent study this coaxial LC-polymer electrospinning approach was extended for spinning coaxial fibers with the smectic-forming 8CB in the core [202]. The fibers were spun at room temperature, with 8CB in the SmA phase. Finding a correct LC flow rate was found to be key to ensure continuous LC filling, yet maintaining good overall fiber morphology, see figure 38. At very low LC flow rates, the fibers were discontinuously filled, whereas at too high LC flow rate, the fibers became deformed and appeared 'smeared out'. X-ray diffraction on oriented fibers showed that the smectic layers were perpendicularly oriented to the fiber axis, a rather unexpected finding considering that SmA flows the easiest along the layers (section 2.1.3). As discussed in section 4.1.4, an interesting hysteresis effect was observed upon heating and cooling between the N and SmA phases.
Figure 38. Microscopy photographs of characteristic samples when varying the flow rate of the LC while retaining the flow rate of the polymer solution constant. Upper row: sample seen without polarisers. Lower row: same sample position seen between crossed polarisers. Reproduced from [202]. CC BY 2.0.
Download figure:
Standard image High-resolution imageScalia and co-workers [197] studied the effects of varying spinning distance, polymer concentration and the presence/absence of sol-gel precursors on the morphology of coaxially electrospun PVP fibers with LC core. The morphology changed considerably, with high polymer concentration and/or large spinning distance yielding premature solvent evaporation with a consequent flat ribbon fiber morphology, whereas the opposite conditions resulted in soft fibers landing on the substrate, where they collapsed into a hemicylinder shape. In some fibers a distinctly porous sheath was detected, a phenomeon that the authors explained as a result of the spinning atmosphere being saturated with solvent. The solvent then re-condenses as liquid droplets on the fiber, leaving a porous surface after final evaporation.
The optical properties and responsiveness of LC core polymer sheath fibers can be further improved by introducing short-pitch cholesterics in the core as shown by Enz et al [193]. The PVP fibers, with diameters in the range of a few microns, showed selective reflection in the visible spectrum. Similar to the case when smectic LCs were used as the core, the LC filling greatly depends on flow rates which in turn affect the overall fiber thickness. When the LC flow rate was high enough, close to that of the sheath solution, the selective reflection from the macroscopic fiber mats could be observed by the naked eye, see figure 39. For thinner fibers, less than ∼7 μm in diameter, light scattering from the sheath dominates over the selective reflection, such that the reflected colors are only detectable with a microscope.
Figure 39. Fiber mat with the selective reflection of an encapsulated short-pitch N* LC visible even macroscopically by the naked eye, in reflection (a), transmission (b), and reflection after heating the LC to the isotropic phase (c). Reproduced from [193] by permission of The Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageInterestingly, the selective reflection color of the fibers with diameter in the micron range varied across the full visible spectrum, although the reflection color of the bulk N* phase was blue. This was explained as a result of quantization of the helix pitch p (not necessarily at its equilibrium value p0) within the fiber core, due to the cylindrical boundary conditions imposed by the polymer sheath [193]. The effect is identical to that described by Kitzerow and co-workers [192], discussed in section 4.1.3. Because there is a certain random variation in the diameter of the electrospun fibers, we see the full spectrum of colors. Even variations on the scale of tens of nanometers yield visible color changes, as p must always adjust to the actual fiber diameter. The relation between the selective reflection color and the core size and shape was investigated in much greater detail in a follow-up study by Scalia and co-workers [196], in which Focused Ion Beam (FIB) was used to dissect the core-sheath fibers at selected locations, allowing nanoscale imaging of the interior of the fibers.
Kye et al [272] further demonstrated that spinning with dual core channels containing two different types of LCs within the same polymer sheath held further potential to increase the multifunctionality of LC-fibers fabricated through the coaxial electrospinning method, see figure 40. The authors produced fibers with adjacent N* and N cores, the former showing visible selective reflection, as well as fibers with adjacent cores filled with the nematic LCs 5CB and E7, respectively, clearing at distinctly different temperatures. The greatest challenge with this multi-core spinning concept was to counteract mixing of the two core fluids and to maintain a wall between the cores that was intact throughout the fiber, even after heating. To this end the fibers were collected on hydrophobic substrates, because Kim and Lagerwall showed in an earlier study that the wetting of water condensed from the atmosphere during spinning promotes fiber spreading and loss of core content [273].
This allowed Kye et al to maintain core integrity, see figure 40. Moreover, the authors noted that, if a surfactant had been added to the PVP sheath solution (to reduce surface tension), then even in fibers with intact wall between the cores the two LCs appeared to be contaminated. The authors proposed that this was due to diffusion of surfactant and condensed water from the sheath to the core solutions during spinning. This assumption was corroborated when single-core fibers without surfactant in the sheath solution were spun with 5CB and E7, and on heating clearing points were close to the bulk values of the pure LCs.
Figure 40. (Left:) photo of Taylor cone during spinning of fibers with N* LC in one core and a black dye-doped nematic in the other. (Top right:) Scanning Electron Microscopy image of a fractured dual-core fiber (coated with platinum for imaging purposes) deposited on a hydrophobic substrate, after the LC has been evaporated. (Bottom right:) reflection polarizing microscopy image of a single dual core-fiber, with N* core along the top and N core along the bottom. Reproduced from [272] by permission of The Royal Society of Chemistry.
Download figure:
Standard image High-resolution imageReyes et al [190] showed that coaxially electrospun fibers with PVP and 5CB could be used as effective optically responsive platforms for gas sensing, as will be discussed in detail in section 4.4.1. The authors investigated aligned and randomly-aligned mats of fibers with morphology varying from uniform cylindrical with continuous LC-filled core to strongly beaded character, where the LC is mainly in the beads. Beading was promoted either by spinning at high relative humidity or by increasing the LC flow rate in relation to that of the polymer sheath. The LC inside partially beaded fibers with continuous LC core show interesting textures, see figure 41. Defect lines running perpendicular to the fiber axis are seen repeatedly along the fibers, in particular at the widest diameter points. The investigation of these defects is still on-going. Considering that we here have essentially cylindrical fibers with modulated diameter in the μm range, but inducing planar rather than homeotropic LC alignment, it is interesting to compare with the related situation for homeotropic boundary conditions studied by Matthias et al [180] (see section 4.1.1).
Figure 41. Thick (A) and thin (B) coaxially electrospun fibers with 5CB core and PVP sheath can show a continuous LC filling but partially beaded character if spun under the appropriate conditions. In this case defects, running roughly perpendicular to the fiber axis, appear, in particular in every bead. The origin of the defect structure is under investigation. These samples were electrospun in 25% humidity, 23°C, with 12.5% PVP in ethanol sheath solution flowing at 0.9 ml h−1, and the 5CB at 0.5 ml h−1. Scale bar 20 μm.
Download figure:
Standard image High-resolution imageWhen co-electrospinning LCs that are crystalline at room temperature, other factors such as miscibility with the sheath's solvent must be considered. Although finding a solvent for a non-room temperature LC may be trivial, its compatibility with the solvent of the sheath fluid to be coaxially electrospun alongside it, may prevent fiber formation. If the core and sheath solvents are miscible, but the sheath solvent is a non-solvent for the LC, a rapid coagulation of the LC results, analogous to the coagulation of polymer fibers during wet spinning. Examples are shown in figure 42.
Figure 42. Coaxial electrospinning of LC materials that are crystalline at room temperature are challenging to spin, as they must be either heated or dissolved prior to spinning. Here are examples of chloroform-dissolved LC falling out of solution in the Taylor cone when the core fluid comes in contact with ethanolic PVP sheath solution. The LC is the nematic single compound EBBA in (A) and the N* single compound cholesteryl nananoate in (B)–(D). A wrinkled 'skin' may form (yellow highlight) in the Taylor cone after voltage is applied. In these situations (the humidity was above 25%) it was either not possible to obtain fibers containing LC, or no fibers were formed. Scale bars: 0.5 mm.
Download figure:
Standard image High-resolution imageAn alternative way of introducing LCs into electrospun fibers was devised by Buyuktanir et al [234]. A chloroform-acetone solution of 5CB as LC and polylactide (PLA) was electrospun to obtain birefringent fibers (diameter ∼0.5–2 μm). The PLA concentration was kept constant while 5CB to PLA ratio (7–86%) was varied for optimum spinnability. During spinning, the LC phase separates from the polymer, giving a core–sheath morphology to the fiber. However, phase separation was not always complete and the sheath was in some cases a mixture of PLA and 5CB. The director was generally aligned along the fiber but there was strong beading. Recently, the same group made a more systematic investigation of the balance between beaded and cylindrical morphology in electrospun LC core fibers produced via the phase separation route [274]. By controlling humidity and optimizing flow rate and solution composition, the authors succeeded in reproducibly spinning LC-filled fibers with morphologies varying from uniform cylindrical to beaded.
The simplicity of the phase separation route is attractive, as a standard spinneret can be used. The recent success is therefore important for the further development of LC-functionalized fibers. At the same time, coaxial electrospinning offers more detailed and dynamic control, and it is more versatile in the LCs and polymer solutions that can be combined. The two methods can be considered largely complimentary, each with its benefits and limitations.
The West and Jakli team also demonstrated air brushing as a facile (non-spinning) way of producing LC core–polymer sheath fibers with average diameter of 5–10 μm [275]. Two types of polymers, PLA and PVP, were dissolved together with E7 nematic LC, in a chloroform/acetone solvent mixture for PLA or in isopropanol for PVP. The obtained fibers were investigated for optical, electro-optical, and morphological characteristics by POM and SEM, respectively. The core-sheath morphology was confirmed as a pipe structure in SEM, demonstrating that LC was phase separated and forms a core.
The fibers obtained were uniformly birefringent with planar anchoring conditions of E7 at the polymer sheath and average LC alignment along the fiber axis. The authors also applied an electric field perpendicular to the fiber axis with the aim to control the optic axis direction; since E7 has positive dielectric anisotropy,  should reorient away from the fiber axis, reducing the effective birefringence, ultimately yielding a dark state between crossed polarizers. However, the latter condition could not be reached with the available fields, a result the authors explained with the voltage drop over the polymer sheath. Fibers were also produced with short-pitch cholesteric LC core, and they showed visible selective reflection.
should reorient away from the fiber axis, reducing the effective birefringence, ultimately yielding a dark state between crossed polarizers. However, the latter condition could not be reached with the available fields, a result the authors explained with the voltage drop over the polymer sheath. Fibers were also produced with short-pitch cholesteric LC core, and they showed visible selective reflection.
4.3.2. High molar mass LCs and LCPs in fibers.
The first approach to incorporate liquid crystallinity into fibers that might come to mind is to electrospin liquid crystal polymers (LCPs). Although there are only a few examples of lyotropic LCPs that have been known to form fibers using electrospinning, several types of thermotropic nematic, smectic, and cholesteric LCPs have been electrospun. For instance, Canejo et al [231] showed that electrospinning a lyotropic LC solution of 60 wt.% acetoxypropylcellulose (APC) with dimethylacetamide (DMAc) as solvent successfully formed chiral birefringent fibers with an average diameter of 3 μm and a helically twisted morphology. Fibers with different diameters had different helical pitch and the authors observed spontaneous helical twisting with both left- and right-handed twist. About 75% of the fibers were right-handed. Interestingly, according to the theory developed to support the experiments, the presence of more right-handed fibers did not come from the natural twisting sense of APC.
Rather, it was attributed to the spontaneous helical winding of the polymer chain in the presence of the electrical field, with the twisting sense determined by a chiral coupling constant depending on the enantiomer of the polymer chain, when the solution concentration is sufficiently high. This finding further establishes the importance of tuning electrospinning parameters; the properties of the solution do not only influence the choice of processing parameters, the processing parameters can also influence the development of the fibers at sub-molecular levels (refer to section 4.2.2).
Tsuboi et al [276] showed another example of fibers electrospun from a lyotropic LCP; poly(γ-benzyl- L-glutamate) (PBLG), a synthetic polypeptide that forms a rod-like α-helical conformation in organic solvents. Nanofibers were electrospun from an isotropic and biphasic PBLG /dichloromethane-pyridine solution under various spinning conditions. For fibers averaging sizes from 0.65 to 1.67 μm, it was counter- intuitively observed that  increased with decreasing fiber diameter, which was attributed to improved uniaxial molecular orientation of PBLG from undulated molecular orientation. A further interesting finding was that the fiber orientation and internal structure could be controlled by changing the spinning solution from isotropic to biphasic solution, which was confirmed by wide-angle x-ray diffraction (WAXD) analysis, and polarized micro-Raman spectroscopy. The nanofibers spun from an isotropic solution generally showed lower orientational order than nanofibers spun from the biphasic solutions, in which the the hexagonal lattice of α helices was uniaxially aligned along the fibers.
increased with decreasing fiber diameter, which was attributed to improved uniaxial molecular orientation of PBLG from undulated molecular orientation. A further interesting finding was that the fiber orientation and internal structure could be controlled by changing the spinning solution from isotropic to biphasic solution, which was confirmed by wide-angle x-ray diffraction (WAXD) analysis, and polarized micro-Raman spectroscopy. The nanofibers spun from an isotropic solution generally showed lower orientational order than nanofibers spun from the biphasic solutions, in which the the hexagonal lattice of α helices was uniaxially aligned along the fibers.
Commercially available LCPs, such as Vectra and Kevlar, have also been used to obtain birefringent nanofibers via electrospinning [277–279]. In preliminary work shown by Reneker's group, an isotropic solution of poly(p-phenylene terephthalamide) (PPTA), commercially known as Kevlar 49®, in concentrated sulfuric acid, was electrospun into a water-bath as a collection target [277]. Using transmission and scanning electron microscopy, TEM and SEM, respectively, they found the average fiber sizes ranged from 40 nm to a few hundreds of nanometers, much smaller than the fibers obtained from conventionally spun  . Although this method produced thermally stable ordered fibers with smaller diameter, the surface roughness of the fibers was of the same order as of commercially obtained fibers.
. Although this method produced thermally stable ordered fibers with smaller diameter, the surface roughness of the fibers was of the same order as of commercially obtained fibers.
For obtaining Vectra fibers, a melt electrospinning setup equipped with a CO2 laser was used by Ogata et al [278] to obtain micron size fibers of polyalirate commercially known as  . The microfibers analyzed by x-ray diffraction were found to have
. The microfibers analyzed by x-ray diffraction were found to have  oriented along the fibers. Interestingly, the diameter of the fibers decreased upon increasing the laser intensity. Due to limitation of the set-up fibers with diameters smaller than 1 μm could not be formed.
oriented along the fibers. Interestingly, the diameter of the fibers decreased upon increasing the laser intensity. Due to limitation of the set-up fibers with diameters smaller than 1 μm could not be formed.
Araujo and co-workers [279] continued the work on electrospinning  and employed a host-guest approach using blends of Vectra with polyethylene oxide (PEO) to electrospin Vectra-PEO nanofibers. Rather than employing melt spinning and the required strong heating, a two-solvent system of chloroform and pentafluorophenol (70:30 ratio) was used to dissolve the commercial Vectra sample. This solution was mixed with a chloroform solution containing PEO, and then the authors electrospun fibers with a Vectra:PEO ratio of 8.19:1, by weight. After spinning, a heat treatment was used to remove the PEO portion of the fibers, and to impose mechanical stability and ordering onto the amorphously spun Vectra fibers.
and employed a host-guest approach using blends of Vectra with polyethylene oxide (PEO) to electrospin Vectra-PEO nanofibers. Rather than employing melt spinning and the required strong heating, a two-solvent system of chloroform and pentafluorophenol (70:30 ratio) was used to dissolve the commercial Vectra sample. This solution was mixed with a chloroform solution containing PEO, and then the authors electrospun fibers with a Vectra:PEO ratio of 8.19:1, by weight. After spinning, a heat treatment was used to remove the PEO portion of the fibers, and to impose mechanical stability and ordering onto the amorphously spun Vectra fibers.
The heat treatment also improved the fibers' thermal stability and increased their tensile strength by more than 300% and elongation at break points by around 150%. The tensile modulus of the fibers, however, was found to be similar to that of conventional Vectra microfibers. It was hypothesized that the increase in tensile strength is due to PEO acting as plasticizer during Vectra fiber spinning, and contributed to the ductile behavior of the untreated mats. Annealing after the complete removal of the PEO enhanced the structural order and resulted in stiffer fibers, hence, improved mechanical properties.
Summarizing the results from electrospinning of Vectra and Kevlar fibers, the overall conclusion is that the functionality of the produced fibers is limited, disappointing in the sense that the fibers do not demonstrate superior properties compared to current commercial Kevlar or Vectra fibers, produced following melt spinning or extrusion. These limitations have ultimately dissuaded many researchers from continuing studies to produce nanoscale fibers made from Kevlar and Vectra.
Rather than using these famous high-performance LCPs, which are difficult to dissolve in compatible solvents, Wu and co-workers chose to electrospin blends of polysiloxane based side-chain cholesteric LCPs with triethylamine and PEO, respectively, dissolved in chloroform [280]. The PEO was added to increase the spinnability of LCPs. In order to obtain uniform fibers another LC was added, triethylamine (Et3N), and different parameters were optimized, such as the PEO concentration, along with the processing parameters like applied voltage and collector distance. Although the addition of a small amount of LC successfully increased the spinnability of the LCP solution, initially only beaded fibers were obtained.
The authors also studied the effect of conductivity of the spinning solution, which affects the net charge density of the jet and hence the quality of fibers produced. As observed by POM the addition of Et3N in the presence, and absence, of trace amounts of water had a great effect on morphology and optical properties of the obtained fibers. It was ultimately found that at a low added volume of Et3N (0.05 ml), uniform fibers formed, while beaded fibers were seen after the addition of more Et3N (0.1 ml). In the presence of trace water Et3N (0.05 ml) is protonated and converts to Et3NH+ , which acts an electrolyte. This increases the birefringence and the morphology of the fibers improved as high enough electrolyte concentration increases the conductivity and hence the spinnability. However, the fibers, with an average size of 1 μm, were brittle and hence not suitable for mechanical characterization. When anhydrous Et3N was used, without trace water present, the LCP solution could not be electrospun.
WXRD analysis showed that while the polymer chains within the fibers were aligned through the electrospinning process, the degree of orientational order was lower compared to fibers prepared by conventional drawing processes. A significant amount of annealing was necessary to increase the level of crystallinity and mechanical stability in the thin electrospun LCP fibers; the Young's modulus of a single fiber increased from 2.00 to 3.93 GPa. In addition to finding optimal processing parameters needed to electrospin LCPs, varying degrees of after treatment processes (annealing, drying...etc) may thus be required to reach satisfactory performance.
Finally, attempts were also made to electrospin main-chain smectic [281] and nematic [230] LCPs. Nakashima et al [281] studied the effects that changing fiber diameter had on the internal structure and molecular orientation of smectic LCP, BB-5(3-me) spun from HFIP solvent, or 1,1,1,1,3,3,3- hexafluro-2-propanol. With concentrations varying from 3–25wt.%, fibers with diameters ranging from 0.13 to 4.71 μm were observed. Under optimal spinning conditions, fibers with diameters ranging from 0.11 to 0.69 μm were found. Interestingly, this polymer was known to form an anticlinic tilted smectic phase, SmCa, in melt spun fibers, but the pristine electrospun fibers showed only SmA order. However, this SmA phase was metastable, and after annealing it was found to transform into the stable SmCa phase also in the electrospun fibers.
Alternatively, while electrospinning main-chain nematic LCPs with photocrosslinkable moieties, Krause et al [230] were able to obtain aligned LCE microfibers after exposing them with UV light for in situ crosslinking. A 5 wt.% solution of LCP in chloroform yielded beaded fibers with average diameter sizes of 450 nm, but upon increasing the concentration to 7 wt.%, uniform fibers were observed with average diameter 1.5 μm. Although the fibers were found to be insoluble in chloroform, proving that the fiber mat was successfully crosslinked, and had uniform director alignment along the fiber axis as confirmed by polarizing microscopy, no tests of actuation were reported. The authors tested actuation only on films prepared in parallel from the same LCE material, without commenting on the lack of actuation data for the fibers. One may speculate that this may have been due to the fibers being fixed to the substrate on which they were collected, thus precluding actuation. It remains an important challenge to electrospin free-hanging LCE fibers and study their actuation behavior.
4.4. Applications of liquid crystal-functionalized fibers
If liquid crystals can be integrated within textile-grade fibers, their extraordinary responsiveness could be put to use in realizing a new generation of wearable technology devices. 'Wearable tech' has been used as a buzz-word throughout many fields and industries looking to capitalize on society's growing interests in seamlessly integrating sensors, tracking devices and other electronics into apparel and accessories. While wearable tech has been successful in creating multifunctional Bluetooth integrated smart-accessories, like smartwatches and fitness bands [282–284], and showing that such accessories and clothing can be fashionable [285], the field has in many respects disappointed. Its products do not appear to be as functionally necessary or as irreplaceable as many hoped they could be [286]. A smart watch can be replaced by a less expensive smart phone containing the same level of functionality, and haute couture fiber-optic fashion, while stylish, is not justifiable in neither cost nor function to many consumers.
In fact, consumer conscious wearable tech creates more wearable electronic accessories right now, than it does true clothing based technology, involving responsive fibrous textiles which actually seek to minimize external electrical sources and dependence on other mobile devices in order to function. Clearly, this is where liquid crystals embedded within individual fibers, introduced already during the actual fiber fabrication, can potentially fill an important niche in creating the next generation of wearable technology. Wrist watches have been with us for two centuries, so in many respects smart watches and the likes can be considered evolution rather than revolution. While important challenges remain to be addressed for bringing LC-functionalized fibers to applications—in particular in terms of transitioning from the research polymers used in today's lab experiments to true textile-grade polymers—they offer some very interesting opportunities, with potentially revolutionary potential. They introduce an entirely different form factor, perfectly adapted for textile garments, and they offer autonomous, non-electronic, functionality. This opens for clothing-integrated devices that are fundamentally different from today's dominating technology, fully independent of batteries and power supplies. We here cover two illustrative examples of the possibilities: gas sensors made from LC-core fibers and actuating fibers made from LCEs.
4.4.1. Gas sensing with liquid crystal-filled fibers.
Based on the observation that light scattering by an electrospun mat of PVP sheath–5CB core fibers is visibly reduced (change easily seen by naked eye) upon exposure to toluene or other organic solvent vapor, Kim et al proposed that LC-core fibers could be used as wearable sensors/detectors of hazardous gases [287]. A recent detailed follow-up study by Reyes et al [190] showed that the morphology of the fibers (beaded or uniformly cylindrical) is very important for the behavior. Interestingly, it was found that beaded fiber mats had visible scattering responses without the need for polarizers, while the response of non-beaded fiber mats could only be visualized with polarizers. Although the latter response thus requires additional components (polarizers) it is very interesting, because it is extremely fast (response and relaxation time below seconds) and highly sensitive [190]. While the alignment effects of the fiber sheath encapsulating the 5CB are still under investigation, as well as the limits to the fiber mats' functionality, the concept of integrating LCs into fibers for furthering ideas in wearable technology is steadily advancing. In terms of developing LC-fiber based gas sensors as a viable concept, the two key challenges are to ensure specificity (response only to the analyte gas) and enhance sensitivity. To reach these critical goals, a good starting point is to survey the work done on gas sensing with liquid crystals in flat non-fibrous samples.
Liquid crystals, on their own, have been used for gas sensing in a research context since the 1990s [288–291]. If issued patents on the usage of LCs for gas sensing are taken into account, then the idea was present decades before, since the 1970s [292–294]. Many of the early works regarding detection of aromatic and halogenated organic vapors at room temperature exploited the use of short-pitch cholesterics because of their ability to change p0, and therefore their color, depending on how much organic vapor came in contact with the samples. The early pioneering works from Dickert and his group [288, 289, 295] demonstrated quantitative correlation between analyte concentration, determined in situ using quartz crystal microbalance (QCM), and p0, calculated from the optical reflection band as determined by UV-VIS spectroscopy. More recent work from the TU Eindhoven group demonstrated that the principle can be used even with fluctuations in atmospheric humidity and temperature [296, 297]. These and other reports [291, 298, 299] have ensured that the idea that LCs could be used for optically detecting harmful volatile organic compounds (VOCs) has grown in popularity throughout the years.
The critical problem of specificity was, however, largely left unaddressed in the early work. Likewise, it remained an open question how LC-based gas sensors can be tailored to respond to different gaseous analytes of interest. During the last decade, the interest in LC based gas sensing applications has been revitalized, largely thanks to a new approach that solves the specificity problem, presented by the Abbott group at the University of Wisconsin-Madison. In their work, they characterized organophosphate and organic gas vapor responses in thin films of 5CB with one side exposed to the air, the other supported on a substrate decorated by perchlorate salt. Due to complexation of the salt by 5CB as well as by the analyte gas, the latter forming a much stronger complex than the former, a sensitive and specific response can be ensured. The substrates vary from polystyrene [300] to photolithography masked PDMS and polyurethane micro-wells [301–303]. The team successfully quantified the chemo-optical transitions induced upon gas exposure from as low as ppb level concentrations under various humidity settings [300, 302–305]. Thus, throughout the years Abbott's group has influenced other groups to extend, and they themselves have extended, their initial micro-level LC-VOC sensing concept. Apart from gas sensing they study sensing of biomolecular phenomena such as protein binding energies [305, 306] and enzymatic activities using nematic LCs [307].
While the Abbott group VOC sensing approach is based on an analyte-triggered change in boundary conditions, resulting in a change of LC alignment through the bulk, other groups have instead focused on sensitizing the bulk LC to specific analytes. This may be disadvantageous for the sensitivity and speed of the sensor, but it obviously gives more freedom to how the boundaries are designed. Moreover, it is an interesting alternative that serves to expand the range of VOCs that can be detected by LCs. Dirk Broer's group demonstrated high selectivity using functionalized chiral dopants added to the standard nematic mixture E7. Depending on the choice of chiral dopant they could detect carbon dioxide or oxygen [308]. Later on the same concept was used to sense increases in temperature [296] and humidity [296, 297]. The Broer group has also experimented with different form factors of LC containment in creating thin LCP responsive films for sensing [296].
If the above strategies, or alternative ones, to ensure specificity can be transferred to LCs in fibers, the new form factor should be most attractive, in particular in implementing LC sensors into non-laboratory environments. While Abbott et al demonstrated VOC sensitivity of perchlorate-sensitized 5CB films down to the ppb level, microscope and video equipment are still necessary to detect the anchoring rearrangement upon gas exposure. Since LC-filled fibers can yield a response that is visible to the naked eye, they may offer a means to take the concept out of the lab. Moreover, with a textile polymer sheath, a mat of appropriately LC-functionalized fibers can easily be incorporated in clothing, for instance uniforms of persons who risk exposure to hazardous gases in their working environment. Because the sensing requires no electrical power, the garment does not need to carry any power supply, battery or electrical wiring to drive the sensor. And with the large surface-to-volume ratio that thin fibers provide, we may expect both a sensitive and rapid response if all parameters are optimized.
Table 1 gives an overview of available and currently developing gas sensing devices, with their respective advantages and disadvantages. This can give a more succinct perspective of the progress and highlight the possibilities LCs have for integration into wearable sensing technology. The primary aspects of gas selectivity, robust form factor containment, and gas sensitivity are the main three issues which need to be addressed for creating commercially viable LC-based gas sensors. Fundamentally, as applied LC research has primarily targeted displays and related technologies, requiring electrodes and assuming hard impermeable (usually glass) substrates to encase the LCs, this novel type of LC application poses a challenge quite different from the ordinary.
Table 1. Current state of the art regarding portable/wearable gas sensing technologies, with and without LCs.
| Sensing device | Pros | Cons |
|---|---|---|
| Traditional gas sensors | + Large variety commercially available and thorough understanding of functionality [314] | − Each type has flaws: |
| + Metal oxide (MOX) sensors: low fabrication cost, high sensitivity, wide analyte range [315, 316] | − MOX sensors: high energy consumption, unstable in uncontrolled environments [316, 317] | |
| + Polymer sensors: low energy consumption, low fabrication cost, very sensitive | − Polymer sensors: issues with selectivity and long-term stability [318] | |
| + CNTs: high surface-to-volume-ratio, low cost, portable | − CNT sensors: high costs, reproducibility problems [319] | |
| LC Based Gas Sensors | + High sensitivity and selectivity demonstrated for relevant VOCs (DMMP [304, 320], nerve agents [299, 302], toluene [190, 298, 300], THF [295], chloroform [289]) | − Generic LC sensors have issues with specificity [287, 302] |
| + Various types of LCs may be employed; dopants can ensure specificity | − Form factor challenges: flexible yet robust LC containment allowing exposure to environment | |
| + Require no electrical components or power source to function; room temperature operation | − Many current solutions require polarizing microscopy analysis | |
| + Small devices possible | ||
| + N*-sensors enable immediate detection by human sight (color change) | ||
| LC Gas Sensors in Fiber Form | + Potential solution to form factor challenge: demonstrated function in non-woven mats [190, 287] | − Reproducibility problems [190] |
| + Response visible at room temperature, with/without additional optics [190] | − Response function needs further investigation [190, 287] | |
| + Response and relaxation within seconds [190] | − Sensitivity needs development [190] | |
| + Long shelf life possible (minimum two months demonstrated [190]) | − Transition to robust textile-grade polymers needed; washability issues | |
| Current non-LC-based Wearable Gas Sensors | + Conductive liquid/interdigitated electrodes for capacitive/resistive sensing: can be woven into garments; some level of flexibility [321, 322] | − Reproducibility problems; time-consuming production for non-printed sensors [323, 324] |
| + Inkjet printed CNT-based electrodes: fast, low-cost production; integration into garments; good lifetime with coin cell batteries due to low power requirements | − Capacitive/resistive response speed can be slow [321] | |
| − Read-out of sensing response requires further electronics | ||
| − Sensing limited (so far) to water vapor, sweat, and ammonia [325, 326] | ||
| − Form factor issues: not true textiles but rather PDMS rubber; breathability and reusability issues [326, 327] | ||
| − High cost |
4.4.2. Liquid crystal elastomer fiber actuators.
There are a number of LCE materials and fabrication methods that have been explored for making actuators that are capable of either thermal, photo-mechanical, or photo-thermo-mechanical actuation. Undoubtedly, these types of LCE actuators show promise in fields like soft robotics [21, 309], and performance comparable to that of skeletal muscles has been demonstrated [16]. As discussed in section 2.4, a commonly used method for obtaining monodomain LCE networks is the two-step crosslinking approach pioneered by Küpfer and Finkelmann [40]. When the target is to make LCE fibers, this approach is convenient, the fibers being stretched during the second crosslinking stage. However, connected to the fiber production another unique way to form LCE fibers arises, based on mechanically orienting a non-crosslinked but reactive LC polymer by flow while drawing fibers, and then quickly crosslinking the fibers to prevent the orientational loss. While some have tried simply drawing fibers using tweezers [26], and toothpicks [310], others have used more sophisticated methods like melt extrusion [25], and even wet-spinning driven by microfluidic setups [311–313].
Naciri et al [26] showed the first examples of LCE fibers obtained through the simple approach of drawing from a melted viscous mixture of a nematic LC terpolymer and crosslinker. The samples were left in the stretched state for 120 hours for crosslinking to complete. The obtained fibers, with average diameter of 300 μm, were found to be birefringent with  along the fiber axis. Thermoelastic measurements to determine the mechanical properties were conducted on the elastomeric fibers in the nematic phase at 50 °C, yielding a Young's modulus of 4.37 MPa. Furthermore, under constant applied stress the length was monitored, and the resulting strain calculated, as the fibers were heated from the nematic into the istoropic phase. The length did not change in the nematic phase, it started to reduce on approaching the clearing transition at TNI, where it sharply decreased, revealing a transition-induced strain up to 35%. The actuation behavior of the LCE fiber was also demonstrated by mounting it inside a heating coil and attaching a 200 mg weight to one end. When the fiber was heated above the N-isotropic transition, the fiber contracted and the weight was lifted.
along the fiber axis. Thermoelastic measurements to determine the mechanical properties were conducted on the elastomeric fibers in the nematic phase at 50 °C, yielding a Young's modulus of 4.37 MPa. Furthermore, under constant applied stress the length was monitored, and the resulting strain calculated, as the fibers were heated from the nematic into the istoropic phase. The length did not change in the nematic phase, it started to reduce on approaching the clearing transition at TNI, where it sharply decreased, revealing a transition-induced strain up to 35%. The actuation behavior of the LCE fiber was also demonstrated by mounting it inside a heating coil and attaching a 200 mg weight to one end. When the fiber was heated above the N-isotropic transition, the fiber contracted and the weight was lifted.
Ohm et al [311] introduced a technique similar to the classic wet-spinning fiber formation process by instead using a microfluidics based mechanism (shown in figure 22) to obtain oriented main-chain LCE fibers from a main-chain photocrosslinkable smectic LCP. A solution of LCP (30 wt.%) and photo-initiator (3wt.%) in dichloromethane (DCM), was injected into a stream of silicone oil within a glass capillary. The co-flowing 'bath' of silicone oil, similar in one of its two functions to the precipitation bath that wet-spun fibers are extruded into prior to being collected, coagulated the fibers. Due to the miscibility of DCM and silicone oil, the solvent is removed from the LCP, which thus enters its LC state (the co-flowing system was kept at 40 °C, within the SmA phase). The result is a continuous LCP filament that is pulled and aligned by the silicone oil stream (its second function), prior to UV exposure for initiating the crosslinking.
The resulting LCE filaments were collected on a winding spool and checked for their optical and actuation behaviors. The fibers obtained had thickness between 20 and 50 μm, which was varied by changing the flow rate of the oil phase. With POM experiments it was also confirmed that the director orientation was along the fiber axis. After heating above 80 °C, to the isotropic phase, the fiber lost its birefringence and a reduction in fiber length was observed. Surprisingly, although the fiber regained its birefringence upon cooling back to 50 °C, the deformation in length was irreversible. The authors proposed that the irreversibility was due to the high activation energy required to form new smectic layers.
Theoretically, this activation energy could be overcome by an external force. To check this, the authors did another actuation experiment in which a single LCE fiber was glued at both ends, with a 'u'-shaped 25 mg weight hanging from the center, the entire setup kept inside a thermo-regulating box, see figure 43. Upon heating the air inside the box above TNI, the weight was lifted as the fiber length reduced from 19.4 mm to 16.3 mm. On cooling, the fiber now regained its original length at a temperature of 50 °C, indicating a reversible actuation. This work showed that the continuous microfluidics based spinning method has the capability of making LCE fibers with reproducible and regular thickness which can act as actuators and lift objects more than one thousand times its own weight. Ultimately, it demonstrates a method for producing versatile and useful soft actuators.
Figure 43. Schematic setup (a) and results (b) of a heating experiment performed on a single SmA LCE filament, glued between two static substrates inside a heatable metal box. A small, U-shaped weight was clipped to the sample. The temperature in the box was cycled while observing the sample with a camera. Between 50 (b) and 80 °C (c) the weight was lifted up while the substrates remained stationary. Upon cooling back to 50 °C (d) the sample went back to it's original height, proving the reversibility of the actuation. Reproduced from [311] with permission of The Royal Society of Chemistry
Download figure:
Standard image High-resolution imageA more detailed mechanical and optical study on LCE fibers with thickness of 30 ± 1 μm, based on the same material, was done by Stannarius et al [312]. One of the findings was strain induced birefringence;  could either be increased or decreased upon stretching and compressing of the samples in an axial direction. However, the effect was reversible only once the fiber had been heated into the SmA state at 40 °C. The slow dynamics of the room temperature glassy state does not allow the dynamic coupling between strain and orientational order parameter that the varying birefringence signifies.
could either be increased or decreased upon stretching and compressing of the samples in an axial direction. However, the effect was reversible only once the fiber had been heated into the SmA state at 40 °C. The slow dynamics of the room temperature glassy state does not allow the dynamic coupling between strain and orientational order parameter that the varying birefringence signifies.
Mechanical studies indicated that the relaxation of the fibers after stretching at room temperature shows glassy behavior and plastic deformation, as the initial length is not recovered. However, if the fiber is then heated above its glass transition temperature, it reaches its original relaxed length within one minute. When the fiber is further heated to TNI, it shortens and a suspended weight is lifted accordingly. A very small stress of 80 μN is required to stretch the sample during the transition to the smectic phase. This shape memory effect is attributed to the formation of a polydomain structure in the SmA phase and a structural reorganization of smectic layers during cooling, similar to chiral SmC* LCEs [328, 329] and nano-sized shape-changing LCE colloids [147]. However, the authors did not provide any x-ray data to confirm this particular hypothesis.
To the best of our knowledge, there has been only one report, so far, on side-chain nematic LCE fibers [313]. This was fabricated in a microfluidic set-up using a side-chain UV-crosslinkable LCP exhibiting a nematic phase between 40 and 56 °C. The LCP was mixed with 0.4 wt.% chlorobenzene and 5 wt.% photoinitiator and injected through a fused silica tube into co-flowing silicone. The set-up was immersed in a water bath for temperature control. Crosslinking was done at different temperatures within the nematic phase. POM analysis showed that fibers crosslinked deep in the N phase were uniaxially oriented whereas fibers crosslinked at a temperature closer to TNI were not. Depending on the exact combination of precursor LCPs and on the crosslinking time, some fibers did not actuate upon heating above the clearing point, whereas others actuated several 100%. The relevant parameter is the crosslinking density, which must not be too high, as this prevents actuation. Thus, fibers obtained from LCPs with lower numbers of crosslinkable units showed the best actuation upon heating, see figure 44.
Figure 44. Overview of the contraction behavior of nematic side-chain LCE fibers crosslinked for 13 s. (A) Fibers made from polymer CrP1 (45 mol%) do not contract because this prepolymer yields too many crosslinks. ((B)–(D)) Fibers made from polymers CrP2-CrP4 with reduced amounts of crosslinkable units (31 to 9 mol%) contract when heated to  °C. Scale bars: 100 μm. Reproduced from [313] John Wiley & Sons. © 2014 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
°C. Scale bars: 100 μm. Reproduced from [313] John Wiley & Sons. © 2014 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim.
Download figure:
Standard image High-resolution imageConclusively, for actuation, it seems like fiber orientation and a softer network that allows deformation are the key factors. The orientation of the LC phase in the fibers can also be optimized by crosslinking at low temperatures in the nematic phase, for example. Actuation can be tuned by either varying the degree of crosslinking, or varying the UV exposure time when the crosslinker amount is lowered.
5. Outlook
Based on the steadily increasing interest in droplets, shells and fibers of liquid crystals, together with the continuous innovation in production and characterization technologies adapted to these fascinating geometries for LC research and applications, we can expect a stimulating development over the next few years. As described above, we have already seen several examples of unexpected director field configurations arising by strong confinement with curved interfaces, and the new opportunities for characterizing topological defects even with nanoscale resolution, for instance via polymerization of reactive mesogens that aggregate in defects, may yield further intriguing surprises. While much valuable information on spheres and cylinders of LCs can be found in the pioneering studies from the 70s–90s, today's ability to produce monodisperse LC droplets, and even shells, with controlled diameter has opened a colorful physics toolbox that is far from fully explored. Likewise, the introduction of electrospinning allows us to scale down the cylindrical confinement to the μm range and below, still using optical methods to probe the response of the LC. This may well reveal confinement phenomena that do not take place in the capillaries of the early studies, one or two orders of magnitude larger in diameter. We may also expect interesting new phenomena as lyotropic LCs start to be explored in droplets, shells and fibers.
So far the emphasis has been primarily on fundamental physics while the applied research has just started to take off. Some very promising results have been put forward in terms of soft actuators based on microfluidics-produced curved LCEs, unclonable pattern formation from regular arrangements of cholesteric shells, or gas sensing from LC-functionalized fiber mats. The challenges until commercial exploitation can be realistically considered are, however, still considerable. For wearable technology applications of LC core fibers a transition to textile-grade polymers is essential, and for many applications it may be wise to move from electrospinning, convenient on the lab scale, to conventional high-throughput spinning methods like wet spinning. As the interest in soft robotics is surging world-wide, the opportunities for LCE-based actuators are enormous, but so far the soft robotics community knows very little about the promise of LCEs. This is an area where we hope LCs will fill an important new role. Apart from advancements in LCE chemistry, which is still very limited in terms of what is commercially available, such a scenario will require a fruitful cross fertilization between the LC and robotics communities.
It is our hope that this review article can contribute in fostering such boundary crossing, also in the other relevant application areas, like wearable technology, materials science or security research. If this happens, the currently unconventional LC geometries that we have discussed above may well become mainstream technology, with potential to revolutionize many aspects of our lives.
Acknowledgments
We acknowledge financial support from the European Research Council ERC (project INTERACT, grant code 648763, for CGR, AS, VSRJ and JPFL), from the Fonds National de la Recherche (project DISGONA, grant code 9170337, for MU; project ULISCO, grant code 6992111, for JN) and the University of Luxembourg (project UNIQUE, for YG and JPFL).
Footnotes
- 2
We thank Ralf Stannarius for pointing out this rarely recognized impact of local variations in K24.
- 3
The polar configuration in LC cylinder research is comparable to the axial configuration for LC droplets (section 3.3.1).