CoRe optimizer: an all-in-one solution for machine learning

The CoRe optimizer [13] is a first-order gradient-based optimizer for stochastic and deterministic iterative optimizations. It adapts the learning rates individually for each weight w_ξ depending on the optimization progress. These learning rate adjustments are inspired by the Adam optimizer [12], RPROP [14, 15], and the synaptic intelligence method [64].

Exponential moving averages of the loss function gradient and its square,

$$\begin{align} g_\xi^\tau& = \beta_1^\tau\cdot g_\xi^{\tau-1}+\left(1-\beta_1^\tau\right)\frac{\partial L^t}{\partial w_\xi^{t-1}}\ , \end{align} \tag{ 1 }$$

$$\begin{align} h_\xi^\tau& = \beta_2\cdot h_\xi^{\tau-1}+\left(1-\beta_2\right)\left(\frac{\partial L^t}{\partial w_\xi^{t-1}}\right)^2\ , \end{align} \tag{ 2 }$$

with decay rates $\beta_1^\tau,\beta_2\in[0,1)$, are employed in minimization in analogy to the Adam optimizer. For maximization, the sign of the loss function gradient in equation (1) has to be inverted. In the CoRe optimizer, β₁ is a function of the individual weight update counter τ,

$$\begin{align} \beta_1^\tau = \beta_1^\mathrm{b}+\left(\beta_1^\mathrm{a}-\beta_1^\mathrm{b}\right)\exp\left[-\left(\frac{\tau-1}{\beta_1^\mathrm{c}}\right)^2\right]\ , \end{align} \tag{ 3 }$$

whereby τ can vary from the counter of gradient calculations t if some optimization steps do not update every weight. The initial decay $\beta_1^\mathrm{a}\in[0,1)$ is converted by a Gaussian with width $\beta_1^\mathrm{c}\gt 0$ to the final decay $\beta_1^\mathrm{b}\in[0,1)$. The smaller $\beta_1^\tau$, the higher is the dependence on the current gradient, while a larger $\beta_1^\tau$ leads to a slower decay of previous gradient contributions.

The Adam-like adaption of the weight-specific learning rates,

$$\begin{align} u_\xi^\tau = \frac{g_\xi^\tau}{1-\left(\beta_1^\tau\right)^\tau}\left\{\left[\frac{h_\xi^\tau}{1-\left(\beta_2\right)^\tau}\right]^{\tfrac{1}{2}}+\epsilon\right\}^{-1}\ , \end{align} \tag{ 4 }$$

employs the quotient of the moving averages $g_\xi^\tau$ and $(h_\xi^\tau)^{\tfrac{1}{2}}$, which are corrected with respect to their initialization bias toward zero ($g_\xi^0,h_\xi^0 = 0$). For numerical stability $\epsilon\gtrapprox0$ is added in the denominator. This quotient is invariant to gradient rescaling and introduces a form of step size annealing. Therefore, $u_\xi^\tau$ changes from ±1 in the first optimization step τ = 1 toward zero in well-behaving optimizations.

The plasticity factor,

$$\begin{align} P_\xi^\tau = \begin{cases}0& \quad \begin{array}{l}\mathrm{for}\ \tau\gt t_\mathrm{hist}\\ \land\ S_\xi^{\tau-1}\ \mathrm{top}\text{-}n_{\mathrm{frozen},\chi}\ \mathrm{in}\ \mathbf{S}_\chi^{\tau-1}\end{array}\\ 1& \quad \begin{array}{l}\mathrm{otherwise}\end{array}\end{cases}\ , \end{align} \tag{ 5 }$$

aims to improve the stability-plasticity balance by regularization in the weight updates. Therefore, weight groups χ are specified—for example, a layer in a neural network—and the weight-specific importance scores $\mathbf{S}_\chi^{\tau-1}$ (see equation (8) below) are compared within these groups. When $\tau\gt t_\mathrm{hist}\gt 0$, $P_\xi^\tau$ can freeze the weights with the $n_{\mathrm{frozen},\chi}\unicode{x2A7E}0$ highest importance scores in their group in update τ to mitigate forgetting of previous knowledge.

The RPROP-like learning rate adaption,

$$\begin{align} s_\xi^\tau = \begin{cases}\mathrm{min}\left(\eta_+\cdot s_\xi^{\tau-1},s_\mathrm{max}\right)&\mathrm{for}\ g_\xi^{\tau-1}\cdot g_\xi^\tau\cdot P_\xi^\tau\gt 0\\ \mathrm{max}\left(\eta_-\cdot s_\xi^{\tau-1},s_\mathrm{min}\right)&\mathrm{for}\ g_\xi^{\tau-1}\cdot g_\xi^\tau\cdot P_\xi^\tau\lt 0\\s_\xi^{\tau-1}&\mathrm{for}\ g_\xi^{\tau-1}\cdot g_\xi^\tau\cdot P_\xi^\tau = 0\end{cases}\ , \end{align} \tag{ 6 }$$

depends only on the sign of the gradient moving average $g_\xi^\tau$ and not on its magnitude leading to a robust optimization. Sign inversions from $g_\xi^{\tau-1}$ to $g_\xi^\tau$ often signalize a jump over a minimum in the previous update. Hence, the step size $s_\xi^{\tau-1}$ is reduced by the decrease factor $\eta_-\in(0,1]$ in this case, while it is enlarged by the increase factor $\eta_+\unicode{x2A7E}1$ for constant signs to speed up convergence. The updated step size $s_\xi^\tau$ is bounded by the minimal and maximal step sizes $s_\mathrm{min},s_\mathrm{max}\gt 0$. For $g_\xi^{\tau-1}\cdot g_\xi^\tau\cdot P_\xi^\tau = 0$, the step size update is omitted. The initial step size $s_\xi^0 = s_\xi^1$ is a hyperparameter of the optimization.

The weight decay,

$$\begin{align} w_\xi^t = \left(1-d_\chi\cdot\left|u_\xi^\tau\right|\cdot P_\xi^\tau\cdot s_\xi^\tau\right)w_\xi^{t-1}-u_\xi^\tau\cdot P_\xi^\tau\cdot s_\xi^\tau\ , \end{align} \tag{ 7 }$$

with group-specific hyperparameter $d_\chi\in[0,(s_\mathrm{max})^{-1})$, targets to reduce the overfitting risk by prevention of strong weight in- or decreases. It is proportional to the product of d_χ and the absolute weight update $|u_\xi^\tau|\cdot P_\xi^\tau\cdot s_\xi^\tau$, i.e. the more stable the weight value the less it is affected by the weight decay. Subsequently, the signed weight update $u_\xi^\tau\cdot P_\xi^\tau\cdot s_\xi^\tau$ is subtracted to obtain the updated weight $w_\xi^t$. The weight values are therefore bound between $-(d_\chi)^{-1}$ and $(d_\chi)^{-1}$ in well-behaving optimizations, i.e. $u_\xi^\tau\unicode{x2A7D}\pm1$.

The importance score value,

$$\begin{align} S_\xi^\tau = \begin{cases} \quad \begin{array}{l}S_\xi^{\tau-1}+\left(t_\mathrm{hist}\right)^{-1}g_\xi^\tau\cdot u_\xi^\tau\cdot P_\xi^\tau\cdot s_\xi^\tau\end{array}& \quad \mathrm{for}\ \tau\unicode{x2A7D} t_\mathrm{hist}\\ \quad \begin{array}{l}\left[1-\left(t_\mathrm{hist}\right)^{-1}\right]S_\xi^{\tau-1}\\ +\left(t_\mathrm{hist}\right)^{-1}g_\xi^\tau\cdot u_\xi^\tau\cdot P_\xi^\tau\cdot s_\xi^\tau\end{array}& \quad \mathrm{otherwise}\end{cases}\ , \end{align} \tag{ 8 }$$

ranks the weight importance by taking into account weight-specific contributions to previously estimated loss function decreases. This ansatz is inspired by the synaptic intelligence method. The importance scores enable to identify the most important weights in previous updates, which can be frozen by the plasticity factors (equation (5)) in following updates to improve the stability-plasticity balance. The product of gradient moving average and signed weight update is employed to estimate the loss function decrease. Since the weight update sign is not inverted, the higher positive the importance score, the larger is the loss function decrease. Starting with $S_\xi^0 = 0$, the mean of $g_\xi^\tau\cdot u_\xi^\tau\cdot P_\xi^\tau\cdot s_\xi^\tau$ over $\tau\unicode{x2A7D} t_\mathrm{hist}$ is calculated. For $\tau\gt t_\mathrm{hist}$, the importance score is determined as exponential moving average with decay $1-(t_\mathrm{hist})^{-1}$.

We note that the relative large number of hyperparameters in the CoRe optimizer is, on the one hand, an advantage to obtain good results even in very difficult or edge cases. On the other hand, the hyperparameter tuning is more complicated. However, a set of generally applicable values, which are provided in this work, can overcome this drawback.

SGD [5] subtracts the product of a constant learning rate γ and the loss function gradient from the weights $w_\xi^{t-1}$ in the weight updates,

$$\begin{align} w_\xi^t = w_\xi^{t-1}-\gamma G_\xi^\tau\ , \end{align} \tag{ 9 }$$

with

$$\begin{align} G_\xi^\tau = \frac{\partial L^t}{\partial w_\xi^{t-1}}\ .\end{align} \tag{ 10 }$$

An additional momentum (Momentum) [6] can be introduced in SGD by replacing $G_\xi^\tau$ in equation (9) by

$$\begin{align} m_\xi^\tau = \mu\cdot m_\xi^{\tau-1}+G_\xi^\tau\ , \end{align} \tag{ 11 }$$

with the momentum factor µ and $m_\xi^1 = G_\xi^1$ [34].

NAG [7, 8] is SGD with Nesterov momentum, i.e., $G_\xi^\tau$ in equation (9) is substituted by

$$\begin{align} n_\xi^\tau = \mu\cdot m_\xi^{\tau}+G_\xi^\tau\ .\end{align} \tag{ 12 }$$

The algorithm of the Adam optimizer [12] is given by equations (1) (with constant β₁), (2), (4), and (9), whereby $G_\xi^\tau$ in equation (9) is replaced by $u_\xi^\tau$. In comparison to the CoRe optimizer, Adam misses the τ dependence of the decay rate β₁, the plasticity factors $P_\xi^\tau$, the RPROP-like learning rate adaption $s_\xi^\tau$, and the weight decay. The latter can be introduced in Adam as well as in many other optimizers also by adding $d\cdot w_\xi^{t-1}$ to the loss function gradient as second operation of an optimization iteration after the possible sign inversion for maximization. A further alternative is to subtract instead $d\cdot\gamma\cdot w_\xi^{t-1}$ from $w_\xi^{t-1}$ as in AdamW [22].

The difference of the AdaMax optimizer [12] compared to Adam is that the term in curly brackets in equation (4) is replaced by the infinity norm,

$$\begin{align} k_\xi^\tau = \mathrm{max}\left(\beta_2\cdot k_\xi^{\tau-1},\left|G_\xi^\tau+\epsilon\right|\right)\ , \end{align} \tag{ 13 }$$

with $k_\xi^0 = 0$.

In RMSprop [11] the loss function gradient is divided by the moving average of its magnitude,

$$\begin{align} w_\xi^t = w_\xi^{t-1}-\gamma G_\xi^\tau \left[\left(h_\xi^\tau\right)^{\tfrac{1}{2}}+\epsilon\right]^{-1}\ . \end{align} \tag{ 14 }$$

Hence, the difference to the Adam optimizer is that the loss function gradient $G_\xi^\tau$ is applied instead of the gradient moving average $g_\xi^\tau$ and the initialization bias correction is omitted.

The AdaGrad optimizer [9] differs from RMSprop by the replacement of $h_\xi^\tau$ in equation (14) by

$$\begin{align} b_\xi^\tau = b_\xi^{\tau-1}+\left(G_\xi^\tau\right)^2\ , \end{align} \tag{ 15 }$$

with $b_\xi^0 = 0$.

The adaptive learning rate in the AdaDelta optimizer [10] is established by

$$\begin{align} w_\xi^t = w_\xi^{t-1}-\gamma G_\xi^\tau\left(\frac{l_\xi^{\tau-1}+\epsilon}{h_\xi^\tau+\epsilon}\right)^{\tfrac{1}{2}}\ , \end{align} \tag{ 16 }$$

with

$$\begin{align} l_\xi^\tau = \beta_2\cdot l_\xi^{\tau-1}+\left(1-\beta_2\right)\frac{l_\xi^{\tau-1}+\epsilon}{h_\xi^\tau+\epsilon}\left(G_\xi^\tau\right)^2 \end{align} \tag{ 17 }$$

and $l_\xi^0 = 0$. Hence, in comparison to the RMSprop algorithm the factor $(l_\xi^{\tau-1}+\epsilon)^{\tfrac{1}{2}}$ is applied additionally in the weight update and the order of adding ε to $h_\xi^\tau$ and taking the square root is inverted.

RPROP [14, 15] is based on equation (6), whereby $G_\xi^{\tau-1}\cdot G_\xi^\tau$ is employed instead of $g_\xi^{\tau-1}\cdot g_\xi^\tau\cdot P_\xi^\tau$. In addition, a backtracking weight step is applied by setting $G_\xi^\tau = 0$ when $G_\xi^{\tau-1}\cdot G_\xi^\tau\lt 0$. The weight update is given by

$$\begin{align} w_\xi^t = w_\xi^{t-1}-s_\xi^\tau\cdot\mathrm{sgn}\left(G_\xi^\tau\right)\ . \end{align} \tag{ 18 }$$

A generally applicable set of CoRe optimizer hyperparameter values has been obtained from our benchmark on nine ML tasks including seven different models and six different data sets. The training processes span the entire range from learning on small mini-batches to full data set batch learning. Based on this benchmark we generally recommend the hyperparameter values $\beta_1^\mathrm{a} = 0.7375$, $\beta_1^\mathrm{b} = 0.8125$, $\beta_1^\mathrm{c} = 250$, $\beta_2 = 0.99$, $\epsilon = 10^{-8}$, $\eta_- = 0.7375$, $\eta_+ = 1.2$, $s_\mathrm{min} = 10^{-6}$, $s_\xi^0 = 10^{-3}$, $d_\chi = 0.1$, and $t_\mathrm{hist} = 250$. The number of frozen weights per group $n_\mathrm{frozen,\chi}$ can often be specified as a fraction of frozen weights per group $p_\mathrm{frozen,\chi}$. Well working values of $p_\mathrm{frozen,\chi}$ are typically in the interval between 0 (without stability-plasticity balance) and about $10\%$. The maximal step size $s_\mathrm{max}$ is recommended to be 10⁻³ for mini-batch learning, 1 for batch learning, and 10⁻² for intermediate cases. $s_\mathrm{max}$ is the main hyperparameter like the learning rate γ in many other optimizers.

To assess the performance of the CoRe optimizer in comparison to nine other optimizers with in total 16 different hyperparameter settings, relative accuracy scores for nine ML tasks were calculated for these optimizers (figures 1(a) and (b)). For mini-batch learning on small batch sizes ($0.1\%$ for AED, AEF, ICD, and ICF) the popular Adam optimizer and our CoRe optimizer perform best, while especially RPROP yields poor accuracy because it cannot handle well stochastic gradient fluctuations. RPROP is intended for batch learning which becomes obvious by the high accuracy scores for SS and TS. For these ML tasks, RPROP and the CoRe optimizer achieve the highest accuracy scores. In the intermediate case, i.e. mini-batch learning with rather large batch sizes ($5\%$ for SR and $10\%$ for lMLP training (figure 4)), both Adam and RPROP perform well with Adam having a small advantage over RPROP. However, the CoRe optimizer outperforms both in this case.

Zoom In Zoom Out Reset image size

Moreover, the learning speed and reliability of the CoRe optimizer in reinforcement learning (NR and RA) is also better than for the other optimizers (figures 1(a) and (b)). RPROP is not able to learn the task in the maximal number of episodes for NR in any training. The CoRe optimizer's convergence speed of the mean test set errors for the other ML tasks is similar to Adam for mini-batch learning and similar to RPROP for batch learning (see figures S1–S7 and S9 in the supporting information).

In total, the CoRe optimizer achieves the highest final accuracy score in six tasks and lMLP training, Adam$^*$ in two tasks, and RPROP$^*$ in one task (figures 1(a) and (b)). However, in the six cases where the CoRe optimizers performs best, the second best optimizer is always within the uncertainty interval of the CoRe optimizer's accuracy score. Still, there is no single optimizer which is always within the uncertainty interval. For example, Adam, RMSprop, RMSprop$^*$, and SGD are within the uncertainty interval for ML task ICF, only AdaMax$^*$ for SR, and AdaMax$^*$, RPROP, and RPROP$^*$ for TS, whereas the CoRe optimizer is always within the uncertainty interval of the best optimizer for the other three ML tasks. Hence, even if there is no clear dominance for individual ML tasks, the CoRe optimizer is among the best optimizers in all these ML tasks resulting in, on average, the best performance and the broadest applicability. Therefore, the CoRe optimizer is well-rounded and achieves the highest overall accuracy score (figure 2). The overall accuracy score of Adam is second highest, while those of AdaMax$^*$ and Adam$^*$ are almost equal to that of Adam. The uncertainty interval of the CoRe optimizer's overall accuracy score overlaps slightly with that of the Adam optimizer. We note that the uncertainty interval of the Adam optimizer's results is also the largest among all results.

Zoom In Zoom Out Reset image size

In general, for the chosen set of ML tasks the optimizers which combine momentum and individually adapted learning rates (CoRe, Adam, and AdaMax) perform better than those which only apply individually adapted learning rates (RMSprop, AdaGrad, and AdaDelta) (figure 2). However, the differences among the CoRe optimizer, Adam, and AdaMax are larger than that of RMSprop and AdaMax. The final accuracy obtained by pure SGD is significantly worse than that of the aforementioned optimizers. However, for these nine ML tasks it is still slightly better than that of the optimizers which employ only momentum (Momentum and NAG). The overall accuracy of RPROP is in between those applying individually adapted learning rates and SGD for these ML tasks. However, this order is, of course, dependent on the fraction of mini-batch and batch learning ML tasks.

The best single model performances obtained by the CoRe optimizer are provided in table S5 and figures S10 (a), (b) and S11 in the supporting information. For SS we can compare the final accuracy directly to the original work with $81.5\%$ correct test set classifications [48]. Due to training by the CoRe optimizer, the best graph convolutional network for SS achieves a test set classification accuracy of $84.2\%$.

The CoRe optimizer's hyperparameters were tuned on this set of ML tasks, while the general hyperparameter recommendations of PyTorch for the other optimizers were not based on this benchmark set. To provide a fair comparison, we also applied hyperparameter values for the other optimizers which were adjusted on this set of ML tasks. The adjusted hyperparameters of AdaDelta$^*$, AdaMax$^*$, Momentum$^*$, and RPROP$^*$ yielded an improvement of their overall accuracy scores (figure 2). However, the gain is not sufficient to reach the overall accuracy scores in the next better class of optimizers described in the last section. Therefore, the choice of the optimization algorithm is confirmed to be crucial for the final accuracy of the ML model. The highest overall accuracy scores of Adam, NAG, and RMSprop were obtained with their generally recommended hyperparameter values. The second best choices of the hyperparameters yielded very similar overall accuracy scores.

Another difference between the CoRe optimizer and the other optimizers was the application of a weight decay. However, figures S13 and S14 in the supporting information show that the standard weight decay algorithm of Adam employed with four different hyperparameter values in general reduces the accuracy score for Adam. Only the weight decay algorithm of AdamW can lead to a small increase of the overall accuracy score. However, the gain is only a fraction of the overall accuracy score difference between the CoRe optimizer and the Adam optimizer. The weight decay of the CoRe optimizer only marginally affects the final accuracy on average (figures S13 and S14 in the supporting information).

In the analysis of individual ML task performances, we note that RPROP and the CoRe optimizer show a slow convergence in the initial epochs of SS training (see figure S6 in the supporting information). The reason is that large weight changes are required in the optimization and the initial step size $s_\xi^0$ is only set to 0.001. Higher values of $s_\xi^0$ result in faster convergence to a similar final accuracy, with $s_\xi^0 = 0.1$ yielding a much faster convergence than obtained with Adam (see figure S7 in the supporting information). However, this ML task is an extreme example with few weight updates to adjust $s_\xi^\tau$ in batch learning and the need of large weight changes. Still, as the final accuracy is the same and in most applications $s_\xi^\tau$ is fast adapted in a relatively small fraction of weight updates, the initialization of $s_\xi^0$ is in general noncritical.

Another edge case can be obtained for high maximal step size values $s_\mathrm{max}$ in the CoRe optimizer. While $s_\mathrm{max} = 1$ yields a high final accuracy in TS training when early stopping is applied, the training can become unstable when continued (see figure S8 in the supporting information). However, reducing $s_\mathrm{max}$ to 0.1 already solves this issue (see figure S9 in the supporting information).

In the training of lMLPs rather large fractions of training data ($10\%$) were employed in the loss function gradient calculation. In line with the results of the PyTorch ML task examples, this kind of training best suits the CoRe optimizer followed by Adam$^*$, Adam, Adamax$^*$, and RPROP$^*$ (figures 3(a), (b) and 4). Moreover, the general trend is confirmed that adaptive and momentum based optimizers perform best, while only adaptive optimizers still yield better results than only momentum based optimizers. In contrast to the PyTorch ML task examples, where the stability-plasticity balance of the CoRe optimizer with $p_\mathrm{frozen}$ around 0.025 can only marginally improve the accuracy scores for AED, AEF, and SR and worsens the final accuracy for ICD and ICF (see figure S12 in the supporting information), the lMLP training largely benefits from the stability-plasticity balance with $p_\mathrm{frozen} = 0.1$. We note that tuning $p_\mathrm{frozen}$, in addition to the maximal step size, extends the hyperparameter optimization capability for $\mathrm{CoRe}^{p_\mathrm{frozen} = 0.1}$ compared to CoRe and all other optimizers, for which only the maximal step size/learning rate was adjusted while all other hyperparameters were taken from the PyTorch ML task example results. This higher degree of freedom can also contribute to the optimization performance. However, a significant performance improvement was not obtained for any other hyperparameter tuning with the exception of tuning $\eta_-$.

Zoom In Zoom Out Reset image size

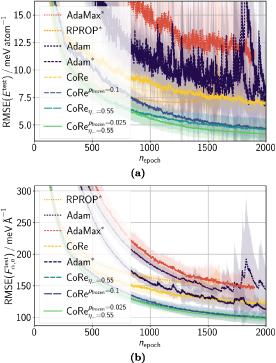
Zoom In Zoom Out Reset image size

Moreover, the stability-plasticity balance smoothens the training convergence as shown in the test set root mean square errors (RMSEs) of energies and atomic force components as a function of the training epochs (figures 5(a) and (b)). The CoRe optimizer yields smoother convergence than Adam, which is beneficial, for example, in lifelong ML where the lMLP needs to be ready for application in every training stage. The accuracy scores in figures 3(a), (b) and 4 take into account the convergence smoothness (see section 3) in contrast to the accuracy scores in figures S15 and S16 in the supporting information which are only based on the individual lMLP early stopping results. The latter is beneficial for the Adam results but still the CoRe optimizer with stability-plasticity balance outperforms Adam. The convergence speed is also higher for the CoRe optimizer than for Adam. This observation is in line with the convergence of the SR ML task (see figure S5 in the supporting information) which also represents a training case between mini-batch and batch learning. To demonstrate the benefit of more stabilized learning in lMLP training, we additionally decreased the $\eta_-$ value which smoothens and improves the training process similarly. Both, a large $p_\mathrm{frozen}$ and a small $\eta_-$, lead also to a better interplay with the lifelong adaptive data selection. However, this interplay is only a minor factor of the large accuracy score improvement since the improvement is similar in training with random data selection (see figure S17 in the supporting information). Lifelong adaptive data selection increases the final accuracy in general. In conclusion, a very smooth convergence is desired in lMLP training making a smaller $\eta_-$ value beneficial. However, the final accuracy and convergence speed and smoothness are already higher than those of other state-of-the-art optimizers when the generally recommended hyperparameter values with a stability-plasticity balance enabled by $p_\mathrm{frozen}$ are applied.

Zoom In Zoom Out Reset image size

In comparison to our previous work, where the best 10 of 20 lMLPs yielded $\mathrm{RMSE}(E^\mathrm{test})$ and $\mathrm{RMSE}(F_{\alpha,n}^\mathrm{test})$ to be $(4.5\pm0.6)\,\mathrm{meV\,atom}^{-1}$ and $(116\pm4)\,\mathrm{meV}\,\unicode{x00C5}^{-1}$ after 2000 training epochs with the CoRe optimizer, the generally recommended hyperparameters of this work in combination with $p_\mathrm{frozen} = 0.1$ ($\mathrm{CoRe}^{p_\mathrm{frozen} = 0.1}$) improved the accuracy to $(4.1\pm0.7)\,\mathrm{meV\,atom}^{-1}$ and $(90\pm5)\,\mathrm{meV}\,\unicode{x00C5}^{-1}$. With an adjusted $\eta_-$ value for even smoother training ($\mathrm{CoRe}_{\eta_- = 0.55}^{p_\mathrm{frozen} = 0.025}$) the respective test set RMSE values decreased to only $(3.4\pm0.4)\,\mathrm{meV\,atom}^{-1}$ and $(92\pm4)\,\mathrm{meV}\,\unicode{x00C5}^{-1}$.

Finally, the comparison of computation time for training with Adam and the CoRe optimizer shows that not only the final accuracy but also the accuracy-cost ratio of the CoRe optimizer is better than that of Adam. For comparison of multiple trainings with the lMLP software, the time fraction of model fitting in the entire training process (including initialization, descriptor calculation, model fitting (about $87\%$), final prediction, and finalization) is calculated to reduce the influence of different computers and computation loads. The resulting speed is the same within the uncertainty interval for Adam and the CoRe optimizer. The additional operations in the CoRe optimizer algorithm cause only little increase of computational cost which is not significant in comparison to the cost for evaluating the loss function gradient. For the presented lMLP example, an optimizer step requires less than $0.2\%$ of the time needed for a loss function gradient calculation. Since the CoRe optimizer requires only the loss function gradient as input like Adam and the other optimizers, the computation time per training epoch is similar for all optimizers.