Generation of conformational ensembles of small molecules via surrogate model-assisted molecular dynamics

Accurately predicting molecular properties is an important task with applications across the sciences. Some prominent examples are drug discovery and material design. Estimating such properties relies on sampling from the underlying Boltzmann distribution. However, generating unbiased and independent samples from the Boltzmann distribution efficiently remains a challenging open problem.

Currently, molecular dynamics (MD) [1] and Markov chain Monte Carlo [2] are the key techniques to draw samples from the Boltzmann distribution. While these techniques asymptotically generate samples from the Boltzmann distribution, many simulation steps are often needed to generate just one independent sample. This problem is particularly prescient for high-dimensional and meta-stable molecular systems. Despite their limitations, these techniques are widely used, especially in combination with enhanced sampling methods [3], which offer different strategies to speed up the generation of independent samples. Important enhanced sampling methods include replica-based approaches [4, 5], flooding [6], meta-dynamics [7], and umbrella sampling [8].

With the advent of deep generative models (DGMs) [9–13], a family of new methods to generate unbiased one-shot equilibrium samples of the Boltzmann distribution were proposed under the name of Boltzmann Generators (BG) [14–17]. These methods approximate the Boltzmann distribution of a molecular system with a DGM which allows efficient sampling and exact likelihood evaluation, commonly Normalizing Flows [11]. Efficient sampling allows to side-step iterative simulation methods, and exact likelihood evaluation allows to recover unbiased samples through importance sampling or importance weighing [14]. Previous work has successfully used BGs to sample from large molecules such as proteins [14] or solids [18]. However, these approaches currently do not generalize to different molecular systems, and designing models that are transferable across different molecules remains a challenging task. Another family of recent related methods, such as implicit transfer operator learning (ITO) [19] or Timewarp [20], tackles the sampling problem by modeling the generative process in MD simulations, yet on much longer time-scales. Nevertheless, currently, these approaches similarly suffer from limited transferability.

Other approaches focus on enumerating the local minima of a potential energy function, so-called conformers. Different architectures have been proposed, such as CGVAE [21], GeoMol [22], or GeoDiff [23]. These methods are transferable across different molecular systems, however, as the generated states represent local minima of potential energy, they are unable to capture entropic effects due to thermal fluctuations, which makes them unsuitable for computing many molecular properties.

Large-scale conformational rearrangements in molecules can be represented by changes in torsion angles (dihedrals), which correspond to rotations occurring around flexible bonds. For example, the structures of biomolecules such as proteins or RNA are compared and analyzed in terms of such angles, using the Ramachandran plot and probabilistic models of local structure [24, 25] as prominent examples. Transitions between different conformations usually account for the slowest processes in simulations. Therefore, generating representative ensembles of torsions is time-consuming and challenging. For this reason, models focusing on torsion angles are useful means to conformational sampling. Recent work encoding conformations in small molecules using torsions include GeoMol [22], Torsional Diffusion [26], Tora3D [27], and VonMisesNet [28]. Apart from capturing major conformational changes, torsion angles are attractive as they reduce the dimensionality of conformational space and are intrinsically invariant to rigid body symmetries. However, even if some of these methods can generate equilibrium samples, they still cannot model stochastic fluctuations in the local structure, and their evaluation as surrogates of the Boltzmann distribution is limited.

In this work, we present surrogate model-assisted molecular dynamics (SMA-MD), a method for generating equilibrium ensembles of molecules. In SMA-MD, generative models are used to sample a diverse ensemble of initial conditions for short molecular simulations. SMA-MD follows a two-step procedure: first, a generative model mixes efficiently across degrees of freedom which exchange slowly in molecular simulations. Second, we reweight samples against the Boltzmann distribution and run short MD simulations to equilibrate the local structure and ensure sampling statistics are unbiased with respect to the target Boltzmann distribution. In this manner, SMA-MD is able to capture entropic effects occurring in all degrees of freedom in a molecule, which are critical for the computation of thermodynamic quantities such as free energy differences. We implement SMA-MD using torsional surrogate models and restrict ourselves to working with small non-cyclic molecules. We probe our method by measuring geometric and thermodynamical (potential and implicit solvation free energies) properties and comparing them to the baseline of classic MD simulations, used as the source of training data. We empirically show that our method can generate diverse and physically realistic ensembles. Equilibrium ensembles generated with SMA-MD present higher conformational coverage and lower average energy than those obtained with conventional MD simulations of similar runtime, closely matching long replica exchange (RE) simulations.

Our main contributions are:

• Introducing SMA-MD: a new approach that combines generative models for slow degrees of freedom with statistical reweighting and short simulations to produce equilibrium conformational ensembles for molecules.
• Evaluation of our method by comparison with ensembles generated by MD and RE simulations.
• Generating a new dataset: consisting of MD simulations of 12530 k non-cyclic small molecules that we use as training data, along with data splits for benchmarking.
• Showcasing a downstream application: estimating relevant observables such as geometrical quantities and free energies of solvation.

2.1. Sampling and molecular properties

Experimental observables (molecular properties) often correspond to averages over the ensemble of 3D arrangements (conformations, x) molecules can adopt, which follow the Boltzmann distribution,

$$\begin{align} \mu\left(\mathbf{x}\right) = \mathcal{Z}^{-1} \exp\left(-\beta U\left(\mathbf{x}\right)\right), \text{with } \mathcal{Z} = \int \mathrm{d}\mathbf{x}\, \exp\left(-\beta U\left(\mathbf{x}\right)\right), \end{align} \tag{ 1 }$$

where $U(\mathbf{x})$ is the potential energy and β is the inverse temperature. We conveniently define the reduced potential $u(x) = \beta U(\mathbf{x})$. Given independent and identically distributed (i.i.d.) conformations sampled from the Boltzmann distribution, thermodynamical quantities can be computed with the Monte Carlo estimator:

$$\begin{align} O = \mathbb{E}_{\mathbf{x}\sim \mu\left(\mathbf{x}\right)}\left[o\left(\mathbf{x}\right)\right] \approx \frac{1}{N}\sum_{i = 1}^No\left(\mathbf{x}_i\right), \hspace{0.15cm} \mathbf{x}_i \overset{\text{i.i.d.}}{\sim} \mu\left(\mathbf{x}\right), \end{align} \tag{ 2 }$$

where $o(\mathbf{x})$ computes the microscopic contribution of a property for a conformation. Generating i.i.d. samples from the Boltzmann distribution is challenging. However, if a surrogate model $p(\mathbf{x})$ overlaps with $\mu(\mathbf{x})$, unbiased Boltzmann-distributed samples can be generated by reweighting the surrogate distribution [14]. This reweighing or resampling, can be achieved with various algorithms, but the simplest one is known as importance sampling, in which samples from $p(\mathbf{x})$ are assigned statistical weight $w = e^{-u(\mathbf{x})}/p(\mathbf{x})$.

2.2. Boltzmann surrogate model

A Boltzmann surrogate is a generative model trained to generate samples from the Boltzmann distribution. In this work, we consider models that generalize across different molecular systems. We use a torsional generative model and therefore, we structure the generation process in the following two sub-steps.

2.2.1. Local structure generation

We define the local structure of a non-terminal atom as the relative geometry of the atoms connected to it. The local structure of a given atom can be specified as a set of internal coordinates (distances, angles, and dihedral angles). In this work, we restrict ourselves to molecules that do not have rings as cyclic molecules would require special considerations. Local structures around non-terminal atoms are very constrained and highly dependent on the hybridization of the central atom. For this reason, we use a simple method for generating the local structure of molecules:

• Distances and angles are set to the equilibrium force field parameters.
• Dihedral angles are chosen based on the hybridization of the central atom. For example, if an atom is sp² hybridized, its local structure will be planar but if it is sp³ hybridized, it will follow a tetrahedron shape. We provide further details in supplementary material.

2.2.2. Rotatable bond generation: Torsional Diffusion

In this work, following conventions from previous contributions in the context of small molecules [22, 26], we consider a bond to be rotatable if it connects two non-terminal atoms in the chemical graph. In this step, we generate the remaining degrees of freedom, the torsion angles of rotatable bonds, using a DGM to model potentially complex multi-modal distributions. We choose this DGM to be a diffusion model [12, 13, 29]. Torsion angles lie on the circle and therefore the set of torsions of rotatable bonds within a molecule lies on a hyper-torus. Previous work adapted the formalism of diffusion models to operate on this Riemannian manifold [30]. Based on this work, Torsional Diffusion [26], a diffusion model tailored for modeling torsions, was proposed. One of the main innovations behind Torsional Diffusion is the use of 3D-aware torsional updates which are invariant to the choice of reference atoms. Moreover, a new model architecture exploiting symmetries around rotatable bonds, the pseudo-torque layer, was introduced. Because of these beneficial characteristics and excellent performance in similar tasks, in this work, we use Torsional Diffusion as a model for torsion angles around rotatable bonds.

2.2.3. Training

Since the local structure generation module has no learnable parameters, in this section we solely elaborate on how we train the rotatable bonds model. We train Torsional Diffusion models against a set of target conformations with torsions $\tau_0 \sim p_0$. During training, noise with intensity t is added, resulting in noisy torsions τ_t . Model optimization is performed by minimizing the denoising score matching loss [13, 31],

$$\begin{equation} J_{DSM} \left(\theta\right) = \mathbb{E}_t \left[ \lambda\left(t\right) \mathbb{E}_{\boldsymbol{\tau}_0 \sim p_0, \boldsymbol{\tau}_t \sim p_{t \vert 0}\left(\cdot \vert\ \boldsymbol{\tau}_0\right) } \left[ \vert \vert s\left(\boldsymbol{\tau}_t, t\right) - \nabla_{\boldsymbol{\tau}_t} \log p_{t\vert0} \left(\boldsymbol{\tau}_t\vert \boldsymbol{\tau}_0\right) \vert \vert^2 \right] \right], \end{equation} \tag{ 3 }$$

where noise level t is uniformly sampled, $\lambda(t) = 1/\mathbb{E}_{\boldsymbol{\tau} \sim p_{t \vert 0} (\cdot \vert 0)} \left[ \vert\vert \nabla_{\boldsymbol{\tau}_t} \log p_{t\vert0} (\boldsymbol{\tau\vert \boldsymbol{0}}) \vert \vert^2 \right]$, $s(\boldsymbol{\tau}_t, t)$ is the neural network prediction for the score and $p_{t\vert0} (\boldsymbol{\tau}_t\vert \boldsymbol{\tau}_0)$ is the perturbation kernel. More details about training can be found in supplementary material.

Please note that, if we directly trained a model using molecular conformations obtained from simulations (or other methods), we would create a distribution shift between training and inference. Therefore, to compensate for this, during training, we substitute the local structures from target conformations with the ones generated by our local structure model.

2.3. SMA-MD

In this work, we present SMA-MD as an approach to efficiently sample from the Boltzmann distribution. The overall workflow of SMA-MD is summarized in figure 1 and consists of two main steps. In the first step, we use a generative model trained to emulate the Boltzmann distribution of molecules (the Boltzmann surrogate) to generate conformations. These conformations are constructed in two sub-steps: starting by generating local geometries with a deterministic algorithm and then sampling the torsion angles using a DGM to mix across the molecules' 'slow degrees of freedom'. Next, in the second step, we use short parallel MD simulations to thermalize and mix the fast degrees of freedom. Combining simulations with an exact reweighting scheme enables us to generate unbiased samples from the Boltzmann distribution of the molecule. These ensembles can then be used to compute thermodynamic properties of interest.

Zoom In Zoom Out Reset image size

2.3.1. Sampling from the surrogate model

We first generate the degrees of freedom corresponding to the local structure and then we sample the torsions, τ . The torsions are sampled through integration of the probability flow (neural) ODE (ordinary differential equation), corresponding to the Torsional Diffusion model, which further enables exact reweighting through sample likelihood calculation. We denote $p_0(\boldsymbol{\tau})$ the neural ODE sampler likelihood in torsional space. However, the Boltzmann distribution is generally specified as a function of the 3D coordinates of the atoms in a molecule, x. Therefore, to allow for compatibility with the Boltzmann measure, we need to express $p_0(\boldsymbol{\tau})$ in Euclidean space instead. As all the generated geometric quantities correspond to internal coordinates, and the local structure is generated deterministically, the Euclidean likelihood can be computed as

$$\begin{equation} p \left(\mathbf{x}\right) = p_0\left(\boldsymbol{\tau}\right) / \vert \det\left(J_{\text{int} \rightarrow \text{euc}}\left(\mathbf{x}\right)\right) \vert, \end{equation} \tag{ 4 }$$

where $J_{\text{int} \rightarrow \text{euc}}(\mathbf{x})$ is the Jacobian of the transformation from internal to Euclidean coordinates. For details about the sampling procedure, see supplementary material.

2.3.2. Reweighting and MD fine-tuning

After generating molecular conformations with the surrogate model, we post-process them by taking two extra steps which we have observed to be critical to generate physically realistic structures.

2.3.2.1. Reweighting according to Boltzmann weights

Given a set of sampled conformers, we compute per-sample weights with

$$\begin{equation} w\left(\mathbf{x}\right) = \frac{e^{-u\left(\mathbf{x}\right)}}{p\left(\mathbf{x}\right)}. \end{equation} \tag{ 5 }$$

We note that reweighting only guarantees improvement in the case of complete domain coverage, which is not fulfilled in general. However, we observe that the surrogate model tends to broadly cover the domain, even generating high-energy metastable conformations. One important role of the reweighting step is ruling out these states as we illustrate in supplementary material.

2.3.2.2. MD fine-tuning: short parallel simulations

Generally, we expect reweighting to align the generated ensemble more closely to the target Boltzmann distribution. However, the ensemble still misses two fundamental ingredients in our implementation: stochastic fluctuations in the local structure and the coupling of these fluctuations with the rotatable bonds. We hypothesize that these two features can be recovered in short simulations. Therefore, we run parallel simulations on the reweighted ensemble using the REFORM library extending OpenMM [32, 33]. For the experiments performed in this work, we run 1 ns simulations per sample.

2.4. The MDQM9-nc dataset

3.1. The impact of the different components of SMA-MD for sampling equilibrium conformations of molecular systems

We showcase the contribution of the different components of SMA-MD by analyzing state populations and potential energies for a molecule in the test set at the two different sampling stages (sampling from the surrogate model and applying post-processing). To find the slowest transitions between metastable states, we use time-lagged independent component analysis (TICA) [37], a linear dimensionality reduction technique that identifies the linear combinations of molecular features that maximizes the autocorrelation. In figure 2(a) we observe that the Boltzmann surrogate captures the relevant states, potentially transitioning to each other in slow processes. Moreover, reweighting and running short simulations adjust the populations and reduce the energy of the ensemble, matching ground-truth long RE simulations figure 2(b).

Zoom In Zoom Out Reset image size

3.2. SMA-MD generates similar local structures to MD

3.3. SMA-MD outperforms MD in conformer generation

As previously introduced, a conformer is a local minimum in the molecular energy landscape. Therefore, they are also local maxima of the density landscape. Given an ensemble, we can extract its conformers by finding these local minima. Following this logic, we retrieve conformers from ensembles generated by SMA-MD and MD.

To obtain a set of conformers from an ensemble, we first find modes in the marginal distributions of torsions. Then, we check how many of the possible combinations of modes in the marginal distributions appear in the ensemble. Next, we refine the set of extracted conformers eliminating duplicates corresponding to atom permutations or global inversions of the geometry. Finally, we check that all conformers satisfy a dissimilarity threshold in their relative root mean square deviation (RMSD). We provide additional details about this procedure in supplementary material.

In table 2 we show the average minimum RMSD (AMR) and coverage (COV) of our method in precision and recall modes, see supplementary material for precise definitions. We report remarkable agreement of SMA-MD with RE, clearly outperforming the training-set-like MD trajectories (MD (15 min)). Because the runtime of SMA-MD (using a single GPU) is longer (20 min) than that of the training set simulations (15 min), see supplementary material for details, we further challenged SMA-MD by comparing to longer MD simulations of comparable runtime. We observe that SMA-MD still clearly outperforms these longer simulations (MD (20 min)) by recovering 6$\%$ more conformers in the ground-truth ensemble. In figure 3 we compare the Coverage for different threshold values. Here we observe that SMA-MD achieves the best Coverage among the three methods independently of the choice of threshold and the improvement margin becomes greater as we reduce the threshold.

Zoom In Zoom Out Reset image size

Table 2. Average minimum root square deviation (AMR) and coverage (COV) of the ensembles generated by SMA-MD and MD simulations of different runtimes against replica exchange. For COV, the threshold is set to δ = 0.75 Å. Bold values indicate best results.

	MD (15 min)		SMA-MD (20 min)		MD (20 min)
	Precision	Recall	Precision	Recall	Precision	Recall
AMR (Å,$\downarrow$)	0.14 ± 0.02	0.24 ± 0.03	0.08 ± 0.01	0.10 ± 0.02	0.13 ± 0.01	0.21 ± 0.02
COV ($\uparrow$)	0.95 ± 0.02	0.87 ± 0.02	0.98 ± 0.01	0.96 ± 0.01	0.97 ± 0.01	0.90 ± 0.02

3.4. Covering conformations separated by high free-energy barriers

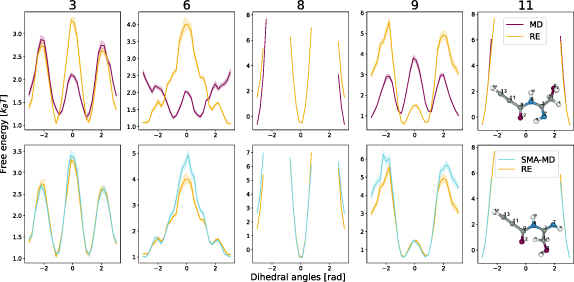
The conformer generation results above, suggest that our generative model covers the local free energy minima of small molecules well and that we may cover the conformational space of small molecules faster than regular MD simulations. We illustrate that this indeed is the case through the following example. We find SMA-MD samples states present in the long RE simulations separated by barriers that are never overcome in MD simulations of comparable runtime to SMA-MD. In figure 4, we show how SMA-MD samples a state (torsion 8) that is not sampled by MD. Overall, the marginal distributions of MD do not match RE, suggesting the simulated ensembles are not fully equilibrated. However, SMA-MD shows remarkable agreement. The difference in mean ensemble energy w.r.t. to RE is −0.37 $k_\textit{B}\textit{T}$ for SMA-MD and +3.15 $k_\textit{B}\textit{T}$ for MD.

Zoom In Zoom Out Reset image size

3.5. SMA-MD generates more diverse and energetically favorable ensembles than MD

In section 3.1 we have shown that SMA-MD outperforms conventional MD simulations in conformer generation, presenting better precision and recall w.r.t. ground-truth simulations. Moreover, we have illustrated in section 3.4 how SMA-MD is able to sample across high-energy barriers, where MD falls short.

Furthermore, we show that SMA-MD generates samples in a more statistically efficient manner by comparing the ensemble potential energies. We do this by computing the difference in average ensemble energies and the Jensen-Shanon divergence (Div) between energy histograms. We show in figure 5(a) that SMA-MD generates more similar energy averages and distributions to RE than MD, and that the agreement with RE is very high.

Zoom In Zoom Out Reset image size

We attribute a number of factors to the improved performance of SMA-MD compared to MD. First, SMA-MD combines data aggregation and post-processing. On the one hand, even if simulations used as training data are not fully converged, it is possible to learn relevant structures from similar molecules. On the other, reweighting and short simulations help to equilibrate the populations and compensate for small deviations in the geometries generated by the surrogate. Combining these two elements, SMA-MD shows robustness against training on biased data (non-converged simulations). Second, SMA-MD does not need initial conditions. One important limitation of MD simulations is their sensitivity to the initial coordinates, often obtained from an experimental crystal structure. Indeed, a main success of Markov state modeling [38] is its ability to use simulation data from different initial conditions to make quantitative predictions. In contrast, SMA-MD not only does not require an initial condition but provides a way of initializing simulations with several different representative initial structures to boost convergence. Third, SMA-MD allows for parallelization. MD simulations are intrinsically sequential, however, all the individual components in SMA-MD allow for parallelization, which makes SMA-MD a more suitable method for modern computing hardware.

3.6. Prediction of molecular properties using SMA-MD: solvation free energy

A major bottleneck of SMA-MD remains the computational cost per sample in comparison to MD. However, as previously discussed, while MD is intrinsically sequential, the SMA-MD framework is fully parallelizable (except for the short individual simulations) and therefore allows for an efficient way to use modern computing hardware, including GPUs. Indeed, this divide-and-conquer strategy is successfully applied in the Markov state modeling community [41–44]. Nevertheless, SMA-MD, in the context presented here does not outperform the state-of-the-art RE in terms of runtime, see supplementary material. This limitation is related to the high cost of sampling from the generative model and the low sample efficiency. Due to continual improvements in the field of DGMs, we believe both of these issues will be resolved in the near future.

Currently, SMA-MD is limited to non-cyclic molecules. This limitation comes from the difficulty of generating realistic ring structures when representing molecules in internal coordinates, e.g. distance, angles, and torsions. This problem is particularly prescient for non-aromatic ring structures, including sugars, which are highly restrained but may undergo concerted slow conformational transitions. While heuristics are available to overcome this problem in e.g. rule-based conformer generations, these methods do not readily allow for the extraction of equilibrium statistics. Therefore, we leave accurate modeling of rings for future work. If modeling non-aromatic rings does not entail significant extra computational cost, we foresee that SMA-MD will be scalable to drug-like molecules. Drug-like molecules in the GEOM-Drugs dataset [45] contain 1.7 aromatic rings and 1.3 non-aromatic rings per molecule. Consequently, the number of rotatable bonds in molecules studied here and those of drug-like molecules, 6.3 and 7.9 respectively, remain comparable.

Finally, we consider training Boltzmann surrogates with large-scale data a promising direction. With data sharing taking an increasing priority, simulation data using similar protocols are deposited in scientific data repositories. Although these simulations may not be fully converged, they still contain valuable information to build general transferable Boltzmann surrogates. Indeed, the data we used to train our model is clearly not converged, however, we can still learn a useful surrogate. Mining this data to train Boltzmann surrogates could increase the transferability and therefore the usefulness of these systems.

In this work, we have introduced SMA-MD, an efficient method for generating equilibrium conformational ensembles for molecules. SMA-MD combines a transferable surrogate from the Boltzmann distribution with a statistical reweighting and short simulation post-processing step. The goal is to mix between slow degrees of freedom using the surrogate model and refine the ensemble through reweighting and brief simulations. Here, we implement SMA-MD using torsional generative models and show that this method outperforms conventional MD simulations in diversity and ensemble energy. We showcase the applications of this method in downstream tasks by successfully estimating solvation free energies. Even if the work presented here is limited to small non-cyclic molecules, we believe it motivates further research on solving remaining scientific problems and paves the way towards the adoption of similar methods in practical applications, especially drug-discovery pipelines.

Code is available at https://github.com/olsson-group/sma-md.

The authors thank Rocío Mercado for discussions and early contributions to this work. This work was partially supported by the Wallenberg AI, Autonomous Systems and Software Program (WASP) funded by the Knut and Alice Wallenberg Foundation. The computations in this work were enabled by the Berzelius resource provided by the Knut and Alice Wallenberg Foundation at the National Supercomputer Centre.

The data that support the findings of this study are openly available at the following URL/DOI: https://github.com/olsson-group/mdqm9-nc-loaders.