Predictive models for inorganic materials thermoelectric properties with machine learning

Delchere Don-tsa; Messanh Agbeko Mohou; Kossi Amouzouvi; Malik Maaza; Katawoura Beltako

doi:10.1088/2632-2153/ad6831

1. Introduction

As the energy demand continues to rise and concerns about environmental sustainability grow [1], it has become increasingly alarming to observe that a significant amount of this energy, approximately 66%, is dissipated in the form of unused heat within industrial processes, modes of transportation and in electronic components [2–4]. This energy loss is attributed to the inefficiency of existing thermoelectric materials and has prompted scientists to explore more efficient thermoelectric materials or to optimize existing ones [1, 5–8]. Thermoelectric generators stand as solid-state devices without moving parts, presenting a viable alternative for harnessing wasted heat [9–11]. The generator consists of two different types of semiconductors: one with n-type conductivity and the other with p-type conductivity. These two materials are joined together with provisions for electricity and heat transfer located between a hot source at temperature $T_{\mathrm{hot}}$ and a cold sink at temperature $T_{\mathrm{cold}}$ . The efficiency of a thermoelectric generator is considerably influenced by both the temperature difference, $T_{\mathrm{hot}} - T_{\mathrm{cold}}$ , and the inherent material properties, often summarized in the figure of merit ZT, given by the following formula;

$\begin{align} ZT = \frac{\sigma S^2 T}{\kappa},\end{align} \tag{ 1 }$

where S, σ, T, and κ represent the Seebeck coefficient, the electrical conductivity, the absolute temperature, and the thermal conductivity, respectively.

An efficient thermoelectric material aims to maximize the electrical conductivity and the Seebeck coefficient while minimizing the thermal conductivity, so that ZT is high. Traditional methods for discovering and designing energy materials typically involve laboratory experiments and simulations, which are time-intensive and yield a limited number of new material samples [12]. Furthermore, these methods have a low success rate [13]. Over the past few decades, the density functional theory (DFT) has been widely used to screen new materials due to its ability to handle extensive searches and offer high computational accuracy. However, DFT calculations also come with drawbacks, such as significant computational costs [14]. In recent years, there has been a significant change in how we explore and design materials [15]. This change has been driven the emergence of the growing influence of artificial intelligence, particularly machine learning [16–19](ML) that involves computer algorithms that enhance their performance autonomously through learning from experience and the utilization of data. Both classification and regression tasks, in conjunction with various machine learning models, have been employed to predict thermoelectric properties of materials. Researchers have adopted diverse strategies for data collection, utilizing existing databases such as Material Project [20], Open Quantum Materials Database (OQMD) [21], Crystallography Open Database (COD)[22], Aflow [23], and NIST Materials Data Repository [24]. Alternatively, some have conducted experimental work to generate their datasets. Other valuable resource in this domain is the matminer Python library [25], designed for efficient data mining. Moving beyond data collection, the selection of machine learning models has been crucial in refining the predictions of materials thermoelectric properties. Researchers explored an array of Machine Learning algorithms, including Random Forest, Ada Boost, Gradient Boost, light gradient boosting, Support Vector Machine, and K-Nearest Neighbor used to predict thermoelectric figure of merit, Seebeck coefficient and power factor of several compounds. Among these models, Random Forest has emerged as the most suitable, achieving an R² value of 0.95 in predicting the thermoelectric figure of merit of layered $IV-V-VI$ semiconductors. [4, 26–33] Classification has been used by Chernyavsky et al [34] to classify thermoelectric materials into distinct binary classes. This approach facilitates determining where a material possesses a high or low Seebeck coefficient, electrical conductivity, or thermal conductivity based on the threshold value set by Gaultois et al [35]. Tao Fan et al [36]. have also perform a classification in order to identify promising thermoelectric materials from others and The prediction on test sets show that all the trained models can achieve classification accuracy higher than 85%. Inspired by existing machine learning models, some researches have developed more promising methods for predicting material properties. For instance, CraTENet, CraTENet+gap, Random Forest+ gap [33] developed by Luis Antunes et al to predict Seebeck coefficient, electrical conductivity of n and p doped material. The CraTENet+gap, Random Forest+ gap demonstrated higher accuracy compared to the standard CraTENet and simple Random Forest in predicting Seebeck coefficient, Thermoelectric power factor and electrical conductivity of p and n doping inorganic materials. Similarly, Liu et al [37] developed the DopNet model for analogous purpose, comparing its performance with Gradient Boosting Tree Regression, Gaussian Process Regression, and Support Vector Regression. The DopNet model surpassed all other machine learning models, achieving R² values of 0.86 and 0.64 for Seebeck coefficient and electrical conductivity of inorganic compounds respectively. The potent capabilities of ML in speeding up material development are evident, as they efficiently manage vast datasets and conduct complex analyses. These advancements collectively forge a new path towards identifying energy-efficient materials and hastening progress in this vital field [34, 37, 38].

In this article, unsupervised machine learning algorithm such as Density-Based Spatial Clustering Application with Noise(DBSCAN) was used in order to clustering the dataset. And furthermore, supervised Machine Learning models such as linear regression, exponential regression, random forest are used to predict transport properties by natural clustering and to propose key physical and governing laws specific to each cluster that will contribute to faster and more accurate predictions of thermoelectric properties, thereby facilitating the discovery of efficient materials. By harnessing the power of machine learning and data analysis, we can expedite the search for promising materials and revolutionize the design of more efficient and durable thermoelectric devices. Our work is structured as follows: First, we collect our dataset. Next, we perform the cluster analysis to group thermoelectric materials based on their properties. Within these clusters, we study the relationship between thermoelectric properties. Additionally, we conduct an exponential regression on the entire dataset to determine the maximum Seebeck coefficient given the electrical conductivity, and vice versa. Subsequently, we perform a linear regression specifically on cluster D2 to predict the Seebeck coefficient, power factor, and electrical conductivity of n-doped materials based on the properties of p-doped materials, and vice versa. Finally, we apply the random forest model to both the whole dataset and dataset D1 to predict the Seebeck coefficient and power factor.

2. Methods: data analysis and machine learning

In this work, we used ML techniques to achieve our goal, which consists essentially of data collection, data cleaning, exploratory data analysis, model building, and deployment.

2.1. Data collection

This study uses the boltztrap_mp dataset from matminer [25] which was thoughtfully compiled and made publicly available by Ricci et al in 2017 [39]. This dataset presents a comprehensive collection of electronic and thermoelectric properties for 8924 inorganic compounds extracted from the Materials Project database [20]. By employing the BoltzTraP software package in conjunction with GGA-PBE or GGA+U density functional theory calculations [40, 41] under a constant relaxation time(CRTA), the dataset offers crucial insights into the effective mass ratio, which is the ratio between the n-type and the conduction band effective mass for n type doping material, and between the p-type and the valence band effective mass for p-type doping material, thermoelectric power factors, and Seebeck coefficients for both n-type and p-type materials. The reported properties are specifically documented at a temperature of 300 Kelvin, and a carrier concentration of 10¹⁸ cm^-3. The full description of the dataset is given in table 1 of the supporting information(SI).

Approximations such as the GGA and CRTA, may not accurately predict electronic transport properties when compared to real-world experiments. GGA tends to underestimate band gaps and overestimate bandwidths, leading to an overestimation of electronic conductivity [42, 43]. Similarly, CRTA, especially could overlooks important differences in scattering mechanisms between different materials [44, 45]. Consequently, any machine learning model trained on this dataset may inherit these inaccuracies, potentially impacting the reliability of its predictions when compared to experimental results. To overcome this, we only used materials compositions and effective mass ratio in our model which give the opportunity to have viable prediction with more accurate dataset.

2.2. Machine learning model

The built machine learning models classify our datasets into clusters and predict the Seebeck coefficient, electrical conductivity and thermoelectric power factor of inorganic materials using the dataset described in section 1. The machine learning model consists of clustering analysis, linear regression, exponential regression, random forest classification, and regression. For cluster analysis, we use the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) method. DBSCAN identifies clusters based on the density of data points, using a defined radius eps and a minimum number of points min_samples. It classifies points as core points, border points, or noise points based on their local density. This method is particularly effective at detecting clusters of arbitrary shapes and handling outliers (noise). Unlike other algorithms, DBSCAN does not require specifying the number of clusters beforehand.

Assuming that the properties of p-doped materials are known, Linear regression was use on cluster $D2$ to predict those of n-doped materials. Similarly, assuming we have the value of the Seebeck coefficient, exponential regression method was used to find the maximum value of electrical conductivity. Please refer to the supporting information(S.I) for more explanation about linear regression and exponential regression method.

We use random forest model on cluster $D1$ and the whole dataset in order to predict the target variables (Seebeck coefficient and thermoelectric power factor n and p) also denoted as Y given the descriptor variables in the dataset(effective mass ration and formula) also denoted as X. Pymatgen and matminer programmes was used to break down a given formula into its component part in order to create new features. This was created based on material composition. We applied two kind of featurizations,

The first was made by using some randomly selected properties that are the row, group, atomic radius, boiling point, melting point, and electronegativity for each element in the composition. Then, we compute the mean and standard deviation based on the set of elemental properties for each composition. These statistical quantities of the elemental properties then become the new features of that material. According to Antunes et al [33], adding a band gap as input to the model outperforms those without the band gap. So, based on that information, We retrieve the band gap of all those materials in Material Project database, along with the effective mass ratio of p and n doping material and added them to the statistical quantities. and this was used as input feature to the first model.

For the second one, the materials agnostic platform for informatics and exploration (MAGPIE) was utilized to compute elemental property attributes. which builds an object that can autonomously engineer 132 new features based on the technique developed by Ward et al [46]. It accomplishes this by first figuring out each component's attribute. The mean, minimum, maximum, and other statistical variables are then calculated based on the set of elemental attributes for each mixture. The new features for that material are then derived from these statistical quantities of the elemental properties. The featurize_dataframe method may then be used by the ElementProperty object to produce all the columns with features. We proceed by removing correlated features, the missing values along with all the columns having the sum of null value greater than 50. If two features have a correlation greater than 0.80, just one of them is keep for further analysis. The remaining features at the end of all these process were 35, and was used as input for the second model. The featurization process is illustrated in figure 1.

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** Process of featurization based composition.
Download figure:
Standard image High-resolution image

So, the random forest model was trained for both classification and regression using those features mentioned above. In order to find the suitable hyperparameter for the model, the grid search method was used and the number of estimator was set to 700, the maximum depth to 10, the minimum sample leaf to 3 and the minimum sample split to 2.

Formally, for the regression task, the goal is to learn a function $f: \mathcal{X} \to \mathcal{Y}$ where $\mathcal{X}$ represents the multi-dimensional input space and $\mathcal{Y}$ represents the corresponding multi-dimensional target space. The training set $\mathcal{D}$ consists of k labeled examples $(\mathbf{x}_i, \mathbf{y}_i)$ , where x_i describes the features of an exemplar in $\mathcal{X}$ , and y_i represents the associated target in $\mathcal{Y}$ . The training procedure involves finding the function f by adjusting the parameters W and b during training. Here, W denotes the weights and b represents the biases of the model. The function f is defined as:

$\begin{align} \hat{\mathcal{Y}} = f\left(\mathcal{X}; W; b\right)\end{align} \tag{ 2 }$

where $\hat{\mathcal{Y}}$ is the predicted output obtained by applying the model to the input data $\mathcal{X}$ .

The optimization process aims to minimize the loss L, which quantifies the disagreement between the true values $\mathcal{Y}$ and the predicted values $\hat{\mathcal{Y}}$ . The loss function L is defined as the mean squared error, computed using the following equation:

$\begin{align} L = \frac{1}{N} \sum_{j = 1}^{N}\left(\mathcal{Y}_j - \hat{\mathcal{Y}}_j\right)^2\end{align} \tag{ 3 }$

where N is the number of samples in the training set, $\mathcal{Y}_j$ is the true target for the jth sample, and $\hat{\mathcal{Y}}_j$ is the corresponding predicted output.

The optimization process involves adjusting the parameters W and b to minimize the loss function. This is typically achieved through iterative optimization algorithms such as gradient descent. The update rule for the parameters during each iteration can be expressed as:

$\begin{align} W \leftarrow W - \alpha \frac{\partial L}{\partial W}\end{align} \tag{ 4 }$

$\begin{align} b \leftarrow b - \alpha \frac{\partial L}{\partial b}\end{align} \tag{ 5 }$

where α is the learning rate, and $\frac{\partial L}{\partial W}$ and $\frac{\partial L}{\partial b}$ denote the gradients of the loss with respect to the weights and biases, respectively. The gradients are computed using the chain rule of calculus and the backpropagation algorithm. The training process continues iteratively until the loss converges to a minimum or reaches a satisfactory level. To achieve this, we have used random forest model.

For the classification model, we applied random forest to features obtained after the second featurization in order to classify materials as either $D1$ or $D2$ . Given the pronounced class imbalance in our dataset, with the majority class comprising 8605 data points and the minority class only 132 data points, it was crucial to adopt a technique to mitigate this imbalance. Although random forests inherently have some capability to handle imbalanced data, we chose to employ the Synthetic Minority Over-sampling Technique (SMOTE) to further address this issue. SMOTE is specifically designed to handle imbalanced datasets by generating synthetic samples for the minority class. This technique helps prevent overfitting and enriches the model with more information. To reliably evaluate the model's performance, we used the Area Under the Receiver Operating Characteristic (AUC-ROC) curve. The ROC curve is a probability curve, and the AUC represents the degree of separability between the classes. It indicates how well the model can distinguish between classes. For detailed classification results, please refer to the supplementary information (SI). Figure 2 show the method we have used in each cluster.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** Flowchart of the method choose based cluster.
Download figure:
Standard image High-resolution image

3. Results and discussions

This section is dedicated to data analysis and the development of machine learning models for the prediction of thermoelectric properties such as the Seebeck coefficient, electrical conductivity, and thermoelectric power factor.

3.1. Clusters and data analysis

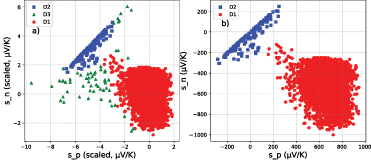
Figure 3 presents the scatter plot of the entire dataset for the Seebeck coefficient of n-type and p-type doping materials. Analysis of the figure 3 reveals a natural clustering pattern. And so we performed the DBSCAN method with ε = 0.5 and min_samples $= 10$ in order to group our datasets into classes, and we found they can be categorized into two main groups: the largest cluster labeled as D1, shown in red circles, and the linear square-shaped cluster colored blue and labeled as D2. We also have some points that do not belong to any cluster, shown in green triangles.

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.** DBSCAN method: (a) clusters with Noise, (b) clusters without Noise.
Download figure:
Standard image High-resolution image

Each cluster falls within the following ranges:

$\begin{align*} \text{D1:} \quad & S_n \in \left[-250, -1000\right] \quad \text{and} \quad\, S_p \in \left[250, 1000\right] \\ \text{D2:} \quad & S_n \in \left[-200, 500\right] \qquad\,\,\, \text{and} \quad S_p \in \left[300, 800\right].\end{align*}$

It is worth to notice from the figure 3 that some of the p-doped materials end up with a negative Seebeck coefficient, and some n-doped materials end up with a positive Seebeck coefficient. Even though this is not the conventional behavior of thermoelectric materials, this was explained by Bin Xu et coworkers [47]. They have shown that there are materials where the sign of their Seebeck coefficient does not depend on the type of charge carrier but on the energy dependence of the electron lifetime. Examples of such materials are Lithium, Copper, Silver, Gold, that have positive Seebeck coefficients when n-doped. Another explanatory route, is the class of materials capable of switching from a positive Seebeck coefficient to a negative Seebeck coefficient and vice versa depending on the imposed physical conditions. Examples of such is CoSbS which p-type turns out that for certain proportions of sulfur, the material ends up with a negative Seebeck coefficient [48]. Using all the data from the Ricci et al database [39], curves of temperature versus Seebeck coefficient for different doping levels have been plotted. These curves can be found in the MPContribs Explorer tab of the Materials Project for materials exhibiting such behavior. We have illustrated this through figure 4 for few of these materials in our database. Figures 4(a) and (b) represent the temperature and doping level dependence of the n-type Seebeck coefficient on the temperature and doping. The same behavior is observe in figures 4(c) and (d) which represents the temperature and doping level dependence of the p-type Seebeck coefficient. Therefore the unconventional Seebeck coefficients of these materials exhibiting this peculiar behavior is intrinsic to these materials.

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.** Temperature and doping level dependence:(a), (b) of the n-type Seebeck coefficient, (c), (d) of the p-type Seebeck coefficient.
Download figure:
Standard image High-resolution image

3.2. Thermoelectric properties

Our analysis focus on the two primary large clusters D1 and D2.

Using the Seebeck coefficient and the power factor, we computed the electrical conductivity of both n and p doping materials with equation (11), where PF represents the power factor, S is the Seebeck coefficient, and σ is the electrical conductivity.

$\begin{align} PF = {\sigma }\cdot S^2.\end{align} \tag{ 6 }$

Figure 5 shows the scatter plot of various thermoelectric properties of each cluster for better understanding of their relationships. A deep analysis of figure 5(a) which is the scatter plot of the power factor and Seebeck coefficient of n type doping materials, reveals that materials in cluster D1 exhibit a negative S_n, while materials in cluster D2 may exhibit either negative or positive values for both S_n and S_p. Figures 5(b) and (c) are the relationship between the Seebeck coefficient and the electrical conductivity of n doping and p doping material respectively. As expected, the absolute value of the Seebeck coefficient and the electrical conductivity are inversely proportional. We also observe that materials in cluster D1 stand out with exceptionally low electrical conductivity values. Specifically for n-type doping, conductivity values are below $24 (\Omega \cdot \text{cm})^{-1}$ and for p-type doping, they could reach up to $87 (\Omega \cdot \text{cm})^{-1}$ . However these materials in D1 exhibit a large absolute values of Seebeck coefficients. This trend might suggests that for materials in cluster D1, the electronic contribution to the power factor and thermal conductivity is very low with respect to their thermal response. Conversely, materials in cluster D2 display a much broader range of electrical conductivity value (up to $500 (\Omega \cdot \text{cm})^{-1}$ ) but with a moderate range for the Seebeck coefficient. This analysis suggests that for materials in cluster D2, thermal contribution to the power factor and thermal conductivity is not high with respect to their electronic response. Figures 5(d)–(f) represent respectively the relationship between the power factor, the Seebeck coefficient and the electrical conductivity for n and p doped materials. We observe that materials in cluster D2, exhibit a linear trend in all cases (strong positive correlation: about 0.89), indicating that the power factor, Seebeck coefficient and electrical conductivity of materials in cluster D2 are less or not at all influenced by the material doping type. This behavior implies that factors increasing thermoelectric properties of n doping materials are likely to also increase the thermoelectric properties of p doping materials, allowing for simultaneous optimization. By targeting modifications that affect both coefficients, such as specific dopants or level of doping, it is possible to streamline the development process, reducing the need for separate experiments for n and p doping material. This not only accelerates material optimization but also cuts costs and development time. On the other hand, materials in cluster D1 exhibit a more scattered distribution (weak correlation) especially for figures 5(d) and (e). Furthermore, we observed that the range of the Seebeck coefficient of p and n doping materials in cluster D1 are symmetrically opposed, suggesting that they are highly affected by the material doping type. The conclusion at this stage of the analysis comes as follow: The natural cluster observed from the Seebeck coefficients scatter plot 3 is strongly and intrinsically related to the physical and thermoelectric properties of the analyzed materials. On one side the low electrical conducting and doping and thermal dependent materials cluster D1. On the other hand the high electrical conductivity, doping independent and electronic related materials in cluster D2.

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.** Relationship between thermoelectric properties: (a) power factor and Seebeck coefficient of n doped material, (b) seebeck coefficient and electrical conductivity of n doped material, (c) seebeck coefficient and electrical conductivity of n doped material, (d) power factor of p and n doped material, (e) seebeck coefficient of n doped and Seebeck coefficient of p doped material, (f) electrical conductivity of n and p doped material.
Download figure:
Standard image High-resolution image

3.3. Clusters and effective mass ratio

Figures 6(a) and (b) represent respectively the scatter plot of the Seebeck coefficient vs. the effective mass ratio and the electrical conductivity vs. the effective mass ratio of p doping materials . We observe that there is no linear dependence between thermoelectric properties and the effective mass ratio. Notably, materials within cluster D2 are characterized by a low effective mass ratio, with approximately 90 percent possessing an effective mass ratio less than 200. In contrast, materials in cluster D1 exhibit a wide range of effective mass ratio values. The detailed analysis of materials properties within clusters D1 and D2 has provided valuable insights into their distinct behaviors.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.** Scatter plot of (a) seebeck coefficient and effective mass ratio of p doping material, (b) electrical conductivity and effective mass ratio of p doping material .
Download figure:
Standard image High-resolution image

3.4. Correlations between the electrical conductivity and Seebeck coefficient

Figures 7(a) and (b) represent respectively the scatter plot of the Seebeck coefficient vs. to the electrical conductivity of n and p doping type material for materials in all our database. As shown previously, the Seebeck coefficient and the electrical conductivity are inversely proportional. These figures also shows that for a given value of the Seebeck coefficient, there is a maximum limit value for the electrical conductivity( $\sigma^{\mathrm{max}}$ ) and inversely. This maximum limit obey to an exponential law that is determined with an exponential regression fitting as shown in equation (7) for n type doping and in equation (8) for p type doping materials represented in figures (a) and (b) in orange dash line

$\begin{align} \sigma_{n}^{\text{max}} & = 8937.831 \cdot e^{-0.0258 \cdot S_n} + 17.735\end{align} \tag{ 7 }$

$\begin{align} \sigma_{p}^{\text{max}} & = 2650.540 \cdot e^{-0.0145 \cdot S_p} + 7.316.\end{align} \tag{ 8 }$

Figure 7. Refer to the following caption and surrounding text. — **Figure 7.** Scatter plot of (a) seebeck coefficient and electrical conductivity of p and n-type doping materials , (b) seebeck coefficient and electrical conductivity of p-type doping materials.
Download figure:
Standard image High-resolution image

Using these thermoelectric power laws in equations (7) and (8), it is possible to predict the maximum value of the electrical conductivity ( $\sigma^{\mathrm{max}}$ ) for a given Seebeck coefficient and vice versa. This established laws will mainly help for a quick scanning of the thermoelectric relevance of a given material with a known electrical conductivity or Seebeck coefficient.

3.5. Predictive models for thermoelectric properties

Given the relevance of clusters in the materials properties prediction, a proposed random forest classification model allows to know exactly to which cluster a material belongs.

Given the consistent linear trends observed in the Seebeck coefficient, power factor, and electrical conductivity across all D2 materials, the choice of using linear regression fitting was a logical decision for capturing and modeling the underlying relationships among these thermoelectric properties. We adopted a random forest as a prediction model of D1's properties due to its ability to model more complex relationship and its robustness in handling data variability.

3.6. Linear regression on cluster D2

Figure 8 illustrate the relationship between the true and the predicted value of the Seebeck coefficient, power factor, electrical conductivity of n type doping material given p type doping material properties. We applied a linear regression fitting on material in D2, and we found a relationship as in equation (9) for the Seebeck coefficient, equation (10) for the power factor, and finally equation (11) for the electrical conductivity using dataset D2 as illustrated in figures 8(a)–(c) along with the respective r-square value and the mean absolute error

$\begin{align} S_n &= 0.96S_p -17.63\end{align} \tag{ 9 }$

$\begin{align} P_n &= 0.99P_p + 0.01\end{align} \tag{ 10 }$

$\begin{align} \sigma_n &= 1.01\sigma_p + 1.91.\end{align} \tag{ 11 }$

Figure 8. Refer to the following caption and surrounding text. — **Figure 8.** Relationship between: (a) true and predicted value of Seebeck coefficient n type doping using dataset D2, (b) true and predicted value of Power factor n type doping using dataset D2, (c) true and predicted value of Electrical conductivity n type doping using dataset D2.
Download figure:
Standard image High-resolution image

Using these equations, one can very accurately predict with a very high R-square the value of the electrical conductivity, Seebeck coefficient and thermoelectric power factor of n doping material given the value of p doping material properties and vice versa. This thorough analysis underscores the equation's accuracy in precisely estimating the Seebeck coefficient, power factor, and electrical conductivity of n-doped materials, particularly when we possess information about the power factor of p-doped materials and vice versa. The small mean absolute error and the high R-squared value validate the model's reliability, establishing it as a valuable tool for predicting these thermometric properties.

3.7. Random forest on cluster D1

Figure 9 is the result of the prediction of the Seebeck coefficient. As describe in the method section, we used two (02) groups of features, the first group include the mean and the standard deviation of group, atomic radius, boiling point, melting point and electronegativity along with band gap and effectives mass. The second group consist of magpie featurization with effective mass and the result of the prediction using those features are represented in figures 9(a) and (b) for the whole dataset. The model without magpie featurization perform with an R-square of 0.76 and a MAE of 45.70. However with magpie featurization as one can see in 9(b), the R-square is improved to 0.79 and the MAE as well. Figures 9(c) and (d) represented the true and predicted value of the Seebeck coefficient n doped material for the dataset D1 with and without magpie featurization. Those figures reveal that magpie features give more accurate R-square 0.83 than the first group of feature as in the case of the whole dataset. We also found that model prediction through cluster is more accurate than the model prediction of the whole dataset which shows the relevance of cluster based prediction.

Figure 9. Refer to the following caption and surrounding text. — **Figure 9.** Result of the prediction of Seebeck Coefficient of n doping material: (a) and (c) using random selected feature, (b) and (d) using magpie featurization for the entire Dataset and D1.
Download figure:
Standard image High-resolution image

We also build a model for the prediction of the Seebeck coefficient p and the power factor p doping type and the result is illustrated in figure 10 using only magpie featurization and we found a low R-square value shown that the model performance is not good on p doping type material properties and this can be explained by the result of the feature importance in the supporting information. From that result, the importance of the features on p doping materials are very small compare to the importance of features on n doping materials.

Figure 10. Refer to the following caption and surrounding text. — **Figure 10.** Result of the prediction of (a): seebeck Coefficient of p dopped materials, (b) power Factor of p dopped material using Dataset1.
Download figure:
Standard image High-resolution image

D1 model is not highly accurate due to the small sample points on that domains and the model of the whole dataset is not highly accurate due to the fact that data is grouped by categories, each with its own unique characteristics. From these different predictions, it emerges that cluster predictions are better than predictions of the whole data set, which makes clustering an interesting option.

3.8. Good thermoelectric material

According to the criteria defined by Gaultois et al ( $|S| \gt 100 \, \mu\mathrm{V} \, \mathrm{K}^{-1}$ , $\sigma \gt 10^{2} \, (\textrm{S cm}^{-1})$ , $\kappa \lt 10 \, \mathrm{W} \cdot \mathrm{m}^{-1}$ $\cdot \mathrm{K}^{-1}$ , $E_g \gt 0 \, \mathrm{eV}$ , all at room temperature) [35], for a material to be suitable for thermoelectric applications, we extracted potentially good thermoelectric materials from our dataset given by the following chemical formulas: $Li_2Ag_3F_6$ , NaFePCO₇, $Cu_2O_3$ , LiCoSiO₄, $V_4O_7F_5$ , $Mn_6OF_{11}$ . We found that the extracted potential good thermoelectric materials belong to dataset D2 and are all suitable for $n-$ type or $p-$ type doping. All these materials belong to the class of materials that are able to switch from positive to negative Seebeck. Example of such materials are $Cu_2O_3$ , $Mn_6OF_{11}$ , LiCoSiO₄ and $V_4O_7F_5$ with negative Seebeck coefficient p and negative Seebeck coefficient n but NaFePCO₇ and $Li_2Ag_3F_6$ have positive Seebeck coefficient n and positive Seebeck coefficient p. It has been proof by Kousar et al [48] that such material are promising for thermoelectric device which confirm our analysis. The materials extracted from our analysis are all crystallize in the monoclinic phase, consistent with the investigations conducted by Ogunbunmi et al [49] and Mahmoud et al [50], where good thermoelectric materials were found to crystallize in the monoclinic phase as well. Due to the very low electrical conductivity of materials in cluster D1, we could not find any material that meets those criteria.

According to another criterion define by Fan and Oganov [36] $(PF \unicode{x2A7E} 5 \, \mu \text{W} \cdot \text{cm}^{-1} \cdot \text{K}^{-2})$ for a material to be good thermoelectric material, we found some good thermoelectric material in our datasets which are: $CsSnI_3, VO_2F, SnSe, Li_4Co(OF)_2, KPrPCO_7$ . Notably, SnSe has already been studied and confirmed to be a good thermoelectric material. Additionally, CsSnI₃ has been investigated and demonstrated to be a promising thermoelectric material [51], due to it ultralow value of thermal conductivity $(0.69 \, \textrm{W m}^{-1}\ \textrm{K}^{-1} )$ with a ZT value of 0.08 at 300K. By utilizing the experimentally obtained thermal conductivity value of CsSnI₃, we computed a ZT of 0.31 at 300K using the power factor from our dataset, which is significantly higher compared to the existing value. We believe that employing a thermal conductivity obtained through material doping will further increase this ZT value.

4. Conclusion

Through this study we brought in data analytics and predictive models able of accelerating the design and discovery of good thermoelectric materials. The use of cluster based method has proven to be highly effective in analyzing our data, showcasing its immense promise in the quest for quality thermoelectric materials. Notably, we have identified two distinct clusters D1 and D2 each revealing unique thermoelectric behaviors. Cluster D1 characterized by a high thermal contribution but an exceptionally low electrical contribution, even with doping. This distinctive characteristic makes it difficult in identifying high-performing thermoelectric materials within this cluster. Conversely, cluster D2 materials exhibits an electrically high contribution along with an average thermal contribution, significantly increasing the likelihood of discovering promising thermoelectric materials within such a cluster. Our proposed models are robust and highly accurate for cluster-based predictions of thermoelectric materials features. In essence, our research contributes as valuable insights and tools that propel the search for optimal thermoelectric materials, paving the way for advancements in energy conversion technologies.

Acknowledgments

This document has been produced with the financial support of the European Union (Grant no. DCI-PANAF/2020/420-028), through the African Research Initiative for Scientific Excellence (ARISE), pilot programme. ARISE is implemented by the African Academy of Sciences with support from the European Commission and the African Union Commission. The contents of this document are the sole responsibility of the author(s) and can under no circumstances be regarded as reflecting the position of the European Union, the African Academy of Sciences, and the African Union Commission. Additionally, The authors would like to express sincere gratitude to Guangzong Xing for his invaluable feedback and constructive suggestions during the preparation of this paper. Their insightful comments and recommendations played a pivotal role in refining the content and clarity of the manuscript.

Data availability statement

All data used in this paper are publicly available in matminer website as $boltztrap\_mp$ https://hackingmaterials.lbl.gov/matminer/dataset_summary.html.

Author e-mails

Author affiliations

Author notes

ORCID iDs

Dates

Peer review information