Exploring the potential of contemporary deep learning methods in purifying polluted information

The ANN framework employed in this study is similar to that described by Dueben and Bauer [5]. This ANN architecture consists of four hidden layers, each of which has 100 neurons with a tanh activation function. The input and output layer to the ANN have 8 neurons. This ANN is stateless, i.e. there is no hidden variable that tracks temporal evolution. Following the procedure used in Dueben and Bauer which involves relating $X\left( t \right)$ to its change in $X\left( t \right)$ at the next time step, rather than the raw value $X\left( {t + \Delta t} \right)$, this ANN training architecture implicitly contains a reference to the previous time step. Therefore, this ANN's inputs/outputs are chosen to be pairs of $X{\left( t \right)^{{\text{train}}}}$ and $\Delta X{\left( t \right)^{{\text{train}}}} = X{\left( {t + \Delta t} \right)^{{\text{train}}}} - X{\left( t \right)^{{\text{train}}}}$. During the prediction phase, by using $X{\left( t \right)^{{\text{test}}}}$ which is either known from the initial condition or has been previously calculated, $\Delta X{\left( t \right)^{{\text{test}}}}$ will be predicted. The obtained $\Delta X{\left( t \right)^{{\text{test}}}}$ is passed through an Adams–Bashforth integration scheme to estimate the next state $X{\left( {t + \Delta t} \right)^{{\text{test}}}} = X{\left( t \right)^{{\text{test}}}} + \frac{1}{2}\left[ {3\Delta X{{\left( t \right)}^{{\text{test}}}} - \Delta X{{\left( {t - \Delta t} \right)}^{{\text{test}}}}} \right].$ The training process for the ANN was executed using a stochastic gradient descent optimizer, with a learning rate set to 0.001 and a batch size of 100. Mean absolute error was primarily used as the loss function, although using the mean squared error yielded comparable outcomes.

The LSTM [7] is a deep-learning algorithm suited for predicting sequential data [13]. A major improvement over regular recurrent neural networks (RNNs) is that LSTM has gates that control the information flow into the neural network from previous steps of the time series [14]. The LSTM architecture used in this study closely mirrors the one proposed by Vlachas et al [4], which has 50 hidden layers in each cell. The input to the LSTM consists of a time-delay-embedded matrix of $X\left( t \right)$, with an embedding dimension $q$, which is also referred to as the look-back parameter. Through extensive hyper-parameter optimization, mainly through trial and error, the optimal value of $q$ was determined to be 3, as this value provided the longest prediction horizon with the best performance (tested over a range of $q = 1\sim22$). The LSTM model predicts $X\left( {t + \Delta t} \right)\,$ by using the previous $q$ time steps of $X\left( t \right)$. The weights for the LSTM layers are determined during the training process. During testing, the prediction for $X\left( {t + \Delta t} \right)$ is generated from the preceding $q$ observations $\left[ {X\left( {t - \left( {q - 1} \right)\Delta t} \right), \ldots ,X\left( {t - \Delta t} \right),\,X\left( t \right)} \right]$ that are either known from the initial condition or have been previously predicted. It was found that the best results came from a stateless LSTM, meaning that the state of the LSTM was reset at the beginning of each training batch. We also experimented with a stateful LSTM, where the states were carried over from one batch to the next, but the stateless configuration performed better during training. There was no evidence of overfitting, as the training and testing accuracies remained consistent throughout.

Reservoir computing (RC) is a deep-learning algorithm designed to process information generated by dynamical systems using time-series data [15]. NG-RC [8] builds upon traditional RC by replacing the recurrent neural network reservoir with a more efficient nonlinear vector auto-regression (NVAR) approach. Instead of relying on random matrices and optimizing multiple meta-parameters, NG-RC builds a feature vector from time-delay embeddings of the input data. This feature vector includes both linear and nonlinear transformations of the past $k$ observations:

$$\begin{align}{{\boldsymbol{O}}_{{\text{lin}}}}\left( t \right) & = \left[ {X\left( t \right),{ }X\left( {t + \Delta t} \right), \ldots ,X\left( {t - \left( {k - 1} \right)\Delta t} \right)} \right]\end{align}$$

$$\begin{align}{}_{{\boldsymbol{O}}^{\left( 2 \right)}_{\text{nonlin}}}\left( t \right) & = {{\boldsymbol{O}}_{{\text{lin}}}}\left( t \right) {\boldsymbol{\otimes}} {{\boldsymbol{O}}_{{\text{lin}}}}\left( t \right)\end{align}$$

$$\begin{align}{{\boldsymbol{O}}_{{\text{total}}}}\left( t \right) & = {\boldsymbol{c}} {\boldsymbol{\oplus}} {{\boldsymbol{O}}_{{\text{lin}}}} {\boldsymbol{\oplus}} {{\boldsymbol{O}}_{{\text{nonlin}}}}.\end{align}$$

The total feature vector is then used to predict the next state via a linear transformation: $\hat X\left( {t + \Delta t} \right) = {W_{{\text{out}}}}{{\boldsymbol{O}}_{{\text{total}}}}\left( t \right)$, where ${W_{{\text{out}}}}$ is optimized through ridge regression:

$$\begin{align}{W_{{\text{out}}}} = {\left( {{\boldsymbol{O}}_{{\text{total}}}^T{{\boldsymbol{O}}_{{\text{total}}}} + \alpha I} \right)^{ - 1}}{\boldsymbol{O}}_{{\text{total}}}^T{Y_d}.\end{align}$$

Here, $\alpha$ is a regularization parameter to avoid overfitting. By eliminating the need for a neural network reservoir, NG-RC reduces computational costs and requires fewer training data. NG-RC retains the ability to model complex dynamics with fewer data points and a simplified structure, providing robust predictions with much lower computational overhead than traditional RC methods.

The RC-ESN [9] is a type of recurrent neural network (RNN) characterized by its reservoir of $D$ neurons. These neurons are sparsely connected according to an Erdős–Rényi random graph configuration, with the connectivity described by an adjacency matrix $A$ of size $D \times D$. This matrix is normalized using its largest eigenvalue (${\Lambda _{{\text{max}}}}$) and scaled by a factor $\rho$, typically ranging from 0.05 to 0.7. The RC-ESN is unique because only the output-to-reservoir weights, ${\boldsymbol{W}_{\mathbf{out}}}$ are trained. The input-to-reservoir and reservoir-to-output weights (${\boldsymbol{W}_{\mathbf{in}}}\;{\text{and}}\;A$) remain fixed after being initialized randomly. The state of the reservoir, denoted as $r\left( t \right)$, is updated using a hyperbolic tangent function. The reservoir processes the input observables, generating a high-dimensional representation, $r\left( {t + \Delta t} \right)$, which is then used to predict $X\left( {t + \Delta t} \right)$ using a linear transformation. The training process for RC-ESN is notably efficient because it does not involve backpropagation through time. Instead, ${\boldsymbol{W}_{\mathbf{out}}}$ is computed in a single step using ridge regression, minimizing the difference between the predicted and actual states. This simplicity in training, combined with the avoidance of vanishing and exploding gradients, makes RC-ESN a powerful tool for time series prediction, especially in dynamic systems.

The DSDL [12] is an innovative approach that utilizes the dynamical information embedded in chaotic time series and integrates deep learning's capacity to model complex, nonlinear relationships to achieve the long-term accurate and interpretable predictions of chaotic dynamical systems. The DSDL framework starts with $n$-dimensional time series data $\left\{ {{x_1}\left( {\text{t}} \right),{x_2}\left( {\text{t}} \right), \ldots ,{x_n}\left( {\text{t}} \right)} \right\}$ from the target system. These time series are treated as primitive system variables, which are used to construct a feature set ${\boldsymbol{X}} = \left\{ {{x_1},{x_2}, \ldots ,{x_n}} \right\}$. In chaotic systems, due to dissipation, the steady-state dynamics are often constrained to a subspace known as the attractor ${\boldsymbol{A}}$, which can be reconstructed using phase-space reconstruction techniques. Based on the delayed embedding theory, a 'delayed attractor' is reconstructed by the time-lagged coordinates of the target variable ${x_k}\left( t \right)$, $k \in \left[ {1,\,n} \right]$ in the form of $\mathcal{D}$(${x_k}\left( t \right),{ }{x_k}\left( {t + \tau } \right),{x_k}\left( {t + 2\tau } \right),\, \ldots$) with suitable embedding dimension $L$ and time delay interval $\tau$. Using the generalized embedding theorem, a 'non-delayed attractor' is reconstructed by multiple variables in the form of $\mathcal{N}$ (${x_i}\left( t \right),{ }{x_j}\left( t \right),{x_s}\left( t \right),\, \ldots$), $i,{ }j,\,s,\, \ldots \in \left[ {1,\,n} \right]$. This dual reconstruction approach allows DSDL to capture both the temporal and spatial dimensions of chaotic systems, providing a more comprehensive understanding of the system's underlying dynamics.

Ma et al [16] randomly selected index tuple $l = \left( {i,{ }j,\,s,\, \ldots } \right)$, considering only the linear relationships among system variables. To fully capture the nonlinear interactions among variables, we construct a multi-layer nonlinear network to obtain the candidate variable set ${{\boldsymbol{X}}_{\boldsymbol{N}}}$. For each layer $i\,\left( {i \in \left[ {1,\,m} \right]} \right)$, the candidate variable subset is denoted as ${\boldsymbol{X}}_{{{\boldsymbol{N}}_{{L_i}}}}^{{L_i}}$, including all monomials of ith-order based on ${\boldsymbol{X}},$ when $i \unicode{x2A7E} 2$ the monomials are nonlinear. However, not all variables in the set ${{\boldsymbol{X}}_{\boldsymbol{N}}}$ have a positive impact on predictions of the target variable ${x_k}\left( t \right)$, thus we select the key variables set ${{\boldsymbol{X}}_{{\boldsymbol{K}},{\boldsymbol{\,\,}}{{\boldsymbol{x}}_{\boldsymbol{k}}}}}$ that significantly influence the evolution of ${x_k}\left( t \right)$ from ${{\boldsymbol{X}}_{\boldsymbol{N}}}$ by using the cross-validation-based stepwise regression (CVSR) method. This approach helps identify critical information and eliminate redundancies, thereby reducing the complexity and enhancing interpretability of the DSDL model. As a result, the non-delayed attractor $\mathcal{N}$ is constructed by those key variables we selected.

The DSDL model establishes a diffeomorphic mapping between the two reconstructed attractors, that is, ${\boldsymbol{\Phi }}:{ }\mathcal{N} \to \mathcal{D}$, since both attractors are topologically conjugated to the original attractor ${\boldsymbol{A}}$. On this basis, we can obtain the DSDL prediction model for the target variable ${x_k}\left( t \right),$

$$\begin{align}{x_k}\left( {t + \tau } \right) = \varphi \left( {{x_i}\left( t \right),{ }{x_j}\left( t \right),{x_s}\left( t \right),\, \ldots } \right).\end{align}$$

Here, $\varphi$ represents the mapping learned from the training data. Unlike typical 'black-box' deep learning models, DSDL aligns more closely with physical models by learning deterministic rules from training data. This structured approach makes it particularly effective for successive predictions, offering a transparent and explainable path from inputs to outputs.

To assess the predictive abilities of various deep learning methods, we employ the effective prediction time (EPT) as an indicator of the model's performance. The EPT is defined as the time it takes for the corresponding prediction error $E\left( t \right)$ to first exceed a predefined error threshold $\varepsilon$, calculated as follows:

$$\begin{align}E\left( t \right) & = \left| {X\left( t \right) - \tilde X\left( t \right)} \right|,\end{align}$$

$$\begin{align}{\text{EPT}} & = {\text{Time}}\left[ {E\left( t \right) \unicode{x2A7D} \varepsilon } \right],\end{align}$$

where $\,X\left( t \right)$ represents the actual time series, and $\tilde X\left( t \right)$ denotes the predicted series. The error threshold $\varepsilon$ is set to one standard deviation of the predicted time series, which is used to determine where the model's accurate prediction stops, so it cannot be too large or too small to avoid overestimating or underestimating the model's predictive ability. Through testing, we found that when the error threshold is one standard deviation, the predicted sequence and the original sequence have basically separated, and subsequent predictions will no longer be accurate. A higher EPT indicates a stronger predictive ability of the model. The EPT is expressed in model time units (MTUs), where 1 MTU $=$ 100 $\,\Delta t$. To ensure robustness, we compute the mean EPT from 100 distinct training/testing sets to evaluate the predictive performance.

To evaluate the predictive performance of several contemporary deep learning methods, we utilize the Lorenz system as our target system. As a paradigmatic chaotic dynamical system, the Lorenz system exhibits deterministic chaos, forming a strange attractor in its phase space trajectory [17]. To challenge the deep learning methods, we introduce five interference systems with distinct properties to contaminate the input dataset: the Rössler system [18], Rucklidge system [19], Hyperchaotic Lorenz system [20], periodic system (trigonometric functions), and stochastic system (random sequences with normal distributions).

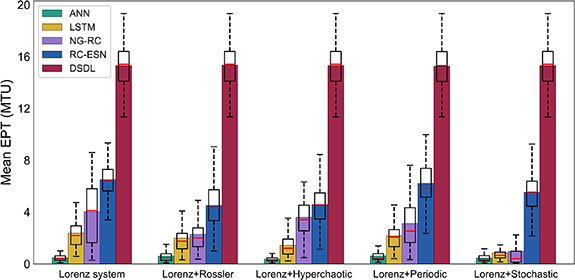
When there is no interfering information, the prediction performance of the DSDL method is the best for the Lorenz system, while other deep learning methods also have varying degrees of effective prediction time (figure 1, table 1). When the input dataset is polluted by one interference system, the DSDL method consistently achieves the highest predictive performance across all interference scenarios. Its mean EPT remains stable and basically unaffected by the introduction of invalid information, underscoring its robustness. The DSDL method's ability to effectively exploit the nonlinear interactions among system variables and removes redundant information by selecting key variables to capture the underlying deterministic rules of the target system enables it to maintain high accuracy.

Zoom In Zoom Out Reset image size

Table 1. Comparison of predictive performance and stability among different deep learning methods for the Lorenz system without and with one interference systems. EPT is measured by dimensionless time units (DTU).

Methods	ANN		LSTM		NG-RC		RC-ESN		DSDL
Evaluation indicators	EPT	CV	EPT	CV	EPT	CV	EPT	CV	EPT	CV
Lorenz	0.63	0.69	2.38	0.52	4.03	0.58	6.51	0.24	15.35	0.12
Lorenz + R${\ddot {\mathbf{o}}}$ssler	0.62	0.98	2.00	0.59	2.30	0.63	4.52	0.38	15.32	0.12
Lorenz + Hyperchaotic	0.36	0.84	1.43	0.62	3.61	0.42	4.58	0.38	15.30	0.13
Lorenz + Periodic	0.59	0.72	2.17	0.53	3.12	0.62	6.22	0.29	15.33	0.13
Lorenz + Stochastic	0.50	0.73	0.84	0.84	0.98	1.53	5.53	0.32	15.32	0.12

In contrast, the ANN, LSTM, NG-RC, and RC-ESN methods exhibited a decline in the mean EPT when faced with interference. The LSTM and NG-RC methods, in particular, struggled with stochastic signal pollution, whereas the RC-ESN method demonstrated resilience against periodic and stochastic systems but faltered with chaotic interference. This highlights DSDL's superiority as a dynamics-based deep learning method in identifying the dynamical attributes of the target system.

We also compared the predictive stability of these five methods using the coefficient of variation (CV), a standardized measure of data dispersion defined as the ratio of the standard deviation of EPTs (achieved by 100 different training/test sets) to the mean value. As shown in figure 2 and table 1, the CV of the DSDL method is the lowest and remains almost unchanged in each scenario, indicating the most stable prediction results despite various invalid information. Notably, the NG-RC method exhibits the highest CV when facing stochastic systems, suggesting significant instability in its predictions due to stochastic signals.

Zoom In Zoom Out Reset image size

To further illustrate the predictive performance of these methods, figure 3 presents the evolution of mean prediction error over time. The ANN and NG-RC methods often lose the original chaotic properties of the target system, failing to capture its deterministic evolution rules. Conversely, the LSTM, RC-ESN, and DSDL methods retained these characteristics, with DSDL showing the longest time to reach the error threshold, confirming its optimal performance.

Zoom In Zoom Out Reset image size

In this study, we focus more on the accurate predictions that different deep learning methods can provide in the presence of other interfering systems. But there is no doubt that capturing the long-term evolution behavior of chaotic systems is also an important criterion for evaluating the quality of deep learning methods. For example, when the interfering system is the Rössler system, figure 4 illustrates the long-term behavior of the predicted sequences provided by five contemporary deep learning methods. We can clearly see that the prediction results of ANN and NG-RC methods quickly overflow the attractor orbit of the target system, while the prediction sequence of LSTM method, although roughly on the attractor orbit, is actually unstable and has disturbances that deviate from the orbit. The prediction results of RC-ESN and DSDL methods are completely follow the Lorenz attractor orbit, indicating that these two methods can effectively capture the long-term evolution behavior of the target system. However, it can be evidently seen in figures 4(D) and (E) that the long-term behavior of the DSDL predicted sequence coincides better with the Lorenz attractor orbit than the RC-ESN method, especially around the equilibrium points. What's more, as shown in figure 1, the accurate predictions provided by DSDL are far superior to those of the RC-ESN method, which means that the predictive performance of the DSDL method is better than that of the EC-ESN method.

Zoom In Zoom Out Reset image size

To further test the capacities of different deep learning methods, we introduce two interference systems simultaneously, increasing the complexity of the dataset. As shown in figure 5 and table 2, the DSDL method continued to exhibit the best predictive performance, remaining largely unaffected by the increased complexity. Compared to figure 1 and table 1, its mean EPT did not significantly decline, showcasing its robustness in handling complex, contaminated datasets. The performance of the other methods generally declined with increasing complexity. The ANN and NG-RC methods lost the chaotic properties of the Lorenz system in all scenarios, while the LSTM and RC-ESN methods retained some properties but with reduced mean EPT compared to scenarios with one interference system.

Zoom In Zoom Out Reset image size

Figure 6 and table 2 show that the CV of the DSDL method remained the lowest and most stable across all scenarios with two interference systems. In contrast, the CV of the other methods increased, indicating higher instability with more complex invalid information. Figure 7 presents the mean prediction error in scenarios with two interference systems. The ANN and NG-RC methods showed significant performance degradation, failing to maintain the chaotic properties of the target system. The LSTM and RC-ESN methods performed better but still showed reduced EPT. The DSDL method's predictive performance remained robust, highlighting its ability to handle complex data contamination.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Chaotic systems have a wide range of applications across various fields, including physics, engineering, finance, and so on. For instance, recent studies have explored the use of chaotic systems in secure communications [21] and video encryption [22, 23]. In order to improve the reliability of this study, we further used another chaotic system with different properties from the Lorenz system as the target system to conduct a simple verification of our results, which is the Chua's circuit system. Chua's circuit is currently the most representative one among many chaotic circuits. It has been applied in secure communications, random number generation, pattern recognition and sensing. The equations of Chua's circuit [21] are as follows:

$$\begin{align}\left\{ \begin{array}{*{20}{c}} {\frac{{{\text{d}}x}}{{{\text{d}}t}} = \alpha \left( {y - x - f\left( x \right)} \right)} \\ {\frac{{{\text{d}}y}}{{{\text{d}}t}} = x - y + z} \\ {\frac{{{\text{d}}z}}{{{\text{d}}t}} = - \beta y} \\ {f\left( x \right) = {m_1}x + 0.5\left( {{m_0} - {m_1}} \right)\left( {\left| {x + 1} \right| - \left| {x - 1} \right|} \right)} \end{array}\right.,\end{align}$$

where $\alpha = 15.6,\,\beta = 28,\,{m_0} = - \frac{8}{7},\,{m_1} = - \frac{5}{7}$. Using a fourth-order Runge–Kutta scheme with a time step $\Delta t = 0.01$ dimensionless time units (TUs), we integrate forward for ${10^7}$ steps starting from $\left( {x,{ }y,{ }z} \right) = { }$ (0.7, 0, 0) to generate a large dataset for training and testing, and we discard the first 5000 time points to ensure the chaos of time series.

Focusing on the Chua's circuit, we obtained the results presented in figure 8. To investigate the ability of modern deep learning methods to purify polluted information, we introduced several contamination scenarios into the Chua's circuit system. When no interfering information is present, the DSDL method demonstrates the best predictive performance, outperforming other deep learning methods. However, when the input dataset is contaminated by interference systems with different characteristics, the DSDL method consistently maintains the highest predictive performance across all scenarios, remaining stable and unaffected by any form of invalid information. In contrast, methods such as ANN, LSTM, NG-RC, and RC-ESN exhibit a noticeable decline in EPT when facing interference. Specifically, ANN and LSTM methods struggle with stochastic signal pollution, while the NG-RC method shows difficulties in handling other dynamical information for predicting the Chua's circuit. These results underscore DSDL's superiority in capturing the deterministic rules governing the Chua's circuit system, even in the presence of contamination.

Zoom In Zoom Out Reset image size