Communication impacting financial markets

The quote "In the short run, the market is a voting machine, but in the long run it is a weighing machine" is attributed to Benjamin Graham¹ . Graham himself used the quote to argue that investors should use the so-called fundamental value investment approach and concentrate on analyzing accurately the worth of a given financial asset. That is, he suggested ignoring the short run "voting machine" part, and instead concentrate on the long run, where somehow the "weighing machine"of the market would ensure to end up with a pricing of the true worth of an asset. The interesting part of Graham's quote is the allusion to the decision making of people and its impact on the markets. Graham however does not refer to how the decision making process actually takes places, and this will be our focus in the following.

In situations of uncertainty people often consult others to get more information and thereby a better understanding of the situation. This is in particular true with respect to financial markets, where market participants consult the media or other colleagues to get an idea of the origin behind price movements, or to assess which impact a given information could have on the markets. For example, copying the behavior of others is one of the predominant mechanisms in decisions to purchase [1]. Social households, i.e. those that interact with their neighbors, have also been shown to have an impact in the level of stock market investments. In [2] it was shown how the stock market participation rates were higher in places that had a higher sociability. However the sole knowledge of the role of imitation is not sufficient to describe in an operative frame the price dynamics of financial markets since indeed the rules governing opinion dynamics and group decisions still needs to be understood and identified in more detail. In [3] interpersonal communication were found to be extremely important in investors decisions. Questionnaire surveys of institutional and individual investors were found to reveal a strong influence by word-of-mouth communications. In [4] it was shown that among fund managers in Germany information exchange with other financial and industry experts was the second most important factor influencing their investment decisions, complemented by conversations with their colleagues and reports from media. More recently impact of large scale human network structes and its flow of information were shown to have an impact on the asset pricing [5]. Different modeling effort was presented in [6] where a spin model was introduced to take into account local interaction between different market participants to explain the formation of bubbles in financial markets. A follow-up study was presented in [7] showing aperiodic switching between bull markets and bear markets due to the local heterogeneous interaction of traders. A different view of interaction between market participants was presented in an "ant recruitment" model of herding/epidemics in [8]. In similar vein models of social opinion dynamics and agent based models of investor sentiments was presented in [9–14]. It should be noted however that only the work of [10,12] keep the price and sentiments as two distinguished variables which we find important since sentiment (as well as price) can be obtained empirically. In the following we will introduce a socio-financial [15] model that in a quantitative manner does exactly this.

Consider a population of market participants, shown schematically as circles in fig. 1(a). We will proceed as in the so-called Galam model of opinion formation [16–18] and for simplicity imagine that people have just two different opinions on the market, which we can characterize as either "bullish" (black circles) or "bearish" (white circles). Letting B(t) denote the proportion of bullishness in a population at time t, the proportion of bearishness is then $1-B(t)$.

Zoom In Zoom Out Reset image size

Figure 1(a) represents the opinions of the participants at the beginning of a given day. During the day people meet in random subgroups of different sizes, as illustrated by the different boxes in fig. 1(b), to update their view of the market. Take, for example, the leftmost box in fig. 1(b) with six persons, two bullish, four bearish, who we can imagine are sitting around a table, or having a conference call, discussing the latest market developments. The outcome of the discussions for the different groups are illustrated in fig. 1(c). For simplicity we have illustrated the case where a majority opinion in a given subgroup manages to polarize the opinion of the group by changing the opinion of those who had an opinion belonging to the minority. If we take the afore mentioned group of six persons we can see that after discussing, because of the majority polarizing rule, they have all become bearish. More realistically, we will in the following instead assume that is a certain probability for a majority opinion to prevail, and that even under certain conditions a minority could persuade a part of the majority to change their opinion.

For a given group of size k with j agents having a bullish opinion and $k - j$ a bearish opinion, we let m_k,j denote the transition probability for all $(k)$ members to adopt the bullish opinion as a result of their meeting. After one update taking into account communications in all groups of size k with j bullish agents, the new probability of finding an agent with a bullish view in the population can therefore be written:

$$\begin{equation} B(t+1) = m_{k,j} (t) C_j^k B(t)^j [1 - B(t)]^{k-j}, \end{equation} \tag{ 1 }$$

where

$$\begin{equation} C^k_j \equiv {k! \over j! (k-j)! } \end{equation} \tag{ 2 }$$

are the binomial coefficients. Notice that the transition probabilities m_k,j depend on time, since we assume that they change as the market performance changes (this point will be explained further below).

Taking the sum over different groups of different sizes and different composition of bullishness within each group (see fig. 1(b)) one obtains a general term, $B(t+1)$, for the bullishness in a population at time t + 1 due to the outcome of meetings of groups with different sizes and different composition of bullishness:

$$\begin{eqnarray} B(t+1) &= \sum_{k=1}^{L} a_k \sum_{j=0}^k m_{k,j} (t) C^k_j B(t)^j [1-B(t)]^{k-j},\quad\end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray} \sum_{k=1}^L a_k &= 1 ;\qquad a_k \equiv {1 \over L}, \end{eqnarray} \tag{ 4 }$$

with L denoting the size of the largest group and a_k denoting the weight of the group of size k. The link between communication and its impact on the markets can then be taken into account by assuming that the price return r(t) changes whenever there is a change in the bullishness. The idea is that the bullishness itself is not the relevant factor determining how prices will change. Those feeling bullish would naturally already hold long positions on the market. Rather, when people change their opinion, say becoming more negative about the market, or less bullish, this will increase their tendency to sell. The fact that the absolute sentiment can act as a contrarian indictor (and the change in sentiment as an indicator) for future market returns is well known among practitioners, see e.g. [19] which present a sentiment index used for contrarian predictions of future market returns.

Assuming the return to be proportional to the percentage change in bullishness, RB(t), as well as economic news, $\eta (t)$, the return r(t) is given by

$$\begin{equation} r(t) = { RB(t) \over \lambda} + \eta (t) , \qquad \lambda > 0, \end{equation} \tag{ 5 }$$

with $RB(t) = {B(t)-B(t-1) \over B(t-1)}$ the change or "return" of the bullishness. The variable $\eta(t) = r(t) - {RB(t) \over \lambda}$ is assumed to be Gaussian distributed with a mean $\mu \equiv 0$ and a standard deviation that varies as a function of time depending on changes in sentiment. We will assume that the market will react to fundamental economic news represented by η but that the amplitude of the reaction depends on changes in the sentiment RB(t):

$$\begin{eqnarray} \sigma (t) & = \sigma_0 \exp{\left({|RB(t)| \over \beta}\right)} ,\quad \sigma_0 > 0,\quad \beta >0. \end{eqnarray} \tag{ 6 }$$

The influence of the financial market on decision-making can now be included in a natural way by letting the strength of persuasion depend on how the market has performed since the last meeting of the market participants. The idea is that, if for example the market had a dramatic downturn at the close yesterday, then in meetings the next morning, those with a bearish view will be more likely to convince even a bullish majority of their point of view. In the formal description below, this is taken into account by letting the transition probabilities for a change of opinion, i.e., the probabilities of transitions like fig. 1(b) → fig. 1(c), depend on the market return over the last period:

$$\begin{eqnarray} \begin{array}{rcl} &m_{k,j} (t) = \displaystyle m_{k,j} (t-1) \exp{\left({r(t) \over \alpha}\right)};\\ &m_{k,j} (t=0) \equiv j/k ,\qquad \alpha > 0, \end{array} \end{eqnarray} \tag{ 7 }$$

where α defines the scale for which a given return r(t) impacts the transition probabilities. The condition $m_{k,j} (t=0) \equiv j/k$ describes the initially unbiased case where in average no market participant changes opinion.

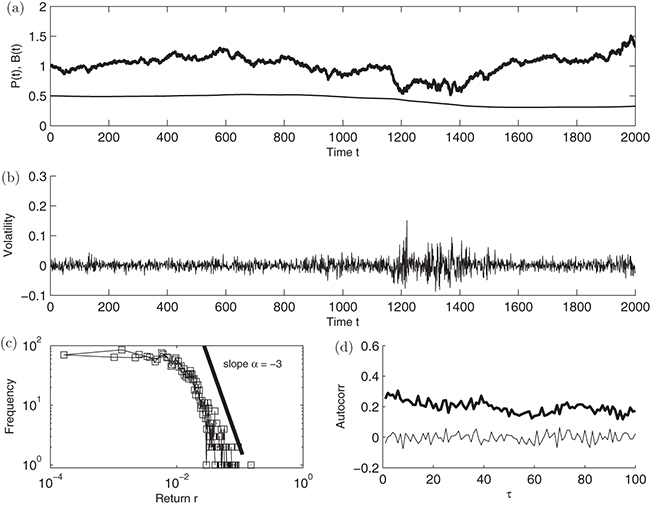
As a first demonstration of the properties of the model, eqs. (3)–(7), fig. 2(a) shows an illustration of the link between the bullishness of the market participants obtained through communication (thin solid line) and market prices (thick solid line). One observes a clear almost continuous decrease in bullishness, whereas the market itself first increases, then decreases, to finally end with an overall gain over the whole period. This illustrates the competition between persistence through memory effects in the bullishness (1)–(7) and the randomness of the return via the $\eta (t)$-term in (5). It should be noted that $B=0,1$ act as repulsive fix points: if B converges towards these two extremes the derivative of B goes to zero and one can neglect the sentiment part in the pricing formula (5). In that case any fundamental negative news $(\eta < 0)$ will not further impact the sentiment in a bearish population (say $B \approx. 0$) whereas any positive fundamental news will lead to a change towards more positive sentiments via (7), (3). The decaying rate of the return of the bullishness over the last part of the time period and the simultaneous rise of the prices illustrates indeed the complex and highly nonlinear relationship between returns and sentiments. The model is able to reproduce the most important of the so-called stylized facts seen in real financial market data [20]. Figure 2(b) illustrates clustering of the volatility of the return of the time series in fig. 2(a). Furthermore the returns show fat-tailed behavior in the returns (fig. 2(c)), with fat tail exponents similar to what is found in real markets [21]. Finally let us also mention that there are no arbitrage possibilities within the framework of the model seen by the zero autocorrelations of returns (thin line, fig. 2(d)), whereas long memory effects are seen in the volatility, seen via the slowly decaying autocorrelations of volatility (thick line, fig. 2(d)). It should be noted that fixing the other parameters we find the pairwise $(L=2)$ case to show similar behavior as the general L case (we have only studied L < 20). A similar conclusion was found using different distributions of a_k, which seems to indicate a robustness of contagion effects on those two parameters somewhat similar to what was reported in [9].

Zoom In Zoom Out Reset image size

Using inference based on maximum likelihood (see appendix) we first conducted a series of simulations in order to ensure indeed to be able to retrieve the parameter values used to generate the simulated data [22]. Next, we examined an empirical application of the proposed socio-financial model to the FTSE-20 Athens stock exchange index. The idea is to consider a very volatile market to study abrupt and large changes in market performance and map the corresponding evolution in sentiments. The data consists of 1247 daily prices over the 7/11/2008–6/11/2013 period. The results showed evidence of convergence of the maximization algorithm since the estimates found by using different starting values are very similar, and the value of the gradient of the log-likelihood evaluated at the parameter estimates is near zero. We then estimated the proportion of bullishness across time and the time-varying conditional volatilities. In fig. 3, we present the FTSE-20 prices P(t), the corresponding returns r(t), the estimated bullishness proportions $\widehat{B}(t)$ and the estimated conditional volatilities $\widehat{\sigma }(t)$, which are based on the parameter estimates of the socio-financial model. Comparing the FTSE-20 price evolution fig. 3(a) and the estimated bullishness proportions fig. 3(c), one observes a steady decline in the bullishness proportions even after a relatively long (two years: from mid-2011 to mid-2013) and stable price evolution. We consequently suggest to consider this as indicating a "bad signal" for the following FTSE-20 price levels. Finally, comparing the observed volatility of the FTSE-20, fig. 3(b), and the estimated volatility from the model, fig. 3(d), one notices that periods of high volatility of the market is indeed detected by volatility estimates of the socio-financial model. Therefore our proposed model can be seen as introducing an alternative measure to capture volatility clustering phenomena observed in return series of financial market data.

Zoom In Zoom Out Reset image size

Based on the parameter estimates and their corresponding standard errors one can conclude that for the given parameter choices the main part of the RB(t) choice is not on the return but on the volatility. However different choices of $\gamma, \sigma_0$ and β could make a stronger impact on the sentiments changes directly on the returns on a shorter time scale. As such the model can be imagined to describe a slow (say monthly/yearly) impact of changes of sentiments on the returns due to possible real economic factors, and a faster (i.e. on a higher frequency, say daily) change in the susceptibility of reaction to economic news depending on changes in sentiments. The ratio $\lambda/\beta$ therefore controls the slow vs. fast time scale of the price formation.

We emphasize here that the econometric analysis presented above is just an illustration of the empirical properties of the proposed model and not a thorough statistical analysis that would require careful assessment of the assumptions adopted. In a preliminary analysis we have found that the density of $\eta(t)$ could be replaced by a student-t density producing better fit to the particular data; this is not surprising as it is well known that in the popular GARCH models a student-t error distributional assumption is preferred to normal.

The main parts of traditional finance as well as behavioral finance, prospect theory [23] included, understand pricing in financial markets through individual investment behavior, thereby ignoring any interaction between market participants. We have on the contrary proposed a socio-financial model that focus on interaction between market participants via communication. Opinion formation of the market participants is modeled by communication that takes place in subgroups of different sizes. Nonlinear feedback effects were introduced to describe how market performance can change sentiments and vice versa. Our socio-financial model was shown to be able to reproduce the main stylized facts of financial market data. By estimating the model parameters via the maximum-likelihood method we are able to study extreme behavior of markets swings and sentiments illustrated by a case of the FTSE-20 Athens stock index over the last five years. Recent price behavior of the FTSE-20 index seems to indicate a reversal of the bearish trend whereas the sentiment measure obtained from our method seems to indicate that the market still has room for further downturns. Finally our model introduces a new volatility measure apt of capturing volatility clustering seen in the real financial market data.

The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7-SSH/2007-2013) under grant agreement No. 320270 SYRTO.

In the following we present an inferential method adopted to estimate the parameters of the model (3)–(7) based on the maximization of the conditional likelihood. Below we describe the calculation of the likelihood function for the model for a sample of T observations ${r=\left(r(1),r(2),\ldots,r(T)\right)}$ under the assumption of a normal distribution for the error process $\eta (t)$.

Consider the probability distribution of r(1), the first observation in the sample. Since $\eta (t)$ is assumed Gaussian, the density of the first observation, conditional on B(0) and $m_{k,j}(0)=j/k$ (corresponding to the neutral case), takes the form

$$\begin{eqnarray*} &f\left[r(1)|B(0),m_{k,j}(0),\mathbf{\theta }\right]= \\ &\frac{1}{\sqrt{2\pi }\sigma (1)}\exp \left\{ -\frac{1}{2\sigma (1)^{2}}\left[ r(1)-\frac{1}{\lambda }RB(1)\right] ^{2}\right\}, \end{eqnarray*}$$

where $\mathbf{\theta =(}\lambda$, $\sigma _{0}$, β, $\alpha)^{\prime}$ denotes the parameter vector to be estimated. Next, conditioning on r(1), the density of the second observation r(2) is

$$\begin{eqnarray*} &f\left[ r(2)|r(1),B(0),m_{k,j}(0),{\theta}\right]=\\ &\frac{1}{\sqrt{2\pi}\sigma (2)}\exp \left\{ -\frac{1}{2\sigma (2)^{2}}\left[ r(2)-\frac{1}{\lambda }RB(2)\right] ^{2}\right\}. \end{eqnarray*}$$

Proceeding in this fashion, the conditional density of the t-th observation can be calculated as

$$\begin{eqnarray*} &f\left[ r(t)|r(t-1),\ldots,r(1),B(0),m_{k,j}(0),\mathbf{\theta }\right]=\\ &\frac{1}{\sqrt{2\pi }\sigma (t)}\exp \left\{ -\frac{1}{2\sigma (t)^{2}}\left[ r(t)-\frac{1}{\lambda }RB(t)\right] ^{2}\right\}. \end{eqnarray*}$$

Therefore, the likelihood of the complete sample can be written as

$$\begin{eqnarray*} &f\left[ r|B(0),m_{k,j}(0),\mathbf{\theta }\right]=\left( 2\pi \right) ^{-\frac{T}{2}}\prod\limits_{t=1}^{T}\sigma (t)^{-1}\\ &\cdot\, \exp \left\{ -\frac{1}{2}\sum\limits_{t=1}^{T}\frac{1}{\sigma (t)^{2}}\left[ r(t)-\frac{1}{\lambda }RB(t)\right] ^{2}\right\}. \end{eqnarray*}$$

The log-likelihood function, denoted by $L_{T}\left( r|\mathbf{\theta }\right)$, can be written as

$$\begin{eqnarray*} L_{T}\left( r|\mathbf{\theta }\right)&=-\frac{T}{2}\ln \left( 2\pi \right)-\sum\limits_{t=1}^{T}\ln \sigma (t)-\frac{1}{2}\sum\limits_{t=1}^{T}\frac{1}{\sigma (t)^{2}}\\ &\quad \times\,\left[ r(t)-\frac{1}{\lambda }RB(t)\right] ^{2}. \end{eqnarray*}$$

Clearly, the value of θ that maximizes the conditional likelihood is identical to the value that maximizes the conditional log-likelihood.

The population dynamics enters in $L_{T}(r | \theta)$ via RB(t) and $\sigma (t)$ through (1) and (6).