A distributed optical fibre dynamic strain sensor based on phase-OTDR

A Masoudi; M Belal; T P Newson

doi:10.1088/0957-0233/24/8/085204

1. Introduction

Distributed temperature and strain sensors have proven to be an efficient means for interrogating a large number of points along a single optical fibre, a capability which has attracted substantial interest from industries involved in oil, gas and structural health monitoring. The majority of such distributed optical fibre sensors have utilized either Raman scattering [1, 2] or Brillouin scattering [3–6] and have operated at low bandwidths.

Dynamic strain sensing has most successfully been explored using coherent Rayleigh scattering [7] and a number of commercial devices are now available that are capable of detecting strain perturbations. These have applications in areas such as perimeter monitoring by identifying disturbance caused by intruders as well as leak detection in oil and gas pipelines. The induced strain causes a change in the coherent Rayleigh backscattered trace and the change is detected and spatially located. Whilst multiple disturbances can be detected simultaneously allowing a moving disturbance to be tracked, such systems to date do not provide a measure of the magnitude of strain-induced perturbation. An optical time domain reflectometry (OTDR) system based on the phase of the coherent Rayleigh noise (CRN), first proposed by Posey et al [8], provided a means to quantify the strain, but in the presented form was only able to monitor the dynamic strain at a single section of the fibre at any one time. This paper builds on this work, utilizing the same proposed phase demodulation scheme but capturing the entire backscattered trace and hence the true distributed measurement of dynamic strain. It is this fact which makes it possible to quantify and track multiple moving objects along the fibre. The underlying principles of the proposed scheme are detailed in section 2, followed by a description of the experimental layout in section 3. Experimental results including the 3D plot of the sensing fibre under strain are presented in section 4, while section 5 discusses and analysis the experimental results. Finally, section 6 highlights the outcome of the study.

2. Principles

The basic principle governing the operation of the dynamic strain sensor is based on detecting the phase change induced between the coherent Rayleigh scattering from two points of the sensing fibre. Like any OTDR system, a short pulse of light is launched into the fibre and the backscattered coherent Rayleigh light is fed through an imbalanced Mach–Zehnder fibre interferometer and onto a detector. The signal is therefore the summation of light emanating from two regions of fibre and its magnitude is dependent on their relative phases. The change in phase is directly related to the change in strain between the two points. Therefore, the gauge length is defined by L_delay/2, where L_delay is the length of the delay fibre of the Mach–Zehnder interferometer (MZI). This assumes that the pulse width is shorter compared to the length of the delay fibre.

As the pulse of light propagates along the sensing fibre, the detector output tracks the phase between the two points separated by the gauge length. To avoid signal fading, the differential and cross-multiply phase demodulation system is used in which a three port MZI and three detectors are used. Three channels of information are stored for each pulse. Post-processing allows the changing phase and hence dynamic strain at any particular position to be determined. Figure 1 illustrates this concept. In this figure, two groups A and B of scattering centres with separation of L metres are shown. To compare the phase difference between the backscattered light from the two sections, an MZI with a path imbalance of twice this length 2L is used. Neglecting fibre loss, the backscattered electric field from A and B at the photodetector is given by

$\begin{eqnarray} E_{A} &=& E_{0}\exp [{\rm i}(\omega t+\phi _{A})]\nonumber \\ E_{B} &=& E_{0}\exp [{\rm i}(\omega t+\phi _{B})], \end{eqnarray} \tag{ 1 }$

where ϕ_A and ϕ_B are the phases of the backscattered light from A and B, respectively, ω is the angular frequency of the backscattered light and E₀ is the magnitude of the electric field of the backscattered light. The intensity of the combined backscattered light is given by

$\begin{eqnarray} I_{det} &=& (E_{A}+E_{B})(E_{A}+E_{B})^{\star }\nonumber\\ &=& 2E_{0}^{2}\cos (\phi _{A}-\phi _{B}). \end{eqnarray} \tag{ 2 }$

Equation (2) shows that the detected intensity depends on the cosine of the phase difference between the two groups of scatterers. Any external disturbances (e.g. acoustic vibration) within the gauge length changes the phase of the backscattered light. This phase change Δϕ can be detected by monitoring the backscattered signal after interaction. The advantage of this technique which is referred to as phase-OTDR (φ-OTDR) is its capability of not only detecting the perturbation, but also of quantifying its magnitude and frequency.

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** Principle of dynamic strain sensing using φ-OTDR. This figure shows the graphical representation of two groups of scatterers in a section of the sensing fibre (a) before external perturbation and (b) after external perturbation.
Download figure:
Standard image High-resolution image

To avoid the fading problem, an MZI with a three output port coupler was used (figure 2). The output intensity of the three arms of the 3 × 3 coupler can be written as [9]

$\begin{eqnarray} I_{1} &=& I_{0}[M+N\cos (\varphi )]\nonumber \\ I_{2} &=& I_{0}\left[M+N\cos \left(\varphi +\frac{2\pi }{3}\right)\right]\nonumber \\ I_{3} &=& I_{0}\left[M+N\cos \left(\varphi -\frac{2\pi }{3}\right)\right], \end{eqnarray} \tag{ 3 }$

where M and N are constant, φ is the phase difference of the light returning through the two arms of the MZI and I₀ is the intensity of the input signal.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** Schematic of the setup used to eliminate signal fading in interferometer by using a symmetric 3 × 3 coupler at the output of the interferometer.
Download figure:
Standard image High-resolution image

The phase detection scheme known as the differentiate and cross-multiply demodulation scheme [10] was used which is depicted in figure 3. By using the three outputs of the 3 × 3 coupler, the phase difference between the two arms of the MZI (i.e. φ in equation (3)) can be measured directly. The output voltage V_Ph is directly proportional to the phase:

$\begin{equation} V_{{\rm Ph}}=\sqrt{3}\varphi . \end{equation} \tag{ 4 }$

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.** Block diagram of the phase detector used, adopted from [9].
Download figure:
Standard image High-resolution image

3. Experimental arrangement

3.1. Experimental setup

The experimental setup is shown in figure 4.

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.** Experimental arrangement. EDFA: erbium-doped fibre amplifier, PD: photodetector, FBG: fibre Bragg grating, PC: polarization controller, C: circulator, DFB: distributed feedback.
Download figure:
Standard image High-resolution image

10 ns optical pulses with a peak power of 10 mW at a repetition rate of 10 μs were generated by directly modulating the injection current of a DFB laser diode operating at 1550 nm biased just below the threshold. 90% of the output pulses were fed into a 28 dB gain erbium-doped fibre amplifier (EDFA1). An optical isolator after the laser diode was used to prevent any backward ASE (amplified spontaneous emission) generated in the EDFA from causing instabilities or damage to the laser diode. 10% of the optical output from the laser diode was used to trigger the oscilloscope.

ASE from EDFA1 was filtered out (3 dB bandwidth of 7 nm), and the optical pulses (∼5 W peak power) were launched into the sensing fibre.

The sensing fibre included two regions of lengths 3.5 m and 7 m, respectively, subjected to dynamic strain using a disc PZT arrangement and a cylindrical PZT arrangement, respectively. 320 m of unstrained–unheated fibre was used to separate the two strained regions and further 400 m and 280 m lengths of unstrained–unheated fibre were added before and after the 7 m and the 3.5 m strained sections of fibre, respectively.

The backscattered light from the sensing fibre was fed via a circulator into a 20 dB gain erbium-doped fibre amplifier, EDFA2. ASE from the amplified backscattered signal was removed by reflecting the amplified signal off a fibre Bragg grating (FBG), before being fed into the imbalanced MZI via a 3 dB coupler. The output of the 3 × 3 coupler was connected to three similar detectors (90 dB gain, 125 MHz bandwidth) and fed into an oscilloscope with a sampling rate of 300 MSa s⁻¹.

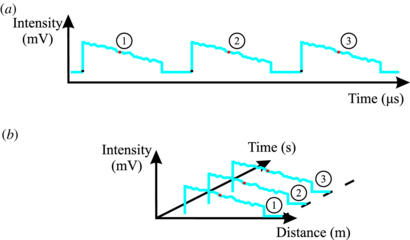
The acquired signals on each detector consisted of a train of backscattered traces. The length of each trace was proportional to the length of the sensing fibre, and the repetition rate was equal to the repetition rate of the pulse generator (figure 5(a)). The sequence of traces was redrawn to provide a 3D plot of the backscattered traces and allows the output at a particular position to be determined as a function of time (figure 5(b)).

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.** Rearrangement of a two-dimensional train of traces, (a) into a three-dimensional diagram, (b) depicting the sequence of traces.
Download figure:
Standard image High-resolution image

The differentiate and cross-multiply demodulation scheme was implemented digitally along the lines of the algorithm as shown in figure 3 for one particular position along the fibre. A fast Fourier transform was performed to identify the frequency components of any phase perturbation occurring within the gauge length of this point. This process was then repeated for each point along the sensing fibre and drawn as a 3D plot showing the frequency spectrum of the perturbations along the sensing fibre.

3.2. Experimental procedure

Both the disc and the ring PZTs were initially characterized using an MZI to determine the voltage–strain relationship of them at different frequencies before being included in the experimental setup. The applied voltages to the PZTs were initially adjusted to stretch the fibre by approximately 750 nm or π rad corresponding to 350 n epsilon strain. Data were acquired for a range of frequencies with the repetition rate of 10 μs for 12 ms. To investigate the linearity of the sensor, the input frequency of the disc PZT was set to a fixed value and different voltages were applied to strain the fibre over the range of 100 n epsilon –1.5 μ epsilon .

4. Results

Figure 6(a) depicts the FFT of the processed signal in a 3D diagram where the axes show the distance and the frequency of perturbation and its magnitude. The two peaks in the figure correspond to the two strained regions in the sensing fibre, i.e. one at a distance of 400 m and the other at a distance of 720 m from the front end of the fibre under test (FUT). Figure 6(b) shows the output of the phase detector for the 3.5 m section of the sensing fibre, which is located at a distance of 720 m from the front end of the sensing fibre.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.** (a) 3D plot of FFT of the phase-detector output of the experimental setup. (b) 3D plot of the phase-detector output in the time domain for the section of the FUT at 720 m.
Download figure:
Standard image High-resolution image

A 2D view of these 3D plots is depicted in figure 7. Figure 7(a) shows the frequency components corresponding to the applied strain at 400 m (red trace) and 720 m (blue trace), respectively, from the front end. Figure 7(b) shows the phase-detector output at the same points.

Figure 7. Refer to the following caption and surrounding text. — **Figure 7.** (a) 2D cross section of figure 6(a) at points 400 and 720 m. (b) 2D cross section of the phase-detector output at the same points.
Download figure:
Standard image High-resolution image

Figure 8 shows the response of the sensor when the disc PZT is subjected to a sinusoidal disturbance at 900 Hz sinwave of varying amplitude. A correlation coefficient of 0.9979 was determined.

Figure 8. Refer to the following caption and surrounding text. — **Figure 8.** PZT input voltage versus sensor output for the input sinusoidal signal at a frequency of 900 Hz.
Download figure:
Standard image High-resolution image

The frequency response of the disc PZT for the 0.7 V_PP input voltage is plotted in figure 9. In this figure, the distributed sensor output is shown in the blue trace, while the red trace shows the disc PZT frequency response characterized by using an MZI.

Figure 9. Refer to the following caption and surrounding text. — **Figure 9.** Frequency response of the PZT for the input voltage of 0.7 V_PP where the red trace shows the frequency response of the FUT using an MZI and the blue trace shows that of the distributed sensor.
Download figure:
Standard image High-resolution image

5. Discussion

5.1. Interpretation of 3D figures

The two peaks of figure 6(a) correspond to the strains applied by the two PZTs to the FUT. The 2D plot shown in figure 7(a) confirms that the peaks on the 3D diagram are accurately indicating the frequency and the amplitude of the strains applied to the FUT. In addition, the 3D diagram of figure 6(b) shows that the output of the phase detector follows the sinusoidally applied strain to the fibre. The 2D cross sections of the phase-detector output at 400 and 720 m are shown in figure 7(b), which illustrates the behaviour of fibre at those points as a function of time.

5.2. Strain range and strain resolution of the sensor

Figure 8 shows a linear relationship between the amplitude of the applied strain on the FUT and the sensor output at 900 Hz. Similar experiments at other frequencies (i.e. 1400, 1900 and 2300 Hz) verified that this linear relationship is independent of the frequency. The R² value of 0.9979 for the fitted line confirms a high level of linearity. The minimum detectable strain was measured to be 80 nε with a signal-to-noise ratio of 1. The strain resolution was measured to be 20 nε.

The limiting factors for the minimum detectable strain and the strain resolutions are the digitization level of the oscilloscope and noises in the setup such as ASE noise, detector noise and CRN. The CRN noise depends on the linewidth of the DFB laser source and the pulse width. A broad band laser source or a shorter pulse width can be used to reduce the CRN. In addition, ASE noise can be improved by using a narrower FBG filter.

The maximum detectable strain depends on both the length of the FUT and the frequency of the strain. The length of the FUT determines the repetition rate of the interrogating pulse which itself determines the sampling rate for each point along the FUT. In addition, since the magnitude of the strain perturbation governs the phase change and hence the number of fringes, perturbation with higher magnitudes behaves like a high frequency signal. Therefore, the relationship between the frequency of the strain, f_strain, the length of the FUT, L, and the maximum detectable strain, ε_max, is governed by

$\begin{equation} \varepsilon _{{\rm max}}\times \, f_{{\rm strain}}\times \, L=K, \end{equation} \tag{ 5 }$

where K is a constant. Therefore, in order to keep track of large perturbations, the minimum sampling rate (S_eff) at the output of the MZI is given by

$\begin{equation} S_{{\rm eff}}=2\pi \times f_{{\rm strain}}\times N_{{\rm fringe}} , \end{equation} \tag{ 6 }$

where f_strain is the frequency of the imposed strain, N_fringe is the number of fringes at the output of the MZI. The factor π arises from taking into account the fact that the rate of changes of strain is nonuniform during a cycle. Equations (5) and (6) explain the limitations imposed on the maximum detectable strain range of the sensor. First of all, the maximum repetition rate of any OTDR system is limited by the round trip of the pulse light inside the FUT. As a result, the maximum sampling rate in equation (6) is determined by the length of the FUT. Therefore, for any setup with a fixed length of fibre and at any given frequency, the maximum detectable strain is determined by equation (5). In order to maintain the linear relationship between the sensor output and the imposed strain, it is essential to keep the strain below this maximum value. Then to measure larger strains, the gauge length should be reduced in order to reduce the phase change and consequently the lower fringe count.

According to figure 9, the blue and the red traces show good correlation. This demonstrates that the strain amplitude measured using the distributed sensor agrees with the data collected using the MZI.

5.3. Spatial and frequency resolution of the sensor

In the current setup, the length of the delay fibre was 4 m with an interrogating pulse width of 10 ns, providing a spatial resolution of 2 m. This value agreed with the experimental results. The spatial resolution can be improved by reducing the pulse width duration and the length of the delay fibre simultaneously.

The frequency resolution of the sensor is governed by the number of traces the oscilloscope can capture per channel. So, the higher the number of captured traces, the smaller the frequency step that can be resolved. For the current experimental setup, the oscilloscope was set to capture 1200 traces per channel with the repetition rate of 10 μs. This corresponds to a theoretical frequency resolution of 83 Hz. A frequency resolution of 90 Hz was measured experimentally. The frequency range of the sensor was measured to be 500–5000 Hz. The higher frequency limit of 5000 Hz is governed by the wavelength of the induced strain, since the measured strain is equal to the net extension over the gauge length. For high-frequency strains with wavelength much shorter than the sensor gauge length, the net extension is small, since there are multiple oscillations within the gauge length. To increase the frequency range of the sensor, the gauge length of the sensor needs to be reduced.

6. Conclusions

A distributed optical fibre dynamic strain sensor has been demonstrated using phase-sensitive OTDR. The problem of signal fading was overcome by a cross-multiply and differentiate demodulator. The experimental results show that the sensor is capable of measuring the frequency and amplitude of multiple perturbations along 1 km of the sensing fibre simultaneously with a spatial resolution of 2 m over a frequency range of 500–5000 Hz. Based on these specifications, the proposed sensor is capable of quantifying and tracking multiple moving objects along the fibre. Rail network control and monitoring can be mentioned as one of the potential applications for this sensor where it can replace the current signaling system. With the repetition rate of 100 μs, this sensor is capable of tracking a train with a speed of 360 km h⁻¹ once every 10 cm over 10 km and in addition to the location, it can report possible problems with the train or the railway track based on the acoustic vibration.

Author e-mails

Author affiliations

Dates