In this paper, we first consider the inverse eigenvalue problem as follows: find a matrix A with specified eigenpairs, where A is a Hermitian and generalized skew-Hamiltonian matrix. The sufficient and necessary conditions are obtained, and a general representation of such a matrix is presented. We denote the set of such matrices by 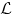Script LS. Then we discuss the best approximation problem for the inverse eigenproblem. That is, given an arbitrary Ã, find a matrix A∗ ∊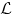Script LS which is nearest to à in the Frobenius norm. We show that the best approximation is unique and provide an expression for this nearest matrix.