Abstract
The purpose of this study is to present a novel perspective on decision support based on the conventional SEIR pandemic model paradigm considering the risks and opportunities as physical forces deviating the expected performance trajectory of a system. The impact of a pandemic is measured by the deviation of the social system's performance trajectory within the geometrical framework of its Key Performance Indicators (KPIs). According to the overall premise of utilizing Ordinary Differential Equations to simulate epidemics, the deviations are connected to several alternative interventions. The model is essentially built on two sets of parameters: (i) social system parameters and (ii) pandemic parameters. The ultimate objective is to propose a multi-criteria performance framework to control pandemics that includes a combination of timely measures. On the one hand, the current study optimizes prospective strategies to manage the potential future pandemic, while on the other hand, it explores the COVID-19 epidemic in the state of Georgia (USA).
Keywords: Decision Support System (DSS), optimization, pandemic, performance management, risk management, SEIR
1. Introduction
Transmission of infectious diseases has long been a cause of worry and a hazard to public health. It has presented severe risks to the survival of humans and social development. Following pandemic crises such as the Cholera (1817-1923), Spanish Flu (1918-1919), COVID-19 (2019-present), and others [1], [2], implementing pandemic preparedness measures has become a top concern for worldwide public health. Pandemic prevention and containment techniques fall into three major categories: antiviral (chiefly a drug or treatment effective against viruses), vaccination (treatment with a vaccine to produce immunity against disease), and non-pharmaceutical (isolation of the infected cases, quarantine, closure of school and workplaces, and travel restrictions) [3]. A critical step in controlling a ”non-pharmaceutical” infectious disease outbreak is attempting to reduce the epidemic peak, which reduces the danger of overburdening healthcare systems and allows for more time for the development of a vaccine and treatment [4]. A thorough assessment of the pandemic-contaminated area and the pandemic itself can provide insight into the scope of the pandemic threat and potential control strategies. The proposed study considers a pandemic-contaminated region as a system and a pandemic as a potential that may affect system KPIs in a multi-dimensional performance space. The Physics-of-Decision (POD) paradigm proposed in [5] is used in this study. Risks and opportunities, according to the original POD framework, may be viewed as physical forces applied to the system trajectory that could push or pull it in its performance space by varying the system's KPIs [6].
The primary goal of this study is to present a tentative Decision Support System (DSS) by tuning a well-known Susceptible-Exposed-Infected-Recovered (SEIR) pandemic model to the POD framework through Ordinary Differential Equations (ODEs). To this aim, by putting the POD principles into practice, researchers may be able to study various strategies that might impact the performance of the considered system and assist them in successfully intervening in the control of future pandemics.
The paper is structured as follows. Section 2 focuses on current research efforts and scientific contributions that are related to the topic at hand. Section 3 first introduces the pandemic modeling through ODEs then tunes the presented model into the POD framework. Section 4 provides a specific POD framework process for a Decision Support System. Section 5 shows the value of the POD as a strategies management framework for the COVID-19 pandemic in the State of Georgia (USA) and to control potential future pandemics efficiently. Finally, Section 6 provides conclusive remarks and proposes areas for further research.
2. Background and Related Works
Effective management of emerging pandemic infectious disease issues in the absence of treatment or vaccine is primarily dependent on government preventive strategies [7]. Scientific understanding is scarce regarding these strategies in the field of infectious disease control. There is also little information on whether theories and measurements created for risk perception studies on chronic diseases, for example, can be used for infectious diseases [8]. Such information, however, is critical for the successful management of newly developing infectious illnesses, because the capacity to promote health-protective behavioral change is conditional on the understanding of major drivers of such behavior [9]. In recent years, epidemiological models have been the subject of significant research. Compartmental models, such as the SEIR model (see subsection 3.2), have been utilized often for epidemic analysis among the many models. The early dynamics of disease transmission, from initial infected cases through the potential of the intervention to limit disease spread, are the primary focus of epidemic modeling approaches [10].
This study looks at a simplified version of the SEIR pandemics model implemented through ODEs in which no one has preexisting immunity, and every infected one has immunity after recovery. The objective is to characterize the pandemic model to investigate the possible interventions to control the outbreak through finding the most desirable solutions considering the limits of their execution. International travel restrictions [11], contact reduction [12], isolation of sick persons from the outset [13], and the use of masks [14] are some of the most common measures for controlling a non-pharmaceutical pandemic. The current research delves into the SEIR model to distinguish the model's inputs from its outputs, and it looks at the mentioned pandemic control strategies with the assumption that changes in system inputs generate changes in its outputs. Some modified SEIR models such as [15], [16], and [17] attempt to thoroughly assess various intervention techniques. The inputs of the pandemic model are divided into two categories: virus and society. The influence of virus-related elements and the characteristics of the pandemic-affected region as a society on the epidemic, are examined in this study. To investigate a behavioral dynamic epidemic model for multidimensional policy analysis that includes endogenous viral transmission, various simulation-based assessments of outbreak reactions and tactics are established [18]. Understanding the interaction between factors in nonlinear systems attempts to investigate ”what-if” possibilities based on the community and region's capabilities. The wearing masks as an example among the non-pharmaceutical intervention measures has been studied in [19] for the COVID-19 epidemic. In the SEIR model, population transmission through dynamic flows has been established using various ODEs. Various pandemics are represented by different input values for the equations, as mentioned in [20].
The foundation of system diagnostics is the characterization of the system and the relationship between its parameters. Controlling the system, necessitates the identification of such linkages and their impact on the system's performance. The varied circumstances of the system across time are defined by system states [21]. Over the last few decades, the field of risk management has produced a number of acknowledged outcomes that are now regarded as reliable contributions [5]. According to [22], risk is defined as a mix of the severity of the system's consequences on the one hand and the likelihood of occurrence on the other. The Physics of Decision (POD), which is based on physical principles and mathematical equations, is a novel performance management technique in the field of risk management [5]. The POD framework is a multi-criteria, time-dependent approach for performance analysis that quantifies the impact of various pandemic control methods. When compared to earlier researches, the innovation of this approach is the ability to measure the influence of multiple strategies (simultaneously) on system performance in a multi-dimensional framework and then determine the optimum strategies while keeping the execution restrictions in mind.
3. Physics-Based Decision Support System
The term “Risk” is used in many ways and is given different definitions depending on the field and context. Common to most definitions of risk is uncertainty and undesirable outcomes. From a reciprocal perspective, those uncertainties that could bring benefits if they were to occur are known as “Opportunities” [23]. The definition of opportunity is: “an uncertainty that could have a positive effect leading to benefits or rewards”. The opportunity could be seen as just another form of risk: a risk with negative impacts is a threat, whereas a risk with a positive impact is an opportunity [24].
Decision Support Systems (DSSs) are at the heart of risk/opportunity management projects [25]. The necessity of such systems is critical to deal with the complexities due to massive data and interconnectivity between the system's components and its environment [26].
In this section, the Physics Of Decisions (POD) is presented and illustrated as an innovative approach for decision support in context of instability and uncertainty. POD considers that risks and opportunities can be created by spontaneous or intentional changes in the system's parameters or in its environment parameters. These changes may push or pull the system in its performance space by varying systems KPIs. Essentially, these variations’ consequences are observed through the deviation of the system “trajectory” within the multidimensional performance space of its KPIs.
3.1. Preliminaries, Basic Concepts, and Notation
System characterization and identification are fundamental problems in systems theory. The problem of characterization is concerned with the mathematical representation of a system. A model of a system can be expressed as a function  from an input space
from an input space  into an output space
into an output space  [27]. The function F is defined implicitly by the specified input-output pairs. The method of representing time-depended systems by vector differential or differential equations is well established in systems theory and applies to a fairly large class of systems [28]. For example, the differential equation:
[27]. The function F is defined implicitly by the specified input-output pairs. The method of representing time-depended systems by vector differential or differential equations is well established in systems theory and applies to a fairly large class of systems [28]. For example, the differential equation:

|
where  ,
,  , and
, and  , represents a
, represents a  input,
input,  output system of order
output system of order  with
with  representing the inputs,
representing the inputs,  the state variables, and
the state variables, and  the outputs of the system.
the outputs of the system.  and
and  are static nonlinear maps defined as
are static nonlinear maps defined as  and
and  . The vector
. The vector  denotes the state of the system at time
denotes the state of the system at time  and is determined by the state at time
and is determined by the state at time  and the input
and the input  defined over the interval
defined over the interval  . The output
. The output  is determined by the state of the system at time
is determined by the state of the system at time  . Eq. (1) is referred to as the input-state-output representation of the system [27], [28]. This paper is concerned with discrete-time systems which can be represented by differential equations corresponding to the differential equation given in (1). These take the form
. Eq. (1) is referred to as the input-state-output representation of the system [27], [28]. This paper is concerned with discrete-time systems which can be represented by differential equations corresponding to the differential equation given in (1). These take the form

|
where  ,
,  , and
, and  are discrete-time sequences. Fig. 1 illustrates a time-dependent input-states-output system.
are discrete-time sequences. Fig. 1 illustrates a time-dependent input-states-output system.
Fig. 1.
Mathematical representation of input-state-output of a system.
3.2. Pandemic Modeling Through Ordinary Differential Equations
Quantitative studies on mechanisms of disease transmissions provide a foundation for pandemic prevention and control. The Epidemic Dynamics formulates mathematical models based on the occurrence and progressions of diseases to its surroundings to characterizing the infectious agents, describing the transmission processes, analyzing origins of the diseases and factors involved in the transmissions, and predicting the prevalence of the diseases and their patterns [10]. Dynamic models for infectious diseases are mostly based on compartment structures [10]. To formulate a dynamic model for the transmission of an epidemic disease, the population in a given region is often divided into several different groups or compartments. Such models describing the dynamic relations among these compartments are called compartment models. The population is assigned to compartments with labels – for example, S, I, or R, (Susceptible, Infectious, or Recovered). The population may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example, SEIS means ıSusceptible, Exposed, Infectious, then Susceptible again. The numbers of individuals are presented in the compartments S, E, I, and R, at time t, as S(t), E(t), I(t), and R(t), respectively [29]. This section introduces the generic version of pandemics model including Susceptible, Exposed, Hospitalized, Recovered, and Dead as common compartments of different pandemics shown in Fig. 2.
Fig. 2.
Flow chart of the SEIR model.
This model postulates rules on how populations in each category move to the next categories. Based on Fig. 2, the transitions of the population through the flows from left to right are as follows:
(i) Exposing flow  The individuals move from S to E through this flow (Fig. 2) at the exposure rate, i.e., the population in category S decreases concerning time t and the population in E correspondingly increases at the same rate. The exposure rate grows with I, the number of infected individuals. A standard hypothesis is that exposure rate is the product of the transmission rate (or contact rate (cr)) and the probability of infection given that contact occurred (infectious rate (ir)) divide by latency due to infectious duration (id) [30].
The individuals move from S to E through this flow (Fig. 2) at the exposure rate, i.e., the population in category S decreases concerning time t and the population in E correspondingly increases at the same rate. The exposure rate grows with I, the number of infected individuals. A standard hypothesis is that exposure rate is the product of the transmission rate (or contact rate (cr)) and the probability of infection given that contact occurred (infectious rate (ir)) divide by latency due to infectious duration (id) [30].

|
(ii) Infecting flow  The Exposed individuals progress to the Infected category through this flow after the latent period (lp), the period at which exposed hosts become infected [30].
The Exposed individuals progress to the Infected category through this flow after the latent period (lp), the period at which exposed hosts become infected [30].

|
(iii) Hospitalizing flow  The individuals with lower immunity in case of virus infection, called severe infected group, progress to the Hospitalized compartment with the rate of fraction hospitalized (fh).
The individuals with lower immunity in case of virus infection, called severe infected group, progress to the Hospitalized compartment with the rate of fraction hospitalized (fh).

|
(iv) Recovering 1 flow  The lightly Infected individuals (non-severe cases), those who don't need to be Hospitalized, progress to the Recovery compartment directly after the infectious duration (id).
The lightly Infected individuals (non-severe cases), those who don't need to be Hospitalized, progress to the Recovery compartment directly after the infectious duration (id).

|
(v) Recovering 2 and Dying flows  The Hospitalized individuals, depending on the fatality rate (fr) of the virus, either recover (Recovering 2 flow) or die after infectious duration (Dying flow). The hospitalized fatality rate (hfr) is calculated by dividing the fatality rate (fr) of the virus by the fraction hospitalized (fh), hfr = (fr)/(fh).
The Hospitalized individuals, depending on the fatality rate (fr) of the virus, either recover (Recovering 2 flow) or die after infectious duration (Dying flow). The hospitalized fatality rate (hfr) is calculated by dividing the fatality rate (fr) of the virus by the fraction hospitalized (fh), hfr = (fr)/(fh).

|
The basic reproductive number (denoted  ), in epidemiological modeling, is the expected number of cases directly caused by one case in a community where everyone is susceptible. In the majority of commonly used epidemic models, a pandemic can spread in a population if
), in epidemiological modeling, is the expected number of cases directly caused by one case in a community where everyone is susceptible. In the majority of commonly used epidemic models, a pandemic can spread in a population if  , but not if
, but not if  . The basic reproductive number for the SEIR model is shown in Eq. (8), assuming that the latency period is a random variable with exponential distribution with parameter
. The basic reproductive number for the SEIR model is shown in Eq. (8), assuming that the latency period is a random variable with exponential distribution with parameter  (i.e., the average latency period is
(i.e., the average latency period is  , or
, or  ),
),  ,
,  , and
, and  are the rates of infection (the number of contacts per person per time (cr/id), multiplied by the probability of disease transmission in a contact between a susceptible and an infectious subject (ir)), recovery, and mortality, respectively [30].
are the rates of infection (the number of contacts per person per time (cr/id), multiplied by the probability of disease transmission in a contact between a susceptible and an infectious subject (ir)), recovery, and mortality, respectively [30].

|
Since the natural mortality rate is not included in the presented SEIR model in Fig. 2 ( ). According to the “Recovery 1” and “Recovery 2” flows in Fig. 2 and Eqs. (6) and (7), the
). According to the “Recovery 1” and “Recovery 2” flows in Fig. 2 and Eqs. (6) and (7), the  is obtained using Eq. (9).
is obtained using Eq. (9).

|
Finally, the reproductive number of the presented model is obtained through Eq. (10).

|
Given that the disease spreads in a closed environment; the paper considers there is no emigration nor immigration and neither birth nor death in the population so that the total population remains a constant  for all t, that is:
for all t, that is:

|
Instead of establishing the system for a specific total number of the population, the paper simplifies the Eq. (11) by dividing the sides of the equation by total population  to be efficient for any population size. Therefore, the following proportions are obtained.
to be efficient for any population size. Therefore, the following proportions are obtained.

|
Based on Fig. 2 and Eqs. (3), (4), (5), (5), and (7), there are six parameters involved in the flows. The vector  presents those parameters as inputs for derived equations.
presents those parameters as inputs for derived equations.

|
The rate of change in the compartments in Fig. 2 from left to right according to the transmission of individuals are represented in Eq. (14) through Ordinary Differential Equations (ODEs) based on equations and the input vector  (13).
(13).

|
The ordinary differential equations (ODEs) system in Eq. (14), together with some initial conditions (values of the input variables of the model (vector  ) at initial starting time
) at initial starting time  ), make up an Initial Value Problem, or IVP. IVPs are ubiquitous in modeling systems that evolve in time. They encapsulate how a future state of a system is determined by the present state (the initial data) plus certain rules on how quantities evolve (the ODEs) [31]. As soon as the preliminary infected (or exposed) cases appear in the region, the pandemic starts to spread. The ODEs in Eq. (14) are supplemented with some initial conditions. For example, some percentage of the whole population (
), make up an Initial Value Problem, or IVP. IVPs are ubiquitous in modeling systems that evolve in time. They encapsulate how a future state of a system is determined by the present state (the initial data) plus certain rules on how quantities evolve (the ODEs) [31]. As soon as the preliminary infected (or exposed) cases appear in the region, the pandemic starts to spread. The ODEs in Eq. (14) are supplemented with some initial conditions. For example, some percentage of the whole population ( ) is infected (or exposed) and the rest are susceptible to be infected.
) is infected (or exposed) and the rest are susceptible to be infected.

|
The modeling through ODEs has been completed. The following are some remarks on specific hypotheses.
(i) The simple version of the presented SEIR model in this section considers that the recovered individuals gain permanent immunity. However, for bacterial diseases, such as encephalitis, and gonorrhea, the recovered individuals don't gain permanent immunity and can be reinfected [10].
(ii) The paper considers there is not an emigration or immigration, and neither birth nor death in the population and the population size remains a constant  for all t.
for all t.
(iii) The presented model considers all the individuals are susceptible to be infected. It might be a portion of the population is immune to the virus and so not susceptible to it. Besides, depending on the type of the virus, due to the sensitivity of the virus to some parameters such as age category, the health status of the population in the region; some individuals might be more susceptible and some not.
(iv) The exposed compartment could be distinguished to individuals with and without symptoms and the Infected group, in addition to the light and severe groups, could include infected individuals that don't carry the virus.
(v) The severely infected individuals could be hospitalized and ICU sections. The model doesn't consider differentiation between these two groups, while it might be the limit capacity for the ICU bed in hospitals.
In addition to the above remarks, there may be other hypotheses for the epidemic model that are not considered in this study. This paper considers one of the simplest cases that is common to most epidemics. It's important to point out that the paper does not cover all the possible versions of epidemics models. This is mostly due to the fact that the study's focus is on the model's application rather than its relevance.
3.3. Physics of Decision Theory and Its Tuning to Pandemic Performance Management
The Physics Of Decision (POD) framework introduced in Section 2 is a mathematical representation of a system considering internal system connections and communication of the system with its environment. The next step after characterization and identification of the system is to evaluate the system performance. The three modes are considered to assess the system performance: (i) Inertia mode: The performance could change due to its normal behavior and the associated consumption. In this mode, the system is not facing any perturbation. (ii) Passive mode: In addition to the performance changes of Inertia, the performance might change because there is (are) perturbation(s) in the system or its environment, (iii) Active mode: In addition to the performance changes of Inertia, the performance could change because the system is facing some perturbations (passive changes) and also because of some taken decisions to manage the consequences of those perturbations. In the case of a pandemic crisis, the change of population size due to migration, or natural birth/death is considered Inertia, the sudden change of the population because of the pandemic issues is considered Passive, and the change of the population due to some intervention in comparison to the Passive mode is considered as Active mode. The POD framework defines two spaces in which a system can be positioned.
The Description Space describes the parameters of the system and the scope of their variation. The  -input vector
-input vector  represents the input system parameters (Section 3.1). Description Space generally refers to what is happening in and around the monitored system. The parameters of the Description Space refer to the “System” and are known as “Attributes”. A monitored system with particular attributes could be affected by several circumstances. These circumstances are known as “Potentials”. A potential could have positive or negative impacts on the system (Risks and Opportunities). The parameters of systems’ potentials are known as ”Characteristics”. State variable
represents the input system parameters (Section 3.1). Description Space generally refers to what is happening in and around the monitored system. The parameters of the Description Space refer to the “System” and are known as “Attributes”. A monitored system with particular attributes could be affected by several circumstances. These circumstances are known as “Potentials”. A potential could have positive or negative impacts on the system (Risks and Opportunities). The parameters of systems’ potentials are known as ”Characteristics”. State variable  is one set of input parameters including Attributes (system's parameters) and Characteristics (potentials’ parameters) that describes the mathematical “states” of a system under function
is one set of input parameters including Attributes (system's parameters) and Characteristics (potentials’ parameters) that describes the mathematical “states” of a system under function  (See Fig. 3 and Eq. (2)).
(See Fig. 3 and Eq. (2)).
Fig. 3.

Description and Performance Spaces of POD framework.
The Performance Space under function  describes the system performance with an
describes the system performance with an  -output vector
-output vector  . The output vector
. The output vector  is determined by the system state in the Description Space (vector
is determined by the system state in the Description Space (vector  ) at time
) at time  .
.
The relationship between the two spaces is determined by the map function  of the state variables,
of the state variables,  (one set of input parameters including Attributes and Characteristics) to the outputs,
(one set of input parameters including Attributes and Characteristics) to the outputs,  . This map function could be known (e.g., is formulated with equations from inputs to outputs), or it could be unknown but estimable (e.g., through simulation analysis, approximation function, Neural Network, etc.).
. This map function could be known (e.g., is formulated with equations from inputs to outputs), or it could be unknown but estimable (e.g., through simulation analysis, approximation function, Neural Network, etc.).
The Description Space in Fig. 3 represents a system with a  -input vector composed by one vector of Attribute (system) and
-input vector composed by one vector of Attribute (system) and  vector of potentials (system's environment). The vector of each potential is represented with its characteristics:
vector of potentials (system's environment). The vector of each potential is represented with its characteristics:
-
(i)
 characteristics for potential
characteristics for potential  (on-axis) and the
(on-axis) and the  possible state variables for each
possible state variables for each  at specific time
at specific time  shown with colored points in Fig. 3 (oval marked with “Environment”),
shown with colored points in Fig. 3 (oval marked with “Environment”), -
(ii)
 Attributes (on-axis) of the system
Attributes (on-axis) of the system  and
and  possible state variables for these Attributes at specific time
possible state variables for these Attributes at specific time  shown with colored points in Fig. 3 (oval marked with “System”).
shown with colored points in Fig. 3 (oval marked with “System”).
Eq. (16) presents the number of inputs  of the input vector
of the input vector 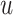 and the number of possible system states
and the number of possible system states  for the generic version of the POD framework presented in Fig. 3.
for the generic version of the POD framework presented in Fig. 3.

|
According to the state variables of Attributes and Characteristics, 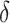 and
and  respectively,
respectively,  possible initial system states exist at time
possible initial system states exist at time  in the Description Space (
in the Description Space ( ).
).
The Performance Space, according to Fig. 3, describes:
(i) on the top, in the case of “no perturbation,” the “Inertia” trajectory is shown in green. Besides, the  possible passive trajectories have been depicted according to
possible passive trajectories have been depicted according to  possible initial system states in the Description Space. In this case, the system goes through its own “passive” trajectories in the system's KPIs space according to the
possible initial system states in the Description Space. In this case, the system goes through its own “passive” trajectories in the system's KPIs space according to the  given colored points for the Attributes of the system
given colored points for the Attributes of the system  and
and  given colored point of Characteristics for each potential
given colored point of Characteristics for each potential  ,
,
(ii) on the bottom, “active” trajectory, in the sense that one movement at specific time  from one colored point to another one has been made through green edge in order to deviate the passive trajectory (blue trajectory as one of possible
from one colored point to another one has been made through green edge in order to deviate the passive trajectory (blue trajectory as one of possible  passive trajectories). The same process continues at
passive trajectories). The same process continues at  from the new state of the system to another state through another edge (e.g., purple edge).
from the new state of the system to another state through another edge (e.g., purple edge).
The system might be destabilized by unforeseen changes. These changes are due to the existence of perturbations that create a passive trajectory. The passive trajectory is determined by the instance in question, with the most likely case being chosen. The changes related to decisions mainly refer to the varying of system parameters including Attributes and Characteristics (changing the system state by moving the colored points through edges) and consequently, deviation from the system's passive trajectory. Any deviation from that trajectory is considered an active one for the system.
Section 3.2 presented the ODEs modeling for the pandemic that disease spread in a closed environment. In the perspective of the presented POD framework in this section, the system is the “region” contaminated by a “pandemic”. The “Attributes” are related to the parameters of the region and there is only one “Potential” which is a pandemic and means,  in Eq. (15) (at the same period, the potentials except pandemic could be other similar negative potentials (risks) such as hurricanes, earthquakes, etc., or positive potentials (opportunities) such as the development of agriculture and industry, increasing social security, improving the standard of living acts, etc.).
in Eq. (15) (at the same period, the potentials except pandemic could be other similar negative potentials (risks) such as hurricanes, earthquakes, etc., or positive potentials (opportunities) such as the development of agriculture and industry, increasing social security, improving the standard of living acts, etc.).
According to Fig. 2 (or Eq. (13)), all the compartments (or left sides of ODEs) could be a KPI in the POD performance space ( ). Besides, the system's inputs, represented in vector
). Besides, the system's inputs, represented in vector  (Eq. (12)), are parameters of the:
(Eq. (12)), are parameters of the:
-
(i)Potential
 pandemic, including the following Characteristics: latent period, infectious duration, fatality rate, and infectious rate of the virus,
pandemic, including the following Characteristics: latent period, infectious duration, fatality rate, and infectious rate of the virus,

-
(ii)
System
 region, including contact rate and hospitalized fraction as attributes
region, including contact rate and hospitalized fraction as attributes

|
In other words, in the POD framework for the presented ODEs of pandemic,  ,
,  , and
, and  (see Eq. (16)).
(see Eq. (16)).
4. Physics of Decision Methodology
In the perspective of the POD framework, deviations from the system passive trajectory happen due to changes in the system state in the Description Space (moving the colored point in Fig. 3). A movement of a colored point is considered a “strategy”. According to the performance space in Fig. 3, the passive trajectory is formed by inputs of the pandemic (vector  in Eq. (17)) and inputs of the region (vector
in Eq. (17)) and inputs of the region (vector  in Eq. (18)).
in Eq. (18)).
The key objective of the POD management theory is to use the results of a model-based system on the paradigm of input-states-output to develop a management strategy. The main expected benefit of this vision is to enable decision-makers to manage the performance trajectory of a considered system by visualizing and combining the impact of risks and opportunities. This section develops an original process of the presented approach on a considered system that might face instabilities (Risks and Opportunities). This POD process is applied to the considered problem in the sequential steps presented as follows.
4.1. System Establishment
The first step of the POD process is understanding the observed system and its environment. First, the system which is supposed to be studied is determined; The boundaries of the system in terms of precise study must be clear. The environment of the selected system refers to its potentials (Risks and Opportunities). Once the system and its potentials are determined, the associate parameters of the system to the considered potentials must be appointed (i.e., characterizing the  inputs of the system). Similarly, the inputs of the system's potentials have to be specified (i.e., characterizing the
inputs of the system). Similarly, the inputs of the system's potentials have to be specified (i.e., characterizing the  ). Section 3.2 is dedicated to performing this step for the pandemic (potential) in a closed environment (system).
). Section 3.2 is dedicated to performing this step for the pandemic (potential) in a closed environment (system).
4.2. System Characterization
The established system includes the inputs of the system (Attributes) and its potentials (Characteristics). These inputs could be categorized into two groups in terms of their movement in the Description Space.
(i) The changes (i.e., movements in the Description Space) of inputs more related to the potential are known as “elusive” changes. The elusive changes are considered out of control changes (or at least hard to perform). Table 1 shows that the inputs  to
to  are connected to the virus's features (potential), and it is impossible to change them unless the virus itself has a mutation (e.g., fatality rate of the COVID-19 (1%-3.4%) is different from Ebola (50%) [34]). Roughly speaking, elusive changes look like impossible (or hard) strategies. The consequences resulted from elusive movements could be in two categories, (i) Inflicted consequences that are imposed on the system's outputs and unmanageable, (ii) Managed consequences that might be controlled through some potentialities (e.g., the infectious rate,
are connected to the virus's features (potential), and it is impossible to change them unless the virus itself has a mutation (e.g., fatality rate of the COVID-19 (1%-3.4%) is different from Ebola (50%) [34]). Roughly speaking, elusive changes look like impossible (or hard) strategies. The consequences resulted from elusive movements could be in two categories, (i) Inflicted consequences that are imposed on the system's outputs and unmanageable, (ii) Managed consequences that might be controlled through some potentialities (e.g., the infectious rate,  , is related to the nature of the virus while the Mask and Social Distance potentialities could reduce it).
, is related to the nature of the virus while the Mask and Social Distance potentialities could reduce it).
TABLE 1. Physics of Decision Process Applied on the Pandemic Model Presented in Section 3.2.
| Input |

|
Vector | Variation (Min, Avg, Max) | Movement Type | Consequence Type | Considered Potentiality |
|---|---|---|---|---|---|---|
| Latent Period |

|

|
(3, 7, 11) [days] [20], [32], [33] | Elusive | Inflicted | Mutation |
| Infectious Duration |

|

|
(7, 12, 17) [days] [20], [32], [33] | Elusive | Inflicted | Mutation |
| Fatality Rate |

|

|
(1, 5, 9) [percent] [20], [32], [33] | Elusive | Inflicted | Mutation |
| LightCyan Infectious Rate |

|

|
(40, 60, 80) [percent] [32], [33] | Elusive | Managed | Mask/Social Distance |
| LightCyan Contact Rate |

|

|
(5, 10, 15) [person/day] | Driver | Managed | Lockdown/Curfew |
| LightCyan Fraction Hospitalized |

|

|
(5, 10, 15) [percent] [20], [33] | Driver | Managed | Partial Lockdown |
(ii) The changes more related to the system are known as “driver” changes. The driver changes (more possible strategies) mainly create deviations in the passive trajectories. In other words, driver changes (and also the elusive changes with “Managed” consequence) make the active trajectories (Fig. 3). The consequences of the driver changes are mainly managed consequences but are essentially related to the limits of the system (see Section 4.3).
4.3. System Intending
The consequences of elusive and driver movements in the Description Space appear as a deviation in the trajectory of the system in the Performance Space. This step is related to (i) Which outputs (KPIs) the system manager is looking for to study (e.g., the number of Hospitalized and Dead cases in the SEIR model), (ii) What constraints might exist for the movement in the Description Space; In cases where the system must not be positioned in some states  forever or for a specific period in the Description Space (e.g., the region allowed to be in confinement only for one month, i.e., the (cr) value can't be close to zero more than one month), (iii) Which movement is preferable to the other if there is any specific priority and/or preference (e.g., wearing mask potentiality to reduce infectious rate is more feasible than confinement potentiality to reduce contact rate), and (iv) The onset of changes and periods that the system stays after the changes until the next change (e.g., the region can't be quarantined until two months after the onset of the pandemic and must return to no-quarantine status after one month).
forever or for a specific period in the Description Space (e.g., the region allowed to be in confinement only for one month, i.e., the (cr) value can't be close to zero more than one month), (iii) Which movement is preferable to the other if there is any specific priority and/or preference (e.g., wearing mask potentiality to reduce infectious rate is more feasible than confinement potentiality to reduce contact rate), and (iv) The onset of changes and periods that the system stays after the changes until the next change (e.g., the region can't be quarantined until two months after the onset of the pandemic and must return to no-quarantine status after one month).
4.4. Strategy Exploration
When the relationship between inputs in the Description Space and outputs in the Performance Space is specified (either formulated or estimated), this step would be the final step in the POD process. The last step of the POD process is dedicated to exploring all possible movements in the Description Space through experiment analysis to find the most desirable ones to be as close as possible to the optimum outputs. This is necessarily dependent on clear information about the following elements presented in the previous steps. (i) Inputs (what are they, which type they have, and which type of consequences might they have in terms of movement in the Description Space), (ii) Outputs (which ones are considered to study and which one is more important to optimize), and (iii) The constraints (the limits of movements, their preferences, onset and period of the movements).
Table 1 presents the POD process (the first and second steps) for the presented model in Sections 3.2 and 3.3. Table 1 presents an overview of the system and possible potentialities for system management. The managers of the system identify the “Managed” consequences and adopt strategies that are related to the inputs that their movement in the Description Space lead to this group of consequences. The highlighted rows in Table 1 refer to such inputs with such properties for the pandemic model. The third and fourth steps of the POD process for the presented pandemic model is more investigated in Section 5. In the POD approach, the key point is to locate the system (region) and the faced potential (pandemic) within the Description Space in order to parametrize and initialize the Decision Support System. The approach addresses the identified system with all of its constraints and the possible strategies to explore when it comes to automated functioning. Finally, following the strategy exploration (4.4), the best-fit strategies to execute will be offered automatically.
5. Experiments and Results
The main experiments are centered on strategy exploration to find the most desirable outcomes to the objectives of the system. The exploration in this context is to study the possible movements in the Description Space and finally propose the best ones at any time  that divert the passive trajectory toward the objective of the system in the Performance Space.
that divert the passive trajectory toward the objective of the system in the Performance Space.
The input vector for the presented well-known SEIR model in Section 3.2 includes the “Attribute,” the parameters of the system, and “Characteristics,” the parameters of the system's potential. The “Attributes” and “Characteristics” refer to region and pandemic respectively.
The Description Space
 for the presented SEIR model includes the inputs of the pandemic and the region with vectors
for the presented SEIR model includes the inputs of the pandemic and the region with vectors  and
and  respectively.
respectively.

|
The given vector  illustrates the state
illustrates the state  of the system and its potentials in the specific time
of the system and its potentials in the specific time  through function
through function  .
.
The Performance Space
 for the presented SEIR model indicates by vector
for the presented SEIR model indicates by vector  in a given
in a given  through function
through function  . This vector includes some notable KPIs.
. This vector includes some notable KPIs.

|
The vector  presents the current position of the system at time
presents the current position of the system at time  in its multi-dimensional KPI space (Performance Space). Different perspectives might be considered for the strategy exploration step of a specific system. Which KPIs are considered to study (it could be all of them at the same time) and which one between selected ones is prior to another one to optimize (they may not have priority): These are two essential questions that must be answered before strategy exploration.
in its multi-dimensional KPI space (Performance Space). Different perspectives might be considered for the strategy exploration step of a specific system. Which KPIs are considered to study (it could be all of them at the same time) and which one between selected ones is prior to another one to optimize (they may not have priority): These are two essential questions that must be answered before strategy exploration.
Sensitivity analysis of the inputs and outputs depicted in Fig. 4, (e.g., through simulation campaign) presents the correlation between them. This analysis proposes the priority for the movements in the Description Space. The inputs with “Managed” consequences (See Table 1) are highlighted in blue frame in Fig. 4. The correlation between inputs ( ) and the outputs (KPIs presented with
) and the outputs (KPIs presented with  vector) are as follows: on average 0.035, 0.012, and 0.0036 for the contact rate (cr), infectious rate (ir), and fraction hospitalized (fh) respectively.
vector) are as follows: on average 0.035, 0.012, and 0.0036 for the contact rate (cr), infectious rate (ir), and fraction hospitalized (fh) respectively.
Fig. 4.
Input-Output correlations of the presented SEIR model in Section 3.2.
According to these values, the impact of “contact rate” is more than the impact of “infectious rate,” which is greater than the impact of “hospitalized fraction”. In other words, potentialities are equally important as following commands, according to the “Considered Potentiality” column in Table 1; Lockdown/Curfew comes first, followed by Mask/Social Distance, and then Partial Lockdown.
To examine the POD framework, the three most dominant KPIs in terms of management, including  ,
,  , and
, and  compartments (Infected, Hospitalized, and Dead) are selected to study the possible movements (strategies) through potentialities, considering the onset and period of the strategies in the 3D performance space. The POD perspective for the selected KPIs is to minimize them as much as possible without any preferences between them. The rest of this section is centered on this objective. According to this objective, the foremost objective is the minimum value for each KPI at any time
compartments (Infected, Hospitalized, and Dead) are selected to study the possible movements (strategies) through potentialities, considering the onset and period of the strategies in the 3D performance space. The POD perspective for the selected KPIs is to minimize them as much as possible without any preferences between them. The rest of this section is centered on this objective. According to this objective, the foremost objective is the minimum value for each KPI at any time  . In the 3D Performance Space, the reference to study different possible movements (strategies) would be the origin of the space, the (0,0,0) coordinates for each axis.
. In the 3D Performance Space, the reference to study different possible movements (strategies) would be the origin of the space, the (0,0,0) coordinates for each axis.
According to Table 1, on the one hand, the linked potentiality to vector  's inputs (pandemic), involves wearing masks or keeping a safe distance from other people in the community (social distance), both of which might lower the infectious rate
(ir). Lockdown and/or Curfew to minimize contact rate
(cr) or Partial lockdown of the fragile group to receive the virus, to lower the fraction hospitalized
(fh), on the other hand, are associated potentialities to the inputs of vector
's inputs (pandemic), involves wearing masks or keeping a safe distance from other people in the community (social distance), both of which might lower the infectious rate
(ir). Lockdown and/or Curfew to minimize contact rate
(cr) or Partial lockdown of the fragile group to receive the virus, to lower the fraction hospitalized
(fh), on the other hand, are associated potentialities to the inputs of vector  (region). These strategies are applied to the ODEs of the presented SEIR model which is equivalent to changing the system states in the Description Space through the movements (See Section 5.2).
(region). These strategies are applied to the ODEs of the presented SEIR model which is equivalent to changing the system states in the Description Space through the movements (See Section 5.2).
The POD will be ready to investigate strategies once the possible potentialities and their implementation limits, such as their start time and duration, have been defined.
5.1. Potential Positioning
Understanding the possible effects of potential on the system trajectory in the Performance Space is the first step in the experiment analysis. Various viruses may have different parameters as inputs in vector  [2], [20]. According to column “Variation” in Table 1, considering that 1% of the total population is infected at first (
[2], [20]. According to column “Variation” in Table 1, considering that 1% of the total population is infected at first ( in Eq. (15)), the Fig. 5 presents the different trajectories of Minimum, Average, and Maximum values for the
in Eq. (15)), the Fig. 5 presents the different trajectories of Minimum, Average, and Maximum values for the  ,
,  ,
,  , and
, and  in purple, yellow, and black colors respectively. The values for non-varying inputs of “Potential” (e.g., in the case of
in purple, yellow, and black colors respectively. The values for non-varying inputs of “Potential” (e.g., in the case of  trajectories in Fig. 5, the
trajectories in Fig. 5, the  ,
,  , and
, and  ) as well as the “System” inputs are considered on “Average” in Table 1.
) as well as the “System” inputs are considered on “Average” in Table 1.
Fig. 5.

Pandemic positioning results for its inputs and their distances from the system objective, (0,0,0) coordinates.
The inverse impact of  and proportionate impact of
and proportionate impact of  ,
,  , and
, and  on the selected KPIs (I, H, and D) are shown in Fig. 5 (In the proportional impact, the distance between the points and the origin (0,0,0) grows as the value of input grows, and vise versa for the inverse impact). In addition, Table 2 shows that
on the selected KPIs (I, H, and D) are shown in Fig. 5 (In the proportional impact, the distance between the points and the origin (0,0,0) grows as the value of input grows, and vise versa for the inverse impact). In addition, Table 2 shows that 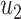 and
and  have bigger fluctuations on the KPIs than
have bigger fluctuations on the KPIs than  and
and  .
.
TABLE 2. Pandemic Positioning Results for Its Inputs and the Sum of Distance From the System Objective, (0,0,0) Coordinates.
| Input | u | Min | Avg | Max |
|---|---|---|---|---|
| Latent Period |

|
8.82 | 8.62 | 8.50 |
| Infectious Duration |

|
5.34 | 8.62 | 11.48 |
| Fatality Rate |

|
8.62 | 8.62 | 8.63 |
| LightCyan Infectious Rate |

|
6.99 | 8.62 | 9.17 |
Table 2 presents an overview of the potential impacts on the selected KPIs (I, H, and D). Except the “infectious rate” row, the value of other rows would be on average for the system positioning (Section 5.2). Because this parameter is the only potential parameter that could have “Managed” consequence in terms of movement in the Description Space (i.e., between the “Elusive” inputs, there is only “feasible potentiality” for infectious rate which could be wearing mask and social distance potentialities).
The experiments cover the period from the initial observation of infected cases to 180 days (six months) afterwards. In other words, each point of the given curves in Fig. 5 represents the values for one day of the selected KPIs (daily cases), and the results in Table 2 are the total sum of the distance between the point (0,0,0) and the 180 points of the curves.
The results presented in Fig. 5 show the system passive trajectories of daily KPIs. In this case, the initial position of the system (region, on the average value) and potential (pandemic) remain constant for the period of study (180 days).

|
5.2. System Positioning
The impact of potential inputs on KPIs is discussed in the preceding section in the absence of any strategy (no movement on the axis related to the system in the Description Space has been taken). This section investigates the active trajectory by examining the results of several possible movements in the Description Space of the COVID-19 (potential) for the state of Georgia (region) as alternative strategies that the system manager could take to control the system's trajectory in the Performance Space based on the selected system objectives.
The average considered value of the “latent period” and “infectious duration” for the COVID-19 are 6 days and 12 days respectively [19] (these values could vary, for example, the infectious duration is shorter when children or less severe cases are involved [32]).
The study uses real data from the COVID-19 virus in the state of Georgia between July 2020 and April 2021 to obtain the values of “fatality rate” and “fraction hospitalized” experimentally [35], [36].
The average value for the fatality rate (fr) indicated in the red plot in Fig. 6, is 2%. Also indicated in blue is the fraction hospitalized (fh), which is 10% on average. In Eq. (7), the “hospitalized fatality rate” (hfr) is calculated by dividing the (fr) by (fh), as illustrated in the black plot. Based on what has been mentioned so far, the input vector of the Covid-19 potential in the state of Georgia is as follows (see Table 1 for the units of input vector).

|
Fig. 6.
Fraction Hospitalized and Fatality Rate of the COVID-19 in the State of Georgia.
The three highlighted inputs with “Managed” consequences of vector  are presented in Table 1. The wearing mask potentiality, to reduce “infectious rate” (
are presented in Table 1. The wearing mask potentiality, to reduce “infectious rate” ( ) and the lockdown potentiality, to reduce “contact rate” (
) and the lockdown potentiality, to reduce “contact rate” ( ) are considered to study the active trajectories through these two potentialities.
) are considered to study the active trajectories through these two potentialities.
The three related alternatives to these potentialities are being investigated to determine the ideal timing for movements equivalent to the considered potentialities in the Description Space of the COVID-19 (Potential) in the state of Georgia (System).
-
(i)
The two-week lockdown potentiality from week
 th to two weeks after (6 months contains 24 weeks starting at the first day after week-first),
th to two weeks after (6 months contains 24 weeks starting at the first day after week-first), -
(ii)
The wearing mask obligation starting from week
 th until the end of the study (6 months),
th until the end of the study (6 months), -
(iii)
The two potentialities (i) and (ii) simultaneously.
The results are presented assuming that the managers can only carry out the potentialities (changing the colored point(s) in the Description Space) on the first day of the week for the pandemic-affected region. In other words, the state of the system is altered at the following set.

|
The passive trajectory of the COVID-19 in the state of Georgia is shown in blue in Fig. 7. This trajectory is the result of the “potential positioning” presented in Section 5.1 and the reference to examine specified alternatives. The active trajectories in Fig. 7 are related to alternatives (i), (ii), and (iii) of daily KPIs depicted in brown, yellow, and red respectively. It's important to note that these alternatives may have an influence on potential (virus) and system inputs, which isn't reflected in the results (e.g., lockdown and wearing mask potentialities may reduce the fatality rate and fraction hospitalized).
Fig. 7.

Region positioning results for its inputs and their distances from the system objective, (0,0,0) coordinates.
The system positioning related to alternatives of week 2, week 3, week 5, and week 10 after week-first of outset ( to
to  ) is presented in Fig. 7. The following are some related observations.
) is presented in Fig. 7. The following are some related observations.
-
(i)
The active trajectories correspond to the passive trajectory (blue) until the moment of activation,
 ,
,  ,
,  , and
, and  linked to the specified weeks,
linked to the specified weeks, -
(ii)
The deviations of the active trajectories related to the “wearing mask” potentiality from the moment of execution to the end of the path are smooth,
-
(iii)
In the early weeks, the deviations of the active trajectories associated with the “lockdown” potentiality are like a forth and back break (deviation), and as we move away from the early weeks, these deviations become smoother,
-
(iv)
The later the movement of colored points in the Description Space (taking the strategies), the closer the active trajectories are to the passive trajectory.
Fig. 8 shows the final results of the study for the considered potential strategies for the state of Georgia to containment the COVID-19 in this region. Since the less the sum of the distances from the origin, the better the movement in the Description Space, the following results can be deduced from Fig. 8.
-
(i)
Week 5th is the ideal time for movement on the “cr” axis, which is the lockdown strategy (starting lockdown after two months),
-
(ii)
The sooner the “wearing mask obligation” strategy (movement on the “ir” axis) is implemented, the better. Over the weeks, the total distance from the target, (0,0,0) has increased,
-
(iii)
The best time to implement two strategies simultaneously is the 4th week,
-
(iv)
From about the 11th week onwards, the implementation of strategies has very little influence on pandemic control (the sum of the distances is approximately equal to the passive mode).
Fig. 8.
The considered potentialities for the COVID-19 in the State of Georgia and the sum of the distances from system objective for given potentiality in the 3D framework during 6 months (week 1 to week 24).
6. Conclusion and Perspectives
In this paper, a simplified version of the SEIR model for pandemic spread through Ordinary Differential Equation (ODEs) has been introduced to support a wide range of instances of viruses and populations. The considered parameters allow covering a wide range of scenarios by assessing the consequence of an observed pandemic on the KPIs of a given population. The POD vision has been established to examine the influence of mitigation measures on the evaluation of these KPIs to control COVID-19 in the state of Georgia (USA) and a potential future pandemic. Within the system KPIs framework, this prediction may be visually displayed as a performance trajectory. Furthermore, decisions may be represented as “what if” scenarios, and their influence, as well as the deviation of the performance trajectory, can be predicted. The next stage in this research is first, to look at the addition vector of the impacts of several simultaneous actions on the performance trajectory in the performance space, and second, to employ this pandemic model as a data supplier for neural network systems. The primary idea is to perform large-scale combinatory simulation campaigns to collect big datasets concerning the general situation of a pandemic-affected social system. Using this data to train neural network systems will allow us to create a formal system capable of simulating any social system affected by a pandemic and implementing any mitigation actions. Optimization algorithms may be used with these tools to determine the best set of actions to do in each given situation (whatever social system is hit by any virus). Finally, the ultimate goal is to develop a modeling system that can characterize the population affected by a specific virus and suggest a combination of timed measures, which can be viewed as physical forces pushing or pulling the observed system's performance trajectory within the performance framework, to optimize its response to the looming pandemic.
Contributor Information
Nafe Moradkhani, Email: [email protected].
Frederick Benaben, Email: [email protected].
Benoit Montreuil, Email: [email protected].
Matthieu Lauras, Email: [email protected].
Julien Jeany, Email: [email protected].
Louis Faugre, Email: [email protected].
References
- [1].Arnold D., “Pandemic India: Coronavirus and the uses of history,” J. Asian Stud., vol. 79, no. 3, pp. 569–577, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Pitlik S. D., “COVID-19 compared to other pandemic diseases,” Rambam Maimonides Med. J., vol. 11, no. 3, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ullah R., Zaman G., and Islam S., “Prevention of influenza pandemic by multiple control strategies,” J. Appl. Math., vol. 2012, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Anderson R. M., Heesterbeek H., Klinkenberg D., and Hollingsworth T. D., “How will country-based mitigation measures influence the course of the COVID-19 epidemic?,” Lancet, vol. 395, no. 10228, pp. 931–934, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Benaben F. et al. , “Instability is the norm! a physics-based theory to navigate among risks and opportunities,” Enterprise Inf. Syst., pp. vol. 16, pp. 1–28, 2022. [Google Scholar]
- [6].Moradkhani N., Faugère L., Jeany J., Lauras M., Montreuil B., and Benaben F., “A physics-based enterprise modeling approach for risks and opportunities management,” in Proc. IFIP Work. Conf. Pract. Enterprise Model., 2020, pp. 339–348. [Google Scholar]
- [7].Brug J., Aro A. R., and Richardus J. H., “Risk perceptions and behaviour: Towards pandemic control of emerging infectious diseases,” 2009. [DOI] [PMC free article] [PubMed]
- [8].Brug J., Oenema A., and Ferreira I., “Theory, evidence and intervention mapping to improve behavior nutrition and physical activity interventions,” Int. J. Behav. Nutr. Phys. Activity, vol. 2, no. 1, pp. 1–7, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Krumkamp R. et al. , “Evaluation of national pandemic management policies–a hazard analysis of critical control points approach,” Health Policy, vol. 92, no. 1, pp. 21–26, 2009. [DOI] [PubMed] [Google Scholar]
- [10].Ma Z., Dynamical Modeling and Analysis of Epidemics. Singapore: World Science, 2009. [Google Scholar]
- [11].Chinazzi M. et al. , “The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak,” Science, vol. 368, no. 6489, pp. 395–400, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hellewell J. et al. , “Centre for the mathematical modelling of infectious diseases COVID-19 working group. feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts,” Lancet Glob. Health, vol. 8, no. 4, pp. e488–e496, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Nam N. H. et al. , “Early centralized isolation strategy for all confirmed cases of COVID-19 remains a core intervention to disrupt the pandemic spreading significantly,” PLoS One, vol. 16, no. 7, 2021, Art. no. e0254012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Eikenberry S. E. et al. , “To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic,” Infect. Dis. Modelling, vol. 5, pp. 293–308, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Yang Z. et al. , “Modified seir and ai prediction of the epidemics trend of COVID-19 in China under public health interventions,” J. Thoracic Dis., vol. 12, no. 3, 2020, Art. no. 165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].López L. and Rodo X., “A modified SEIR model to predict the COVID-19 outbreak in Spain and Italy: Simulating control scenarios and multi-scale epidemics,” Results Phys., vol. 21, 2021, Art. no. 103746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].de Camino-Beck T., “A modified SEIR model with confinement and lockdown of COVID-19 for Costa Rica,” medRxiv, 2020.
- [18].Struben J., “The coronavirus disease (COVID-19) pandemic: Simulation-based assessment of outbreak responses and postpeak strategies,” Syst. Dyn. Rev., vol. 36, no. 3, pp. 247–293, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Li T., Liu Y., Li M., Qian X., and Dai S. Y., “Mask or no mask for COVID-19: A public health and market study,” PLoS One, vol. 15, no. 8, 2020, Art. no. e0237691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Vyasarayani C. P. and Chatterjee A., “New approximations, and policy implications, from a delayed dynamic model of a fast pandemic,” Physica D: Nonlinear Phenomena, vol. 414, 2020, Art. no. 132701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Ferreira A. and Otley D., “The design and use of performance management systems: An extended framework for analysis,” Manage. Accounting Res., vol. 20, no. 4, pp. 263–282, 2009. [Google Scholar]
- [22].Benaben F., Lauras M., Montreuil B., Faugère L., Juanqiong G., and Mu W., “Physics of organization dynamics: An AI framework for opportunity and risk management,” in Proc. IEEE Int. Conf. Ind. Eng. Syst. Manage., 2019, pp. 1–6. [Google Scholar]
- [23].Olsson R., “In search of opportunity management: Is the risk management process enough?,” Int. J. Project Manage., vol. 25, no. 8, pp. 745–752, 2007. [Google Scholar]
- [24].Hillson D., Exploiting Future Uncertainty: Creating Value From Risk. Evanston, IL, USA: Routledge, 2017. [Google Scholar]
- [25].Fang C. and Marle F., “A simulation-based risk network model for decision support in project risk management,” Decis. Support Syst., vol. 52, no. 3, pp. 635–644, 2012. [Google Scholar]
- [26].Yuthas K., “Tamara bekefi, marc j. epstein and,” 2008.
- [27].Haaser N. B., Real analysis. Courier Corporation, 1991. [Google Scholar]
- [28].Kumpati S. N. et al. , “Identification and control of dynamical systems using neural networks,” IEEE Trans. Neural Netw., vol. 1, no. 1, pp. 4–27, Mar. 1990. [DOI] [PubMed] [Google Scholar]
- [29].Tolles J. and Luong T., “Modeling epidemics with compartmental models,” Jama, vol. 323, no. 24, pp. 2515–2516, 2020. [DOI] [PubMed] [Google Scholar]
- [30].Bjϕrnstad O. N., Shea K., Krzywinski M., and Altman N., “The seirs model for infectious disease dynamics,” Nature Methods, vol. 17, no. 6, pp. 557–559, 2020. [DOI] [PubMed] [Google Scholar]
- [31].Bourgois A., “Safe & collaborative autonomous underwater docking,” Ph.D. dissertation, ENSTA Bretagne-École nationale supérieure de techniques avancées Bretagne, 2021. [Google Scholar]
- [32].Byrne A. W. et al. , “Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases,” BMJ Open, vol. 10, no. 8, 2020, Art. no. e039856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Piret J. and Boivin G., “Pandemics throughout history,” Front. Microbiol., vol. 11, 2021, Art. no. 3594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Abiad A., Arao R. M., and Dagli S., “The economic impact of the COVID-19 outbreak on developing Asia,” 2020.
- [35].Georgia COVID-19 data hub. Accessed: May 11, 2021. [Online]. Available: https://covid-hub.gio.georgia.gov/
- [36].COVID-19 Georgia metrics | tableau public. Accessed: May 11, 2021. [Online]. Available: https://public.tableau.com/app/profile/dima.nazzal/viz/COVID-19GeorgiaMetics/GeorgiaCOVID-19Dashboard







