Abstract
Accurately dating when the first bilaterally symmetrical animals arose is crucial to our understanding of early animal evolution. The earliest unequivocally bilaterian fossils are ≈555 million years old. In contrast, molecular-clock analyses calibrated by using the fossil record of vertebrates estimate that vertebrates split from dipterans (Drosophila) ≈900 million years ago (Ma). Nonetheless, comparative genomic analyses suggest that a significant rate difference exists between vertebrates and dipterans, because the percentage difference between the genomes of mosquito and fly is greater than between fish and mouse, even though the vertebrate divergence is almost twice that of the dipteran. Here we show that the dipteran rate of molecular evolution is similar to other invertebrate taxa (echinoderms and bivalve molluscs) but not to vertebrates, which significantly decreased their rate of molecular evolution with respect to invertebrates. Using a data set consisting of the concatenation of seven different amino acid sequences from 23 ingroup taxa (giving a total of 11 different invertebrate calibration points scattered throughout the bilaterian tree and across the Phanerozoic), we estimate that the last common ancestor of bilaterians arose somewhere between 573 and 656 Ma, depending on the value assigned to the parameter scaling molecular substitution rate heterogeneity. These results are in accord with the known fossil record and support the view that the Cambrian explosion reflects, in part, the diversification of bilaterian phyla.
Although the Cambrian explosion is of singular importance to our understanding of the history of life, it continues to defy explanation (1). This defiance stems, in part, from our inability to distinguish between two competing hypotheses: whether the Cambrian explosion reflects the rapid appearance of fossils with animals having a deep but cryptic precambrian history, or whether it reflects the true sudden appearance and diversification of animals in the Cambrian (2). Because each hypothesis makes a specific prediction of when animals arose in time, one way to distinguish between these two hypotheses is to date animal diversifications by using a molecular clock (2). A number of previous clock studies (reviewed in refs. 3 and 4) have suggested that the last common ancestor of bilaterians (LCB) lived well over one billion years ago (5, 6), whereas others suggest that LCB arose ≈900 million years ago (Ma) (e.g., refs. 7–10), and still others are more consistent with an origination closer to the Cambrian (11–13). These deep estimates for the origin of LCB raise the question of how hundreds of millions of years of bilaterian evolution can escape detection, given that LCB and its near relatives should have had the capability of leaving both body and trace fossils (14–16).
Because molecular clocks have several inherent problems, including how the clock is calibrated, how molecular substitution rates are estimated, and how heterogeneity in these rates is detected and corrected (3, 4), as well as an inherent statistical bias for overestimating dates (4, 17), a much more recent date for LCB may not yet be refuted. Of crucial importance for clock accuracy is the calibration of the clock itself, which requires not only accurate paleontological estimates (18) but also rate homogeneity between the calibrated and uncalibrated taxa. When estimating the origination date for LCB, virtually all analyses use the vertebrate fossil record to calibrate the clock and ask when vertebrates diverged from dipterans. However, genome-wide sequence comparisons have shown that the average sequence identity of nuclear protein-coding genes between dipterans is lower than that of bony fish, even though the dipteran divergence time, estimated at 235 Ma (19), is only about half as long as the divergence of bony fish at 450 Ma (20). It is usually assumed that dipterans increased their rate of molecular evolution with respect to vertebrates (21), but it is possible that the vertebrate sequences decreased their rate of molecular evolution. If so, then any estimate of an invertebrate divergence (including LCB) derived from a vertebrate calibration will be artifactually twice too deep, a value suspiciously close to the observed molecular estimates of LCB vs. paleontological observations (4).
Here, we test this hypothesis by first showing that a pronounced rate difference exists between vertebrates and dipterans. Next, we show that using concatenated amino acid sequences of seven nuclear-encoded genes, the dipteran rate of sequence evolution is similar to two other invertebrate groups, echinoderms and bivalve molluscs, but all three differ significantly from the vertebrate rate of sequence evolution. Finally, using 11 invertebrate calibration points from all three major clades of bilaterians and across the Phanerozoic, we estimate that LCB arose ≈570 Ma, an estimate in remarkable accord with the fossil record of metazoans.
Materials and Methods
Cloning. Total RNA from 17 taxa was prepared from live animals by using a one-step TRIzol method (GIBCO/BRL) or RNAzol (Leedo Medical Laboratories, Houston). Taxa were purchased from Marine Biological Laboratory (Woods Hole, MA; Nucula proxima, Stylochus sp., Obelia sp., and Metridium senile), Gulf Specimen Aquarium and Marine Biological Supply (Panacea, FL; Encope michenlini, Eucidaris tribuloides, and Modiolus americanus), or Charles Hollahan (Santa Barbara, CA, Dendraster excentricus, Strongylocentrotus purpuratus, Mytilus edulis, and Mytilus califorianus). Saccoglossus kowalevskii clones, Monosiga brevicollis cDNA, Antedon mediterrania cDNA, Asterina miniata cDNA, and Priapulis caudatis animals were kind gifts of John Gerhart (Harvard University, Cambridge, MA), Nicole King and Sean Carroll (University of Wisconsin, Madison), Ina Arnone (Stazione Zoologica Anton Dohrn, Napoli, Italy), Veronica Hinman and Eric Davidson (California Institute of Technology, Pasadena, CA), and Graham Budd (University of Uppsala, Uppsala, Sweden), respectively. Ptychodera flava, Chaetopterus sp., Enallagma aspersum, Lestes congener, and Clypeatula cooperensis were already in the collections of K.J.P. and M.A.M. cDNA synthesis was performed with RETROscript (Ambion, Austin, TX) following the manufacturer's instructions by using 1–2 μg of total RNA as indicated above.
Partial fragments of seven nuclear-encoded genes were PCR amplified, cloned, and sequenced by using standard techniques: aldolase (200 aa), triosephosphate isomerase (217 aa), phosphofructokinase (175 aa), methionine adenosyltransferase (348 aa), elongation factor 1-α (418 aa), ATP synthase β chain (430 aa), and catalase (264 aa) (we were unable to amplify all seven from the choanoflagellate, M. califorianus, and S. kowalevskii). These genes were chosen because they had previously been shown to support the monophyly of Ecdysozoa or did not significantly support an alternative arrangement (9, 22) and/or had shown potential clock-like behavior (23). We stress that no molecule or region of a molecule was excluded from the analysis, and the successful amplification and cloning of only these seven (of 12 tested) proved tractable from this diversity of taxa using standard techniques. Gene-specific primers (sequences available on request) and 1 or 10 μl of cDNA plus the TaqPlus Precision PCR system (Stratagene) were mixed and used in touchdown style PCR. PCR fragments of the predicted sizes were excised, purified (Qiagen, Valencia, CA), ligated at 16°C overnight into the pGEM-T-Easy vector according to the manufacturer's instructions (Promega), and electroporated into DH10B cells. Clones containing the correct insert size were sequenced on an ABI373 model sequencer. Sequences were edited, translated, and aligned by using macvector, Ver. 7.0 (Genetics Computer Group).
Phylogenetic Analyses. Dipteran, vertebrate, and plant [Arabidopsis (mustard weed) and Oryza (rice)] sequences were searched by using blast, all significant hits were downloaded, and the inferred amino acid sequences of each gene were analyzed. The topology of each individual gene as deduced by neighbor-joining suggests that each is a case of “many-to-many orthologues” (21). The 50-gene data set was compiled from previous studies (9, 10); the sea urchin genes for this data set were acquired from the Sea Urchin Genome Project web site (http://sugp.caltech.edu). Distance methods used mega, Ver. 2.1, with pairwise deletion (24), and both the Poisson correction and γ distance models [the parameter scaling molecular substitution rate heterogeneity, α, ranged from ∞ (= Poisson distributed) to 0.28]; maximum likelihood (ML) used quartet puzzle, Ver. 5.0 (25) or paml (26). ML analyses used the Jones et al. (27) matrix of amino acid substitution, allowing the analysis to estimate the parameter for substitution rate heterogeneity; all amino acid substitution models gave effectively the same tree (analyses not shown). Relative rates tests used the output of quartet puzzle. Bootstrap values were derived by using 1,000 replications, and 1,000 puzzling steps were performed. Analyses of covariance were performed by using sas, Ver. 6.1 (SAS Institute, Cary, NC).
Divergence Estimates. Date estimates for uncalibrated nodes in phylogenies were derived by using r8s, Ver. 1.5 (M. J. Sanderson, http://ginger.ucdavis.edu/r8s). This software uses multiple calibration points to derive estimates of uncalibrated nodes by using various algorithms. All algorithms for estimating divergence times gave very similar results, and so we report only those derived by the Langley–Fitch likelihood method. Confidence intervals for divergence dates are based on the curvature of the likelihood surface (6) as implemented in r8s.
Results
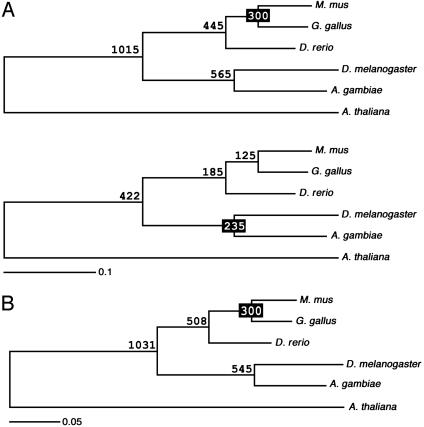
Rate Heterogeneity Between Vertebrates and Insects. To first ask whether a significant molecular rate difference exists between vertebrates and dipterans, as suggested by comparative genomics (21), we assembled a data set consisting of the concatenation of 50 different nuclear-encoded protein sequences (7,613 aa) taken from the analyses of Wang et al. (9) and Nei et al. (10). The ML analysis of this data set is shown in Fig. 1. As expected, the correct topology is realized and strongly supported. We applied standard relative rates tests to examine whether rate differences exist between the vertebrate and dipteran lineages, using Arabidopsis as the outgroup. All pairwise tests for differences between the two lineages were significant (all P < 0.005), indicating strong rate heterogeneity between the lineages leading to vertebrates and dipterans. However, all pairwise relative rates tests comparing taxa within these lineages (e.g., comparing fish and mouse with Drosophila as the outgroup) were not significant (all P > 0.05), suggesting no rate heterogeneity within the two lineages.
Fig. 1.
Rate heterogeneity between vertebrates and dipterans, as assessed by untenable estimates for the divergences of the uncalibrated taxa. (A) ML analysis of the 50-gene data set for vertebrates and dipterans using Arabidopsis as the outgroup. (Upper) Values derived for the origin of bony fish, Diptera, and Bilateria if the tree is calibrated using the amniote divergence at 300 Ma. (Lower) Values derived for the origin of bony fish, amniotes, and bilaterians if the tree is calibrated by using the dipteran divergence at 235 Ma. (B) ML analysis of the seven-gene data set from the same taxa. If the tree is calibrated by using the amniote divergence at 300 Ma, qualitatively similar values as found in A are derived for the origin of bony fish, dipterans, and bilaterians.
If the bird/mammal divergence (300 Ma) is used to calibrate the tree, we find that Osteichthyes arose 445 Ma, an estimate congruent with the paleontological record (20) (Fig. 1 A Upper). In addition, we find that LCB arose 1,015 Ma, which is close to previous estimates (e.g., refs. 9 and 10). Nonetheless, we find that dipterans, which are near the apex of the insect tree (19, 28), arose 565 Ma, almost 200 million years (Myr) before the first appearance of insects in the fossil record (19). If instead the dipteran divergence is used to calibrate the tree, then the vertebrate divergences are far too shallow, with amniotes originating in the Early Cretaceous (125 Ma) and Osteichthyes originating during the Early Jurassic (185 Ma) (Fig. 1 A Lower).
Vertebrates Significantly Slowed Their Rate of Molecular Evolution. Because the presence of dipterans in the precambrian and the absence of bony fish in the Paleozoic are both untenable, these taxa must differ substantially in the rate of molecular evolution of the included sequences, as suggested by the relative rates tests. Although it is possible that insects increased their rate of molecular evolution with respect to vertebrates, possibly because of their faster generation time (20), it seems as likely that vertebrates slowed their rate of evolution with respect to dipterans.
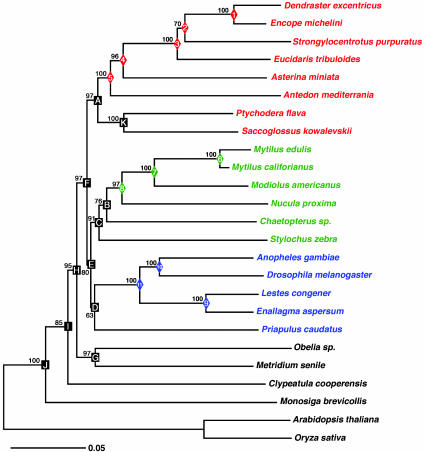
To distinguish between these two alternatives, we analyzed seven of the 50 sequences discussed above from 14 invertebrate taxa from all three major bilaterian groups chosen specifically to maximize the number of calibration points across the Phanerozoic (Lowest Ordovician through Miocene) within a known phylogeny: Deuterostomia (five echinoderm calibrations), Ecdysozoa (two additional insect calibrations), and Spiralia (three bivalve calibrations); these calibration points are numbered 1–11 on Figs. 2 and 3 and are listed in Table 1. The seven different sequences were concatenated (2,052 aa) and analyzed with ML and minimum evolution; both analyses were accurate and, for most nodes, precise (Figs. 2 and 3). Furthermore, analyses of this data set gave qualitatively similar results when compared to the 50-gene data set (Figs. 1 and 2).
Fig. 2.
ML tree of the seven concatenated protein sequences from 18 in-group taxa by using Arabidopsis as the outgroup. Bootstrap values for ML (Upper) as well as distance (Lower) are given to the left of the respective nodes. Nodes 1–11 are calibration points, whose distances are plotted against the divergence times derived from the fossil record (Table 1) in the regression analysis. The two vertebrate divergences (300 Ma for Amniota and 450 Ma for Osteichthyes) give the vertebrate line whose midpoint value is significantly displaced from the invertebrate line. The open diamonds indicate the position of the node when analyzed with the 50-gene data set; note that it is qualitatively similar to the seven-gene data set (filled diamonds). Echinoderms are shown in red, bivalves in green, and insects in blue; vertebrates are in orange.
Fig. 3.
Distance (Poisson) phylogram of the seven concatenated protein sequences from 23 in-group taxa by using Arabidopsis and Oryza as outgroups. Bootstrap values are given to the left of the respective nodes. Nodes 1–11 are calibration points (see Fig. 2); the ages of nodes A–K are estimated by using r8s and are given in Table 1 and shown in Fig. 4. Deuterostomes are shown in red, spiralians in green, and ecdysozoans in blue.
Table 1. Calibrations and estimates in millions of years.
| Estimated ages (95% confidence intervals)§
|
|||||
|---|---|---|---|---|---|
| Node* | Calibrations age†, Myr | Refs.‡ | Node* | α = ∞ | α = 0.28 |
| 1 | Eocene (50) | 50, 51 | A | 526 (513, 558) | 567 (551, 586) |
| 2 | Early Jurassic (190) | 51, 52 | B | 519 | 548 (534, 564) |
| 3 | Late Permian (260) | 51, 53 | C | 538 (523, 554) | 580 (563, 598) |
| 4 | Early Ordovician (475) | 28, 54 | D | 542 (521, 565) | 599 (578, 621) |
| 5 | Early Ordovician (485) | 54, 55 | E | 560 (544, 593) | 623 (604, 643) |
| 6 | Miocene (20) | 56, 57 | F | 573 (556, 592) | 656 (636, 678) |
| 7 | Late Carboniferous (325) | 56, 57 | G | 548 (519, 579) | 595 (561, 626) |
| 8 | Early Ordovician (485) | 57, 58 | H | 615 (592, 643) | 724 (697, 756) |
| 9 | Early Cretaceous (120) | 19 | I | 653 (625, 684) | 832 (796, 880) |
| 10 | Middle Triassic (235) | 19 | J | 744 (705, 783) | 987 (940, 1,033) |
| 11 | Late Carboniferous (325) | 19 | K | 404 (370, 436) | 412 (381, 442) |
Numbered and lettered nodes from Fig. 3
Calibration points are derived from the first occurrence of a member of the crown group. For example, although Permian dipterans are known (19), it is unclear whether they are crown-group dipterans. The first unequivocal crown-group dipterans are Middle Triassic (19), and hence this was used as the calibration point. The 1999 Geological Time Scale (Geological Society of America, www.geosociety.org/science/timescale/timescl.htm.) was used for dates
References are for both the age and the phylogenetic position of the node
Nodes where R8S could not converge on a solution for the 95% confidence intervals are left blank
The regression analysis of calibration dates to distance derived from the ML analysis is also shown in Fig. 2. The dipteran divergence (node 10) is not an outlier from the regression line for the invertebrate calibration points (nodes 1–11); analysis of covariance among the lines generated from echinoderms (red), insects (blue), or spiralians (green) shows that neither the slope (F3,5 = 1.35, P > 0.35) nor the elevation (F2,7 = 3.10, P > 0.10) is significantly different among these taxa. However, analysis of covariance for the regressions of vertebrate vs. invertebrate calibration points shows that the vertebrate regression is displaced significantly above the invertebrate regression (F1,8 = 35.81, P < 0.0001) (Fig. 2). This result demonstrates that rather than evolutionary rates increasing in insects (21), molecular evolutionary rates significantly decreased in vertebrates before the origin of crown-group Osteichthyes.
Molecular Clock Estimates of Metazoan Divergence Times. To estimate the origination date of Bilateria, as well as several other invertebrate divergences, we used the r8s software package to analyze the concatenated seven-gene data set for 23 in-group taxa (Fig. 3). Using the option in r8s that the calibration points are fixed, we estimate that LCB (node F, Fig. 3) evolved between 573 and 656 Ma, depending on the specified value of the rate heterogeneity parameter (Table 1). However, because the calibration points derived from the fossil record are paleontological minima (i.e., the first occurrence of a recognizable member of a total group), the estimates derived from these points must be minima as well. Estimating maxima for divergences is difficult (3). Nonetheless, if we specify in r8s that the calibration points are variable, then estimates scale linearly with the error; e.g., if a 10% error is associated with the calibration points, then all estimated dates are increased 7–12%. To ask whether the size of the data set changes the estimate for LCB, we added the sea urchin S. purpuratus to the 50-gene data set and reanalyzed the data without the vertebrates. Calibrating the resulting ML tree with the dipteran divergence gives an estimate of 541 Ma for the last common ancestor of S. purpuratus and Diptera, which is equivalent to LCB.
Finally, to address which γ parameter estimate (Table 1) might be more accurate, we had r8s estimate the origin of crown-group echinoderms (node 5) using both α = ∞ and α = 0.28. The predicted value based on the fossil record of echinoderms (Fig. 4) is between 485 (the minimum value based on the first occurrence of crinoids, Table 1) and 525 Ma (the maximum value that corresponds to the first occurrence of echinoderm skeletal material in the fossil record; ref. 29). Using α = ∞, r8s estimated the age of crown-group echinoderms at 508 ± 12 Ma, whereas with α = 0.28, r8s estimated the age at 527 ± 12 Ma. Thus, the simpler model of molecular evolution gives an estimate more consistent with the fossil record.
Fig. 4.
Metazoan divergence estimates with metazoan diversity and phylogeny placed into the geological context of the Neoproterozoic/Cambrian transition. Tree nodes are positioned according to age estimates derived from the Poisson analysis (Table 1). Thick lines are the known fossil record, and thin lines are the lineage extensions as deduced from the molecular clock analysis. N-D, Nemakit–Daldynian; T/A, Tommotian/Atdabanian; B/T, Botominan/Toyonian; M, Middle; L, Late (adapted from ref. 1).
Discussion
Rate Heterogeneity Between Vertebrates and Invertebrates. Our data suggest that, inconsistent with most molecular clock estimates but consistent with paleontological predictions (e.g., refs. 13 and 14), bilaterians do not have a significant precambrian evolutionary history. The deep precambrian estimates for LCB derived from analyses that use nuclear protein-encoding genes calibrated to the vertebrate fossil record (e.g., refs. 9 and 10) are clearly artifacts associated with the significant rate reduction in the molecular evolution of the vertebrate genome.
Martin and Palumbi (30) argued that much of the rate heterogeneity that exists between species can be accounted for by differences in metabolic rates. Although no single factor can fully account for rate variation (30), we note that a difference in metabolic rates is unlikely to be the primary explanation in this case because the teleost fish Danio rerio is evolving at a similar rate to that of the two endothermic amniotes, and the molecular clock estimate of the origin of Osteichthyes is concordant with the vertebrate fossil record (Fig. 1 A). Given the metabolic rate difference between amniotes and fishes (31), we would expect a greater disparity between the clock estimate and the vertebrate fossil record if this were a significant driving factor. One possible explanation for the rate heterogeneity seen between vertebrates and invertebrates is the duplication of the vertebrate genome (12), which occurred sometime between the last common ancestor of cephalochordates and vertebrates and the last common ancestor of Osteichthyes (32). Despite the fact that gene duplication events are thought to increase rather than decrease the rate of molecular evolution (33), a genome duplication event would (at least initially) increase the number of interactors for each protein, potentially slowing the rate of molecular evolution across the entire genome (34).
Phylogenetic Considerations. Our protein tree (Fig. 3) gives the correct topology, where known (Table 1), and finds support for clades such as Ambulacraria (Echinodermata + Hemichordata), Spiralia, and Ecdysozoa, as well as Protostomia. This is now the third independent molecular data set supporting the monophyly of these clades, because all four are found with 18S rDNA analyses and Hox gene duplications, in addition to many newly elucidated characters (reviewed in ref. 35). We are not able to recover a monophyletic Deuterostomia when vertebrates are included into the analysis (Fig. 2), possibly because of the relatively few number of genes analyzed (36) and the pronounced rate heterogeneity detected with the vertebrate sequences (Fig. 2). Nonetheless, an analysis of the 50-gene data set, which includes both the sea urchin and the three vertebrates, results in a monophyletic but weakly supported Deuterostomia (not shown).
Tempo and Mode of Early Animal Evolution. Although the use of molecular clocks to infer divergence times is fraught with difficulties (3, 4), this analysis fulfills the suggested requirements of Shaul and Graur (37) for a molecular clock analysis: (i) the use of multiple primary calibration points; (ii) the accommodation of rate variation; and (iii) the calculation of confidence intervals associated with the estimates. Interestingly, both our analysis and the analyses of Aris-Brosou and Yang (11, 12) conclude that LCB evolved ≈570 Ma and split from cnidarians somewhere between 600 and 630 Ma (Fig. 4). Moreover, both analyses agree that the last common ancestor of protostomes evolved ≈550 Ma, and both analyses agree that phylum-level splits within Spiralia and Deuterostomia occurred 520–530 Ma. The congruence between these two clock studies and the fossil record is striking, although possibly not surprising given that both studies use multiple calibration points scattered across both phylogeny and time and account for rate heterogeneity either by removing vertebrates from the analysis, as was done here, or by using a Bayesian approach to account for rate change across lineages (11, 12). Because of this congruence, the Cambrian explosion must reflect, at least in part, the diversification of bilaterian phyla.
We extrapolate the origin of total-group Bilateria to be ≈615 Ma, almost 45 Myr before the appearance and rapid diversification of the crown group and ≈60 Myr before their first unequivocal appearance in the fossil record. This cryptic precambrian history suggests that these stem-group bilaterians must have been “micrometazoans,” because, although benthic (38, 39), they were seemingly incapable of leaving trace fossils (see also ref. 40). The bilaterian trace fossil record would commence only after the invention of pattern formation mechanisms that potentiated the evolution of larger body size in multiple animal clades near the end of Neoproterozoic (41, 42). Whether the origin of bilaterians or any other metazoan group can be triggered by environmental perturbations such as “snowball Earth” (43, 44) remains highly speculative at the moment, given the uncertainty about the exact number and ages of Neoproterozoic glaciations (45). Nonetheless, if the “Marinoan” glaciation interval is younger than 590 Ma (46), then an increase in bilaterian body size might have been facilitated by the greater productivity of the marine ecosystem after the glacial melt (47, 48). This increase in both body size and planktonic productivity would then allow for the evolution of broadcast spawning and external fertilization and, by ≈525 Ma, planktotrophic development. The absence of precambrian planktonic metazoans is consistent with our Early Cambrian estimate for the origin of the last common ancestor of living cnidarians, a population of animals whose life cycle lacked a medusa stage and thus was entirely benthic (49). The development of this new planktonic food web (47), coupled with the evolution of a dispersal stage and the reappearance of exposed continental shelf, may have provided the environmental stimuli necessary for the rapid evolution of disparate bilaterian body plans and ultimately the Cambrian explosion itself.
Acknowledgments
We thank S. Bengtson, D. Campbell, K. Cottingham, N. Christie-Blick, E. Davidson, M. Dietrich, D. Erwin, D. Evans, D. Jablonski, M. LaBarbera, A. Rivera, B. Runnegar, A. Smith, and J. Sprinkle for comments and discussion. We also thank the individuals who provided or procured material for us and C. Hanselman and V. Moy for technical assistance. K.J.P. is supported by the National Science Foundation, National Aeronautical and Space Administration–Ames, and Dartmouth College. M.A.M. is supported by the National Science Foundation.
Abbreviations: LCB, last common ancestor of bilaterians; ML, maximum likelihood; Ma, million years ago; Myr, million years.
Data deposition: The sequences reported in this paper have been deposited in the GenBank database (accession nos. AY580167-AY580307).
References
- 1.Knoll, A. H. & Carroll, S. B. (1999) Science 284, 2129-2137. [DOI] [PubMed] [Google Scholar]
- 2.Runnegar, B. (1982) J. Geol. Soc. Aust. 29, 395-411. [Google Scholar]
- 3.Smith, A. B. & Peterson, K. J. (2002) Annu. Rev. Earth Planet. Sci. 30, 65-88. [Google Scholar]
- 4.Benton, M. J. & Ayala, F. J. (2003) Science 300, 1698-1700. [DOI] [PubMed] [Google Scholar]
- 5.Wray, G. A., Levinton, J. S. & Shapiro, L. H. (1996) Science 274, 568-573. [Google Scholar]
- 6.Cutler, D. J. (2000) Mol. Biol. Evol. 17, 1647-1660. [DOI] [PubMed] [Google Scholar]
- 7.Runnegar, B. (1982) Lethaia 15, 199-205. [Google Scholar]
- 8.Gu, X. (1998) J. Mol. Evol. 47, 369-371. [DOI] [PubMed] [Google Scholar]
- 9.Wang, D. Y.-C., Kumar, S. & Hedges, S. B. (1999) Proc. R. Soc. London Ser. B 266, 163-171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nei, M., Xu, P. & Glazko, G. (2001) Proc. Natl. Acad. Sci. USA 98, 2497-2502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aris-Brosou, S. & Yang, Z. (2002) Syst. Biol. 51, 703-714. [DOI] [PubMed] [Google Scholar]
- 12.Aris-Brosou, S. & Yang, Z. (2003) Mol. Biol. Evol. 20, 1947-1954. [DOI] [PubMed] [Google Scholar]
- 13.Ayala, F. J., Rzhetsky, A. & Ayala, F. J. (1998) Proc. Natl. Acad. Sci. USA 95, 606-611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Conway Morris, S. (1998) Am. Zool. 38, 867-877. [Google Scholar]
- 15.Budd, G. E. & Jensen, S. (2000) Biol. Rev. Camb. Philos. Soc. 75, 253-295. [DOI] [PubMed] [Google Scholar]
- 16.Erwin, D. H. (1999) Am. Zool. 39, 617-629. [Google Scholar]
- 17.Rodriguez-Trelles, F., Tarrio, R. & Ayala, F. J. (2002) Proc. Natl. Acad. Sci. USA 99, 8112-8115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee, M. S. Y. (1999) J. Mol. Evol. 49, 385-391. [DOI] [PubMed] [Google Scholar]
- 19.Rasnitsyn, A. P. & Quicke, D. L. J. (eds.). (2002) History of Insects (Kluwer, Dordrecht, The Netherlands).
- 20.Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J. M., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A., et al. (2002) Science 297, 1301-1310. [DOI] [PubMed] [Google Scholar]
- 21.Zdobnov, E. M., von Mering, C., Letunic, I., Torrents, D., Suyama, M., Copley, R. R., Christophides, G. K., Thomasova, D., Holt, R. A., Subramanian, G. M., et al. (2002) Science 298, 149-159. [DOI] [PubMed] [Google Scholar]
- 22.Mushegian, A. R., Garey, J. R., Martin, J. & Liu, L. X. (1998) Genome Res. 8, 590-598. [DOI] [PubMed] [Google Scholar]
- 23.Nikoh, N., Iwabe, N., Kuma, K., Ohno, M., Sugiyama, T., Watanabe, Y., Yasui, K., Shi-cui, Z., Hori, K., et al. (1997) J. Mol. Evol. 45, 97-106. [DOI] [PubMed] [Google Scholar]
- 24.Kumar, S., Tamura, K., Jakobsen, I. B. & Nei, M. (2001) mega2: Molecular Evolutionary Genetics Analysis (Arizona State University, Tempe), Ver. 2.1. [DOI] [PubMed]
- 25.Strimmer, K. & von Haeseler, A. (1996) Mol. Biol. Evol. 13, 964-969. [Google Scholar]
- 26.Yang, Z. (1997) Comput. Appl. Biosci. 13, 555-556. [DOI] [PubMed] [Google Scholar]
- 27.Jones, D. T., Taylor, R. W. & Thornton, J. W. (1992) Comput. Appl. Biosci. 8, 275-282. [DOI] [PubMed] [Google Scholar]
- 28.Wheeler, W. C., Whiting, M., Wheeler, Q. D. & Carpenter, J. M. (2001) Cladistics 17, 113-169. [DOI] [PubMed] [Google Scholar]
- 29.Smith, A. B. (1988) in Echinoderm Phylogeny and Evolutionary Biology, eds. Paul, C. R. C. & Smith, A. B. (Clarendon, Oxford), pp. 85-97.
- 30.Martin, A. P. & Palumbi, S. R. (1993) Proc. Natl. Acad. Sci. USA 90, 4087-4091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gillooly, J. F., Brown, J. H., West, G. B., Savage, V. M. & Charnov, E. L. (2001) Science 293, 2248-2251. [DOI] [PubMed] [Google Scholar]
- 32.Holland, P. W. H., Garcia-Fernàndez, J., Williams, N. A. & Sidow, A. (1994) in The Evolution of Developmental Regulatory Mechanisms, eds. Akam, M., Holland, P., Ingham, P. & Wray, G. (Company of Biologists, Cambridge, U.K.), Vol. 1994 Supplement, pp. 125-133. [Google Scholar]
- 33.Pollard, S. L. & Holland, P. W. (2000) Curr. Biol. 10, 1059-1062. [DOI] [PubMed] [Google Scholar]
- 34.Fraser, H. B., Hirsh, A. E., Steinmetz, L. M., Scharfe, C. & Feldman, M. W. (2002) Science 296, 750-752. [DOI] [PubMed] [Google Scholar]
- 35.Eernisse, D. J. & Peterson, K. J. (2004) in Assembling the Tree of Life, eds. Cracraft, J. & Donoghue, M. J. (Oxford Univ. Press, New York).
- 36.Rokas, A., Williams, B. L., King, N. & Carroll, S. B. (2003) Nature 425, 798-804. [DOI] [PubMed] [Google Scholar]
- 37.Shaul, S. & Graur, D. (2002) Gene 300, 59-61. [DOI] [PubMed] [Google Scholar]
- 38.Rigby, S. & Milson, C. (1996) Geology 24, 52-54. [Google Scholar]
- 39.Valentine, J. W., Jablonski, D. & Erwin, D. H. (1999) Development (Cambridge, U.K.) 126, 851-859. [DOI] [PubMed] [Google Scholar]
- 40.Valentine, J. W. (2002) Annu. Rev. Ecol. Syst. 30, 285-306. [Google Scholar]
- 41.Davidson, E. H., Peterson, K. J. & Cameron, R. A. (1995) Science 270, 1319-1325. [DOI] [PubMed] [Google Scholar]
- 42.Martin, M. W., Grazhdankin, D. V., Bowring, S. A., Evans, D. A. D., Fedonkin, M. A. & Kirschvink, J. L. (2000) Science 288, 841-845. [DOI] [PubMed] [Google Scholar]
- 43.Hoffman, P. F., Kaufman, A. J., Halverson, G. P. & Schrag, D. P. (1998) Science 281, 1342-1346. [DOI] [PubMed] [Google Scholar]
- 44.Hoffman, P. F. & Schrag, D. P. (2002) Terra Nova 14, 129-155. [Google Scholar]
- 45.Evans, D. A. D. (2000) Am. J. Sci. 300, 347-433. [Google Scholar]
- 46.Schaefer, B. F. & Burgess, J. M. (2003) J. Geol. Soc. London 160, 825-828. [Google Scholar]
- 47.Butterfield, N. J. (1997) Paleobiology 23, 247-262. [Google Scholar]
- 48.Knoll, A. H. (1994) Proc. Natl. Acad. Sci. USA 91, 6743-6750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Collins, A. G. (2002) J. Evol. Biol. 15, 418-432. [Google Scholar]
- 50.Mooi, R. (1990) Paleobiology 16, 25-48. [Google Scholar]
- 51.Littlewood, D. T. J. & Smith, A. B. (1995) Phil. Trans. R. Soc. London Ser. B 347, 213-234. [DOI] [PubMed] [Google Scholar]
- 52.Smith, A. B. & Hollingworth, N. T. J. (1990) Proc. Yorkshire Geol. Soc. 48, 47-60. [Google Scholar]
- 53.Smith, A. B. & Anzalone, L. (2000) Palaeontology 43, 303-324. [Google Scholar]
- 54.Littlewood, D. T. J., Smith, A. B., Clough, K. A. & Emson, R. H. (1997) Biol. J. Linn. Soc. 61, 409-438. [Google Scholar]
- 55.Guensburg, T. E. & Sprinkle, J. (2001) Geology 29, 131-134. [Google Scholar]
- 56.Carter, J. G. & Seed, R. (1998) in Bivalves: An Eon of Evolution, eds. Johnston, P. A. & Haggart, J. W. (Univ. of Calgary Press, Calgary, AL, Canada), pp. 87-117.
- 57.Cope, J. C. W. (2000) in The Evolutionary Biology of the Bivalvia, eds. Harper, E. M., Taylor, J. D. & Crame, J. A. (Geological Society, London), Vol. 177, pp. 81-95. [Google Scholar]
- 58.Cope, J. C. W. (1997) Palaeontology 40, 713-746. [Google Scholar]