Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CO2 incorporation in hydroxide and hydroperoxide containing water clusters—a unifying mechanism for hydrolysis and protolysis†
Mauritz J.
Ryding
* and
Einar
Uggerud
*
Mass Spectrometry Laboratory and Centre for Theoretical and Computational Chemistry, Department of Chemistry, University of Oslo, P.O. Box 1033 Blindern, N-0315 Oslo, Norway. E-mail: [email protected]; [email protected]
First published on 24th March 2014
Abstract
The reactions of CO2 with anionic water clusters containing hydroxide, OH−(H2O)n, and hydroperoxide, HO2−(H2O)n, have been studied in the isolated state using a mass spectrometric technique. The OH−(H2O)n clusters were found to react faster for n = 2,3, while for n >3 the HO2−(H2O)n clusters are more reactive. Insights from quantum chemical calculations revealed a common mechanism in which the decisive bicarbonate-forming step starts from a pre-reaction complex where OH− and CO2 are separated by one water molecule. Proton transfer from the water molecule to OH− then effectively moves the hydroxide ion motif next to the CO2 molecule. A new covalent bond is formed between CO2 and the emerging OH− in concert with the proton transfer. For larger clusters, successive proton transfers from H2O molecules to neighbouring OH− are required to effectively bring about the formation of the pre-reaction complex, upon which bicarbonate formation is accomplished according to the concerted mechanism. In this manner, a general mechanism is suggested, also applicable to bulk water and thereby to CO2 uptake in oceans. Furthermore, this mechanism avoids the intermediate H2CO3 by combining the CO2 hydrolysis step and the protolysis step into one. The general mechanistic picture is consistent with low enthalpy barriers and that the limiting factors are largely of entropic nature.
Introduction
The pH and temperature dependent distribution of carbon dioxide between the gaseous and aqueous states is critical for maintaining vital functions such as cell respiration and the climate-regulating balance between the amount of CO2 in the atmosphere and the amount of CO2 dissolved in the oceans. At equilibrium, the sequence of elementary steps that are usually written down to account for the relevant chemical transformations is the following:| CO2(g) ⇌ CO2(aq) | (1) |
| CO2(aq) + H2O ⇌ H2CO3(aq) | (2) |
| H2CO3(aq) + H2O ⇌ HOCO2−(aq) + H3O+(aq) | (3) |
| HOCO2−(aq) + H2O ⇌ CO32− + H3O+(aq). | (4) |
Among these species, carbonic acid, H2CO3(aq), remains the more elusive, inferred to have a concentration of a few per mil relative to CO2(aq). It has been difficult to characterize and quantify this species, and the most recent estimates based on state-of-the-art time-resolved spectroscopy and simulations could indicate that it has a lifetime of one nanosecond in water.1,2 Despite these facts, it has been difficult to substantiate its role during CO2 hydrolysis and protolysis, as implied in the equations above. At least mathematically, it is possible to eliminate H2CO3 completely from these considerations by simply adding eqn (2) and (3). Multiplication of the expressions for the corresponding equilibrium constants, (see ESI,† additional information) and rearranging leads to the equation,
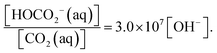 | (5) |
In other words, in neutral water at pH = 7, bicarbonate is the dominating species compared to CO2(aq). At pH = 8.5—a typical value for surface oceanic water—the situation is even more slanted towards bicarbonate. The higher concentration of OH− and the fact that OH− is more nucleophilic than H2O, therefore suggest that a direct route to bicarbonate formation may exist, at least under basic conditions:
| CO2(aq) + OH−(aq) ⇌ HOCO2−(aq). | (6) |
As a matter of fact, measurements have indicated that this reaction, being first order in both reactants, is the dominating one above pH 11;3 at lower pH the experimental data available were originally interpreted such that a second unimolecular reaction was also proposed to be operative. However, since the reaction rate is strongly dependent upon the ionic strength of the solutions under investigation,3–5 this interpretation was seriously questioned, and Ho and Sturtevant5 concluded that it is not necessary at all to include the carbonic acid molecule in the mechanistic picture at high pH. Furthermore, quantum chemical calculations (QCC) indicate that hydrolysis of CO2(aq) has an energy barrier >120 kJ mol−1 and involves a transition state of CO2 and two water molecules:6
| CO2(aq) + 2H2O → HOCO2−(aq) + H3O+(aq). | (7) |
The purpose of the present work is to better understand the mechanism of the bimolecular reaction (eqn (6)). We decided to conduct a systematic series of experiments in which we studied the reaction of CO2 with hydrated OH− in the form of size-selected clusters, OH−(H2O)n. Increasing n in steps, starting with the naked anion (n = 0), bridges the domains of gas phase chemistry and condensed phase chemistry; a more detailed understanding of solvent–solute interactions at the molecular level can hopefully be obtained thus. In order to provide an even closer mechanistic insight, we also chose to conduct QCC to establish a consistent description of the kinetics and thermodynamics at the molecular level.
For comparison and benchmark purposes we also performed similar experiments with HO2−(H2O)n. The hydroperoxide anion is known to be an even stronger nucleophile than hydroxide – in aqueous solution,7,8 in the isolated gas phase,9 and in the microsolvated state.10 It would therefore be of interest to see if this is also the case in the reaction with CO2. The experimental part of our study is also intended to be more comprehensive and consistent than previous studies including HO2−(H2O)n, for which only limited experiments have been reported.11
It is already established that the direct reaction between OH− and CO2 is kinetically more favourable for the isolated species than when the reactants are dissolved in water.12–18 Above pH = 10, the direct reaction in water (eqn (6)) is—as already mentioned—first order in both reactants, and an Arrhenius activation energy of 55 kJ mol−1 has been estimated.3 The microsolvation effect of water has been studied in three previous reports on CO2 reactivity towards OH−(H2O)n clusters.19–21 The computational part of this study is also intended to give a better understanding of the mechanism and the nature of the microsolvation effect.
Results and discussion
Reaction products
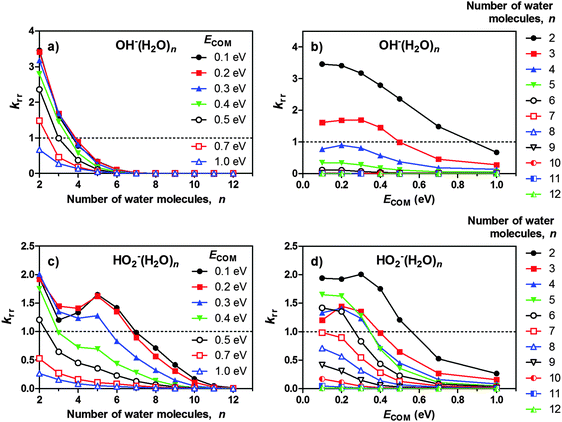
In the experiments presented, the cluster ions were made to collide with CO2 under high-vacuum conditions and at different centre-of-mass collision energies, ECOM. Fig. 1 and 2 show the relative (to the reactant ion) background-corrected signal intensities of the various products observed for OH−(H2O)n + CO2 and HO2−(H2O)n + CO2. The curves correspond to the combined signal intensity of the different product channels, meaning that “Total + CO2 − xH2O” combines the intensity of all reaction channels where the cluster incorporates CO2 and loses any number of H2O molecules. Likewise, “Total − xH2O” combines the intensity of all reaction channels where the cluster is observed to lose water molecules without the incorporation of CO2, i.e., collision induced dissociation (CID). Note that neither OH−(H2O)1 nor HO2−(H2O)1 are included among the products, since their m/z values are too low to allow transmission and detection with the current experimental setup. For HO2−(H2O)n, the relative intensity of ion signals due to loss of H2O2 has also been included; however, these product channels are quite insignificant.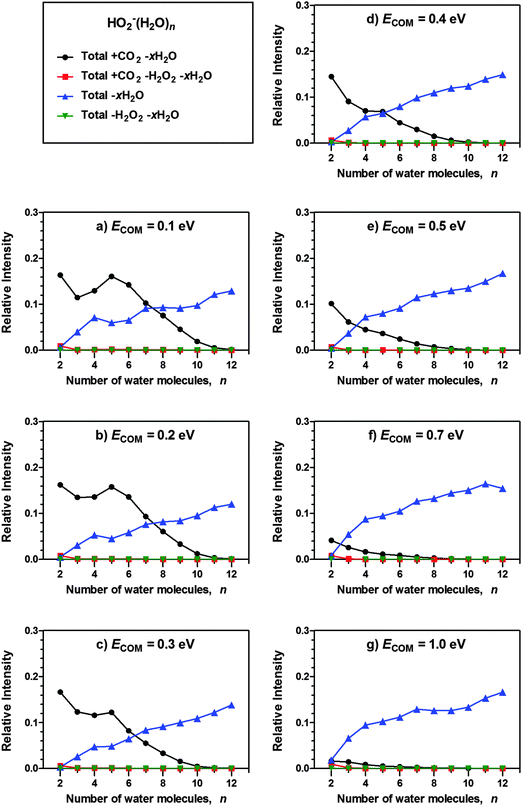 | ||
| Fig. 2 Relative signal intensities of products observed to result from reactive and non-reactive encounters for HO2−(H2O)n + CO2 at various nominal collision energies (centre-of-mass frame). | ||
Both hydroxide- and hydroperoxide-containing water clusters show the same behaviour – as the cluster size increases, CO2 incorporation (Total + CO2 − xH2O) decreases while collisionally induced H2O loss (Total − xH2O) increases, in agreement with previous studies on OH−(H2O)n.21
Reaction rates
Fig. 3 shows the relative reaction rate coefficients for the reaction of OH−(H2O)n and HO2−(H2O)n with CO2 as obtained by the procedure detailed in the ESI† (eqn (S10)), i.e., the reaction rates are expressed relative to the OH−(H2O)3 ion at ECOM = 0.5 eV. Fig. 3a shows the results regarding OH−(H2O)2–12, as a function of the number of water molecules in the cluster, n. The rate coefficient decreases as the cluster size increases, in general agreement with previous results of Yang and Castleman21 who used a flowing afterglow apparatus and reported thermal rate coefficients for n ≤ 3 at 300 K, n ≤ 4 at 200 K and n ≤ 15 at 130 K. It should also be mentioned that Fehsenfeld and Ferguson19 obtained thermal rate coefficients at 296 K for n = 2–4, and that Hierl and Paulson20 obtained rate coefficients for lab-frame collision energies of 0.15–25 eV with n ≤ 3. The shape of the curve differs from that of Yang and Castleman, in the sense that they observed CO2 incorporation up to n = 15, whereas in our measurements, the reactivity falls off more quickly with size. In considering these differences it should be taken into account that our rate coefficients are obtained under essentially single-collision conditions, while Yang and Castleman conducted their study under multiple-collision conditions.Fig. 3c shows the relative reaction rate coefficient for HO2−(H2O)n + CO2, also for n = 2–12. Generally, the HO2−(H2O)n clusters show lower reaction rates for the very smallest values of n (2 and 3) compared to OH−(H2O)n; however, the former has a weaker size dependence and retains CO2 incorporation for significantly larger cluster sizes. It should be noted that the higher reactivity of HO2−(H2O)n compared to OH−(H2O)n for n ≥ 4 becomes less pronounced as ECOM increases.
For the reaction, HO2−(H2O)n + CO2, Yang and Castleman11 reported room temperature rate coefficients for n = 0–2. A slight decrease in the reaction rate coefficients reported by Yang and Castleman was evident as hydration increased from zero to two water molecules.
For both OH−(H2O)n and HO2−(H2O)n, we note that the reaction rate coefficient is not necessarily monotonically dependent upon ECOM, which is especially evident for n = 2,3 (Fig. 3b and d). It is clear that for some clusters, the reaction rate coefficient has a local maximum within the collision energy range investigated. This is a consequence of the competition between incorporation of CO2 and water loss due to CID. A slight increase in collision energy seems to promote the passage of the free energy barrier associated with making the core-ion available for reaction. On the other hand, too high collision energy only leads to fragmentation of the original cluster. As such, there is a collision energy “sweet spot” where the two tendencies are balanced. It seems that the position of the collision energy–sweet spot generally decreases with the increasing cluster size. This may result from the reasonable assumption that the sensitivity of the cluster to CID increases more rapidly with size, but could also reflect intricate dynamics of the CO2 incorporation reaction, indicating that the kinetic barrier is not only of enthalpic origin.
In addition to the local maxima discussed above, there are also local minima and maxima occurring for the reaction HO2−(H2O)n + CO2 with regard to the cluster size (Fig. 3c). At lower collision energies, the reaction rate decreases in the region from n = 2 to n = 3,4, followed by an increase, with a local maximum at n = 5. This size trend is most evident for ECOM = 0.1 eV; the resulting kink in the curve then flattens out for ECOM = 0.2–0.3 eV, and has almost disappeared at ECOM = 0.4 eV. Considering that the minima and maxima of the curves are mirrored by, respectively, maxima and minima in the abundance of water loss due to CID (Fig. 2a–d), a likely explanation is that the cluster's sensitivity to fragmentation does not increase monotonically with size, but both increases and decreases in the size range in question. However, a look at the abundance spectra and the evaporation rate for HO2−(H2O)n (see the ESI†) does not suggest that this cluster would be particularly unstable in the indicated size region, therefore, another explanation cannot be ruled out.
Thermochemistry
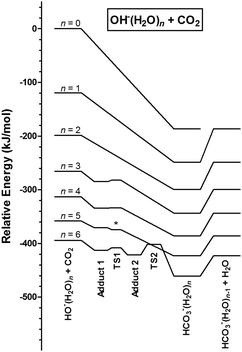
The addition of carbon dioxide to the isolated hydroxide anion results in the direct formation of the bicarbonate anion (Scheme 1). Our QCC confirm that there is no barrier to this process anywhere along the reaction coordinate. In close analogy, addition of the hydroperoxide anion, HO2−, to carbon dioxide gives the peroxybicarbonate anion, HOOCO2−. According to the calculation, the latter reaction is slightly more exothermic than the former. Some key bond parameters are presented in Table 1, showing the close resemblance between the two adduct-forming reactions. The abbreviations B3 and G4 refer to calculations performed using the hybrid density functional B3LYP in conjunction with the 6-311++G(2d,2p) basis set and the Gaussian-4 theory compound method, respectively (please refer to the Methods section).In order to provide insights into the mechanisms of CO2 addition to OH−(H2O)n and HO2−(H2O)n clusters, we performed QCC for n = 1–6 for the former, and n = 6 for the latter.
We will first describe the addition, OH−(H2O)n + CO2 → HOCO2−(H2O)n. The structural features of both reactant and product clusters have been well characterized in previous studies.23–25 For OH−(H2O)n we re-optimized the lowest energy structures reported, using B3. For HOCO2−(H2O)n we applied the lowest energy cluster-structures reported in the quantum chemical part of the IR action spectroscopic study by Garand et al.,26 also re-optimizing them with B3. As expected, only minor structural changes occurred during geometry optimization with B3 for both reactant and product structures. For addition of CO2 to OH−(H2O)n with n = 1 and 2, we find that there is a straight downhill path leading towards the product cluster without any intermediate energy barrier anywhere along the reaction coordinate, as was the case for n = 0. For n = 3–6, we were able to identify minima for the rather weakly bonded adducts, OH−(H2O)n(CO2), indicating that there is no direct downhill path to the bicarbonate cluster for these cluster sizes. This is illustrated in the potential energy diagrams in Fig. 4. In fact, for n = 3–6, the water molecules efficiently form hydrogen bonds to the OH− core and block the direct access of CO2 to the lone pairs of the nucleophile OH− from all sides. In all these intermediate OH−(H2O)n(CO2) clusters the CO2 entity is weakly C–O coordinated to one water molecule, with contact distances in the range 2.6–2.7 Å. In other words, it is more appropriate to term these weakly bonded H2O–CO2 complexes rather than covalently bonded +H2O–CO2− zwitterions. Furthermore, the larger the cluster, the more water molecules are available as CO2 coordination sites, resulting in an increasing number of possible pre-reaction complexes. This adds to the already complex situation of searching for relevant reaction routes on a multidimensional potential energy surface, which therefore effectively becomes prohibitive already for n > 6. We have considered two possible mechanisms for forming the crucial HOCO2− structural motif within these clusters, starting from the OH−(H2O)n(CO2) intermediates. These mechanisms are:
(i) A water molecule rearrangement mechanism in which at least one of the hydrogen bonds to OH− is broken, leading to OH− becoming sufficiently de-solvated to allow for it to concurrently or subsequently form a covalent C–O bond to the incoming CO2.
(ii) A proton transfer mechanism in which a water molecule, hydrogen-bonded to OH− and to which the CO2 is coordinated, transfers a proton to OH−, thereby itself becoming a OH− (while the original OH− becomes H2O). The formation of a covalent C–O bond between CO2 and the new OH− happens concurrently or subsequently to the proton transfer.
Fig. 4 shows the potential energy diagrams corresponding to the lowest energy reaction pathways for OH−(H2O)n + CO2 with n = 0–6. On the very left hand side, the spacing between the curves corresponds to the enthalpies of successive addition of water molecules to OH− at 0 K. For each curve, the lowest point corresponds to the most stable HOCO2−(H2O)n product configuration, and the spacing between the curves correspond to the hydration enthalpies of the bicarbonate anion, which are clearly lower than those of the reactant for small n. In qualitative terms this can be understood from the larger size of the bicarbonate ion compared to the hydroxide ion. As a result of this, the diagrams also show that addition of CO2 becomes gradually less exothermic with the cluster size. Uphill from the water–bicarbonate cluster, on the right hand side in each curve, we have indicated the enthalpy of the product pair HOCO2−(H2O)n−1 + H2O. Also this reaction is exothermic (relative to the reactants) for all sizes investigated. For n = 5, the transition state structure for the transition of the adduct OH−(H2O)n(CO2) into the product HOCO2−(H2O)n is calculated to be slightly below the energy level of the adduct when the ZPVE is included. However, this anomaly is lifted when the ZPVE is not included, in the sense that it is then a small barrier of 1 kJ mol−1. Reaction enthalpies (denoted ΔHrxn) and the enthalpies of step-by-step dehydration (denoted ΔHdehyd) are summarized in Table 2.
| n | ΔHdehyd, OH−(H2O)n | ΔHrxn, OH−(H2O)n + CO2 → HOCO2−(H2O)n | ΔHdehyd, HOCO2−(H2O)n |
|---|---|---|---|
| 0 | −186.6 | ||
| 1 | 119.2 | −129.5 | 62.1 |
| 2 | 79.4 | −101.0 | 50.9 |
| 3 | 67.1 | −77.9 | 44.0 |
| 4 | 47.6 | −72.6 | 42.4 |
| 5 | 44.8 | −65.0 | 37.2 |
| 6 | 36.0 | −66.6 | 37.7 |
Experimental estimates of the enthalpy changes for the reaction OH−(H2O)n + CO2 → HOCO2−(H2O)n−x + xH2O for values of n = 0–5, x = 0–3 are known from the literature.22,27–30 Aqueous phase reaction enthalpies have been determined in a direct reaction by Pinsent,3 but can more accurately be estimated from the well-established formation enthalpies.31 A comparison of our QCC values—presented in Table 2—to these experimentally determined values is given in Fig. 5. It can be seen (upper panel) that our B3 estimates of the enthalpies for successive hydration/dehydration of OH− are in good agreement with the experimental series of Meot-Ner and Speller,30 while our computed reaction enthalpies seem to approach the tabulated bulk value in an asymptotic fashion (lower panel).31 In summary, this provides support for the computed reaction energies, and thereby an indication of the accuracy of the method used.
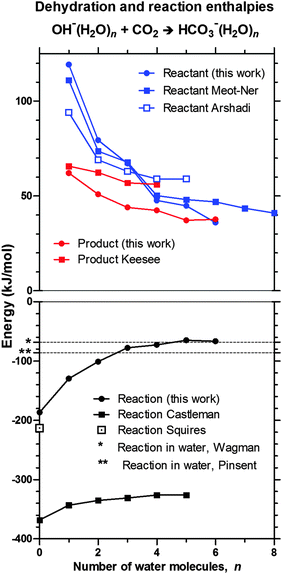 | ||
| Fig. 5 Comparison of dehydration (upper panel) and reaction (lower panel) enthalpies for OH−(H2O)n + CO2 → HOCO2−(H2O)n as calculated in this work (B3, including ZPVE) and as reported in experimental investigations: Meot-Ner,30 Arshadi,28 Keesee,29 Castleman,21 Squires22 (298 K), and Pinsent3 (293 K) or, as calculated from well-established tabulated values – Wagman31 (293 K). The dehydration enthalpy of the reactant OH−(H2O)n is shown in blue, the dehydration enthalpy of the product HCO3−(H2O)n is shown in red, and the reaction enthalpy is shown in black. One major reason for the discrepancy of the reaction energies of Castleman is most likely that ref. 21 uses an erroneous value for the enthalpy of formation of the bicarbonate anion originating from ref. 20. | ||
Water loss during reaction and collision
For reactive encounters between OH−(H2O)n (n = 2–6) and CO2, we observe that on an average the immediate product cluster [HOCO2−(H2O)n]* loses two water molecules, as seen in Fig. 6. According to the energy diagram of Fig. 4, the loss of one water molecule is exothermic at 0 K, while the loss of two water molecules is endothermic. When we also take other sources of energy into account, including the thermal energy of the reactants (see ESI,† Table S2) plus the COM collision energy, the total energy available also allows for the loss of a second water molecule. Also in this respect, the quantum chemical model is in good accord with observation. It is also interesting to note that as the COM energy increases toward 1.0 eV the total energy after addition of CO2 approaches a level where it allows for the loss of a third water molecule. The branching ratio model (see ESI†) is also seen to be in fairly good agreement with the experimental data (see Fig. 6). The same considerations given above for OH−(H2O)n are also valid for HO2−(H2O)n (see ESI,† Fig. S4).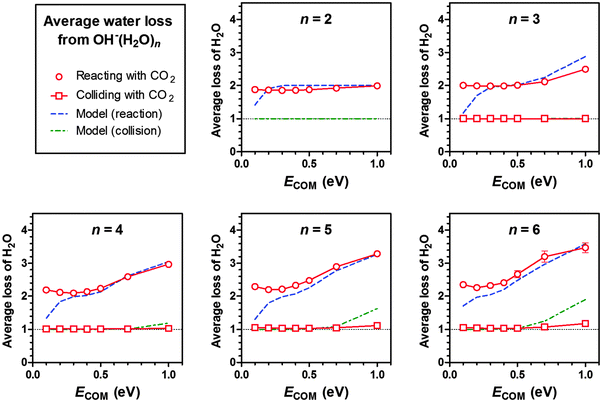 | ||
| Fig. 6 Experimental data and results of branching ratio modelling (see ESI†) showing the average number of water molecules lost from OH−(H2O)n when the cluster incorporates CO2 (circles) or collides with CO2 without incorporating it, resulting in water loss (squares). Data given for different cluster sizes, n, as a function of nominal centre-of-mass collision energy ECOM. Error bars corresponding to one standard deviation (from count statistics) are included for all data points. | ||
As seen in Fig. 6, in most of the CID events the collision energy is too low to result in the detachment of one—and certainly not two—water molecules; therefore the average number of water molecules lost due to CID is made up of the few detected instances where one single water molecule left the cluster. The modelled average CID shown in Fig. 6 is designed to reflect this as well. As the distribution of cluster–gas collision-energies reaches the limit for detachment of a second H2O molecule, an increase in the average CID water-loss above unity is observed.
Reactivity and mechanistic considerations
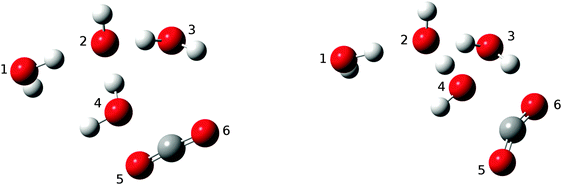
As mentioned above, for n ≥ 3 the addition complexes OH−(H2O)n(CO2) give rise to local energy minima en route to the products. This means there is at least one potential energy barrier separating this intermediate and the product HOCO2−(H2O)n. In all cases, 2 < n < 6, the lowest energy pathway found corresponds to the proton transfer mechanism, type (ii), as explained above. Despite being unable to locate transition structures of lower energy for the alternative mechanism type (i) for any of the cluster sizes investigated, we will be careful not to exclude the possibility that this mechanism, which requires water molecule rearrangements to allow for the CO2 to diffuse towards the OH− core, may have some significance, especially for larger clusters. This will be discussed below. The fact that the motion of one single water molecule affects the motion of all the other molecules in the hydrogen bond network in these clusters makes it extremely difficult to map out all possible reaction routes with full confidence.In addition to the enthalpic preference of the type (ii) proton transfer mechanism, it is also attractive from a probabilistic (entropic) point of view, as it does not require molecular rearrangements since the proton transfer occurs via the established hydrogen bond network of the lowest energy structural form. Fig. 7 shows a simple but illustrative example found for HO−(H2O)3, depicting the structures of the intermediate adduct and the transition state. Note that the formation of the covalent C–O bond occurs in concert with the proton transfer from H2O to OH−. This single proton transfer mechanism was also identified for HO−(H2O)4 and HO−(H2O)5.
For n = 6, we find no transition state structure for a direct pathway, either by a one-step single proton transfer or by two synchronous proton transfers (Grotthuss mechanism) from any of the initial OH−(H2O)n(CO2) adduct configurations, which leads directly to HOCO2−(H2O)n. Instead, we find that the lowest energy pathway requires two successive proton transfer steps, both having transition states below the reactant state in energy. In the first step the OH− moiety is effectively brought closer to the CO2 moiety by the transformation (H2O)4(OH−)(H2O)(H2O)(CO2) → (H2O)5(OH−)(H2O)(CO2), while the covalent C–O bond formation is only realized upon the second proton transfer, then according to a mechanism analogous to the one depicted in Fig. 7. We note that the transition state energy of the second proton transfer is rather high in energy compared to the situation in the smaller clusters, being only 7 kJ mol−1 lower in energy than the separated reactants OH−(H2O)6 + CO2 (Fig. 4). For the presumed rate determining step, the transition state energies relative to the separated reactants are ETS = −16, −20, −16 and −7 kJ mol−1 for n = 3, 4, 5 and 6, respectively. More important than the slightly more unfavourable increase of the effective enthalpic barrier towards reaction is the fact that an asynchronous two-step proton transfer makes the overall kinetics by far more ineffective compared to a one step mechanism. This shift in mechanism may explain why we do not observe significant CO2 uptake for clusters larger than n = 6. In any case, from n = 6 and onwards, it is clear that the OH− moiety becomes increasingly more shielded by the surrounding water molecules, and therefore increasingly less accessible for binding to the incoming CO2 molecule. We therefore suggest that the effective activation enthalpy is probably not the limiting factor—a situation that is likely to be valid for clusters of any size, including bulk water—and that it is the unfavourable entropical factor associated with a multistep mechanism which is the main reason behind the experimentally observed trend in reactivity.
In these considerations proton tunnelling has not been taken into account. It is well known that this quantum mechanical effect may lower the effective proton transfer reaction barrier height, even at room temperature.32,33 The computed imaginary frequencies of vibration are in the range 350–520 cm−1, which indicates a relatively low curvature of the potential energy in the direction of the reaction coordinate and thereby only a moderate probability for tunnelling.
According to a previous computational study of HO2−(H2O)n clusters, there is a slight preference for small clusters of this kind to accommodate the OH−(H2O)n−1(H2O2) configuration rather than the assumed HO2−(H2O)n.34 This preference is surprising taking into account the fact that hydrogen peroxide is a stronger acid than water both in the isolated gas phase and in aqueous solution. However, the two forms are close in energy, within a few kJ mol−1. From the same computational study it also appeared that for a given value of n the OH− entity is somewhat less strongly solvated in OH−(H2O)n−1(H2O2) than in pure hydroxide–water clusters, and that the H2O2 preferably sits on the surface of the cluster, at least up to n = 20. These qualitative considerations may indicate why the reaction is observed to occur for nominal HO2−(H2O)n up to larger values of n compared to OH−(H2O)n. Recently, Thomsen et al.10 studied the SN2 reaction between X−(H2O) and CH3Cl (X− = OH− and HO2−), both experimentally and computationally; it was elegantly demonstrated that the barrier for HO2− indeed is lower, in agreement with the fact that HO2− is the better nucleophile, as mentioned in the Introduction. Interestingly, while the most stable reactant configuration for the microsolvated hydrogen peroxide is (H2O2)(OH−) the actual reaction was seen to occur from the (HO2−)(H2O) configuration. Due to this complicating issue of the mobile proton, arising from the favourable protolysis of HO2−, we considered it too complicated to pursue a systematic quantum chemical survey of the potential surfaces for the reactions of HO2−(H2O)n clusters with CO2 as we did for OH−(H2O)n. In addition to the n = 0 case referred to above—which has already revealed that direct addition of HO2− to CO2 is more exothermic compared to addition of OH− to CO2—we conducted a limited study of n = 6, starting from the re-optimized lowest energy (H2O)5(OH−)(H2O2) structure of Anick.34 The calculations revealed a one-step proton transfer mechanism in analogy to that found for the hydroxide–water clusters containing 3–5 H2O molecules. A pre-reaction complex, (H2O)5(OH−)(H2O2)(CO2), at −13 kJ mol−1 relative to the isolated reactants was found to connect to the (H2O)6(HOOCO2−) product via a transition state at −1 kJ mol−1. Despite the fact that the transition state of this single HO2−(H2O)6 configuration is computed to be at a higher relative energy compared to the transition states of HO−(H2O)6, the former requires one proton transfer while the latter requires two consecutive and uncoupled proton transfers, which clearly is kinetically unfavourable as already suggested. If the single proton transfer mechanism of HO2−(H2O)n also persists for n > 6 this may explain why hydroperoxide–water clusters in this size-range are observed to react to a significantly larger extent than the hydroxide–water clusters do, in agreement with HO2− being a stronger nucleophile than OH−. The fact that only an insignificant amount of H2O2 is seen to evaporate from the product clusters upon inclusion of CO2 is consistent with the notion that the peroxide moiety is incorporated in the central (HOOCO2−) moiety of the product cluster.
Relationship to CO2 uptake in water
The findings reported here have a direct bearing on the mechanism for uptake of carbon dioxide in the oceans. At pH = 8.5 we have [OH−(aq)] = 3.2 × 10−6 M. At equilibrium and under ambient conditions, assuming a CO2 concentration in the gas phase of 390 ppm by volume and using a tabulated35 equilibrium constant of 29.4 M atm−1, we have [CO2(aq)] = 1.3 × 10−5 M. Since the concentrations of OH− and CO2 only differ by a factor of four, a bimolecular reaction seems to be the most significant. The diffusion coefficients for the two species are also of similar magnitude, respectively, 5.3 × 10−9 m2 s−1 and 1.9 × 10−9 m2 s−1,36,37 indicating that diffusion of both species is of importance for their relative motion. The interaction between CO2 and the surrounding water molecules is weak and essentially hydrophobic, so diffusion of CO2 requires for the most part reordering of the water molecules by relative rotation.38,39 On the other hand, transport of OH− follows a more composite mechanism, involving both water molecule rotation/reordering and incoherent proton hopping via the intermediate [H–O–H–O–H]−.40,41 Neither of these mechanisms is likely to have an enthalpic barrier much above that necessary for breaking one single hydrogen bond, which is around 20 kJ mol−1. On this background we may then consider the actual chemical transformation HO−(aq) + CO2(aq) → HOCO2−(aq) in accordance with the cluster mechanism outlined above, namely that the reaction may occur when the two reacting species have diffused to a point where one or two water molecules separate them and that C–O bond formation is then accomplished according to the mechanism:| (HO−)(H–OH)(CO2) → (H–O–H–OH–CO2)− → (HOH)(HOCO2−). | (8) |
Further support for this scenario comes from a Car–Parrinello dynamics simulation of the process by Stirling42 for which a transition state configuration involving H–O–H–O–H−, much in line with the mechanism of Fig. 7, was clearly identified. It was also concluded that the free energy barrier is predominantly hydration related and significantly entropic in origin. A direct comparison with the results of Pinsent et al.3 mentioned in the Introduction turns out to be difficult, due to the general crudeness of an Arrhenius plot. Analysis of the measured reaction rates as a function of inverse temperature in a limited temperature range (T = 273–313 K) gave an Arrhenius activation energy EA = 55 kJ mol−1,3 as already mentioned. Wang et al. analysed the results of stopped-flow kinetics experiment of the hydration of CO2 (using optical detection by means of added indicators) and reported a value of EA = 64 kJ mol−1.43 If our mechanism is correct, it is unlikely that the enthalpy of activation is much above 20 kJ mol−1, as already indicated. It should also be mentioned that the alternative mechanism (denoted type (i) above) has also been subject to various quantum chemical model calculations including QM/MM and continuum solvation models,15,44 resulting in activation enthalpies apparently in good agreement with the experimentally derived parameter of Pinsent et al.3 However, this apparent agreement may be coincidental. In fact, the relationship between a phenomenological Arrhenius activation energy obtained in a narrow temperature range and the energy of activation for the rate-determining step at best is very unclear.
As a final note on this part we recognize the shortcomings of our quantum chemical reaction model which is based on a potential energy surface survey of the molecular clusters in question. We have made no efforts in explicitly incorporating potentially important kinetic and dynamic effects. The fact that the B3 model may be in error of several kJ mol−1 in the estimates of the potential energy barriers makes RRKM theory estimates of the rate coefficients highly uncertain. More important is the detailed reaction dynamics which could be uncovered in ab initio reaction trajectory simulations (Born–Oppenheimer molecular dynamics). Such simulations, required to run well into the nanosecond domain in order to be compatible with our experiments, will obviously have a huge demand for computer resources. We have just started this work and realize it will take quite some time before it will be finished. In such simulations the nuclei are treated according to classical mechanics, even though it is well known that proton transfers may be subject to quantum mechanical tunnelling or reflection, which may be important for quantitative agreement. Despite this, we consider the present model to contain the essential mechanism.
Methods
Experimental procedure
The experiments were performed using a quadrupole–time-of-flight mass spectrometer (QTOF2, Micromass/Waters, Manchester UK), as previously used by us.45–50 The instrument has been modified to allow for volatile and semi-volatile gases to be injected into the instrument's collision-cell via a stainless steel inlet system.Cluster ions were produced at atmospheric pressure by means of the Z-configuration electrospray ionization (ESI) unit fitted to the instrument. The ESI unit was operated at room temperature, and water (HiPerSolv CHROMANORM for HPLC, VWR BDH Prolabo) was fed through the electrospray capillary at a rate of 25 μL min−1. A voltage of 3.0–3.5 kV was applied to the electrospray needle, leading to a weak corona discharge at the needle tip and the formation of several series of anion–water clusters, e.g., OH−(H2O)n, HO2−(H2O)n, and O2−(H2O)n. The resulting clusters were transferred into the high vacuum part of the instrument, where the quadrupole mass filter—operating at better than unit resolution—acted either as a ramped high pass filter for measuring abundance spectra, or, allowed for transmission of a single cluster size based on the cluster's mass-to-charge ratio (m/z) for the reaction studies.
The ions were introduced into the collision cell (length 16 cm, with a hexapole ion guide) at a well-defined lab-frame kinetic energy. For the reaction experiments, CO2 (industrial grade, AGA) was introduced into the collision cell via an ultra-high vacuum leak-valve. The CO2 pressure was adjusted to limit double collisions while maintaining a sufficiently high collision frequency to avoid problems with count statistics and signal-to-noise ratios. Typically, approximately 10% of the reactant ions react with CO2. The unreacted clusters and reaction products were analysed in the time-of-flight (TOF) unit on the basis of their m/z ratio. Due to limitations in the TOF unit setup, the smallest ions in the reaction studies were OH−(H2O)2 and HO2−(H2O)2.
For each single reaction measurement, a corresponding background measurement was performed, using the same cluster and kinetic energy, but with an empty collision cell. Also the abundance spectra were collected with an empty collision cell. Every 5th or 6th measurement in the reaction studies and background measurements was a reference measurement, performed on the cluster OH−(H2O)3 at 1.3 eV lab-frame collision energy (centre-of-mass energy, ECOM = 0.5 eV). The use of a reference measurement allowed us to monitor changes in the CO2 pressure. We estimate the partial pressure of CO2 from readings before and after the opening of the leak valve to lie between 0.5 × 10−5 and 1.0 × 10−5 mbar.
Prior to the measurements, the voltages on the micro-channel-plate detector in the TOF unit were adjusted to secure that the isotopic pattern of Cl−(NaCl)n clusters was faithfully reproduced, this ensured that no bias towards larger or smaller mass spectrum peaks existed. The sodium chloride clusters were produced from a 30 mM NaCl(aq) solution (NaCl: 99.5%, Prolabo).
For some of the reaction measurements, the parent ion had isobaric overlaps with contamination species. In particular, this was observed for OH−(H2O)6 and HO2−(H2O)6, having overlaps with, respectively, NaOOC–CH2–COO− (124.99 Th) and KOOC–CH2–COO− (140.96 Th). The resolution of the QTOF2 (m/Δm ≈ 5000 at full-width-half-maximum) is sufficient to separate the isobaric overlap; furthermore, none of the contaminating species were observed to react with CO2.
All measurements have been repeated on either two or three separate occasions, separated by several months, to verify the reproducibility.
Quantum chemical calculations
Quantum chemical calculations were carried out using the GAUSSIAN 09 program system.51 All structures (reactants, transition structures, and products) were characterized by complete geometry optimization using the hybrid density functional B3LYP in conjunction with the 6-311++G(2d,2p) basis set, here abbreviated B3.52 The character of each stationary point (transition state structure or minimum energy structure) was identified from analysis of the eigenvalues of the molecular Hessian and by visual inspection. Relative energies were corrected by including unscaled zero-point vibrational energies (ZPVE) obtained from the harmonic frequencies. Furthermore, for each transition structure that was localized, the reaction coordinate was followed to verify that the minimum potential reaction path leads to the expected reactant and product minima.In the case of carbonate adduct formation, more accurate estimates of the association energies were obtained using the G4 (Gaussian-4 theory) compound method, for which geometry optimization is performed with B3LYP/6-31G(2df,p).53 Then, the equilibrium structure obtained is subject to a sequence of single point energy calculations – performing CCSD(T) calculations with a moderate sized basis set and MP4 calculations with a relatively large basis set. Finally, the results of the calculations are combined using an extrapolation scheme (also including ZPVE corrections) to approximate the energies of more expensive calculations, estimated to be accurate within ± 10 kJ mol−1.
Conclusions
We have reported reactions of the anionic clusters, OH−(H2O)n and HO2−(H2O)n, with CO2 for values of n = 2–12 and shown that OH−(H2O)n has a significantly larger reaction rate than HO2−(H2O)n for n = 2,3. However, the reaction rate of the former cluster drops off more quickly with size and for n ≥ 4 we find that HO2−(H2O)n reacts faster. For OH−(H2O)n, the reaction is not observed for n ≥ 7, while HO2−(H2O)n retains noticeable reactivity with CO2 up to n = 11. In addition, while the reaction rate of OH−(H2O)n is a monotonically decreasing function of cluster size, the reaction rate of HO2−(H2O)n shows a local minimum for n = 3,4, and a local maximum for n = 5, the exact reason for this is not determined as of yet.The QCC reproduce the reaction enthalpy for naked OH− with CO2 in good agreement with an experimental value;22 furthermore, as the degree of hydration is increased the calculated reaction enthalpy approaches the value for OH− in bulk water asymptotically.
Within the clusters studied here, the shielding of the core ion from CO2 by the water molecules presents an obstacle to reaction. Of the two mechanisms considered for the cluster reaction, OH−(H2O)n + CO2 → HOCO2−(H2O)n−x + xH2O, a general mechanism is clearly identified (denoted type (ii)). In the reaction adduct, OH−(H2O)n(CO2), proton transfer from a H2O molecule in the innermost solvation shell of CO2 to OH− positioned in the second solvation shell of CO2 initiates the ultimate formation of the O–C bond of bicarbonate. As observed already for n = 6, previous proton transfers are required to bring the OH− in position. It is the entropic factor owing to successive proton transfers that seems to limit the reaction rate, and not the modest enthalpic requirements. The proposed dominant mechanism for reaction between the hydroxide anion and CO2 in clusters by proton transfer within the hydrogen bonded OH−/H2O network is likely to be valid also in the limit of n → ∞, i.e., in bulk-water, as also supported by the simulations of Stirling.42 It should be emphasized that the reaction mechanism avoids any intermediate H2CO3 during CO2 hydrolysis, and that bicarbonate formation and protolysis occur in one common step, at odds with the common notion that carbonic acid is prerequisite for the formation of HCO3− and CO32−.
Acknowledgements
This work was supported by the Norwegian Research Council by the Grants No. 205512/F20, Nano-solvation in Hydrogen-Bonded Clusters and No. 179568/V30 to the Centre of Theoretical and Computational Chemistry through their Centre of Excellence program; and the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K).References
- K. Adamczyk, M. Premont-Schwarz, D. Pines, E. Pines and E. T. J. Nibbering, Science, 2009, 326, 1690–1694 CrossRef CAS PubMed.
- P. P. Kumar, A. G. Kalinichev and R. J. Kirkpatrick, J. Phys. Chem. B, 2009, 113, 794–802 CrossRef CAS PubMed.
- B. R. W. Pinsent, L. Pearson and F. J. W. Roughton, Trans. Faraday Soc., 1956, 52, 1512–1520 RSC.
- M. Eigen, K. Kustin and G. Maass, Z. Phys. Chem., 1961, 30, 130 CAS.
- C. Ho and J. M. Sturtevant, J. Biol. Chem., 1963, 238, 3499–3501 CAS.
- M. T. Nguyen, G. Raspoet, L. G. Vanquickenborne and P. T. VanDuijnen, J. Phys. Chem. A, 1997, 101, 7379–7388 CrossRef CAS.
- J. E. Dixon and T. C. Bruice, J. Am. Chem. Soc., 1971, 93, 6592–6597 CrossRef CAS.
- J. M. Garver, S. Gronert and V. M. Bierbaum, J. Am. Chem. Soc., 2011, 133, 13894–13897 CrossRef CAS PubMed.
- J. M. Garver, Z. B. Yang, C. M. Nichols, B. B. Worker, S. Gronert and V. M. Bierbaum, Int. J. Mass Spectrom., 2012, 316, 244–250 CrossRef PubMed.
- D. L. Thomsen, J. N. Reece, C. M. Nichols, S. Hammerum and V. M. Bierbaum, J. Am. Chem. Soc., 2013, 135, 15508–15514 CrossRef CAS PubMed.
- X. Yang and A. W. Castleman, Chem. Phys. Lett., 1991, 179, 361–366 CrossRef CAS.
- D. A. Palmer and R. Vaneldik, Chem. Rev., 1983, 83, 651–731 CrossRef CAS.
- Z. Peng and K. M. Merz, J. Am. Chem. Soc., 1993, 115, 9640–9647 CrossRef CAS.
- M. M. Davidson, I. H. Hillier, R. J. Hall and N. A. Burton, Mol. Phys., 1994, 83, 327–333 CrossRef CAS.
- A. V. Nemukhin, I. A. Topol, B. L. Grigorenko and S. K. Burt, J. Phys. Chem. B, 2002, 106, 1734–1740 CrossRef CAS.
- K. Leung, I. M. B. Nielsen and I. Kurtz, J. Phys. Chem. B, 2007, 111, 4453–4459 CrossRef CAS PubMed.
- K. Iida, D. Yokogawa, H. Sato and S. Sakaki, Chem. Phys. Lett., 2007, 443, 264–268 CrossRef CAS PubMed.
- B. Jonsson, G. Karlstrom and H. Wennerstrom, J. Am. Chem. Soc., 1978, 100, 1658–1661 CrossRef CAS.
- F. C. Fehsenfeld and E. E. Ferguson, J. Chem. Phys., 1974, 61, 3181–3193 CrossRef CAS PubMed.
- P. M. Hierl and J. F. Paulson, J. Chem. Phys., 1984, 80, 4890–4900 CrossRef CAS PubMed.
- X. Yang and A. W. Castleman, J. Am. Chem. Soc., 1991, 113, 6766–6771 CrossRef CAS.
- R. R. Squires, Int. J. Mass Spectrom. Ion Processes, 1992, 117, 565–600 CrossRef CAS.
- S. S. Xantheas, J. Am. Chem. Soc., 1995, 117, 10373–10380 CrossRef CAS.
- C. Chaudhuri, Y. S. Wang, J. C. Jiang, Y. T. Lee, H. C. Chang and G. Niedner-Schatteburg, Mol. Phys., 2001, 99, 1161–1173 CrossRef CAS.
- T. H. Choi, R. Liang, C. M. Maupin and G. A. Voth, J. Phys. Chem. B, 2013, 117, 5165–5179 CrossRef CAS PubMed.
- E. Garand, T. Wende, D. J. Goebbert, R. Bergmann, G. Meijer, D. M. Neumark and K. R. Asmis, J. Am. Chem. Soc., 2010, 132, 849–856 CrossRef CAS PubMed.
- R. G. Keesee and A. W. Castleman, J. Phys. Chem. Ref. Data, 1986, 15, 1011–1071 CrossRef CAS PubMed.
- M. Arshadi and P. Kebarle, J. Phys. Chem., 1970, 74, 1483–1485 CrossRef CAS.
- R. G. Keesee, N. Lee and A. W. Castleman, J. Am. Chem. Soc., 1979, 101, 2599–2604 CrossRef CAS.
- M. Meot-Ner and C. V. Speller, J. Phys. Chem., 1986, 90, 6616–6624 CrossRef CAS.
- D. D. Wagman, W. H. Evans, V. B. Parker, R. H. Schumm, I. Halow, S. M. Bailey, K. L. Churney and R. L. Nuttall, J. Phys. Chem. Ref. Data, Suppl., 1982, 11, 2–38 Search PubMed and 32–83.
- R. P. Bell, The proton in chemistry, Chapman and Hall, London, 2nd edn, 1973 Search PubMed.
- D. Jose and A. Datta, Angew. Chem., Int. Ed., 2012, 51, 9389–9392 CrossRef CAS PubMed.
- D. J. Anick, J. Phys. Chem. A, 2011, 115, 6327–6338 CrossRef CAS PubMed.
- R. Sander, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. M. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, USA, http://webbook.nist.gov, accessed December 12, 2013 Search PubMed.
- E. Samson, J. Marchand and K. A. Snyder, Mater. Struct., 2003, 36, 156–165 CrossRef CAS.
- W. J. Lu, H. R. Guo, I. M. Chou, R. C. Burruss and L. L. Li, Geochim. Cosmochim. Acta, 2013, 115, 183–204 CrossRef CAS PubMed.
- M. I. H. Panhuis, C. H. Patterson and R. M. Lynden-Bell, Mol. Phys., 1998, 94, 963–972 CrossRef.
- S. T. Moin, A. B. Pribil, L. H. V. Lim, T. S. Hofer, B. R. Randolf and B. M. Rode, Int. J. Quantum Chem., 2011, 111, 1370–1378 CrossRef CAS.
- M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929 CrossRef CAS PubMed.
- N. Agmon, Chem. Phys. Lett., 2000, 319, 247–252 CrossRef CAS.
- A. Stirling, J. Phys. Chem. B, 2011, 115, 14683–14687 CrossRef CAS PubMed.
- X. G. Wang, W. Conway, R. Burns, N. McCann and M. Maeder, J. Phys. Chem. A, 2010, 114, 1734–1740 CrossRef CAS PubMed.
- S. Miertus, O. Kysel and M. Krajci, Chem. Zvesti, 1981, 35, 3–7 CAS.
- P. U. Andersson, M. J. Ryding, O. Sekiguchi and E. Uggerud, Phys. Chem. Chem. Phys., 2008, 10, 6127–6134 RSC.
- A. S. Zatula, P. U. Andersson, M. J. Ryding and E. Uggerud, Phys. Chem. Chem. Phys., 2011, 13, 13287–13294 RSC.
- M. J. Ryding, A. S. Zatula, P. U. Andersson and E. Uggerud, Phys. Chem. Chem. Phys., 2011, 13, 1356–1367 RSC.
- M. J. Ryding, K. Ruusuvuori, P. U. Andersson, A. S. Zatula, M. J. McGrath, T. Kurten, I. K. Ortega, H. Vehkamaki and E. Uggerud, J. Phys. Chem. A, 2012, 116, 4902–4908 CrossRef CAS PubMed.
- M. J. Ryding, A. M. Jonsson, A. S. Zatula, P. U. Andersson and E. Uggerud, Atmos. Chem. Phys., 2012, 12, 2809–2822 CrossRef CAS.
- A. S. Zatula, M. J. Ryding, P. U. Andersson and E. Uggerud, Int. J. Mass Spectrom., 2012, 330, 191–199 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 2007, 126 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on the experimental methods and results, including a discussion on abundance spectra, evaporation patterns and magic numbers. In addition, tabulated energy levels and Cartesian coordinates are given for all structures and transition states. See DOI: 10.1039/c4cp00100a |
| This journal is © the Owner Societies 2014 |