1 4 Angles and Their Measures What you



















- Slides: 41

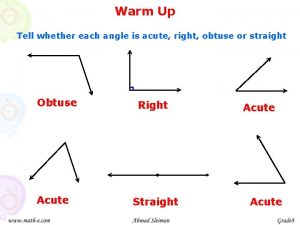
1. 4 Angles and Their Measures What you should learn GOAL 1 Use Angle Postulates GOAL 2 Classify angles as acute, right, obtuse, or straight. Why you should learn it To solve real-life problems about angles, such as the field of vision of a horse wearing blinkers.

1. 4 GOAL Angles and Their Measures 1 USING ANGLE POSTULATES An _____ angle consists of two different rays that have the same initial point. The rays are the _____ sides of the angle and the initial point is the ______. vertex The three names for this C angle are A The sides are B The vertex is point A.

EXAMPLE 1 Name angles Name three angles in the diagram. WXY, or YXW YXZ, or ZXY WXZ, or ZXW You should not name any of these angles X because all three angles have X as their vertex.

EXAMPLE 1 Extra Example 1 Name the angles in the figure. M N O P Click for the answers. 1. 2. 3. should not be used to name any angle in the figure. Why not? All three angles have N as the vertex, so could mean any of the angles.

Measuring Angles The expression is read as “the ____ measure of angle A. ” IMPORTANT!!! Note the difference in notation between an angle and its measure. Always use the correct notation!!! The tool used to measure angles is called a _____. protractor The units used to measure angles are called _______, degrees and the symbol for them is a _.

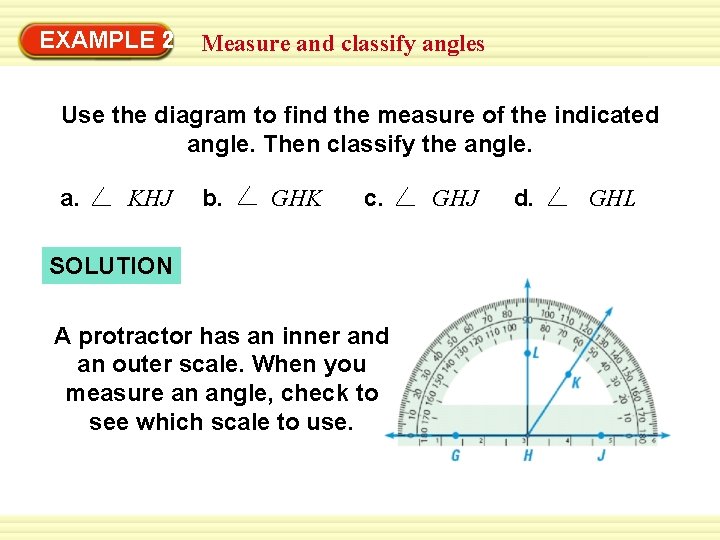
EXAMPLE 2 Measure and classify angles Use the diagram to find the measure of the indicated angle. Then classify the angle. a. KHJ b. GHK c. SOLUTION A protractor has an inner and an outer scale. When you measure an angle, check to see which scale to use. GHJ d. GHL

EXAMPLE 2 Measure and classify angles o a. HJ is lined up with the 0 on the inner scale of the protractor. HK passes through 55 o on the inner scale. So, m KHJ = 55 o. It is an acute angle. b. HG is lined up with the 0 o on the outer scale and HK passes through 125 oon the outer scale. So, m GHK = 125 o. It is an obtuse angle. c. mo GHJ = 180. It is a straight angle. d. m o GHL= 90. It is a right angle.

Measuring Angles Let’s measure some angles. R Y Q Since congruent _____. M T S we say that the angles are Remember: Angles are congruent, measures are equal. Incorrect: Correct: and

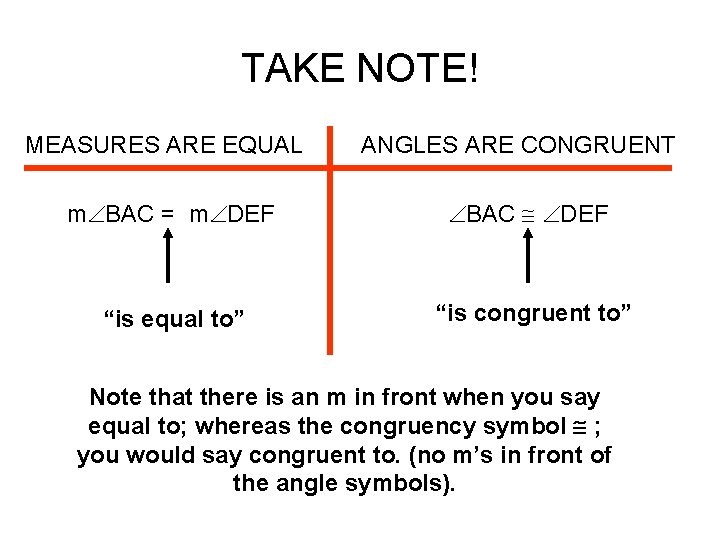
TAKE NOTE! MEASURES ARE EQUAL ANGLES ARE CONGRUENT m BAC = m DEF BAC DEF “is equal to” “is congruent to” Note that there is an m in front when you say equal to; whereas the congruency symbol ; you would say congruent to. (no m’s in front of the angle symbols).

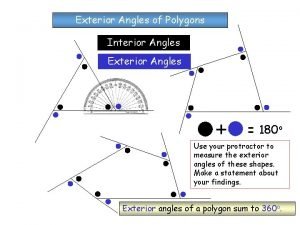
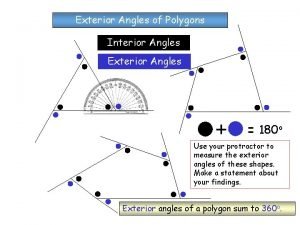
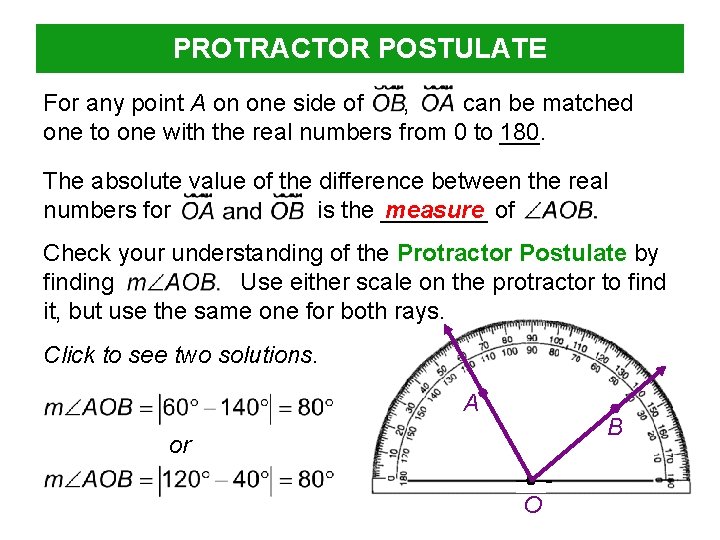
PROTRACTOR POSTULATE For any point A on one side of , can be matched one to one with the real numbers from 0 to 180 ___. The absolute value of the difference between the real numbers for is the ____ measure of Check your understanding of the Protractor Postulate by finding Use either scale on the protractor to find it, but use the same one for both rays. Click to see two solutions. A B or O

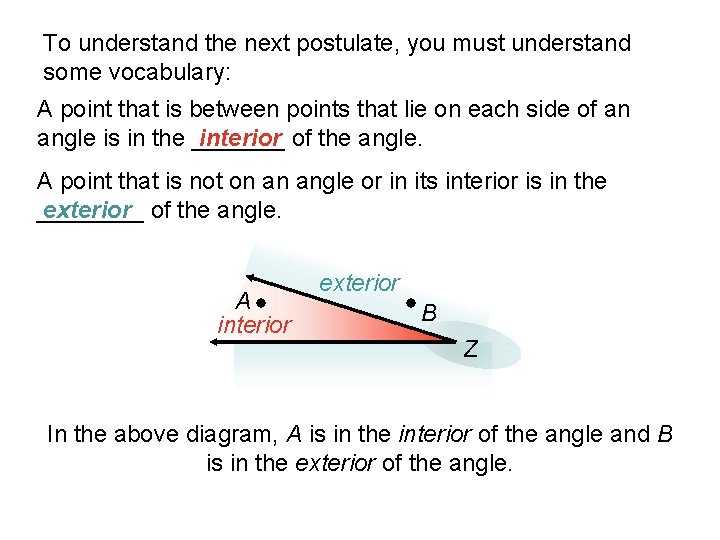
To understand the next postulate, you must understand some vocabulary: A point that is between points that lie on each side of an angle is in the _______ interior of the angle. A point that is not on an angle or in its interior is in the ____ exterior of the angle. A interior exterior B Z In the above diagram, A is in the interior of the angle and B is in the exterior of the angle.

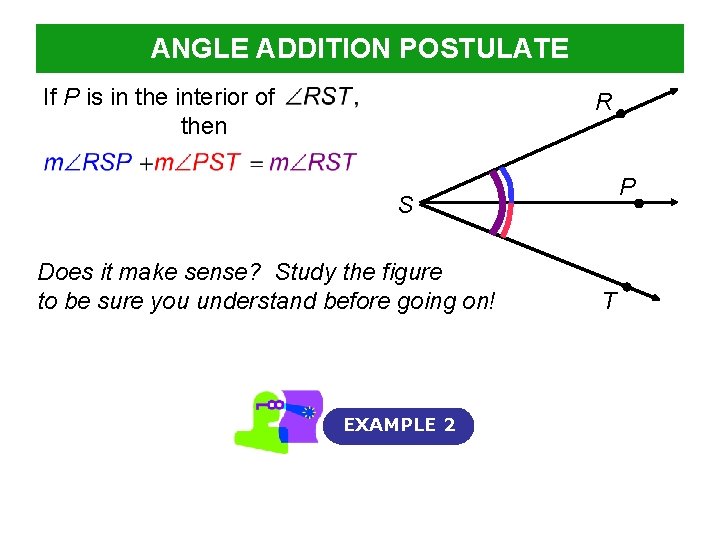
ANGLE ADDITION POSTULATE If P is in the interior of then R P S Does it make sense? Study the figure to be sure you understand before going on! EXAMPLE 2 T

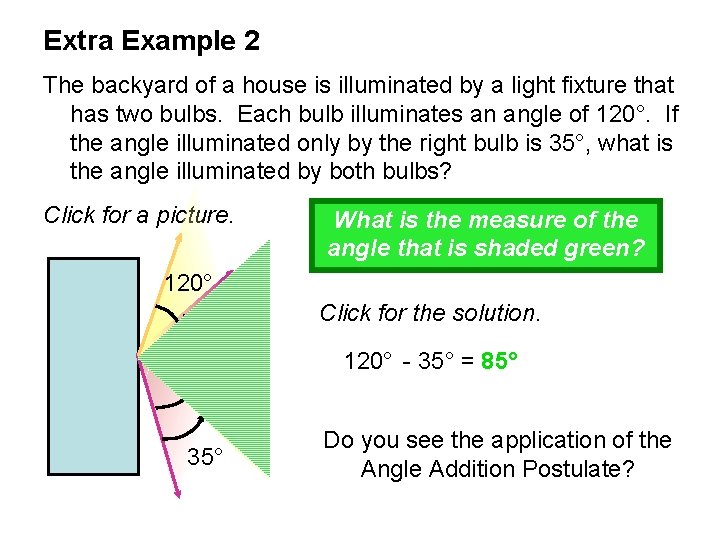
Extra Example 2 The backyard of a house is illuminated by a light fixture that has two bulbs. Each bulb illuminates an angle of 120°. If the angle illuminated only by the right bulb is 35°, what is the angle illuminated by both bulbs? Click for a picture. What is the measure of the angle that is shaded green? 120° Click for the solution. 120° - 35° = 85° 35° Do you see the application of the Angle Addition Postulate?

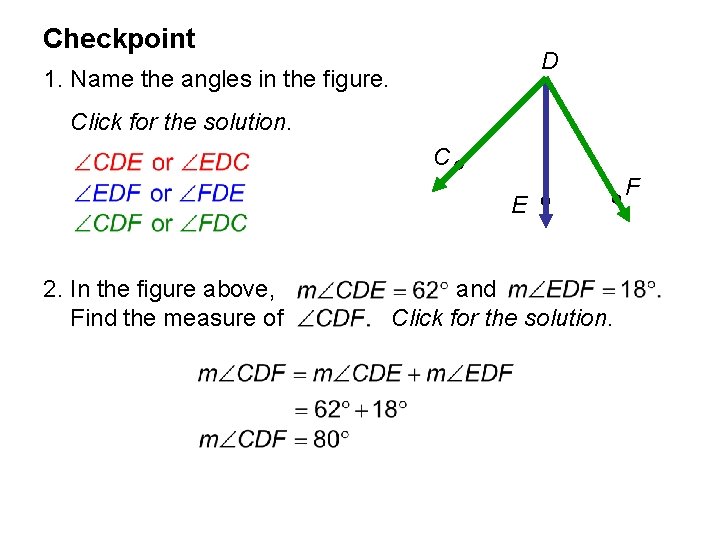
Checkpoint D 1. Name the angles in the figure. Click for the solution. C E 2. In the figure above, Find the measure of and Click for the solution. F

1. 4 GOAL Angles and Their Measures 2 CLASSIFYING ANGLES We can classify all angles by their measure as follows: acute Angles with measures between 0 and 90 degrees: _____ 90 degree angles: _____ right Angles with measures between 90 and 180 degrees: ______ obtuse 180 degree angles: _______ straight

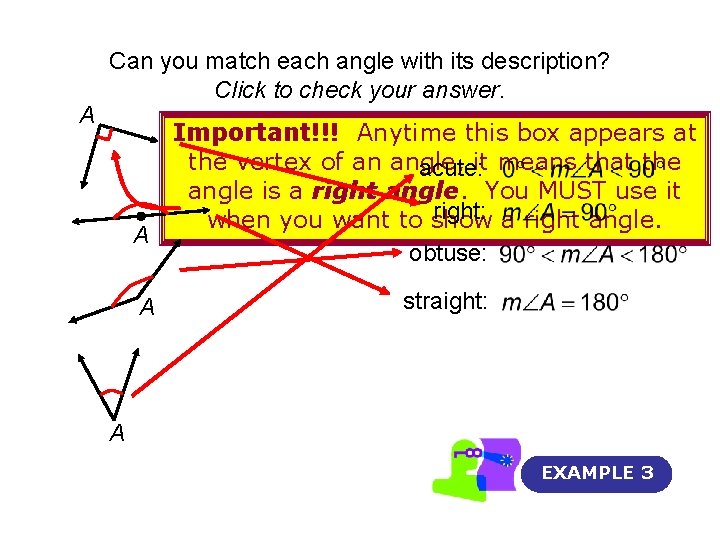
A Can you match each angle with its description? Click to check your answer. Important!!! Anytime this box appears at the vertex of an angle, acute: it means that the angle is a right angle. You MUST use it right: a right angle. when you want to show A obtuse: A straight: A EXAMPLE 3

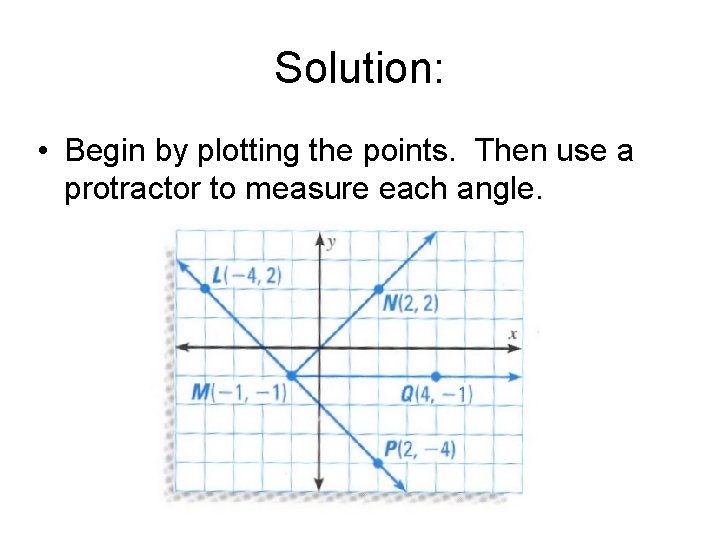
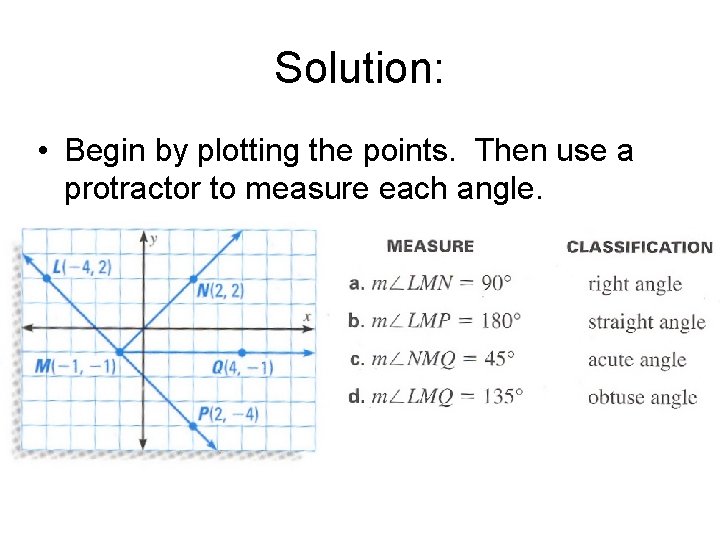
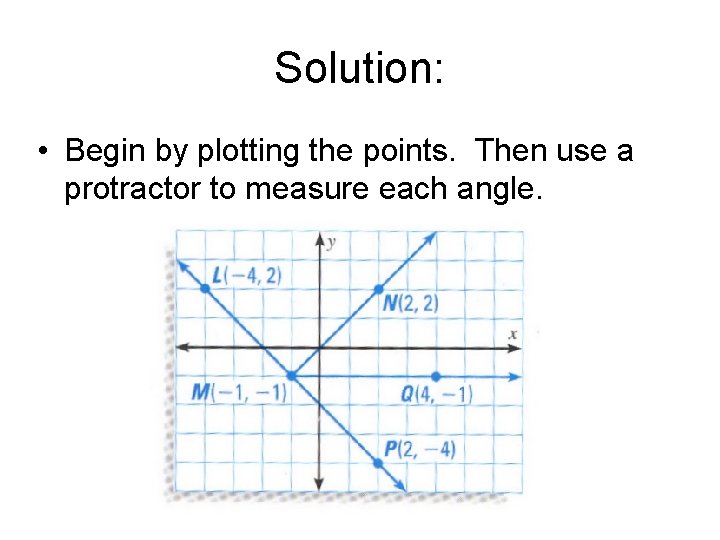
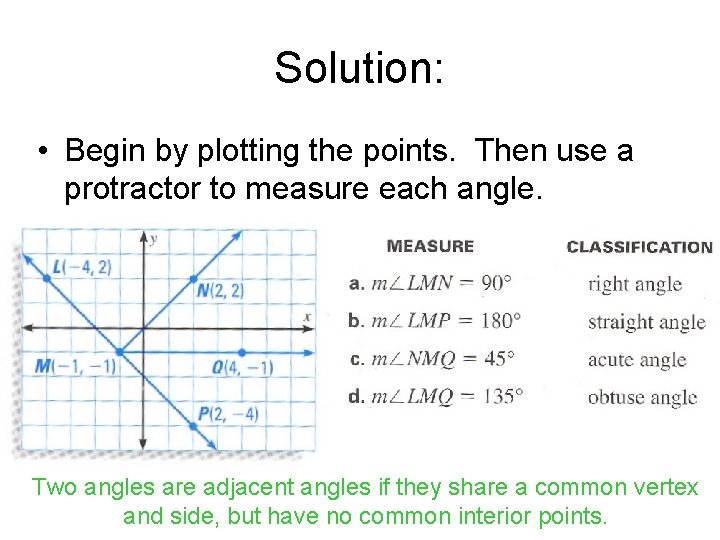
Classifying Angles in a Coordinate Plane • a. b. c. d. Plot the points L(-4, 2), M(-1, -1), N(2, 2), Q(4, -1), and P(2, -4). Then measure and classify the following angles as acute, right, obtuse, or straight. LMN LMP NMQ LMQ

Solution: • Begin by plotting the points. Then use a protractor to measure each angle.

Solution: • Begin by plotting the points. Then use a protractor to measure each angle.

Extra Example 3 Plot the points A(-3, -1), B(-1, 1), C(2, 4), D(2, 1), and E(2, -2). Then measure and classify the following angles as acute, right, obtuse, or straight. Click for each answer. a. 45°, acute b. 90°, right c. 180°, straight d. 135°, obtuse Reminder: Be sure you understand the material before going on to the next slide. If you need to review, do so NOW!

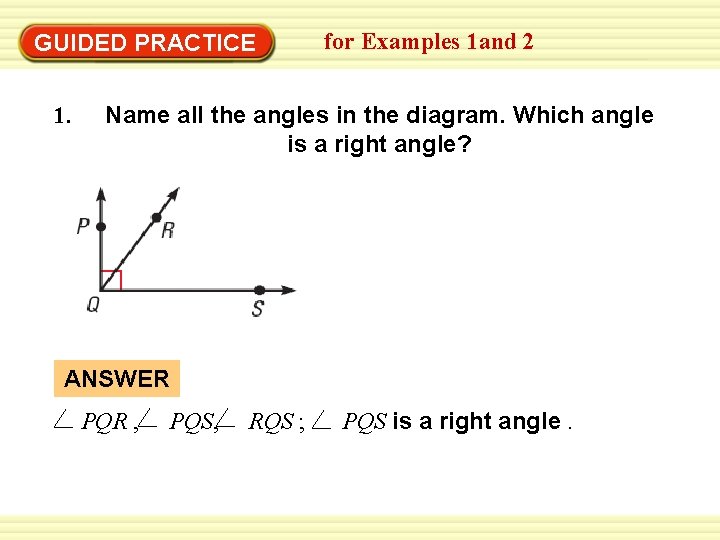
GUIDED PRACTICE 1. for Examples 1 and 2 Name all the angles in the diagram. Which angle is a right angle? ANSWER PQR , PQS, RQS ; PQS is a right angle.

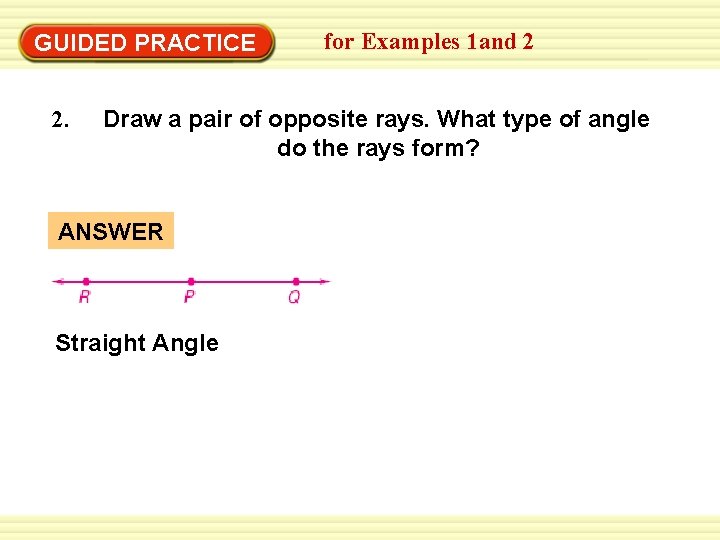
GUIDED PRACTICE 2. for Examples 1 and 2 Draw a pair of opposite rays. What type of angle do the rays form? ANSWER Straight Angle

EXAMPLE 3 Find angle measures ALGEBRA Given that m and m o LKN =145 , find m MKN. LKM SOLUTION STEP 1 Write and solve an equation to find the value of x. m LKN = m LKM + m MKN o o 145 = (2 x + 10)o + (4 x – 3) 145 = 6 x + 7 138 = 6 x 23 = x Angle Addition Postulate Substitute angle measures. Combine like terms. Subtract 7 from each side. Divide each side by 6.

EXAMPLE 3 Find angle measures STEP 2 Evaluate the given expressions when x = 23. m m LKM = (2 x + 10)° = (2 23 + 10)° = 56° MKN = (4 x – 3)° = (4 23 – 3)° = 89° ANSWER So, m LKM = 56° and m MKN = 89°.

GUIDED PRACTICE for Example 3 Find the indicated angle measures. 3. Given that KLM is a straight angle, find m and m NLM. ANSWER 125°, 55° KLN

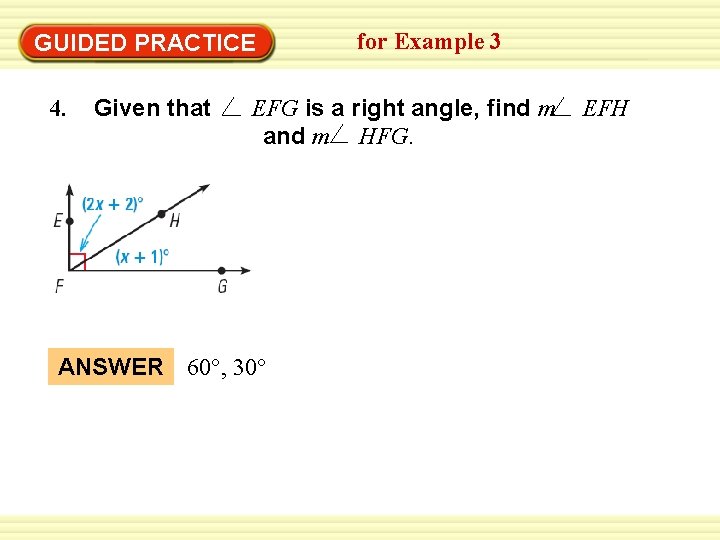
GUIDED PRACTICE 4. Given that for Example 3 EFG is a right angle, find m and m HFG. ANSWER 60°, 30° EFH

EXAMPLE 4 Identify congruent angles Trapeze The diagram shows some of the angles formed by the ropes in a trapeze apparatus. Identify the congruent angles. If m DEG = 157° , what is m GKL? SOLUTION There are two pairs of congruent angles: DEF ~ JKL and DEG ~ GKL. Because DEG ~ GKL, m DEG = m GKL. So, m GKL = 157°.

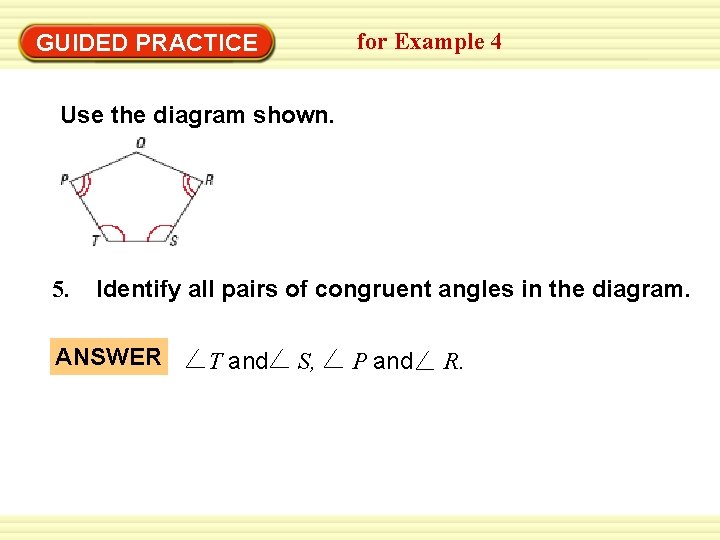
for Example 4 GUIDED PRACTICE Use the diagram shown. 5. Identify all pairs of congruent angles in the diagram. ANSWER T and S, P and R.

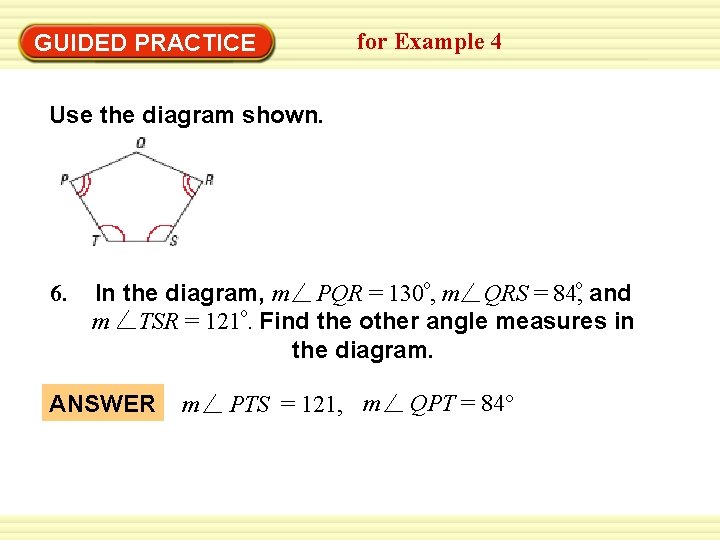
GUIDED PRACTICE for Example 4 Use the diagram shown. 6. In the diagram, m PQR = 130 o, m QRS = 84, o and o m TSR = 121. Find the other angle measures in the diagram. ANSWER m PTS = 121, m QPT = 84°

An ANGLE BISECTOR is a ray that divides an angle into two angles that are congruent. 1. Draw and label an acute angle, . 2. Fold the paper so that MN is on top of LM. 3. Draw a point P on the folded side. Connect it with M. 4. Measure the angles formed.

EXAMPLE 5 Double an angle measure In the diagram at the right, YW bisects XYZ, and o m XYW = 18. Find m XYZ. SOLUTION By the Angle Addition Postulate, XYZ = m XYW + m WYZ. Because YW bisects you know that XYW ~ WYZ. m So, m m XYW = m WYZ, and you can write XYZ = m XYW + m WYZ = 18°+ 18° = 36°. XYZ

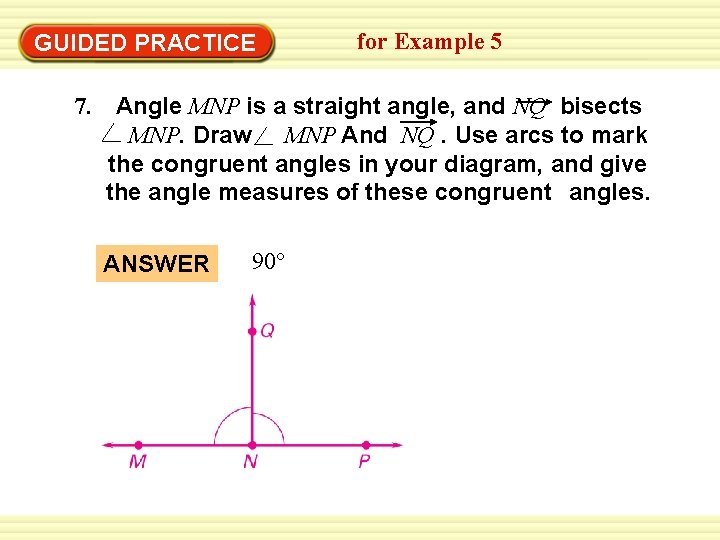
GUIDED PRACTICE 7. for Example 5 Angle MNP is a straight angle, and NQ bisects MNP. Draw MNP And NQ. Use arcs to mark the congruent angles in your diagram, and give the angle measures of these congruent angles. ANSWER 90°

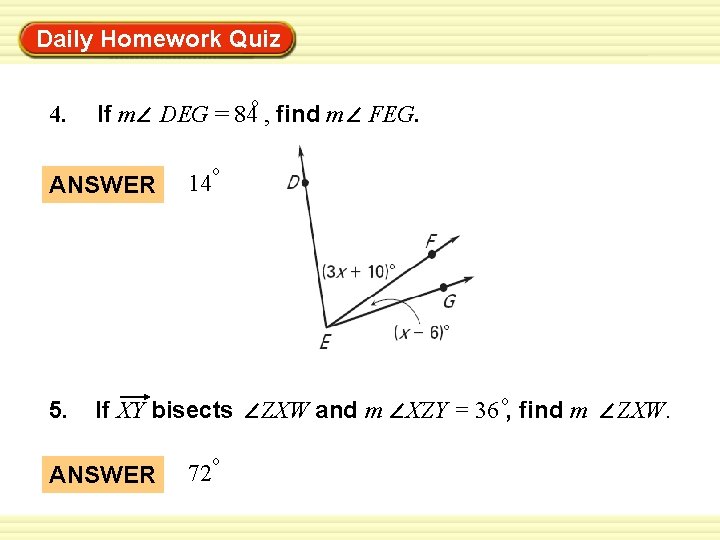
Daily Homework Quiz Classify each angle as acute, obtuse , right or straight. 1. m ANSWER o A = 90 right o 2. m B = 62 ANSWER acute 3. m ANSWER o C = 119 obtuse

Daily Homework Quiz 4. If m ANSWER 5. o DEG = 84 , find m o 14 If XY bisects ANSWER FEG. o 72 ZXW and m o XZY = 36 , find m ZXW.

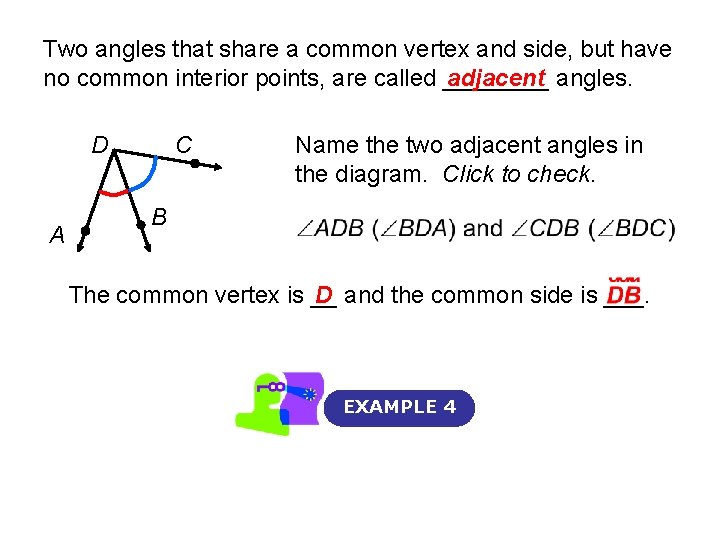
Two angles that share a common vertex and side, but have no common interior points, are called ____ adjacent angles. D A C Name the two adjacent angles in the diagram. Click to check. B The common vertex is __ D and the common side is ___. EXAMPLE 4

Classifying Angles in a Coordinate Plane • a. b. c. d. Plot the points L(-4, 2), M(-1, -1), N(2, 2), Q(4, -1), and P(2, -4). Then measure and classify the following angles as acute, right, obtuse, or straight. LMN LMP NMQ LMQ

Solution: • Begin by plotting the points. Then use a protractor to measure each angle.

Solution: • Begin by plotting the points. Then use a protractor to measure each angle. Two angles are adjacent angles if they share a common vertex and side, but have no common interior points.

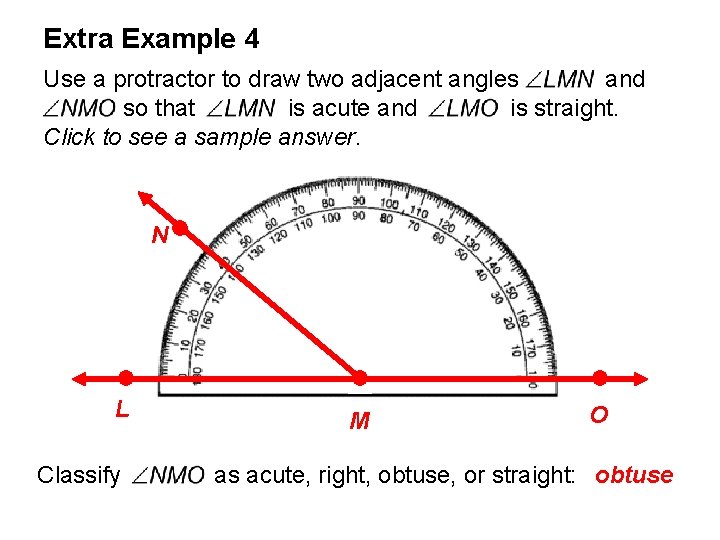
Extra Example 4 Use a protractor to draw two adjacent angles and so that is acute and is straight. Click to see a sample answer. N L Classify M O as acute, right, obtuse, or straight: obtuse

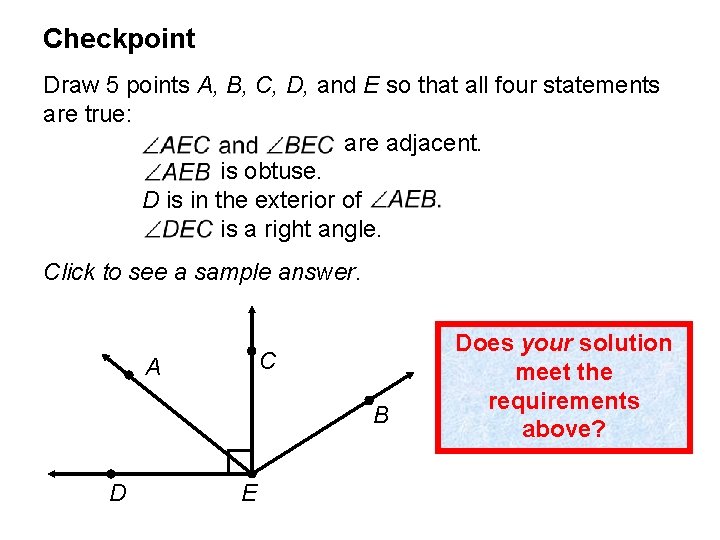
Checkpoint Draw 5 points A, B, C, D, and E so that all four statements are true: are adjacent. is obtuse. D is in the exterior of is a right angle. Click to see a sample answer. C A B D E Does your solution meet the requirements above?

QUESTIONS?
 Vertical angles
Vertical angles Vertically opposite angles are congruent
Vertically opposite angles are congruent Anova repeated measures
Anova repeated measures Module 15 angles and segments in circles
Module 15 angles and segments in circles Black classification cavities
Black classification cavities Kites and trapezoids are parallelograms
Kites and trapezoids are parallelograms The diagonals of rhombus wxyz intersect at v
The diagonals of rhombus wxyz intersect at v Extemporaneous compounding
Extemporaneous compounding Classify each angle as acute obtuse right or straight
Classify each angle as acute obtuse right or straight A pair of adjacent complementary angles
A pair of adjacent complementary angles Answers
Answers Tell me what you eat and i shall tell you what you are
Tell me what you eat and i shall tell you what you are Romeo + juliet prologue
Romeo + juliet prologue You say you love the rain but you open your umbrella
You say you love the rain but you open your umbrella You are what you eat do you agree or disagree
You are what you eat do you agree or disagree If you think you can you can poem
If you think you can you can poem Follow you wherever you may go
Follow you wherever you may go Teaspoon abbreviation
Teaspoon abbreviation Find the refrence angle
Find the refrence angle You will know them by their fruit
You will know them by their fruit Match the word with the definition mug burglary
Match the word with the definition mug burglary Vertical angles
Vertical angles Weights and measure training
Weights and measure training Finding segment lengths find the value of x
Finding segment lengths find the value of x Secant tangent angle
Secant tangent angle 10-6 secants tangents and angle measures
10-6 secants tangents and angle measures Measures to correct excess demand and deficient demand
Measures to correct excess demand and deficient demand Liceo scientifico fermo
Liceo scientifico fermo Fuller's formula for concrete
Fuller's formula for concrete Tom minka
Tom minka Demolition hazards and control measures
Demolition hazards and control measures Department of measurement standards
Department of measurement standards Segment lengths in circles
Segment lengths in circles A suitcase measures 24 inches long
A suitcase measures 24 inches long Numerical measure of how alike two data objects are
Numerical measure of how alike two data objects are Belief and plausibility measures in fuzzy
Belief and plausibility measures in fuzzy Local reliability protocols
Local reliability protocols California weights and measures
California weights and measures Measures of central tendency and variation
Measures of central tendency and variation Measures of central tendency and variation
Measures of central tendency and variation Operating performance measures
Operating performance measures Statutory and non statutory welfare measures
Statutory and non statutory welfare measures