Chapter 12 Thermal Energy Section 12 1 Temperature














































































- Slides: 91

Chapter 12 Thermal Energy

Section 12. 1 Temperature and Thermal Energy The study of heat transformations into other forms of energy is called thermodynamics. Although the study of thermodynamics began in the eighteenth century, it was not until around 1900 that the concepts of thermodynamics were linked to the motion of atoms and molecules in solids, liquids, and gases. This is why this field is so “new”

Section 12. 1 Temperature and Thermal Energy There are numerous molecules moving freely in a gas, resulting in many collisions. Therefore, it is convenient to discuss the total energy of the molecules and the average energy per molecule. The total energy of the molecules is called thermal energy, and the average energy per molecule is related to the temperature of the gas.

Section 12. 1 Temperature and Thermal Energy Hot Objects What makes an object hot? When you fill up a balloon with helium, the rubber in the balloon is stretched by the repeated pounding from helium atoms. Each of the billions of helium atoms in the balloon collides with the rubber wall, bounces back, and hits the other side of the balloon wall.

Section 12. 1 Temperature and Thermal Energy Hot Objects If you put a balloon in sunlight, the balloon gets slightly larger. The energy from the Sun makes each of the gas atoms move faster and bounce off the rubber walls of the balloon more often. Each atomic collision with the balloon wall puts a greater force on the balloon and stretches the rubber. Thus, the balloon expands.

Section 12. 1 Temperature and Thermal Energy Hot Objects On the other hand, if you refrigerate a balloon, you will find that it shrinks slightly. Lowering the temperature slows the movement of the helium atoms. Even though the balloon contains the same number of atoms, the balloon shrinks.

Section Temperature and Thermal Energy 12. 1 Solids The atoms in solids also have kinetic energy, but they are unable to move freely as gas atoms do. If a solid has N number of atoms, then the total thermal energy in the solid is equal to the average kinetic energy and potential energy per atom times N.

Section 12. 1 Temperature and Thermal Energy and Temperature A hot object has more thermal energy than a similar cold object. This means that, as a whole, the particles in a hot object have greater thermal energy than the particles in a cold object. This does not mean that all the particles in an object have exactly the same amount of energy; they have a wide range of energies.

Section 12. 1 Temperature and Thermal Energy Temperature is a property of atoms themselves, and therefore, it does not depend on the number of atoms in an object. Temperature depends only on the average kinetic energy of the particles in the object. Consider two blocks of steel. The first block has a mass of 1 kg, and the second block has a mass of 2 kg. If the 1 -kg block is at the same temperature as the 2 -kg block, the average kinetic energy of the particles in each block is the same.

Section 12. 1 Temperature and Thermal Energy Temperature However, the 2 -kg block has twice the mass of the 1 -kg block. Hence, the 2 -kg block has twice the amount of particles as the 1 -kg block. Thus, the total amount of kinetic energy of the particles in the 2 kg block is twice that of the 1 -kg mass. Therefore, thermal energy in an object is proportional to the number of particles in it.

Section 12. 1 Temperature and Thermal Energy Equilibrium and Thermometry How do you measure your body temperature? If you suspect that you have a fever, you might place a thermometer in your mouth and wait for a few minutes before checking thermometer for your temperature reading. The atomic level process involved in measuring temperature involves collisions and energy transfers between thermometer and your body.

Section 12. 1 Temperature and Thermal Energy Equilibrium and Thermometry Energy is then transferred from your skin to the glass particles by the process of conduction, which is the transfer of kinetic energy when particles collide. The thermal energy of the particles that make up thermometer increases, while at the same time, thermal energy of the particles in your skin decreases.

Section 12. 1 Temperature and Thermal Energy Thermal Equilibrium As the particles in the glass gain more energy, they begin to give some of their energy back to the particles in your body. At some point, the rate of transfer of energy between the glass and your body becomes equal, and your body and thermometer are then at the same temperature.

Section 12. 1 Temperature and Thermal Energy Thermal Equilibrium At this point, your body and thermometer are said to have reached thermal equilibrium, the state in which the rate of energy flow between two objects is equal and the objects are at the same temperature, as shown below. >

Section 12. 1 Temperature and Thermal Energy Temperature Scales: Celsius and Kelvin Over the years, scientists developed temperature scales so that they could compare their measurements with those of other scientists. A scale based on the properties of water was devised in 1741 by Swedish astronomer and physicist Anders Celsius. On this scale, now called the Celsius scale, the freezing point of pure water is defined to be 0°C. The boiling point of pure water at sea level is defined to be 100°C.

Section 12. 1 Temperature and Thermal Energy Temperature Limits The wide range of temperatures present in the universe is shown in the figure. Temperatures do not appear to have an upper limit. The interior of the Sun is at least 1. 5× 107°C. Temperatures do, however, have a lower limit.

Section 12. 1 Temperature and Thermal Energy Temperature Limits If an ideal gas, such as helium in a balloon is cooled, it contracts in such a way that it occupies a volume that is only the size of the helium atoms at – 273. 15°C. At this temperature, all thermal energy that can be removed has been removed from the gas. It is impossible to reduce the temperature any further. Therefore, there can be no temperature lower than 273. 15°C, which is called absolute zero.

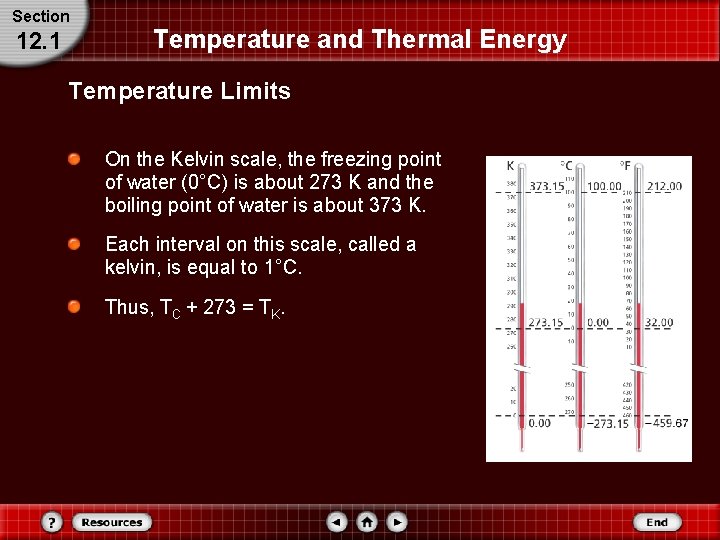
Section 12. 1 Temperature and Thermal Energy Temperature Limits The Celsius scale is useful for day-to-day measurements of temperature. It is not conducive for working on science and engineering problems, however, because it has negative temperatures. Negative temperatures suggest a molecule could have negative kinetic energy, which is not possible because kinetic energy is always positive. The solution to this issue is to use a temperature scale based on absolute zero. The zero point of the Kelvin scale is defined to be absolute zero.

Section 12. 1 Temperature and Thermal Energy Temperature Limits On the Kelvin scale, the freezing point of water (0°C) is about 273 K and the boiling point of water is about 373 K. Each interval on this scale, called a kelvin, is equal to 1°C. Thus, TC + 273 = TK.

Section 12. 1 Temperature and Thermal Energy Heat and the Flow of Thermal Energy When two objects come in contact with each other, they transfer energy. The energy that is transferred between objects when they come in contact is called heat. The symbol Q is used to represent an amount of heat, which like other forms of energy is measured in joules. If Q has a negative value, heat has left the object; if Q has a positive value, heat has been absorbed by the object.

Section 12. 1 Temperature and Thermal Energy Conduction If you place one end of a metal rod in a flame, the hot gas particles in the flame conduct heat to the rod. The other end of the rod also becomes warm within a short period of time. Heat is conducted because the particles in the rod are in direct contact with each other.

Section 12. 1 Temperature and Thermal Energy Convection This motion of fluid in a liquid or gas caused by temperature differences is called convection. Thunderstorms are excellent examples of large-scale atmospheric convection.

Section 12. 1 Temperature and Thermal Energy Radiation The third method of thermal transfer does not depend on the presence of matter. The Sun warms Earth from over 150 million km away via radiation, which is the transfer of energy by electromagnetic waves. These waves carry the energy from the hot Sun to the muchcooler Earth.

Section 12. 1 Temperature and Thermal Energy Specific Heat Some objects are easier to heat than others. When heat flows into an object, its thermal energy and temperature increase. The specific heat of a material is the amount of energy that must be added to the material to raise the temperature of a unit mass by one temperature unit. In SI units, specific heat, represented by C, is measured in J/kg. K. What else is measured in C?

Section 12. 1 Temperature and Thermal Energy Specific Heat Liquid water has a high specific heat compared to the specific heat of other substances. A mass of 1 kg of water requires 4180 J of energy to increase its temperature by 1 K. The same mass of copper requires only 385 J to increase its temperature by 1 K.

Section 12. 1 Temperature and Thermal Energy Specific Heat The heat gained or lost by an object as its temperature changes depends on the mass, the change in temperature, and the specific heat of the substance. By using the following equation, you can calculate the amount of heat, Q, that must be transferred to change the temperature of an object. Heat Transfer Q = m. CΔT = m. C (Tf – Ti)

Section 12. 1 Temperature and Thermal Energy Calorimetry: Measuring Specific Heat In an isolated, closed system, the change in thermal energy is equal to the heat transferred because no work is done. Therefore, the change in energy for each block can be expressed by the following equation: ΔE = Q = m. CΔT The increase in thermal energy of block A is equal to the decrease in thermal energy of block B. Thus, the following relationship is true: m. ACAΔTA + m. BCBΔTB = 0

Section 12. 1 Temperature and Thermal Energy Calorimetry: Measuring Specific Heat The change in temperature is the difference between the final and initial temperatures; that is, ΔT = Tf – Ti. If the temperature of a block increases, Tf >Ti, and ΔT is positive. If the temperature of the block decreases, Tf <Ti, and ΔT is negative. The final temperatures of the two blocks are equal. The following is the equation for the transfer of energy: m. ACA(Tf – TA) + m. BCB(Tf – TB) = 0

Section 12. 1 Temperature and Thermal Energy Transferring Heat in a Calorimeter A calorimeter contains 0. 50 kg of water at 15°C. A 0. 040 -kg block of zinc at 115°C is placed in the water. What is the final temperature of the system?

Section 12. 1 Temperature and Thermal Energy Transferring Heat in a Calorimeter Let zinc be sample A and water be sample B. Sketch the transfer of heat from the hotter zinc to the cooler water.

Section 12. 1 Temperature and Thermal Energy Transferring Heat in a Calorimeter Identify the known and unknown variables. Known: m. A = 0. 040 kg CA = 388 J/kg·ºC TA = 115 ºC m. B = 0. 500 kg CB = 4180 J/kg·ºC TB= 15. 0 ºC Unknown: Tf = ?

Section 12. 1 Temperature and Thermal Energy Transferring Heat in a Calorimeter Determine the final temperature using the following equation.

Section 12. 1 Temperature and Thermal Energy Transferring Heat in a Calorimeter Substitute m. A = 0. 040 kg, CA = 388 J/kg·ºC, TA = 115 ºC, m. B = 0. 500 kg, CB = 4180 J/kg·ºC, TB= 15. 0 ºC.

Section 12. 1 Section Check Question 1 Distinguish between thermal energy and temperature.

Section Check 12. 1 Answer 1 Thermal Energy 1. 2. 3. Temperature The total energy of the 1. molecules is called thermal energy. Thermal energy is proportional 2. to the number of particles in an object. Two blocks of steel of different 3. masses kept together have different thermal energies depending upon the number of particles present in the blocks The average energy per molecule is related to the temperature of the gas. Temperature does not depend on the number of particles in an object. Two blocks of steel of different masses kept together may have the same temperature depending upon the surrounding.

Section Check 12. 1 Question 2 When one end of a metal rod is kept in a flame, the other end also becomes warm within a short period of time. What causes this? A. Conduction B. Convection C. Radiation D. Thermal equilibrium

Section 12. 1 Section Check Answer 2 Answer: A Reason: Conduction is a process in which heat is conducted when particles are in direct contact with each other. In a metal rod, all the particles are in direct contact with each other. Hence, the other end of the rod also becomes warm within a short period of time, because of conduction.

Section 12. 1 Section Check Question 3 Define specific heat of a material.

Section 12. 1 Section Check Answer 3 The specific heat of a material is the amount of energy that must be added to a material to raise the temperature of a unit mass by one temperature unit. In SI units, specific heat represented by C is measured in J/Kg·K.

Section 12. 2 Changes of State and the Laws of Thermodynamics Changes of State The three most common states of matter are solids, liquids, and gases. As the temperature of a solid is raised, it usually changes to a liquid. At even higher temperatures, it becomes a gas. When thermal energy of a solid is increased, the motion of the particles also increases, as does the temperature.

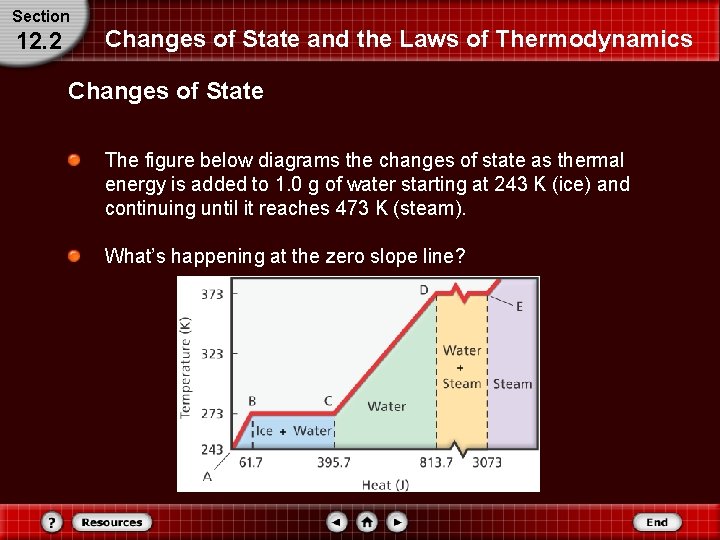
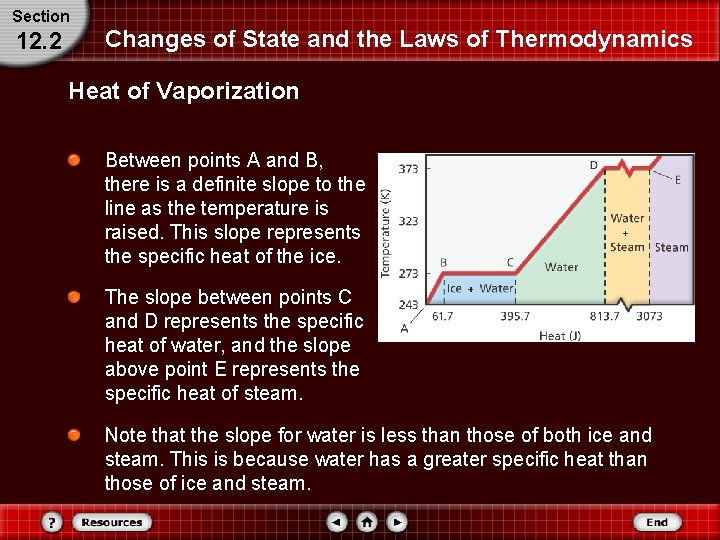
Section 12. 2 Changes of State and the Laws of Thermodynamics Changes of State The figure below diagrams the changes of state as thermal energy is added to 1. 0 g of water starting at 243 K (ice) and continuing until it reaches 473 K (steam). What’s happening at the zero slope line?

Section 12. 2 Changes of State and the Laws of Thermodynamics Changes of State At some point, the added thermal energy causes the particles to move rapidly enough that their motion overcomes the forces holding the particles together in a fixed location. The particles are still touching each other, but they have more freedom of movement. Eventually, the particles become free enough to slide past each other.

Section 12. 2 Changes of State and the Laws of Thermodynamics Melting Point At this point, the substance has changed from a solid to a liquid. The temperature at which this change occurs is the melting point of the substance. When a substance is melting, all of the added thermal energy goes to overcome the forces holding the particles together in the solid state. None of the added thermal energy increases the kinetic energy of the particles.

Section 12. 2 Changes of State and the Laws of Thermodynamics Melting Point This can be observed between points B and C in the figure, where the added thermal energy melts the ice at a constant 273 K. Because the kinetic energy of the particles does not increase, the temperature does not increase between points B and C.

Section 12. 2 Changes of State and the Laws of Thermodynamics Boiling Point Once a solid is completely melted, there are no more forces holding the particles in the solid state. Adding more thermal energy again increases the motion of the particles, and the temperature of the liquid rises. In the diagram, this process occurs between points C and D.

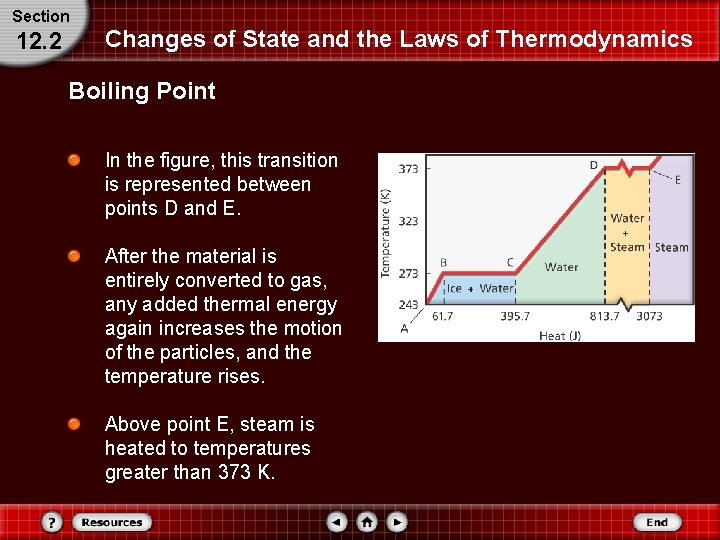
Section 12. 2 Changes of State and the Laws of Thermodynamics Boiling Point As the temperature increases further, some particles in the liquid acquire enough energy to break free from the other particles. At a specific temperature, known as the boiling point, further addition of energy causes the substance to undergo another change of state. All the added thermal energy converts the substance from the liquid state to the gaseous state. As in melting, the temperature does not rise while a liquid boils.

Section 12. 2 Changes of State and the Laws of Thermodynamics Boiling Point In the figure, this transition is represented between points D and E. After the material is entirely converted to gas, any added thermal energy again increases the motion of the particles, and the temperature rises. Above point E, steam is heated to temperatures greater than 373 K.

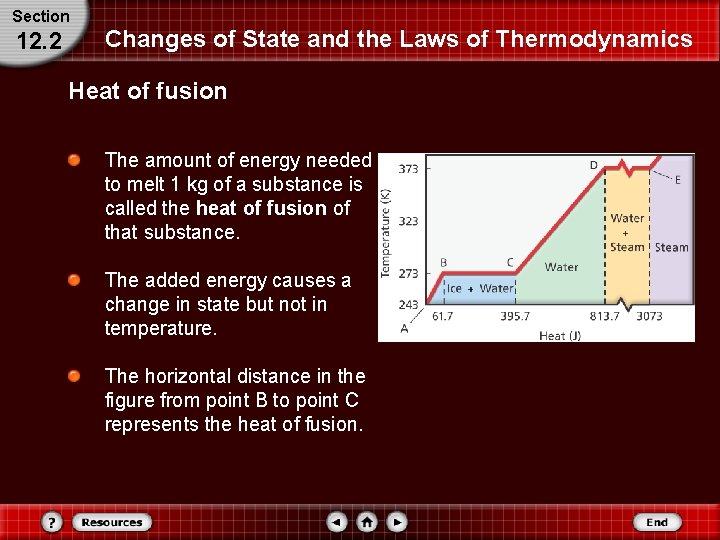
Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of fusion The amount of energy needed to melt 1 kg of a substance is called the heat of fusion of that substance. The added energy causes a change in state but not in temperature. The horizontal distance in the figure from point B to point C represents the heat of fusion.

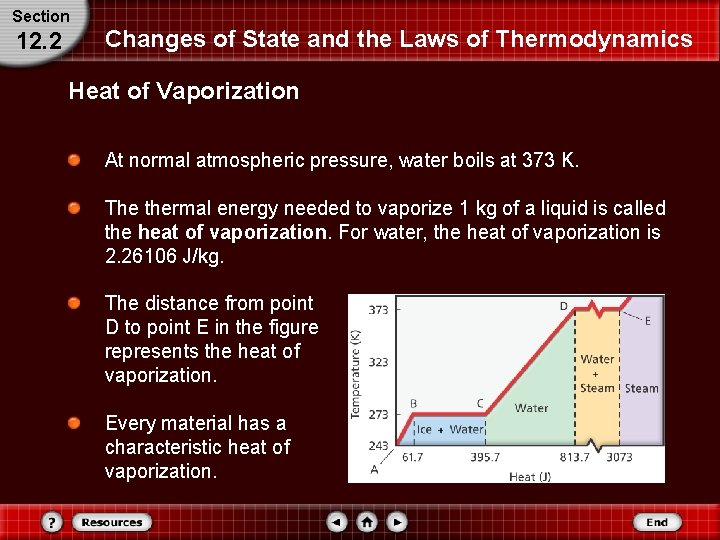
Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization At normal atmospheric pressure, water boils at 373 K. The thermal energy needed to vaporize 1 kg of a liquid is called the heat of vaporization. For water, the heat of vaporization is 2. 26106 J/kg. The distance from point D to point E in the figure represents the heat of vaporization. Every material has a characteristic heat of vaporization.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization Between points A and B, there is a definite slope to the line as the temperature is raised. This slope represents the specific heat of the ice. The slope between points C and D represents the specific heat of water, and the slope above point E represents the specific heat of steam. Note that the slope for water is less than those of both ice and steam. This is because water has a greater specific heat than those of ice and steam.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization The heat, Q, required to melt a solid of mass m is given by the following equation. Heat Required to Vaporize a Liquid Q = m. Hf The heat required to melt a solid is equal to the mass of the solid times the heat of fusion of the solid.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization Similarly, the heat, Q, required to vaporize a mass, m, of liquid is given by the following equation. Heat Required to Melt a Solid Q = m. Hv The heat required to vaporize a liquid is equal to the mass of the liquid times the heat of vaporization of the liquid.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization When a liquid freezes, an amount of heat, Q = –m. Hf, must be removed from the liquid to turn it into a solid. The negative sign indicates that the heat is transferred from the sample to the external world. In the same way, when a vapor condenses to a liquid, an amount of heat, Q = –m. Hv, must be removed from the vapor.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat of Vaporization The values of some heats of fusion, Hf, and heats of vaporization, Hv, are shown in the table below.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Suppose that you are camping in the mountains. You need to melt 1. 50 kg of snow at 0. 0°C and heat it to 70. 0°C to make hot cocoa. How much heat will be needed?

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Sketch the relationship between heat and water in its solid and liquid states.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Sketch the transfer of heat as the temperature of the water increases.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Identify the known and unknown variables. Known: m. A = 1. 50 kg Ti = 0. 0 ºC C = 4180 J/kg· ºC Unknown: Qmelt ice = ? Qheat liquid = ? Hf = 3. 34× 105 J/kg Qtotal = ? m. B = 0. 500 kg Tf= 70. 0 ºC

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Calculate the heat needed to melt ice. Qmelt ice = m. Hf

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Substitute m. A = 1. 50 kg, Hf = 3. 34× 105 J/kg. Qmelt ice = (1. 50 kg) (3. 34× 105 J/kg) = 5. 01× 105 J = 5. 01× 102 k. J

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Calculate the temperature change. ΔT = Ti – Tf

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Substitute Tf = 70. 0 ºC, Ti = 0. 0 ºC ΔT = 70. 0 ºC – 0. 0 ºC = 70. 0 ºC

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Calculate the heat needed to raise the water temperature. Qheat liquid = m. CΔT

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Substitute m. A = 1. 50 kg, C = 4180 J/kg· ºC, ΔT = 70. 0 ºC. Qheat liquid = (1. 50 kg) (4180 J/kg· ºC) (70. 0 ºC) = 4. 39× 105 J = 4. 39× 102 k. J

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Calculate the total amount of heat needed. Qtotal = Qmelt ice + Qheat liquid

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Substitute Qmelt ice = 5. 01× 102 k. J, Qheat liquid = 4. 39× 102 k. J. Qtotal = 5. 01× 102 k. J + 4. 39× 102 k. J = 9. 40× 102 k. J

Section 12. 2 Changes of State and the Laws of Thermodynamics The First Law of Thermodynamics The first law of thermodynamics states that the change in thermal energy, ΔU, of an object is equal to the heat, Q, that is added to the object minus the work, W, done by the object. Note that ΔU, Q, and W are all measured in joules, the unit of energy. The First Law of Thermodynamics ΔU = Q – W The change in thermal energy of an object is equal to the heat added to the object minus the work done by the object.

Section 12. 2 Changes of State and the Laws of Thermodynamics The First Law of Thermodynamics also involves the study of the changes in thermal properties of matter. The first law of thermodynamics is merely a restatement of the law of conservation of energy, which states that energy is neither created nor destroyed, but can be changed into other forms.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Engines The warmth that you experience when you rub your hands together is a result of the conversion of mechanical energy into thermal energy. However, the reverse process, the conversion of thermal energy into mechanical energy, is more difficult. A device that is able to convert thermal energy to mechanical energy, continuously, is called a heat engine.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Engines

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Engines When the automobile engine is functioning, the exhaust gases and the engine parts become hot. As the exhaust comes in contact with outside air and transfers heat to it, the temperature of the outside air is raised. In addition, heat from the engine is transferred to a radiator. Outside air passes through the radiator and the air temperature is raised.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Engines All of this energy, QL, transferred out of the automobile engine is called waste heat, that is, heat that has not been converted into work. When the engine is working continuously, the internal energy of the engine does not change, or ΔU = 0 = Q – W. The net heat going into the engine is Q = QH – QL. Thus, the work done by the engine is W = QH – QL.

Section 12. 2 Changes of State and the Laws of Thermodynamics Refrigerators Heat flows spontaneously from a warm object to a cold object. However, it is possible to remove thermal energy from a colder object and add it to a warmer object if work is done. A refrigerator is a common example of a device that accomplishes this transfer with the use of mechanical work. Electric energy runs a motor that does work on a gas and compresses it.

Section 12. 2 Changes of State and the Laws of Thermodynamics Refrigerators According to the first law of thermodynamics, the sum of the heat removed from the refrigerator’s contents and the work done by the motor is equal to the heat expelled, as shown in the figure.

Section 12. 2 Changes of State and the Laws of Thermodynamics Heat Pumps A heat pump is a refrigerator that can be run in two directions. In the summer, the pump removes heat from a house and thus cools the house. In the winter, heat is removed from the cold outside air and transferred into the warmer house. In both cases, mechanical energy is required to transfer heat from a cold object to a warmer one. Most homes in Fl use heat pumps to heat AND cool

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics Many processes that are consistent with the first law of thermodynamics have never been observed to occur spontaneously. Two such processes are presented below.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics If heat engines completely converted thermal energy into mechanical energy with no waste heat, then the first law of thermodynamics would be obeyed. However, waste heat is always generated, and randomly distributed particles of a gas are not observed to spontaneously arrange themselves in specific ordered patterns.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics In the nineteenth century, French engineer Sadi Carnot studied the ability of engines to convert thermal energy into mechanical energy. He developed a logical proof that even an ideal engine would generate some waste heat. Carnot’s result is best described in terms of a quantity called entropy, which is a measure of the disorder in a system.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics Entropy, like thermal energy, is contained in an object in kelvins. If heat is added to an object, entropy is increased. If heat is removed from an object, entropy is decreased. If an object does work with no change in temperature, the entropy does not change, as long as friction is ignored.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics The change in entropy, ΔS, is expressed by the following equation, in which entropy has units of J/K and the temperature is measured in kelvins. Change in Entropy The change in entropy of an object is equal to the heat added to the object divided by the temperature of the object.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics The second law of thermodynamics states that natural processes go in a direction that maintains or increases the total entropy of the universe. That is, all things will become more and more disordered unless some action is taken to keep them ordered.

Section 12. 2 Changes of State and the Laws of Thermodynamics The Second Law of Thermodynamics The increase in entropy and the second law of thermodynamics can be thought of as statements of the probability of events happening. The figure illustrates an increase in entropy as foodcoloring molecules, originally separate from the clear water, are thoroughly mixed with the water molecules over time.

Section Check 12. 2 Question 1 The amount of energy needed to melt 1 kg of ice is called _____. A. Melting point of ice B. Boiling point of water C. Heat of vaporization D. Heat of fusion

Section Check 12. 2 Answer 1 Answer: D Reason: The amount of energy needed to melt 1 kg of a substance is called heat of fusion of that substance. Heat of fusion is measured in J/kg. For example, the heat of fusion of ice is 3. 34× 106 J/kg. If 1 kg of ice absorbs 3. 34× 106 J at its melting point, 273 K, the ice becomes 1 kg of water at the same temperature, 273 K.

Section Check 12. 2 Question 2 Which of the following is true for the first law of thermodynamics? A. The change in thermal energy of an object is equal to the work done by the object minus the heat added to the object. B. The change in thermal energy of an object is equal to the heat added to the object minus the work done by the object. C. The change in temperature of an object is equal to the work done by the object minus the heat added to the object. D. The change in temperature of an object is equal to the heat added to the object minus the work done by the object.

Section Check 12. 2 Answer: B Reason: The first law of thermodynamics states that the change in thermal energy of an object is equal to the heat added to the object minus the work done by the object. U = Q – W Note that the change in internal energy, U, heat added, Q, and work done, W, are all measured in joules (J), the unit of energy.

Section Check 12. 2 Question 3 When a solid is heated, it changes to a liquid. The temperature at which this happens is called its _____. A. Melting point B. Boiling point C. Heat of vaporization D. Heat of fusion

Section Check 12. 2 Answer 3 Answer: A Reason: The temperature at which a solid changes to a liquid is called the melting point of the substance. When a solid is heated, at a particular temperature, even though thermal energy is added to the solid, the kinetic energy of the solid does not increase as all of the added thermal energy goes to overcome the forces holding the particles together and, hence, the solid melts. The temperature at which this change occurs is called the melting point.

Section Check 12. 2 Question 4 At melting point, even if you add more thermal energy, the temperature of the solid does not increase until the solid completely changes to a liquid. Why? A. At melting point, the added thermal energy escapes in the form of steam. B. At melting point, the added thermal energy is utilized to acquire the liquid state. C. At melting point, the added thermal energy goes to overcome the force holding the particles together in solid state. D. At melting point, the added thermal energy is utilized to increase the intermolecular distance.

Section 12. 2 Section Check Answer 4 Answer: C Reason: At melting point, even if more thermal energy is added, the temperature does not increase until the solid completely changes to a liquid, because all the added thermal energy is used to overcome the force holding the particles together in solid state. The added thermal energy does not increase the kinetic energy of the particle. Because the kinetic energy of the particle does not increase, the temperature does not increase.

Chapter 12 End of Chapter
 Section 3 using heat worksheet answers
Section 3 using heat worksheet answers Thermal energy in states of matter
Thermal energy in states of matter Heat thermal energy and temperature
Heat thermal energy and temperature Thermal energy vs heat
Thermal energy vs heat Thermal energy vs heat energy
Thermal energy vs heat energy Heat vs thermal energy vs temperature
Heat vs thermal energy vs temperature Thermal energy vs temperature
Thermal energy vs temperature Thermal energy vs temperature
Thermal energy vs temperature Thermal energy vs temperature
Thermal energy vs temperature Which reverses the normal flow of thermal energy
Which reverses the normal flow of thermal energy Section 1 matter and thermal energy
Section 1 matter and thermal energy Thermal energy and mass
Thermal energy and mass Thermal transfer vs direct thermal printing
Thermal transfer vs direct thermal printing Thermal cycler temperature verification system
Thermal cycler temperature verification system Chapter 12 thermal energy study guide answers
Chapter 12 thermal energy study guide answers Chapter 12 thermal energy answers
Chapter 12 thermal energy answers Chapter 16 thermal energy and heat
Chapter 16 thermal energy and heat Mass and thermal energy
Mass and thermal energy Chapter 14 section 1 heat and temperature answers
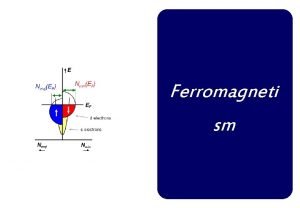
Chapter 14 section 1 heat and temperature answers Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Difference between curie temperature and neel temperature
Difference between curie temperature and neel temperature Ferrimagnetism
Ferrimagnetism Work and energy section 2 describing energy answer key
Work and energy section 2 describing energy answer key Section 1 how organisms obtain energy
Section 1 how organisms obtain energy Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis What is the difference between thermal energy and heat?
What is the difference between thermal energy and heat? How does conduction transfer heat
How does conduction transfer heat Specific heat capacity of lead j/kg c
Specific heat capacity of lead j/kg c Difference between heat and thermal energy
Difference between heat and thermal energy Thermal energy depends on
Thermal energy depends on What is todays temperature
What is todays temperature Thermal energy definition
Thermal energy definition Flannel shirt conductor or insulator
Flannel shirt conductor or insulator How to calculate change in thermal energy
How to calculate change in thermal energy How to measure heat energy
How to measure heat energy Sound energy examples
Sound energy examples Thermal energy in states of matter
Thermal energy in states of matter Thermal energy formula
Thermal energy formula Heat transfer jeopardy
Heat transfer jeopardy What is specific heat capacity
What is specific heat capacity Thermal energy formula
Thermal energy formula How heat moves
How heat moves Types of thermal energy transfers
Types of thermal energy transfers Radiation heat transfer examples
Radiation heat transfer examples Thermal energy vs heat
Thermal energy vs heat Thermal heat formula
Thermal heat formula Conclusion of thermal energy
Conclusion of thermal energy Energy videos bill nye
Energy videos bill nye Thermal energy examples
Thermal energy examples Gravitational potential energy
Gravitational potential energy Examples of thermal kinetic energy
Examples of thermal kinetic energy Forms of energy foldable
Forms of energy foldable Control measures of thermal pollution
Control measures of thermal pollution Thermal energy in states of matter
Thermal energy in states of matter A thermal energy reservoir (ter) has
A thermal energy reservoir (ter) has How to measure heat energy
How to measure heat energy Insulate cantilevered floor
Insulate cantilevered floor Energy efficiency in thermal utilities
Energy efficiency in thermal utilities Thermal energy transfer
Thermal energy transfer Thermal bypass checklist
Thermal bypass checklist The science duo physical and chemical changes
The science duo physical and chemical changes Thermal energy depends on
Thermal energy depends on Specific heat capacity equation triangle
Specific heat capacity equation triangle How is thermal energy created
How is thermal energy created Thermal energy system
Thermal energy system Chemistry of life
Chemistry of life Thermal energy flows from
Thermal energy flows from Thermal energy notes
Thermal energy notes Renewable resources definition
Renewable resources definition Thermal energy
Thermal energy Thermal energy notes
Thermal energy notes During conduction, thermal energy is transferred
During conduction, thermal energy is transferred Thermochemistry gaussian
Thermochemistry gaussian Thermal energy transfer
Thermal energy transfer Internal thermal energy
Internal thermal energy Thermal energy balance
Thermal energy balance Me 495
Me 495 Thermal energy
Thermal energy Examples of radiation heat transfer
Examples of radiation heat transfer Define thermal energy
Define thermal energy Thermal energy summary
Thermal energy summary Thermal energy is measured in ______.
Thermal energy is measured in ______. What has more thermal energy an iceberg or hot water
What has more thermal energy an iceberg or hot water Chapter 10 section 1 meiosis worksheet answer key
Chapter 10 section 1 meiosis worksheet answer key Chapter 2 section 2 flow of energy in an ecosystem
Chapter 2 section 2 flow of energy in an ecosystem Section 1 the nature of energy
Section 1 the nature of energy Chapter 4 section 1 work and machines answer key
Chapter 4 section 1 work and machines answer key Chapter 8 section 1 how organisms obtain energy answer key
Chapter 8 section 1 how organisms obtain energy answer key Chapter 8 section 1 how organisms obtain energy
Chapter 8 section 1 how organisms obtain energy Chapter 8 section 1 how organisms obtain energy
Chapter 8 section 1 how organisms obtain energy Gibbs free energy vs temperature
Gibbs free energy vs temperature