Chapter 4 Annuities START EXIT 4 1 Mc












































































































- Slides: 137

Chapter 4 Annuities START EXIT 4 -1 Mc. Graw-Hill/Irwin Copyright © 2008 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Chapter Outline 4. 1 4. 2 4. 3 4. 4 4. 5 What Is an Annuity? Future Values of Annuities Sinking Funds Present Values of Annuities Amortization Tables Chapter Summary Chapter Exercises 4 -2

4. 1 What Is an Annuity? • All of the situations we have considered so far, whether simple interest, simple discount, or compound interest, have had something in common. • In every case, a sum of money is lent and then the loan is repaid in full at once at the maturity date. • However, take a car loan, for example. Suppose you borrow $14, 500 at 8% compounded monthly for 5 years to buy a car. • It’s highly unlikely that you will get $14, 500 up front, do nothing for 5 years, and then repay the entire loan. Instead, you would be making monthly payments. 4 -3

4. 1 What Is an Annuity? • Definition 4. 1. 1 An annuity is any collection of equal payments made at regular time intervals. • Examples – Car loan – Student loan – Mortgage – Paycheck (salary) – Rent – Pension or Social Security • These are NOT annuities: – Monthly credit card payment – Utility bills 4 -4

4. 1 What Is an Annuity? • Definition 4. 1. 2 A sum of money to which an annuity’s payments and interest accumulate in the end is called the annuity’s future value. A sum of money paid at the beginning of an annuity, to which the annuity’s payments are accepted as equivalent, is called the annuity’s present value. 4 -5

4. 1 What Is an Annuity? Example 4. 1. 1 • Problem – Dylan deposits $25 from each paycheck into a 401(k) savings plan at work. He will keep this up for the next 40 years, at which time he plans to retire, hopefully having accumulated a large balance in his account. Since equal payments are being made into the account at regular intervals, this is an annuity. Is the value of the account when Dylan retires a present value or a future value? • Solution – The value of the account when Dylan reaches retirement would be the future value. 4 -6

4. 1 What Is an Annuity? Example 4. 1. 1 Cont. • Problem – Terri borrowed $160, 000 to buy a house. To pay off this mortgage loan, she agreed to make payments of $1, 735. 52 per month for 30 years. Since her mortgage payments are all equal and are made at regular intervals, they constitute an annuity. Was the amount she borrowed this annuity’s present value or future value? • Solution – The $160, 000 was received at the start of the annuity payments. Therefore, it would be the present value of the annuity. 4 -7

4. 1 What Is an Annuity? • Definition 4. 1. 3 An ordinary annuity is an annuity whose payments are made at the end of each time period. However, end of the month refers to a month counted from the date the annuity begins, not necessarily the end of the calendar month. An annuity due is an annuity whose payments are made at the beginning of each time period. 4 -8

4. 1 What Is an Annuity? Example 4. 1. 2 • Problem – John took out a car loan on May 7. Payments will be made monthly. The first payment is not due until June 7 (the second will be due on July 7, etc. ). Is this an ordinary annuity or an annuity due? • Solution – Because his first payment is not made until the end of the first month, the second at the end of the second month, and so on, his car payments are an ordinary annuity. 4 -9

4. 1 What Is an Annuity? Example 4. 1. 2 Cont. • Problem – Jenna won a lottery jackpot which will pay her $35, 000 per year for the next 26 years. She does not have to wait an entire year to get her first check – she will be paid the first $35, 000 right away. Her second payment will come a year from now, at the start of the second year, and so on. Is this an ordinary annuity or an annuity due? • Solution – Since the payments come at the start of each year, her prize payout is an annuity due. 4 -10

Section 4. 1 Exercises Problem 1: The Definition of an Annuity Problem 2: Present and Future Values Problem 3: Ordinary Annuities vs. Annuities Due Problem 4: Grab Bag 4 -11

Problem 1 • You just bought a car and will make monthly payments for the next five years. Is this an annuity? CHECK YOUR ANSWER 4 -12

Solution 1 • You just bought a car and will make monthly payments for the next five years. Is this an annuity? • Yes, an annuity is any collection of equal payments made at regular time intervals. BACK TO GAME BOARD 4 -13

Problem 2 • You just bought a house and took out a mortgage loan, agreeing to pay $738 every month for the next 30 years. Is this a present or future value? CHECK YOUR ANSWER 4 -14

Solution 2 • You just bought a house and took out a mortgage loan, agreeing to pay $738 every month for the next 30 years. Is this a present or future value? • It is a present value because the loan has been received at the start of the annuity payments. BACK TO GAME BOARD 4 -15

Problem 3 • Your rent is due at the end of each month. Is this an ordinary annuity or an annuity due? CHECK YOUR ANSWER 4 -16

Solution 3 • Your rent is due at the end of each month. Is this an ordinary annuity or an annuity due? • It’s an ordinary annuity because payments are made at the end of each time period. BACK TO GAME BOARD 4 -17

Problem 4 • You sponsor an orphan by paying $32 every month to www. compassion. com. Is this an annuity? CHECK YOUR ANSWER 4 -18

Solution 4 • You sponsor an orphan by paying $32 every month to www. compassion. com. Is this an annuity? • Yes, equal payments are made at the regular time intervals. BACK TO GAME BOARD 4 -19

4. 2 Future Values of Annuities • Suppose that you deposit $1, 200 at the end of each year into an investment account that earns 7. 2% compounded annually. Assuming you keep the payments up, how much would your account be worth in 5 year? • Your annual payments constitute an ordinary annuity. • Since we are asking about their accumulated value with interest at the end, we are looking for the future value. 4 -20

4. 2 Future Values of Annuities • Approach 1: The Chronological Approach – A natural way to approach the problem described on a previous slide is to build up the account value year by year, crediting interest as it comes due and adding new payments as they are made. – At the end of the first year, $1, 200 is deposited. No interest would be paid since there was no money in the account prior to this deposit. – At the end of the second year, 1 year’s worth of interest would be paid on the $1, 200, raising the account value to $1, 200(1. 072) = $1, 286. 40. In addition, $1, 200 comes in from the second-year deposit, bringing the total to $2, 486. 40. – It’s obvious, however, that it’s a very tedious process. 4 -21

4. 2 Future Values of Annuities • Approach 2: The Bucket Approach – Suppose now that you opened a new account for each year’s deposit, instead of making them all to the same account. – The bucket approach arises from an observation that keeping separate accounts would make no difference whatsoever in the total end result; the final balance would be the same. – The first payment of $1, 200 is placed in the first bucket. This money is kept on deposit from the end of year 1 until the end of year 5, a total of 4 years. At the end of the fifth year, the bucket will contain a total of $1, 200(1. 072)4 = $1, 584. 75. – We do same for each of the other five payments. – However, this approach is still rather tedious if there are numerous payments. 4 -22

4. 2 Future Values of Annuities • Approach 3: The Annuity Factor Approach – There is a third alternative. Suppose that instead of payments of $1, 200, you made a payment of $3, 600, three times as much. So to find the future value of the $3, 600 annuity, we wouldn’t need to start from scratch; we could just multiply the $1, 200 annuity’s future value by 3 to get FV = 3($6, 928. 48) = $20, 785. 44 – If you have any doubts about this, you can verify it for yourself by working through the future value of a $3, 600 annuity using either of the approaches we used above. – In general, a larger or smaller payment changes the future value proportionately. – Exploiting this, we can define the future value annuity factor. 4 -23

4. 2 Future Values of Annuities • Definition 4. 2. 1 – For a given interest rate, payment frequency, and number of payments, the future value annuity factor is the future value that would accumulate if each payment were $1. We denote this factor with they symbol sn/i where n is the number of payments and i is the interest rate per payment period. – When we find annuity factors, we carry the results out to more than the usual two decimal places, to avoid losing too much in the rounding. – It is conventional not to write a dollar sign in front of the annuity factor. 4 -24

4. 2 Future Values of Annuities FORMULA 4. 2. 1 The Future Value of an Ordinary Annuity FV = PMTsn/i where FV represents the FUTURE VALUE of the annuity PMT represents the AMOUNT OF EACH PAYMENT and sn/i is the ANNUITY FACTOR 4 -25

4. 2 Future Values of Annuities • Table of Annuity Factors – One way to find annuity factors is simply to have a table listing the factors for certain interest rates and numbers of payments. – See Sample Table of Annuity Factors on page 186 of your textbook. – This table shows us to look up the value of the appropriate annuity factor for any of the interest rates and values of n that the table includes. – For example, if we need the annuity factor for a 15 -year annual annuity at 8%, we would look in the n=15 row and 8% column and see that the value is 27. 15211393. 4 -26

4. 2 Future Values of Annuities Example 4. 2. 1 • Problem – How much will I have as a future value if I deposit $3, 000 at the end of each year into an account paying 6% compounded annually for 30 years? • Solution – The payments are equal and at regular intervals, and their timing is at the end of each period, so we have an ordinary annuity. – FV = PMTsni – FV = ($3, 000)s 30/0. 06 = $3, 000 x 79. 05818622 = $237, 174. 56 4 -27

4. 2 Future Values of Annuities FORMULA 4. 2. 2 The Future Value Annuity Factor sn/i = where i represents the INTEREST RATE PER PAYMENT PERIOD and n represents the NUMBER OF PAYMENTS 4 -28

4. 2 Future Values of Annuities Example 4. 2. 2 • Problem – Find the future value annuity factor for a term of 20 years with an interest rate of 7. 9% compounded annually. • Solution 4 -29

4. 2 Future Values of Annuities Example 4. 2. 3 • Problem – Suppose that $750 is deposited each year into an account paying 7. 9% interest compounded annually. What will the future value of the account be? • Solution FV = PMTsn/i = $750 x 45. 258204619 = $33, 943. 65 4 -30

4. 2 Future Values of Annuities Example 4. 2. 4 • Problem – Find the future value of quarterly payments of $750 for 5 years, assuming an 8% interest rate. • Solution i = 0. 08/4 = 0. 02 n = 5 x 4 = 20 FV = PMTsn/i = $750 x 24. 2973698 = $18, 223. 03 4 -31

4. 2 Future Values of Annuities Example 4. 2. 5 • Problem – Find the future value annuity factor for a monthly annuity, assuming the term is 15 years and the interest rate is 7. 1% compounded monthly. • Solution i = 0. 071/12 = 0. 005916667 n = 15 x 12 = 180 4 -32

4. 2 Future Values of Annuities Example 4. 2. 6 • Problem – Each month, Carrie deposits $250 into a savings account that pays 4. 5% (compounded monthly). Assuming that she keeps this up, and that the interest rate does not change, how much will her deposits have grown to after 5 years? • Solution i = 0. 045/12 = 0. 00375 n = 5 x 12 = 60 FV = PMTsn/i = $250 x 67. 14555214 = $16, 786. 39 4 -33

4. 2 Future Values of Annuities Example 4. 2. 7 • Problem – How much total interest did Carrie earn? • Solution – We first observe that the money in her account comes from two sources: the money she deposits and the interest she earns. – She made monthly deposits for 5 years, for a total of n = 60 deposits. – Each one was for $250, so in total she deposited 60 x $250 = $15, 000. – The rest must have come from interest. – Carrie’s Total Interest = $16, 786. 39 -- $15, 000 = $1, 786. 39 4 -34

4. 2 Future Values of Annuities • • With an annuity due, payments are made at the beginning of each period rather than the end. Each payment is made earlier, so it stands to reason that an annuity due would have a larger future value than an ordinary annuity, since the payments have longer to earn interest. To see how much more, let’s revisit the 5 year, $1, 200 per year annuity with 7. 2% interest. This time, though, as an annuity due. The first payment would earn interest from the start of the first year until the end of the fifth year, for a total of 5 years. The second payment would earn interest for 4 years, the third payment for 3 years, and so on. Since there is an extra year to earn interest, the maturity value is $7, 427. 33 instead of $6, 928. 48. See table on page 186 in your textbook. 4 -35

4. 2 Future Values of Annuities FORMULA 4. 2. 3 Future Value for an Annuity Due FV = PMTsn/i(1 + i) where FV represents the future value of the annuity PMT is the amount of each payment i is the interest rate period and sn/i is the annuity factor 4 -36

4. 2 Future Values of Annuities Example 4. 2. 8 • Problem – On New Year’s Day 2004, Max resolved to deposit $3, 000 at the start of each year into a retirement savings account. Assuming that he sticks to this resolution, and that his account earns 8 ¼% compounded annually, how much will he have after 40 years? • Solution – The payments are equal and made at the start of each year, so this is an annuity due. FV = PMTsn/i(1 + i) FV = $3, 000 x 276. 72205752 x (1 + 0. 0825) = $898, 654. 88 4 -37

Section 4. 2 Exercises Problem 1: Problem 2: Finding Future Values by Future Values for Non. Using Annuity Factors: Annual Ordinary Annuities Problem 3: Finding Total Interest Earned Problem 4: Finding Future Values by Using Annuity Factors: Annuities Due 4 -38

Problem 1 • You decided to invest $500 at the end of each year into an investment account that earns 5% interest compounded annually for 20 years. Find the future value of the annuity. CHECK YOUR ANSWER 4 -39

Solution 1 • You decided to invest $500 at the end of each year into an investment account that earns 5% interest compounded annually for 20 years. Find the future value of the annuity. • i = 0. 05 • n = 20 FV = PMTsn/i FV = $500 x 33. 0659541 = $16, 532. 98 BACK TO GAME BOARD 4 -40

Problem 2 • At the end of each month, Laura deposits $100 into her savings account that pays 2. 5% interest. Assuming that she keeps doing it for the next 10 years, how much will her deposits grow to? CHECK YOUR ANSWER 4 -41

Solution 2 • At the end of each month, Laura deposits $100 into her savings account that pays 2. 5% interest. Assuming that she keeps doing it for the next 10 years, how much will her deposits grow to? • • i = 0. 025/12 = 0. 002083333 n = 12 x 10 = 120 FV = PMTsn/i FV = $100 x 136. 1719618 = $13, 617. 20 BACK TO GAME BOARD 4 -42

Problem 3 • How much total interest would Laura earn? CHECK YOUR ANSWER 4 -43

Solution 3 • • How much total interest would Laura earn? Total Payments = $100 x 120 = $12, 000 Future Value = $13, 617. 20 Total Interest = $13, 617. 20 -- $12, 000 = $1, 617. 20 BACK TO GAME BOARD 4 -44

Problem 4 • Suppose Laura deposits $100 into her savings account that pays 2. 5% interest. However, she does it on the first day of each month. Assuming that she keeps doing it for the next 10 years, how much will her deposits grow to? CHECK YOUR ANSWER 4 -45

Solution 4 • Suppose Laura deposits $100 into her savings account that pays 2. 5% interest. However, she does it on the first day of each month. Assuming that she keeps doing it for the next 10 years, how much more will she earn? • i = 0. 025/12 = 0. 002083333 • n = 12 x 10 = 120 FV = PMTsn/i(1 + i) FV = $100 x 136. 1719618(1 + 0. 002083333) = $13, 645. 57 -- $13, 617. 20 = $28. 37 BACK TO GAME BOARD 4 -46

4. 3 Sinking Funds • So far, we have looked at annuities from the point of view that the payments determine the future value. • If instead we set up an annuity with a future value goal in mind, we would need to look at things in the opposite direction. • We call such annuities sinking funds. • Definition – A sinking fund is an annuity for which the amount of the payments is determined by the future value desired. 4 -47

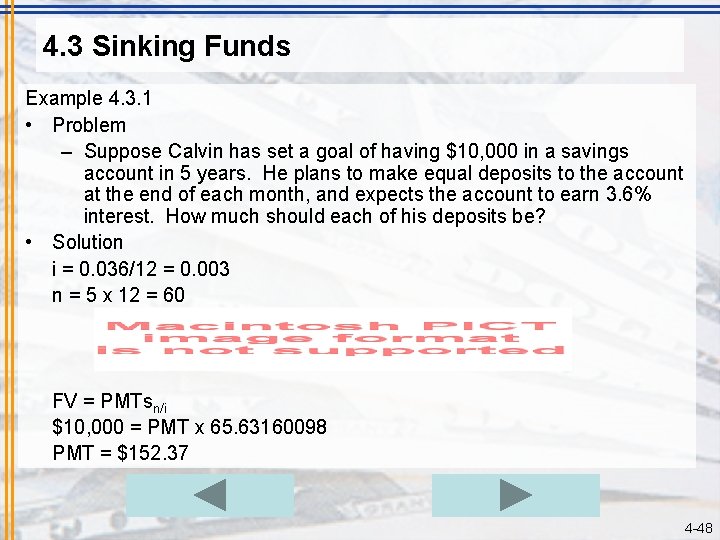
4. 3 Sinking Funds Example 4. 3. 1 • Problem – Suppose Calvin has set a goal of having $10, 000 in a savings account in 5 years. He plans to make equal deposits to the account at the end of each month, and expects the account to earn 3. 6% interest. How much should each of his deposits be? • Solution i = 0. 036/12 = 0. 003 n = 5 x 12 = 60 FV = PMTsn/i $10, 000 = PMT x 65. 63160098 PMT = $152. 37 4 -48

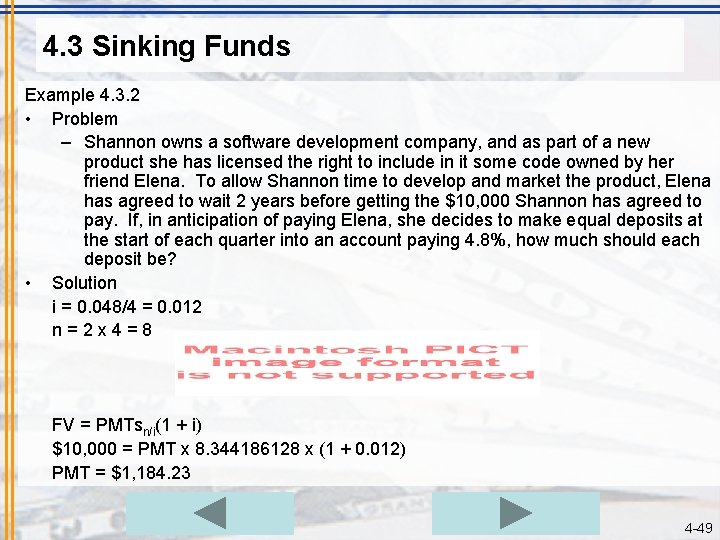
4. 3 Sinking Funds Example 4. 3. 2 • Problem – Shannon owns a software development company, and as part of a new product she has licensed the right to include in it some code owned by her friend Elena. To allow Shannon time to develop and market the product, Elena has agreed to wait 2 years before getting the $10, 000 Shannon has agreed to pay. If, in anticipation of paying Elena, she decides to make equal deposits at the start of each quarter into an account paying 4. 8%, how much should each deposit be? • Solution i = 0. 048/4 = 0. 012 n=2 x 4=8 FV = PMTsn/i(1 + i) $10, 000 = PMT x 8. 344186128 x (1 + 0. 012) PMT = $1, 184. 23 4 -49

4. 3 Sinking Funds • Sinking Funds with Loans – Knowing that her company had a large expense ahead on the horizon, it was prudent of Shannon to set up a fund to be able to meet it, rather than just wait and then get hit with a major expense all at once. – She may or may not have been under any obligation to do this. – However, what if Elena is concerned with Shannon’s inability to come up with a payment at the end of 2 years? Given this possibility, Elena has a good reason to want Shannon to be building up that balance along the way, so it’s possible that Elena might insist that Shannon sets up a sinking fund and makes regular payments. 4 -50

4. 3 Sinking Funds Example 4. 3. 3 • Problem – The Smithville Water and Sewer District has borrowed $1. 5 million from a group of investors. The note carries an interest rate of 5. 52% compounded annually, and matures in 7 years. The deal requires the district to establish a sinking fund and make semiannual deposits. As required, the district set up an account at the local bank which offers an interest rate of 3. 8%. How much should each of the deposits be? 4 -51

4. 3 Sinking Funds Example 4. 3. 3 Cont. • Solution – We must first determine the future value to be accumulated. It would be the $1. 5 million borrowed, together with the interest that it accumulates. FV = PV(1 +i)n = $1, 500, 000 x 1. 05527 = $2, 184, 915. 96 i = 0. 038/2 = 0. 019 n = 7 x 2 = 14 FV = PMTsn/i $2, 184, 915. 96 = PMT x 15. 86753836 PMT = $137, 697. 22 4 -52

4. 3 Sinking Funds • Sinking Funds and Retirement Planning – Suppose that Joe is now 25 years old, and hopes to be able to retire 45 years from now, at age 70. To ensure that he can do so comfortably, he has decided to start making deposits into an investment account which he assumes can earn an average of 9%. – The deposits will be automatically deducted from his paycheck when he receives it on the first and fifteenth of each month. – To get some sense of how large his deposits should be, he has set a goal of having $1, 000 in the account. 4 -53

4. 3 Sinking Funds Example 4. 3. 4 • Problem – Using the scenario described on a previous slide, determine how much Joe should deduct from each paycheck to reach his goal. • Solution i = 0. 09/24 = 0. 00375 n = 24 x 45 = 1, 080 FV = PMTsn/i $1, 000 = PMT x 14923. 819794054 PMT = $67. 01 4 -54

4. 3 Sinking Funds Example 4. 3. 5 • Problem – For the scenario of the previous example, determine how much total interest Joe would be earning. • Solution – He is making 1, 080 deposits of $67. 01 each, so his total deposits add up to $72, 370. 80. – Total Interest = $1, 000 -- $72, 370. 80 = $927, 629. 20 4 -55

Section 4. 3 Exercises Problem 1: Sinking Funds Problem 2: Sinking Funds with Loans Problem 3: Sinking Funds and Retirement Planning Problem 4: Grab Bag 4 -56

Problem 1 • Nicolas plans to start medical school in 5 years after obtaining an undergraduate degree and figures that he needs to save as much money as possible to help pay for his tuition and living expenses and minimize the amount to be borrowed through student loans. • After carefully analyzing his monthly budget, he determined that he can invest $700 at the beginning of each month. How much money will he have at maturity, assuming that his savings earn 6%? CHECK YOUR ANSWER 4 -57

Solution 1 • i = 6%/12 = 0. 5% = 0. 005 • n = 5 x 12 = 60 FV = PMTsn/i(1 + i) FV = $700 x 69. 77003051(1 + 0. 005) FV = $49, 083. 22 BACK TO GAME BOARD 4 -58

Problem 2 • Jen’s parents loaned her $20, 000 to make a down payment on the house. She would like to repay the loan in 3 years so she decided to set up a sinking fund which pays 4. 5%, compounded quarterly. How much should she deposit every quarter? CHECK YOUR ANSWER 4 -59

Solution 2 • i = 4. 5%/4 = 0. 01125 • n = 3 x 4 = 12 FV = PMTsn/i $20, 000 = PMT x 12. 7710614 PMT = $1, 566. 04 BACK TO GAME BOARD 4 -60

Problem 3 • Gabriel hopes to retire in 30 years at the age of 65 and would like to set up a retirement account and deposit $200 at the end of each week. If his savings account pays 6. 3%, how much money will he have? CHECK YOUR ANSWER 4 -61

Solution 3 • i = 6. 3%/52 = 0. 001211538 • n = 30 x 52 = 1, 560 FV = PMTsn/i FV = $200 x 4631. 960228 FV = $926, 392. 45 BACK TO GAME BOARD 4 -62

Problem 4 • Nancy borrowed $7, 000 from her friends to buy her first car. She would like to repay the loan in 3 years and decided to open a sinking fund so she can accumulate the full amount over a period of time. If the account pays 3. 8%, compounded monthly, how much money should she deposit at the beginning of each month in order to have the full amount in 3 years? CHECK YOUR ANSWER 4 -63

Solution 4 • • i = 3. 8%/12 = 0. 003166667 n = 3 x 12 = 36 FV = PMTsn/i(1 + i) $7, 000 = PMT x 38. 068507603(1 + 0. 003166667) $7, 000 = PMT x 38. 18905355 PMT = $183. 30 BACK TO GAME BOARD 4 -64

4. 4 Present Values of Annuities • Definition 4. 4. 1 – For a given interest rate, payment frequency, and number of payments, the present value annuity factor is the present value of an annuity at this rate, payment frequency, and number of payments if each payment were $1. – We denote this factor with the symbol an/i where n is the number of payments and i is the interest rate per payment period. 4 -65

4. 4 Present Values of Annuities FORMULA 4. 4. 1 The Present Value of an Ordinary Annuity PV = PMTan/i where PV represents the PRESENT VALUE OF THE ANNUITY PMT represents the AMOUNT OF EACH PAYMENT and an/i is the PRESENT VALUE ANNUITY FACTOR 4 -66

4. 4 Present Values of Annuities FORMULA 4. 4. 2 The Present Value of an Annuity Due PV = PMTan/i(1 + i) where PV represents the PRESENT VALUE OF THE ANNUITY PMT represents the AMOUNT OF EACH PAYMENT and an/i is the PRESENT VALUE ANNUITY FACTOR 4 -67

4. 4 Present Values of Annuities FORMULA 4. 4. 3 The Present Value Annuity Factor 4 -68

4. 4 Present Values of Annuities Example 4. 4. 4 • Problem – Find an/i when n = 36 and i = 0. 0035 • Solution 4 -69

4. 4 Present Values of Annuities Example 4. 4. 5 • Problem – Use the annuity factor calculated in Example 4. 4. 4 to find the monthly payment on an $8, 000 car loan at 4. 2% for 3 years. • Solution PV = PMTan/i $8, 000 = PMT(33. 7681092) PMT = $236. 91 4 -70

4. 4 Present Values of Annuities FORMULA 4. 4. 4 The Present Value Annuity Factor (Traditional Formula) 4 -71

4. 4 Present Values of Annuities Example 4. 4. 6 • Problem – Find the present value annuity factor for a 5 -year annuity with quarterly payments and a 9% interest rate. • Solution 4 -72

4. 4 Present Values of Annuities Example 4. 4. 7 • Problem – Cathy is thinking about buying a condominium. She figures that she can afford monthly loan payments of $650, and that she would be taking out a 30 -year loan with an interest rate of 8. 4%. What is the most she can afford to borrow? If she has $7, 500 to use as a down payment, what is the most she can afford to pay for the condo? • Solution PV = PMTan/i PV = $650(131. 2615606) = $85, 320. 01 Therefore, the most she can afford is $85, 320. 01 + $7, 500 = $92, 820. 01 4 -73

4. 4 Present Values of Annuities Example 4. 4. 8 • Problem – Pat and Tracy are buying a house, and will need to take out a $158, 000 mortgage loan. They plan to take out a standard 30 -year mortgage loan, on which their interest rate will be 7. 2%. If they make all their payments as scheduled, how much total interest will they pay over the course of the 30 years? • Solution – First, we need to determine their monthly payments: n = 30 x 12 = 360 and i = 0. 072/12 = 0. 006 PV = PMTan/i $158, 000 = PMT(147. 3213568) PMT = $1, 072. 49 Total Interest = $1, 072. 49 x 360 -- $158, 000 = $228, 096. 40 4 -74

4. 4 Present Values of Annuities Example 4. 4. 9 • Problem Suppose that Pat and Tracy from Example 4. 4. 8 decided instead to try to save some of the interest by paying off their loan more quickly. If they were to go with a 15 -year loan rather than a 30 -year loan, how much higher would their payments need to be (assuming the same interest rate)? How much interest would they save? • Solution PV = PMTan/i $158, 000 = PMT(109. 884466016) PMT = $1, 437. 87 So they would need to increase their payments by $1, 437. 87 -- $1, 072. 49 = $365. 38. Their total interest would be $1, 437. 87 x 180 – $158, 000 = $100, 816. 60 The savings are $228, 096. 40 – $100, 816. 60 = $127, 279. 80 4 -75

4. 4 Present Values of Annuities Example 4. 4. 10 • Problem Charlie has accumulated $557, 893 in his 401(k) retirement savings account. Now that he has retired, he is planning to start using this fund to provide him with some income. He expects that the account can continue to earn 4 ½% interest, and plans to make monthly withdrawals from the account over the next 20 years. How much can he afford to withdraw each month? • Solution PV = PMTan/i $557, 893 = PMT(158. 065436810) PMT = $3, 529. 51 4 -76

4. 4 Present Values of Annuities Example 4. 4. 11 • Problem The New York State Lotto Jackpot is advertised to be $52 million. However, this jackpot is not paid out all at once as a single lump sum. Rather, it’s paid out in equal annual installments for 26 years (beginning immediately). The advertised $52 million is the total of all the payments. When you buy a ticket, you can choose to have the jackpot paid to you as a lump sum should you win, but in that case you receive the present value of the payments. If the interest rate used is 6%, what is the value of the jackpot as a lump sum? 4 -77

4. 4 Present Values of Annuities Example 4. 4. 11 Cont. • Solution Since the jackpot annuity is 26 equal payments totaling $52 million, each payment would be $52, 000/26 = $2, 000 PV = PMTan/i(1 + i) PV = $2, 000(13. 003166187)(1 + 0. 06) PV = $27, 566, 712. 32 4 -78

Section 4. 4 Exercises Problem 1: Finding Present Value Annuity Factors Problem 2: Present Values and Loans Problem 3: Present Values and Retirement Savings Problem 4: Grab Bag 4 -79

Problem 1 • Find a present value annuity factor if – the payments are quarterly – the interest rate is 4. 6% – the term is 15 years CHECK YOUR ANSWER 4 -80

Solution 1 • Find a present value annuity factor if – the payments are quarterly – the interest rate is 4. 6% – the term is 15 years BACK TO GAME BOARD 4 -81

Problem 2 • Eric, a 20 -year-old college student, ran up a credit card debt, but insists on making only the minimal monthly payment of $50 so he can enjoy life. His accountant, in an attempt to modify Eric’s irresponsible behavior, told him that it would take 40 years to pay off the current balance if only minimal payments are made. The credit card interest rate is 16. 8%. What is Eric’s balance? CHECK YOUR ANSWER 4 -82

Solution 2 • i = 16. 8%/12 = 0. 014 • n = 12 x 40 = 480 • PV = PMTan/i • PV = $50(71. 33827855) = $3, 566. 91 BACK TO GAME BOARD 4 -83

Problem 3 • Elaine is looking forward to retiring soon and hopes she will have enough in her retirement savings account to be able to withdraw $1, 500 monthly for 30 years. How much will she need in her account when she retires in order to do that? Assume that the interest rate is 4. 8%. CHECK YOUR ANSWER 4 -84

Solution 3 PV = PMTan/i PV = $1, 500(190. 5976813) = $285, 896. 52 BACK TO GAME BOARD 4 -85

Problem 4 • Eric, a 20 -year-old college student, ran up a credit card debt, but insists on making only the minimal monthly payment of $50 so he can enjoy life. His accountant, in an attempt to modify Eric’s irresponsible behavior, told him that it would take 40 years to pay off the current balance if only minimal payments are made. The credit card interest rate is 16. 8%. If Eric agrees to pay off the balance in two years, what would be his monthly payment? CHECK YOUR ANSWER 4 -86

Solution 4 • i = 16. 8%/12 = 0. 014 • n = 12 x 2 = 24 • PV = PMTan/i • $3, 566. 91 = PMT(20. 26497738) PMT = $176. 01 BACK TO GAME BOARD 4 -87

4. 5 Amortization Tables In section 4. 4, we compared a 30 -year to a 15 -year mortgage and found that despite the commonsense expectation that halving the time would require doubling the payments, the 15 -year loan’s payments were not anywhere near twice the 30 year’s. We attributed the difference to the shorter term allowing for less interest, which generally makes sense, but is a bit vague. Unfortunately, our annuity factor formula allows us only to calculate payments from the present value. We might have a conceptual idea of what is going on as the payments are made-each payment chips away at the amount owed until the debt is entirely paid off-we don’t have a way to look more specifically at the details. Being able to do so would provide a better understanding of how all this works. 4 -88

4. 5 Amortization Tables Amortization tables are a tool to do this!!! The word amortization actually comes from the French phrase à morte, meaning towards death. A fitting name for a look at how we kill off debt (alternatively and perhaps equally fitting, for looking at how debt can kill you). There are columns for the amount of each payment, the amount of the payment that goes toward interest, the amount that goes toward principal, and the remaining balance after the payment is made. 4 -89

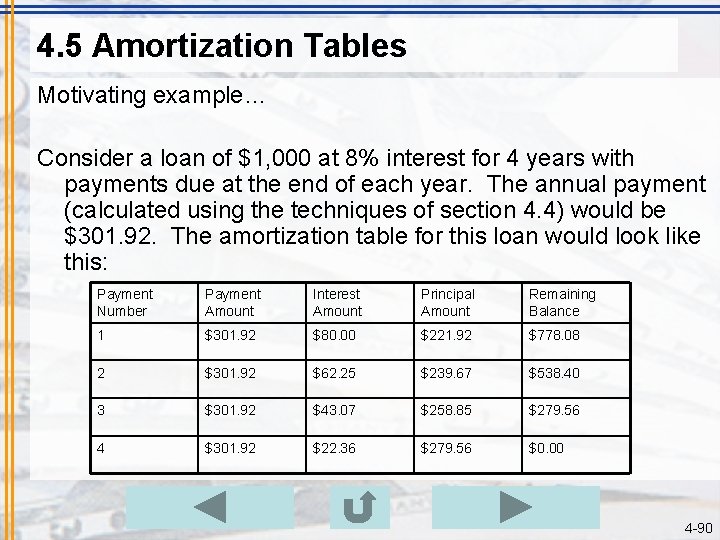
4. 5 Amortization Tables Motivating example… Consider a loan of $1, 000 at 8% interest for 4 years with payments due at the end of each year. The annual payment (calculated using the techniques of section 4. 4) would be $301. 92. The amortization table for this loan would look like this: Payment Number Payment Amount Interest Amount Principal Amount Remaining Balance 1 $301. 92 $80. 00 $221. 92 $778. 08 2 $301. 92 $62. 25 $239. 67 $538. 40 3 $301. 92 $43. 07 $258. 85 $279. 56 4 $301. 92 $22. 36 $279. 56 $0. 00 4 -90

4. 5 Amortization Tables We can see from the table how each payment is split up between interest and principal, and that the balance owed declines with each payment until it reaches zero after the last payment is made. How, though, is the split between interest and principal determined? To answer this question, let’s walk through the calculations of the entries in the first two rows. In the first year, the amount owed is the original $1, 000, since no payments are made until the end of that year. Interest is assumed to compound annually, and so no compounding goes on during the year. The interest owed would be: I = PRT = (1, 000)(0. 08)(1) = $80. 00 4 -91

4. 5 Amortization Tables Since $80. 00 must go to pay interest, the remainder of the payment is left to go towards principal: $301. 92 - $80. 00 = $221. 92. Taking that off of the loan’s balance, we get: $1, 000 - $221. 92 = $778. 08. These amounts agree with those shown in the first row of the table. Moving on to the second row…. . 4 -92

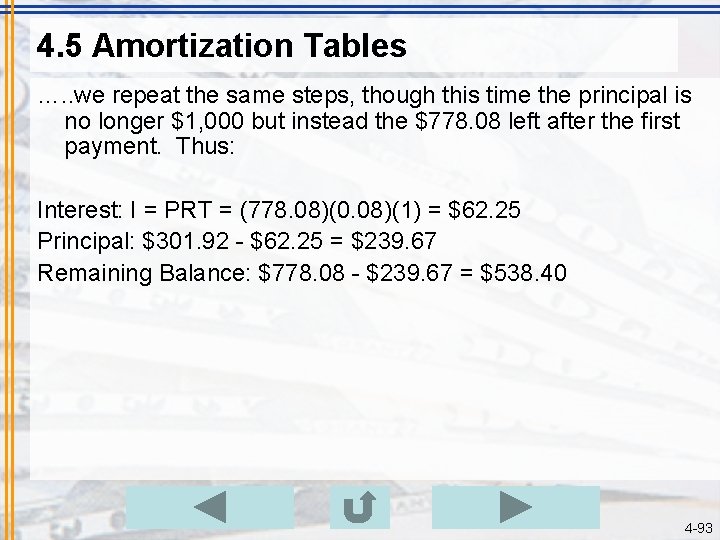
4. 5 Amortization Tables …. . we repeat the same steps, though this time the principal is no longer $1, 000 but instead the $778. 08 left after the first payment. Thus: Interest: I = PRT = (778. 08)(0. 08)(1) = $62. 25 Principal: $301. 92 - $62. 25 = $239. 67 Remaining Balance: $778. 08 - $239. 67 = $538. 40 4 -93

4. 5 Amortization Tables • The amount of each payment is the same, but the split between interest and principal changes with each payment. • As the balance is paid down, the portion of each payment dedicated to interest declines. A larger share of early payments will thus go toward interest than later payments. • As interest’s share of the payments decreases, principal’s share of the payments increases. So not only does each payment reduce the amount owed, but also the pace of the reduction is accelerating. • We might have expected that the interest would be compound interest; however, since each payment must cover the entire amount of interest for the period, interest never gets a chance to compound upon itself. 4 -94

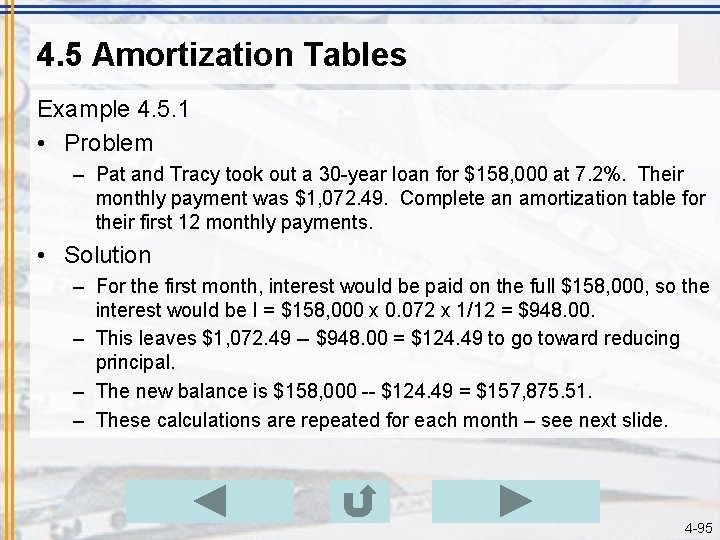
4. 5 Amortization Tables Example 4. 5. 1 • Problem – Pat and Tracy took out a 30 -year loan for $158, 000 at 7. 2%. Their monthly payment was $1, 072. 49. Complete an amortization table for their first 12 monthly payments. • Solution – For the first month, interest would be paid on the full $158, 000, so the interest would be I = $158, 000 x 0. 072 x 1/12 = $948. 00. – This leaves $1, 072. 49 -- $948. 00 = $124. 49 to go toward reducing principal. – The new balance is $158, 000 -- $124. 49 = $157, 875. 51. – These calculations are repeated for each month – see next slide. 4 -95

4. 5 Amortization Tables Example 4. 5. 1 Cont. Pmt # Pmt Amt Interest Principal Balance 1 $1, 072. 49 $948. 00 $124. 49 $157, 875. 51 2 $1, 072. 49 $947. 25 $125. 24 $157, 750. 27 3 $1, 072. 49 $946. 50 $125. 99 $157, 624. 28 4 $1, 072. 49 $945. 75 $126. 74 $157, 497. 54 5 $1, 072. 49 $944. 99 $127. 50 $157, 370. 04 6 $1, 072. 49 $944. 22 $128. 27 $157, 241. 77 7 $1, 072. 49 $943. 45 $129. 04 $157, 112. 73 8 $1, 072. 49 $942. 68 $129. 81 $156, 982. 92 9 $1, 072. 49 $941. 90 $130. 59 $156, 852. 33 10 $1, 072. 49 $941. 11 $131. 38 $156, 720. 95 11 $1, 072. 49 $940. 33 $132. 16 $156, 588. 79 12 $1, 072. 49 $939. 53 $132. 96 $156, 455. 83 4 -96

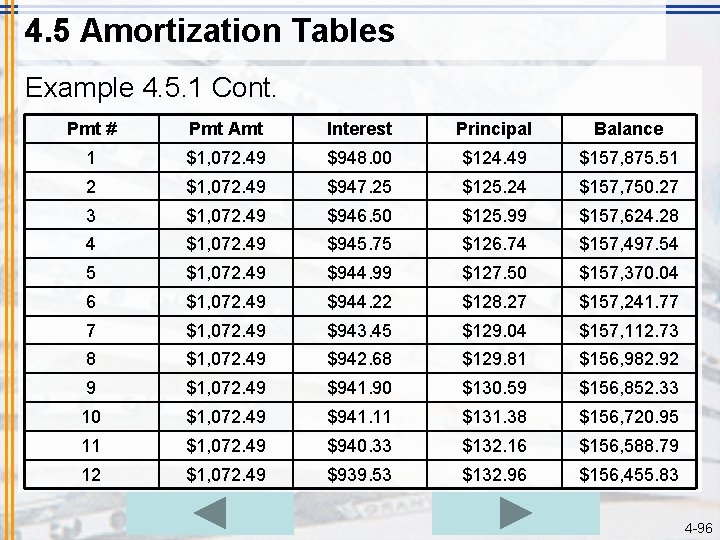
4. 5 Amortization Tables Example 4. 5. 2 • Problem – Suppose Pat and Tracy took out a 15 -year mortgage instead, also for $158, 000, and at a 7. 2% rate. Their monthly payment would then be $1, 437. 87. – Construct an amortization table for their first 12 monthly payments. • Solution (see next slide) 4 -97

4. 5 Amortization Tables Payment Number Payment Amount Interest Amount Principal Amount Remaining Balance 1 $1, 437. 87 $948. 00 $489. 87 $157, 510. 13 2 $1, 437. 87 $947. 25 $490. 62 $157, 019. 51 3 $1, 437. 87 $946. 50 $491. 37 $156, 528. 14 4 $1, 437. 87 $945. 75 $492. 12 $156, 036. 02 5 $1, 437. 87 $944. 99 $492. 88 $155, 543. 14 6 $1, 437. 87 $933. 26 $504. 61 $155, 038. 53 7 $1, 437. 87 $930. 23 $507. 64 $154, 530. 89 8 $1, 437. 87 $927. 19 $510. 68 $154, 020. 21 9 $1, 437. 87 $924. 12 $513. 75 $153, 506. 46 10 $1, 437. 87 $921. 04 $516. 83 $152, 989. 63 11 $1, 437. 87 $917. 94 $519. 93 $152, 469. 70 12 $1, 437. 87 $914. 82 $523. 05 $151, 946. 65 4 -98

4. 5 Amortization Tables $1, 437. 87 is only a few hundred dollars more than $1, 072. 49. When we looked at this comparison in section 4. 4, it was surprising that those few hundred dollars could cut the loan’s term in half. Now, looking at the amortization table, we can see why. Every penny of the extra money went toward principal. The amount going to principal jumped from $129. 49 all the way up to $489. 87! The enormous gain in the amount going toward principal is the reason for the surprisingly large impact of the higher payment. 4 -99

4. 5 Amortization Tables • In most circumstances, a borrower can choose to pay more than the required monthly payment on a loan and enjoy the interest saving benefits of doing so. • The ability to do this is a consequence of an approach to interest on a loan sometimes referred to as the United States Rule. • For most financial situations in the United States, for each time period you pay the interest only on the amount that you actually owe. If you pay extra to reduce the balance, this reduces the amount of interest you pay. • Some loans, however, have what are known as prepayment penalties. • The term amortized loan refers to any loan whose payments are calculated by using the annuity factors and whose progress toward payoff therefore follows what is illustrated in an amortization table. 4 -100

4. 5 Amortization Tables “FORMULA” 4. 4. 5 The Remaining Balance of a Loan At any point in the term of an amortized loan, the amount owed is equal to the present value of the remaining payments. 4 -101

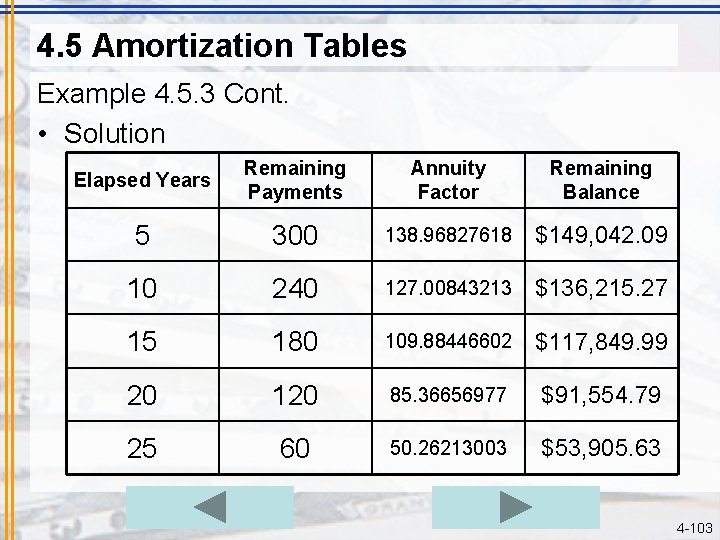
4. 5 Amortization Tables Example 4. 5. 3 • Problem – Assuming that Pat and Tracy make all their payments as scheduled, how much will they owe on their mortgage after 5 years? 10 years? 15 years? 20 years? 25 years? • Solution – After 5 years, they will have made 5 x 12 = 60 payments, so 300 payments remain (30 x 12 = 360). – The amount they owe is the present value of those payments, so: PV = PMTan/i PV = $1, 072. 49 x a 300/0. 006 PV = $1, 072. 49 x 138. 96827618 PV = $149, 042. 09 – The remaining calculations are essentially the same; see next slide. 4 -102

4. 5 Amortization Tables Example 4. 5. 3 Cont. • Solution Elapsed Years Remaining Payments Annuity Factor Remaining Balance 5 300 138. 96827618 $149, 042. 09 10 240 127. 00843213 $136, 215. 27 15 180 109. 88446602 $117, 849. 99 20 120 85. 36656977 $91, 554. 79 25 60 50. 26213003 $53, 905. 63 4 -103

4. 5 Amortization Tables Example 4. 5. 4 • Problem – Suppose Kim has 12 years remaining on a business loan at 15%, on which the quarterly payments are $2, 531. 00. If she refinances this debt with a new 12 -year loan at 8%, what will her new quarterly payment be? How much total interest will she save by doing this? • Solution – There are 12 x 4 = 48 remaining payments PV = PMTan/i PV = $2, 531 x a 48/0. 0375 PV = $2, 531 x 22. 11112866 PV = $55, 963. 27 – So $55, 963. 27 is the amount she needs to pay off the old loan. 4 -104

4. 5 Amortization Tables Example 4. 5. 4 Cont. • Solution – Borrowing $55, 963. 27 at 8% with quarterly payments for 12 years would require payments of PV = PMTan/i $55, 963. 27 = PMT x a 48/0. 02 $55, 963. 27 = PMT x 30. 67311957 PMT = $1, 824. 51 – This results in a savings of $2, 531 -- $1, 824. 51 = $706. 49 for a total of $706. 49 x 48 = $33, 911. 52 4 -105

4. 5 Amortization Tables Example 4. 5. 5 • Problem – Andrea has a car payment of $288. 95 a month at 9% with 37 months remaining, a student loan of $353. 08 at 5. 4% with 108 months remaining, and a mortgage payment of $1, 104. 29 at 7. 35% with 19 years remaining. – A finance company suggests that she could refinance her mortgage and consolidate it with her other loans to lower her monthly payments. They propose that she take out a new 30 -year mortgage loan at 7. 75%, borrowing enough to pay off all three existing loans. – What would her new monthly payment be? 4 -106

4. 5 Amortization Tables Example 4. 5. 5 Cont. • Solution – We first need to calculate the amounts she owes on her existing loans. For the sake of space, we will not show all those calculations her. These amounts can be found as in our previous examples, by taking the present value of the remaining payments. – Doing this, we find that she owes • $9, 306 on the car • $30, 149 on the student loan • $135, 486 on the house – She would need to borrow a total of $174, 941. – Calculating the monthly payment on this present value using 30 years and 7. 75%, we determine that her new payment would be $1, 253. 30. 4 -107

4. 5 Amortization Tables Example 4. 5. 6 • Problem – How much, in total, will Andrea save by doing this consolidation? • Solution – With the new loan, she will make 360 payments of $1, 253. 30 each, totaling $451, 188. – With her old loans, her remaining payments would total: Loan Payment Remaining Pmts Total Remaining Car $288. 95 37 $10, 691 Student $353. 08 108 $38, 133 $1, 104. 29 228 $251, 778 Mortgage Total $300, 602 4 -108

4. 5 Amortization Tables Example 4. 5. 6 Cont. • Solution – We see that she will actually not save anything by consolidating. – Actually, the total she would pay with the new loan is over $150, 000 more than what she would pay on her existing loans! – The reason lies in the number of months. By consolidating, she would lower her monthly payment. – However, she would take debts that would be paid off in 19 years, and just over 3 years and convert them into a debt that will take 30 years to pay off. – Does this mean that consolidating and/or refinancing is a bad idea? – Absolutely not! Andrea may decide that freeing up $500 cash in her monthly budget is well worth extending her final payoff farther into the future. Money might be tight now and she may plan to make extra payments later. 4 -109

Section 4. 5 Exercises Problem 1: The Remaining Balance on a Loan Problem 2: Consolidation and Refinancing 4 -110

Problem 1 • Natalie’s 30 -year mortgage payment is $478. 90 and the interest rate is 6. 8%. If she made all her payments as scheduled and has 15 years of monthly payments left, what is her remaining balance? CHECK YOUR ANSWER 4 -111

Solution 1 • • • Natalie’s 30 -year mortgage payment is $478. 90 and the interest rate is 6. 8%. If she made all her payments as scheduled and has 15 years of monthly payments left, what is her remaining balance? Natalie has 15 x 12 = 180 payments left The amount she owes is the present value of those payments: PV = PMT x an/i PV = $478. 90 x 112. 6525777 = $53, 949. 32 BACK TO GAME BOARD 4 -112

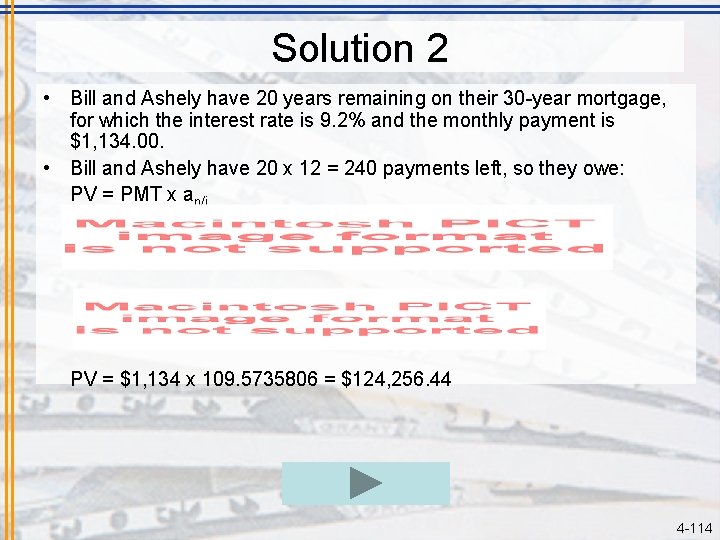
Problem 2 • Bill and Ashley have 20 years remaining on their 30 -year mortgage, for which the interest rate is 9. 2% and the monthly payment is $1, 134. 00. They have made all of their payments as scheduled. • If they refinance their loan by replacing it with a new 20 year loan at 6%, what will their new monthly payment be? • How much, if anything, will they save by doing this? CHECK YOUR ANSWER 4 -113

Solution 2 • Bill and Ashely have 20 years remaining on their 30 -year mortgage, for which the interest rate is 9. 2% and the monthly payment is $1, 134. 00. • Bill and Ashely have 20 x 12 = 240 payments left, so they owe: PV = PMT x an/i PV = $1, 134 x 109. 5735806 = $124, 256. 44 4 -114

Solution 2 • So their new mortgage would be for $124, 256. 44 (principal only). PV = PMT x an/i $124, 256. 44 = PMT x 139. 5807717 PMT = $890. 21 Balance w/out refinancing = 240 x $1, 134 = $272, 160 Balance after refinancing = 240 x $890. 21 = $213, 650. 40 Therefore, they will save $58, 509. 60 if they refinance. BACK TO GAME BOARD 4 -115

Chapter 4 Summary • Annuities, Uses and Terminology • The Future Value of an Ordinary Annuity • The Future Value Annuity Factor Formula • Finding Total Interest Earned • The Future Value of an Annuity Due • Sinking Funds and Retirement Planning • The Present Value of an Ordinary Annuity • The Present Value Annuity Factor Formula • Finding Loan Payments • Finding Total Interest Paid • Amortization Tables • The Remaining Balance of a Loan • Consolidation and Refinancing 4 -116

Chapter 4 Exercises Section 4. 1 Section 4. 2 Section 4. 3 Section 4. 4 Section 4. 5 $100 $100 $200 $200 EXIT 4 -117

Section 4. 1 -- $100 • At the end of each quarter, Reynolds Electric, Inc. pays its shareholders a dividend of $1 for each share owned. • Is this an ordinary annuity or an annuity due? CHECK YOUR ANSWER 4 -118

Section 4. 1 -- $100 • It’s an ordinary annuity because payments are made at the end of each time period. BACK TO GAME BOARD 4 -119

Section 4. 1 -- $200 • Sam deposits a certain amount from each paycheck into a 401(k) savings plan. He will keep doing it for the next 30 years. Is the value of the account when Sam retires a present value or a future value? CHECK YOUR ANSWER 4 -120

Section 4. 1 -- $200 • It would be the future value because it’s a sum of money to which an annuity’s payments and interest accumulate in the end. BACK TO GAME BOARD 4 -121

Section 4. 2 -- $100 • Calculate sn/i if n = 10 and i = 0. 034 CHECK YOUR ANSWER 4 -122

Section 4. 2 -- $100 • Calculate sn/i if n = 10 and i = 0. 034 BACK TO GAME BOARD 4 -123

Section 4. 2 -- $200 • If you deposit $50 each week into an account that earned 3% interest for 30 years, what would be the future value? CHECK YOUR ANSWER 4 -124

Section 4. 2 -- $200 • If you deposit $50 each week into an account that earned 3% interest for 30 years, what would be the future value? • FV = PMTsn/i FV = $50 x 2528. 872765 = $126, 443. 6382 BACK TO GAME BOARD 4 -125

Section 4. 3 -- $100 • Ariel would like to accumulate a balance of $200, 000 in her savings account in the next 20 years. Deposits will be made every month and the interest rate is 5%. How much should each deposit be? CHECK YOUR ANSWER 4 -126

Section 4. 3 -- $100 • Ariel would like to accumulate a balance of $200, 000 in her savings account in the next 20 years. Deposits will be made every month and the interest rate is 5%. How much should each deposit be? • FV = PMTsn/I $200, 000 = PMT x 411. 0336346 PMT = $486. 58 BACK TO GAME BOARD 4 -127

Section 4. 3 -- $200 • Alan wants to save $50, 000 for his son’s college expenses. How much should he invest every quarter to reach this goal in 10 years if the interest rate is 3. 6%? CHECK YOUR ANSWER 4 -128

Section 4. 3 -- $200 • Alan wants to save $50, 000 for his son’s college expenses. How much should he invest every quarter to reach this goal in 10 years if the interest rate is 3. 6%? • FV = PMTsn/I $50, 000 = PMT x 47. 89145744 PMT = $1, 044. 03 BACK TO GAME BOARD 4 -129

Section 4. 4 -- $100 • If n = 60 and i = 0. 00386, find the present value annuity factor. CHECK YOUR ANSWER 4 -130

Section 4. 4 -- $100 • If n = 60 and i = 0. 00386, find the present value annuity factor. BACK TO GAME BOARD 4 -131

Section 4. 4 -- $200 • Arlene figured out that the most she can afford to pay each month for a car loan is $310. If her credit union offers a 7 -year car loan with an interest rate of 6%, what is the most she can afford to borrow? CHECK YOUR ANSWER 4 -132

Section 4. 4 -- $200 • Arlene figured out that the most she can afford to pay each month for a car loan is $310. If her credit union offers a 7 -year car loan with an interest rate of 6%, what is the most she can afford to borrow? • PV = PMT x an/i • PV = $310 x 68. 45304243 = $21, 220. 44 BACK TO GAME BOARD 4 -133

Section 4. 5 -- $100 • Sasha’s car loan payment is $217. 34 and the interest rate is 8. 2%. If she made all her payments as scheduled and still has 3 years of monthly payments left, how much does she owe today? CHECK YOUR ANSWER 4 -134

Section 4. 5 -- $100 • Sasha’s car loan payment is $217. 34 and the interest rate is 8. 2%. If she made all her payments as scheduled and still has 3 years of monthly payments left, how much does she owe today? • She has 3 x 12 = 36 payments left • PV = PMT x an/i • PV = $217. 34 x 31. 81804032 = $6, 915. 33 BACK TO GAME BOARD 4 -135

Section 4. 5 -- $200 • Sasha’s car loan payment is $217. 34 and the interest rate is 8. 2%. She has made all her payments as scheduled and still has 3 years of monthly payments left. If she refinances this debt with a new 3 -year loan at 5%, how much money, if any, will she save? CHECK YOUR ANSWER 4 -136

Section 4. 5 -- $200 • The current balance on her existing loan is $6, 915. 33 so that’s how much she will need to borrow. • Her new monthly payment would be: • PV = PMT x an/i • • • $6, 915. 33 = PMT x 33. 36569857 PMT = $207. 26 Total Payments w/out refinancing = $217. 34 x 36 = $7, 824. 24 Total Payments after refinancing = $207. 26 x 36 = $7, 461. 36 Savings = $362. 88 BACK TO GAME BOARD 4 -137
 Means of egress definition
Means of egress definition Exit exit access and exit discharge
Exit exit access and exit discharge Gcu annuity
Gcu annuity Annuities definition
Annuities definition Kids on beach
Kids on beach Annuities bloomfield hills
Annuities bloomfield hills Annuities definition
Annuities definition Rumus anuitas bertumbuh
Rumus anuitas bertumbuh But we gotta start somewhere
But we gotta start somewhere Jump start in field traige assessment
Jump start in field traige assessment Chapter 8 great gatsby analysis
Chapter 8 great gatsby analysis 3 2 1 exit ticket
3 2 1 exit ticket Drivers ed module 5 topic 3
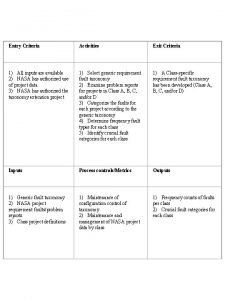
Drivers ed module 5 topic 3 Project exit criteria
Project exit criteria Cps algebra exit exam
Cps algebra exit exam Sap conversion exit
Sap conversion exit How to ace an exit interview
How to ace an exit interview Mcoles shooting qualification
Mcoles shooting qualification Exit taxiway
Exit taxiway Risk-benefit analysis in professional ethics
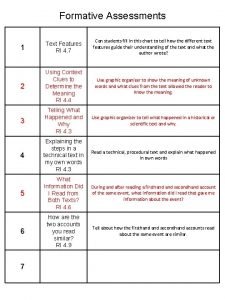
Risk-benefit analysis in professional ethics Text features assessment
Text features assessment Exit ticket app
Exit ticket app Exit the map
Exit the map Project exit criteria
Project exit criteria Eet699 speaking test
Eet699 speaking test Eet background
Eet background Wood badge ticket examples
Wood badge ticket examples Exit policy
Exit policy Gip inspection artifacts
Gip inspection artifacts Client exit interview
Client exit interview Pleasure curve
Pleasure curve Exit policy mrsm
Exit policy mrsm 1910 subpart e
1910 subpart e Uat metrics
Uat metrics Press esc to exit
Press esc to exit Marissa just bought 100 acres of land
Marissa just bought 100 acres of land Udinus
Udinus Bullet entrance and exit holes
Bullet entrance and exit holes Wlan exit point
Wlan exit point Senior exit project ideas
Senior exit project ideas Exit_saplkedrcopa_001
Exit_saplkedrcopa_001 Lesson 1 exit ticket answer key
Lesson 1 exit ticket answer key Spread of islam through architecture exit slip
Spread of islam through architecture exit slip Exit site scoring system
Exit site scoring system Lesson 2 estimate products
Lesson 2 estimate products Chapter 16 driving on highways
Chapter 16 driving on highways Fork() wait() exec() and exit() system calls
Fork() wait() exec() and exit() system calls Exit summary example
Exit summary example Round the factors and estimate the products exit ticket
Round the factors and estimate the products exit ticket Excess capacity graph
Excess capacity graph Exit condition
Exit condition Senior exit interview
Senior exit interview California high school exit examination
California high school exit examination Chapter 7 section 1 perfect competition worksheet answers
Chapter 7 section 1 perfect competition worksheet answers Exit procedure steps
Exit procedure steps Free entry and exit
Free entry and exit Lab safety exit ticket
Lab safety exit ticket Have i played the part well then applaud me as i exit
Have i played the part well then applaud me as i exit Exit summary declaration
Exit summary declaration Exit quiz
Exit quiz Monopolists may be artists
Monopolists may be artists Press esc to exit
Press esc to exit Panic exit hardware
Panic exit hardware Exit controlled loop flowchart
Exit controlled loop flowchart Free entry and exit
Free entry and exit Descargar exit
Descargar exit Exit schweiz mitgliedschaft
Exit schweiz mitgliedschaft Smart guides adobe illustrator
Smart guides adobe illustrator Free entry and exit
Free entry and exit Second empire furniture no exit
Second empire furniture no exit 31 spinal nerves
31 spinal nerves What are exit interviews
What are exit interviews Exit sentence
Exit sentence Menu pull down exit terdapat pada menu..
Menu pull down exit terdapat pada menu.. Koloid liofil contoh
Koloid liofil contoh Sa block
Sa block Exit kolmas kausi
Exit kolmas kausi Exit interview process flowchart
Exit interview process flowchart Pstn feature exit
Pstn feature exit Bed exit alarm effectiveness
Bed exit alarm effectiveness Entry and exit criteria in software testing
Entry and exit criteria in software testing Chapter 52 pride and prejudice
Chapter 52 pride and prejudice Start.php?chapter=
Start.php?chapter= Compare and contrast hook example
Compare and contrast hook example Formal email
Formal email How to make an expository paragraph
How to make an expository paragraph How to finish a formal email
How to finish a formal email How to start opinion paragraph
How to start opinion paragraph Informal letter business
Informal letter business Essay discussing the advantages and disadvantages
Essay discussing the advantages and disadvantages What is persuasive essay
What is persuasive essay What are the parts of a friendly letter
What are the parts of a friendly letter Similarity paragraph example
Similarity paragraph example When did ww2 start
When did ww2 start Why did the industrial revolution start in britain
Why did the industrial revolution start in britain Head start pir
Head start pir Where does the pacific time zone start
Where does the pacific time zone start When did the internet start
When did the internet start Welcome we will begin shortly
Welcome we will begin shortly How to start an opening statement
How to start an opening statement Spools of suffering
Spools of suffering Polovysoký start
Polovysoký start Past participle past
Past participle past Unit 6 lesson 4 fast start
Unit 6 lesson 4 fast start Aug methionine start codon
Aug methionine start codon Adverbial sentence openers
Adverbial sentence openers Bce and bc timeline
Bce and bc timeline Think big act now
Think big act now Sumerian civilization
Sumerian civilization Jump start triage system
Jump start triage system What started the renaissance
What started the renaissance A person who supports artists especially financially
A person who supports artists especially financially Prefix un words
Prefix un words How did language start
How did language start Forefather of internet
Forefather of internet Describe katniss’s quarters.
Describe katniss’s quarters. Introduction to a comparative essay
Introduction to a comparative essay Jesus timeline
Jesus timeline When did the gold rush start and end in australia
When did the gold rush start and end in australia Tek butonla start stop
Tek butonla start stop Utterance
Utterance How to start an opening statement
How to start an opening statement How do you start a story
How do you start a story How to write an enduring issue essay
How to write an enduring issue essay How to write a counterclaim
How to write a counterclaim How to start topic sentence
How to start topic sentence Start with heart
Start with heart 6 word biography examples
6 word biography examples Repulsion start induction run motor
Repulsion start induction run motor Piccola noria maxiemergenza
Piccola noria maxiemergenza Running start spscc
Running start spscc Running start pros and cons
Running start pros and cons Prefix examples mis
Prefix examples mis Protestant reformation quiz
Protestant reformation quiz Density property of real numbers examples
Density property of real numbers examples How to start a counterclaim paragraph
How to start a counterclaim paragraph Pseudocode
Pseudocode What does the symbol oval means in the flowchart?
What does the symbol oval means in the flowchart?