Geometrical Event Biasing 1 Geometrical Event Biasing a

Geometrical Event Biasing 1. Geometrical Event Biasing a) Importance Sampling b) Weight Window and Energy biasing 2. Examples 3. Options 4. Shortcomings? 5. Discussion Alex Howard ETH, Zurich Geometrical Event Biasing Overview Geant 4 Collaboration Workshop ESTEC 6 th October 2010 Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 1

Geometric Biasing The purpose of geometry based event biasing is to save computing time by sampling less often the particle histories entering “less important” geometry regions, and more often in more “important” regions. * Importance sampling technique * Weight window technique Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 2

Importance sampling technique Importance sampling acts on particles crossing boundaries between “importance cells”. The action taken depends on the importance value assigned to the cell. In general, a track is either split or plays Russian roulette at the geometrical boundary depending on the importance value assigned to the cell. I=1 I=2 W=1 W=0. 5 Splitting W=0. 5 P=2 P = 0. 5 Russian Roulette X W=1 W=0. 5 Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 3

Importance sampling technique Importance sampling acts on particles crossing boundaries between “importance cells”. The action taken depends on the importance value assigned to the cell. In general, a track is either split or plays Russian roulette at the geometrical boundary depending on the importance value assigned to the cell. I=1 I=2 W=1 W=0. 5 Survival probability (P) is defined by the ratio of importance value. P = Ipost / Ipre The track weight is changed to W/P. W=0. 5 P=2 P = 0. 5 X W=1 W=0. 5 Splitting a track ( P > 1 ) Ø E. g. creating two particles with half the ‘weight’ if it moves into volume with double importance value. Russian-roulette (P < 1 ) in opposite direction Ø E. g. Kill particles according to the survival probability (1 - P). Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 4

Weight Window Weight based enhancement to importance sampling Particles either split or Russian Roulette played based on space-energy cells User defines a weight window for each space cell, and optionally for different energies Can help control weight fluctuations introduced by other variance reduction techniques Maintains similar weights in a given region, which makes computation more efficient – (equal CPU per weight) Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 5
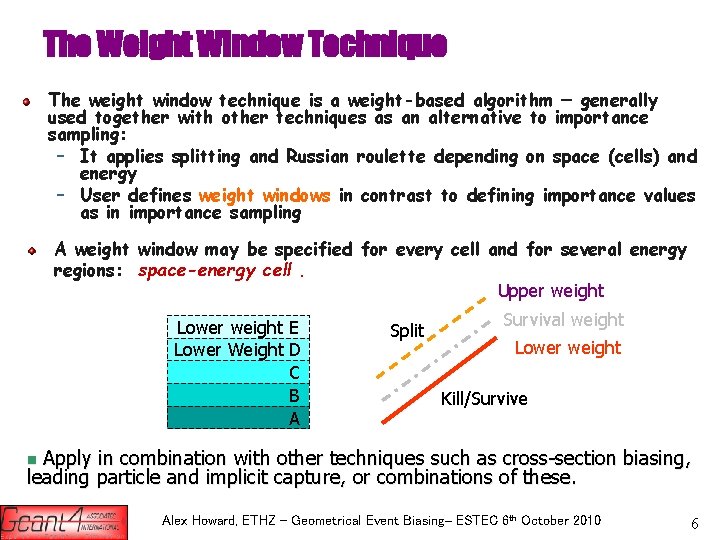
The Weight Window Technique The weight window technique is a weight-based algorithm – generally used together with other techniques as an alternative to importance sampling: – It applies splitting and Russian roulette depending on space (cells) and energy – User defines weight windows in contrast to defining importance values as in importance sampling A weight window may be specified for every cell and for several energy regions: space-energy cell. Upper weight Upper Energy Survival weight Upper Energy Lower weight E Split Lower weight Lower Weight D C B Kill/Survive A Lower weight Apply in combination with other techniques such as cross-section biasing, leading particle and implicit capture, or combinations of these. n Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 6

The weight window technique (continue) Checks the particle weight – Compare the particle weight with a ‘window’ of weights defined for the current energy-space cell – Play splitting or roulette in case if it is outside, resulting in 0 or more particles ‘inside’ the window § E. g. WL is a lower weight bound of a cell. CU and CS are upper limit factor and survival factor, respectively. • W > WL*CU Split track • W < WL*WL Roulette WL*CU WL*CS P = W / (WL*CS) WL Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 7

Examples Extended/Biasing contains 2 examples of biasing – B 01 (one geometry biasing) – B 02 (biasing in the parallel world) § Both looking at 10 Me. V neutrons travelling through concrete shielding Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 8

Biasing example B 01 Shows the importance sampling in the mass (tracking) geometry Option to show weight window 10 Me. V neutron shielding by cylindrical thick concrete material Geometry – 80 cm high concrete cylinder divided into 18 slabs – Importance values assigned to 18 concrete slabs in the Detector. Construction for simplicity. – The G 4 Scorer is used for the checking result § Top level class uses the framework provided for scoring. Air 1 1 2 4 8 16 32 64 ………. . 2 n Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 9
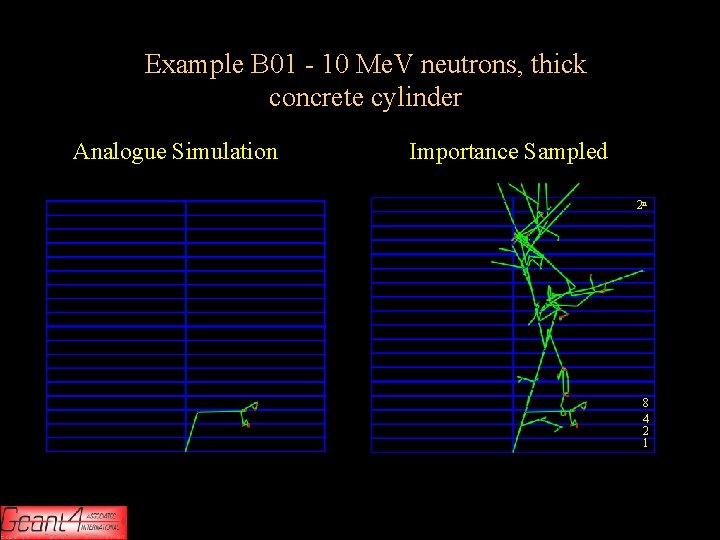
Example B 01 - 10 Me. V neutrons, thick concrete cylinder Analogue Simulation Importance Sampled 2 n 8 4 2 1 Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 10
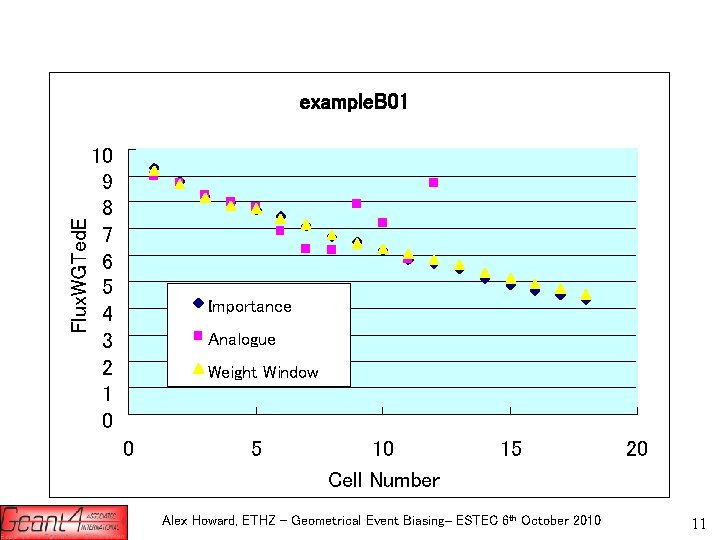
Flux multiplied by Kinetic energy of particle Flux. WGTed. E (Me. V) example. B 01 10 9 8 7 6 5 4 3 2 1 0 Importance Analogue Weight Window 0 5 10 Cell Number 15 Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 20 11

Example B 02 Shows importance sampling in a parallel geometry Includes a customized scoring making use of the scoring framework Mass geometry consists of a 180 cm high simple bulk concrete cylinder A parallel geometry is created to hold importance values for slabs of width 10 cm and for scoring The scoring uses the G 4 Cell. SCorer and one customized scorer for the last slab Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 12

Shortcomings Statistical analysis/accuracy of result/convergence of result Performance improvement measure Interface – command line? Why in physics list? Sensible weight values? Protection against “dumb” users? Real Examples Validation for given use cases in terms of CPU, Variance reduction and physics performance Documentation Publicity Alex Howard, ETHZ – Geometrical Event Biasing– ESTEC 6 th October 2010 13
- Slides: 13