Linear Programming What is Linear Programming What is

Linear Programming

What is Linear Programming?

What is Linear Programming? Say you own a 500 square acre farm. On this farm you can grow wheat, barley, corn or some combination of the 3. You have a limited supply of fertilizer and pesticide, both of which are needed (in different quantities) for each crop grown. Let’s say wheat sells at $7 a bushel, barley is $3, and corn is $3. 50. So, how many of each crop should you grow to maximize your profit?

What is Linear Programming? A mathematical tool for maximizing or minimizing a quantity (usually profit or cost of production), subject to certain constraints. Of all computations and decisions made by management in business, 5090% of those involve linear programming.

Background on Linear Programming • As a field of mathematics, LP is still a small child (in math years) • Developed by Leonid Kantorovich around the time of WWII • Further developed over following decades • Today, easily the most commonly used field for optimization • Economics, business management, transportation, technology, planning, production, … the list goes on…

Maximizing Profit Problem where a limited number of resources are used to produce a combination of products to maximize profit from the sale Production of… • Pretty much anything

• Maximizing Problems consist of… 1. 2. 3. 4. 5. Resources Products Recipes Profit Objective

Setting Up A toy manufacturer can produce skateboards and dolls. Both require the precious resource of plastic, of which there are 60 units available. Skateboards take five units of plastic and make $1 profit. Dolls take two units of plastic and make $0. 55 profit. The company wants to make at least 1 doll and at least 1 skateboard. What is the number of dolls and skateboards the company can produce to maximize profit?

Setting Up Mixture Problems First identify components of the problem: 1. Variables (Products) 2. Constraints (Resources and Recipes) 3. Profits 4. Objective – Maximize profit

Make Mixture Chart or Formulas Products Resources Plastic (60) Profit Skateboards (x units) 5 $1. 00 Dolls (y units) 2 $0. 55 2 Groups of Equations: - Profit Equation (profit equation) - Constraint Inequalities With these, create Feasible Region

Feasible Region – region which consists of all possible solution choices for a particular problem Using the constraint equation we get the following graph: Constraints: 5 s + 2 d ≤ 60 s>0 d>0

Corner Point Principle Which point is optimal? Corner Point Principle The maximal value always corresponds to a corner point

Corner Point Principle Plug in corner points to profit formula:

Quick Practice A clothing company has 100 yards of cloth and produces shirts (x units) and vests (y units). Shirts require 10 units and have profit value of $5, while vests require 4 units and have profit value of $4. What is the optimal production solution? Steps 3 & 4: Feasible Region & Corner Points ( 0, 25 ) ( 10, 0 ) ( 0, 0 ) Point (0, 0) Calculation of Profit Formula $5. 00 x + $4. 00 y = P $5. 00 (0) + $4. 00 (0) = $0. 00 (0, 25) $5. 00 (0) + $4. 00 (25) = $100. 00 (10, 0) $5. 00 (10) + $4. 00(0) = $50. 00

Quick Practice What if the company decides to also put a “non-zero constraint” on all production? Must produce at least 3 shirts and 10 vests. Constraints become: 10 x + 4 y ≤ 100 … x≥ 3 y ≥ 10 Feasible Region becomes: Corner Points: Point ( 3, 17. 5 ) Calculation of Profit Formula $5. 00 x + $4. 00 y = P (3, 10) $5. 00 (3) + $4. 00 (10) = $55. 00 (3, 17. 5) $5. 00 (3) + $4. 00 (17) = $83. 00 (6, 10) $5. 00 (6) + $4. 00(10) = $70. 00 ( 6, 10 ) ( 3, 10 ) Great Job!

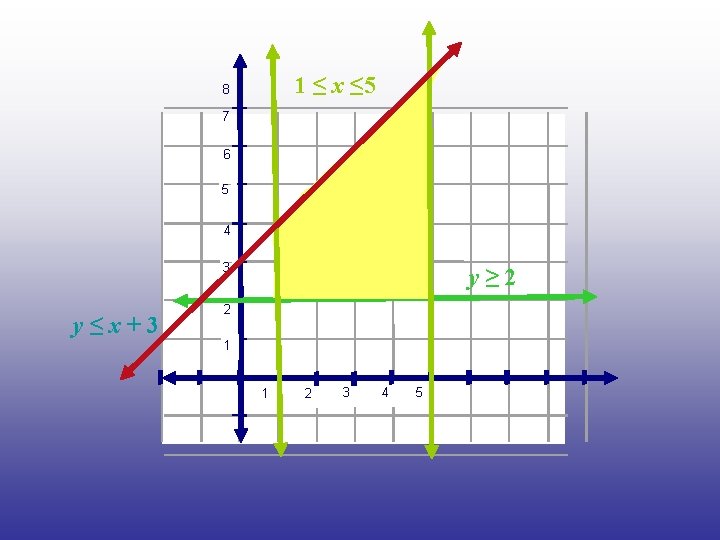
Linear Programming • Find the minimum and maximum values by graphing the inequalities and finding the vertices of the polygon formed. • Substitute the vertices into the function and find the largest and smallest values.

1 ≤ x ≤ 5 8 7 6 5 4 3 y≤x+3 y≥ 2 2 1 1 2 3 4 5

Linear Programming • The vertices of the quadrilateral formed are: (1, 2) (1, 4) (5, 2) (5, 8) • Plug these points into the function P = 3 x - 2 y

Linear Programming • • P = 3 x - 2 y P(1, 2) = 3(1) - 2(2) = 3 - 4 = -1 P(1, 4) = 3(1) - 2(4) = 3 - 8 = -5 P(5, 2) = 3(5) - 2(2) = 15 - 4 = 11 P(5, 8) = 3(5) - 2(8) = 15 - 16 = -1

Linear Programming • f(1, 4) = -5 minimum • f(5, 2) = 11 maximum