Abstract
Machine learning methods have helped to advance wide range of scientific and technological field in recent years, including computational chemistry. As the chemical systems could become complex with high dimension, feature selection could be critical but challenging to develop reliable machine learning based prediction models, especially for proteins as bio-macromolecules. In this study, we applied sparse group lasso (SGL) method as a general feature selection method to develop classification model for an allosteric protein in different functional states. This results into a much improved model with comparable accuracy and only 28 selected features comparing to 289 selected features from a previous study. The accuracy achieves 91.50 % with 1936 selected feature, which is far higher than that of baseline methods. In addition, grouping protein amino acids into secondary structures provides additional interpretability of the selected features. The selected features are verified as associated with key allosteric residues through comparison with both experimental and computational works about the model protein, and demonstrate the effectiveness and necessity of applying rigorous feature selection and evaluation methods on complex chemical systems.
Keywords: Protein States, Function-Related Residues, Sparse Group Lasso, Classification, Feature Selection
Graphical Abstract

Applying machine learning and feature selection to identify the allostery related residues are a relatively new research direction. The amino acid residues in the protein divided into secondary structures is considered as additional label for feature selection procedure. The selected features are verified as associated with key allosteric residues. This article demonstrates the effectiveness of sparse group lasso as general feature selection method for complex biomolecular systems.
1. INTRODUCTION
Proteins are important macro-molecules in biological systems to carry out wide range of biological functions in all forms of lives on earth. It is critical to understand protein functions as basic knowledge and for potential bio-engineering applications. Protein structures form the foundation of the understanding in protein function. However, proteins carry out their functions through constant dynamical processes1–4. Quantitative characterization of protein dynamics remains as the focus of structural and computational biology. Protein allostery is one of dynamical phenomena in which signals or regulation are transmitted from distal perturbation sites to functional sites in proteins5–16. Many computational and experimental techniques were developed to probe protein allostery17,17–33. Molecular dynamics simulations are the main computational method to explore protein dynamics thanks to the increasing computing powers. Accordingly, effective and efficient analysis methods are indispensable to interrogate simulations data to delineate protein functions and their relations with structures, especially individual residues34,35. Dimensionality reduction methods are effective means to inspect and visualize overall distribution of the simulations36–41. However, there is an urgent need for analysis method to shed lights on the relations between the protein functions and individual residues. Recently, we introduced machine learning methods to develop classification models to differentiate protein’s allosteric states with high accuracy. In addition to the prediction power, the machine learning methods also provide feature importance for each feature, which is directly related to individual amino acid residues, employed for the model development.
In this regard, applying machine learning and feature selection to identify the allostery related residues are a relatively new research direction. Recent literature42–44shows that the use of efficient machine learning algorithms such as random forest42,44, support vector machine43 and neural network43,45 allows promising learning result in terms of classification result in chemistry. For example, Zhang et al.46 applied the convolutional neural networks method to identify the DNA-protein binding sites. Li et al.47 proposed an improved artificial bee colony algorithm to optimize protein secondary structure. As some of the classifiers such as lasso48, decision tree49 and support vector machine50 are built-in feature selector at the same time, features used to build the learning model can be further analyzed for meaningful interpretation.
Furthermore, there are three categories of supervised feature selection: 1) wrapper method, 2) filter method and 3) embedded method. Wrapper method uses a predictive model to score feature subsets. Each new subset is used to train a model, which is tested on a hold-out set. Counting the number of mistakes made on that hold-out set (the error rate of the model) gives the score for that subset. Subset of features with the best performance are selected. The advantages of wrapper method are that the performance score is easy to compute and it identifies an optimal subset to build the learning model without specifying the number of features required beforehand. However, it is relatively slower than the other two methods. Examples include sequential forward selection (SFS) and sequential backward selection (SBS). Filter method uses a proxy measure instead of the error rate to score a feature subset. This measure is chosen to be fast to compute, while still capturing the usefulness of the feature set. A performance score will be assigned to each features, and features with the highest score will be chosen. Filter method is fast and intuitive, but the number of features needs to be specified. Examples include minimum redundancy maximum relevance (mRMR)51, Pearson’s correlation, linear discriminant analysis (LDA) and ANOVA. Embedded method combines the qualities of filter and wrapper methods. It is implemented by algorithms that have their own built-in feature selection methods. Examples include lasso48, support vector machine and sparse group lasso as applied in this work. The advantages of using embedded method include 1) the measure of learning performance (e.g. accuracy, specificity) can be used for parameter tuning instead of using a proxy measure or a measure which is not relevant to the learning performance (as in wrapper and filter methods), and 2) sparse learning can be easily achieved in the embedded method to achieve effectively learning model, thus reducing the possibility of over-fitting. For example, Li et al.52 proposed an adaptive sparse group lasso which can effectively perform grouped gene selection.
Continued from Zhou et al.45, this work aims at selecting and analyzing the function-related residue for protein-state recognition with sparse group learning. In this study, to differentiate protein’s allosteric, we use sparse group lasso to select important features, and use the selected feature to train a classifier to achieve high performance. The experimental results demonstrate that our method achieves a high prediction performance through using minor features and outperforms baseline methods.
The main contributions in this paper can be summarized as follows:
The large number of atomic distances from protein be grouped into relatively small number of structures.
We use sparse group lasso to develop classification models to differentiate protein’s allosteric states with high accuracy. In addition to the prediction power, the SGL method also provide feature importance for each feature, which is directly related to individual amino acid residues. The highly ranked features have high likelihood to play important role in protein allostery.
Bayesian hyperparameter optimization is used to tune the parameters of sparse group lasso model and support vector machine algorithm to achieve a higher performance.
To evaluate the classification performance of our method, it is compared against baseline algorithms. The experimental results demonstrate that the used approach outperforms other algorithms in terms of identification of protein-states.
The remainder of this paper is organized as follows. Section 2 introduces the data materials and the methodology. Section 3 presents the experimental result to verify the effectiveness of the proposal method, and then analyze the selected features, followed by a discussion. Finally, the conclusions are drawn in Section 4.
2. DATA COLLECTION AND METHODOLOGY
In this section, we first introduce the data sources. Subsequently, the details of methods of this paper are given. By using the sparse group lasso, the features are selected during the training phase, and then the selected features are used as training feature set to train the classifier. Next, the whole experiment process is presented. Finally, the baseline methods are introduced.
2.1. Data Collection Using Molecular Dynamics Simulation
In this study, we employed the second PDZ domain (PDZ2) in the human PTP1E protein as the data source to develop feature selection and prediction models. The PDZ2 protein is a typical dynamics-driven allosteric protein upon binding with its allosteric effectors. This type of protein has extensively experimental and computational investigations in protein research. We adopted the PDZ2 protein as a test case to develop and evaluate the proposed structured sparse learning based feature selection and classification model to identify key features that potentially drive the allostery of the PDZ2 protein. As the developed machine learning method is a general approach, it can be conveniently used as an effective machine learning tool for other protein research studies.
The initial structures for PDZ2 protein are 3LNX and 3LNY for unbound and bound states, respectively. Both unbound and bound states are immersed in explicit water boxes using TIP3P model (ref), and sodium cations and chloride anions were added to the simulation boxes to neutralize the simulation boxes. Total of 13 independent sets simulations each with length 34ns were carried out for both state and subjected to machine learning model analysis. The canonical ensemble (NVT) Langevin MD simulations were used for the production run. For all simulations, 2 femtosecond (fs) step size was used and bond for hydrogen atoms were constrained. Frames were saved every 10 picoseconds. Periodic Boundary Condition (PBC) was applied in the simulations. All simulations were carried out using CHARMM simulation package version 40b1 and the CHARMM22 force field. For all the 34ns simulation, the initial 4 nanoseconds were treated as equilibrium. Therefore, each simulation set subjected to analysis is 30ns with 3000 frames extracted. Among 13 simulations of each state, ten simulations were randomly selected as training sets, and remaining three simulations were used as testing sets.
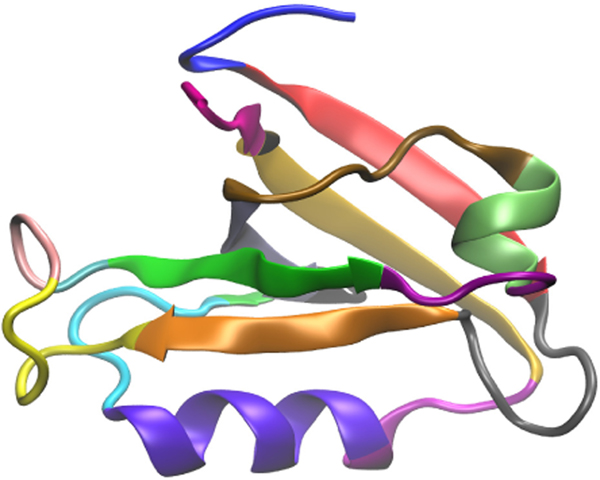
In previous work45, there are 60,000 training observations and 18,000 testing observations. The training and testing observations were combined together as a single dataset for better evaluation with cross validation (as introduced later). The total number of features is 4743: the 1st − 4371th features are the inter-distance among the 94 residues, the 4372nd−4464th features are the sine values of Phi angles along the protein backbone, the 4465th − 4557th features are the cosine values of Phi angles along the protein backbone, the 4558th − 4650th features are the sine values of the Psi angles along the backbone, and the 4651st − 4743th features are the cosine values of the Psi angles along the backbone. Detail can be found in Table 1. To summarize, each residue can be assigned to one of the 19 groups, as shown in Table 2. PDZ2 structure with these 19 groups is illustrated in Fig. 1. In this study, the features are grouped into feature groups. The details of the 189 inter-residual groups can be found in Table 3.
Table 1:
Features in this Study.
| Features | Type |
|---|---|
| 1 – 4371 | Pairwise distance between the 94 residues (i.e. 1–2, 1–3, ..., 93–94) |
| 4372 – 4464 | Inter-residue Phi Angle (sin) between 94 residues (i.e. 1–2, 2–3, ..., 93–94) |
| 4465 – 4457 | Inter-residue Phi Angle (cos) between 94 residues (i.e. 1–2, 2–3, ..., 93–94) |
| 4458 – 4650 | Inter-residue Psi Angle (sin) between 94 residues (i.e. 1–2, 2–3, ..., 93–94) |
| 4651 – 4743 | Inter-residue Psi Angle (cos) between 94 residues (i.e. 1–2, 2–3, ..., 93–94) |
Table 2:
A List of All 94 Protein Residues and the Group Assignment.
| Group No | Group | Residue |
|---|---|---|
| 1 | Loop 1 | P1 |
| K2 | ||
| P3 | ||
| G4 | ||
| D5 | ||
| 2 | Beta-strand 1 | I6 |
| F7 | ||
| E8 | ||
| V9 | ||
| E10 | ||
| L11 | ||
| A12 | ||
| 3 | Loop 2 | K13 |
| N14 | ||
| D15 | ||
| N16 | ||
| S17 | ||
| L18 | ||
| G19 | ||
| 4 | Beta-strand 2 | I20 |
| S21 | ||
| V22 | ||
| T23 | ||
| G24 | ||
| 5 | Loop 3 | G25 |
| V26 | ||
| N27 | ||
| T28 | ||
| S29 | ||
| V30 | ||
| 6 | Alpha-helix 1 | R31 |
| H32 | ||
| G33 | ||
| 7 | Loop 4 | G34 |
| 8 | Beta-strand 3 | I35 |
| Y36 | ||
| V37 | ||
| K38 | ||
| A39 | ||
| V40 | ||
| 9 | Loop 5 | I41 |
| P42 | ||
| Q43 | ||
| G44 | ||
| 10 | Alpha-helix 2 | A45 |
| A46 | ||
| E47 | ||
| S48 | ||
| D49 | ||
| 11 | Loop 6 | G50 |
| R51 | ||
| I52 | ||
| H53 | ||
| K54 | ||
| G55 | ||
| D56 | ||
| 12 | Beta-strand 4 | R57 |
| V58 | ||
| L59 | ||
| A60 | ||
| V61 | ||
| 13 | Loop 7 | N62 |
| G63 | ||
| 14 | Beta-strand 5 | V64 |
| S65 | ||
| 15 | Loop 8 | L66 |
| E67 | ||
| G68 | ||
| A69 | ||
| T70 | ||
| 16 | Al pha-helix 3 | H71 |
| K72 | ||
| Q73 | ||
| A74 | ||
| V75 | ||
| E76 | ||
| T77 | ||
| L78 | ||
| R79 | ||
| 17 | Loop 9 | N80 |
| T81 | ||
| G82 | ||
| Q83 | ||
| 18 | Beta-strand 6 | V84 |
| V85 | ||
| H86 | ||
| L87 | ||
| L88 | ||
| L89 | ||
| E90 | ||
| 19 | Loop 10 | K91 |
| G92 | ||
| Q93 | ||
| S94 |
Figure 1:
PDZ2 structure with 19 groups highlighted.
Table 3:
A list of 189 groups of inter-residual groups used in sparse group lasso for feature selection. Please note that duplicated groups such as 1–2 and 2–1 have been consolidated as one. The name of each residual group can be found in Table 2.
| Group 1 | Group 2 | Final Group |
|---|---|---|
| 1 | 1 | 1–1 |
| 2 | 2 | 2–2 |
| 3 | 3 | 3–3 |
| 4 | 4 | 4–4 |
| 5 | 5 | 5–5 |
| 6 | 6 | 6–6 |
| 7 | 7 | 7–7 |
| 8 | 8 | 8–8 |
| 9 | 9 | 9–9 |
| 10 | 10 | 10–10 |
| 11 | 11 | 11–11 |
| 12 | 12 | 12–12 |
| 13 | 13 | 13–13 |
| 14 | 14 | 14–14 |
| 15 | 15 | 15–15 |
| 16 | 16 | 16–16 |
| 17 | 17 | 17–17 |
| 18 | 18 | 18–18 |
| 19 | 19 | 19–19 |
| 1 | 2 | 1–2 |
| 1 | 3 | 1–3 |
| 2 | 3 | 2–3 |
| 1 | 4 | 1–4 |
| 2 | 4 | 2–4 |
| 3 | 4 | 3–4 |
| 1 | 5 | 1–5 |
| 2 | 5 | 2–5 |
| 3 | 5 | 3–5 |
| 4 | 5 | 4–5 |
| 1 | 6 | 1–6 |
| 2 | 6 | 2–6 |
| 3 | 6 | 3–6 |
| 4 | 6 | 4–6 |
| 5 | 6 | 5–6 |
| 1 | 7 | 1–7 |
| 2 | 7 | 2–7 |
| 3 | 7 | 3–7 |
| 4 | 7 | 4–7 |
| 5 | 7 | 5–7 |
| 6 | 7 | 6–7 |
| 1 | 8 | 1–8 |
| 2 | 8 | 2–8 |
| 3 | 8 | 3–8 |
| 4 | 8 | 4–8 |
| 5 | 8 | 5–8 |
| 6 | 8 | 6–8 |
| 7 | 8 | 7–8 |
| 1 | 9 | 1–9 |
| 2 | 9 | 2–9 |
| 3 | 9 | 3–9 |
| 4 | 9 | 4–9 |
| 5 | 9 | 5–9 |
| 6 | 9 | 6–9 |
| 7 | 9 | 7–9 |
| 8 | 9 | 8–9 |
| 1 | 10 | 1–10 |
| 2 | 10 | 2–10 |
| 3 | 10 | 3–10 |
| 4 | 10 | 4–10 |
| 5 | 10 | 5–10 |
| 6 | 10 | 6–10 |
| 7 | 10 | 7–10 |
| 8 | 10 | 8–10 |
| 9 | 10 | 9–10 |
| 1 | 11 | 1–11 |
| 2 | 11 | 2–11 |
| 3 | 11 | 3–11 |
| 4 | 11 | 4–11 |
| 5 | 11 | 5–11 |
| 6 | 11 | 6–11 |
| 7 | 11 | 7–11 |
| 8 | 11 | 8–11 |
| 9 | 11 | 9–11 |
| 10 | 11 | 10–11 |
| 1 | 12 | 1–12 |
| 2 | 12 | 2–12 |
| 3 | 12 | 3–12 |
| 4 | 12 | 4–12 |
| 5 | 12 | 5–12 |
| 6 | 12 | 6–12 |
| 7 | 12 | 7–12 |
| 8 | 12 | 8–12 |
| 9 | 12 | 9–12 |
| 10 | 12 | 10–12 |
| 11 | 12 | 11–12 |
| 1 | 13 | 1–13 |
| 2 | 13 | 2–13 |
| 3 | 13 | 3–13 |
| 4 | 13 | 4–13 |
| 5 | 13 | 5–13 |
| 6 | 13 | 6–13 |
| 7 | 13 | 7–13 |
| 8 | 13 | 8–13 |
| 9 | 13 | 9–13 |
| 10 | 13 | 10–13 |
| 11 | 13 | 11–13 |
| 12 | 13 | 12–13 |
| 1 | 14 | 1–14 |
| 2 | 14 | 2–14 |
| 3 | 14 | 3–14 |
| 4 | 14 | 4–14 |
| 5 | 14 | 5–14 |
| 6 | 14 | 6–14 |
| 7 | 14 | 7–14 |
| 8 | 14 | 8–14 |
| 9 | 14 | 9–14 |
| 10 | 14 | 10–14 |
| 11 | 14 | 11–14 |
| 12 | 14 | 12–14 |
| 13 | 14 | 13–14 |
| 1 | 15 | 1–15 |
| 2 | 15 | 2–15 |
| 3 | 15 | 3–15 |
| 4 | 15 | 4–15 |
| 5 | 15 | 5–15 |
| 6 | 15 | 6–15 |
| 7 | 15 | 7–15 |
| 8 | 15 | 8–15 |
| 9 | 15 | 9–15 |
| 10 | 15 | 10–15 |
| 11 | 15 | 11–15 |
| 12 | 15 | 12–15 |
| 13 | 15 | 13–15 |
| 14 | 15 | 14–15 |
| 1 | 16 | 1–16 |
| 2 | 16 | 2–16 |
| 3 | 16 | 3–16 |
| 4 | 16 | 4–16 |
| 5 | 16 | 5–16 |
| 6 | 16 | 6–16 |
| 7 | 16 | 7–16 |
| 8 | 16 | 8–16 |
| 9 | 16 | 9–16 |
| 10 | 16 | 10–16 |
| 11 | 16 | 11–16 |
| 12 | 16 | 12–16 |
| 13 | 16 | 13–16 |
| 14 | 16 | 14–16 |
| 15 | 16 | 15–16 |
| 1 | 17 | 1–17 |
| 2 | 17 | 2–17 |
| 3 | 17 | 3–17 |
| 4 | 17 | 4–17 |
| 5 | 17 | 5–17 |
| 6 | 17 | 6–17 |
| 7 | 17 | 7–17 |
| 8 | 17 | 8–17 |
| 9 | 17 | 9–17 |
| 10 | 17 | 10–17 |
| 11 | 17 | 11–17 |
| 12 | 17 | 12–17 |
| 13 | 17 | 13–17 |
| 14 | 17 | 14–17 |
| 15 | 17 | 15–17 |
| 16 | 17 | 16–17 |
| 1 | 18 | 1–18 |
| 2 | 18 | 2–18 |
| 3 | 18 | 3–18 |
| 4 | 18 | 4–18 |
| 5 | 18 | 5–18 |
| 6 | 18 | 6–18 |
| 7 | 18 | 7–18 |
| 8 | 18 | 8–18 |
| 9 | 18 | 9–18 |
| 1 | 18 | 1–18 |
| 2 | 18 | 2–18 |
| 3 | 18 | 3–18 |
| 4 | 18 | 4–18 |
| 5 | 18 | 5–18 |
| 6 | 18 | 6–18 |
| 7 | 18 | 7–18 |
| 8 | 18 | 8–18 |
| 9 | 18 | 9–18 |
| 10 | 18 | 10–18 |
| 11 | 18 | 11–18 |
| 12 | 18 | 12–18 |
| 13 | 18 | 13–18 |
| 14 | 18 | 14–18 |
| 15 | 18 | 15–18 |
| 16 | 18 | 16–18 |
| 17 | 18 | 17–18 |
| 1 | 19 | 1–19 |
| 2 | 19 | 2–19 |
| 3 | 19 | 3–19 |
| 4 | 19 | 4–19 |
| 5 | 19 | 5–19 |
| 6 | 19 | 6–19 |
| 7 | 19 | 7–19 |
| 8 | 19 | 8–19 |
| 9 | 19 | 9–19 |
| 10 | 19 | 10–19 |
| 11 | 19 | 11–19 |
| 12 | 19 | 12–19 |
| 13 | 19 | 13–19 |
| 14 | 19 | 14–19 |
| 15 | 19 | 15–19 |
| 16 | 19 | 16–19 |
| 17 | 19 | 17–19 |
| 18 | 19 | 18–19 |
2.2. Machine Learning Methods
2.2.1. Feature Selection by Sparse Group Lasso
Under this context, sparse learning refers to the use of L1-norm () on the learning model (β), whereas group learning53 refers to the use of group norm (, where k refers to the kth group in the group structure) on the learning model.
Lasso (least absolute shrinkage and selection operator)48, as the basis of sparse learning, was originally developed as a regression analysis method. It minimizes the usual sum of squared errors, with a bound on the sum of the absolute values of the coefficients. A L1-norm penalty in the formulation is an effective way to alleviate the problem of over-fitting. In addition, lasso involves solving an easy convex optimization problem. The formulation of the lasso optimization problem with least-square loss is as follows, where N is the number of observations, M is the
number of features, , , and :
| (1) |
Lasso was later generalized to many variants such as elastic nets54 and group lasso55. Group lasso consists of predefined groups of covariates regularized by an L2-norm, where and :
| (2) |
As for group learning, the group lasso with L2-norm penalty was extended to the one with L∞-norm penalty56, where :
| (3) |
Both the L2-norm and L∞-norm of βg become zero when βg = 0; hence when λ is appropriately tuned, the penalty term can effectively remove unimportant groups. However, the limitation of using the L2-norm and L∞-norm penalties is that, when one variable in a group is selected, all other variables in the same group tend to be selected, better known as an ”all-in-all-out” property57. Once a component of βg is non-zero, the value of the two norm functions are no longer zero.
To select variables inside a group (instead of choosing all in a group as in group lasso), sparse group lasso (SGL)55,58 has an additional L1-norm penalty (See Eq. 4 for details). The resulting model of using both L1-norm and group norm is better known as sparse group learning53,58–60, with SGL using the least square loss (see Eq.4 for details).
As sparse group learning considers the inherent group structure of the data (e.g. the kth group of pairwise distances of different residues45), learning models are trained according to the entire group of features - if a particular group of features is irrelevant to the learning performance, group norm - which is essentially to apply a L2-norm on the pre-defined group of features - will force its norm and thus every element the entire group vector (βk) to be zero, according to the singularity of L2-norm when parameters are appropriately tuned. On the other hand, the presence of L1-norm ensures sparsity of the model vector β. Thus, both group-norm and L1norm ensure inter-group and within-group sparsity of the model vector β. Moreover, features selected in the model vector can be analyzed in groups - all features in the irrelevant group tend not to be selected as a whole, whereas only a small amount of features are selected in the relevant group, as seen in the later section of this work and others. This is why the use of sparse group learning has gained traction in various application areas of research (particularly in bioinformatics) in recent years, and why SGL is proposed for feature selection as a continuance of the meaningful protein-state recognition project45.
Sparse group lasso (SGL)58,61 was used to select the important features among the entire set of 4743 features. The formulation of SGL is as follows:
| (4) |
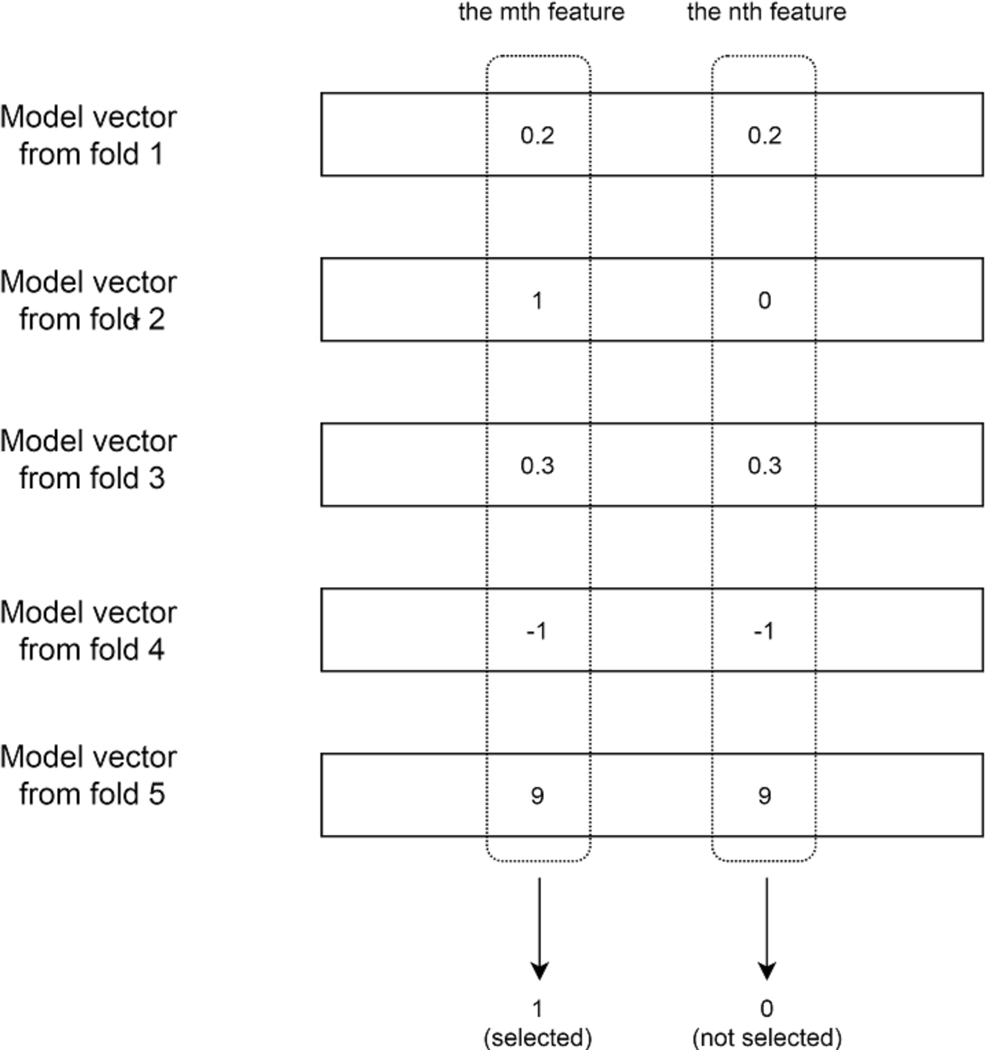
where y represents the categorical response, A is the observed feature vector. Implementation by Matlab-based SLEP toolbox61 was used. SGL by SLEP toolbox was implemented with accelerated gradient descent (AGD)62, a computationally efficient mathematical optimization algorithm. For a given function f(x), the idea of AGD is that instead of updating the gradient directly as in gradient descent, where γi is the step size in each iteration of the optimization), AGD attempts to update the gradient through a proximal operator (). The convergence rate of AGD is O(1/N2) as opposed to O(1/N) for gradient descent, which is more favorable in terms of computational efficiency. This is the main reason why SLEP toolbox is used. After solving Eq. 4, the intersection set of features with non-zero value in feature vector x from each fold will be chosen for model building and evaluation as illustrated in Fig. 2.
Figure 2:
Visualization of how features are selected with SGL. Firstly, 5-fold cross validation was run. In each run, there would be a model vector built for the particular fold. After that, if a particular feature is selected across all 5 folds (i.e. coefficient of that feature is non-zero for all 5 folds), then that feature is selected for the final model building. In this example, the nth feature is not selected because the coefficient value of model vector at fold 2 is zero.
2.2.2. Classification with Support Vector Machine
The selected subset of features with SGL were used to train the classification model. Among various classification model, SVM model has been frequently used because its classification performance is very high63–65. The goal of SVM classification is to create decision boundaries in the feature space that divide data points into multiple classes. Its aim is to make an ideal separating hyperplane among multiple classes in order to decrease generalization error and increase margin. The unique difference between L1-norm regularized SVM and L2-norm SVM is that the regularization term of L2-SVM is the square sum of slack variables. L2-SVM is differentiable and imposes a bigger loss for points which violate the margin66. The related researches demonstrated that training the classifier using the L2-SVM objective function outperforms L1-SVM67. In this paper, we choose the L2-regularized support vector machine by Matlab-based LIBLINEAR package68. Its formulation is as follows. The outcome variable is binary variable, which represents whether a protein is bound or unbound.
| (5) |
The L2-regularized support vector machine was solved via a trust region Newton method. The kernel function is linear kernel. The parameter C is optimized in the cross validation under different parameters and find the best one. For details of optimization method, please refer to the LIBLINEAR Practical Guide68.
2.3. Bayesian Hyperparameter Optimization
Bayesian Hyperparameter Optimization is used to tune the hyperparameters of sparse group lasso model and SVM. Comparing with the random or grid search, Bayesian hyperparameter optimization can efficiently conduct a search of a global optimization problem at finding the hyperparameters.
In the sparse group lasso model, the parameter λ1 control the within-group sparsity of model vector, the parameter λ2 control the between-group sparsity of model vector. It means that the sparsity of feature groups to be chosen can be controlled by adjusting this number. The parameters λ1 and λ2 are adjusted by the Bayesian hyperparameter optimization method with the training dataset using a five-fold cross validation to provide a realistic estimation of prediction errors and to prevent over-fitting. By adjusting the parameters(λ1, λ2), the number of features to be chosen in each group and the number of groups to be chosen can be controlled respectively while maintaining similar classification accuracy to the most optimal result. After running all possible combinations of parameters, the combination with the highest accuracy would be chosen. It can be a powerful application for chemists to design and consider different new design regarding protein residues.
2.4. Experimental Design
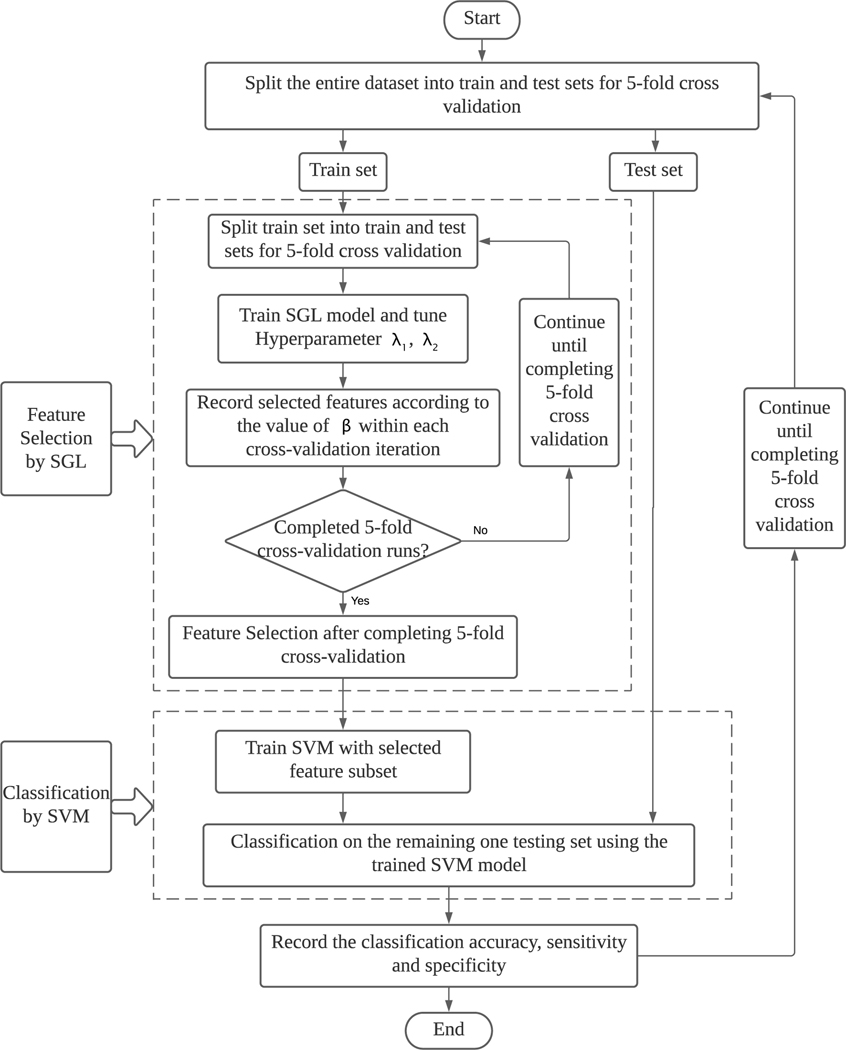
As shown in Fig. 3, we conduct standard 5-folds cross-validation on the entire dataset. In each time, the 4 folds were used as training set which is used for feature selection conducted by the sparse group lasso method. The training set can be further split into 5 folds to adjust the parameter λ1 and the λ2 by Bayesian hyperparameter optimization method. Based on the selected features by the sparse group lasso method, the SVM classification model are trained on the training set to make the final classification. The remaining one fold of the data set was used as testing set to calculate the classification accuracy, the sensitivity and the specificity with the trained SVM model.
Figure 3:
Flowchart of the Experimental Design
2.5. Comparison with Baseline Methods
To illustrate the advantages of the proposed method, the method in the previous work45 was compared. Feature selection using an extra-trees classifier in Scikit-Learn package69 of Python was first applied on all 4743 features. After that, two other baseline prediction models were built and evaluated.
Decision Tree: Often referred to as CART or Classification and Regression Trees, decision tree is a non-parametric machine learning algorithm. It uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item’s target value (represented in the leaves).
Artificial neural network (ANN): An ANN is based on a collection of connected units or nodes called artificial neurons which loosely model the neurons in a biological brain. The word ”artificial” was added to differentiate the human neural network from the neural network for machine learning. In essence, ANN can be considered as a black-box learning algorithm. When appropriately tuned, ANN can outperform other machine learning algorithms if vast amount of data is available.
More details of the baseline methods can be found in the previous work45.
3. EXPERIMENTAL RESULTS AND DISCUSSION
In this section, we first introduce the details of evaluation criterion. Next, we present the performance of our proposed method, followed the performance comparison with baseline methods. Then, we analyze the selected features by sparse group lasso. Lastly, the significance of the results of the study is discussed.
3.1. Evaluation Criterion
There are four evaluation indexes used in this regard. 1) Accuracy (Acc) refers to the ratio between the number of correctly classified number of protein states and total number of protein states; 2) Sensitivity (Sen) stands for the proportion of positives that are correctly identified; 3) Specificity (Spe) refers to the proportion of negatives that are correctly classified number of protein states; and 4) Density of model vector β (or feature vector) is defined as the ratio between the number of non-zero elements of the feature vector and that of the length. Model is deemed to be good if accuracy, sensitivity and specificity are high and density of feature vector is low (but not too low that the necessary features are not included in the selection result).
Sen, Spe and Acc are calculated according to the following formulate:
| (6) |
| (7) |
| (8) |
where TP refers to the number of true positives, TN stands for the number of true negatives, FP refers to the number of false positives, FN stands the number of false negatives.
For an example of understanding what overall density and group density of model vector is, it is assumed that there are 10 features in 2 groups for differentiating an apple from an orange, and the selection result (in the form of model vector β) is as follows:
| (9) |
Since all elements in feature vector of group 1 (β1) are all zero, feature group 1 is deemed to be irrelevant in differentiating an apple from an orange. On the other hand, feature group 2 deserves more attention as two elements out of the total five in the feature vector of group 2 (β2) are not zero. Feature density of group 1 is 0, whereas feature density of group 2 is 2/5 = 0.4 (2 out of all 5 elements are non-zero). Last but not least, overall density is 2/10 = 0.2. The same is applied to the problem of protein-state recognition.
3.2. Performance of different features
Using the proposed method, we use the Bayesian optimization search method to adjust the parameter λ1 and λ2 in different range to control the sparsity and thus obtain various number of selected features. Given a certain range of the parameter λ1 and λ2, we can obtain the number of feature density and the corresponding accuracy, sensitivity and specificity. The results are summarized in Table 4. According to Table 4, as the number of features go up, the accuracy is higher. It can be observed that 28 selected features achieve 81.04% for classification accuracy, 79.90% for sensitivity and 82.18% for specificity. Furthermore, the classification accuracy achieves 91.50% when the number of selected features is 1936, and the corresponding sensitivity is 91.68%.
Table 4:
The performance for various number of features
| No. of features | No. of Density(%) | Accuracy(%) | Sensitivity(%) | Specificity (% ) |
|---|---|---|---|---|
|
| ||||
| 1936 | 40.82 | 91.50 | 91.68 | 91.31 |
| 373 | 7.86 | 87.30 | 87.32 | 87.28 |
| 158 | 3.33 | 85.41 | 84.87 | 85.95. |
| 94 | 1.98 | 84.58 | 83.90 | 85.26 |
| 35 | 0.74 | 81.78 | 80.45 | 83.11 |
| 28 | 0.57 | 81.04 | 79.90 | 82.18 |
3.3. Performance comparison with Baseline methods
We compare our proposed method against the previous work45. As shown in Table 5, we can see that the proposed sparse group lasso method can achieve better classification accuracy with less selected features comparing with baseline methods. When the number of selected features is 28, the accuracy of our method is improvement of approximately 1.04%. In addition, the accuracy of our method improves 11.5% when the number of selected features is 1936.
Table 5:
Performance comparison between the proposed method and baseline methods.
3.4. Feature analysis
In these studies, feature selection is more or less an implicit procedure to ensure the prediction quality and accuracy. Due to the large size of proteins with much more atoms in small molecules, including all the atomic distances as features for machine learning models is not feasible. Although in some special cases, some predefined reaction coordinates could be constructed manually as features. In general, a robust feature selection procedure would be desirable for many machine learning prediction models for protein simulation. However, more systematic and thorough investigation for feature selection of high dimensional system presented in the current study is still necessary.
There are 94 residues which can be categorized in 19 groups (Table 2). This work focuses on the feature groups which contribute the most to the differentiation of protein states. Therefore, if the density of a model vector for a particular feature group is significantly higher than zero, that particular feature group deserves more attention for further interpretation.
Using SGL method, total of 28 features were selected to achieve 81.4% of accuracy. 28 features are inter-residue distances, as shown in Table 6. The inter-residue distances are illustrated in Fig. 4. The distance features are located between Groups 1 (Loop 1) and 3 (Loop 2), Groups 1 (Loop 1) and 4 (Beta-strand 2), Groups 1 (Loop 1) and 8 (Beta-strand 3), Groups 1 (Loop 1) and 9 (Loop 5), Groups 1 (Loop 1) and 10 (Alpha-helix 2), Groups 1 (Loop 1) and 11 (Loop 6), Groups 2 (Beta-strand 1) and 14 (Beta-strand 5), Groups 2 (Beta-strand 1) and 16 (Alpha-helix 3), Groups 10 (Alpha-helix 2) and 15 (Loop 8), Groups 10 (Alpha-helix 2) and 16 (Alpha-helix 3), Groups 10 (Alpha-helix 2) and 17 (Loop 9), Groups 10 (Alpha-helix 2) and 18 (Beta-strand 6), Groups 10 (Alpha-helix 2) and 19 (Loop 10). In Table 6, it also shows the corresponding protein residues. Feature density of each group is calculated as the number of non-zero elements over the length of the model vector of the particular group. A higher feature density indicates that the importance of the group is more high. The final coefficient is multiple of coefficients from the 25 fold, which indicates the importance of each selected feature. For example, if αi is the model vector from fold i, then the final coefficient element-wise products from all 25 folds ()
Table 6:
The details of 28 features selected by SGL.
| Group Name | Protein Residues | Group Feature Density | Final Coefficient | |||
|---|---|---|---|---|---|---|
|
| ||||||
| Inter Residual Group | Group 1 | Group 2 | Residual1 | Residual2 | ||
|
| ||||||
| 1–3 | Loop 1 | Loop 2 | P1 | N16 | 2.86% | 9.6036E-31 |
| 1–4 | Loop 1 | Beta-strand 2 | P1 | I20 | 8% | 1.2559E-26 |
| 1–4 | Loop 1 | Beta-strand 2 | P1 | G24 | 8% | -1.5256E-12 |
| 1–8 | Loop 1 | Beta-strand 3 | K2 | K38 | 3.33% | -7.6462E-46 |
| 1–9 | Loop 1 | Loop 5 | K2 | P42 | 10% | 2.3101E-73 |
| 1–9 | Loop 1 | Loop 5 | K2 | Q43 | 10% | -1.0090E-60 |
| 1–10 | Loop 1 | Alpha-helix 2 | K2 | A46 | 4% | 7.2234E-54 |
| 1–11 | Loop 1 | Loop 6 | K2 | G50 | 2.22% | 2.1611E-59 |
| 2–14 | Beta-strand 1 | Beta-strand 5 | I6 | S65 | 7.14% | 8.6464E-36 |
| 2–16 | Beta-strand 1 | Alpha-helix 3 | I6 | A74 | 1.59% | 5.8091E-30 |
| 10–15 | Alpha-helix 2 | Loop 8 | A45 | L66 | 8% | 6.5626E-66 |
| 10–15 | Alpha-helix 2 | Loop 8 | A45 | E67 | 8% | 1.2873E-70 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | Q73 | 15.56% | 7.7743E-58 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | A74 | 15.56% | 6.4350E-56 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | V75 | 15.56% | 5.8432E-49 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | E76 | 15.56% | 1.4509E-46 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | T77 | 15.56% | 7.9182E-56 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | L78 | 15.56% | 2.1162E-57 |
| 10–16 | Alpha-helix 2 | Alpha-helix 3 | A45 | R79 | 15.56% | 1.0561E-55 |
| 10–17 | Alpha-helix 2 | Loop 9 | A45 | N80 | 5% | 3.2852–81 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | V84 | 17.14% | 6.5555E-57 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | V85 | 17.14% | 3.9407E-50 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | H86 | 17.14% | 5.3979E-72 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | L87 | 17.14% | 2.3291E-80 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | L88 | 17.14% | 8.3000E-57 |
| 10–18 | Alpha-helix 2 | Beta-stand 6 | A45 | L89 | 17.14% | 6.4652–74 |
| 10–19 | Alpha-helix 2 | Loop 10 | A45 | Q93 | 10% | 1.5272E-73 |
| 10–19 | Alpha-helix 2 | Loop 10 | A45 | S94 | 10% | 4.6970E-67 |
Figure 4:
Key inter-residue distances selected using SGL method
In Fig. 5, different colors of ideogram represents different groups. Each group includes different number of protein residues. It shows not only the inter-residual feature density (pairwise distance) but also the inter-group feature density for various combination of parameters with accuracy higher than 81%. Fig. 5(a), Fig. 5(b), Fig. 5(c), Fig. 5(d), Fig. 5(e), Fig. 5(f) indicate the visualization of inter-residual feature density and inter-group feature density when the number of selected features is 28, 35, 94, 158, 373 and 1936 respectively. The Inter-Group Feature Density illustrated in Fig. 5 provides straightforward representations for the important groups among all the groups. In addition, Inter-Residual Feature Density illustrated in Fig. 5 could provide much finer presentation about important feature distribution of the system.
Figure 5:
Visualization of Inter-Residual Feature Density (Pairwise Distance) for various combination of paramaters.
On the whole, the inter-residual features between alpha-helix 2 and alpha-helix 3, alpha-helix2 and beta-strand 6 exist in most of the plots, indicating its importance in discriminating the protein states. The protein residues P1, K2, I6, N16, I20, G24, K38, P42, Q43, A45, A46, G50, S65, L66, E67, Q73, A74, V75, E76, T77, L78, R79, N80, V84, V85, H86, L87, L88, L89 from the above mentioned groups are critical for allostery of PDZ2 in various experimental studies. Such observation is indeed in agreement with the result of inter-group feature selection as in Table 6. With the increase of accuracy, the more inter-residual features are chosen.
3.5. Discussion
One of the innovations in the current study is grouping and labeling large number of atomic distances from protein (4371 for PDZ2 as the model system in this study) with relatively small number of secondary structures (19 for PDZ2, Fig. 1). This further labeling of the general features significantly simplified the data processing and interpretation of the machine learning model developed in this study. In the current study, Groups 1, 10, 16, and 18 are identified with the most contributions to the top important features (Table 6). Some of the residues from these Groups have been reported as critical for allostery of PDZ2 in various experimental studies, including Ala45 in Group 10,70 and Q73, Ala74, Val75, E76, Thr77, Leu78, R79 in Group 1670–73. In addition, there are more residues associated with high importance revealed in the current study that are also identified as key allosteric residues in the experimental characterization of PDZ2 allostery: N16, I20, G24, Q43, L66, N8071,73.
The key residues identified through sparse group lasso also large overlap with findings from several computational studies. The most prominent observation is that the Alpha-helix 3 as Group 16 consisting residues Q73 through R79 highlighted in this study is also identified as containing many hot residues through Perturbation Response Scanning study23, and part of allosteric path through Protein Structure Network (PSN) and Elastic Network Model (ENM)-based strategy.74 Similarly, part of beta-strand 2 as group 4 (residues 20 and 24) and beta-stand 6 as group 18 (residues V84, V85, L87 and L88 ) are associated with important features in this study, and are also identified as hot residues,23 or part of allosteric path74. Numerous other residues associated with high importance from this study are also highlighted by these computational studies, including P1, K2, I6, K38.
These agreements between our refined feature selections and experimental as well as other computational studies about PDZ2 provide necessary and reassuring validation for this study, rendering our strategy as a general approach applicable for other allosteric proteins. These presentations based on the rigorous feature selection procedure presented in this study, provide comprehensive and innovative ways to build reliable and informative machine learning models for complicated biological systems.
4. CONCLUSIONS
Machine learning models have started to be applied in many computational chemistry studies. Due to the complexity of molecular systems, especially biomacromolecules such as proteins, rigorous feature selections procedure remains as a challenging problem but is necessary for reliable model building. In this study, we applied sparse group lasso (SGL) method as feature selection method to develop reliable classification model for protein allostery using allosteric PDZ2 protein as model system. Comparing to a previous machine learning study about the same protein, this study demonstrated that the SGL method could be used to develop classification models differentiating protein in different allosteric states with the comparable accuracy but with much fewer features. Four balanced performance measures were used to evaluate the selected features, including classification accuracy, specificity, sensitivity and feature density. The final classification models using support vector machine method provide the same classification accuracy (81%) with merely 28 features among total of 4743 features, which is much smaller than 289 features used in a previous study. Dividing the amino acid residues in the protein into secondary structures as additional label for feature selection procedure is shown as an effective and informative way to illustrate important feature distribution. This study demonstrates the effectiveness of SGL as general feature selection method for complex biomolecular systems, and warrant further investigations to develop more novel and thorough feature selection approaches in computational chemistry.
5. DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.
6. ACKNOWLEDGMENTS
This work was supported by National Institute of General Medical Sciences of the National Institutes of Health [grant number R15GM122013]; the National Science Foundation [grant number 1537504]; the National Science Foundation [grant number 1434401]; and Southern Methodist University Dissertation Fellowship, Dallas, TX.
References
- 1.Frauenfelder H; McMahon B Proc. Natl. Acad. Sci 1998, 95(9), 4795–4797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Campbell E; Kaltenbach M; Correy GJ; Carr PD; Porebski BT; Livingstone EK; Afriat-Jurnou L; Buckle AM; Weik M; Hollfelder F; others. Nat. Chem. Biol 2016, 12(11), 944–950. [DOI] [PubMed] [Google Scholar]
- 3.Hensen U; Meyer T; Haas J; Rex R; Vriend G; Grubmüller H PloS one 2012, 7(5), e33931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kubitzki MB; de Groot BL; Seeliger D In From Protein Structure to Function with Bioinformatics; Springer Netherlands: Dordrecht, 2017; pages 393–425. [Google Scholar]
- 5.Perutz MF Nature. 1970, 228(5273), 726–734. [DOI] [PubMed] [Google Scholar]
- 6.Bacon F J mol biol 1965, 12, 88–118. [DOI] [PubMed] [Google Scholar]
- 7.Monod J; Changeux JP; Jacob FJ Mol. Biol 1963, 6(4), 306–329. [DOI] [PubMed] [Google Scholar]
- 8.Cooper A; Dryden DTF Eur. Biophys. J 1984, 11(2), 103–109. [DOI] [PubMed] [Google Scholar]
- 9.Cui Q; Karplus M Protein Sci. 2008, 17(8), 1295–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gunasekaran K; Ma BY; Nussinov R Proteins. 2004, 57(3), 433–443. [DOI] [PubMed] [Google Scholar]
- 11.Nussinov R; Tsai C-J; Liu JJ Am. Chem. Soc 2014, 136(51), 17692–17701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Volkman BF; Lipson D; Wemmer DE; Kern D Sci. 2001, 291(5512), 2429–2433. [DOI] [PubMed] [Google Scholar]
- 13.Fenton AW Trends Biochem. Sci 2008, 33(9), 420–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goodey NM; Benkovic SJ Nat. Chem. Biol 2008, 4(8), 474–482. [DOI] [PubMed] [Google Scholar]
- 15.Tzeng S-R; Kalodimos CG Curr. Opin. Struct. Biol 2011, 21(1), 62–67. [DOI] [PubMed] [Google Scholar]
- 16.Manley G; Loria JP Arch. Biochem. Biophys 2012, 519(2), 223–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Collier G; Ortiz V Arch. Biochem. Biophys 2013, 538(1), 6–15. [DOI] [PubMed] [Google Scholar]
- 18.De Los Rios P; Cecconi F; Pretre A; Dietler G; Michielin O; Piazza F; Juanico B Biophys J 2005, 89(1), 14–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ota N; Agard DA J. Mol. Biol 2005, 351(2), 345–354. [DOI] [PubMed] [Google Scholar]
- 20.Sharp K; Skinner JJ Proteins: Struct., Funct., Bioinf 2006, 65(2), 347–361. [DOI] [PubMed] [Google Scholar]
- 21.Kidd BA; Baker D; Thomas WE Plos Comput. Bio 2009, 5(8),e1000484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kong Y; Karplus M Proteins: Struct., Funct., Bioinf 2009, 74(1), 145–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gerek ZN; Ozkan SB PLoS Comput. Biol 2011, 7(10), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rader AJ; Brown SM Mol. BioSyst 2011, 7(2), 464–471. [DOI] [PubMed] [Google Scholar]
- 25.Feher VA; Durrant JD; Van Wart AT; Amaro RE Curr. Opin. Struct. Biol 2014, 25, 98–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Johnson QR; Lindsay RJ; Nellas RB; Fernandez EJ; Shen T Biochemistry 2015, 54(7), 1534–1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ma X; Qi Y; Lai L Proteins. 2015, 83(8), 1375–1384. [DOI] [PubMed] [Google Scholar]
- 28.Dokholyan NV Chem. Rev 2016, 116(11), 6463–6487. [DOI] [PubMed] [Google Scholar]
- 29.Stetz G; Verkhivker GM J. Chem. Inf. Model 2016, 56(8), 1490–1517. [DOI] [PubMed] [Google Scholar]
- 30.Stolzenberg S; Michino M; LeVine MV; Weinstein H; Shi L Biochimica et Biophysica Acta (BBA) - Biomembranes 2016, 1858(7, Part B), 1652–1662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.La Sala G; Decherchi S; De Vivo M; Rocchia W ACS Cent. Sci 2017, 3(9), 949–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Greener JG; Sternberg MJE Curr. Opin. Struct. Biol 2018, 50, 1–8. [DOI] [PubMed] [Google Scholar]
- 33.Dong Z; Zhou H; Tao P Protein Sci. 2017, 27, 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kalescky R; Liu J; Tao PJ Phys. Chem. A 2015, 119(9), 1689–1700. [DOI] [PubMed] [Google Scholar]
- 35.Kalescky R; Zhou H; Liu J; Tao P PLoS Comput. Biol 2016, 12(4), e1004893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tenenbaum JB; De Silva V; Langford JC Sci. 2000, 290(5500), 2319–2323. [DOI] [PubMed] [Google Scholar]
- 37.Hinton GE; Salakhutdinov RR Sci. 2006, 313(5786), 504–507. [DOI] [PubMed] [Google Scholar]
- 38.Levy RM; Srinivasan AR; Olson WK; McCammon JA Biopolymers.1984, 23 6, 1099–112. [DOI] [PubMed] [Google Scholar]
- 39.Naritomi Y; Fuchigami SJ Chem. Phys 2011, 134(6), 065101. [DOI] [PubMed] [Google Scholar]
- 40.Coifman RR; Lafon S; Lee AB; Maggioni M; Nadler B; Warner F; Zucker SW Proc. Natl. Acad. Sci. U.S.A 2005, 102(21), 7426–7431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zhou H; Wang F; Tao PJ Chem. Theory Comput 2018, 14(11), 5499–5510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kalyoncu S; Keskin O; Gursoy A BMC Bioinform. 2010, 11(1), 357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Daqrouq K; Alhmouz R; Balamesh A; Memic A PLoS One. 2015, 10(4), e0122873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kalyoncu S; Keskin O; Gursoy A In Health Informatics and Bioinformatics (HIBIT), 2010 5th International Symposium on, pages 121–124. IEEE, 2010. [Google Scholar]
- 45.Zhou H; Dong Z; Tao PJ Comput. Chem 2018, 39(20), 1481–1490. [DOI] [PubMed] [Google Scholar]
- 46.Zhang Y; Qiao S; Ji S; Han N; Liu D; Zhou J Eng. Appl. Artif. Intell 2019, 79, 58–66. [Google Scholar]
- 47.Li B; Li Y; Gong L Eng. Appl. Artif. Intell 2014, 27, 70–79. [Google Scholar]
- 48.Tibshirani RJ R. Stat. Soc. Ser. B-Stat. Methodol 1996, 58(1), 267–288. [Google Scholar]
- 49.Stone CJ Wadsworth International Group. 1984, 8, 452–456. [Google Scholar]
- 50.Cortes C; Vapnik V Mach. Learn 1995, 20(3), 273–297. [Google Scholar]
- 51.Peng H; Long F; Ding C IEEE Trans. Pattern Anal. Mach. Intell 2005, 27(8), 1226–1238. [DOI] [PubMed] [Google Scholar]
- 52.Li J; Dong W; Meng D IEEE-ACM Trans. Comput. Biol. Bioinform 2017, 15(6), 2028–2038. [DOI] [PubMed] [Google Scholar]
- 53.Huang J; Breheny P; Ma S Stat. Sci 2012, 27(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zou H; Hastie TJ R. Stat. Soc. Ser. B-Stat. Methodol 2005, 67(2), 301–320. [Google Scholar]
- 55.Yuan M; Lin YJ R. Stat. Soc. Ser. B-Stat. Methodol 2006, 68(1), 49–67. [Google Scholar]
- 56.Zhao P; Rocha G; Yu B Department of Statistics, UC Berkeley, Tech. Rep 2006, 703. [Google Scholar]
- 57.Zhou N; Zhu J Stat. Interface 2010, 3(4), 557–574. [Google Scholar]
- 58.Simon N; Friedman J; Hastie T; Tibshirani RJ Comput. Graph. Stat 2013, 22(2), 231–245. [Google Scholar]
- 59.Kronvall T; Jakobsson A Signal Process. 2018, 151, 107–118. [Google Scholar]
- 60.S En, M U; Erdogan H Pattern Recognit. Lett 2013, 34(3), 265–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Liu J; Ji S; Ye J; others. Arizona State University. 2009, 6(491), 7. [Google Scholar]
- 62.Beck A; Teboulle M SIAM J. Imaging Sci 2009, 2(1), 183–202. [Google Scholar]
- 63.Magnin B; Mesrob L; Kinkingnéhun S; Pélégrini-Issac M; Colliot O; Sarazin M; Dubois B; Lehéricy S; Benali H Neuroradiology. 2009, 51(2), 73–83. [DOI] [PubMed] [Google Scholar]
- 64.Davatzikos C; Bhatt P; Shaw LM; Batmanghelich KN; Trojanowski JQ Neurobiol. Aging 2011, 32(12), 2322.e19–2322.e27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Pradhan D; Sahoo B; Misra BB; Padhy S Appl. Soft. Comput 2020, 96, 106664. [Google Scholar]
- 66.Tang Y CoRR, abs/1306.0239 2013, 2, 1. [Google Scholar]
- 67.Koshiba Y; Abe S In Proceedings of the International Joint Conference on Neural Networks, 2003., Vol. 3, pages 2054–2059. IEEE, 2003. [Google Scholar]
- 68.Fan R-E; Chang K-W; Hsieh C-J; Wang X-R; Lin C-JJ Mach. Learn. Res 2008, 9(Aug), 1871–1874. [Google Scholar]
- 69.Pedregosa F; Varoquaux G; Gramfort A; Michel V; Thirion B; Grisel O; Blondel M; Prettenhofer P; Weiss R; Dubourg V; others. J. Mach. Learn. Res 2011, 12(Oct), 2825–2830. [Google Scholar]
- 70.Fuentes EJ; Der CJ; Lee AL J. Mol. Biol 2004, 335(4), 1105–1115. [DOI] [PubMed] [Google Scholar]
- 71.Lockless SW; Ranganathan R Sci. 1999, 286(5438), 295–299. [DOI] [PubMed] [Google Scholar]
- 72.Fuentes EJ; Gilmore SA; Mauldin RV; Lee AL J. Mol. Biol 2006, 364(3), 337–351. [DOI] [PubMed] [Google Scholar]
- 73.Stucki-Buchli B; Johnson PJM; Bozovic O; Zanobini C; Koziol KL; Hamm P; Gulzar A; Wolf S; Buchenberg S; Stock GJ Phys. Chem. A 2017, 121 49, 9435–9445. [DOI] [PubMed] [Google Scholar]
- 74.Raimondi F; Felline A; Seeber M; Mariani S; Fanelli FJ Chem. Theory Comput 2013, 9(5), 2504–2518. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.