Abstract
In a computer-aided diagnosis (CADx) scheme for evaluating the likelihood of malignancy of clustered microcalcifications on mammograms, it is necessary to segment individual calcifications correctly. The purpose of this study was to develop a computerized segmentation method for individual calcifications with various sizes while maintaining their shapes in the CADx schemes. Our database consisted of 96 magnification mammograms with 96 clustered microcalcifications. In our proposed method, a mammogram image was decomposed into horizontal subimages, vertical subimages, and diagonal subimages for a second difference at scales 1 to 4 by using a filter bank. The enhanced subimages for nodular components (NCs) and the enhanced subimages for both nodular and linear components (NLCs) were obtained from analysis of a Hessian matrix composed of the pixel values in those subimages for the second difference at each scale. At each pixel, eight objective features were given by pixel values in the subimages for NCs at scales 1 to 4 and the subimages for NLCs at scales 1 to 4. An artificial neural network with the eight objective features was employed to enhance calcifications on magnification mammograms. Calcifications were finally segmented by applying a gray-level thresholding technique to the enhanced image for calcifications. With the proposed method, a sensitivity of calcifications within clustered microcalcifications and the number of false positives per image were 96.5% (603/625) and 1.69, respectively. The average shape accuracy for segmented calcifications was also 91.4%. The proposed method with high sensitivity of calcifications while maintaining their shapes would be useful in the CADx schemes.
Keywords: Computerized segmentation, Calcification, Magnification mammogram, Multiresolution analysis, Artificial neural network
Introduction
Clustered microcalcifications are present in 30% to 50% of all cancers found in a mammography examination. [1, 2] However, it is very difficult for radiologists to correctly distinguish between benign and malignant clustered microcalcifications because they are often small and subtle. In the USA, the positive predictive value of mammography, i.e., the ratio of the number of found breast cancers to the number of lesions diagnosed as malignant case on mammograms, is typically between 15% and 30%. [3, 4] Therefore, many investigators have developed computer-aided diagnosis (CADx) schemes [5] which present radiologists objective indices for a diagnostic aid by computer analysis in order to improve the positive predictive value of the mammography. [6–13] As a CADx scheme, Jiang et al. [6] developed a computerized method for estimating the likelihood of malignancy of clustered microcalcifications by using an artificial neural network (ANN) with eight image features on mammograms. Chan et al. [7, 8] proposed a classification method for analyzing malignant and benign calcifications by using various feature classifiers with morphologic and texture features. Nakayama et al. [9–11] developed a computerized scheme for identifying histological classifications of clustered microcalcifications based on the differences in both the image features and the growth speeds among histological classifications. Muramatsu et al. [12, 13] developed a computerized method for providing images of lesions of a known disease that have a similar appearance to lesions of an unknown disease. In most of the CADx schemes, objective features were extracted from segmented calcifications to analyze clustered microcalcifications. Therefore, it is important to segment all calcifications accurately within the clustered microcalcifications on mammograms. It is also necessary to segment individual calcifications while maintaining their shapes because the information on their shapes is an important finding in distinguishing between benign and malignant clustered microcalcifications. [14] Previously, some studies have demonstrated a computerized segmentation method for calcifications while maintaining their shapes. [15, 16] However, it would be difficult for these methods to extract the shapes of calcifications with subtle edge accurately because these methods used the edge information of individual calcifications.
Calcifications on mammograms have various sizes and shapes. To accurately segment individual calcifications within clustered microcalcifications, therefore, it is necessary in the segmentation method to analyze both size information and shape information. Nakayama et al. [17] developed a new filter bank for analyzing not only the size information but also the shape information. In their study, the degree of nodular structures which were contained in a region of interest (ROI) was quantified as nodular features (N features). The degree of both nodular structures and linear structures which were contained in the ROI was also quantified as nodular and linear features (NL features). From this filter bank at different scales, they obtained the N features and the NL features for structures with size corresponding to the filter size at the scale. Although those N features and NL features were shown to be useful in distinguishing between an abnormal ROI with calcifications and a normal ROI without calcifications, the method could not segment individual calcifications while maintaining their shapes within clustered microcalcifications.
In order to extract accurate shapes of calcifications with various sizes, each pixel instead of ROI on magnification mammograms was evaluated whether it belongs to a calcification or not by use of the objective features obtained from the filter bank at different scales in our study. We evaluated the sensitivity and the shape accuracies for the segmented calcifications within clustered microcalcifications by applying the proposed method to 625 calcifications.
Related Work
There have been many studies for region extraction. [15, 16, 18–25] A region-growing technique [15, 18] is one of the region extraction methods which have been widely used for medical images. In the region-growing technique, a pixel on a target region is first set as an initial seed point. This technique then determines whether the neighboring pixels should be added to the same region as the initial seed point by use of predefined criteria such as the range of pixel values. This procedure is repeated while there is an added pixel. Although a region-growing technique is a simple and powerful tool for region extraction, the selection of the criteria is very difficult for indistinct calcifications. A Snakes is also one of the region extraction methods which are used for medical images. [19–25] The Snakes is a deformable spline controlled by the evaluation functions based on constraint condition with several parameters. The border line for the Snakes continues to shrink or extend actively and dynamically until the energy functional which consisted of the internal strain energy and the image energy is minimized. The region wrapped by the border line is then determined as the extracted region when the energy functional is minimum. It would be difficult for the Snakes to extract the edges of calcifications with fine irregular shape in detail because the border line is given by an approximated curve based on a spline curve.
Materials and Methods
Materials
In clinical practice, magnification mammograms are frequently used for evaluating clustered microcalcifications in detail after radiologists detect them on standard mammograms. [14] Magnification mammograms were also used in some CADx schemes. [9–11] Therefore, our database consisted of 96 magnification mammograms with 70 malignant clustered microcalcifications and 26 benign clustered microcalcifications at the Breastopia Namba Hospital, Miyazaki, Japan. It included a total of 1,563 calcifications. The magnification mammograms were acquired with a Kodak MinR-2000/MinR-2000 screen/film system. The magnification factor was 1.8. All mammograms were digitized to a 512 × 512 matrix size with a 0.0275-mm pixel size and 12-bit gray scale by use of an EPSON ES-8000 digitizer (optical resolution 800 × 1,600 dpi, optical density range 0.0 to 3.3 D). The locations and the shapes of individual calcifications were determined by an experienced radiologist. In order to train and evaluate the proposed method, we divided our database randomly into a training set and a test set. Each set included 48 mammograms. The number of calcifications in the training set and that in the test set were 938 and 625, respectively.
Methods
Overall Scheme for Segmentation of Calcifications
Figure 1 shows a schematic diagram of the proposed method for the segmentation of individual calcifications within clustered microcalcifications on magnification mammograms. The mammogram image was first decomposed into horizontal subimages, vertical subimages, and diagonal subimages for a second difference at scales 1 to 4 by the filter bank [17] because the average pixel size of maximum chords of calcifications included in our database was smaller than the filter size at scale 4. The enhanced subimages for nodular components (NCs) and the enhanced subimages for both nodular and linear components (NLCs) at scales 1 to 4 were obtained from an analysis of a Hessian matrix composed of the pixel values in those subimages for the second difference at the corresponding scale. At each pixel, the pixel values in the enhanced subimages for NCs at scales 1 to 4 were defined as the N features at scales 1 to 4, respectively. Note that pixel values in the enhanced subimages for NCs were used instead of the degree of nodular structures which were contained in a ROI in Nakayama’s study. [17] The pixel values in the enhanced subimages for NLCs at scales 1 to 4 were also defined as the NL features at scales 1 to 4, respectively. An artificial neural network [26] with the N features and the NL features at scales 1 to 4 was employed to evaluate the likelihood that the pixel belongs to a calcification. Calcifications were segmented by applying a gray-level thresholding technique [27] to the enhanced image for calcifications defined by the output values of the ANN.
Fig. 1.
Schematic diagram of the proposed method for the segmentation of individual calcifications within clustered microcalcifications on magnification mammograms
Filter Bank
Calcifications on magnification mammograms present nodular structures and have various sizes. Therefore, we used a filter bank [17] for analyzing both the size information and the shape information, as shown in Fig. 2. Here, z−j represented the delay of j sampling period in a digital filter. The first derivative on the digital image corresponds to the first difference. HH(zj), FH(zj) were the filters for the first difference at scale j, which were given as
 |
1 |
 |
2 |
Therefore, 
was the filter for the second difference, which was
 |
3 |
was also the filter for the smoothing operator, which was given as
 |
4 |
was an original image. The smoothed subimage 
at scale j was obtained by applying the sequential applications of the horizontal smoothing operator and the vertical smoothing operator to
. The horizontal subimage 
at scale j was obtained by applying the second difference filter in the vertical direction to 
, whereas the vertical subimage 
at scale j was obtained by applying the second difference filter in the horizontal direction to 
. The diagonal subimage 
at scale j was also obtained by applying the first difference in the vertical direction followed by the first difference in the horizontal direction to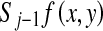 
. Figure 3 shows the subimages obtained from the analysis bank of the filter bank at scales 1 to 4. The pixel values in these subimages 
, 
, and 
correspond to the elements of a Hessian matrix H which was defined as
 |
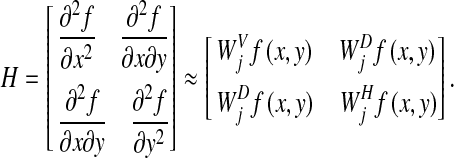5 |
Here, f(x, y) presents a continuous function. The smallest value and the largest value of the second derivatives in all directions at a pixel were able to be calculated approximately by small eigenvalue 
and large eigenvalue 
of the Hessian matrix H. The following formulas indicated the conditions that the two eigenvalues 
and 
must satisfy for a nodular structure and a linear structure, respectively. [17]
 |
6 |
 |
7 |
Fig. 2.
Filter bank for analyzing both the size information and the shape information (from scales 1 to 3)
Fig. 3.
Subimages obtained from the analysis bank of the filter bank at scales 1 to 4
The enhanced subimage for nodular structures at scale j was defined by 
the sign of which was inverted. The enhanced subimage for both nodular and linear structures at scale j was also defined by 
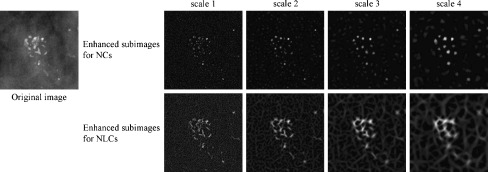
the sign of which was inverted. Figures 4 and 5 show the enhanced subimages for NCs and the enhanced subimages for NLCs at scales 1 to 4, which were obtained from an abnormal ROI with clustered microcalcifications and a normal ROI with blood vessels. The pixels on the nodular structures such as calcifications in the original image appeared to have high pixel values in the enhanced subimages for NCs, whereas the pixels on the nodular structures or the linear structures such as blood vessels appeared to have high pixel values in the enhanced subimages for NLCs. The pixels on the large structures in the original image also tended to have high pixel values at higher scales. Therefore, it would be possible to evaluate whether a pixel belongs to calcifications with various sizes by using the pixel values in these enhanced subimages.
Fig. 4.
Example of enhanced subimages for NCs and for NLCs at scales 1 to 4, which were obtained from a ROI with clustered microcalcifications
Fig. 5.
Example of enhanced subimages for NCs and for NLCs at scales 1 to 4, which were obtained from a ROI with blood vessels
Segmentation of Calcifications
An ANN [26] which was a three-layered, feed-forward network with a back propagation algorithm was employed to evaluate the likelihood that each pixel belongs to a calcification on magnification mammogram. The parameters for the ANN (the coefficient of the momentum term, 0.2; the learning rate, 0.2; the slant of the sigmoid function, 1.0; the number of the hidden layer neurons, 9; and the number of the training iterations, 280) were determined by taking into account the greatest areas under free-response receiver operating characteristic (FROC) curves [28] with various combinations of the parameters. Here, the coefficient of the momentum term and the learning rate were varied from 0.1 to 1.0, whereas the slant of the sigmoid function was varied from 0.5 to 3.0. The number of the hidden layer neurons was varied from 4 to 10. The ANN was also trained up to 1,000 iterations. For the input of the ANN at each pixel, we used eight objective features (N features and NL features at scales 1 to 4) given by the pixel values in the enhanced subimages for nodular structures and the enhanced subimages for both nodular and linear structures at scales 1 to 4. The ANN was trained by using 30,498 abnormal pixels of interest (POIs) on 938 calcifications and 30,000 normal POIs on normal tissues in the training set. Abnormal POIs were all pixels on calcifications included in the training set, whereas normal POIs were selected randomly on normal breast tissues. Here, a supervised signal for calcifications and that for normal tissues were given as 0.95 and 0.05, respectively. The output value of the ANN would be higher when the pixel was on calcifications in the original image. The enhanced image for calcifications was then defined by the output value of the ANN at each pixel. Figure 6 shows an example of an enhanced image for calcifications. Calcifications were finally segmented by applying a gray-level thresholding technique [27] to the enhanced image.
Fig. 6.
Example of an enhanced image for calcifications. a Original image, b enhanced image
Evaluation of Detection Performance and Shape Accuracy
A FROC curve [28] was usually used to summarize quantitatively the detection performance of the computerized scheme. The FROC curve shows the relationship between true-positive fraction (sensitivity) and the average number of false positives (FPs) per image when varying the threshold value continuously in a computerized scheme. In this study, the threshold value was varied in the segmentation of calcifications. When a segmented candidate for calcification overlapped with a true calcification region determined by an experienced radiologist, this candidate was considered to have been “truly” detected. When a candidate did not overlap with a true calcification region, this candidate was considered a false positive. The shape accuracy for a segmented calcification was also defined as
 |
8 |
Here, A was the calcification region segmented by the proposed method, whereas B was the true calcification region determined by an experienced radiologist. The change in the average shape accuracies was also evaluated by varying the threshold value in the segmentation of the candidates for calcifications.
Results
Figure 7 shows the relationships between the N features and the NL features at scales 1 to 4. These objective features were obtained from 100 abnormal POIs and 100 normal POIs. These abnormal POIs were selected randomly on calcifications in the training set, whereas these normal POIs were selected randomly on normal breast tissues in the training set. Both of the N features and the NL features for calcifications at all scales tended to be larger than those for normal tissues. Most of the normal POIs which had as high NL features as the abnormal POIs were selected from blood vessels. The difference in the N features and the NL features at scale 2 between calcifications and normal tissues appeared large. This would imply that the number of calcifications with the size corresponding to the filter size at scale 2 was large in our database. Table 1 shows the result of test for univariate equality of group means. This test was evaluated by using the objective features in Fig. 7. The Wilk’s lambdas [29] for the NL features at scale 2 were smaller than those for the other objective features. The F value [29] for the NL features at scale 2 was also larger than those for any other features. This result would indicate that the NL features at scale 2 made a larger contribution to evaluate whether a pixel belongs to a calcification or normal tissue. On the other hand, the N features at scale 4 had the largest Wilk’s lambda and the smallest F value. We considered that most of calcifications contained in our database were smaller than filter size at scale 4. However, the p value for the N features at scale 4 reached the level of statistical significance (p < 0.001). Thus, these eight objective features were statistically useful for evaluating the likelihood that a pixel belongs to a calcification. With the proposed method using a threshold value of 0.5 in applying the gray-level thresholding technique to the enhanced images for calcifications, the sensitivity and the number of false positives per image were 96.5% (603/625) and 1.69, respectively. The average shape accuracy for the proposed method also was 91.4%.
Fig. 7.
Relationship between N features and NL features a at scale 1, b at scale 2, c at scale 3, and d at scale 4
Table 1.
Tests for univariate equality of group means.
| Wilk’s lamda | F value | p value | |
|---|---|---|---|
| N features at scale 1 | 0.611 | 125.8 | <0.001 |
| N features at scale 2 | 0.585 | 140.2 | <0.001 |
| N features at scale 3 | 0.629 | 116.7 | <0.001 |
| N features at scale 4 | 0.765 | 60.7 | <0.001 |
| NL features at scale 1 | 0.483 | 211.6 | <0.001 |
| NL features at scale 2 | 0.467 | 226.3 | <0.001 |
| NL features at scale 3 | 0.584 | 141.2 | <0.001 |
| NL features at scale 4 | 0.677 | 94.6 | <0.001 |
Discussion
In many previous studies for detecting calcifications, computerized methods have been developed by the use of only the features related to the nodular structure. In order to investigate the usefulness of the combination of the N features and the NL features in terms of the sensitivity, we evaluated not only the detection performance with the proposed method but also that with a computerized method using only four N features at scales 1 to 4 and that with a computerized method using only four NL features at scales 1 to 4. Figure 8 shows the FROC curves obtained by applying the three different computerized methods to 48 magnification mammograms in the test set. The detection performance with the proposed method was much higher than that with the computerized method with four N features or with four NL features. Although calcifications with irregular structure tended not to be detected by the computerized method based on only the features related to the nodular structure, most of them were detected correctly by the combination of the features related to the nodular structure and the linear structure in the proposed method.
Fig. 8.
FROC curves obtained by three different computerized methods with N features and NL features, N features, and NL features at scales 1 to 4
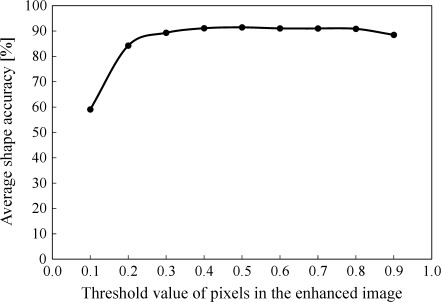
Figure 9 shows the average shape accuracy for segmented calcifications when threshold value for a gray-level thresholding technique varied from 0.1 to 0.9. The average shape accuracies did not change rapidly within the range of appropriate threshold values. This result would indicate that proposed method had high robustness. With a threshold value of 0.3, the sensitivity was relatively high (98.71%), although the average shape accuracy and the number of false positives per image were low and large (89.29% and 9.54). With a threshold value of 0.9 though the sensitivity and shape accuracy were low and low (84.93%, 88.47%). Therefore, we considered that a threshold value between 0.35 and 0.85 would be appropriate in CADx schemes. Figure 10 shows an example of a segmented image by use of the proposed method with a threshold value of 0.5 (the average shape accuracy, 91.4%).
Fig. 9.
Change in the average shape accuracies for segmented calcifications by the proposed method
Fig. 10.
Example of a segmented image for calcifications. a Original image, b true calcification regions determined by an experienced radiologist, c segmented calcifications by the proposed method
We also investigated the change in the sensitivity, the shape accuracy, and the false positive for the proposed method when each of the ANN parameters was varied as mentioned in the section of the segmentation of calcifications. With a threshold value of 0.5 in the segmentation of calcifications, the average sensitivity, the average shape accuracy, and the average false positive per image were 94.57%, 91.05%, and 2.13, respectively. The standard deviation of the sensitivities, that of the shape accuracies, and that of the false positives per image were also 3.99, 3.29, and 3.44, respectively. These results would imply the performance of the proposed method was not influenced substantially by the parameters for the ANN.
In order to investigate the adequacy of scales used for the filter bank, we compared the performances of the computerized methods with six objective features at scales 1 to 3, eight objective features at scales 1 to 4 (the proposed method), and ten objective features at scales 1 to 5. Figure 11 shows the FROC curves obtained by applying the three computerized methods to 48 magnification mammograms in the test set. Figure 12 also shows the average shape accuracies for segmented calcifications obtained by the three computerized methods. Here, the ANN parameters for each of the three computerized methods were determined by taking into account the greatest areas under the FROC curves. Although the highest shape accuracy for the proposed method with scales 1 to 4 was slightly higher than that for the other computerized methods, the sensitivity and the average FPs for the proposed method were comparable to those for the other computerized methods.
Fig. 11.
FROC curves obtained by three different computerized methods with the N features and the NL features at scales 1–3, scales 1–4, and scales 1–5
Fig. 12.
Change in the average shape accuracies for segmented calcifications obtained by three different computerized methods
The pixel size of magnification mammograms used in this study was 0.0275 mm. The filter sizes at scales 1, 2, 3, 4, and 5 which were showed to be useful for the segmentation of calcifications were 0.1375, 0.2475, 0.3575, 0.4675, and 0.5775 mm, respectively. If a standard mammogram with a pixel size of 0.05 mm is used, scales 4 and 5 might be not useful since the filter sizes at scales 1, 2, 3, 4, and 5 are 0.25, 0.45, 0.65, 0.85, and 1.05 mm, respectively. Therefore, it would be necessary to change the scales of the filter bank by taking into account the pixel size of the image. However, we believe that it would not be necessary to adjust the parameters for the ANN substantially in images with different resolution because the sensitivities and the shape accuracies hardly changed in this study even when the parameters were varied.
To investigate the usefulness of evaluating the possibility for belonging to a calcification at each pixel in terms of the shape accuracy, the proposed method was compared with the Snakes. An initial border line for the Snakes was given by a circle area with a diameter larger than any calcifications included in our database. In the Snakes, the initial border line was first set at the center of each calcification in the magnification mammograms. Sixty different combinations of parameters were used for the energy function in the Snakes. The average shape accuracy for extracted calcifications was 79.3% when it was the highest in the 60 combinations. The average shape accuracy for the Snakes was lower than that 91.4% of the proposed method. The Snakes is a method that is influenced strongly by edge strength. Therefore, when a calcification with low contrast and a calcification with high contrast exist near each other, the border line of the calcification with low contrast did not shrink or extend appropriately due to the information of the edge of the calcification with higher contrast. On the other hand, the proposed method of evaluating each pixel is not influenced by the surrounding information. Although we evaluated the shape accuracy for extracted calcifications by use of the 60 different combinations of parameters for the Snakes, it may be improved by using more optimal combination of the parameters. However, it would be very difficult to find.
There are some limitations in this study. One limitation is that we used magnification mammograms instead of standard mammograms as materials and proposed a computerized segmentation method for them. Radiologists frequently use magnification mammograms in distinguishing between benign and malignant clustered microcalcifications after they detect clustered microcalcifications in standard mammograms. On the other hand, there are radiologists and researchers who promote the diagnosis of clustered microcalcifications in standard mammograms in order to reduce the cost and the time of taking magnification mammograms. In a future study, it will be necessary to modify the proposed method in order to deal with standard mammograms by changing the scales in the filter bank and relearning the ANN. Another limitation is that we could not check whether calcifications in our database have all possible shapes. However, we believe that our database included most of possible shapes because it included many malignant calcifications which tend to have various irregular shapes.
Conclusion
In this study, we developed a computerized segmentation method for individual calcifications while maintaining their shapes within clustered microcalcifications on magnification mammograms. We showed the usefulness of the N features and the NL features for evaluating the likelihood that a pixel belongs to a calcification. The proposed method was shown to have high sensitivity with high shape accuracy for segmented calcifications, and would be useful in a CADx scheme for a diagnostic aid.
Acknowledgment
We are grateful to Kiyoshi Namba, MD, at Hokuto Hospital and, Ryoji Watanabe, MD, at Hakuaikai Hospital, for their help and valuable suggestions. We thank Mark LaForge at Suzuka University of Medical Science, for improving the manuscript.
References
- 1.Sickles EA. Mammographic features of early breast cancer. AJR AM J Roentgenol. 1984;143:461–464. doi: 10.2214/ajr.143.3.461. [DOI] [PubMed] [Google Scholar]
- 2.Sickles EA, Mammographic features of 300 consecutive nonpalpable breast cancers, AJR AM J Roentgenol, 661–663 (1986). [DOI] [PubMed]
- 3.Adler D.D., Helvie M.A., Mammographic biopsy recommendations, Current Opinion in Radiology, 123–129 (1992). [PubMed]
- 4.Kopans DB. The positive predictive value of mammography. AJR AM J Roentgenol. 1992;158:521–526. doi: 10.2214/ajr.158.3.1310825. [DOI] [PubMed] [Google Scholar]
- 5.Doi K, MacMahon H, Katsuragawa S, Nishikawa RM, Jiang Y. Computer-aided diagnosis in radiology: potential and pitfall. European J Radiology. 1999;31:97–109. doi: 10.1016/S0720-048X(99)00016-9. [DOI] [PubMed] [Google Scholar]
- 6.Jiang Y, Nishikawa RM, Wolverton DE, Metz CE, Giger ML, Schmidt RA, Vyborny CJ, Doi K. Malignant and benign clustered microcalcifications: automated feature analysis and classification. Radiology. 1996;198:671–678. doi: 10.1148/radiology.198.3.8628853. [DOI] [PubMed] [Google Scholar]
- 7.Chan HP, Sahiner B, Petric N, Heavie MA, Lam KL, Adler DD, Goodsitt MM. Computerized classification of malignant and benign microcalcifications on mammograms: texture analysis using an artificial neural network. Phys Med Biol. 1997;42:549–567. doi: 10.1088/0031-9155/42/3/008. [DOI] [PubMed] [Google Scholar]
- 8.Chan HP, Sahiner B, Lam KL, Petric N, Helvie MA, Goodsitt MM, Adler DD. Computerized analysis of mammographic microcalcifications in morphological and texture feature spaces. Medical Physics. 1998;25:2007–2019. doi: 10.1118/1.598389. [DOI] [PubMed] [Google Scholar]
- 9.Nakayama R, Uchiyama Y, Watanabe R, Katsuragawa S, Namba K, Doi K. Computer-aided diagnosis scheme for histological classification of clustered microcalcifications on magnification mammograms. Medical Physics. 2004;31:789–799. doi: 10.1118/1.1655711. [DOI] [PubMed] [Google Scholar]
- 10.Nakayama R, Watanabe R, Namba K, Takeda K, Yamamoto K, Katsuragawa S, Doi K. Computer-aided diagnosis scheme for identifying histological classification of clustered microcalcifications by use of follow-up magnification mammograms. Acad Radiol. 2006;13:1219–1228. doi: 10.1016/j.acra.2006.07.005. [DOI] [PubMed] [Google Scholar]
- 11.Nakayama R, Watanabe R, Namba K, Takeda K, Yamamoto K, Katsuragawa S, Doi K. An improved computer-aided diagnosis scheme using the nearest neighbor criterion for determining histological classification of clustered microcalcifications. Methods Inf Med. 2007;46:716–722. [PubMed] [Google Scholar]
- 12.Muramatsu C, Li Q, Schmidt R, Suzuki K, Shiraishi J, Newstead G, Doi K. Experimental determination of subjective similarity for pairs of clustered microcalcifications on mammograms: observer study results. Medical Physics. 2006;33:3460–3468. doi: 10.1118/1.2266280. [DOI] [PubMed] [Google Scholar]
- 13.Muramatsu C, Li Q, Schmidt RA, Shiraishi J, Suzuki K, Newstead GM, Doi K. Determination of subjective similarity for pairs of masses and pairs of clustered microcalcifications on mammograms: comparison of similarity ranking scores and absolute similarity ratings. Medical Physics. 2007;34:2890–2895. doi: 10.1118/1.2745937. [DOI] [PubMed] [Google Scholar]
- 14.Kopans DB. Breast Imaging. 2. New York: Lippincott-Raven; 1997. [Google Scholar]
- 15.Shen L, Rangayyan RM, Desautels JEL. Application of shape analysis to mammographic calcifications. IEEE Trans Med Image. 1994;13:263–274. doi: 10.1109/42.293919. [DOI] [PubMed] [Google Scholar]
- 16.Muramatsu C, Li Q, Schmidt R, Shiraishi J, Doi K. Investigation of psychophysical similarity measures for selection of similar images in the diagnosis of clustered microcalcifications on mammograms. Medical Physics. 2008;35:5695–5702. doi: 10.1118/1.3020760. [DOI] [PubMed] [Google Scholar]
- 17.Nakayama R, Uchiyama Y, Yamamoto K, Watanabe R, Namba K. Computer-aided diagnosis scheme using a filter bank for detection of microcalcification clusters in mammograms. IEEE Trans Biomedical Engineering. 2006;53(2):273–283. doi: 10.1109/TBME.2005.862536. [DOI] [PubMed] [Google Scholar]
- 18.Zhang H, Foo SW. Computer aided detection of breast masses from digitized mammograms. IEICE. 2006;E89-D(6):1955–1961. [Google Scholar]
- 19.Kass M, Witkin A, Terzopoulos D. Snake: active contour models. Int J Compu Vis. 1987;1:321–331. doi: 10.1007/BF00133570. [DOI] [Google Scholar]
- 20.Xu C and Prince J.L, “Gradient vector flow: A new external force for snakes.” in IEEE Proc. Conf. on Computer Vision and Pattern Recognition, 66–71 (1997).
- 21.Xu C, Prince JL. Snakes, shapes, and gradient vector flow. IEEE Trans Image Processing. 1998;7(3):359–369. doi: 10.1109/83.661186. [DOI] [PubMed] [Google Scholar]
- 22.Chucherd S, Rodtook A, Makhanov SS. Phase portrait analysis for multiresolution generalized gradient vector flow. IEICE. 2010;E93-D(10):2822–2835. [Google Scholar]
- 23.Cheng HD, Shan J, Ju W, Guo Y, Zhang L. Automated breast cancer detection and classification using ultrasound images. Pattern Recognition. 2010;43(1):299–317. doi: 10.1016/j.patcog.2009.05.012. [DOI] [Google Scholar]
- 24.Tang J. A multi-direction gvf snake for the segmentation of skin cancer images. Pattern Recognit. 2009;42(6):1172–1179. doi: 10.1016/j.patcog.2008.09.007. [DOI] [Google Scholar]
- 25.Caselles V, Catte F, Coll T, Dibos F. A geometric model for active contours. Numerische Mathematik. 1993;66:1–31. doi: 10.1007/BF01385685. [DOI] [Google Scholar]
- 26.Duda RO, Hart PE, Stork DG. Pattern Classification. New York: Wiley; 2001. pp. 282–349. [Google Scholar]
- 27.Gonzales RC, Woods RE. Digital Image Processing. 2. MA: Addison-Wesley; 1992. pp. 567–643. [Google Scholar]
- 28.Chakraborty DP, Winter LHL. Free-response methodology: alternate analysis and a new observer- performance experiment. Radiology. 1990;174:873–881. doi: 10.1148/radiology.174.3.2305073. [DOI] [PubMed] [Google Scholar]
- 29.Johnson RA, Wichern DW. Applied Multivariate Statistical Analysis. Englewood cliffs: Prentice-Hall; 1992. [Google Scholar]