Abstract
Macroscopic pKa values were calculated for all compounds in the SAMPL6 blind prediction challenge, based on quantum chemical calculations with a continuum solvation model and a linear correction derived from a small training set. Microscopic pKa values were derived from the gas-phase free energy difference between proto- nated and deprotonated forms together with the Conductor-like Polarizable Continuum Solvation Model and the experimental solvation free energy of the proton. pH- dependent microstate free energies were obtained from the microscopic pKas with a maximum likelihood estimator and appropriately summed to yield macroscopic pKa values or microstate populations as function of pH. We assessed the accuracy of three approaches to calculate the microscopic pKas: direct use of the quantum mechanical free energy differences and correction of the direct values for short-comings in the QM solvation model with two different linear models that we independently derived from a small training set of 38 compounds with known pKa. The predictions that were corrected with the linear models had much better accuracy [root-mean-square error (RMSE) 2.04 and 1.95 pKa units] than the direct calculation (RMSE 3.74). Statistical measures indicate that some systematic errors remain, likely due to differences in the SAMPL6 data set and the small training set with respect to their interactions with water. Overall, the current approach provides a viable physics-based route to estimate macroscopic pKa values for novel compounds with reasonable accuracy.
Keywords: pKa, pH, quantum chemistry, SAMPL challenge
1. Introduction
The SAMPL (Statistical Assessment of the Modeling of Proteins and Ligands) challenges allow the molecular modeling community to assess, in “blind” conditions, the accuracy and efficiency of current computational chemistry methods and tools, leading to continuous improvements of the available computational methods. The previous SAMPL challenges [1–5] involved hydration free energy calculations, with the exception of the last edition, SAMPL5, which was dedicated to the prediction of distribution coefficients [6]. Our past participations in SAMPL challenges [7–9] represented unique opportunities for us to test our approaches and to develop and improve new computational tools. In 2018, the SAMPL6 challenge focused on the prediction of microscopic and macroscopic pKa values for fragment-like organic compounds.
The equilibrium acid dissociation reaction in aqueous solution
| (1) |
with acid dissociation constant is of broad importance in biological systems, in synthetic chemistry, and pharmacology [10–14]. The pKa, defined as
| (2) |
for the standard state concentration c0 = 1 mol/l, measures thermodynamic acidity. The theoretical prediction of pKa values is an ongoing challenge [15]. In the narrow realm of protein biochemistry, good progress has been made in calculating the physiologically important changes in pKas of standard amino acid residues in different environments with accuracies better than 1 pKa unit [12], especially with constant pH molecular dynamics simulations [16–19], which have been applied to study a wide range of phenomena [20–22]. Absolute pKa calculations of arbitrary molecules using physics-based quantum chemistry approaches (as opposed to machine learning (ML) ones) have been more challenging and accuracy of 1 pKa unit has been difficult to achieve consistently [15, 23] whereas a range of methods can achieve “chemical accuracy” (defined as 2.5 pKa units by Ho and Coote [15]). The clear advantage of ab initio approaches is that they can be applied to any novel compound. Here we report on pKa calculations of the 24 compounds in the SAMPL6 challenge (Fig. 1) with a quantum-chemical approach originally developed by Muckerman et al [24]. The SAMPL6 compounds are, however, chemically more complex and 23 contain multiple titratable protons and, in some cases, tautomers so that macroscopic pKa have to be calculated.
Fig. 1.
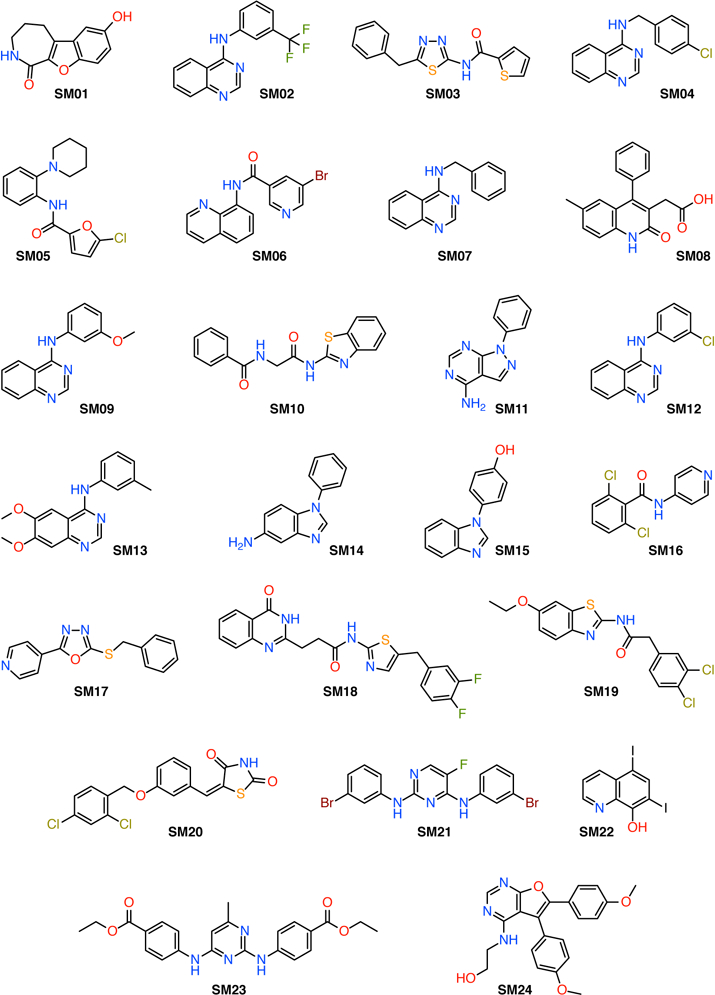
Chemical structures of the SAMPL6 data set. SM20 is the only compound that contains a single titratable proton; all other compounds contain multiple titratable protons and, in some cases, tautomers.
The calculation of microscopic pKas, i.e., the free energy difference for the deprotonation reaction Eq. 1 at the standard state (concentration 1 mol/l and temperature T = 298.15 K, indicated by the superscript “*”)
| (3) |
is straightforward using quantum chemical gas-phase calculations. However, it is well-known [15, 23] that direct calculations lead to large errors in the calculated pKas, mainly due to the poor continuum solvation models that have to be employed in order to obtain free energies in solution. One approach to correct for these systematic errors is to generate a model to correct the raw quantum chemical free energies [24]. We generated linear models from a training set with 38 simple compounds with experimentally known pKa (Fig. 2 and 3). We fit a global model to all the data (the global linear model) and we split the training set with a simple classifier, namely the charge of the acid, yielding a piecewise linear model with separate linear functions for neutral and cationic acids. We calculated the macroscopic pKas for all 24 SAMPL6 compounds and compared the accuracy of the three approaches [QM computed (raw), linear fit global, and linear fit piecewise].
Fig. 2.

Chemical structures of the QM1 training data set (neutral acids); see also Table 1.
Fig. 3.
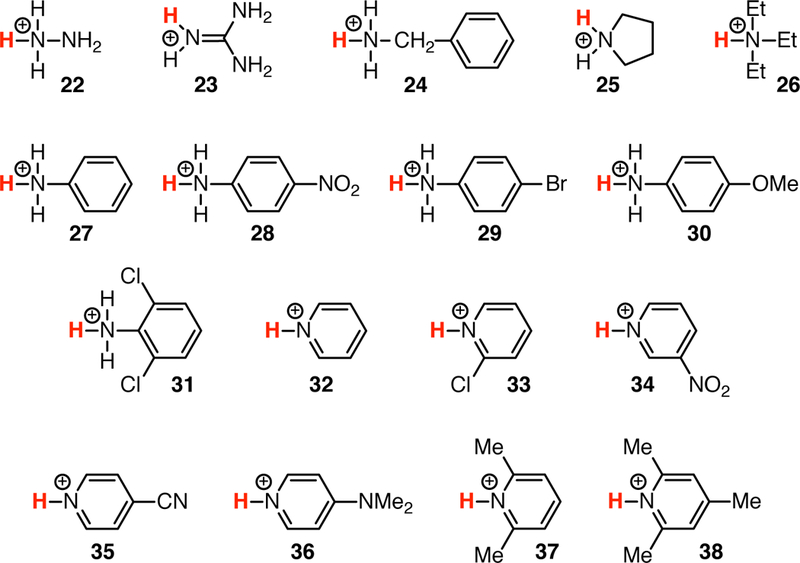
Chemical structures of the QM2 training data set (cationic acids); see also Table 1.
2. Methods
Following Muckerman et al [24], our strategy was to compute gas-phase free energy differences
| (4) |
(denoted as standard state free energies at 1 atm pressure and 298.15 K) for the deprotonation reaction for all titratable protons,
| (5) |
To obtain solution free energy differences corresponding to Eq. 1,
| (6) |
(where the standard state refers to 1 mol/l), a solvation free energy contribution is added to the gas-phase free energies of the acid HA and the base A− from Eq. 4,
| (7) |
with accounting for the change in standard state in the gas phase. The free energy of the proton in the gas phase is calculated analytically in the ideal gas limit (the Sackur-Tetrode equation [25]), and for the solvation free energy of the proton we chose the same value as Muckerman et al [24], G*(HA(s)) = −272.2 kcal/mol although other values are also discussed in the literature [15, 26]. With , the pKa is calculated from Eq. 3.
As described in detail in Section 2.2, the directly calculated pKa values have fairly poor accuracy and thus we derive a simple linear estimator to correct for shortcomings in the solvation model [24]. The linear model is based on our own training data set (described in the next section) and the resulting estimator ℒ is applied to the pKa from Eq. 3 to obtain improved predictions for the SAMPL6 data set, .
2.1. Data sets
The QM1 subset of the training set contains 21 neutral acids belonging to several chemical families (Fig. 2): mono- (1), di- (2) and tri- (3) protic inorganic acids, aliphatic (4) and aromatic (5) sulfonic acids, diversely substituted carboxylic acids (6–11) and alcohols (12–17), phenols (18 and 19), phthalimide (20) and uracil (21). The experimental pKa values of these compounds range from −3.00 to 17.10 (Table 1). The QM2 subset contains 17 compounds that are cationic acids (Fig. 3): hydrazine (22), guanidine (23), aliphatic mono- (24), di- (25) and tri- (26) substituted amines, diversely substituted aromatic amines (27–31) and pyridines (32–38). These compounds possess experimental pKa values from 0.49 to 13.60 (Table 1).
Table 1.
Experimental and computed pKa values for the compounds from the QM1 (Fig. 2) and QM2 (Fig. 3) training data sets. The difference Δ (Eq. 20) between computed and experimental pKa values is shown for each compound. The experimental values were taken from Muckerman et al [24] and from Lundblad and Macdonald [35]. The root-mean-square error (RMSE), the mean absolute error (MAE), and the signed mean error (ME) were calculated according to Eqs. 21–23.
| id | Exp. | QM computed | Linear fit global | Linear fit piecewise | ||||
|---|---|---|---|---|---|---|---|---|
| pKa | pKa | Δ | pKa | Δ | pKa | Δ | ||
| 1 | −1.40 | −4.01 | −2.61 | 3.56 | 0.43 | 1.83 | −0.31 | 1. 09 |
| 2 | 2.15 | 1.75 | −0.40 | 0.54 | 2.88 | 0.73 | 2.14 | −0.01 |
| 3 | −3.00 | −10.32 | −7.32 | 9.98 | −0.68 | 2.32 | −1.41 | 1.59 |
| 4 | −1.90 | −2.92 | −1.02 | 1.39 | 0.08 | 1.98 | −0.65 | 1.25 |
| 5 | −2.80 | −3.44 | −0.64 | 0.88 | −0.54 | 2.26 | −1.27 | 1.53 |
| 6 | 3.77 | 5.16 | 1.39 | −1.89 | 4.00 | 0.23 | 3.26 | −0.51 |
| 7 | 4.76 | 7.27 | 2.51 | −3.42 | 4.69 | −0.07 | 3.94 | −0.82 |
| 8 | 1.68 | 4.73 | 3.05 | −4.16 | 2.56 | 0.88 | 1.82 | 0.14 |
| 9 | 0.23 | −1.82 | −2.05 | 2.80 | 1.55 | 1.32 | 0.82 | 0.59 |
| 10 | 1.38 | 4.06 | 2.68 | −3.65 | 2.35 | 0.97 | 1.61 | 0.23 |
| 11 | 4.21 | 6.77 | 2.56 | −3.49 | 4.31 | 0.10 | 3.56 | −0.65 |
| 12 | 15.54 | 23.37 | 7.83 | −10.68 | 12. 14 | −3.40 | 11.37 | −4.17 |
| 13 | 15.90 | 22.73 | 6.83 | −9.31 | 12.39 | −3.51 | 11.62 | −4.28 |
| 14 | 12. 43 | 14. 22 | 1.79 | −2.44 | 9.99 | −2.44 | 9.22 | −3.21 |
| 15 | 17.10 | 22.61 | 5.51 | −7.51 | 13.22 | −3.88 | 12.44 | −4.66 |
| 16 | 9.30 | 8.57 | −0.73 | 0.99 | 7.83 | −1.47 | 7.07 | −2.23 |
| 17 | 5.40 | 4.28 | −1.12 | 1.53 | 5.13 | −0.27 | 4.38 | −1.02 |
| 18 | 9.95 | 14.99 | 5.04 | −6.87 | 8.28 | −1.67 | 7.51 | −2.44 |
| 19 | 7.14 | 8.26 | 1.12 | −1.53 | 6.33 | −0.81 | 5.58 | −1.56 |
| 20 | 8.30 | 13.49 | 5.19 | −7.08 | 7.14 | −1.16 | 6.38 | −1.92 |
| 21 | 9.50 | 13.81 | 4.31 | −5.87 | 7.97 | −1.53 | 7.2 | −2.30 |
| RMSE (QM1) | 3.86 | 1.90 | 2.19 | |||||
| MAE (QM1) | 3.13 | 1.56 | 1.72 | |||||
| ME (QM1) | 1.61 | −0.36 | −1.11 | |||||
| R2 (QM1) | 0.97 | |||||||
| m (QM1) | 1.45 | |||||||
| 22 | 8.12 | 9.05 | 0.93 | −1.26 | 7.01 | −1.11 | 7.93 | −0.19 |
| 23 | 13.60 | 18.94 | 5.34 | −7.28 | 10. 8 | −2.80 | 11.7 | −1.90 |
| 24 | 9.30 | 8.48 | −0.82 | 1.12 | 7.83 | −1.47 | 8.75 | −0.55 |
| 25 | 11.27 | 8.18 | −3.09 | 4.22 | 9.19 | −2.08 | 10.1 | −1.17 |
| 26 | 10.72 | 12. 64 | 1.92 | −2.61 | 8.81 | −1.91 | 9.72 | −1.00 |
| 27 | 4.62 | 2.91 | −1.71 | 2.33 | 4.59 | −0.03 | 5.53 | 0.91 |
| 28 | 0.98 | −4.10 | −5.08 | 6.93 | 2.07 | 1.09 | 3.02 | 2.04 |
| 29 | 3.89 | 1.50 | −2.39 | 3.26 | 4.09 | 0.20 | 5.02 | 1.13 |
| 30 | 5.36 | 5.35 | −0.01 | 0.01 | 5.1 | −0.26 | 6.04 | 0.68 |
| 31 | 1.53 | −3.20 | −4.73 | 6.44 | 2.45 | 0.92 | 3.4 | 1.87 |
| 32 | 5.24 | 4.67 | −0.57 | 0.78 | 5.02 | −0.22 | 5.95 | 0.71 |
| 33 | 0.49 | −0.96 | −1.45 | 1.98 | 1.73 | 1.24 | 2.69 | 2.20 |
| 34 | 0.81 | −1.37 | −2.18 | 2.98 | 1.96 | 1.15 | 2.91 | 2.10 |
| 35 | 1.86 | 0.14 | −1.72 | 2.35 | 2.68 | 0.82 | 3.63 | 1.77 |
| 36 | 9.60 | 11.07 | 1.47 | −2.00 | 8.04 | −1.56 | 8.95 | −0.65 |
| 37 | 6.70 | 7.89 | 1.19 | −1.63 | 6.03 | −0.67 | 6.96 | 0.26 |
| 38 | 7.33 | 8.22 | 0.89 | −1.21 | 6.47 | −0.86 | 7.39 | 0.06 |
| RMSE (QM2) | 2.60 | 1.30 | 1.33 | |||||
| MAE (QM2) | 2.09 | 1.08 | 1.13 | |||||
| ME (QM2) | −0.71 | −0.44 | 0.49 | |||||
| R2 (QM2) | 0.96 | |||||||
| m (QM2) | 1.45 | |||||||
| RMSE (Global) | 3.35 | 1.66 | 1.85 | |||||
| MAE (Global) | 2.66 | 1.35 | 1.46 | |||||
| ME (Global) | 0.58 | −0.40 | −0.40 | |||||
| R2 (Global) | 0.96 | |||||||
| m (Global) | 1.44 | |||||||
The SAMPL6 data set consisted of 24 fragment-like small organic molecules (Fig. 1) with unknown pKa values that were selected for their similarity to kinase inhibitors and for experimental tractability. It was provided by the SAMPL6 organizers through the public repository https://github.com/MobleyLab/SAMPL6 as computer-generated microstates in SMILES format. The protonation state for each microstate was computed with an in-house script using the C ACT VS Chemoinfor- matics Toolkit [27] (Xemistry GmbH, https://www.xemistry.com/), allowing the classification of microstates in two groups, neutral acids and cationic acids, for which different correction factors were applied in the approach using the piecewise linear model.
Three-dimensional coordinates for all compounds were generated in MOL2 format using CORINA version 3.60 (http://www.molecular-networks.com), then converted into the Gaussian input format using an in-house script. The PDF 3d files, which can be visualized with Adobe Acrobat Reader (https://get.adobe.com/fr/reader/) were generated with Cactvs.
2.2. Quantum chemical microscopic pKa calculations
Gas-phase geometry optimization and frequency calculation of the protonated and deprotonated forms were performed at the B3LYP/6–311+G(d,p) level using Gaussian 09 version D.01 [28] to obtain . A single-point free energy evaluation at the same level using the Conductor-like Polarizable Continuum Solvation Model (CPCM) [29–32] and UAHF radii as implemented in Gaussian 09 version D.01 [28] yielded the solvation free energy so that (Eq. 7) and an estimate for the pKa associated with this protonation/deprotonation event could be calculated via Eqs. 6 and 3.
In some cases, the geometry optimization did not converge with Gaussian 09 version D.01, but was successful with the version A.02 of Gaussian 09. Geometry optimization for microstates SM04_micro016, SM07_micro016, SM17_micro008 and SM17_micro009 did not converge in any conditions.
Muckerman et al [24] recognized systematic errors related to the solvation contribution as responsible for poor accuracy, namely the solvation model under-solvates weak acids and over-solvates strong acids. They proposed a physically-motivated correction
| (8) |
to with the linear model
| (9) |
The parameters a0 and a1 are determined from a training set by linear regression. In order to apply the correction Eq. 9 to compounds with unknown pKa, a linear estimator ℒ can be derived by substituting in Eq. 9 and solving for to yield
| (10a) |
| (10b) |
| (10c) |
The linear estimator ℒ with parameters a0 and a1 for the microscopic pKa is
| (11) |
2.3. Microstates vs Macrostates
We consider each tautomer of the acid HA and the base A− as a microstate with label i. The set of microstates with the same total number of protons Ni = N is labeled the macrostate N. The macroscopic pKa characterizes the transitions between any of the microstates with N protons to any microstate with N − 1 protons.
In general, the free energy difference between two states (micro or macro states) that are separated by a single protonation process (i.e., the free energy to go from N to N − 1 associated protons) is
| (12) |
where P(N − 1) and P(N) are the probabilities of observing the system with N − 1 and N associated protons respectively and β = (RT)−1. The Henderson-Hasselbalch equation
| (13) |
can be rewritten in terms of the free energy of protonation (Eq. 12) to give
| (14a) |
| (14b) |
2.4. Calculation of macroscopic pKas from microscopic pKas
The microscopic pKa values correspond to free energy differences between microstates i and j (Eq. 14b); for notational convenience we drop the explicit pH dependence in the following for all free energies. Each state has a pH-dependent associated free energy Gi, which is not known. Constructing the Gi from the differences between them is not straightforward because these calculated free energy differences come with unknown errors that prevent, for example, that the sum along any closed thermodynamic cycle is exactly zero as required by the fact that the Gi are thermodynamic state functions. We construct a set of M microstate free energies that is most consistent with the calculated (“measured”) {ΔGij} using a maximum-likelihood estimator [33] based on the likelihood function
| (15) |
where we assumed normal distribution of errors with constant standard deviation. The product runs over all pairs (i, j) for which calculated ΔGij are available. L is proportional to the probability Ρ({ΔGij}|{Gi}) that we could observe the measured data (all the calculated Δ Gij) if we were given a specific set of the Gi (our model parameters). Maximizing the log-likelihood ln L (using functions in SciPy [34]) as a function of all the Gi provides the set that is most consistent with the given measurements {Δ Gij}. Further details and more general applications of this approach will be published elsewhere (I.M. Kenney et al, in preparation).
In order to calculate the macroscopic pKas, we begin by calculating the free energy of protonation using principles of equilibrium statistical mechanics [25]. The probability of observing a macrostate with N associated protons is
| (16) |
where the sum is over all accessible microstates with free energy Gi, δΝi,N is unity when the microstate i has N protons and null otherwise, and Z is the partition function, defined by
| (17) |
Eq. 16 combined with the general expression for the free energy of protonation (Eq. 12) yields the effective macroscopic protonation free energy as a function of the Gi,
| (18) |
ΔGN-1,N is a function of the pH of the system and the microscopic pKas relevant to the macrostate N. Together with Eq. 14a, Eq. 18 allows us to calculate the macroscopic pKa value for removing the Nth proton from a molecule. With all microstate free energies known for a given pH value it is also straightforward to compute the pH-dependent microstate probabilities
| (19) |
where all terms depend on pH.
2.5. Error analysis
The difference between experimental and computed pKa values (“signed error”) for each compound, labeled with its identification code ‘id’, was calculated as
| (20) |
The root-mean-square error (RMSE) was determined from the individual errors Δ as
| (21) |
the mean absolute error (MAE) as
| (22) |
and the signed mean error (ME, also called the “mean signed error”, MSE) as
| (23) |
We also report the Pearson correlation coefficient R2 and the slope m of a linear regression to the data, as computed with the function scipy.stats.linregress( ) in the SciPy package [34].
The quantum chemical single point free energy calculations do not have a statistical error and we have not yet implemented the calculation of an error bound in the maximum likelihood estimator for the Gi. Therefore, all pKa are provided without a statistical error. Judging from the performance of the training data set and the post- hoc analysis of the SAMPL6 compounds (see Results), the accuracy of the calculated pKa values is 1–2 pKa units.
Calculated pKa were compared to experimental values with the script typeIII_analysis.py as provided by the SAMPL6 organizers in the public repository https://github.com/MobleyLab/SAMPL6. Calculated values were matched to experimental ones with the Hungarian algorithm, which finds the optimum pairing between two sets by minimizing the linear sum of squared errors.
3. Results and Discussion
3.1. Training data set
The first step in our protocol was the design of a training data set containing 38 structurally-diverse, simple organic and inorganic compounds with known pKa values. This global data set could be classified by the charge of the acid and split into two subsets. The neutral acids (named QM1, Fig. 2) contained 21 compounds and the second set, the positively-charged acids (named QM2, Fig. 3), contained the remaining 17 compounds. The structures were chosen from different chemical families in order to obtain for the two subsets a relatively homogeneous distribution of data points over a wide range of values (see Table 1 for the experimental pKas).
Predicted pKa values were computed for all compounds from the training data set using the protocol described by Muckerman et al [24] (see the Methods section for details). The correlation of these computed values with the experimental pKas is shown in (Fig. 4a), with a Pearson correlation coefficient R2 = 0.96 (Table 1). The corresponding values were obtained using Eq. 8 and plotted against the experimental pKa values. A global linear fit model, with a slope of a1 = −0.61 and an intercept of a0 = 2.75 (parameters in Eq. 9), was derived by using all compounds as a single data set (Fig. 4b). Alternatively, a piecewise linear fit model was derived by considering separately the two QM1 and QM2 subsets (Fig. 4c). In this latter case we obtained the parameters in Eq. 9 with a slope of for both subsets and intercept values of for the QM1 and QM2 subsets, respectively.
Fig. 4.
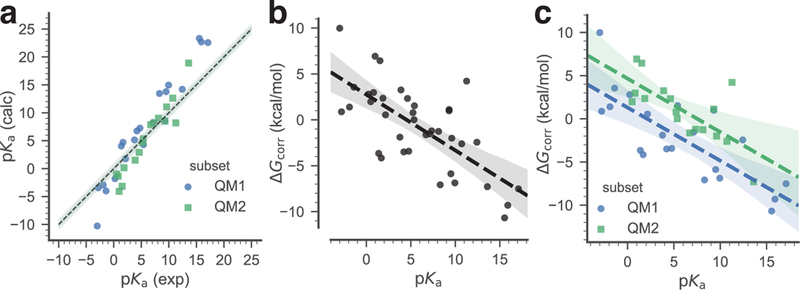
Training data set. The pKa of the training data set compounds are used to derive a simple linear model that relates the free energy correction to the experimental pKa. Two linear models were derived: a global linear model (black dashed line), utilizing all data, and a piecewise linear model that applies to either neutral acids (subset QM1, blue) or to positively charged acids (subset QM2, green). a: Correlation between experimental and calculated pKa of the training data set. The dashed line indicates ideal correlation with the gray band indicating 1 pKa unit deviation. b: Global linear fit of the calculated to the experimental pKa. c: Linear fits of the calculated to the experimental pKa, split between the QM1 and the QM2 subsets. In (b) and (c) the dashed lines are linear models to the data, with shaded bands indicating 95% confidence intervals from 1000 bootstrap samples.
The linear estimators associated with these models (Eq. 10a) were calculated using Eq. 11. These corrections were applied to the whole training set, and to the QM1 and QM2 subsets, respectively, in order to evaluate to which extent the systematic errors related to the prediction method were removed compared with the pKa values obtained directly from the ab initio calculations (Table 1). We can see that in all cases the corrected pKa values are much closer to the experimental values, with the global model behaving slightly better than the piecewise model, as shown by, for instance, the smaller RMSE 1.66 vs 1.85 for the whole training set.
3.2. Macroscopic pKa
The microscopic pKa values for the SAMPL6 data set were computed using the same protocol as for the training data set (595 individual transformations). Again, the corrections from the global linear model were applied to the whole SAMPL6 data set and alternatively, those from the piecewise linear model to individual subsets of the SAMPL6 data set containing the neutral acids and the cationic acids, respectively.
Starting from these three sets of results (obtained directly from ab initio free energies or after correction with the two linear models, global and piecewise) we calculated pH-dependent microstate free energies and macroscopic pKa values (Table 2). These results, formatted using the SAMPL6 submission template, were used as input for the typeIII_analysis.py script in order to compare to the experimental values that were provided by the SAMPL6 organizers together with the analysis scripts. The input files with our results formatted as comma-separated value (CSV) files and the optimized structures for all microstates in MOL2 and pdf3d format are provided in the Electronic Supplementary Material. During the challenge we submitted macroscopic pKa values only for three compounds (SM15, SM20 and SM22). Here we describe the macroscopic pKa predictions for the entire SAMPL6 data set.
Table 2.
Experimental and computed pKa values for the compounds from the SAMPL6 data set (Fig. 1). The difference Δ (Eq. 20) between computed and experimental pKa values is shown for each compound. The experimental values were provided by the SAMPL6 organizers. The root- mean-square error (RMSE), the mean absolute error (MAE), and the signed mean error (ME) were calculated according to Eqs. 21–23. The Pearson correlation coefficient R2 and the slope m were calculated from a linear regression.
| Compound | pKa | Exp. | QM computed | Linear fit global | Linear fit piecewise | |||
|---|---|---|---|---|---|---|---|---|
| ID | ID | pKa | pKa | Δ | pKa | Δ | pKa | Δ |
| SM01 | pKal | 9.53(1) | 15.81 | 6.28 | 12.33 | 2.80 | 11.55 | 2.02 |
| SM02 | pKal | 5.03(1) | 6.97 | 1.94 | 6.21 | 1.18 | 7.14 | 2.11 |
| SM03 | pKa1 | 7.02(1) | 1.40 | −5.62 | 11.06 | 4.04 | 10.27 | 3.25 |
| SM04 | pKa1 | 6.02(1) | 9.58 | 3.56 | 8.06 | 2.04 | 8.98 | 2.96 |
| SM05 | pKa1 | 4.59(1) | 0.95 | −3.64 | 2.02 | −2.57 | 2.17 | −2.42 |
| SM06 | pKa1 | 3.03(4) | 1.54 | −1.49 | 2.54 | −0.49 | 3.81 | 0.78 |
| SM06 | pKa2 | 11.74(1) | 17.43 | 5.69 | 13.45 | 1.71 | 12.95 | 1.21 |
| SM07 | pKa1 | 6.08(1) | 8.44 | 2.36 | 7.23 | 1.15 | 8.15 | 2.07 |
| SM08 | pKa1 | 4.22(1) | 10.17 | 5.95 | 8.43 | 4.21 | 7.80 | 3.58 |
| SM09 | pKa1 | 5.37(1) | 6.99 | 1.62 | 6.23 | 0.86 | 7.16 | 1.79 |
| SM10 | pKa1 | 9.02(1) | 14.82 | 5.80 | 11.81 | 2.79 | 12.31 | 3.29 |
| SM11 | pKa1 | 3.89(1) | 4.39 | 0.50 | 4.53 | 0.64 | 3.75 | −0.14 |
| SM12 | pKa1 | 5.28(1) | 6.55 | 1.27 | 5.96 | 0.68 | 6.89 | 1.61 |
| SM13 | pKa1 | 5.77(1) | 9.23 | 3.46 | 7.79 | 2.02 | 8.72 | 2.95 |
| SM14 | pKa1 | 2.58(1) | −0.31 | −2.89 | 1.16 | −1.42 | 1.56 | −1.02 |
| SM14 | pKa2 | 5.30(1) | 5.68 | 0.38 | 5.34 | 0.04 | 5.15 | −0.15 |
| SM15 | pKa1 | 4.70(1) | 5.51 | 0.81 | 5.21a | 0.51 | 6.14b | 1.44 |
| SM15 | pKa2 | 8.94(1) | 14.49 | 5.55 | 11.41a | 2.47 | 10.64b | 1.70 |
| SM16 | pKa1 | 5.37(1) | 5.04 | −0.33 | 4.88 | −0.49 | 6.17 | 0.80 |
| SM16 | pKa2 | 10.65(1) | 15.92 | 5.27 | 12.40 | 1.75 | 11.69 | 1.04 |
| SM17 | pKa1 | 3.16(1) | 2.26 | −0.90 | 2.96 | −0.20 | 3.90 | 0.74 |
| SM18 | pKa1 | 2.15(2) | 1.91 | −0.24 | 2.80 | 0.65 | 3.29 | 1.14 |
| SM18 | pKa2 | 9.58(3) | 3.54 | −6.04 | 13.27 | 3.69 | 12.49 | 2.91 |
| SM18 | pKa3 | 11.02(4) | 17.14 | 6.12 | 13.88 | 2.86 | 13.54 | 2.52 |
| SM19 | pKa1 | 9.56(2) | 4.81 | −4.75 | 11.78 | 2.22 | 11.00 | 1.44 |
| SM20 | pKa1 | 5.70(3) | 10.04 | 4.34 | 8.34a | 2.64 | 7.58b | 1.88 |
| SM21 | pKa1 | 4.10(1) | 4.68 | 0.58 | 4.63 | 0.53 | 5.56 | 1.46 |
| SM22 | pKa1 | 2.40(2) | −0.10 | −2.50 | 1.32a | −1.08 | 2.02b | −0.38 |
| SM22 | pKa2 | 7.43(1) | 9.44 | 2.01 | 7.93a | 0.50 | 7.41b | −0.02 |
| SM23 | pKa1 | 5.45(1) | 5.53 | 0.08 | 5.23 | −0.22 | 6.16 | 0.71 |
| SM24 | pKa1 | 2.60(1) | 6.13 | 3.53 | 5.65 | 3.05 | 5.25 | 2.65 |
| RMSE | 3.74 | 2.04 | 1.95 | |||||
| MAE | 3.08 | 1.66 | 1.68 | |||||
| ME | 1.25 | 1.24 | 1.42 | |||||
| R2 | 0.58 | 0.87 | 0.86 | |||||
| m | 1.45 | 1.31 | 1.17 | |||||
These results represent our submission 35bdm to SAMPL6.
These results represent our submission pQjba to SAMPL6.
Using this protocol we could predict the macroscopic pKa values for the 24 SAMPL6 compounds with a RMSE of about 2 pKa units when the corrections were applied and of 3.74 pKa units when the ab initio free energies were used directly. The relative poor accuracy when directly using the quantum chemical free energies is in line with previous studies [15, 24].
The signed errors of individual predictions represented in Fig. 5 show that most of the prediction errors after correction are positive, with the notable exception of compound SM05 for which these errors are consistently negative. High prediction errors (3 −4 pKa units) are obtained for compounds SM03 and SM08, whereas compounds SM01, SM04, SM10, SM13, SM18, SM20, and SM24 are predicted with errors of about 2 – 3 pKa units. The representation of the prediction errors in the order of increasing absolute experimental pKa values (Fig. S3, Electronic Supplementary Material) shows that these are not related. Therefore, the source of remaining errors after correction should be sought elsewhere. As shown in Fig. 6, the results for the SAMPL6 data set are fairly insensitive to the fitting approach used (global or piecewise linear model), further indicating some level of robustness. Other statistical measures such as Pearson correlation coefficient R2 = 0.86 and the slope of the linear regression m = 1.17 (for the piecewise linear model, see Table 2 for almost identical values for the global linear model) indicate encouraging correlations but the large mean error (1.42 for the piecewise linear model and 1.24 for the global linear model) hint at remaining systematic errors.
Fig. 5.

Signed error Δid of individual predictions. The calculated pKa was matched to the experimental pKa for each compound (indicated by the SAMPL6 pKa ID) and the deviation from the experimental value represented as a bar. Observations for the same compound have the same color. a: pKa were directly estimated from the quantum mechanical free energy differences. b: The quantum mechanical pKa were corrected with the global linear model. c: compounds were corrected depending on their membership in subsets 1 or 2 with the piecewise linear model.
Fig. 6.
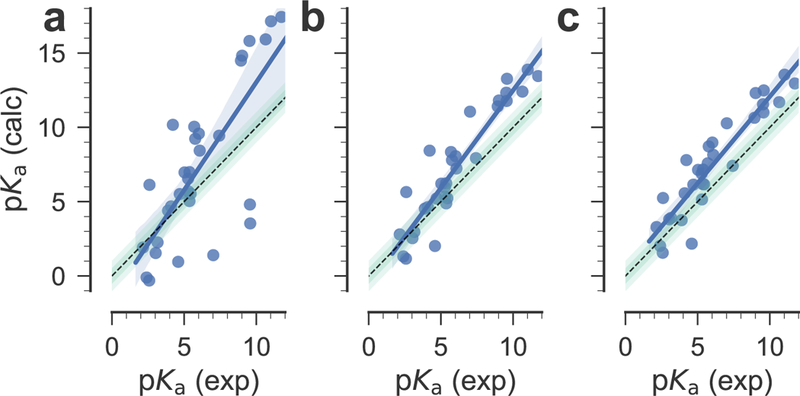
Correlation between experimental and calculated pKa values for the SAMPL6 compounds. a: pKa were directly estimated from the quantum mechanical free energy differences. b: The quantum mechanical pKa were corrected with the global linear model. c: compounds were corrected depending on their membership in subsets 1 or 2. The black dashed line indicates ideal correlation, the shaded green bars show 0.5 and 1 pKa units deviation from ideal. Blue lines are linear regression fits to the data, with the blue shaded area indicating the 95% confidence interval from 1000 bootstrap samples.
The fact that the linear fit did not remove these systematic errors implies that the training data set did not include properties that are important for the SAMPL6 data set and hence the linear or piecewise linear estimator cannot correct model errors related to these properties. In order to quantify similarities and differences between the two datasets we analyzed a number of chemical properties (see section Properties of the training and SAMPL6 data sets with Fig. S1 in the Electronic Supplementary Material file for details). Overall, the most obvious differences between our training and the SAMPL6 data set are the higher flexibility of the SAMPL6 molecules (with a median three and maximum ten rotatable bonds versus a median zero and maximum three, Fig. 7a) and the greater capability to accept hydrogen bonds (median four and maximum eight hydrogen bond acceptors versus median two and maximum ten; Fig. 7b), which correlates with a larger polar surface area (see Fig. S2 in the Electronic Supplementary Material file). However, Fig. 7c shows that the training compounds have more hydrogen bond acceptors for the same number of heavy atoms than the SAMPL6 compounds, i.e., for their larger size, the SAMPL6 compounds have fewer acceptors than one would expect from simple extrapolation of the training compounds. Similarly, the polar surface area of the SAMPL6 compounds would be overestimated from the training set (Fig. S2). These differences suggest that the interactions with water through hydrogen bonds are stronger in the training set than in the SAMPL6 set, which could lead to a systematic error in the estimator that was derived from the training set.
Fig. 7.
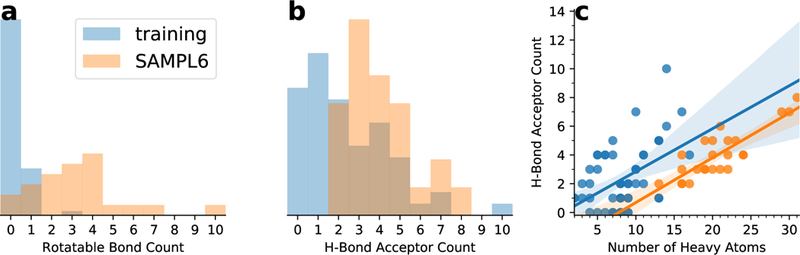
Comparison of chemical properties of the training (light blue) and SAMPL6 (orange) data sets. a: normalized histograms of the number of rotatable bonds; b: normalized histograms of the number of hydrogen bond acceptors; c: correlation between the number of heavy atoms and the number of acceptors with linear regressions shown as solid lines and their 95% confidence interval from 1000 bootstraps indicated by shaded areas.
In the post-challenge analysis, we also tested the introduction of a conformational search step in our protocol and evaluated its influence on the quality of our predictions using two model compounds, SM06 and SM20. The complete results are presented in the Conformational search section of the Electronic Supplementary Material file. In brief, for SM06 the new microscopic pKa value of SM06_micro011 brought no changes in the predicted macroscopic pKa values and for SM20 we obtained macroscopic pKa prediction errors 1.8–2.4 pKa units higher compared with the values obtained without conformational search. It seems that, at least for these two compounds, the conformational search does not yield any substantial improvements in the prediction of macroscopic pKa values.
3.3. Microstate probabilities
The SAMPL6 organizers recently made available experimental assignments of microstates with corresponding microstate pKa for a number of compounds [36] (https://github.com/MobleyLab/SAMPL6/blob/master/physical_properties/pKa/experimental_data/NMR_microstate_determination/). Here we focus on SM14 as an example. Fig. 8 compares our computed microstate probabilities pi (Eq. 19) to the ones derived from the experimental assignments of states SM14_micro003, SM14_micro002, and SM14_micro001. The important calculated microstates (from the linear piecewise model) were SM14_micro003 (N = 3 protons), SM14_micro004 and SM14_micro002, both with N = 2 protons, and SM14_micro001 (N = 1).The calculated microscopic pKa for the deprotonation of SM14_micro003 to SM14_micro002 was 2.1, similar to the experimental value 2.58 ± 0.01. The microscopic pKa corresponding to the deprotonation of SM14_micro002 to SM14_micro001 was calculated as 4.6, also similar to the experimental one, 5.30 ± 0.01. A second microstate SM14_micro005 exists with the same number of protons as SM14_micro002 but both experiment and our computations indicated that this second state is suppressed and plays no role. Our calculations, however, assigned a higher population to SM14_micro004 than to SM14_micro002, in contrast to the experimental findings, which, based on NMR nitrogen chemical shift measurements in the aprotic solvent acetonitrile-d3 under pH titration, identified SM14_micro002 as the dominant intermediate state. The partial agreement between these detailed experiments and our calculations is encouraging but a single comparison does not allow us to draw any broader conclusions except perhaps to highlight the ease with which our partition function-based formalism can be used to compute microscopic populations.
Fig. 8.
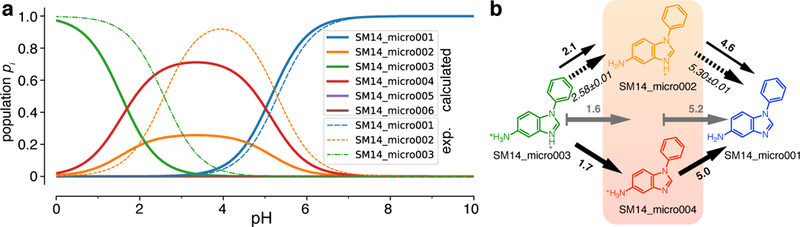
Microstate probabilities pi for SM14. a: Computed microstate probabilities (for the piecewise linear fit) are shown as heavy solid lines and experimentally derived probabilities as thin dashed lines. The experimental pi were calculated in the same way as the calculated ones (Eq. 19) by directly using the experimental microstate pKas. b: Microstate diagram with arrows indicating deprotonation. Bold numbers near solid arrows are the calculated microstate pKa (from (a)) and italic numbers near dashed arrows are the experimental numbers, assigned to the experimentally identified microstate transitions. The gray solid arrows with gray bold numbers indicate the calculated macroscopic pKa from N = 3 protons (microstate SM14_micro003) to N = 2 protons (mixture of SM14_micro002 and SM14_micro004, indicated by the orange box) to N = 1 proton in SM14_micro001 (and SM14_micro005, which is not shown because computation and experiment indicate that it is suppressed relative to SM14_micro001).
3.4. Computation time
The total computational cost required by this project was 641 CPU-days on a Linux cluster making use of Intel Xeon E5–4627 v3 CPUs running at 2.60 GHz. Given that 344 microstates were computed, each microstate required 1.86 CPU-days on average. The calculations were carried out in parallel on 8 cores, so the average wall clock time for a microstate was 5.6 hours in these conditions. The most rigid compound, SM22, was the fastest with 1 CPU-hour for one microstate, whereas one of the biggest and most flexible compounds from the SAMPL6 data set, SM18, required about 3.2 CPU-days for one microstate.
4. Conclusions
Compared to other methods in the SAMPL6 challenge, our approach has below- average accuracy (Fig. 9 and Figs. S4–S7 in the Electronic Supplementary Material) and its computational cost is also higher than ML-based approaches (not considering the cost for compiling and validating the data and training the ML model). A key advantage of our approach is its generality as it does not depend on training on specific data sets although below we note that the quality of the training set for the correction step is a possible concern. With the linear model, which was derived from a very small and simple training set (38 compounds), we remove some of the errors related to the QM method used and its implementation in Gaussian (e.g., the implicit solvation model). The quality of the prediction is mostly independent of the structure, i.e., it can predict organic compounds from different families and even inorganic compounds with similar level of accuracy. In comparison, purely ML-based methods are trained on large experimental data sets (containing several thousands or tens of thousands compounds) and they can be vulnerable to chemical families that are not represented in the training set. Our approach appears reasonably robust because for our training set we obtain the same slope on the global data set and on the individual subsets, which are chemically quite different. The results for the SAMPL6 data set are also fairly insensitive to the fitting approach used (global or piecewise linear model), further demonstrating robustness. The correlations with experimental data are generally good but suffer from systematic errors, possibly from differences between the training set and the SAMPL6 set that bias the estimator that is needed to correct the raw QM pKa values. The statistical measures indicate clear room from improvement. It appears that a better correction scheme, using a larger data set that better matches the test data set with respect to its hydrogen bonding properties and is generally more representative of drug-like molecules could improve the predictions, perhaps in conjunction with more sophisticated classifiers and estimators than simple separation by charge and linear regression. We expect that improvements in the model physics, namely in the treatment of solvation, could also lead to further increases in accuracy.
Fig. 9.
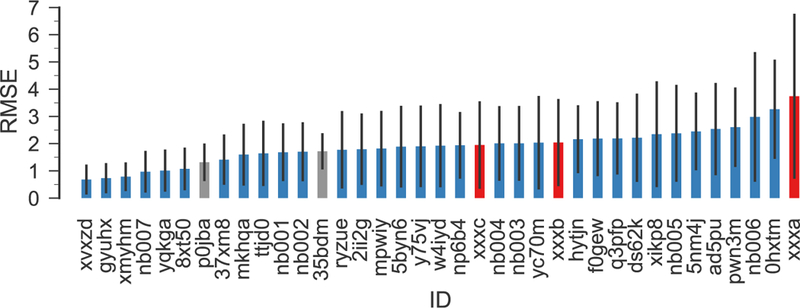
RMSE of all SAMPL6 submissions (blue), including our new calculations for all SAMPL6 compounds (red) and for completeness our original submissions (gray), which only included predictions for SM15, SM20, and SM22 and is only of limited statistical validity because of the large variance of the RMSE itself for only three samples [37]. The submission IDs p0jba and xxxc correspond to the piecewise linear model, 35bdm and xxxb to the global linear model, and xxxa to directly using the quantum chemical free energies. Other IDs belong to other regular SAMPL6 submissions. The error bars indicate 95% confidence intervals from 1000 bootstrap samples.
We currently consider the method described here (and originally developed by Muckerman et al [24]) as an acceptable compromise between speed, accuracy and generality across the chemical space. It seems especially useful when one encounters novel compounds and wants to assess them based on their absolute pKa values. The calculations are tractable with typical computational resources, absolute pKas are accurate to about 2 units (within the “chemical accuracy” range [15]) and do not seem to be biased with respect to specific chemical groups, and thus the relative ordering of compounds is also meaningful.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by the National Institute Of General Medical Sciences of the National Institutes of Health under Award Number R01GM118772 (to OB). BII was supported in part by grants ANR-10-LABX-33 (LabEx LERMIT) and ANR-14-JAMR-0002–03 (JPIAMR) from the French National Research Agency (ANR), and by a grant DIM MAL-INF from the Region Ile-de-France.
Contributor Information
E. Selwa, Institut de Chimie des Substances Naturelles, CNRS UPR 2301, Université Paris-Saclay, Labex LERMIT, 1 Avenue de la Terrasse, 91198 Gif-sur-Yvette, France
I. M. Kenney, Department of Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA
O. Beckstein, Department of Physics and Center for Biological Physics, Arizona State University, P.O. Box 871504, Tempe, AZ 85287-1504, USA, Tel.: +1 480 727 9765, Fax: +1 480 965-4669, [email protected]
B. I. Iorga, Institut de Chimie des Substances Naturelles, CNRS UPR 2301, Université Paris-Saclay, Labex LERMIT, 1 Avenue de la Terrasse, 91198 Gif-sur-Yvette, France, Tel.: +33 1 69 82 30 94, Fax: +33 1 69 07 72 47, [email protected]
References
- 1.Nicholls A, Mobley DL, Guthrie JP, Chodera JD, Bayly CI, Cooper MD, Pande VS (2008) Predicting small-molecule solvation free energies: An infor¬mal blind test for computational chemistry. J Med Chem 51(4):769–779, DOI 10.1021/jm070549+ [DOI] [PubMed] [Google Scholar]
- 2.Guthrie JP (2009) A blind challenge for computational solvation free ener¬gies: Introduction and overview. J Phys Chem B 113(14):4501–4507, DOI 10.1021/jp806724u [DOI] [PubMed] [Google Scholar]
- 3.Geballe MT, Skillman AG, Nicholls A, Guthrie JP, Taylor PJ (2010) The SAMPL2 blind prediction challenge: Introduction and overview. J Comput Aided Mol Des 24(4):259–279, DOI 10.1007/s10822-010-9350-8 [DOI] [PubMed] [Google Scholar]
- 4.Geballe MT, Guthrie JP (2012) The SAMPL3 blind prediction challenge: transfer energy overview. J Comput Aided Mol Des 26(5):489–96, DOI 10.1007/s10822-012-9568-8 [DOI] [PubMed] [Google Scholar]
- 5.Mobley DL, Wymer KL, Lim NM, Guthrie JP (2014) Blind prediction of solvation free energies from the SAMPL4 challenge. J Comput Aided Mol Des 28(3):135–50, DOI 10.1007/s10822-014-9718-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bannan CC, Calabrd G, Kyu DY, Mobley DL (2016) Calculating partition co¬efficients of small molecules in octanol/water and cyclohexane/water. J Chem Theory Comput 12(8):4015–24, DOI 10.1021/acs.jctc.6b00449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Beckstein O, Iorga BI (2012) Prediction of hydration free energies for aliphatic and aromatic chloro derivatives using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 26(5):635–645, DOI 10.1007/s10822-011-9527-9 [DOI] [PubMed] [Google Scholar]
- 8.Beckstein O, Founder A, Iorga BI (2014) Prediction of hydration free energies for the SAMPL4 diverse set of compounds using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 28(3):265–276, DOI 10.1007/s10822-014-9727-1 [DOI] [PubMed] [Google Scholar]
- 9.Kenney IM, Beckstein O, Iorga BI (2016) Prediction of cyclohexane-water dis¬tribution coefficients for the SAMPL5 data set using molecular dynamics simulations with the OPLS-AA force field. J Comput Aided Mol Des 30(11):1045–1058, DOI 10.1007/s10822-016-9949-5 [DOI] [PubMed] [Google Scholar]
- 10.Babic S, Horvat AJ, Mutavdzic Pavlovic D, Kastelan-Macan M (2007) Determination of pKa values of active pharmaceutical ingredients. TrAC Trends in Analytical Chemistry 26(11):1043–1061, DOI https://doi.org/10.1016/j.trac.2007.09.004 [Google Scholar]
- 11.Lee AC, Crippen GM (2009) Predicting pKa. Journal of Chemical Information and Modeling 49(9):2013–2033, DOI 10.1021/ci900209w [DOI] [PubMed] [Google Scholar]
- 12.Alexov E, Mehler EL, Baker N, Baptista AM, Huang Y, Milletti F, Nielsen JE, Farrell D, Carstensen T, Olsson MHM, Shen JK, Warwicker J, Williams S, Word JM (2011) Progress in the prediction of pKa values in proteins. Proteins 79(12):3260–75, DOI 10.1002/prot.23189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rupp M, Korner R, Tetko IV (2011) Predicting the pKa of small molecules. Combinatorial Chemistry & High Throughput Screening 14(5):307–327, DOI 10.2174/138620711795508403 [DOI] [PubMed] [Google Scholar]
- 14.Reijenga J, van Hoof A, van Loon A, Teunissen B (2013) Development of methods for the determination of pKa values. Anal Chem Insights 8:53–71, DOI 10.4137/ACI.S12304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ho J, Coote ML (2009) A universal approach for continuum solvent pKa calculations: are we there yet? Theoretical Chemistry Accounts 125(1–2):3–21, DOI 10.1007/s00214-009-0667-0 [Google Scholar]
- 16.Mongan J, Case DA, McCammon JA (2004) Constant pH molecular dynam¬ics in generalized born implicit solvent. J Comput Chem 25(16):2038–48, DOI 10.1002/jcc.20139 [DOI] [PubMed] [Google Scholar]
- 17.Chen W, Morrow BH, Shi C, Shen JK (2014) Recent development and applica¬tion of constant pH molecular dynamics. Molecular Simulation 40(10–11):830–838, DOI 10.1080/08927022.2014.907492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Swails JM, York DM, Roitberg AE (2014) Constant pH replica exchange molecular dynamics in explicit solvent using discrete protonation states: Implementation, testing, and validation. J Chem Theory Comput 10(3):1341–1352, DOI 10.1021/ct401042b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Radak BK, Chipot C, Suh D, Jo S, Jiang W, Phillips JC, Schulten K, Roux B (2017) Constant-pH molecular dynamics simulations for large biomolecular systems. Journal of Chemical Theory and Computation 13(12):5933–5944, DOI 10.1021/acs.jctc.7b00875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Di Russo NV, Estrin DA, Marti MA, Roitberg AE (2012) pH-dependent con¬formational changes in proteins and their effect on experimental pK(a)s: the case of nitrophorin 4. PLoS Comput Biol 8(11):e1002,761, DOI 10.1371/journal.pcbi.1002761 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Morrow BH, Koenig PH, Shen JK (2013) Self-assembly and bilayer-micelle tran¬sition of fatty acids studied by replica-exchange constant pH molecular dynamics. Langmuir 29(48):14,823–30, DOI 10.1021/la403398n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Huang Y, Chen W, Dotson DL, Beckstein O, Shen J (2016) Mechanism of pH- dependent activation of the sodium-proton antiporter NhaA. Nature Communications 7:12,940, DOI 10.1038/ncomms12940 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Alongi KS, Shields GC (2010) Theoretical calculations of acid dissociation constants: A review article In: Ann Rep Comput Chem, vol 6, Elsevier Science B.V., chap 8, pp 113–138, DOI 10.1016/S1574-1400(10)06008-1 [Google Scholar]
- 24.Muckerman JT, Skone JH, Ning M, Wasada-Tsutsui Y (2013) Toward the accurate calculation of pKa values in water and acetonitrile. Biochimica et Biophysica Acta 1827:882–891, DOI 10.1016/j.bbabio.2013.03.011 [DOI] [PubMed] [Google Scholar]
- 25.McQuarrie DA (1976) Statistical Mechanics. HarperCollins, New York [Google Scholar]
- 26.Zhang H, Jiang Y, Yan H, Yin C, Tan T, van der Spoel D (2017) Free-energy calculations of ionic hydration consistent with the experimental hydration free energy of the proton. The Journal of Physical Chemistry Letters 8(12):2705–2712, DOI 10.1021/acs.jpclett.7b01125, pMID: [DOI] [PubMed] [Google Scholar]
- 27.Ihlenfeldt W, Takahashi Y, Abe H, Sasaki S (1994) Computation and management of chemical properties in CACTVS: An extensible networked approach toward modularity and compatibility. J Chem Inf Comput Sci 34(1):109–116 (http://www.xemistry.com/) [Google Scholar]
- 28.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery JA Jr, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2009) Gaussian 09 Revision D.01. Gaussian Inc. Walling-ford CT [Google Scholar]
- 29.Klamt A, Schuurmann G (1993) COSMO: anew approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J Chem Soc, Perkin Trans 2 pp 799–805, DOI 10.1039/P29930000799 [Google Scholar]
- 30.Andzelm J, Kulmel C, Klamt A (1995) Incorporation of solvent effects into density functional calculations of molecular energies and geometries. The Journal of Chemical Physics 103(21):9312–9320, DOI 10.1063/1.469990 [Google Scholar]
- 31.Barone V, Cossi M (1998) Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. The Journal of Physical Chemistry A 102(11):1995–2001, DOI 10.1021/jp9716997 [Google Scholar]
- 32.Cossi M, Rega N, Scalmani G, Barone V (2003) Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. Journal of Computational Chemistry 24(6):669–681, DOI 10.1002/jcc.10189 [DOI] [PubMed] [Google Scholar]
- 33.Bishop CM (2006) Pattern Recognition and Machine Learning Information Science and Statistics, Springer [Google Scholar]
- 34.Jones E, Oliphant T, Peterson P, et al. (2001-) SciPy: Open source scientific tools for Python. URL http://www.scipy.org/, [Online; accessed 2018–05-31]
- 35.Lundblad R, Macdonald F (2010) Handbook of Biochemistry and Molecular Biology, Fourth Edition Taylor & Francis [Google Scholar]
- 36.Ndukwe IE, Wang X, Reibarkh M, Isik M, Martin GE (2018) NMR characterization of microstates of SM14 Tech. rep., Merck NMR Structure Elucidation Group [Google Scholar]
- 37.Faber NKM (1999) Estimating the uncertainty in estimates of root mean square error of prediction: application to determining the size of an adequate test set in multivariate calibration. Chemometrics and Intelligent Laboratory Systems 49(1):79–89, DOI 10.1016/S0169-7439(99)00027-1 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


