Abstract
Coordinating the movements of different body parts is a challenging process for the central nervous system because of several problems. Four of these main difficulties are: first, moving one part can move others; second, the parts can have different dynamics; third, some parts can have different motor goals; and fourth, some parts may be perturbed by outside forces. Here, we propose a novel approach for the control of linked systems with feedback loops for each part. The proximal parts have separate goals, but critically the most distal part has only the common goal. We apply this new control policy to eye-head coordination in two-dimensions, specifically head-unrestrained gaze saccades. Paradoxically, the hierarchical structure has controllers for the gaze and the head, but not for the eye (the most distal part). Our simulations demonstrate that the proposed control structure reproduces much of the published empirical data about gaze movements, e.g., it compensates for perturbations, accurately reaches goals for gaze and head from arbitrary initial positions, simulates the nine relationships of the head-unrestrained main sequence, and reproduces observations from lesion and single-unit recording experiments. We conclude by showing how our model can be easily extended to control structures with more linked segments, such as the control of coordinated eye on head on trunk movements.
Keywords: Gaze saccades, Eye, Head, Feedback control, Superior colliculus, VOR suppression
1 Introduction
Everyday activities require the coordination of several body parts that are linked together such that movement of one part moves all the more distal parts (e.g., shoulder movement also moves the arm and hand). If one wants to redirect one’s gaze (gaze = eye-in-space = eye-in-head + head-on-trunk+trunk-on-legs+legs-in-space) to a new target of interest, one has to coordinate the movement of all body parts to ensure an accurate direction of gaze (Land 2004, 2009; Anastasopoulos et al. 2009). The coordination of these body segments also needs to account for the different dynamics of each subpart. Furthermore, some subparts may need their own goal (e.g., to satisfy path constraints, or to allow for subgoals, such as biting what you are looking at). One policy for the control of linked systems (LS) would be to divide the overall, or global, goal into subgoals for each segment and let each one be controlled independently. This approach faces problems, e.g., in biological systems a part’s controller may not be able to fully compensate for a given perturbation. Thus, uncompensated perturbations to one part could prevent the system from reaching the global goal. We propose a new architecture for the control of LS, in which subparts have individual goals controlled by feedback, but are also coupled to the most distal (and usually fastest) subpart. The most distal subpart is governed only by feedback of the global goal. Controllers may also interact to achieve better performance. We call this architecture the hierarchical control of linked systems (HCLS), and demonstrate its performance with a simple but well-studied linked system: gaze control with the head unrestrained.
Coordinated eye and head movements are required for many tasks, but the most demanding are the rapid, flicking movements of the eyes (called saccades) used to look around the world. Eye saccades have been studied for over a hundred years. These movements have stereotyped dynamics, with a well characterized relationship (called the main sequence, Bahill et al. 1975) between the amplitude of the eye’s displacement and its duration, peak and average speeds. When the head is unrestrained, cooperative movements of the eyes and head bring the gaze to the target. Interestingly, gaze displacement (change in head position + change in eye position) follows a main sequence with several similarities to that of a head-restrained eye saccade. In contrast, the eye follows a non-stereotypical movement that depends on exactly how the head moves (Bizzi 1979; Bizzi et al. 1971; Freedman and Sparks 1997; Liao et al. 2005; Gandhi 2012). Hence, we will call both the eye movement with head fixed and the gaze movement with head free saccades. (NB: although we have two eyes, when making saccades without vergence changes they move together, so we will usually refer to movements of the eyes as a single eye movement.)
Gaze saccade control is a good candidate to test HCLS for several reasons: first, the eyes and the head have much different dynamics, and thus command timing is crucial (Guitton et al. 1990). Second, head and gaze movements can follow different trajectories toward a common visual target (Goossens and van Opstal 1997; Collins and Barnes 1999). Third, head and gaze, but not eye movements, can have separate goals. Fourth, even if head orientation is perturbed, the final gaze orientation remains accurate (Laurutis and Robinson 1986; Tomlinson and Bahra 1986b; Pèlisson et al. 1989, 1995). We propose a unifying approach for LS and apply it to the 2-D gaze saccade control system to simulate many behavioral observations: gaze and head movements in same/opposite directions; perturbation compensation; gaze and eye velocity profiles dependent on head movement; effects of lesions; and the gaze main sequence. Although some of these observations have been modelled before (see below), no single model has been able to account for all of them. Thus, a new model is needed that can account for all the interactions among the different parts of the saccadic system.
Despite the interest in gaze control and head movement control, surprisingly little attention has been paid to how anatomical structures in the brain control head movements (Freedman 2001; Zangemeister et al. 1981; Viviani and Berthoz 1975; Peng et al. 1996; Goossens and van Opstal 1997). This problem is much harder than controlling eye movements, because many muscles move the head, the motor neurons are in a complicated circuit in the spinal cord, and the load on the head is not necessarily constant. Thus, our new model provides a new, but still oversimplified, hypothesis for head movement control.
HCLS is a control structure in which the different subparts are driven according to their own subgoals, but the most distal part is driven only by the global goal. Feedback from all subparts ensures the accuracy of the overall task goal. Although the HCLS architecture is relatively simple, further complexity must be incorporated here to apply it to a biological system with known neuroanatomical connections. These details are necessary for modeling data from experiments that directly disrupt the brain (e.g., lesions). Even if this complicates the presentation, it has the advantage of showing the efficacy of HCLS for a biological system of great interest to both scientists and clinicians. Furthermore, it provides an example where controllers for different parts interact to achieve improved performance.
1.1 Vestibular drive suppression
An important difference between head-restrained and head-unrestrained gaze movements is that head movements also move the eye in space (i.e., they are linked), and thus interfere with attempts to fixate a target. When unintended head movements (i.e., perturbations) occur, this interference is counteracted by the very short latency vestibuloocular reflex (VOR), which stabilizes gaze when the head is moving. The basic function of the VOR is to send an eye velocity command equal in amplitude (i.e., gain of one) but opposite in direction to the head’s velocity. However, during a large gaze movement (requiring a combined eye and head movement) the VOR would be counterproductive, as it would cancel the eye part of the gaze command. To avoid such opposition, the gain of the VOR is reduced (suppressed) during head-unrestrained saccades with amplitudes more than 40° (e.g., Cullen et al. 2004; Lefèvre et al. 1992; Laurutis and Robinson 1986; Tomlinson and Bahra 1986b). (The lack of suppression of the VOR for smaller saccade amplitudes follows from the fact that the relatively slow head makes very little contribution to small gaze changes). Laurutis and Robinson (1986) pointed out that even though the VOR was not active in these movements, the brain still knew how far the head had turned (because the gaze movement remained accurate). Thus, another system, which they called the vestibulo-saccade reflex (VSR), must have been keeping the gaze movement accurate (Laurutis and Robinson 1986). Here, we propose a more detailed description of the VSR, based on ideas from Cullen’s group (Cullen et al. 2004; Cullen and Roy 2004).
One of the interesting features of VOR suppression is that it is specific to the axis along which the gaze change occurs. Thus, a horizontal gaze saccade suppresses the horizontal VOR, but not the vertical VOR (Tomlinson and Bahra 1986b). The suppression of the VOR may be mediated through the position-vestibular-pause (PVP) neurons of the vestibular system (Roy and Cullen 1998). Most PVP cells pause during ipsilateral head rotations, but interestingly about 22 % also pause completely for contralateral rotations (Roy and Cullen 1998). Thus, it is not surprising that the VOR is suppressed during saccades for perturbations in the same and opposite directions (Laurutis and Robinson 1986).
1.2 Head drive suppression
Above we made the argument that the VOR would make gaze less efficient when the eye and head move in the same direction, and thus should be suppressed. However, If the VOR is suppressed in both directions during a gaze saccade, what is the effect when the eye and head move in opposite directions? Suppose that the eye and head do not start in an aligned position. For example, if the gaze is oriented to the left and the head is oriented to the right of straight ahead with the target located straight ahead, the eye will start far to the left in the head (eye = gaze - head). When the gaze movement is finished, the eye will be centered in the head and the head will be at 0°. Now, if the eye and head movements were independent, the head would move to the left, carrying the eye to the left, if the VOR is suppressed. But the eye has to go to the right, so the head movement has made the eye move farther to get on target. However, gaze could get on target sooner if the leftward part of the head movement is slightly delayed or slowed, so that the eye can move to the target first. The rest of the time that the head took to get to the target would occur while the VOR was on, and thus the eye would naturally counter-roll to its final position without disturbing vision. Thus, an argument can be made that part of the drive signal for the head should be suppressed, just as the VOR eye velocity command is suppressed when the eye and head move in opposite directions, so that a more efficient gaze movement can occur. We include such a mechanism here, whereby the SC output shunts part of the drive to the head, when the head and the eye move in opposite directions. This head drive suppression is one of the most novel predictions we make in our new model.
1.3 Classic gaze control models
Previously, two types of mechanisms were proposed to model gaze behavior. In the first (Fig. 1a), a gaze feedback loop drives both eye and head based on gaze motor error and compensates for any perturbations during saccades (Galiana and Guitton 1992; Lefèvre and Galiana 1992). These models can only generate a head movement along the gaze direction (see below), because a separate head goal is not included. Additionally, its neural structure (based on the superior colliculus) can not explain how it is possible to make accurate saccades (albeit with longer latencies and lower peak velocities) after superior colliculus (SC) lesions (Schiller et al. 1979, 1980; Aizawa and Wurtz 1998; Quaia et al. 1998).
Fig. 1.
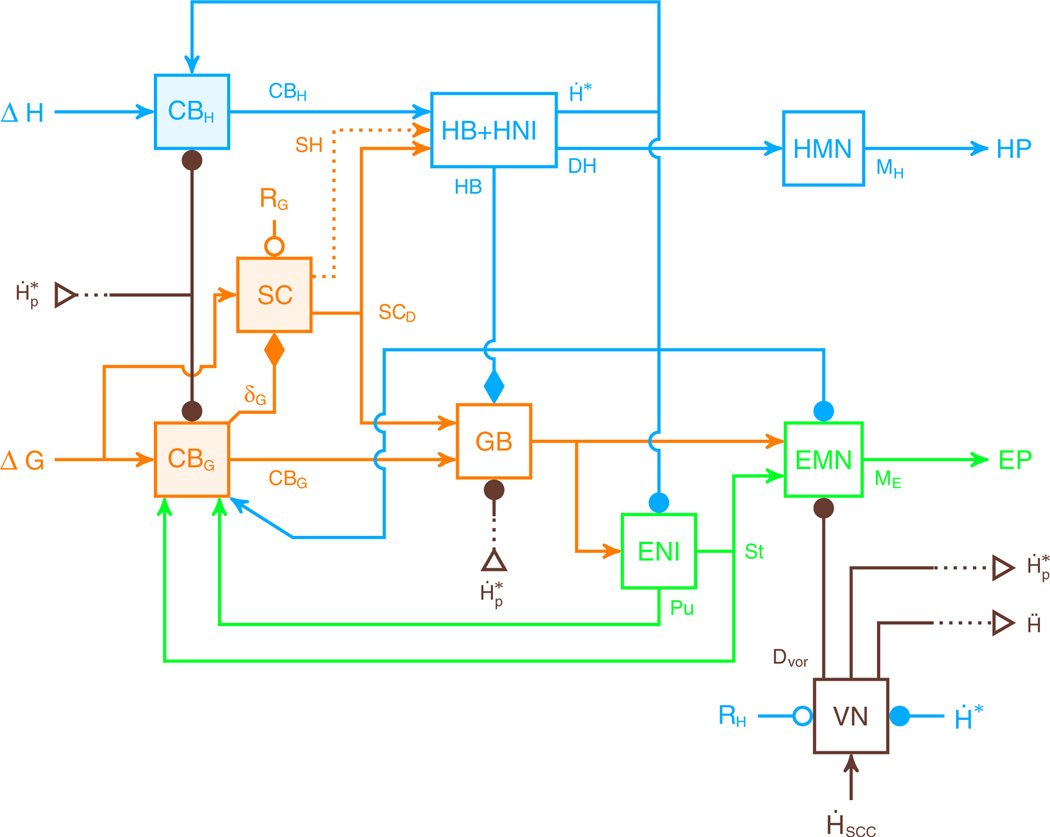
Schematic representation of head unrestrained gaze saccade control schemes. a represents the organization of gaze feedback models. The desired gaze displacement (ΔG) is compared to the actual gaze displacement, and the error causes the superior colliculus (SC) to send a common motor command to the eye and the head (Galiana and Guitton 1992). b represents the feedforward mechanism of Freedman (2001, 2008). The desired gaze displacement is sent to the SC, which sends separate commands to the eye and the head controllers. An inhibition proportional to the head velocity is sent from the head controller to the eye controller (dashed line in panel b) to modulate the maximum eye velocity as a function of the head velocity. c represents the proposed new architecture, based on the concurrent action of three parallel drive pathways head cerebellar pathway CBH, gaze cerebellar pathway CBG and collicular pathway, SC. Orange items represent parts of the models with a discharge related to gaze displacement. Blue items represent structures with a discharge related to head movements. Green items represent parts of the models with a discharge related to eye movements. In this figure, circles with a capital sigma (∑) represent summing operators. Arrowheads correspond to excitation and filled circles correspond to inhibition
In the second mechanism (Fig. 1b), a central gaze controller pre-computes separate desired eye and head displacements to execute a gaze movement (Freedman 2001, 2008). The only interaction between eye and head pathways during gaze shifts is a modulation of the eye-in-head velocity by the head velocity (represented by the dashed line with filled circle tip in Fig. 1b). This model can generate loosely dependent head and gaze trajectories. However, it does not use gaze feedback, and thus can not compensate for all head perturbations (see below). This model also lacks head position feedback, and thus can not guarantee that the head gets on target.
These early models dealt separately with the two key aspects of gaze control: how to make accurate eye and head movements, and how to compensate for perturbations. Unfortunately, neither model alone can solve both problems. Furthermore, many secondary issues have been raised, such as how the brain subdivides the gaze movement into eye and head contributions, and how the system is affected by chemical lesions in specific anatomical structures. We will now give a brief overview of some of the other models that have been proposed. However, none of them addressed all of the empirical studies in a single model, and none proposed a structure that could be easily generalized to the control of linked systems with more parts. We will then present a new, general model that accounts for the key elements, and some of the secondary elements, of gaze control (Fig. 1c). The purpose of this new model is thus to incorporate many experimental results into a single model, and to make predictions about novel effects on behavior that can be tested experimentally.
1.4 Models without head feedback
Moschovakis’ group studied a model of the gaze control system that does not use gaze feedback (Kardamakis and Moschovakis 2009; Kardamakis et al. 2010). The output of the head velocity command couples into the eye’s burst generator, so it has something in common with the model in Fig. 1b. The earlier (lumped) version of their model (Kardamakis and Moschovakis 2009) is not related to the known anatomy (it is a coupled system of four ordinary differential equations). In a later version (Kardamakis et al. 2010) the model has subparts that are related to brain stem anatomy. Kardamakis et al. (2010) showed the simulation of a head-unrestrained main sequence but the simulated relationships are not close to the known data (compare Fig. 6 in Kardamakis et al. 2010 with data from Freedman and Sparks 1997; Gandhi 2012). This issue will be elaborated in the Results section. Finally, they do not show that this model can compensate for head perturbations. Instead, they argue that their model should compensate for perturbations, because they have a neural integrator in the head controller, which would eventually bring the head on target. However, this statement is misleading, because any such compensation would have the time course of their head plant. The results of Sylvestre and Cullen (2006) show that after a brief head brake is applied, the head movement recovers with a time constant of much less than 100 ms. Furthermore, Boulanger et al. (2012) showed that when long duration torques were applied to the head, the head could get on target even before the torque ends. As the model of Kardamakis et al. (2010) used a plant with two time constants (105 and 181 ms) and no head feedback, their model could not reproduce either of these head perturbation studies because the fastest recovery would have a time constant of 105 ms. Exactly the same criticism applies to Freedman’s model (Freedman 2001). Note that this perturbation problem is not shared by models that use gaze feedback (e.g., Laurutis and Robinson 1986). However, common gaze feedback models can not account for the fact that gaze speed is reduced during head-unrestrained saccades (Freedman and Sparks 1997), whereas the coupling models do reproduce such a modified main sequence.
1.5 Two-dimensional control
Most previous models have dealt with gaze control in 1-D. However, this may be an oversimplification, because some aspects of eye-head interaction, such as the modulation of the VOR in directions not along that of the gaze movement, can not be addressed by a 1-D model. An early study modeled 3-D gaze control (Tweed 1997). Tweed’s model used separate eye and head feedback controllers, with a saturation on the eye controller to keep the eye within the limited oculomotor range (OMR ≈ 30–40°). Both eye and head were driven with dynamic gaze error, but the head had another control input, allowing independent goals for gaze and head (as in Fig. 1c). The VOR in this model was also turned off during the gaze saccade. This model works well, and accounts for Donder’s and Listing’s law for the head and eye, respectively. However, it does not relate parts of the model to anatomical structures, it does not deal with the dynamics (i.e., main sequence) of the movements, and it does not examine the rejection of head perturbations. We propose a 2-D model that treats the VOR differently along the direction of the saccade and orthogonal to it, attempts to make correlations between the model parts and brain anatomy, and reproduces the gaze main sequence. Three-dimensional properties are important for the eye, because of their high speed. However, A full 3-D model is not necessary here, because the muscles pass through pulleys before inserting on the globe, allowing the brain to treat eye movements as if they were two-dimensional for purposes of suppressing post-saccadic drift (Quaia and Optican 1998). Three-dimensional properties of the head may be ignored because their low speed mitigates the problem of post-saccadic drifts. (Details of the 3-DVOR itself are outside the scope of this paper, and extension of this model to 3-D awaits further work).
Another model that simulated 2-D gaze saccades was proposed by Goossens and van Opstal (1997). That model included feedback of the gaze orientation, but no separate goal for the head (so it is similar to the model in Fig. 1a). The partial separation between the eye and head was achieved using independent gating and separate feedback loops for the eye and the head. The authors used the same architecture for both horizontal and vertical controllers. How the VOR was modulated was not specified. This model was built to simulate 2-D head-unrestrained gaze saccades in which gaze and head could move in opposite directions. One of their experimental findings was that when the eye and head started from different locations, the initial direction of the head could be influenced by the required initial gaze direction (Fig. 13 of Goossens and van Opstal 1997). In other words, the initial head movement was not toward the target. Thus, this model is strictly functional, neglecting most of what is known about the anatomy and dynamics of the system. Finally, the model was not used to test other key aspects of head-unrestrained gaze saccades (e.g. large amplitudes and rejection of perturbations).
1.6 Recent results
In the last decade more studies have discovered new features of how the brain controls gaze. So far, none of these new observations have been modelled. Gandhi’s lab found that electrical stimulation in a region of the brain stem containing omnipause neurons (OPN), which pause for saccades in all directions, interrupts both eye and gaze movements, but not head movements (Gandhi and Sparks 2007). They also found that inactivation of the SC reduces gaze velocity but increases head velocity (Walton et al. 2008). Later, they showed that the firing rate of horizontal premotor burst neurons was more closely related to gaze velocity than eye velocity (Bechara and Gandhi 2010).
Recently, Gandhi (2012) showed that the velocity profiles of gaze and eye movements were affected by eye blinks. During a normal gaze movement without a blink, eye and gaze velocities are smooth, single-peaked traces. When the gaze movement is accompanied by a blink, the eye and gaze velocities become double-peaked. This is a particularly interesting finding, because previous literature shows either single-peaked (Boulanger et al. 2012; Choi and Guitton 2006; Guitton and Volle 1987a) or double-peaked (Freedman and Spark 1997, 2000) traces. We infer from Gandhi’s study that double-peaked velocity traces may not be a normal feature of eye-head coordination. Thus, our model produces single-peak velocities, and leaves for future development an interaction with the eyelid blink system.
Finally, Boulanger et al. (2012) have shown that long duration torques (up to 700 ms), which oppose or assist intended head movements, can be compensated even before the torque ends. This would not be possible for any head control model without some feedback information about head displacement. We regard this as a definitive experiment proving the existence of feedback control of the head, thus justifying our decision to generalize our earlier model of the feedback control of the eye to the feedback control of head movements.
1.7 Dual-pathway control of gaze with cerebellar feedback
Our new model extends our earlier work on eye-saccade control (Lefèvre et al. 1998; Quaia et al. 1999; Optican and Quaia 2002; Optican 2005) in two ways. First, the model controls gaze displacement, whereas in the original model it controlled eye displacement. Second, the new model adds a similar controller for the head. Our earlier model uses a dual-pathway controller for saccades, i.e., there are two drive commands, one from the SC and one from the cerebellum. The dual-pathway idea is well established experimentally (Schiller et al. 1979, 1980), although few models have included both pathways (Fujita 2005; Lefèvre et al. 1998; Quaia et al. 1999; Optican and Quaia 2002; Optican 2005). Instead, models either do not specify anatomical locations for their elements, or they have a colliculo-centric organization, with the saccade drive coming from the SC, and the cerebellum acting only as a side path controlling gain (e.g., Schweighofer et al. 1996; Scudder et al. 2002). We have chosen to include the dual-drive architecture in our model, where it will arise naturally in the gaze controller. Furthermore, it has been argued that a good candidate for the second drive is the cerebellum (cf. Lefèvre et al. 1998). This new model uses the old cerebellar dual-pathway for eye control to control gaze, and adds a new cerebellar controller for the head. There is no feedback controller for the eye (i.e., the model cannot specify a goal for the eye itself). Here, we justify our decisions to use feedback through the cerebellum and to use a dual-pathway controller for the head.
Several arguments are commonly given for ruling out a role in the feedback pathway for the cerebellum. However, all of these have one thing in common, they account for feedback action through some other (usually brain stem) feedback loop. Thus, they can not account for the effects of cerebellar and superior collicular lesions. First, accurate saccades can be made after SC lesions following a few days of recovery time, albeit with a reduction in peak velocity and an increase in latency with the head fixed (Hanes et al. 2005; Quaia et al. 1998) or free to move (Walton et al. 2008). Also, there is no doubt that cerebellar lesions result in saccadic dysmetria (Optican and Robinson 1980). Indeed, long- and short-lead burst and burst-tonic activity linked to saccades has been recorded on mossy fibers projecting to the oculomotor parts of the cerebellar vermis (Kase et al. 1980). Furthermore, the midline cerebellum is known to project to the brain stem burst generator (e.g., Robinson et al. 1993). Nonetheless, Scudder et al. (2002) “envision a role for the cerebellum in which the feedback is much weaker than is typically assumed in models of saccade generation. Therefore, most of the work required to produce accurate saccades falls upon feedforward mechanisms”. In fact, there is no evidence that their idea about relative feedback strength is correct. Furthermore, if the cerebellum is not in the feedback path, then there is no way to explain the effects of cerebellar lesions on saccades, or preservation of saccades after SC lesions. Thus, their assumption does not provide a reason for ruling out a feedback pathway through the cerebellum.
Another criticism of the dual-pathway model is that gaze saccades evoked by electrical stimulation in the SC stop before the end of the electrical stimulation, even though the caudal part of the fastigial nuclei (cFN) had been lesioned (Guillaume and Pèlisson 2001). However, this ignores the basic fact that, for example, the ipsilateral movements were actually quite hypermetric, i.e., they did not get on the target. Many mechanisms could stop a saccade, such as fatigue in the latch circuit that holds off the OPNs, thereby allowing them to restart and stop the saccade. Importantly, only a feedback mechanism can guarantee that a saccade gets on target. Thus, the cFN lesion experiments, although in detail quite complicated, clearly reiterate the simple finding that without an intact cerebellum the eye does not land on the target. As the cerebellum is the only place we know of where lesions prevent the saccade from getting on target, it seems reasonable to assume that it lies in the feedback path.
Finally, Kato et al. (2006) electrically stimulated the predorsal bundle (PDB), which carries the output fibers from the SC, and concluded that the horizontal saccadic burst system was located downstream from the SC. Although they imply that the cerebellum is not in the feedback pathway, the PDB projects to the NRTP, which projects to the cerebellum. Indeed, the authors conceded that the dual-pathway model was not ruled out by their study, but they ruled it out by citing the specious argument made by Scudder et al. (2002). We have already shown that those arguments do not rule out a feedback role for the cerebellum (see above). Kato et al. (2006) say that “it is parsimonious to conclude that saccades evoked in response to the electrical stimulation of the cerebellum are due to the engagement of the same circuit that is responsible for the generation of saccades after PDB, SC and possibly cortical stimulation as well, i.e. a burst generator located downstream of all these structures in the brainstem”. Despite its appeal, parsimony alone can not rule out the possibility that the saccadic feedback pathway closes through the cerebellum (whose output is in parallel with a drive from the SC).
The dual-pathway model proposed earlier (Lefèvre et al. 1998; Quaia et al. 1999; Optican and Quaia 2002) already provides a satisfactory explanation for all of these results. It is up to carefully designed experiments to rule out the possibility that the cerebellum is in the feedback loop, determining the context-dependent goal of saccades, keeping track of and steering saccade progress, and stopping the saccade when required. As argued above, we are unaware of any compelling experimental evidence that can rule out this model structure.
1.8 Dual-pathway control of the head
Even if the cerebellar feedback control of gaze is on firm ground, we still need to address the question of how to justify the dual-drive controller for the head. It is beyond the scope of this paper to review all the literature on this topic. Instead, we will address three key points that apply to all models of head control. First, there must be some reflex action through the spinal cord. Second, the head must be under feedback control. Third, the cerebellum must be involved in that control.
The importance of spinal cord reflexes in head movement control has long been recognized (Viviani and Berthoz 1975; Peng et al. 1996). Freedman (2001) used an internal model of the head and a reafference comparator to mimic the neck reflex model of Peng et al. (1996). Such a reflex can compensate, to some extent, for externally applied forces but is not sufficient to compensate for long duration perturbations. Freedman showed, with a simulation, that the neck reflex was enough to maintain gaze amplitude despite a short-duration perturbation of the head (his Fig. 9, Freedman 2001). He argues from this that gaze feedback control may not be necessary, although his simulation could not rule that out. In our model, we also have a spinal cord controller, which is used to compensate for the head plant dynamics (see below), but that is not sufficient to compensate for long duration perturbations
The next question is whether or not the head movement is itself under position feedback control. In other words, is the amplitude of the head movement maintained after head perturbations? We think a recent study gives a definitive answer to this question. Boulanger et al. (2012) applied small torques of long duration to the head during gaze changes. Those torques could either assist or oppose the intended head motion. They found that the amplitude of both the gaze and the head were well controlled. Furthermore, the head could accurately reach its goal even if the torque outlasted the head movement. The authors concluded that such gaze accuracy could not be achieved by models (e.g., Freedman 2001; Kardamakis et al. 2010) that do not include gaze feedback control. A similar argument applies to head reflex models, because a spinal cord reflex (presumably unaware of the head’s goal) could not compensate for a long-duration torque that outlasted the duration of the head movement command. Thus, we regard this experiment as definitive proof that the head is under feedback control.
The final question is: where is the head feedback controller? A full review of the head control literature is not possible here, but suffice it to say that we are unaware of any models that explain both the dynamics and anatomy of head control. Some pathways are well known, such as projections from medullary nuclei to the spinal cord, and from the SC and cerebellum to those medullary nuclei, but full details of how these areas interact are not known. Most critically, the part of the circuit that processes the feedback signals is not known. The feedforward pathways involved in head control have been extensively studied (for a review see Isa and Sasaki 2002). In summary, neurons in the nucleus reticularis gigantocellularis (NRG) and nucleus reticularis pontis caudalis (NRPC) project to neck motor neurons controlling horizontal head turning. Lesions of the NRPC and the NRG impair rapid head turning toward the ipsilateral side. These neurons receive monosynaptic excitation from the contralateral SC, and permanent lesions of the cat’s SC severely impair head turning to the contralateral side (Isa and Sasaki 2002). Cerebral areas also project to the NRG and NRPC, but as the latency through the cortex is presumed to be long, we do not consider this pathway as important for head feedback. We assume it is involved in determining the desired head displacement.
The medial cerebellum (vermis and fastigial nuclei) is involved in head movements, which is interesting because the vermis (and its projection area, the caudal fastigial nucleus, cFN) is also involved in eye and gaze movements. Pèlisson et al. (1998) found that after muscimol injections into the rostral fastigial nucleus (rFN) gaze and head movements became hypermetric to the same side, and hypometric to the opposite side. This is the same effect that cFN lesions have on gaze and head movements (Goffart and Pèlisson 1998). Importantly, it is not just gaze that fails to reach the target after cFN lesions, the head also does not reach the target (Goffart and Pèlisson 1998; Goffart et al. 1998b; Pèlisson et al. 2003). Intraoperative microstimulation of the cerebellum of human patients (Mottolese et al. 2013) found a topographically organized motor representation, with neck muscles responding to stimulation of the declive (vermal lobule VI), which those authors ascribed to feedback control. These results strongly support the hypothesis that control of both gaze and head uses feedback through the cerebellum.
One argument sometimes raised against the use of cerebellar feedback is based on experiments that chemically lesion the cFN and then electrically stimulate the SC to displace gaze before a visually guided saccade (Goffart et al. 1998a; Pèlisson et al. 2003). If the cFN is inside the feedback loop (Lefèvre et al. 1998; Quaia et al. 1999), the argument is that the lesion breaks the loop, and thus the saccade can only get on target using an open-loop mechanism. Their reasoning follows that of an experiment wherein electrical stimulation of the SC displaced the eye before a head-restrained saccade, and yet the saccade to the target was accurate (Mays and Sparks 1980). The problem with this reasoning is that displacing the eye or gaze by electrically stimulating the SC is not the same as compensating for a head perturbation made during the movement. As is clear from their data (cf. Fig. 2 in Goffart et al. 1998b), the gaze first fixates, then is driven to a new position by the electrical stimulation. After a period of time (about 150–200 ms) another movement is made that is accurate (or, in the cFN lesioned case, has the same final error as the unstimulated movement). However, all this proves is that the brain knows that the gaze was moved by the stimulation, and when the new goal is calculated, it is done relative to the correct starting position. (There is an extensive literature on how the cortex may update or remap goals (e.g., Duhamel et al. 1992), but that is outside the scope of this paper).
When analyzing this example, it is important to remember that there are two integrators in the classic saccadic system (Robinson 1975; Jürgens et al. 1981). One of the integrators is in the feedback pathway of the motor controller, and keeps track of how far the eye has moved since the saccade started. This is called the displacement, or resettable, integrator, because it resets before each movement. The other integrator, called simply the neural integrator, is in the feedforward path. It provides the tonic innervation needed to hold the eye at its final position against the elastic restoring forces in the orbit. The output of that integrator is thus proportional to the eye’s current position, and it is often called the efference copy of the eye position. Thus, the SC lesion experiment says nothing about the details of the feedback control of movements, because the knowledge of the current position is already available, as the efference copy from the neural integrator, when the new movement goal is chosen.
1.9 A new gaze control model
A successful model of gaze control must accomplish three key things. First, it must be physiologically plausible, i.e., it must make use of known anatomy and physiology, and to some extent, it must account for degraded performance after lesions of its structure. Second, it must account for as much of the known experimental evidence as possible, i.e., it is not a good idea to have a separate model for each set of data. Finally, it must make some predictions that can be tested experimentally to falsify the model. As we will see below, none of the currently available models of gaze control can meet all of these criteria. We propose here a new model, which, although somewhat simplified,1 can still make that claim. Note that all the models are built from the same anatomical knowledge of brain connections, so one can not expect them to have wildly different structures. However, subtle questions arise about how the different structures in these models interact, and it is these interactions that give a model its unique character. Here we also are careful to consider the frame of reference (eye, head or gaze) for all the signals, so that they can be experimentally tested. Finally, we argue that the HCLS model is a novel paradigm that can be applied to other linked systems, of any depth. Thus, the paradoxical lack of an eye movement controller in our model is a feature of a wider class of control systems, which we would expect to see incorporated into other biological linked systems (e.g., foot-leg-thigh-hip or hand-forearm-arm-shoulder).
2 Models
2.1 Notations
These notations are used throughout the description of the model:
| β | Scalar |
| A | Vector |
| Ah | Horizontal component of vector A |
| Aυ | Vertical component of vector A |
The amplitude of a vector is defined by:
The dot product results in a scalar number and is denoted:
The cross product result is a vector. However, in this study, only the amplitude of the cross product is used and is computed:
The saturation of a signal X between a lower boundary L and an upper boundary U is defined as:
Where equations of motion for both gaze and head are the same, the equation is given once with the index k, which may be replaced by either G for gaze or H for head. Values for all the parameters used in the equations are presented in Table 1.
Table 1.
Model parameters: monkey
| γG | 0.98 | γH | 0.95 | |
| αC,G | 0.5 | τC,G | 55 | |
| ζC,G | 5 | ξC,G | 0.3 | |
| βC,G | 3 | αC,H | −0.7 | |
| τC,H | 45 | ζC,H | 4.5 | |
| ξC,H | 2.0 | βC,H | 1 | |
| TΔG,‖ | 0.0075 | KΔG,‖ | 30.0 | |
| TΔG,⊥ | 0.2 | KΔG,⊥ | 2.0 | |
| ΨΔG,‖ | 1.0 | ΨΔG,⊥ | 1.0 | |
| KΔH,‖ | 0.07 | ϒΔH,‖ | 3.5 | |
| TΔH,‖ | 0.06 | KΔH,⊥ | 2.0 | |
| TEB | 0.01 | 700 | ||
| K0 | 900 | TK | 0.03 | |
| TE,1 | 0.135 | TN | 0.02 | |
| TE,2 | 0.726 | TH | 0.3 | |
| TE,Z | 0.615 | BVN | 900 | |
| αSC,G | 1.0 | αSC,H | 0.02 | |
| G0 | 40 | G1 | 25 | |
| μgh | 30.6 | ϕgh | 600 | |
| τmax,g | 0.021 | τmin,g | 0.001 | |
| Kgh | 5/35 | 400 | ||
| TSC | 0.005 | βsc | 145.5 | |
| γsc | −60/55 | TH,B | 0.03 | |
| Gsh | 2 | Δsh | 0.25 | |
| αr | 0.0025 | βr | 0.2 | |
| KEB | 1.1 |
Model parameters for monkey simulations. This table presents values for all the parameters used in the simulations that reproduce monkey behavior
2.2 Simulation methods
We chose a lumped approach instead of a distributed model to reduce the number of parameters. This approach emphasizes the general properties of the control architecture. Each part of the model will be described using ordinary differential equations (ODEs). The main goal is that each component of the model behaves functionally like the neuronal area it represents, even if it is not always easy to match neuronal firing rates to states in the model.
All the simulations reported in the present paper were performed on a personal computer using the python programming language. The ordinary differential equations are presented in continuous form for the sake of clarity. However, before simulation they were first transformed into a continuous state-space representation (Nth-order ODEs were transformed into a set of N, first-order ODEs). Then, the continuous state-space representation was discretized using a bilinear transform (also called Tustin’s method) with a fixed time step of 0.2 ms (Corriou 2004).
2.3 General architecture
The key components of the new model are given in Fig. 2. The basic structure is an extension of the dual pathway model of head-restrained saccades by Lefèvre et al. (1998) and Quaia et al. (1998) (NB: Our model does not include the cerebral cortex, which is assumed to select the desired gaze and head goals). The proposed circuit for the control of head-unrestrained saccades is a multi-input multi-output (MIMO) control system. It has two inputs: the desired gaze displacement (ΔG) and the desired head displacement (ΔH) and two outputs: the drive sent to the eye muscles (EP) and the drive to the neck muscles (HP). Based on the anatomy, the model includes two pathways to control gaze: one through the superior colliculus (SC) and one through the cerebellum (CBG). There are also two pathways to drive head trajectories (SC and CBH). This novel architecture is thus based on the interactions between two separate feedback controllers: one dedicated to the gaze trajectory and one dedicated to the head trajectory. Importantly, there is no controller for the eye trajectory. Because the head movement is fed back to both the gaze and the head controllers, and the gaze cerebellar controller influences the head trajectory, the new architecture has a hierarchical structure. In the following paragraphs mathematical descriptions of each part of the model are given. Finally, all the areas related to vision in our model, from the retina to the superior colliculus and the cerebellum, are vectorial (their activities are described as an amplitude and an orientation). The division into horizontal and vertical components only arises downstream, in the motor neurons and muscles.
Fig. 2.
New model structure. The model includes three major pathways. Two receive the desired gaze displacement (ΔG) as input: one goes through the superior colliculus (SC) and projects to gaze- and head-related bursters, and one goes through one part of the cerebellum (CBG and orange items) and projects only to gaze-related neural areas. The third pathway (CBH and blue items) has the desired head displacement as input (ΔH); it goes through another part of the cerebellum and only projects to head-related neural areas (NRPC, NRG and HNI). The SC sends a collicular drive in the direction of the desired gaze displacement to both eye and head, but it does not control gaze trajectory. Additionally, the SC sends a collicular shunt to the head bursters (SH, orange dashed line). CBG is the core of the gaze controller; it sends a drive to eye-related neural areas to control gaze trajectory. It also sends a facilitation signal, δG, that mediates the collicular level of activity as a function of the gaze motor error (orange diamond). CBH controls head trajectory and sends a drive to the head-related neural areas. Brown items represent model elements related to head perturbations. Orange items represent parts of the model with a discharge related to gaze displacement. Blue items represent structures with a discharge related to head movements. Green items represent parts of the model with a discharge related to eye movements. In this figure, lines with arrowheads correspond to excitation, lines with filled circles correspond to inhibition, lines with filled diamonds correspond to facilitation, and lines with open circles correspond to reset signals. Open triangles represent cross-page connections. EP eye plant. HP head plant. GB gaze bursters. NRG nucleus reticularis gigantocellularis. NRPC nucleus reticularis pontis caudalis. HNI head neural integrator. ENI eye neural integrator. EMN eye motoneurons. HMN head motoneurons. VN vestibular nuclei. For other details see text
2.4 The superior colliculus
The model of the superior colliculus is a first order transfer function (time constant: TSC) with two inputs: the neocortex gives the desired gaze displacement (ΔG) and the cerebellum gives a disfacilitation signal (δG, see Eq. (12)). The colliculus produces two outputs: an excitatory drive (SCD) that goes to both the head and the gaze bursters, and our hypothesized directional shunt (SH(ΔG)), which modulates the activity of the head bursters. The amplitude of the collicular discharge is modulated by a gain (KSC[ΔG]) that is a linear function (gain: γsc, bias: βsc) of the amplitude of the gaze displacement:
| (1) |
Then, the output drive of the superior colliculus is computed as:
| (2) |
and the directional shunt is computed as:
| (3) |
Equation (3) shows that the directional shunt corresponds to the evolution of the gaze facilitation signal (δG) along the gaze direction . It represents the decay of activity in the superior colliculus.
2.5 Gaze and head displacement cerebellar controllers
The new model includes two similar cerebellar controllers: one for desired gaze displacement (ΔG) and the other for desired head displacement (ΔH). The following paragraphs describe their equations.
2.5.1 Error computation
To control head and gaze trajectories, both controllers compute the current error vector (εΔk) with respect to the desired gaze (ΔG) and head (ΔH) goals. These signals will then be used to compute the appropriate drive sent to either the eye (to control the gaze) or the head (to control the head). First, each controller builds an internal estimate of either the current gaze (ΔG*) or the current head displacement (ΔH*):
| (4) |
| (5) |
Equation (4) represents an internal estimate of the current gaze displacement and Eq. (5) represents an internal estimate of the current head displacement. Ė* (Ḣ*) represents an efference copy of eye-in-head (head) velocity, tG0 (tH0) corresponds to the onset of the gaze (head) movement and tGF (tHF) corresponds to the offset of the gaze (head) movement. The last term of Eq. (4) represents the head displacement not accounted for by the VOR along the gaze trajectory following a head perturbation (corresponding to the VSR (Laurutis and Robinson 1986), see Eqs. (54)–(58)). The second term of Eq. (5) represents an estimate of the head perturbation (see Eq. (54)).
Finally, the current gaze (head) error is evaluated as the difference between the desired gaze (head) displacement and the internal estimate of the current gaze (head) displacement:
| (6) |
| (7) |
2.5.2 Controller architecture: error decomposition
To compute their output drive, both controllers decompose the current error (εΔk) into a component parallel to the desired trajectory (εΔk,‖) and a component normal to the desired trajectory (εΔk,⊥), see Fig. 3:
| (8) |
| (9) |
| (10) |
| (11) |
Equation (8) represents a unit vector parallel to the direction of the desired displacement and Eq. (9) corresponds to a unitary vector normal to the direction of the desired displacement (reminder: k indices can be replaced by either G or H for the gaze or the head component).
Fig. 3.
Error decomposition. Dark arrows show the decomposition of vector error into channels implemented in the gaze cerebellar controller. G0 corresponds to the initial gaze position. GF is the desired final gaze position. εΔG corresponds to the current gaze error. εΔG,‖ is the projection of the error along the desired initial gaze displacement (the vector from G0 to GF). This corresponds to the remaining gaze displacement along the desired displacement (dashed line). εΔG,⊥ corresponds to the perturbation with respect to the desired gaze displacement. A similar decomposition has been implemented for the control of the head trajectory
2.5.3 Controller architecture: reset signals and gaze facilitation signal
To signal the end of the movement, a reset flag is computed for the gaze (RG) and the head (RH). Those signals are computed by comparing the ratio (δk) between the amplitude of the current displacement and the desired displacement with a fixed scalar threshold (γk):
| (12) |
| (13) |
γk was tuned once before simulations and kept constant for all the simulations. δG is also used as the gaze disfacilitation signal sent to the superior colliculus (see Eq. (2)) and used internally in the cerebellum.
2.5.4 Controller architecture: cerebellar choke
When the reset signal is activated, the movement must be stopped. To that goal, our model includes a choke signal (Lefèvre et al. 1998; Quaia et al. 1998). The choke will oppose the current drive to ensure the accuracy of the controlled movement. It is based on the ratio between the current gaze velocity and a function of the current error. Then, the choke is computed for the directions parallel and normal to the desired displacement:
| (14) |
| (15) |
| (16) |
The rational behind relationships (15) and (16) is that for the same velocity, a smaller error generates a larger choke to ensure that the movement ends close to the target. Similarly, for the same error, if the movement is faster, the choke will be bigger to ensure that the movement ends close to the target.
2.5.5 Controller architecture: gaze cerebellar drive
Signals from Sections 2.5.1–2.5.4 are then used to compute the gaze cerebellar drive along the direction parallel to the desired gaze displacement:
| (17) |
Equation (17) generates the drive needed to decrease the gaze error along the direction parallel to desired gaze displacement (εΔG,‖) until the gaze reset flag (RG) switches from 0 to 1. KΔG,‖ represents the constant gain of the parallel controller and TΔG,‖ represents the integration time constant of the parallel controller. ΨΔG,‖ is a gain used to modify the decay time of the activity when RG switches to 1.
The gaze cerebellar drive along the direction normal to the gaze displacement is computed as proportional+integral control of the gaze error normal to the direction of the desired gaze displacement (εΔG,⊥):
| (18) |
in Eq. (18), TΔG,⊥ represents the integration time constant and KΔG,⊥ represents the gain of the controller. As in (17), δG corresponds to the gaze facilitation signal. When the gaze reset flag switches to 1, this drive decays towards 0. The rate of decay is tuned by ΨΔG,⊥.
The choke normally acts downstream on the burst neurons to slow down the saccade at the end of the movement (Lefèvre et al. 1998; Quaia et al. 1999). Because our model is unilateral, this is equivalent to removing the value of the choke from the output of the cerebellum. Therefore, to simplify the representation of the gaze cerebellar activity, the vectorial output of the gaze cerebellar controller is computed as the combination of Eqs. (8)–(9) and (15)–(16) with Eqs. (17)–(18):
| (19) |
2.5.6 Controller architecture: head cerebellar drive
The head cerebellar drive parallel to the desired head displacement is a first order transfer function (time constant: TΔH,‖) with one zero and a constant gain (ϒΔH,‖) of the head displacement parallel error (εΔH,‖). It is computed as:
| (20) |
The head cerebellar drive normal to the desired head displacement is a proportional controller of the normal head displacement error (εΔH,⊥). The gain of the controller is the product of a constant factor (KΔH,⊥) with the head facilitation signal (internal cerebellar signal, not shown in the figures: δH). It is written as:
| (21) |
As for the gaze cerebellar controller, we combined the action of the head cerebellar drive and the head choke to compute the output of the head cerebellar controller. Therefore, the output of the head cerebellar controller is computed as the combination of Eqs. (8)–(9) and (15)–(16) with Eqs. (20)–(21):
| (22) |
2.6 Gaze burster neurons
The model used to represent the activity of the gaze burster neurons is based on the decomposition of the input activity into its horizontal and vertical components. The gaze burster’s input is computed as the sum of the gaze cerebellar activity (CBΔG) and the collicular drive (SCD) multiplied by a constant gain (αSC,G):
| (23) |
| (24) |
θG,in in Eq. (24) represents the orientation of the gaze input discharge. The amplitude of the discharge (‖BG, in‖) is then modulated by two gains. The first one, KVN, is used to represent the sensitivity of the gaze bursters to the activity of vestibular neurons (Sylvestre and Cullen 2006). The second, KH, is used to simulate the decay of the peak and average gaze velocity during head-unrestrained gaze shifts with an amplitude larger than 25° (Freedman and Sparks 1997; Gandhi 2012).
| (25) |
| (26) |
In Eq. (25), and K0 are burster parameters (see Table 1). The rational behind KH is that the gaze movement must be slowed down to ensure that the head starts its movement and contributes significantly to the gaze displacement before the end of the gaze saccade. Therefore, KH will be bigger and decay more slowly for large gaze shifts. KH is computed as:
| (27) |
| (28) |
In Eqs. (27)–(28), μgh, φgh, τmax,g, τmin,g, τgh and Kgh are the parameters used to tune the sensitivity of the gaze bursters to the head drive (‖HB‖). Finally, KVN is computed as:
| (29) |
with BVN the sensitivity to the vestibular activity, the head perturbation along the gaze trajectory (see Eq. (55)) and GVOR,‖ corresponds to the VOR gain (see Eq. (57)).
Then, the gaze burst discharge is decomposed into its horizontal and vertical components using:
| (30) |
| (31) |
2.7 Head burster neurons
The head burster neurons in the model are represented by a first order transfer function with a saturated input gated by a collicular shunt (see Eq. (3)). We added a shunt to the head bursters to reproduce the increase of peak head velocity when the colliculus is inactivated (Walton et al. 2008). The rationale behind the shunt comes from the observation that the gaze peak velocity decreases with increasing head-unrestrained gaze shifts while the peak head velocity increases (Freedman and Sparks 1997; Gandhi 2012). Therefore, the head must be slowed down to prevent it from going faster than the gaze. Otherwise, it would reflect on the displacement as a VOR signal because the eyes would roll back in the orbits. More details on the shunt will be given in the results section (see Section 3.5).
The activity of the head burster neurons are modeled through four steps. First we computed the input to the head bursters by combining the collicular activity from Eq. (2) with the head cerebellar activity from Eq. (22):
| (32) |
| (33) |
Second, the amplitude of this drive is multiplied by a recruitment gain function of the amplitude of the head displacement (Rr(ΔH)). This value is then saturated to represent the maximum discharge of the head bursters:
| (34) |
| (35) |
| (36) |
| (37) |
Then we applied the collicular shunt (SH(ΔG)) to the bursters activity B. Equation (38) computes the shunting gain along the direction parallel to the desired gaze displacement:
| (38) |
with:
| (39) |
Equation (39) computes the relative orientation between the collicular shunt and the desired head displacement (θ(SH(ΔG),H)). When the gaze and the head move in the same direction the shunting gain is minimal (θ(SH(ΔG),H) = 1). When the gaze and the head move in opposite direction the shunting gain is maximal (θ(SH(ΔG),H) = −1). Finally, the shunting gain is modulated by the relative current gaze displacement (with ‖SH(ΔG)‖).
The shunting gain along the direction normal to the desired gaze displacement is computed as:
| (40) |
As for Eq. (38), Eq. (40) shows that the shunting gain normal to the desired gaze displacement is proportional to the relative orientation between the collicular shunt and the desired head displacement. SH⊥,G is maximal when head and gaze desired trajectories are parallel and minimal when they are normal.
We combined these signals with:
| (41) |
| (42) |
Equations (41)–(42) project the head drive onto the direction parallel to the gaze displacement and the direction normal to the gaze displacement and apply the corresponding shunting gain to each component.
Then, Eq. (43) reconstructs the head drive in the horizontal-vertical reference frame:
| (43) |
Finally, each component from the drive of Eq. (43) is sent through a first order transfer function (time constant: THB) with a constant gain (KEB):
| (44) |
| (45) |
To maintain the head in an eccentric position, the discharge from the head bursters must be integrated. Currently, the interstitial nucleus of Cajal (INC) seems to be the best candidate to play this role for vertical and torsional head posture (Klier et al. 2002; Farshadmanesh et al. 2007). However, no studies have found a neural structure that plays the role of horizontal head neural integrator. Because no definitive answer has been provided yet concerning the head neural integrator, we simplified its function to its pure mathematical sense. Thus, the head drive Eqs. (44)–(45) is also sent to an internal neural integrator. Finally, we combined the action of the head burster with the output of the neural integrator to compute the drive sent to the spinal cord (DH):
| (46) |
| (47) |
2.8 Eye neural integrator
Studying head-fixed saccades, Robinson (1975) postulated the existence of a neural integrator to hold the eye at an eccentric position after a saccade. Using lesions, it has been shown that the complex medial vestibular nucleus (MVN)/nucleus prepositus hypoglossi (NPH) is a key structure to ensure gaze holding (Cannon and Robinson 1987; Cheron and Godaux 1987). McFarland and Fuchs (1992) reported a majority of NPH neurons in the monkey with a discharge that was modulated by a change in eye position but not when the monkey was canceling its VOR.2 Interestingly, Because during the cancellation of the VOR, the gaze is changing but the eyes remain fixed in the orbit, this study suggests that the discharge of those NPH neurons was correlated with eye-in-head position and not with gaze position. Recently, Dale and Cullen (2013) confirm that NPH neurons discharge with eye movements. Therefore, we modeled the neural integrator for the gaze pathway as an eye position integrator in our new architecture.
The model used for the eye neural integrator is an extension to head-unrestrained conditions of the head-restrained neural integrator of Optican (2009):
| (48) |
| (49) |
| (50) |
| (51) |
in which Ḣ* represents an internal estimate of the head velocity (see Eq. (62)), Pu is the pulse, St is the step, and Sl is the slide of innervation needed to generate tension in the eye muscles and prevent them from drifting at the end of the movement. TE,1 and TE,2 are the time constants of the eye plant model. TE,Z is the zero of the eye plant model (see section on eye plant below).
2.9 Eye motor neurons
To compute the activity of the eye motor neurons, we subtracted the internal estimate of head velocity (see Eq. (62)) from the output of the gaze bursters (see Eqs. (30)–(31)) to build an eye-related drive. Then we added the integrated output of the eye neural integrator (Step, see Eq. (49)). Finally, because a perturbation on the head will affect the accuracy of the head velocity estimate, we also included a drive from the vestibular nuclei (DVOR, see Eq. (58)) to compensate for the effect of the perturbation.
Therefore, the discharge of the eye motor neurons (ME) is modeled as:
| (52) |
2.10 Head motor neurons
The discharge of the lumped head motor neuron (MH) is modeled as a third order transfer function (a double time constant TN and a single one TK), with one zero (TH) that compensates for one of the head time constants (see section on head plant below). The input of the lumped head motor neuron model is the output of the head bursters (DH, see Eq. (47)). The head motor neuron’s activity is modeled as:
| (53) |
This model structure was chosen to reproduce the results from (Freedman and Sparks 2000), the time constants in Eq. (53) were tuned using system identification methods. The specific values of these time constants are not critical for the purpose of this paper. The choice of this model will not be discussed here, because this paper focuses on the interactions between the different feedback loops to control gaze and head trajectories. Details of the head plant model will be given in a subsequent paper.
2.11 Vestibulo-ocular reflex
The model of the vestibulo-ocular reflex (VOR) is based on the decomposition of the unexpected head movement into the direction parallel to the gaze displacement and the direction normal to the gaze displacement:
| (54) |
| (55) |
| (56) |
Tomlinson and Bahra (1986b) and Cullen et al. (2004) reported a reduction of the VOR gain when both gaze and head perturbation were horizontal, but a fully functional VOR when the monkey did vertical gaze saccades with a horizontal head perturbation. To explain those results, the compensatory gain in our model is assumed to be unity along the direction normal to gaze displacement and modulated linearly as a function of the amplitude of the gaze displacement for the direction parallel to the desired gaze trajectory. Supplementary experiments must be conducted to test the VOR gain as a function of the angle between the gaze and the head displacements.
VOR gain along the desired gaze trajectory is computed as:
| (57) |
with G1, the largest amplitude for which the VOR gain is unity and G0, the amplitude at which the VOR gain is equal to zero. Finally, the vector VOR drive is composed as:
| (58) |
2.12 Eye and head plant models
The input-output relationship between the innervation of the ocular muscles and the movement of the eye is modeled as a second order transfer function with three time constants (two poles and a zero, called the 2p1z eye plant model) as in Optican (2009). Therefore, the model of the eye plant is represented in the temporal domain by:
| (59) |
In Eq. (59), E corresponds to the eye-in-head position and ME corresponds to the drive sent to the eye plant (EP) by the eye motor neuron.
The relationship between the complex activation of the neck muscles and the resulting head movement is simplified by a second order transfer function with two identical time constants, as in Lefèvre and Galiana (1992). Thus the head plant is represented by the transfer function:
| (60) |
H corresponds to the head-in-space position and MH corresponds to the drive sent to the neck muscles (head plant).
We lumped agonist and antagonist muscles into one equivalent muscle for both eye and head plants, because the tension exerted by a pair of muscles can be approximated by a linear function of the difference in innervation between the agonist and the antagonist (Haustein 1989).
2.13 Internal head velocity estimator
Because of the dynamics of the head-neck system, the burster activity does not change the head movement instantaneously. Therefore, to estimate correctly head position and head velocity, the system needs a temporally accurate internal representation of the head plant.
The model has an internal forward model to estimate the head velocity from the activity of the head bursters (DH, Eq. (47)). It combines the head motor neurons Eq. (53) and the head plant Eq. (60):
| (61) |
| (62) |
2.14 Internal eye velocity estimator
As for the head, an efference copy of the drive sent to the eye is not sufficient to evaluate the eye position. Therefore, the model also includes an internal representation of the eye plant.
The model makes an estimator of the eye velocity using the output of the eye neural integrator:
| (63) |
3 Results
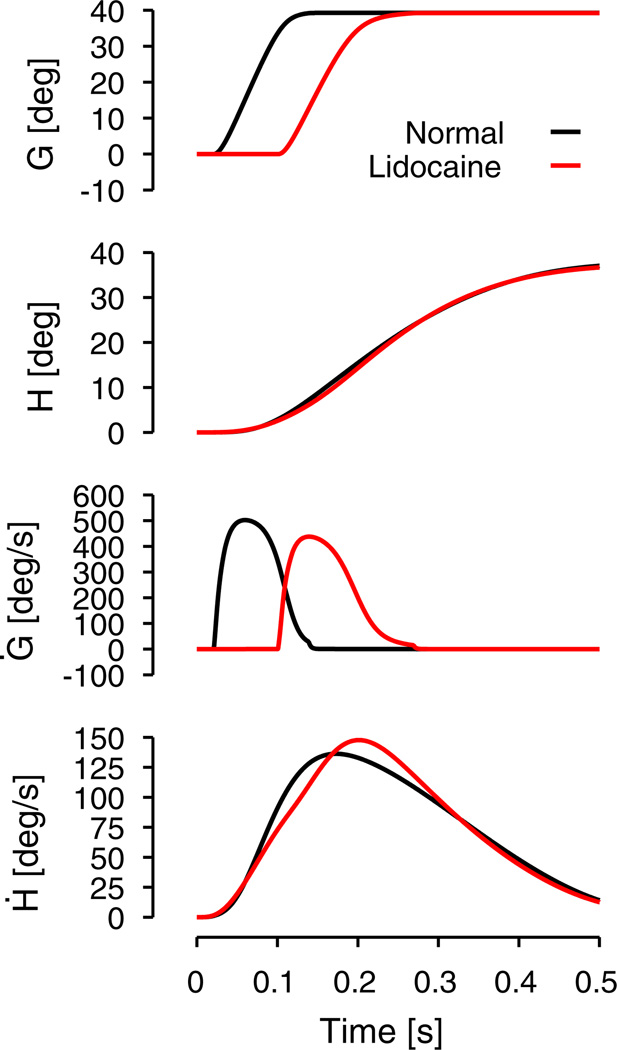
We will present simulations that emphasize the general behavior of the proposed hierarchical controller for linked systems (HCLS), as applied to gaze. First, we will show typical position and velocity profiles for gaze, eye and head for different gaze amplitudes. Next, we will show how the model reproduces the nine metrics of head-unrestrained gaze saccades, the so-called main sequence (Gandhi 2012; Freedman and Sparks 1997). Then we will discuss an example that presents the general interaction between the three loops (gaze, head, vestibular) of the model during an oblique gaze shift. We will then show how the model rejects perturbations and how it reproduces the results from Sylvestre and Cullen (2006). Finally, we will show how the model can explain why a localized inactivation of the superior colliculus by lidocaine can increase the peak head velocity (Walton et al. 2008). The first three simulations show the general properties of HCLS, while the two final simulations reproduce specific behavior determined by biological constraints on the gaze system. Two sets of parameters were tuned for the simulations: one set (Table 1) was used for simulations of monkey data (simulations 1, 2, 4 and 5) and a second set (Table 2) was used for simulations reproducing human behavior (simulation 3).
Table 2.
Model parameters: human
| γG | 0.98 | γH | 0.95 | |
| αC,G | 0.5 | τC,G | 55 | |
| ζC,G | 5 | ξC,G | 0.3 | |
| βC,G | 3 | αC,H | −0.7 | |
| τC,H | 45 | ζC,H | 4.5 | |
| ξC,H | 2.0 | βC,H | 1 | |
| TΔG,‖ | 0.0075 | KΔG,‖ | 30.0 | |
| TΔG,⊥ | 0.2 | KΔG,⊥ | 2.0 | |
| ΨΔG,‖ | 1.0 | ΨΔG,⊥ | 1.0 | |
| KΔH,‖ | 0.06 | ϒΔH,‖ | 3.0 | |
| TΔH,‖ | 0.065 | KΔH,⊥ | 3.0 | |
| TEB | 0.01 | 700 | ||
| K0 | 900 | TK | 0.03 | |
| TE,1 | 0.135 | TN | 0.02 | |
| TE,2 | 0.726 | TH | 0.3 | |
| TE,Z | 0.615 | BVN | 900 | |
| αSC,G | 1.0 | αSC,H | 0.01 | |
| G0 | 40 | G1 | 25 | |
| μgh | 30.6 | ϕgh | 600 | |
| τmax,g | 0.021 | τmin,g | 0.001 | |
| Kgh | 5/35 | 40 | ||
| TSC | 0.005 | βsc | 145.5 | |
| γsc | −60/55 | TH,B | 0.01 | |
| Gsh | 1 | Δsh | 0.125 | |
| αr | 0.0025 | βr | 0.2 | |
| KEB | 1.2 |
Model parameters for human simulations. This table presents values for all the parameters used in the simulations that reproduce human behavior
3.1 Family of horizontal gaze shifts
Figure 4 shows a family of head-unrestrained saccades simulated by the model with the monkey parameters. The desired gaze amplitude was set to 5, 10, 15, 20, 30, 40 and 50° and the corresponding desired head amplitude was set to 0, 4.5, 9, 14.5, 22.5, 31.5 and 41.5° (ΔH = 0.9(ΔG−5)). Because our model does not have a cortex that computes the desired gaze and head displacement as a function of the target position, we arbitrarily chose those values and used them as inputs of our model.
Fig. 4.
Family of simulated horizontal gaze shifts. Left column represents the time course of position and right column represents the time course of velocity for the gaze (first row), the eye-in-head (second row) and the head (third row) for different desired gaze saccade amplitudes (5, 10, 15, 20, 30, 40 and 50°). The corresponding desired head amplitude was set to (0, 4.5, 9, 14.5, 22.5, 31.5 and 41.5°). Peak eye and gaze velocity decline for large gaze shifts. Peak head velocity occurs later for large gaze shifts
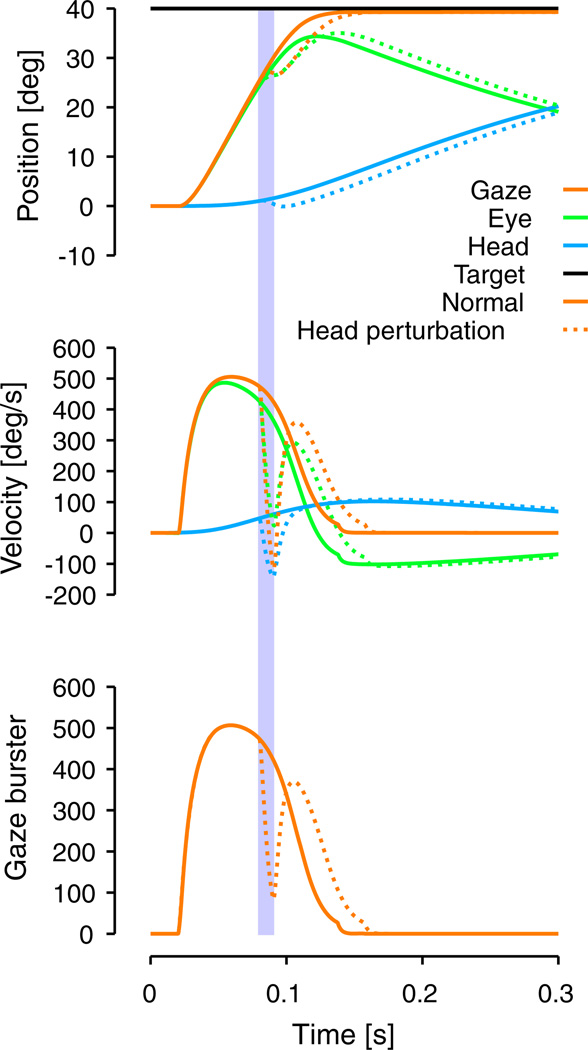
Numerous studies have shown that the latency of head movement with respect to the onset of gaze is not constant, e.g. using stimulations (Corneil et al. 2002) and behavior (Freedman and Sparks 1997). Because our model includes feedback loops to control head and gaze displacements, delay between head and gaze onset does not affect the accuracy of the movement. However, if the delay is too short, the gaze movement would be over before the head could make a significant contribution. Thus, as a simplification, we chose a constant 30 ms delay between head a gaze movement to ensure that the head movement would contribute significantly to the gaze displacement in our simulations.
As shown in the second column of Fig. 4, simulated gaze and eye velocity traces do not have a dip (double-peak velocity profiles) during large gaze saccadic movements as previously observed some experiments (Freedman and Sparks 1997, 2000), but not others (Gandhi 2012).
Figure 4 shows that the model reproduces two key characteristics of head-unrestrained gaze saccades. The decrease of peak gaze and eye velocities with gaze shifts of amplitude bigger than ≈ 30° (Freedman and Sparks 1997; Gandhi 2012). Additionally, as in the monkey data in Fig. 5I and 8E of Freedman (2001), the peak head velocity occurred later with increasing head displacement.
3.2 Main sequence and eye-head contributions
To show how well the model reproduced the average behavior during head-unrestrained gaze saccades, we generated a simulated main sequence and compared our results with monkey data. The main sequence includes two relationships that were first defined to characterize the kinematics of saccadic eye movements (Bahill et al. 1975). The first one is the nonlinear (saturated) relationship between saccade amplitude and saccade peak velocity, whereas the second one is the linear relationship between saccade amplitude and saccade duration. When the head is free to move, those relationships are not as stereotyped as for eye-only saccades, because they depend on exactly how the head moves during each gaze shift. However, a general trend is that the peak velocity increases with increasing gaze shifts up to ≈ 30° and then decreases for larger head-unrestrained saccadic movements (Gandhi 2012; Freedman and Sharks 1997, 2000). Freedman and Sparks (1997) also considered the amplitude-average velocity relationship. Comparing the peak velocity with the average velocity, one can extract information concerning the shape of the movement (e.g., if the average velocity is close to half the peak velocity times the duration, the velocity profile is roughly triangular).
Figure 5 shows the nine main sequence relationships. The first row represents the peak velocity relationship, the second row represents the average velocity relationship and the third row represents the duration relationship. The first column represents the three relationships for the gaze as a function of gaze amplitude. The second column represents the three relationships for the eye as a function of eye amplitude. The third column represents the three relationships for the head as a function of head amplitude. Gray dots were measured from eye movement data kindly provided by Dr. Gandhi (Gandhi 2012) for monkey gaze saccadic movements without blinks. Red lines represent simulations for increasing desired gaze saccade amplitude (ΔG) from 5 to 70° in steps of 1°. The amplitude of the desired head movement (ΔH) was set to 0.9(ΔG − 5). Gaze onset was delayed by 30 ms with respect to the head as in Fig. 4. To match the monkey data, simulated saccades were detected using a velocity threshold of 50° /s for the gaze and of 30° /s for the eye (Gandhi 2012). We used a velocity criterion to detect head movements with a threshold of 15° /s for the onset of head movement and 10° /s for the offset of head movement.
Fig. 5.
Head unrestrained main sequence in monkey. Gray dots represent data provided by Dr. Gandhi (from Gandhi 2012) for blink-free gaze shifts. Red lines represent the simulations of the model. Only by fitting all nine relationships well can a model demonstrate that it fits the shape of the eye, head and gaze trajectories for all amplitudes
Figure 5 shows that the model reproduces the characteristics of the gaze and eye main sequence relationships very well. Gaze and eye peak and average velocities increase with gaze shift amplitude (up to ≈ 600° /s) for gaze shifts of amplitude smaller than 30°. For gaze saccades larger than ≈ 30°, gaze and eye peak and average velocities decrease with increasing gaze shift amplitude (this inflection point in velocity profiles is called the hook). The model also simulates correctly the head main sequence with the increase of peak and average velocities of the head and the saturation of head movement duration with increasing head amplitude.
Figure 6 shows the contribution of the head (upper row) and the eye (bottom row) to the gaze displacement as a function of the gaze amplitude. Gray dots represent the data provided by Dr. Gandhi (2012) for blink-free gaze saccades. Red lines represent the eye and head contributions for the same simulations as in Fig. 5. Figure 6 clearly shows that the model fits the average monkey behavior well.
Fig. 6.
Head and eye contributions to the gaze saccade. Gray dots represent data provided by Dr. Gandhi (from Gandhi 2012) for blink-free gaze shifts. Red lines represent the simulations of the model. This fit demonstrates that the model accounts well for the division of labor between eye and head during gaze shifts, even though the model controls only gaze and head
3.3 Similar versus different orientations for desired head and gaze displacements
Now that we have shown how the model can reproduce the average behavior of horizontal gaze saccades, we will show how it can simulate results from studies that looked at more general types of gaze movements. A simulation of an oblique head-unrestrained gaze saccade is presented in Fig. 7. This example will be used to explain some details of how the model works and how the different pathways of the model interact. Goossens and van Opstal (1997) showed what happened when the initial positions of the gaze and the head were not aligned. Figure 7 shows a simulation of two movements based on their protocol (Fig. 13 of Goossens and van Opstal (1997), second column, first row), one in which the desired gaze and head displacements were in the same direction (dashed lines), and one in which the desired displacements had different directions (solid lines). In the different condition, the gaze started from (−15, 0)° (the first number represents the horizontal coordinate and the second represents the vertical coordinate) and the desired displacement was set to (15, 40)°. The head started from (15, 0)° and the desired head displacement was set to (−15, 30)°. For the same condition, head parameters remained identical but the gaze started at the same place as the head and the desired gaze displacement was set to (−15, 40)°. In Fig. 7, the right column of panel a shows a spatial representation of gaze, eye-in-head and head positions in both situations. The left column of panel Fig. 7a shows the time course of horizontal (top row) and vertical (bottom row) positions of the gaze, eye-in-head and head in both situations. The desired final gaze and head positions were the same in the two cases. The difference in the trajectories arose from a horizontal shift of the initial position of the gaze due to a horizontal shift of the eye-in-head. Therefore, as expected, there were no big differences between the two simulations with respect to the vertical trajectories (lower left panel in Fig. 7a).
Fig. 7.
Gaze saccades simulated by the model when gaze and head displacements are in the same or different directions. a right column: Spatial representation of eye-in-head (green lines), head (blue lines) and gaze (orange lines) positions. a left column: positions as a function of time. Gaze, eye and head displacements in the same direction are represented by dashed lines. Gaze, eye and head displacements in different directions are represented by solid lines. b represents a detailed view of the head movement with the collicular (orange arrows) and the head cerebellar (blue arrows) drives when head and gaze desired trajectories had different desired displacements. c represents a detailed view of the head trajectory with collicular (orange arrows) and head cerebellar (blue arrows) drives when head and gaze had the same desired displacements. For visibility we offset the arrows from the head trace. Note that when the goals are in different directions the SC drive pushes the head away from its ultimate goal
Figure 7b shows a detailed view of the head trajectory with the relative discharge of the collicular (orange arrows) and the cerebellar (blue arrows) head pathways that were summed and sent to the head plant through the head motor neurons, when head and gaze desired displacement were not in the same direction. Figure 7c shows the same detailed view for head and gaze desired displacements when they moved in the same direction.
In the same condition (dashed lines in Fig. 7), the desired gaze displacement and the desired head displacements had similar orientations. Therefore, the SC discharge had the same orientation as the head cerebellar pathway (compare the orientation of orange and blue arrows in Fig. 7c). In this situation, the collicular and the cerebellar head drives had a similar orientation.
In the different condition (solid lines in Fig. 7), the collicular activity did not have the same orientation as the head cerebellar activity (compare the direction of orange and blue arrows in Fig. 7b). Hence, as was observed in Fig. 7, there was a deviation of the head movement (up and to the right) caused by the collicular discharge during the first part of the gaze saccade. This deviation acted as a perturbation on the head controller. Angles between the collicular and the head discharge in Fig. 7b lead to a deviation of initial head movement in the direction of the gaze displacement. As soon as the gaze was on target (gaze stabilization part of the simulated gaze saccade), only the head pathway discharged. Therefore, collicular perturbation of the head ceased and the head cerebellar controller brought the head close to its desired final position.
Our simulations and the behavioral observations of Goossens and van Opstal (1997) (their Fig. 13, first row, second column) match well. As in their recordings, our simulated head movement in the unaligned condition is initially deviated along the gaze direction (although gaze was not represented in Fig. 13 of Goossens and van Opstal 1997), but the head trajectory is corrected and ends close to the aligned situation. Note that, both in their behavioral recordings and in our simulations, the spatial position of the visual target corresponds to the goal of both head and gaze.
As shown in Fig. 7, the model can reproduce the observed initial heading of the head movement when the gaze and the head desired displacements are not in the same direction. As explained in the previous paragraph, the initial deviation of the head movement arose because of the collicular discharge from the gaze pathway that is sent to the head bursters. The sensitivity of the head trajectory to the gaze trajectory is determined in the model by αSC,H (see Eq. (32)). The effect of changing αSC,H is shown in Fig. 8. The left column of Fig. 8 represents spatial trajectories of head movements for different values of αSC,H while keeping other parameters constant (G0 = (−15, 0), ΔG = (15, 40), H0 = (15, 0), ΔH = (−15, 30)). Note that when αSC,H is equal to 0, the gaze loop does not influence the head trajectory and therefore the trajectory is straight. Additionally, the bigger αSC,H is, the more the head is initially deviated in the direction of the gaze. This is quantified in the right column of Fig. 8, which represents the initial orientation of the head movement (100 ms after the onset of the movement) as a function of αSC,H.
Fig. 8.
Sensitivity of head trajectory to the gain from SC to head bursters. Left panel represents the spatial trajectory for increasing values of the SC to head burster gain (αSC,H) while keeping all the other parameters constant. The right panel represents the head’s initial heading (measured 100 ms after movement onset) as a function of αSC,H
3.4 Torque pulse on the head during a gaze shift: compensation for external perturbations
Using a torque pulse on the head during a gaze saccade, (Laurutis and Robinson 1986, Tomlinson and Bahra 1986a, b) showed that the VOR is suppressed during the gaze saccade, and that the final gaze position remains accurate. Later, Lefèvre et al. (1992) and Cullen et al. (2004) reported a more detailed evolution of VOR suppression during gaze saccades. They showed that the VOR gain decreases quickly at saccade onset (Cullen et al. 2004) and increases back to one before saccade offset (Lefèvre et al. 1992). Gaze saccades remain accurate despite perturbations even though the VOR is suppressed. This implies a continuous feedback control of the gaze trajectory. To demonstrate the importance of a gaze feedback circuit in rejecting perturbations on gaze trajectory when the VOR gain is close to zero, we simulated a horizontal torque pulse on the head that occurred shortly after the onset of a gaze saccade. In our model the gain of the VOR is a function of the amplitude of the desired gaze shift (see Eq. (57)). Finally, Sylvestre and Cullen (2006) showed that the activity of the gaze burster neurons in the paramedian pontine reticular formation (PPRF) is quickly modified following a head perturbation. Those changes show that gaze bursters in the PPRF are sensitive to a perturbation of the head movement. This is why the activity of our gaze bursters is modulated by a vestibular drive signal (see Eq. (29)).
Figure 9 presents two simulations: one without perturbation (solid lines) and one with an opposing velocity pulse (smoothed by a second order transfer function with 5 and 1.5 ms time constants) on the head starting 80 ms after saccade onset and lasting for 10 ms. As observed by Tomlinson and Bahra (1986b), the influence of an external perturbation on the head can be clearly seen on head and gaze positions (Fig. 9). Traces in the middle row show a drastic change in head and gaze velocities due to the perturbation. Finally, as reported by Sylvestre and Cullen (2006), the bottom row shows that the gaze burster activity was affected by the head perturbation. As soon as the perturbation was over, the gaze and head controllers corrected the trajectories so that they ended close to the desired final positions. Thus, even with a perturbation, gaze and head trajectories ended close to the unperturbed trajectories (compare solid and dashed lines for head and gaze trajectories), as was found experimentally (Tomlinson and Bahra 1986b). This shows the importance of the three feedback loops for gaze and head trajectories when the VOR gain is smaller than one.
Fig. 9.
Model response to a head perturbation. Upper row represents gaze (orange lines), eye-in-head (green lines) and head (blue lines) positions as a function of time. Middle row represents the velocity time-course for the same signals. Bottom row represents the evolution of gaze burster activity as a function of time. Solid lines represent the normal conditions. Dashed lines represent a simulation with an opposing torque applied to the head for 10 ms starting 80 ms after the onset of the gaze movement. The time during which the torque was applied is represented by the colored rectangle. Gaze and head started at (0, 0)°, the desired gaze displacement was set to (40, 0)° and the desired head displacement was set to (30, 0)°. The same color conventions as in Fig. 7 apply here
3.5 SC inactivation and head velocity
Walton et al. (2008) showed that following a chemical lesion in the superior colliculus peak gaze velocity decreased, gaze latency increased, head latency remained similar but peak head velocity increased. Figure 10 shows a simulation reproducing the conditions of Fig. 3 in Walton et al. (2008). Black lines represent the normal condition. Red lines represent the effect of an inactivation of the model’s SC. Desired gaze and head displacements were set to 40° in both conditions. To simulate the effect of a local lidocaine injection in the colliculus, we decreased the collicular gain to the gaze bursters by 25 % (αSC,G = 0.75), the collicular gain to the head bursters by 50 % (αSC,H = 0.01) and the collicular shunt to the head bursters by 100 % (ξC,H = 0). Additionally, because the model does not include a triggering mechanism based on SC activity, we delayed the onset of the gaze by 80 ms to account for the change in latency observed following the lidocaine injection.
Fig. 10.
Superior colliculus inactivation and head velocity. The top two rows represent the time-course of gaze and head positions. The bottom two rows represent the time-course of gaze and head velocities. Black lines represent a normal saccade while red lines represent saccades after partial SC inactivation. The desired gaze (head) amplitude was set to 45° (35°) for both conditions. The gaze onset was delayed by 80 ms with respect to the healthy situation when the colliculus was lesioned. This simulates well the increase in peak head velocity shown by Walton et al. (2008)
Comparing our simulation in Fig. 10 with the results of Walton et al. (2008), one can see that the model reproduces the changes observed following the lidocaine injection. The peak gaze velocity decreases and the peak head velocity increases. This is the result of the removal of the collicular shunt on the head bursters. Therefore, all the drive coming from the head cerebellar pathway and the remaining collicular drive are sent to the head bursters. This generates, as observed in typical examples of Fig. 3 in Walton et al. (2008), an acceleration of the head when the gaze movement starts, thereby generating an increase of the peak velocity.
4 Discussion
In this paper we have presented a new approach for the hierarchical control of linked systems (HCLS). We demonstrated the soundness of this approach for head-unrestrained gaze saccade control, but we propose that this novel architecture could also apply to the control of any system of linkages, no matter how long. Adding more platforms to the system, e.g., by adding trunk motion to gaze control, would simply augment this model with another cerebellar pathway for controlling the trunk, which would also feed back to the more distal controllers. Figure 11 shows a suggested extension of our coupled-feedback controller for a LS with trunk, head, and eyes.
Fig. 11.
Hierarchical control system augmented for control of gaze, head and trunk movements. The gaze control structure of the model is identical to Fig. 1c. Another feedback loop has been added to account for the control of trunk movement. A possible third projection (dotted line) from the superior colliculus to the trunk plant is in case body movements result from SC stimulation. The head controller (CBH) controls head orientation with respect to an inertial reference frame but projects to the head plant represented in a trunk-fixed reference frame. Arrowheads correspond to an excitation and filled circles correspond to an inhibition
Ever since the first head-unrestrained behavioral recordings (Bizzi et al. 1971), researchers have proposed models of eye-head coordination during saccades. Extending the principle of internal feedback loops introduced by Robinson (1975), Laurutis and Robinson (1986) developed a head-unrestrained gaze saccade model that included an internal, or local, feedback loop of gaze position. In their model, the feedback loop controls the gaze position using a gaze motor error built from the difference between the target position and an estimate of gaze position. Moreover, only the gaze was controlled; head position was an independent input of the model. Based on the observed tight coupling between eye and head movement kinematics (especially in head-unrestrained cats Guitton et al. 1990), Guitton and Galiana extended the principle of Laurutis and Robinson (1986) to the control of both eye and head during gaze saccades (Guitton 1992; Galiana and Guitton 1992; Lefèvre and Galiana 1992). Their models also included a gaze feedback loop (see Fig. 1a) to compute gaze motor error, which predominantly drives both eye and head. As in their model, our model also includes a gaze feedback loop to ensure the accuracy of the gaze movement, but is further extended by adding a head feedback controller. Most importantly, the distal feedback loop controls not eye displacement, but gaze displacement.
4.1 Interconnections
In addition to the two separate feedback loops to control gaze and head, our model has several connections between gaze and head pathways to account for interactions between eye and head during gaze movements. There are two projections from the colliculus to the head bursters: the first one is a drive that pushes the head along the gaze direction (gaze collicular drive), while the second decreases the head bursters’ activity along the direction orthogonal to the desired gaze displacement (collicular shunt). In addition, a projection from the head bursters modulates gaze bursters’ activity to slow down the gaze movement. This gives time for the head to start its movement before the gaze saccade ends, otherwise the head would not contribute significantly to the gaze displacement, requiring the eye to move to a more eccentric position. Thus, this modulation will ensure that the eye does not need to attain large eccentric positions during large gaze saccades. Finally, the vestibular projections inform both feedback loops whether the head is moving as planned or not. All these interactions have a common goal: to redirect the line of sight quickly and accurately from one object of interest to another, while avoiding uncomfortable eye eccentricities.
Note that in our model we do not have a projection from the cerebellar gaze pathway to the head plant, i.e., in Fig. 2 there is no orange line from CBG to the head bursters. We have not included a gaze cerebellar projection to the head because the head’s inertia is so high that it would not have a significant effect on the compensation of the gaze perturbations during the short duration of a head-unrestrained saccade (around 100 ms for a saccade of 30°, Freedman and Sparks 1997). If physiological evidence of such a projection becomes compelling, adding it would constitute a minor change to the model. This connection could also be useful for other species with low head inertia and a smaller oculomotor range: i.e., cat, owl, squirrel monkey, etc.
Even though strong coupling between the eye and head (and therefore between gaze and head) has been observed, there are examples where the two systems have differently oriented trajectories (Goossens and van Opstal 1997), are not temporally synchronized (Freedman and Sparks 1997) or where head movement characteristics change as a function of gaze saccade amplitude (Guitton and Volle 1987b; Freedman and Sparks 1997; Gandhi 2012). From those observations, Freedman (2001 and 2008) proposed a new architecture for head-unrestrained saccade control based on an a priori decomposition of the desired gaze displacement into its eye and head components (see Fig. 1b). Those components are then sent to two separate controllers, one for the head and one for the eye movement. The only interaction between the two separate pathways is an inhibitory signal sent from the head controller to the saccade generator that modulates the maximum eye velocity in proportion to the head velocity. In the Freedman model, the eye displacement is controlled using feedback of the eye motor error as in Robinson (1975), but no feedback is included to control gaze trajectory. Any perturbation of the head is postulated to be rejected by neck reflexes in Freedman’s model. However, this hypothesis is hard to reconcile with several observations. For instance, the experiment of Choi and Guitton (2006) (brake on the head during a large gaze shift while recording in SC) showed that gaze shifts were accurate even when the head remained stationary longer than the duration of the normal eye movement. This result could be simulated by our model, but could not be reproduced by the neck reflex mechanism proposed by Freedman because the eye movement will not be affected by the head perturbation. It is important to stress that without an interaction from the head to the eye movement (and therefore, a form of gaze feedback), it is impossible for any neck reflex mechanism to correct the gaze trajectory to negate long head perturbations (Boulanger et al. 2012). As in Freedman’s models (Freedman 2001, 2008), our model includes a separate pathway to control the head trajectory. However, our model controls head and gaze instead of head and eye (Freedman 2001, 2008). As in Freedman’s models (Freedman 2001, 2008), our model modulates the activity of the gaze bursters as a function of the head movement. However, in Freedman’s model, the gaze bursters are modulated by an open-loop drive while in our model this signal comes from the head bursters located inside the feedback loop (see Section 3).
No previous gaze feedback control architecture could easily simulate movements where gaze and head moved in different directions, and thus some groups have rejected the gaze feedback theory based on this observation. However, our new model takes into account that the head is under volitional control. Thus, one can move one’s head more or less (Fuller 1992), or even move one’s head independently of a gaze movement (Collins and Barnes 1999). However, one can not decide to modulate the speed of gaze movements. Gaze speed is constrained by the target movement during head-unrestrained tracking and it is (with some additional constraints) maximized during head-unrestrained gaze shifts (to minimize the duration of the gaze shift). If the brain controlled the eye and head separately, this constraint would require an internal representation of an infinite number of combinations of eye and head movements for a defined gaze displacement, which seems unlikely. Moreover, it would not be possible to take into account long, unexpected perturbations of the head. Our new control architecture includes two separate inputs with three feedback loops, thus the infinite number of eye and head movement combinations for the same gaze displacement is intrinsically taken into account, as are perturbations of any duration.
4.2 2-D control
Most previous models were designed to simulate 1-D gaze trajectories. A 2-D update of those models is not a trivial task. Furthermore, adding head movements to a head-fixed model requires inclusion of a vestibular system. Nonetheless, simply incorporating these changes does not get us all the way to our solution, nor does it generalize to other multiplatform controllers. The main contribution of our new model is the idea of hierarchical control, where each subcontroller has its own goal, but the most distal effector has only the composite goal, and feedback from each link goes to the next distal link. Thus the 1-D to 2-D update would only produce a controller with eye and head controllers, but would not generalize to other movement controllers. In contrast, our new model has no eye controller, only gaze and head controllers, and would easily generalize to other linked platforms.
In addition, prior models cannot simulate both perturbation rejection and differently oriented gaze and head trajectories in 2-D. Our new architecture, with the parallel control of independent gaze and head trajectories, manages this in an efficient and extensible way. Our model is also the first one that simulates the nine key relationships of the head-unrestrained main sequence (peak velocity, average velocity and duration) for the three components of gaze saccades (eye, head and gaze). As explained in the Section “Results”, only the reproduction of all nine relationships of the main sequence ensures that a model does a good job of reproducing gaze saccade behavior. Finally, our model proposes an explanation for the observation that localized collicular lesions increase head peak velocity while decreasing gaze peak velocity. To reproduce this observation, we proposed that the head bursters may be inhibited slightly by a gaze-related signal from the SC. Our implementation generates a shunt that inhibits the head bursters with the SC activity. However, an identical effect would be obtained if the shunt comes instead from the gaze bursters, because when the collicular discharge decreases so does the activity of the gaze bursters. New experiments are needed to test the existence and pathway of our hypothesized shunt mechanism.
4.3 Fitting the main sequence
The best test of whether a model simulates the dynamics of gaze movements is whether it can fit all the main sequence relationships (e.g., Fig. 5). As shown in the second column of Fig. 4, our simulated gaze and eye velocity traces do not have a dip (double-peak velocity profiles) during large gaze saccadic movements. Such dips were previously observed (Freedman and Sparks 1997, 2000), and Freedman and Sparks (2000) reported that the amplitude of the dip was linked to the head movement. However, Gandhi (2012) recorded eyelid movement during gaze shifts and showed that the occurrence of double-peak velocity profiles was correlated with the occurrence of blinks. Because neither Freedman and Sparks (1997) nor Freedman and Sparks (2000) controlled for blinks during gaze shifts in their experiments, it is possible that the double-peak velocity profiles they observed resulted from the monkey making blinks during the task (Gandhi 2012). Rottach et al. (1998) also showed that blinks could affect saccade velocities when the head was fixed. Therefore, we decided to simulate the blink-free behavior (based on Gandhi 2012) and model only single-peak velocity profiles. However, because gaze and head are under feedback control, if new evidence shows that double-peak velocity profiles occur without blinks, the addition of a double-peak mechanism would not impair the model’s ability to simulate accurate gaze shifts.
At first, it was proposed that the hook in gaze and eye velocity profiles was an outcome of the double-peak velocity profiles. In Freedman’s model those double peaks were caused by a strong (temporally localized) inhibition of the eye burster activity by a head velocity signal (Freedman 2001, 2008). It has been recently shown that even when the monkey did not blink (and therefore, no dip was observed in the velocity profiles), there is still a decrease in the head-unrestrained gaze and eye peak and average velocity relationships for larger gaze shifts (Gandhi 2012). To reproduce this behavior, our model head burster activity also inhibits the gaze burster activity (see Eqs. (27)–(28)). However, a major difference between our model and Freedman’s arises from the nature of the signal used to shunt the gaze bursters. The signal used in Freedman (2001, 2008) is a fixed-duration velocity step precomputed as a function of the amplitude of the head movement, whereas our shunt is an internal signal continuously updated through the feedback loop that controls head movement.
The rationale for our head shunt signal is to slow down the gaze movement to give enough time for the head (which has a bigger inertia and therefore is slower) to start its movement. Therefore, it is critical that the signal that would modulate the gaze burster activity represents the actual head movement. This is not the case in Freedman (2001, 2008), because his open-loop model precomputes a head velocity profile that, if any perturbation occurs, will not be correlated with the actual head movement. Obviously the velocity step would not represent the actual head velocity if the head is held for a duration longer than the duration of the velocity step. Therefore, Freedman’s model (Freedman 2001, 2008) predicts that a reduction in the peak gaze and eye velocity with increasing gaze saccade amplitude will be observed even if the head is blocked at the onset of the gaze saccade for the duration of the saccade, because the decrease of the peak gaze/eye velocity is not linked to the actual head movement but to an independent open-loop command. Our model predicts that the shape of the main sequence is a function of the relative latency between gaze and head velocity profiles, because the tuning of the gaze bursters is linked to the actual head movement. Supplementary experiments must be conducted to test which hypothesis is more likely.
Finally, in the open-loop gaze model of Freedman (2001, 2008), the gaze main sequence is an outcome of the combination of the eye and head main sequences, because eye and head are controlled independently. In our model, gaze and head are under feedback control, thus the eye main sequence is the outcome of the gaze and the head main sequences. It must be pointed out that the inflection point in the main sequence relationships in Fig. 5 comes from the hard saturation in Eq. (27). The rational behind this saturation is that the shunt will have a similar behavior for gaze displacements smaller than a function of the lower threshold (equal to τmin,gφgh + μgh), and could not increase for gaze shifts larger than a function of the upper threshold (equal to τmax,gφgh + μgh). The hard saturation was chosen to simplify the description of the shunt. Using a soft saturation would not change the behavior but would increase the complexity of the equations.
Importantly, just because a model reproduces one of the average velocity or the peak velocity or the duration relationships, there is no guarantee that it can also reproduce the two other relationships. Only the reproduction of the three relationships with the same set of parameters for eye, head and gaze is a guarantee that a model does a good job simulating the behavior of head unrestrained gaze saccades. Currently, no other model reproduces all nine relationships. Freedman (2001) and Freedman (2008) showed average velocity profiles for gaze, eye-in-head and head, but neither the duration nor the peak velocity. Therefore, it is hard to determine if his model reproduces correctly the kinematics of gaze, eye-in-head and head movements during gaze shifts. Additionally, the saturation in Freedman’s model (Freedman 2001, 2008) is on the eye bursters, thus the eye average velocity stays at a lower level for increasing gaze amplitudes larger than ≈ 40°. However, the average gaze velocity increases because of the increase of the average head velocity. In our model, the gaze bursters are saturated, therefore, the gaze peak velocity relationship remains low for saccades with increasing amplitudes larger than 40° and the peak/average eye velocity relationships decay for larger movements (as shown by the data in Fig. 5).
The model by Kardamakis et al. (2010) also showed simulated main sequences. Comparing actual results with their simulations, it can be seen that their main sequence (Fig. 6 in Kardamakis et al. 2010) has a discontinuity (step from ≈ 700° /s for a 16° gaze shift to ≈ 380° /s for an 18° gaze shift) in the peak velocity profiles. This step is not observed in published data (Freedman and Sparks 1997; Gandhi 2012). Kardamakis et al. (2010) does not show the three key relationships of the main sequence for gaze, eye and head. Finally, the simulations in (Kardamakis et al. 2010) are not compared to actual data, therefore, it is not possible to evaluate how well this model reproduces average head unrestrained gaze saccade kinematics. Thus, as Fig. 5 shows, our new model is the only one that has shown that it can reproduce the three key relationships of the main sequence (peak velocity, average velocity and duration) for gaze, eye and head components with the same set of parameters.
4.4 Testing the new model
When one proposes a new model, it is important to point out how it may be falsified. In our case, the effects of SC lesions mentioned above suggest a test. Our model has two inputs for head movements. Thus, whether the head and the eye move toward goals in the same or opposite directions makes a difference. For example, in Fig. 7 the head trace moves directly toward the head goal when the gaze and head have goals in the same direction (dashed blue line); However, when the head goal is in a different direction than the gaze goal, the head is first pushed toward the gaze goal, but then turns around and moves toward the head goal (solid blue line). Thus, it is a prediction of our model that, following a collicular lesion, in addition to the reported increase of peak head velocity (Walton et al. 2008), the effect of the gaze goal on the initial head trajectory should vanish; i.e., for a head goal opposite the gaze goal, the head should not move toward the gaze goal. It would also be possible to test our model by making lesions in the cerebellum and testing the ability of the head and gaze to get on target despite long-duration perturbations. Further tests of signals in the brain stem, to determine whether they are related to eye, head or gaze would also be critical for our model.
Despite its complexity, the neural architecture of our model is still simple compared to the actual connectivity of the gaze control system. For example, the new architecture does not include a model representing the circuitry of the PPRF as in Lefèvre et al. (1998) and Quaia et al. (1999). It is well known that omnipause neuron (OPN) discharge is correlated with saccade duration in head-restrained condition, that they have a tonic activity and that they stop discharging during a saccade (Sparks and Travis 1971; Luschei and Fuchs 1972) independently of saccade direction (Keller et al. 1974). Those results have been extended to head unrestrained conditions; Parè and Guitton (1998) showed that the pause duration was correlated with the duration of the gaze saccade, not with the duration of the eye part of the movement. Prsa and Galiana (2007) proposed a model of the OPNs that reproduces previous electrophysiological recordings; including such an explicit OPN model in our model would not change its behavior regarding the eye-head coordination during head unrestrained saccades, but it was left out to avoid further complicating the model. Finally, our model does not include a quick-phase generator as in Chun and Robinson (1978) and Galiana and Outerbridge (1984). Therefore, the model can not simulate nystagmus.
Our model predicts that there will be a difference between acute and chronic ophthalmoplegia. Gilchrist et al. (1997, 1998) reported recordings of head unrestrained gaze displacements in a patient with chronic ophthalmoplegia while reading. The authors described her movements as: “AIs head movements have a saccadic pattern;…” (Gilchrist et al. 1997). In our model, an acute ophthalmoplegia would result in a gaze movement carried out by the head that would go wherever the head goal was set, which may be less than the desired gaze change. Over time, we assume that adaptation would match gaze and head goals as well as increasing the collicular drive to the head, resulting in gaze-like head movements. This could be tested in an animal model by paralyzing the orbital muscles.
Results from Isa and Sasaki (2002) and from Walton et al. (2008) seem contradictory. Using permanent lesions in cats’ SC, Isa and Sasaki (2002) showed slower head movements towards the contralateral side, whereas the transient lesions in monkeys from Walton et al. (2008) showed an increase in peak velocity. Those conflicting results could be explained by our model if one takes into account two factors. Firstly, adaptation plays a role after chronic lesions. We think that adaptation would compensate for the loss of the collicular shunt by reducing the parallel cerebellar drive to the head. Adaptation has to slow down the head to give enough time for the feedback loops to function properly with a slower gaze movement. This prediction could be tested experimentally. Secondly, the tecto-reticulo-spinal pathway is strong in cats (Grantyn and Berthoz 1985; Munoz and Guitton 1985, 1986) and weaker in monkeys. To simulate this difference, the gain of the collicular drive sent to the head burster could be increased to become stronger than the cerebellar drive. Once this drive is removed, the head movement would be strongly decreased as observed by Isa and Sasaki (2002).
One key difference between our model and previous control schemes is the addition of an explicit representation of the VOR. The action of the VOR at different levels (eye motor neurons, gaze bursters and cerebellar controllers) generates different responses that can modify the gaze trajectory with different time constants. The projection to the cerebellar controllers is more useful during large gaze shifts because the system has time to compensate for a head perturbation that will not be negated by the absent VOR. In contrast, for small amplitudes the cerebellar controllers would not have enough time to compensate for the perturbation. Thus, a quicker response to the perturbation is necessary to ensure gaze accuracy. One way to get a quicker response is to leave the VOR on, and send its output directly to suppress gaze burst neuron activity. This would slow the eye movement, but would not affect the final gaze position, as the gaze cerebellar controller would automatically compensate for this perturbation through the feedback loop. The new model thus provides a possible explanation for why the VOR has to remain operational during small gaze shifts. This hypothesis could be tested by reproducing the experiment of Cullen and Roy (2004) and recording the gaze burster activity while perturbing the head movement during gaze saccades of different amplitudes. Our model predicts that the strength of the modulation should be negatively correlated with the duration of the desired gazes shift.
One of the highest priorities of the oculomotor system is to reorient the line of sight (gaze) from one center of interest to another. Here we give an intuitive demonstration of why the central nervous system controls gaze and head instead of eye and head. Any perturbations that could occur during a gaze movement would affect the correct acquisition of the visual goal. Therefore, these unpredictable effects must be accounted for to ensure clear vision and an efficient execution of the gaze movement. As explained in the introduction, a redirection of the gaze can be accompanied by another goal, e.g. aligning the mouth to bite the visual target in a predator-prey race. In this situation vision is crucial because it informs the predator of the prey’s movements. Therefore, whatever perturbations occur, it is fundamental that gaze remains aligned on the object of interest. Because both head and eye movements are affected by a perturbation on the head, we think that this example clearly shows that it is their sum, the gaze, that must be controlled to ensure clear vision and the achievement of any other goals (in the predator’s case, biting the prey). Because the eyes are carried by the head, a totally separated control of eye and head could not ensure that the gaze movement will be accurate without a correction of these movements based on gaze information. For example, changing the head trajectory will modify the needed displacement of the eye to ensure a correct gaze movement. Therefore, to acquire the visual target when the head is perturbed, the eye trajectory must be changed so the sum of eye and head components at the end of the gaze movement remains unchanged compared to the unperturbed case.
Historically, movement controllers have been focused on independent subsystems, such as the eye and head, or hand and arm. More recent research shows that control of linked systems is complicated by interactions between subsystems. Our hierarchical model presents a framework for representing complicated systems with common drive signals and multiple levels of feedback. Although many models could reproduce the behavior described here, neuroanatomical and neurophysiological studies constrained our model architecture giving it more predictive power. With such a framework, interpreting the results of future experiments may become simpler.
Acknowledgments
We are especially grateful to Dr. N. J. Gandhi for kindly providing the data points used to make our Fig. 5.
Drs. Optican and Daye were supported by the Intramural Research Program of the National Eye Institute.
Dr. Blohm has been supported by the National Science and Engineering Research Council (Canada), the Ontario Research Fund (Canada), the Canadian Foundation for Innovation (Canada) and the Botterell Foundation (Queens University, Kingston, ON, Canada).
Dr. Lefevre has been supported by Fonds National de la Recherche Scientifique, Action de Recherche Concertèe (Belgium). This paper presents research results of the Belgian Network Dynamical Systems, Control and Optimization, funded by the Interuniversity Attraction Poles Programmes, initiated by the Belgian State, Science Policy Office.
Footnotes
One simplification here is that we ignore internal noise in the system, e.g., Harris and Wolpert (1998) showed that optimal control of a system with signal-dependent noise can reproduce the speed-accuracy trade-off for saccades. As we are dealing with rejection of perturbations in linked systems, internal noise is not our primary concern.
To cancel its VOR, the monkey looked at a head-fixed target while sitting on a rotating chair that oscillated sinusoidally
Conflict of interests The authors declare that they have no conflict of interest
Contributor Information
Pierre M. Daye, Email: [email protected], NIH, NEI, Laboratory of Sensorimotor Research, 49 Convent Drive, Room 2A50, Bethesda, MD 20892-4435, USA.
Lance M. Optican, Email: [email protected], NIH, NEI, Laboratory of Sensorimotor Research, 49 Convent Drive, Room 2A50, Bethesda, MD 20892-4435, USA.
Gunnar Blohm, Email: [email protected], Centre for Neuroscience Studies, Queen’s University, Botterell Hall, Room 229, 18 Stuart Street, Kingston, ON K7L 3N6, Canada.
Philippe Lefèvre, Email: [email protected], UCLouvain, ICTeam, IoNS, Euler building, 4 avenue Georges Lemaitre, 1348 Louvain-la-Neuve, Belgium.
References
- Aizawa H, Wurtz R. Reversible inactivation of monkey superior colliculus. I. Curvature of saccadic trajectory. Journal of Neurophysiology. 1998;79(4):2082–2096. doi: 10.1152/jn.1998.79.4.2082. [DOI] [PubMed] [Google Scholar]
- Anastasopoulos D, Ziavra N, Hollands M, Bronstein A. Gaze displacement and inter-segmental coordination during large whole body voluntary rotations. Experimental Brain Research. 2009;193(3):323–336. doi: 10.1007/s00221-008-1627-y. [DOI] [PubMed] [Google Scholar]
- Bahill A, Clark M, Stark L. The main sequence, a tool for studying human eye movements. Mathematical Biosciences. 1975;24(3–4):191–204. [Google Scholar]
- Bechara B, Gandhi N. Matching the oculomotor drive during head-restrained and head-unrestrained gaze shifts in monkey. Journal of Neurophysiology. 2010;104(2):811–828. doi: 10.1152/jn.01114.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bizzi E. Strategies of eye-head coordination. Progress in Brain Research. 1979;50:795–803. doi: 10.1016/S0079-6123(08)60876-6. [DOI] [PubMed] [Google Scholar]
- Bizzi E, Kalil R, Tagliasco V. Eye-head coordination in monkeys: evidence for centrally patterned organization. Science. 1971;173(3995):452–454. doi: 10.1126/science.173.3995.452. [DOI] [PubMed] [Google Scholar]
- Boulanger M, Galiana H, Guitton D. Human eye-head gaze shifts preserve their accuracy and spatiotemporal trajectory profiles despite long-duration torque perturbations that assist or oppose head motion. Journal of Neurophysiology. 2012;108(1):39–56. doi: 10.1152/jn.01092.2011. [DOI] [PubMed] [Google Scholar]
- Cannon S, Robinson D. Loss of the neural integrator of the oculomotor system from brain stem lesions in monkey. Journal of Neurophysiology. 1987;57(5):1383–1409. doi: 10.1152/jn.1987.57.5.1383. [DOI] [PubMed] [Google Scholar]
- Cheron G, Godaux E. Disabling of the oculomotor neural integrator by kainic acid injections in the prepositus-vestibular complex of the cat. The Journal of physiology. 1987;394(1):267–290. doi: 10.1113/jphysiol.1987.sp016870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi W, Guitton D. Responses of collicular fixation neurons to gaze shift perturbations in head-unrestrained monkey reveal gaze feedback control. Neuron. 2006;50(3):491–505. doi: 10.1016/j.neuron.2006.03.032. [DOI] [PubMed] [Google Scholar]
- Chun KS, Robinson D. A model of quick phase generation in the vestibuloocular reflex. Biological Cybernetics. 1978;28(4):209–221. doi: 10.1007/BF00344268. [DOI] [PubMed] [Google Scholar]
- Collins C, Barnes G. Independent control of head and gaze movements during head-free pursuit in humans. The Journal of Physiology. 1999;515(1):299–314. doi: 10.1111/j.1469-7793.1999.299ad.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corneil B, Olivier E, Munoz D. Neck muscle responses to stimulation of monkey superior colliculus. II. Gaze shift initiation and volitional head movements. Journal of Neurophysiology. 2002;88(4):2000–2018. doi: 10.1152/jn.2002.88.4.2000. [DOI] [PubMed] [Google Scholar]
- Corriou J. Process control: theory and applications. London: Springer-Verlag; 2004. ISBN:1-85233-776-1. [Google Scholar]
- Cullen K, Roy J. Signal processing in the vestibular system during active versus passive head movements. Journal of Neurophysiology. 2004;91(5):1919–1933. doi: 10.1152/jn.00988.2003. [DOI] [PubMed] [Google Scholar]
- Cullen K, Huterer M, Braidwood D, Sylvestre P. Time course of vestibuloocular reflex suppression during gaze shifts. Journal of Neurophysiology. 2004;92(6):3408–3422. doi: 10.1152/jn.01156.2003. [DOI] [PubMed] [Google Scholar]
- Dale A, Cullen KE. The nucleus prepositus predominantly outputs eye movement-related information during passive and active self-motion. Journal of Neurophysiology. 2013;109(7):1900–1911. doi: 10.1152/jn.00788.2012. [DOI] [PubMed] [Google Scholar]
- Duhamel JR, Colby C, Goldberg M. The updating of the representation of visual space in parietal cortex by intended eye movements. Science. 1992;255(5040):90–92. doi: 10.1126/science.1553535. [DOI] [PubMed] [Google Scholar]
- Farshadmanesh F, Klier E, Chang P, Wang H, Crawford J. Three-dimensional eye–head coordination after injection of muscimol into the interstitial nucleus of cajal (inc) Journal of Neurophysiology. 2007;97(3):2322–2338. doi: 10.1152/jn.00752.2006. [DOI] [PubMed] [Google Scholar]
- Freedman E. Interactions between eye and head control signals can account for movement kinematics. Biological Cybernetics. 2001;84(6):453–462. doi: 10.1007/PL00007989. [DOI] [PubMed] [Google Scholar]
- Freedman E. Coordination of the eyes and head during visual orienting. Experimental Brain Research. 2008;190(4):369–387. doi: 10.1007/s00221-008-1504-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman E, Sparks D. Eye-head coordination during head-unrestrained gaze shifts in rhesus monkeys. Journal of Neurophysiology. 1997;77(5):2328–2348. doi: 10.1152/jn.1997.77.5.2328. [DOI] [PubMed] [Google Scholar]
- Freedman E, Sparks D. Coordination of the eyes and head: movement kinematics. Experimental Brain Research. 2000;131(1):22–32. doi: 10.1007/s002219900296. [DOI] [PubMed] [Google Scholar]
- Fujita M. Feed-forward associative learning for volitional movement control. Neuroscience Research. 2005;52(2):153–165. doi: 10.1016/j.neures.2005.02.006. [DOI] [PubMed] [Google Scholar]
- Fuller J. Head movement propensity. Experimental Brain Research. 1992;92(1):152–164. doi: 10.1007/BF00230391. [DOI] [PubMed] [Google Scholar]
- Galiana H, Guitton D. Central organization and modeling of eye-head coordination during orienting gaze shifts. Annals of the New York Academy of Sciences. 1992;656(1):452–471. doi: 10.1111/j.1749-6632.1992.tb25228.x. [DOI] [PubMed] [Google Scholar]
- Galiana H, Outerbridge J. A bilateral model for central neural pathways in vestibuloocular reflex. Journal of Neurophysiology. 1984;51(2):210–241. doi: 10.1152/jn.1984.51.2.210. [DOI] [PubMed] [Google Scholar]
- Gandhi NJ. Interactions between gaze-evoked blinks and gaze shifts in monkeys. Experimental Brain Research. 2012;216(3):321–339. doi: 10.1007/s00221-011-2937-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandhi N, Sparks D. Dissociation of eye and head components of gaze shifts by stimulation of the omnipause neuron region. Journal of Neurophysiology. 2007;98(1):360–373. doi: 10.1152/jn.00252.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilchrist I, Brown V, Findlay J. Saccades without eye movements. Nature. 1997;390(6656):130–131. doi: 10.1038/36478. [DOI] [PubMed] [Google Scholar]
- Gilchrist I, Brown V, Findlay J, Clarke M. Using the eye–movement system to control the head. Proceedings of the Royal Society of London Series B: Biological Sciences. 1998;265:1831–1836. doi: 10.1098/rspb.1998.0509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goffart L, Pélisson D. Orienting gaze shifts during muscimol inactivation of caudal fastigial nucleus in the cat. I. Gaze dysmetria. Journal of Neurophysiology. 1998;79(4):1942–1958. doi: 10.1152/jn.1998.79.4.1942. [DOI] [PubMed] [Google Scholar]
- Goffart L, Guillaume A, Pélisson D. Compensation for gaze perturbation during inactivation of the caudal fastigial nucleus in the head-unrestrained cat. Journal of Neurophysiology. 1998a;80(3):1552–1557. doi: 10.1152/jn.1998.80.3.1552. [DOI] [PubMed] [Google Scholar]
- Goffart L, Pélisson D, Guillaume A. Orienting gaze shifts during muscimol inactivation of caudal fastigial nucleus in the cat. II. Dynamics and eye-head coupling. Journal of Neurophysiology. 1998b;79(4):1959–1976. doi: 10.1152/jn.1998.79.4.1959. [DOI] [PubMed] [Google Scholar]
- Goossens H, van Opstal A. Human eye-head coordination in two dimensions under different sensorimotor conditions. Experimental Brain Research. 1997;114(3):542–560. doi: 10.1007/pl00005663. [DOI] [PubMed] [Google Scholar]
- Grantyn A, Berthoz A. Burst activity of identified tecto-reticulo-spinal neurons in the alert cat. Experimental Brain Research. 1985;57(2):417–421. doi: 10.1007/BF00236550. [DOI] [PubMed] [Google Scholar]
- Guillaume A, Pélisson D. Gaze shifts evoked by electrical stimulation of the superior colliculus in the head-unrestrained cat. II. Effect of muscimol inactivation of the caudal fastigial nucleus. European Journal of Neuroscience. 2001;14(8):1345–1359. doi: 10.1046/j.0953-816x.2001.01739.x. [DOI] [PubMed] [Google Scholar]
- Guitton D. Control of eye–head coordination during orienting gaze shifts. Trends in Neurosciences. 1992;15(5):174–179. doi: 10.1016/0166-2236(92)90169-9. [DOI] [PubMed] [Google Scholar]
- Guitton D, Volle M. Gaze control in humans: eye-head coordination during orienting movements to targets within and beyond the oculomotor range. Journal of Neurophysiology. 1987a;58(3):427–459. doi: 10.1152/jn.1987.58.3.427. [DOI] [PubMed] [Google Scholar]
- Guitton D, Volle M. Gaze control in humans: eye-head coordination during orienting movements to targets within and beyond the oculomotor range. Journal of Neurophysiology. 1987b;58(3):427–459. doi: 10.1152/jn.1987.58.3.427. [DOI] [PubMed] [Google Scholar]
- Guitton D, Munoz D, Galiana H. Gaze control in the cat: studies and modeling of the coupling between orienting eye and head movements in different behavioral tasks. Journal of Neurophysiology. 1990;64(2):509–531. doi: 10.1152/jn.1990.64.2.509. [DOI] [PubMed] [Google Scholar]
- Hanes D, Smith M, Optican L, Wurtz R. Recovery of saccadic dysmetria following localized lesions in monkey superior colliculus. Experimental Brain Research. 2005;160(3):312–325. doi: 10.1007/s00221-004-2013-z. [DOI] [PubMed] [Google Scholar]
- Harris C, Wolpert D. Signal-dependent noise determines motor planning. Nature. 1998;394(6695):780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Haustein W. Considerations on listing’s law and the primary position by means of a matrix description of eye position control. Biological Cybernetics. 1989;60(6):411–420. doi: 10.1007/BF00204696. [DOI] [PubMed] [Google Scholar]
- Isa T, Sasaki S. Brainstem control of head movements during orienting; organization of the premotor circuits. Progress in Neurobiology. 2002;66(4):205–242. doi: 10.1016/s0301-0082(02)00006-0. [DOI] [PubMed] [Google Scholar]
- Jürgens R, Becker W, Kornhuber H. Natural and drug-induced variations of velocity and duration of human saccadic eye movements: evidence for a control of the neural pulse generator by local feedback. Biological Cybernetics. 1981;39(2):87–96. doi: 10.1007/BF00336734. [DOI] [PubMed] [Google Scholar]
- Kardamakis A, Moschovakis A. Optimal control of gaze shifts. The Journal of Neuroscience. 2009;29(24):7723–7730. doi: 10.1523/JNEUROSCI.5518-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kardamakis A, Grantyn A, Moschovakis A. Neural network simulations of the primate oculomotor system. v. eye–head gaze shifts. Biological Cybernetics. 2010;102(3):209–225. doi: 10.1007/s00422-010-0363-0. [DOI] [PubMed] [Google Scholar]
- Kase M, Miller D, Noda H. Discharges of purkinje cells and mossy fibres in the cerebellar vermis of the monkey during saccadic eye movements and fixation. The Journal of Physiology. 1980;300(1):539–555. doi: 10.1113/jphysiol.1980.sp013178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato R, Grantyn A, Dalezios Y, Moschovakis A. The local loop of the saccadic system closes downstream of the superior colliculus. Neuroscience. 2006;143(1):319–337. doi: 10.1016/j.neuroscience.2006.07.016. [DOI] [PubMed] [Google Scholar]
- Keller E, et al. Participation of medial pontine reticular formation in eye movement generation in monkey. Journal of Neurophysiology. 1974;37(2):316–332. doi: 10.1152/jn.1974.37.2.316. [DOI] [PubMed] [Google Scholar]
- Klier E, Wang H, Constantin A, Crawford J. Midbrain control of three-dimensional head orientation. Science. 2002;295(5558):1314–1316. doi: 10.1126/science.1067300. [DOI] [PubMed] [Google Scholar]
- Land M. The coordination of rotations of the eyes, head and trunk in saccadic turns produced in natural situations. Experimental Brain Research. 2004;159(2):151–160. doi: 10.1007/s00221-004-1951-9. [DOI] [PubMed] [Google Scholar]
- Land M. Vision, eye movements, and natural behavior. Visual Neuroscience. 2009;26(1):51–62. doi: 10.1017/S0952523808080899. [DOI] [PubMed] [Google Scholar]
- Laurutis V, Robinson D. The vestibulo-ocular reflex during human saccadic eye movements. The Journal of Physiology. 1986;373(1):209–233. doi: 10.1113/jphysiol.1986.sp016043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefèvre P, Galiana H. Dynamic feedback to the superior colliculus in a neural network model of the gaze control system. Neural Networks. 1992;5(6):871–890. [Google Scholar]
- Lefèvre P, Bottemanne I, Roucoux A. Experimental study and modeling of vestibulo-ocular reflex modulation during large shifts of gaze in humans. Experimental Brain Research. 1992;91(3):496–508. doi: 10.1007/BF00227846. [DOI] [PubMed] [Google Scholar]
- Lefèvre P, Quaia C, Optican L. Distributed model of control of saccades by superior colliculus and cerebellum. Neural Networks. 1998;11(7–8):1175–1190. doi: 10.1016/s0893-6080(98)00071-9. [DOI] [PubMed] [Google Scholar]
- Liao K, Kumar A, Han Y, Grammer V, Gedeon B, Leigh R. Comparison of velocity waveforms of eye and head saccades. Annals of the New York Academy of Sciences. 2005;1039(1):477–479. doi: 10.1196/annals.1325.048. [DOI] [PubMed] [Google Scholar]
- Luschei ES, Fuchs AF. Activity of brain stem neurons during eye movements of alert monkeys. Journal of Neurophysiology. 1972;35(4):445–461. doi: 10.1152/jn.1972.35.4.445. [DOI] [PubMed] [Google Scholar]
- Mays L, Sparks D. Saccades are spatially, not retinocentrically, coded. Science. 1980;208:1163–1165. doi: 10.1126/science.6769161. [DOI] [PubMed] [Google Scholar]
- McFarland J, Fuchs A. Discharge patterns in nucleus prepositus hypoglossi and adjacent medial vestibular nucleus during horizontal eye movement in behaving macaques. Journal of Neurophysiology. 1992;68(1):319–332. doi: 10.1152/jn.1992.68.1.319. [DOI] [PubMed] [Google Scholar]
- Mottolese C, Richard N, Harquel S, Szathmari A, Sirigu A, Desmurget M. Mapping motor representations in the human cerebellum. Brain. 2013;136:330–342. doi: 10.1093/brain/aws186. [DOI] [PubMed] [Google Scholar]
- Munoz D, Guitton D. Tectospinal neurons in the cat have discharges coding gaze position error. Brain Research. 1985;341(1):184–188. doi: 10.1016/0006-8993(85)91487-8. [DOI] [PubMed] [Google Scholar]
- Munoz D, Guitton D. Presaccadic burst discharges of tecto-reticulo-spinal neurons in the alert head-free and-fixed cat. Brain Research. 1986;398(1):185–190. doi: 10.1016/0006-8993(86)91267-9. [DOI] [PubMed] [Google Scholar]
- Optican L. Sensorimotor transformation for visually guided saccades. Annals of the New York Academy of Sciences. 2005;1039(1):132–148. doi: 10.1196/annals.1325.013. [DOI] [PubMed] [Google Scholar]
- Optican L. Encyclopedia of neuroscience. Oxford: Academic; 2009. Oculomotor system: models; pp. 25–34. [Google Scholar]
- Optican L, Quaia C. Distributed model of collicular and cerebellar function during saccades. Annals of the New York Academy of Sciences. 2002;956(1):164–177. doi: 10.1111/j.1749-6632.2002.tb02817.x. [DOI] [PubMed] [Google Scholar]
- Optican L, Robinson D. Cerebellar-dependent adaptive control of primate saccadic system. Journal of Neurophysiology. 1980;44(6):1058–1076. doi: 10.1152/jn.1980.44.6.1058. [DOI] [PubMed] [Google Scholar]
- Paré M, Guitton D. Brain stem omnipause neurons and the control of combinedeye-head gaze saccades in the alert cat. Journal of Neurophysiology. 1998;79(6):3060–3076. doi: 10.1152/jn.1998.79.6.3060. [DOI] [PubMed] [Google Scholar]
- Pélisson D, Guitton D, Munoz D. Compensatory eye and head movements generated by the cat following stimulation-induced perturbations in gaze position. Experimental Brain Research. 1989;78(3):654–658. doi: 10.1007/BF00230255. [DOI] [PubMed] [Google Scholar]
- Pélisson D, Goffart L, Guitton D. On-line compensation of gaze shifts perturbed by micro-stimulation of the superior colliculus in the cat with unrestrained head. Experimental Brain Research. 1995;106(2):196–204. doi: 10.1007/BF00241115. [DOI] [PubMed] [Google Scholar]
- Pélisson D, Goffart L, Guillaume A. Contribution of the rostral fastigial nucleus to the control of orienting gaze shifts in the head-unrestrained cat. Journal of Neurophysiology. 1998;80(3):1180–1196. doi: 10.1152/jn.1998.80.3.1180. [DOI] [PubMed] [Google Scholar]
- Pélisson D, Goffart L, Guillaume A, Quinet J. Visuomotor deficits induced by fastigial nucleus inactivation. The Cerebellum. 2003;2(1):71–76. doi: 10.1080/14734220310015629. [DOI] [PubMed] [Google Scholar]
- Peng G, Hain T, Peterson B. A. dynamical model for reflex activated head movements in the horizontal plane. Biological Cybernetics. 1996;75(4):309–319. doi: 10.1007/s004220050297. [DOI] [PubMed] [Google Scholar]
- Prsa M, Galiana H. Visual-vestibular interaction hypothesis for the control of orienting gaze shifts by brain stem omnipause neurons. Journal of Neurophysiology. 2007;97(2):1149–1162. doi: 10.1152/jn.00856.2006. [DOI] [PubMed] [Google Scholar]
- Quaia C, Optican L. Commutative saccadic generator is sufficient to control a 3-d ocular plant with pulleys. Journal of Neurophysiology. 1998;79(6):3197–3215. doi: 10.1152/jn.1998.79.6.3197. [DOI] [PubMed] [Google Scholar]
- Quaia C, Aizawa H, Optican L, Wurtz R. Reversible inactivation of monkey superior colliculus. II. Maps of saccadic deficits. Journal of Neurophysiology. 1998;79(4):2097–2110. doi: 10.1152/jn.1998.79.4.2097. [DOI] [PubMed] [Google Scholar]
- Quaia C, Lefèvre P, Optican L. Model of the control of saccades by superior colliculus and cerebellum. Journal of Neurophysiology. 1999;82(2):999–1018. doi: 10.1152/jn.1999.82.2.999. [DOI] [PubMed] [Google Scholar]
- Robinson DA. Oculomotor control signals. In: Lennerstand G, Bach-y-Rita P, editors. Basic mechanisms of ocular motility and their clinical implications. Vol. 24. Pergamon Press; 1975. pp. 337–374. [Google Scholar]
- Robinson F, Straube A, Fuchs A. Role of the caudal fastigial nucleus in saccade generation. II. Effects of muscimol inactivation. Journal of Neurophysiology. 1993;70(5):1741–1758. doi: 10.1152/jn.1993.70.5.1741. [DOI] [PubMed] [Google Scholar]
- Rottach K, Das V, Wohlgemuth W, Zivotofsky A, Leigh R. Properties of horizontal saccades accompanied by blinks. Journal of Neurophysiology. 1998;79(6):2895–2902. doi: 10.1152/jn.1998.79.6.2895. [DOI] [PubMed] [Google Scholar]
- Roy J, Cullen K. A neural correlate for vestibulo-ocular reflex suppression during voluntary eye-head gaze shifts. Nature Neuroscience. 1998;1(5):404–410. doi: 10.1038/1619. [DOI] [PubMed] [Google Scholar]
- Schiller P, True S, Conway J. Effects of frontal eye field and superior colliculus ablations on eye movements. Science. 1979;206(4418):590–592. doi: 10.1126/science.115091. [DOI] [PubMed] [Google Scholar]
- Schiller P, True S, Conway J. Deficits in eye movements following frontal eye-field and superior colliculus ablations. Journal of Neurophysiology. 1980;44(6):1175–1189. doi: 10.1152/jn.1980.44.6.1175. [DOI] [PubMed] [Google Scholar]
- Schweighofer N, Arbib M, Dominey P. A model of the cerebellum in adaptive control of saccadic gain. I. The model and its biological substrate. Biological Cybernetics. 1996;75(1):19–28. doi: 10.1007/BF00238736. [DOI] [PubMed] [Google Scholar]
- Scudder C, Kaneko C, Fuchs A. The brainstem burst generator for saccadic eye movements. A modern synthesis. Experimental Brain Research. 2002;142(4):439–462. doi: 10.1007/s00221-001-0912-9. [DOI] [PubMed] [Google Scholar]
- Sparks D, Travis R. Firing patterns of reticular formation neurons during horizontal eye movements. Brain Research. 1971;33(2):477. doi: 10.1016/0006-8993(71)90120-x. [DOI] [PubMed] [Google Scholar]
- Sylvestre P, Cullen K. Premotor correlates of integrated feedback control for eye–head gaze shifts. The Journal of Neuroscience. 2006;26(18):4922–4929. doi: 10.1523/JNEUROSCI.4099-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomlinson R, Bahra P. Combined eye-head gaze shifts in the primate. I. Metrics. Journal of Neurophysiology. 1986a;56(6):1542–1557. doi: 10.1152/jn.1986.56.6.1542. [DOI] [PubMed] [Google Scholar]
- Tomlinson R, Bahra P. Combined eye-head gaze shifts in the primate. II. Interactions between saccades and the vestibuloocular reflex. Journal of Neurophysiology. 1986b;56(6):1558–1570. doi: 10.1152/jn.1986.56.6.1558. [DOI] [PubMed] [Google Scholar]
- Tweed D. Three-dimensional model of the human eye-head saccadic system. Journal of Neurophysiology. 1997;77(2):654–666. doi: 10.1152/jn.1997.77.2.654. [DOI] [PubMed] [Google Scholar]
- Viviani P, Berthoz A. Dynamics of the head-neck system in response to small perturbations: analysis and modeling in the frequency domain. Biological Cybernetics. 1975;19(1):19–37. doi: 10.1007/BF00319778. [DOI] [PubMed] [Google Scholar]
- Walton M, Bechara B, Gandhi N. Effect of reversible inactivation of superior colliculus on head movements. Journal of Neurophysiology. 2008;99(5):2479–2495. doi: 10.1152/jn.01112.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zangemeister W, Lehman S, Stark L. Simulation of head movement trajectories: model and fit to main sequence. Biological Cybernetics. 1981;41(1):19–32. doi: 10.1007/BF01836124. [DOI] [PubMed] [Google Scholar]