Abstract
Partial differential equation (PDE) based methods have become some of the most powerful tools for exploring the fundamental problems in signal processing, image processing, computer vision, machine vision and artificial intelligence in the past two decades. The advantages of PDE based approaches are that they can be made fully automatic, robust for the analysis of images, videos and high dimensional data. A fundamental question is whether one can use PDEs to perform all the basic tasks in the image processing. If one can devise PDEs to perform full-scale mode decomposition for signals and images, the modes thus generated would be very useful for secondary processing to meet the needs in various types of signal and image processing. Despite of great progress in PDE based image analysis in the past two decades, the basic roles of PDEs in image/signal analysis are only limited to PDE based low-pass filters, and their applications to noise removal, edge detection, segmentation, etc. At present, it is not clear how to construct PDE based methods for full-scale mode decomposition. The above-mentioned limitation of most current PDE based image/signal processing methods is addressed in the proposed work, in which we introduce a family of mode decomposition evolution equations (MoDEEs) for a vast variety of applications. The MoDEEs are constructed as an extension of a PDE based high-pass filter (Europhys. Lett., 59(6): 814, 2002) by using arbitrarily high order PDE based low-pass filters introduced by Wei (IEEE Signal Process. Lett., 6(7): 165, 1999). The use of arbitrarily high order PDEs is essential to the frequency localization in the mode decomposition. Similar to the wavelet transform, the present MoDEEs have a controllable time-frequency localization and allow a perfect reconstruction of the original function. Therefore, the MoDEE operation is also called a PDE transform. However, modes generated from the present approach are in the spatial or time domain and can be easily used for secondary processing. Various simplifications of the proposed MoDEEs, including a linearized version, and an algebraic version, are discussed for computational convenience. The Fourier pseudospectral method, which is unconditionally stable for linearized the high order MoDEEs, is utilized in our computation. Validation is carried out to mode separation of high frequency adjacent modes. Applications are considered to signal and image denoising, image edge detection, feature extraction, enhancement etc. It is hoped that this work enhances the understanding of high order PDEs and yields robust and useful tools for image and signal analysis.
Keywords: Mode decomposition, Evolution equations, High order PDE transform, Anisotropic diffusion, Total variation, High-pass filter, Partial differential equation
I Introduction
Noise removal, image edge detection, distortion restoration, feature extraction, enhancement, segmentation and pattern recognition are fundamental problems in signal processing, image processing, computer vision, machine vision and artificial intelligence.15, 21, 63 The understanding of these problems and the construction of efficient solutions are essential to optical sorting, automatic control, augmented reality, robotics, sonar, radar, remote sensing, target tracking, surveillance, communication, navigation and a variety of imaging technologies. The primary step toward a solution to these problems is the decomposition of the original signal – image or general data – into various modes according to their frequency distributions. Usually, the subsequent analysis or secondary processing on individual mode components enables us to achieve our goal of processing. Therefore, mode decomposition is a fundamental process in information processing and data analysis.
Fourier analysis15, 41, 53, 63, 69 is one of the oldest techniques and remains one of the most useful techniques for mode decomposition. However, Fourier analysis is subject to a number of limitations. For example, the Fourier method is not suitable for analyzing data of non-stationary nature. Moreover, Fourier analysis is not data adaptive, and it usually lacks the desired information of spatial and temporal localization in many applications. Most importantly, when the signal or image involves abundantly many modes, it becomes very inefficient or even impossible for any non-automatic algorithm to separate individual modes and perform secondary processing on them.
Wavelet transform is another powerful tool for mode decomposition.15, 19, 21, 28, 36, 45, 51, 63, 75 Similar to the Fourier analysis, wavelet transform decomposes a signal or image into frequency sub-bands which correspond to different temporal/spatial scales or resolutions. In this sense, wavelets are often used as filter banks.45 Because the number of sub-bands is usually significantly smaller than that of the Fourier modes, it is much more convenient to carry out the secondary processing on individual sub-band than on individual Fourier mode. Additionally, via appropriate selection of wavelet functions and parameters, wavelet transform is able to provide controlled time-frequency or spatial-temporal localization. Moreover, wavelet analysis can be made fully adaptive and automatic for time varying and non-stationary signal and data. For these reasons, wavelet analysis has become very popular in many applied fields. However, wavelet transform is basically a linear analysis and suffers from many limitations. The down sides include uniformly poor frequency resolution, and sometimes counter-intuitive interpretation.32 In fact, wavelet methods inherit many shortcomings of the Fourier transform since some commonly used wavelets are based on Fourier analysis.
In approximation theory, mode decomposition can be achieved by the projection onto an orthogonal basis normalized in an appropriate norm. The aforementioned Fourier transform can be seen as a form of polynomial projection with harmonic base functions, i.e., trigonometric polynomials. Wavelet bases are usually constructed by a variety of means, such as spline functions and rational functions, in addition to many others. The technique of rational functions is a generalization based on the ratios of polynomial functions. In the Hilbert space analysis, a wide variety of polynomials can be used to construct suitable L2 bases, depending on the geometric property of polynomials. The most commonly used polynomial functions include Chebyshev, Hermite, Legendre and Lagrange.45 Many classical bases are unified in the sense of the Sturm-Liouville theory. In fact, for a well-defined weight function and appropriate geometric domain, one can construct a polynomial basis which is orthogonal with respect to the given weight.
More recently, empirical mode decomposition (EMD)17, 32, 34, 58, 67 has been constructed. Unlike the previous orthogonal decomposition methods, EMD aims to decompose signals and images of arbitrary dimensionality into multiple general hierarchical modes, based on which a secondary processing can be performed. Wang and his coworkers introduced iterative filtering decomposition (IFD).42, 46, 48 EMD and IFD modes are hierarchical in a sense that they are not orthogonal to each other, although there is a perfect reconstruction of the original signal and image from these modes. These modes are called intrinsic mode functions (IMFs).32, 34, 70 Time series or signals are decomposed into a sum of IMFs which have zero mean value and equal (or different by one) number of extrema and zero crossings. Each IMF contains information of instantaneous frequency defined by Hilbert-Huang transforms.20, 33 Additionally, EMD and IFD are highly data adaptive and applicable to non-uniform and non-stationary data.32, 34, 39, 43, 57, 66
Mode decomposition enables one to collect, filter and extract detailed information and knowledge corresponding to various individual modes. These modes could contain information related to frequency distribution, noise distribution, feature allotting, morphology, dynamics and transport of non-stationary signals, and images functions. Apart from applications to signal/image processing, data analysis, remote sensing, target tracking, and surveillance, mode decomposition methods can also be applied to many other fields, such as regression analysis,86 linear programming, machine learning,47, 49 and the solution of partial differential equations.76 Each of these subjects has its own mathematical foundation and fruitful applications in science and engineering. However, a detailed elaboration of these aspects is beyond the scope of the present work.
An elementary operation of signal and image processing is filtering, i.e., the preservation of certain mode components and the elimination of others. Commonly used filters include low-pass, high-pass, band-pass, band-stop and all-pass ones. Among them, low-pass filters are widely used for denoising, whereas high-pass filters are commonly used for image edge detection. A vast variety of filters, such as linear, nonlinear, active, passive, wavelet, Chebyshev, Gaussian, Kalman, Wiener and conjugate filters,27, 64, 65, 86 have been constructed for various applications. The essence that underpins the filtering process is the ability and efficiency of performing mode decomposition or frequency separation. In fact, one can do a lot more than filtering if all mode components are available. For example, one can perform secondary processing on each of the mode components before assembling them into desirable objects. One can also classify individual modes into certain categories, such as noise, image edge, image segment and smooth image before carrying out the secondary processing.
Witkin introduced the diffusion equation for image denoising in 1983.80 The essential idea behind Witkin’s method is that the evolution of an image under a diffusion operator is formally equivalent to the standard Gaussian low-pass filter. Consequently, image denoising can be formulated as an initial value problem of the diffusion equation. The solution to this partial differential equation (PDE) at a later time is a modified smooth image. Nevertheless, the original diffusion equation was not very efficient in denoising — it not only removes the noise but also smears the image edges, which leads to poor vision perception. This problem was addressed by Perona and Malik with an anisotropic diffusion equation,54 in which the constant diffusion coefficient is replaced by a function of image gradients. The essential idea is to make the diffusion coefficient small at the image edges which contribute to large gradients. It was commonly believed that the nonlinear anisotropic diffusion equation facilitates a potentially more effective PDE algorithm for noise removing, image restoration, edge detection, and image enhancement. However, it was shown by further studies that the anisotropic diffusion operator may break down when the gradient generated by noise is comparable to image edges and features.11, 52 One can of course apply a pre-convolution with a smoothing function to the image to reduce grey scale oscillation and to alleviate the instability, but the image quality will inevitably be degraded. One alternative solution introduced by Wei74 is to statistically discriminate noise from image edges by a measure based on the local statistical variance of the image. Such a local statistical variance based edge-stopping works well for image restoration. PDE based methods have attracted great attention in the past two decades.4, 6, 10, 14, 26, 35, 38, 55, 61, 81
Rudin, Osher and Fatemi59 devised image processing as a total variation (TV) problem. The essential idea is that signals and images with extra and possibly spurious components have a relatively large variation or gradient. As such, image processing can be formulated as a problem of minimizing the total energy defined as a functional of the gradient of the image, while preserving important image contents such as edges. The goal of the total energy variation is to reconstruct an image with the best fidelity and the least noise. However, this inverse problem is ill-posed in sense of Hadamard. Regularization procedures are usually used in total variation analysis. The use of different norm measurements for the fidelity term can affect the quality of image restoration. For example, L2 norm based least square algorithms may produce smooth restoration which is inaccurate if the image consists of detailed features such as edges. In contrast, L1 norm algorithms better preserve the edge information in the restored images. The minimization is carried out with the calculus of variations which gives the minimum of the energy functional as the solution of the Euler-Lagrange equation.1, 14 The TV concept provides a rigorous mathematical algorithm to introduce nonlinear diffusion equations and has been employed as a regularization approach for many applications where one needs to preserve discontinuous features.12
To improve the efficiency of noise removing, Wei introduced the first family of arbitrarily high order nonlinear PDEs for image denoising and restoration in 1999.74 Recently, an arbitrarily high order geometric PDE was proposed by Bates et al. for the construction of biomolecular surfaces.5 Many fourth-order evolution equations were introduced in the literature for image analysis.13, 24, 44, 68, 85 These equations were proposed either as a high-order generalization of the Perona-Malik equation5, 74 or as an extension of the TV formulation.13, 44, 68, 85 The essential assumption in these high order equations is that high-order diffusion operators are able to remove high frequency components more efficiently. Mathematical analysis of these high order equations in Sobolev space was carried out by Bertozzi and Greer,7, 24, 25 which proved the existence and uniqueness of the solution to a case with H1 initial data and a regularized operator. Similar analysis was performed by Xu and Zhou.82 Jin and Yang proved the existence of strong solution of Wei’s fourth-order nonlinear operator.37 Witelski and Bowen proposed alternating-direction implicit (ADI) schemes for high order image processing PDEs.79
Image processing PDEs of the Perona-Malik type and total variation type are mostly designed to function as nonlinear low-pass filters. In 2002, Wei and Jia77 introduced coupled nonlinear PDEs to behave as high-pass filters. These coupled PDEs are used for image edge detection. The essential idea behind these PDE based high-pass filters is that when two Perona-Malik type of PDEs evolve at dramatically different speeds, the difference of their solutions gives rise to image edges. This follows from the fact that the difference between an all-pass filter (i.e., identity operator) and a low-pass one is a high-pass filter.77 The speeds of evolution in these equations are controlled by the appropriate selection of the diffusion coefficients. These PDE-based edge detectors have been shown to work extremely well for images with large amount of textures.64, 77
Despite of great progress in PDE based image analysis in the past two decades, a fundamental question is whether one can use PDEs to perform all tasks in the image processing. To certain extent, this is equivalent to ask whether one can devise PDEs to perform a full-scale mode decomposition for signals and images. As discussed earlier, when all the mode components are available, it is trivial to manipulate them for all image processing purposes. The main difficulty at present is that it is still unclear how to formulate PDEs for mode decomposition. The objective of the present work to construct a PDE based algorithm for mode decomposition of signals, images and functions. All of the important building blocks for the construction of the mode decomposition evolution equations (MoDEEs) were developed in our earlier work, i.e., arbitrarily high order PDE filters74 and PDE based high-pass filters.77 The increase in the order of the PDE leads to better frequency localization, which is desirable for certain applications. Additionally, the MoDEEs need to regenerate the initial value in order to systematically extract all IMFs, an algorithm previously used in our mode decomposition via iterative filtering,42, 70 which is equivalent to the use of high order PDE high-pass filters. The MoDEE yields band-frequency components (or modes) by recursively extracting high frequency signals using high order PDEs. The proposed MoDEEs behave like Fourier transform and wavelet transform — the intrinsic modes yielded by the MoDEEs have a perfect reconstruction of the original function. The frequency localization of the MoDEEs is controlled by the order of the PDEs. In addition, with other parameters optimized, MoDEE algorithm is capable of attaining high accuracy besides adaptive robustness. It is worthwhile to note that such optimization is important and useful tool for general applications in mathematics and physical science.83 In this sense, we also call the operation of the MoDEEs a PDE transform. However, the proposed PDE transform is capable of decomposing signals and images into various “functional” modes instead of pure frequency modes like those in Fourier transform. By functional modes, we mean the components which share similar band of frequencies or belong to same category, e.g., noise, edge and trend. But unlike wavelet transform, the proposed PDE transform works like a series of low-pass and/or high-pass filters in the spatial or time domain only. As such, the subsequent secondary processing on each individual mode become robust and controllable, leading to desirable processing effects.
The rest of the present paper is organized as follows. Section II is devoted to the theory and algorithm of the proposed PDE transform or the MoDEEs. We start with a brief review of high order image processing PDEs and PDE based high-pass filters. The MoDEEs are constructed by an appropriate generalization of the PDE based high-pass filters.77 A number of MoDEE systems are presented. The nth order MoDEE system involves the 2nth order PDEs. Computational algorithms are proposed in Section III. As the proposed MoDEEs are coupled nonlinear PDEs involving high order derivatives, their solution is non trivial. We propose many simplified MoDEE systems, including decoupled MoDEEs, linear MoDEEs and algebraic MoDEEs to reduce computational complexity. The Fourier pseudospectral method64, 84 is employed to numerically solve the MoDEE systems. This approach is exact for certain class of PDEs. Numerical tests and validations are presented in Section IV. A benchmark test is to separate adjacent frequency modes in a function or signal. This test becomes difficult when the adjacent modes are of high frequencies. Other tests include image edge detection, denoising and enhancement. We show that the proposed MoDEEs are able to perform well on all these tests. In Section V, applications of proposed PDE transform are considered to the processing of a few medical images. We demonstrate the performance of the proposed MoDEEs for image denoising, restoration and edge detection. This paper ends with some concluding remarks.
II Theory and formulation
This section presents the theoretical formulation of PDE based mode decomposition methods. To establish notation and illustrate concepts, we briefly review high order PDE based nonlinear low-pass filters introduced by Wei74 and PDE based nonlinear high-pass filters introduced by Wei and Jia.77 The construction of mode decomposition evolution equations follows as a natural extension of PDE based nonlinear high-pass filters.
II.A High order PDE based low-pass filters
Motivated by a number of physical phenomena, such as pattern formation in alloys, glasses, polymer, combustion and biological systems, Wei introduced some of the first family of high order nonlinear PDEs for image processing in 199974
| (1) |
where u(r, t) is the image function. Here dq(u(r), |∇u(r)|, t) and e(u(r), |∇u(r)|, t) are edge sensitive diffusion coefficients and enhancement operator respectively. Equation (1) is a generalization of the Perona-Malik equation,54 where the latter is recovered at q = 0 and e(u(r), |∇u(r)|, t) = 0. The hyper diffusion coefficients dq(u(r), |∇u(r)|, t) were chosen as
| (2) |
where the values of constant dq0 depend on the noise level, and σ0 and σ1 were chosen as the local statistical variance of u and ∇u
| (3) |
The notation denotes the local average of X(r) centered at position r. The statistical measure based on the variance is important for discriminating image edges from noise. By using this measure, one can avoid the use of preprocessing, i.e., the convolution of the noise image with a smooth mask. In general, both Neumann type or periodic boundary conditions can be imposed. However, if arbitrarily high order PDEs are devised, periodic boundary conditions are better choices, as are chosen for the application with Fourier pseudospectral methods in this paper. The numerical application of Eq. (1) to image denoising and restoration was demonstrated and the performance of this equation was compared with that of the Perona-Malik equation54 by Wei74 and many other researchers.22, 23, 44 The well-posedness of the generalized Perona-Malik equation was analyzed in terms of the existence and uniqueness of the solution.7, 24, 25, 37, 82 It was argued that the mathematical properties of the generalized Perona-Malik equation differ from those of other high order PDEs.37 The stability of Eq. (1) follows from appropriate choice of diffusion coefficients dq(u(r), |∇u(r)|, t), e.g., the sign of dq should be (−1)q. However, other choices of the signs were also explored in forward-and-backward diffusion processes to achieve simultaneous image denoising and enhancement.22
II.B Nonlinear PDE based high-pass filters
By 2000, there had been a large number of publications that explored PDE based image processing approaches. However, most of the research was focused on the use of even-order partial derivatives as a means to smooth images, i.e., as low-pass filters. These PDE approaches were inefficient for image edge detection, particularly for images with a large amount of texture. This is due to the fact that edge detection is a high-pass filtering operation, while the diffusion process is inherently a low-pass filtering process. Wei and Jia addressed this issue by introducing a pair of weakly coupled nonlinear evolution equations in 200277
| (4) |
| (5) |
where u(r, t) and v(r, t) are scalar fields with Neumann boundary conditions imposed, εu and εv are coupling strengths. F1 and F2 are general nonlinear functions which can be chosen as the Perona-Malik operator
| (6) |
with dj(|∇uj|) = dj0 exp[−|∇uj|2/(2σ2)], u1 = u and u2 = v. The initial values for both scalar fields were chosen to be the same image of interest, i.e., u(r, 0) = v(r, 0) = I(r). In the theory of nonlinear dynamics, Eqs. (4) and (5) constitute a synchronization system. To attain an appropriate image edge contrast, the original image must evolve under dramatically different time scales, i.e., either d10 ≫ d20 or d20 ≫ d10. The coupling strengths ε1 and ε2 were set to be relatively small (i.e., εu ≅ εv ~ 0) so that the rate of change of u or v was dominated by the diffusion process. The coupling term plays the role of relative fidelity. This becomes clear when d10 ~ 0. The image edge was defined as the difference of two dynamical systems
| (7) |
To ensure a normal performance of diffusion operator, one of the diffusion coefficients d10 or d20 must be of similar amplitude as that used in the Perona-Malik dynamics. If we choose d20 to be a normal one, the requirement of d20 ≫ d10 implies that d10 ≈ 0. As such, w(r, t) in Eq. (7) behaves like a band pass filter. In the extreme case, if we set d10 = 0, we have a PDE based high-pass filter
| (8) |
This setting is often used in our practical applications.64, 65 The PDE based high-pass filters have been shown to be very robust and efficient. They provide superior results in image edge detection compared to those obtained by using other existing approaches, such as the Sobel, Prewitt, and Canny operators, and by anisotropic diffusion.77
II.C Mode decomposition evolution equations (MoDEEs)
The high-pass PDE filter discussed above does not discriminate different high frequency modes or components. The goal of the proposed project is to devise a PDE based system for systematic separation of all the mode components, including high order modes. This requires a generalization of the PDE based high-pass PDE filter. To this end, we first cast Eqs. (4) and (5) into a matrix form
| (9) |
where all quantities are same as those defined in the last section. Considering the fact that w ~ u − v, we can arrive at a more compact form
| (10) |
Since εu ≅ εv ~ 0, for simplicity, we drop the coupling strengths (εu + ε1) in the evolution equation of w
| (11) |
where we have relabled variables v and w as v1 and w1, respectively. Note that the PDE for “edge” w in Eq. (11) is very different from the other two genuine PDEs for u and v. The solution of w is easily obtained by integrating the corresponding PDE once only, provided that u and v are given. Equation system (11) is hereafter referred to as the first MoDEE system.
For problems involving high frequency modes, we need to construct the high order MoDEEs. The matrix form (11) can be easily generalized to include fourth order derivatives
| (12) |
where differential equations of u and v2 employ the fourth order nonlinear low-pass filters given in Eq. (1). Here w2 is more sensitive to high frequency components than w1 is. Therefore, w2 contains the information related to the difference between high order modes. As discussed earlier, it is computationally cheaper to solve edge functions w2 than to solve u and v2. We have utilized the fourth order operator designed by Wei74 in the above formulation. The initial values of u and v2 are set to the original image or signal of interest. The initial value of w2 can be set to zero. Equation system (12) is hereafter referred to as the second MoDEE system.
If the task is merely to detect image edges, one may just use the first MoDEE system or the high-pass filter of Wei and Jia to obtain desirable results as demonstrated in our earlier work.64, 77 However, if one wants to separate high frequency modes, the second MoDEE system is a better candidate than the first one.
For highly oscillatory signals, images and functions, in order to separate all the high frequency modes, which is desirable in many applications, we need the MoDEEs containing even higher order PDEs. To this end, we construct an nth order system
| (13) |
Equation (13) can be solved to generate nth edge functions wn. Similar to the first MoDEE system, the nth MoDEE system works when one sets duj+1 ~0, j = 0, · · ·, n − 1, εu ~ 0, and εn ~ 0. Since all PDEs are designated as smoothing operators, all odd diffusion coefficients, such as du1, du3, · · ·, dn1, dn3, · · · are to be positive and all even diffusion coefficients are to be negative. In order to separate high order modes, it is practical to set all duj+1 = 0 and dnj+1 = 0, except for dun and dnn.
III Simplified models and computational algorithms
III.A Linear MoDEEs
In general, we need to solve systems of coupled, nonlinear, high order PDEs as shown in Eq. (13), which can be technically demanding. However, for many practical problems, we can design simplified MoDEE models which also work well. Based on the physical understanding, various simplifications of the MoDEE systems are presented to reduce the computational complexity. Numerical algorithms for solving the high order MoDEEs are also discussed in the following paragraphs.
The first approximation is to set εj = 0 in the MoDEEs. This approximation leads to the decoupling of all MoDEEs. The uncoupled MoDEEs are much easier to solve. The solutions of decoupled PDEs are also easy to interpret, which makes the selection of mode parameters easy.
Another useful approximation is to eliminate nonlinearity and positional dependence of all the diffusion coefficients. The nonlinear models work better for most application as evident from our own experiments. However, for certain class of problems with smooth functions, the nonlinear edge sensitive diffusion coefficients do not play the critical role. Signal processing is a typical example. Therefore, the linear MoDEE systems are computationally favored. As an example, we can obtain a linear form of the nth MoDEE system from Eq. (13):
| (14) |
The linear MoDEE systems can be easily solved with the Fourier pseudospectral methods.65, 84
III.B Algebraic MoDEEs
To further simplify the MoDEE systems, we can make use of the algebraic relation given in the original formulation of Wei and Jia.77 The use of algebraic relations saves the computational cost of integrating the edge equations. We first consider a set of linear equations modified from Eq. (14)
| (15) |
These linear equations offer copies of smoothed image functions. After solving Eq. (15) for u and vn, we determine the mode functions by the simple form of Wei and Jia as that given in Eq. (7)
| (16) |
By the appropriate selection of parameters, wn(r, t) delivers desirable mode functions. It behaves as a band-pass filter.
Another simple choice is to determine the mode functions by the form given in Eq. (8)
| (17) |
where I(r) is an initial value. As such, we do not need to solve the PDE for u. It behaves as a high-pass filter. We expect that wn in Eq. (17) performs similar to wn in Eq. (16) does when the parameters are appropriately selected.
Obviously, there are still many other ways to construct mode vectors. Essentially, for a given application, the selection of appropriate vn for the construction of jth order mode component can be formulated as an optimization problem. It is beyond the scope of the present work to discuss other alternative MoDEEs.
Similar to the IFD algorithm,42, 70 we extract the highest frequency component first, then residual is used as the initial value for u and vn to extract the second highest frequency component. We continue this procedure until all components or intrinsic mode functions are separated. Note that this procedure is inherently nonlinear, even if the linear MoDEEs are used. Unlike the IFD algorithm, no (internal) iteration is used — to extract an intrinsic mode, we only solve the MoDEE once.
We also noted that one can extract the lowest intrinsic mode function first. Then the residual is used as the initial value in the MoDEE to extract second lowest intrinsic mode function. One continues this procedure until all the intrinsic modes are systematically separated one by one.
Using the PDE transform algorithm discussed above, intrinsic mode functions are systematically extracted from residues, a perfect reconstruction is straightforward by summing all the modes and final residue In, i.e.,
| (18) |
In practical computations, either the periodic boundary condition or the Neumann boundary condition can be used in all the proposed MoDEEs. When Fourier spectral methods is used for integration in this paper, periodic boundary condition is applied.
III.C Numerical methods for high-order MoDEEs
The proposed MoDEEs involve many high order PDEs which have to be solved in an appropriate manner to avoid the accumulation of numerical errors. Essentially, there are two important issues in the solution of high order evolution PDEs. The first issue concerns the accuracy of approximating high order derivatives. The rule of thumb here is that to approximate high order derivatives, high order numerical methods are required.72, 87 High order finite difference methods based on the Lagrange polynomials, Fourier pseudospectral methods and local spectral methods are suitable approaches for approximating high order derivatives. The second issue is the stability constraint in solving high order evolution PDEs. When the explicit (forward) Euler type of time discretization is used to solve an nth order evolution PDE, the step size Δt of time is constrained by Δt ~ (Δx)n, where Δt is the spatial grid spacing. Therefore, it is desirable to use alternative direction implicit (ADI) type of implicit methods for the time discretization. ADI type of methods has been previously developed by us to solve high order geometric flow equations.5, 18
To solve the decoupled linear MoDEEs (15), we use the Fourier pseudospectral method. Spectral methods have been a popular choice for the numerical solution of various wave problems in recent years. As global methods, the Fourier spectral methods usually are much more efficient than local methods (e.g., finite difference and finite element methods) for certain classes of nonlinear problems. We applied Fourier pseudospectral method to the solution of the Navier-Stokes equation and other PDEs.65, 84 This approach is unconditionally stable and particularly efficient for solving the high oder MoDEEs proposed in Eq. (15). A windowed Fourier pseudospectral method has been developed for hyperbolic conservation laws, i.e., Euler equations.65
IV Numerical tests and validations
IV.A Intrinsic mode decomposition
In this section, the MoDEE is applied to and validated on several benchmark testing cases to demonstrate the flexibility, efficiency, and accuracy of the method. In this paper, we use Fourier spectral methods to numerically integrate PDEs in one-step.
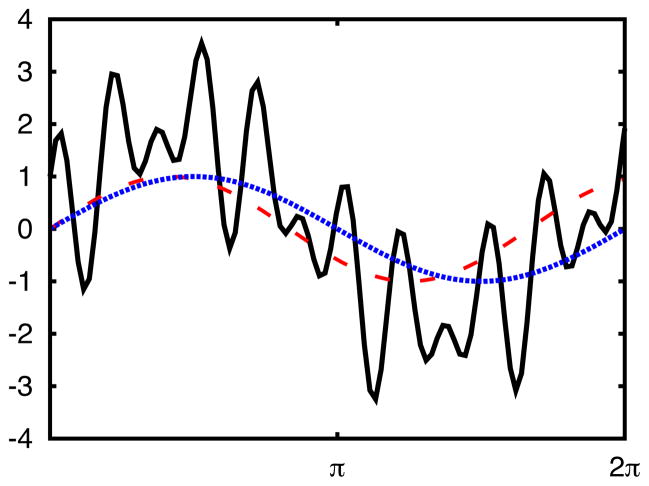
We first illustrate the efficiency and accuracy of the MoDEE algorithm III.B using signal f(x) = sin(x)+ sin(1.2x) + cos(2x) + sin(12x), as shown in Figure 1. In the figure, x-axis is in the domain of [0, 2π]. The total signal f(x) is shown in solid black curve, and the two modes with close frequencies, sin(1.2x) and sin(x), are chosen to be plotted with red dashed and blue dotted lines, respectively. The MoDEE decomposes the original signal into four modes which agree very well with the analytical results, and no visible difference can be observed when the 32nd order PDE is used in the MoDEE. Note that mode 3 of sin(1.2x) and mode 4 of sin(x) are closely embedded in f(x) and are thus difficult to be separated using many methods other than Fourier transform or wavelet methods. To investigate the MoDEE method in detail, various high order PDEs are used to separate the same signal. In Table 1, the MoDEE method illustrates its advances in separating out various modes clearly. When the highest order of the PDE used in the MoDEE is increased from 8 to 32, the L2 error of various modes separated numerically decreases by orders of magnitude. The signal here is perfect candidate for the application of the Fourier method, and the MoDEE gives satisfactory decomposition accurately.
Figure 1.
Mode separation using the MoDEE method with the 32nd order PDE. Black curve shows the signal f(x) = sin(x) + sin(1.2x) + cos(2x) + sin(12x). X-axis is in the unit of π, and the domain of [0, 2π] is shown in the plot. Red dashed and blue dotted lines show the 3rd mode sin(1.2x) and 4th mode sin(x) respectively. All the four modes, including the 3rd and 4th modes which are very close in frequencies, are separated using the MoDEE method using the 32nd order PDE. Numerical results agree well with the exact values with no visible difference. The L2 norm of the errors are smaller than 0.01.
Table 1.
Comparison of the accuracy of mode decomposition using various high order PDEs in the MoDEE scheme.
| Highest order of the PDE | mode number | L2 error |
|---|---|---|
| 8 | 1 | 0.084879 |
| 2 | 0.073587 | |
| 3 | 0.261249 | |
| 4 | 0.209813 | |
|
| ||
| 16 | 1 | 0.006547 |
| 2 | 0.006035 | |
| 3 | 0.106525 | |
| 4 | 0.091147 | |
|
| ||
| 32 | 1 | 0.000020 |
| 2 | 0.000019 | |
| 3 | 0.011317 | |
| 4 | 0.010353 | |
In Figures 2 and 3, plots are shown to compare the effect of high order PDEs on mode separation as illustrated as in Table 1. Mode 1 of sin(12x) is plotted in the Figure 2. Red circles in three panels show the result using the MoDEE method with different highest order of PDEs, and black curves show the analytical results of sin(12x) as reference. The highest order of PDEs as in ∇2n in Eq. (15) are 8, 16, and 32 respectively. For this mode, the use of up to the 16th order PDE is enough for the convergence. Similar plots of the decomposition of the third mode sin(1.2x) from the fourth one sin(x) are shown in Figure 3. A higher order PDE of up to 32nd order is required for the separation of closely overlapping modes 3 and 4. The results illustrate how important it is and when it is necessary to include very high order PDEs for signal processing. In addition, it is shown that the MoDEE using very high order PDEs is still very stable and does not diverge.
Figure 2.
Mode 1 of sin(12x) separated from signal in Figure 1 using the MoDEE with various orders of PDEs. Black curves in three panels show the exact results of mode 1 of sin(12x), and red circles show the MoDEE results. The values of the highest order of PDEs used are 8, 16, and 32 respectively from the left to right panel.
Figure 3.
Mode 3 of sin(1.2x) separated from signal in Figure 1 using the MoDEE with various orders of PDEs. Black curves in three panels show the exact results of mode 1 of sin(1.2x), and red circles show the MoDEE results. The values of the highest order of PDEs used are 8, 16, and 32 respectively from the left to right panel.
Lastly, we illustrate the spectral accuracy achieved by the MoDEE using signal composed of two modes of cos(mπx) and cos((m − 1) πx), where m is the maximum frequency supported by the mesh size (which is 0.05 in this example, and thus m = 20), i.e. two grid points for each oscillation period. In Figure 4, f(x) = cos(mπx) + cos((m − 1) πx) is decomposed into two frequency modes, cos(mπx) and cos((m − 1) πx), using the MoDEE. The comparison of numerical results are shown in Figures 4(b) and 4(c) respectively. Black curve shows the exact values, and red circles show the numerical results. Highly accurate MoDEE decomposition is observed in the figures where the 32nd order PDE is employed in the MoDEE algorithm as in Section III.A.
Figure 4.
Plots of f(x) = cos(mπx) + cos((m − 1) πx) where m = 20 corresponds to the maximum frequency supported by the finite grid mesh size chosen here.
IV.B Image denoising, edge detection and enhancement
Image processing is becoming increasingly important in many areas of research in physical, mathematical and biological sciences.16, 29, 30, 40, 56 In particular, edge detection is a key issue in pattern recognition, computer vision, target tracking and image processing.2, 3, 9, 50, 60, 62 Closely related to edge detection is denoising. PDE methods provide powerful tools image processing. The MoDEE is designed for both accurately decomposing modes with different frequency (or “frequency-modes”) with spectral accuracy and effectively decomposing modes with different functions (of “functional-modes”) for image enhancement like edge detection, denoising, segmentation, etc.
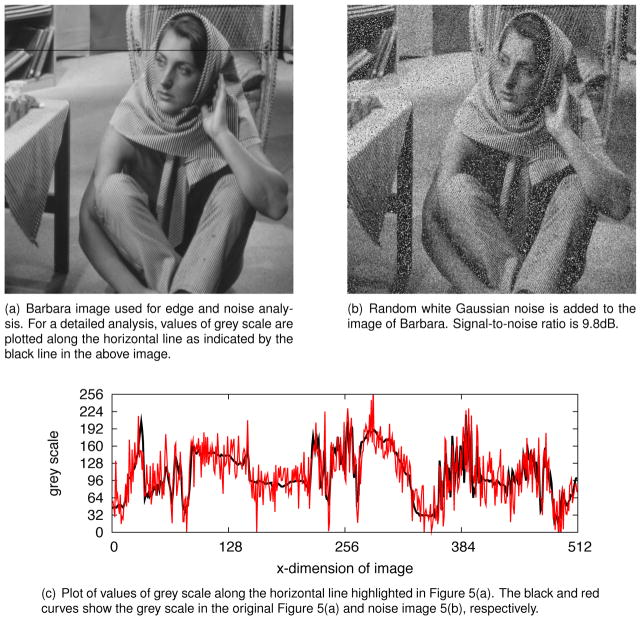
The 512×512 grey-scale Barbara image as shown in Figure 5(a) is used to test the MoDEE algorithm. The same image has been extensively used in the literature due to its fine details associated with multiple edges. In Figure 5(b) random white Gaussian noise with signal to noise ratio (SNR) of 9.8 dB was added to the original image. For a quantitative view of the magnitude of SNR and effect of PDEs on the image enhancement, values of grey scale along a randomly chosen horizontal line is plotted before and after image processing. In Figure 5(a), such a horizontal line is specified by a dark grey line crossing the forehead of the Barbara image. In Figure 5(c), the black curve shows the grey scale values along the chosen horizontal line in the original Barbara image, and the red curve shows the values of the same horizontal line in the noise-added Barbara image 5(b). The added noises overlap closely with the edges of the original image, such that any denoising would smear the fine details of edges.
Figure 5.
Grey scales of the original and noise-added Barbara image.
The MoDEE algorithm in III.A is applied to denoise the image while preserving the edge details as best as possible by taking difference between two PDEs with different diffusion constant and inclusion of high order PDEs. In Figure 6, values of grey scale along the horizontal line Figure 5(a) are plotted. Black solid curves show the original grey scale without noise. Blue curves show the grey scale of the same horizontal line after image processing using the MoDEE algorithm with evolution time Δt = 10, du2 = 0.05 and dn2 = 0.4. Red curves show the grey scale using the same MoDEE algorithm with different value of du2 = 0. It is clear from the image, especially in those intervals as magnified and shown in Figures 6(b), 6(c) and 6(d), that the blue curves capture more details of various image edges with better accuracy than those red curves. The better accuracy illustrates the advantage of employing the difference between two high-pass filters in image processing as is employed in the MoDEE algorithms. For visual observation and comparison, denoised images using the two aforementioned MoDEE equations and parameters are shown in Figures 6(e) and 6(f). SNR is improved from 16.9 dB in Figure 6(e) to 17.4 dB in 6(e). Though the improvement in SNR alone is not very significant, the visual enhancement is more significant due to the improvement in capturing more fine edge details.
Figure 6.
Noise removal in the Barbara image using the MoDEE algorithm.
As given by Eq. (18), the MoDEE algorithm allows straightforward reconstruction of the original image through various modes and residue. In terms of image processing, the MoDEE algorithm automatically extracts noise, denoised image and image edges at the same time. The denoised image is shown in Figure 6(f), and the residual is therefore shown in Figure 7(a) which corresponds to the image edge. In addition, as aforementioned, the MoDEE is a general scheme allowing feature extraction and secondary processing of the decomposed functional modes. The residual in Figure 7(a) which contains image edges can be further post-processed by applying MoDEE algorithm once more. To achieve good performance, both the residue and edge mode from previous MoDEE application are utilized in the second MoDEE application. The reference-assisted “denoised” mode of the image in Figure 7(a) is shown in Figure 7(b). Comparing the two figures, it can be observed that edges in Figure 7(a) are finer and sharper, representing good edge extraction. On the other hand, edges in Figure 7(b) have varying density and look more natural to human eyes with more physical features captured in detail, e.g. the shade on the elbow of the left hand of Barbara. The edges in Figure 7(b) can be seen as an edge “representation” rather than edge extraction, where stronger and more meaningful edges are shown as denser lines while more subtle edges are shown as finer lines. In many applications this representation may prove to be very useful.
Figure 7.
Edge detection and secondary processing using the MoDEE algorithm.
V Applications
In the past two decades advances in medical imaging using magnetic resonance imaging (MRI) or computed tomography (CT) technology have enabled both clinicians and researchers to collect and analyze large collection of medical images. In this section, the MoDEE algorithm is applied to various types of medical images.
V.A Magnetic resonance images
MRI is built upon the physical theory of nuclear magnetic resonance (NMR): a nucleon such as proton possesses spin which has value of multiples of 1/2, and those nuclei with unpaired spins tend to align with the orientation of the externally applied magnetic field. After alignment, high frequency pulses, usually in the range of radio frequency (RF) of MHz, are emitted into a slice plane perpendicular to the external field to excite the aligned spins. RF waves are then turned off such that excited nucleus undergo a relaxation process to resume its original distribution. Different types of biological structures and tissues have different characteristic relaxation time which can be measured by MRI hardware and software to construct associated spatial images. Using MRI technique, each pulse sequence exploits some specific physical or chemical property of the protons of small, mobile molecules like water and lipids. Therefore, one could depict structural and functional information from living tissue at the sub-millimeter scale.
Though the medical imaging techniques have advanced tremendously in terms of spatial resolution, acquisition speed, and signal-to-noise ratio, medical images thus created still need to be carefully enhanced to account for factors like signal intensity inhomogeneities (i.e. bias fields), noise, and other artifacts. Noise, as one example, in MRI enters the data samples in k-space and competes with the NMR signal due to random fluctuations in the receiving coil electronics and in the patient body. In the case of function MRI (fMRI)8 for brain mapping and diffusion tensor imaging (DTI)73, 78 for studying neural fibers, the amount of random thermal noise entering MRI data in the time domain in the acquisitions limits the performance and usefulness of quantitative MRI diagnostics such as voxel-based tissue classification, extraction of organ shape or tissue boundaries, estimation of physiological parameters like tissue perfusion and contrast agent permeability from dynamic imaging.31, 44 Despite of much progress made in post-processing methods for noise reduction and image enhancement, it remains a challenge to find robust and interacting ways for noise removal, boundary preservation applicable to the different MRI acquisition techniques.
In Figure 8, the MoDEE algorithm using PDE (9) is used to detect edges for blur medical images obtained using MRI. Figure 8(a) is obtained using cardiac magnetic resonance imaging (cMRI) for a 21-year old woman referred for clinical management of idiopathic dilated cardiomyopathy (the image is authored by the European society of cardiology). By applying the MoDEE algorithm with evolution time Δt = 10, du2 = 0.2 and dn2 = 0.52, one obtains satisfactory results with enhanced edge detection in Figure 8(b) which shows a dilated left ventricle, without evidence of tissue abnormalities (e.g. scars, patchy fibrosis).
Figure 8.

Edge detection and registration using the MoDEE algorithm.
V.B Magnetic resonance angiography images
Magnetic resonance angiography (MRA) image stands for a group of important techniques based on MRI to image blood vessels. MRA is often used to evaluate the arteries of the neck and brain, the thoracic and abdominal aorta, the renal arteries and the legs to diagnose symptoms like stenosis (abnormal narrowing) and occlusion or aneurysms (vessel wall dilatations, at risk of rupture), etc. An advantage of MRA compared to invasive catheter angiography is the non-invasive character of the examination. In particular, compared to computed tomography and angiography and catheter angiography, MRA does not expose patient to any ionizing radiation. The greatest drawbacks of the method are its comparatively high cost and its somewhat limited spatial resolution. In addition, the length of time the scans take can also be an issue, with computed tomography being far quicker. Therefore, image processing technique is important for post-processing the images generated by MRA to save cost, improve resolution and extract/highlight important features like fine details of edges of arteries.
The image shown in Figure 9(a) is downloaded from the website of Magnetic Resonance and Image Analysis Research Centre, University of Liverpool. The image is used to show the vessels known as the circle of will is in the brain. To test the ability of edge detection and noise removal, original image is added with noise. For a realistic setting the total noise added to the MRA image 9(a) is composed of two parts, η(x, y) = σ (x, y) + γ (x, y), where σ (x, y) is white Gaussian noise with maximum amplitude 25 and zero mean, and γ (x, y) is a periodically oscillating cosine noise given by
Figure 9.
Edge representation in noised image using the MoDEE algorithm.
| (19) |
The noisy image is shown in Figure 9(b). To remove both noises closely embedded in the original image, we apply the MoDEE algorithm in Section III.A including 20th order PDE with du2 = 0.01 and dn2 = 0.47. The resulting enhanced image is shown in Figure 9(c), in which both types of noises have been reduced and edges are clearer for medical diagnosis.
V.C X-ray computed tomography images
Computed tomography (CT) is a technology of using X-rays to image biological and human body. Compared to visible spectra imaging, X-rays have wavelengths between nanometer and picometer scales, which are energetic enough to penetrate biological tissues. Denser structures like the bones are more efficient at absorbing X-rays compared to softer tissues. This leads to the noninvasive medical imaging. CT is a popular technique for reconstructing the X-ray images with delicate hardware design as well as computer software. In CT scanning, a localized X-ray source and corresponding detector are put opposite to each other and rotate around the human body. The 2D slice image is then synthesized from the X-ray signals around all the directions. In the last few decades, CT technique has been widely used in medical imaging of soft tissues, hard bonds, blood vessels, etc.
In Figures 10(a) and 10(c), two different CT abdomen images are shown corresponding to different patient with slightly different shapes and edges of the organ in the abdomen. The MoDEE algorithm using PDE (9) is applied to detect edges in these two original CT images. The same set of MoDEE coefficients are used with du2 = 0.22 and dn2 = 0.5. In particular, figure 10(a) shows the CT image of abdomen of a 68-year old male, image authored by Maclennan, Radiologist, Royal Alexandra Hospital, Paisley, United Kingdom. Edge enhanced image using the MoDEE algorithm is shown in Figure 10(b) which shows with better clarity (e.g. finer edges and tiny circles) the calcific density mass with flat upper margin in neck of gallbladder. The flat margin suggests that whatever is causing the mass is layering under the effect of gravity. Figure 10(c) shows a similar cross-sectional image of abdomen, with image authored by Department of Health and Human Services, using computerized axial tomography (CAT) scanning technique. The MoDEE captures the small differences which are reflected in the final edge-extracted image 10(d). The shape of the tiny circles in the liver are clearly highlighted.
Figure 10.
Edge detection and registration using the MoDEE algorithm.
As a short conclusion, through the applications and images shown in this section, it is illustrated that the MoDEE algorithm provides a robust and powerful tool for various image processing and enhancement tasks of interest to both clinical and research scientists equipped with various types of medical imaging techniques.
VI Concluding remarks
Digital image processing, signal processing and video processing underpin a number of modern technologies for optical sorting, automatic control, augmented reality, robotics, sonar, radar, remote sensing, target tracking, communication, navigation and imaging. Mode decomposition is an elementary operation in image and signal processing, and enables essentially all the other processing tasks such as noise removal, image edge detection, distortion restoration, feature extraction, enhancement, segmentation, and pattern recognition. Although there are many mode decomposition techniques such as empirical mode decomposition (EMD),32 iterative filtering decomposition42, 70, 71 and wavelets, partial differential equation (PDE) approaches have not been discovered. A major obstacle is due to the limited understanding of high order PDEs. High order PDEs have been conventionally considered as computational unstable as well as unnecessary in physical modeling and image analysis. The present work constructs a PDE based framework for mode decomposition of signals, images and functions. We show that it takes an in-depth understanding of the performance and function of arbitrarily high order PDE based low-pass filters74 and nonlinear PDE based high-pass filters77 to construct PDE based methods for mode decomposition analysis. Inspired by our mode decomposition via iterative filtering,42, 70 we propose a family of mode decomposition evolution equations (MoDEEs) in the present paper. The construction of the MoDEEs is equivalent to the design of high order PDE based high-pass filters. The proposed MoDEEs yield band-frequency components (or modes) by recursively extracting high frequency signals using high order PDEs. The MoDEEs behave like Fourier transform and wavelet transform — the intrinsic modes generated from the MoDEEs have a perfect reconstruction of the original function. In this sense, we also call the operation of the MoDEEs a PDE transform. However, the proposed PDE transform is capable of decomposing signals and images into various “functional” modes instead of pure frequency modes like those in Fourier transform. By functional modes, we mean the components which share similar band of frequencies or belong to same category, e.g., noise, edge and trend. But unlike wavelet transform, the proposed PDE transform works like a series of low-pass and/or high-pass filters in the spatial or time domain only. As such, the subsequent secondary processing on each individual mode becomes robust and controllable, leading to desirable processing effects. The Fourier pseudospectral method has been utilized in our numerical solution of high order PDEs. This method is unconditionally stable and very efficient for the linearized MoDEEs.
The present MoDEE approach is carefully validated on several benchmark testing cases to demonstrate its ability, usefulness, and efficiency. We first consider the standard test of mode separation of signals and functions. We have shown that the proposed MoDEEs are able to effectively split high frequency adjacent modes. Such a result enables us to separate noise from signals in many situation and perform many other secondary processing tasks. The applications of the present MoDEEs are considered to image edge detection, feature extraction, denoising and enhancement. The method is also applied to various types of medical images obtained using MRI, MRA and CT.
The proposed MoDEEs can be extended in a number of ways. First, different forms of MoDEEs can be constructed based on the proposed principles. This can be formulated as a problem of variation for a given application. Additionally, the role of nonlinear PDEs will be explored. Anisotropic diffusion type of schemes are expected to yield better results. Moreover, computational methods for the nonlinear high order MoDEEs deserve a further study. Stable scheme is crucial for the implementation of high order PDEs. Furthermore, parameter optimization is an important issue in the MoDEE applications too. For example, frequency localization achieved by increasing the highest order of the MoDEEs may be desirable in certain applications, but may be undesirable when certain functional modes are to be extracted. Finally, the MoDEE algorithm is in a best position, which has been partially verified in this paper, due to its high accuracy and adaptive robustness, to be combined with and optimized by other techniques and applications such as regression analysis, linear programming and machine learning.
Acknowledgments
This work was supported in part by NSF grants CCF-0936830 and DMS-1043034; NIH grant R01GM-090208; MSU Competitive Discretionary Funding Program grant 91-4600.
Literature cited
- 1.Angenent S, Pichon E, Tannenbaum A. Mathematical methods in medical image processing. Bulletin of the American Mathematical Society. 2006;43(3):365–396. doi: 10.1090/s0273-0979-06-01104-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Archibald R, Gelb A, Saxena R, Xiu DB. Discontinuity detection in multivariate space for stochastic simulations. Journal of Computational Physics. 2009;228(7):2676–2689. [Google Scholar]
- 3.Archibald R, Gelb A, Yoon JH. Polynomial fitting for edge detection in irregularly sampled signals and images. SIAM Journal on Numerical Analysis. 2005;43(1):259–279. [Google Scholar]
- 4.Barbu T, Barbu V, Biga V, Coca D. A PDE variational approach to image denoising and restoration. Nonlinear Analysis Real World Applications. 2009;10(3):1351–1361. [Google Scholar]
- 5.Bates PW, Chen Z, Sun YH, Wei GW, Zhao S. Geometric and potential driving formation and evolution of biomolecular surfaces. Journal of Mathematical Biology. 2009;59(2):193–231. doi: 10.1007/s00285-008-0226-7. [DOI] [PubMed] [Google Scholar]
- 6.Bertalmio M. Strong-continuation, contrast-invariant inpainting with a third-order optimal PDE. IEEE Transactions on Image Processing. 2006;15(7):1934–1938. doi: 10.1109/tip.2006.877067. [DOI] [PubMed] [Google Scholar]
- 7.Bertozzi AL, Greer JB. Low-curvature image simplifiers: Global regularity of smooth solutions and laplacian limiting schemes. Communications on Pure and Applied Mathematics. 2004;57(6):764–790. [Google Scholar]
- 8.Buxton RB. Introduction to functional magnetic resonance imaging – principles and techniques. Cambridge University Press; Cambridge, UK: 2002. [Google Scholar]
- 9.Canny J. A computational approach to edge-detection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986;8(6):679–698. [PubMed] [Google Scholar]
- 10.Caselles V, Morel JM, Sapiro G, Tannenbaum A. Introduction to the special issue on partial differential equations and geometry-driven diffusion in image processing and analysis. IEEE Transactions on Image Processing. 1998;7(3):269–273. doi: 10.1109/TIP.1998.661176. [DOI] [PubMed] [Google Scholar]
- 11.Catte F, Lions PL, Morel JM, Coll T. Image selective smoothing and edge-detection by nonlinear diffusion. SIAM Journal on Numerical Analysis. 1992;29(1):182–193. [Google Scholar]
- 12.Chambolle A, Lions PL. Image recovery via total variation minimization and related problems. Numerische Mathematik. 1997;76(2):167–188. [Google Scholar]
- 13.Chan T, Marquina A, Mulet P. High-order total variation-based image restoration. SIAM Journal on Scientific Computing. 2000;22(2):503–516. [Google Scholar]
- 14.Chan T, Shen J. Image processing and analysis: variational, PDE, wavelet, and stochastic methods. Society for Industrial Mathematics; 2005. [Google Scholar]
- 15.Chan Y. Wavelet basics. Springer; 1995. [Google Scholar]
- 16.Chen K, Chen X, Renaut R, Alexander GE, Bandy D, Guo H, Reiman EM. Characterization of the image-derived carotid artery input function using independent component analysis for the quantitation of 18f fluorodeoxyglucose positron emission tomography images. Physics in Medicine and Biology. 2007;52(23):7055–7071. doi: 10.1088/0031-9155/52/23/019. [DOI] [PubMed] [Google Scholar]
- 17.Chen QH, Huang N, Riemenschneider S, Xu YS. A B-spline approach for empirical mode decompositions. Advances in Computational Mathematics. 2006;24(1–4):171–195. [Google Scholar]
- 18.Chen Z, Baker NA, Wei GW. Differential geometry based solvation models I: Eulerian formulation. J Comput Phys. 2010;229:8231–8258. doi: 10.1016/j.jcp.2010.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Daubechies I. Ten Lectures on Wavelets. SIAM; Philadelphia: 1992. [Google Scholar]
- 20.Echeverria JC, Crowe JA, Woolfson MS, Hayes-Gill BR. Application of empirical mode decomposition to heart rate variability analysis. Medical and Biological Engineering and Computing. 2001;39(4):471–479. doi: 10.1007/BF02345370. [DOI] [PubMed] [Google Scholar]
- 21.Farge M. Wavelet transforms and their applications to turbulence. Annual Review of Fluid Mechanics. 1992;24:395–457. [Google Scholar]
- 22.Gilboa G, Sochen N, Zeevi YY. Forward-and-backward diffusion processes for adaptive image enhancement and denoising. IEEE Transactions on Image Processing. 2002;11(7):689–703. doi: 10.1109/TIP.2002.800883. [DOI] [PubMed] [Google Scholar]
- 23.Gilboa G, Sochen N, Zeevi YY. Image sharpening by flows based on triple well potentials. Journal of Mathematical Imaging and Vision. 2004;20(1–2):121–131. [Google Scholar]
- 24.Greer JB, Bertozzi AL. H-1 solutions of a class of fourth order nonlinear equations for image processing. Discrete and Continuous Dynamical Systems. 2004;10(1–2):349–366. [Google Scholar]
- 25.Greer JB, Bertozzi AL. Traveling wave solutions of fourth order PDEs for image processing. SIAM Journal on Mathematical Analysis. 2004;36(1):38–68. [Google Scholar]
- 26.Grimm V, Henn S, Witsch K. A higher-order PDE-based image registration approach. Numerical Linear Algebra with Applications. 2006;13(5):399–417. [Google Scholar]
- 27.Gu Y, Wei GW. Conjugate filter approach for shock capturing. Communications in Numerical Methods in Engineering. 2003;19(2):99–110. [Google Scholar]
- 28.Guan S, Lai C, Wei G. A wavelet method for the characterization of spatiotemporal patterns. Physica D: Nonlinear Phenomena. 2002;163(1–2):49–79. [Google Scholar]
- 29.Guo H, Renaut R, Chen K. An input function estimation method for FDG-PET human brain studies. Nuclear medicine and biology. 2007;34(5):483–492. doi: 10.1016/j.nucmedbio.2007.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Guo H, Renaut RA, Chen K, Reiman E. FDG-PET parametric imaging by total variation minimization. Computerized Medical Imaging and Graphics. 2009;33(4):295–303. doi: 10.1016/j.compmedimag.2009.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic resonance imaging: physical principles and sequence design. Wiley; New York: 1999. [Google Scholar]
- 32.Huang NE, Long SR, Shen Z. The mechanism for frequency downshift in nonlinear wave evolution. Advances in Applied Mechanics. 1996;32:32, 59. [Google Scholar]
- 33.Huang NE, Shen Z, Long SR. A new view of nonlinear water waves: The Hilbert spectrum. Annual Review of Fluid Mechanics. 1999;31:417–457. [Google Scholar]
- 34.Huang NE, Shen Z, Long SR, Wu MLC, Shih HH, Zheng QN, Yen NC, Tung CC, Liu HH. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences. 1998;454(1971):903–995. [Google Scholar]
- 35.Jain AK. Partial-differential equations and finite-difference methods in image-processing .1. image representation. Journal of Optimization Theory and Applications. 1977;23(1):65–91. [Google Scholar]
- 36.Jin JH, Shi JJ. Feature-preserving data compression of stamping tonnage information using wavelets. Technometrics. 1999;41(4):327–339. [Google Scholar]
- 37.Jin ZM, Yang XP. Strong solutions for the generalized Perona-Malik equation for image restoration. Nonlinear Analysis-Theory Methods and Applications. 2010;73(4):1077–1084. [Google Scholar]
- 38.Karras DA, Mertzios GB. New PDE-based methods for image enhancement using SOM and bayesian inference in various discretization schemes. Measurement Science Technology. 2009;20(10):8. [Google Scholar]
- 39.Kopsinis Y, McLaughlin S. Development of EMD-based denoising methods inspired by wavelet thresholding. IEEE Transactions on Signal Processing. 2009;57(4):1351–1362. [Google Scholar]
- 40.Li S. Markov random field modeling in image analysis. Springer-Verlag; New York Inc: 2009. [Google Scholar]
- 41.Liang HL, Lin QH, Chen JDZ. Application of the empirical mode decomposition to the analysis of esophageal manometric data in gastroesophageal reflux disease. IEEE Transactions on Biomedical Engineering. 2005;52(10):1692–1701. doi: 10.1109/TBME.2005.855719. [DOI] [PubMed] [Google Scholar]
- 42.Lin L, Wang Y, Zhou H. Iterative filtering as an alternative algorithm for empirical mode decomposition. Advances in Adaptive Data Analysis. 2009;1(4):543–560. [Google Scholar]
- 43.Liu B, Riemenschneider S, Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mechanical Systems and Signal Processing. 2006;20(3):718–734. [Google Scholar]
- 44.Lysaker M, Lundervold A, Tai XC. Noise removal using fourth-order partial differential equation with application to medical magnetic resonance images in space and time. IEEE Transactions on Image Processing. 2003;12(12):1579–1590. doi: 10.1109/TIP.2003.819229. [DOI] [PubMed] [Google Scholar]
- 45.Mallat S. A Wavelet tour of signal processing. Academic Press; 1999. [Google Scholar]
- 46.Mao D, Rockmore D, Wang Y, Wu Q. Preprint. EMD Analysis for Visual Stylometry. [DOI] [PubMed] [Google Scholar]
- 47.Mao D, Rockmore DN, Wang Y, Wu Q. Preprint. Emd analysis for visual stylometry. [DOI] [PubMed] [Google Scholar]
- 48.Mao D, Wang Y, Wu Q. Preprint. A New Approach for Analyzing Physiological Time Series. [Google Scholar]
- 49.Mao D, Wang Y, Wu Q. Preprint. A new approach for analyzing physiological time series. [Google Scholar]
- 50.Marr D, Hildreth E. Theory of edge-detection. Proceedings of the Royal Society of London Series B-Biological Sciences. 1980;207(1167):187–217. doi: 10.1098/rspb.1980.0020. [DOI] [PubMed] [Google Scholar]
- 51.Meyer FG, Coifman RR. Brushlets: A tool for directional image analysis and image compression. Applied and Computational Harmonic Analysis. 1997;4(2):147–187. [Google Scholar]
- 52.Nitzberg M, Shiota T. Nonlinear image filtering with edge and corner enhancement. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1992;14(8):826–833. [Google Scholar]
- 53.Oppenheim AV, Schafer RW. Digital Signal Process. Englewood Cliffs, NJ: Prentice-Hall; 1989. [Google Scholar]
- 54.Perona P, Malik J. Scale-space and edge-detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1990;12(7):629–639. [Google Scholar]
- 55.Pesenson M, Roby W, McCollum B. Multiscale astronomical image processing based on nonlinear partial differential equations. Astrophysical Journal. 2008;683(1):566–576. [Google Scholar]
- 56.Radke RJ, Andra S, Al-Kofahi O, Roysam B. Image change detection algorithms: A systematic survey. IEEE Transactions on Image Processing. 2005;14(3):294–307. doi: 10.1109/tip.2004.838698. [DOI] [PubMed] [Google Scholar]
- 57.Rezaei D, Taheri F. Experimental validation of a novel structural damage detection method based on empirical mode decomposition. Smart Materials and Structures. 2009;18(4) [Google Scholar]
- 58.Rilling G, Flandrin P, Goncalves P, Lilly JM. Bivariate empirical mode decomposition. IEEE Signal Processing Letters. 2007;14:936–939. [Google Scholar]
- 59.Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60(1–4):259–268. [Google Scholar]
- 60.Saxena R, Gelb A, Mittelmann H. A high order method for determining the edges in the gradient of a function. Communications in Computational Physics. 2009;5(2–4):694–711. [Google Scholar]
- 61.Shih Y, Rei C, Wang H. A novel PDE based image restoration: Convection-diffusion equation for image denoising. Journal of Computational and Applied Mathematics. 2009;231(2):771–779. [Google Scholar]
- 62.Siddiqi K, Kimia BB, Shu CW. Geometric shock-capturing eno schemes for subpixel interpolation, computation and curve evolution. Graphical Models and Image Processing. 1997;59(5):278–301. [Google Scholar]
- 63.Spedding GR, Browand FK, Huang NE, Long SR. A 2D complex wavelet analysis of an unsteady wind-generated surface wavelet analysis of an unsteady wind-generated surface wave field. Dynamics of atmospheres and oceans. 1993;20:55–77. [Google Scholar]
- 64.Sun YH, Wu PR, Wei G, Wang G. Evolution-operator-based single-step method for image processing. Int J Biomed Imaging. 2006;83847:1. doi: 10.1155/IJBI/2006/83847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sun YH, Zhou YC, Li SG, Wei GW. A windowed Fourier pseudospectral method for hyperbolic conservation laws. Journal of Computational Physics. 2006;214(2):466–490. [Google Scholar]
- 66.Tanaka T, Mandic DP. Complex empirical mode decomposition. IEEE Signal Processing Letters. 2007;14(2):101–104. [Google Scholar]
- 67.Tang Y-W, Tai C-C, Su C-C, Chen C-Y, Chen J-F. A correlated empirical mode decomposition method for partial discharge signal denoising. Measure Science Tech. 2010;21:085106. [Google Scholar]
- 68.Tasdizen T, Whitaker R, Burchard P, Osher S. Geometric surface processing via normal maps. Acm Transactions on Graphics. 2003;22(4):1012–1033. [Google Scholar]
- 69.Titchmarsh EC. Introduction to the theory of Fourier integrals. Oxford University Press; 1948. [Google Scholar]
- 70.Wang Y, Wei G, Yang S. Iterative filtering decomposition based on local spectral evolution kernel. Journal of Scientific Computing. doi: 10.1007/s10915-011-9496-0. accepted, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wang Y, Wei G, Yang S. Partial differential equation transform — Variational formulation and Fourier analysis. International Journal for Numerical Methods in Biomedical Engineering. 2011 doi: 10.1002/cnm.1452. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Wang Y, Zhao YB, Wei GW. A note on the numerical solution of high-order differential equations. Journal of Computational and Applied Mathematics. 2003;159(2):387–398. [Google Scholar]
- 73.Wang Z, Vemuri BC, Chen Y, Mareci TH. A constrained variational principle for direct estimation and smoothing of the diffusion tensor field from complex DWI. IEEE Trans Medical Imaging. 2004;23:930. doi: 10.1109/TMI.2004.831218. [DOI] [PubMed] [Google Scholar]
- 74.Wei GW. Generalized Perona-Malik equation for image restoration. IEEE Signal Processing Letters. 1999;6(7):165–167. [Google Scholar]
- 75.Wei GW. Wavelets generated by using discrete singular convolution kernels. Journal of Physics A: Mathematical and General. 2000;33:8577–8596. [Google Scholar]
- 76.Wei GW. Oscillation reduction by anisotropic diffusions. Comput Phys Commun. 2002;144:417–342. [Google Scholar]
- 77.Wei GW, Jia YQ. Synchronization-based image edge detection. Europhysics Letters. 2002;59(6):814–819. [Google Scholar]
- 78.Westin C-F, Maier SE, Mamata H, Nabavi A, Jolesz FA, Kikinis R. Processing and visualization of diffusion tensor MRI. Medical Image Analysis. 2002;6:93. doi: 10.1016/s1361-8415(02)00053-1. [DOI] [PubMed] [Google Scholar]
- 79.Witelski TP, Bowen M. Adi schemes for higher-order nonlinear diffusion equations. Applied Numerical Mathematics. 2003;45(2–3):331–351. [Google Scholar]
- 80.Witkin A. Scale-space filtering: A new approach to multi-scale description. Proceedings of IEEE International Conference on Acoustic Speech Signal Processing; Institute of Electrical and Electronics Engineers; 1984. pp. 150–153. [Google Scholar]
- 81.Wu JY, Ruan QQ, An GY. Exemplar-based image completion model employing PDE corrections. Informatica. 2010;21(2):259–276. [Google Scholar]
- 82.Xu M, Zhou SL. Existence and uniqueness of weak solutions for a fourth-order nonlinear parabolic equation. Journal of Mathematical Analysis and Applications. 2007;325(1):636–654. [Google Scholar]
- 83.Yang S, Coe J, Kaduk B, Martínez T. An “optimal” spawning algorithm for adaptive basis set expansion in nonadiabatic dynamics. Journal of Chemical Physics. 2009;130:134113. doi: 10.1063/1.3103930. [DOI] [PubMed] [Google Scholar]
- 84.Yang S, Zhou YC, Wei GW. Comparison of the discrete singular convolution algorithm and the Fourier pseudospectral method for solving partial differential equations. Computer Physics Communications. 2002;143(2):113–135. [Google Scholar]
- 85.You Y, Kaveh M. Fourth-order partial differential equations for noise removal. IEEE Transactions on Image Processing. 2002;9(10):1723–1730. doi: 10.1109/83.869184. [DOI] [PubMed] [Google Scholar]
- 86.Zhao S, Wei GW. Comparison of the discrete singular convolution and three other numerical schemes for solving fisher’s equation. SIAM Journal on Scientific Computing. 2003;25(1):127–147. [Google Scholar]
- 87.Zhao S, Wei GW. Matched interface and boundary (MIB) for the implementation of boundary conditions in high-order central finite differences. International Journal for Numerical Methods in Engineering. 2009;77(12):1690–1730. doi: 10.1002/nme.2473. [DOI] [PMC free article] [PubMed] [Google Scholar]