Automated Detection of Covid-19 from Chest X-ray scans using an optimized CNN architecture

Sameena Pathan; PC Siddalingaswamy; Tanweer Ali

doi:10.1016/j.asoc.2021.107238

. 2021 Feb 24;104:107238. doi: 10.1016/j.asoc.2021.107238

Automated Detection of Covid-19 from Chest X-ray scans using an optimized CNN architecture

Sameena Pathan ^a, PC Siddalingaswamy ^a, Tanweer Ali ^b,^⁎

PMCID: PMC7903912 PMID: 33649705

Abstract

The novel coronavirus termed as covid-19 has taken the world by its crutches affecting innumerable lives with devastating impact on the global economy and public health. One of the major ways to control the spread of this disease is identification in the initial stage, so that isolation and treatment could be initiated. Due to the lack of automated auxiliary diagnostic medical tools, availability of lesser sensitivity testing kits, and limited availability of healthcare professionals, the pandemic has spread like wildfire across the world. Certain recent findings state that chest X-ray scans contain salient information regarding the onset of the virus, the information can be analyzed so that the diagnosis and treatment can be initiated at an earlier stage. This is where artificial intelligence meets the diagnostic capabilities of experienced clinicians. The objective of the proposed research is to contribute towards fighting the global pandemic by developing an automated image analysis module for identifying covid-19 affected chest X-ray scans by employing an optimized Convolution Neural Network (CNN) model. The aforementioned objective is achieved in the following manner by developing three classification models, (i) ensemble of ResNet 50-Error Correcting Output Code (ECOC) model, (ii) CNN optimized using Grey Wolf Optimizer (GWO) and, (iii) CNN optimized using Whale Optimization + BAT algorithm. The novelty of the proposed method lies in the automatic tuning of hyper parameters considering a hierarchy of MultiLayer Perceptron (MLP), feature extraction, and optimization ensemble. A 100% classification accuracy was obtained in classifying covid-19 images. Classification accuracy of 98.8% and 96% were obtained for dataset 1 and dataset 2 respectively for classification into covid-19, normal, and viral pneumonia cases. The proposed method can be adopted in a clinical setting for assisting radiologists and it can also be employed in remote areas to facilitate the faster screening of affected patients.

Keywords: Covid-19, CNN, Ensemble, ECOC, GWO, SVM, WOA

1. Introduction

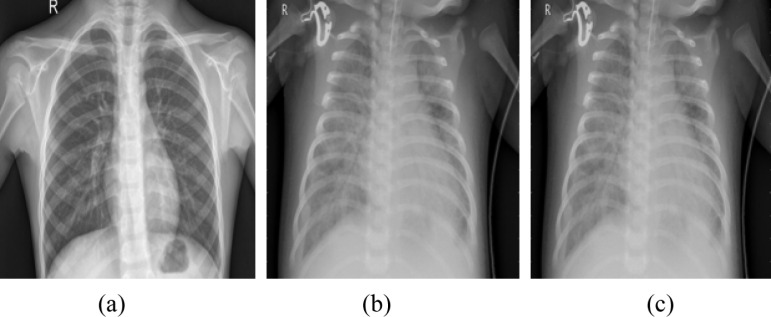
Covid-19, the most talked-about on-going pandemic that has resulted in a major global crisis, and has significantly impacted several lives around the globe. The first case of the lethal virus is reported to have originated from Wuhan, a province in China in December 2019 [1]. In a short period, the virus turned out to be a global pandemic affecting several countries in the world. One of the most common techniques that is currently used in the diagnosis of covid-19 is reverse transcription-polymerase (RT_PCR). Radiological imaging modalities such as Computed Tomography (CT) and X-ray have played vital roles in the early diagnosis of this disease [2]. Since the diagnosing sensitivity of PCR is 60%–70%, X-ray scans have been adopted in the screening of covid-19 cases. Fig. 1, illustrates the three classes of chest x-ray scans namely, normal, viral pneumonia, and covid-19.

Fig. 1 — Illustration of chest X-ray images, (a) Normal, (b) Viral pneumonia (c) Covid-19 [3].

Few recent studies have reported changes in X-ray and CT image scans in patients at the onset of covid-19 symptoms [4]. For instance, Zhao et al. [5] observed dilation and consolidation in addition to ground-glass opacities in covid affected patients. A rapid rise in the number of positive covid-19 cases has aggravated the need for researchers to integrate Artificial Intelligence (AI) along with expert opinion to ease the task of the clinicians. In this regard, deep learning models, have started garnering recognition. Due to the shortage in the number of radiologists in hospitals, AI-based diagnostic models can be helpful to provide timely assistance to the patients. Based on these techniques, numerous studies have been reported in the literature, however, only prominent studies are highlighted here. Seven Convolutional Neural Network (CNN) models, comprising of improved VGG19 and Google MobileNet to diagnose covid-19 form X-ray images was proposed by Hemdan et al. [6]. An accuracy of 92.4% was obtained by Wang et al. [7] in classifying covid-19 images from normal and viral pneumonia cases. Similarly, Ioannis et al. [8] used 224 covid-19 images and obtained a class accuracy of 93.48%. An optimized CNN termed as optconet was proposed in [9] using a total of 2700 images thereby yielding a precision score of 92.8%. A mobilenet CNN model was developed by Apostolopoulous et al. [10] using certain extricated features. Three distinctive CNN models namely inception v3, ResNet50, Inception-ResNet V2 were used for the same purpose of classification in [11]. A transfer learning-based approach using three models such as ResNet18, ResNet50, SqueezeNet, and DenseNet-121 was used in [12] for the classification of covid and non-covid chest X-ray images.

Although all the above-reported state of art techniques are designed using CNN, the methods do not take into account the spatial relationships between the image pixels for training the models. Thus, when the images are subjected to the rotation, certain resize operations, and data augmentation due to the availability of smaller dataset size, the developed CNN models fail to accurately identify the covid-19 cases, form viral pneumonia and normal chest X-ray scans. Although, a certain degree of misclassification in identifying viral pneumonia cases is acceptable, but misclassification of covid-19 cases as normal or viral pneumonia can mislead the treatment performed by clinicians. The proposed work aims to address the aforementioned limitations by developing an automated diagnostic tool for screening of covid-19 patients using chest X-ray scans. The proposed method employs an optimized robust CNN architecture for the classification of chest X-ray images into three classes.

1.1. Novelty and contributions

The novelty of the proposed work is two-fold. The methodology adopted for optimizing the CNN hyper parameters is unique. The major hyper parameters of CNN are tuned using (i) Multilayer perceptron (MLP) and Grey Wolf Optimizer (GWO), and (ii) MLP and Whale optimization $+$ BAT algorithm. The hyper parameter tuning was performed using dataset 1 and the same parameters were used for training and testing of dataset 2. In both cases, good performance metrics were obtained.

The main contributions of this paper are summarized as given below:

a.
An ensemble of ResNet and Error Correcting Output Code (ECOC) classifier is designed for the classification of X-ray images into three classes.
b.
Two optimization algorithms namely GWO and WOA-BAT were used for tuning the hyper parameters of CNN. In contrast to the method in [9], the proposed method determines the values of the hyper parameters by optimizing an MLP trained on the features extracted from the ResNet-50. The best values obtained were used as hyper parameters (Initial Learning Rate, L2 regularization, gradient decay factor, and Maximum epochs).
c.
A thorough comparative analysis is performed between the optimized and un-optimized CNN to prove the efficacy of the proposed method. The optimization parameters are computed using dataset 1, and the same parameters are used for dataset 2. For both the datasets good performance is observed, thereby proving the suitability of the system to be adopted in a clinical setting for initial screening of covid-19 patients.

2. Materials and methods

2.1. Dataset

The study is carried out using two datasets. The first dataset henceforth is referred to as dataset 1, consists of 2905 chest X-ray images. There are 3 classes of image data belonging to covid-19, normal and viral pneumonia images, of which 219 are covid-19 images, 1341 are normal images and 1345 belong to viral pneumonia. The covid-19 images were obtained from the Italian Society of medical and interventional radiology, Joseph Paul Cohen and Morrison Covid-19 dataset and, various publications [13]. The second dataset [3], henceforth referred to as dataset 2, consists of 6432 images, of which 576 belong to covid-19, 4273 belong to viral pneumonia and 1583 belong to normal. All the images of dataset 2 are in jpeg format.

2.2. Optimization and classification

The proposed classification and optimization methodology consist of three different design models as given below:

1.
The first model is designed using an ensemble of ResNet-50 and ECOC classifier.
2.
The second classification model is built by optimizing CNN layer parameters using GWO optimization.
3.
The third classification model is built by optimizing CNN layer parameters using WOA and BAT algorithm.

2.2.1. Ensemble of ResNet-50 and ECOC classifier

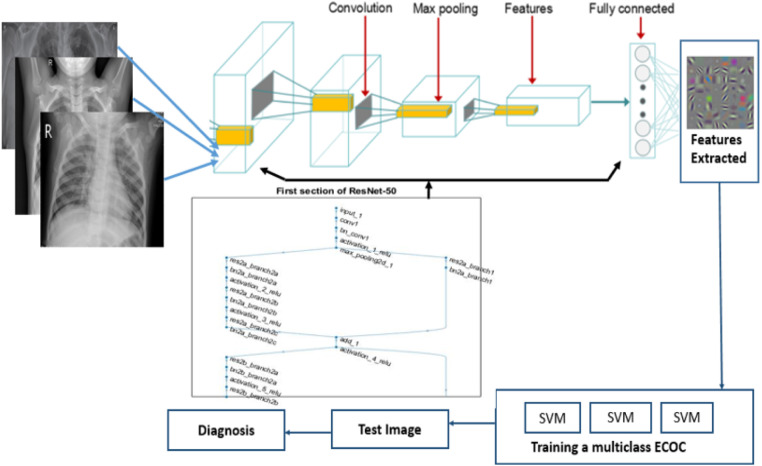
The ResNet models developed by He et al. [14] are prominently known for good convergence with great classification performance. The proposed model-1 in this paper employs a pre-trained ResNet-50 residual network architecture that has 177 layers in total. The dataset is divided into a 30:70 ratio with 30% of data used for training and 70% used for testing. The block diagram of the proposed ensemble of ResNet-50 and ECOC classifier is given in Fig. 2. For the first convolution layer, a patch size of 112 × 112 is used. As the structure evolves deeper, the patch size reduces to 56 × 56. The minimum batch size is 32. The ResNet-50-ECOC ensemble has 64 filters of size 7 × 7 × 3 with stride [2 2] and padding [3 3 3 3]. The fully connected layer before the softmax layer has 1000 neurons with weights 1000 × 2048 and a bias of 1000 × 1. The deep residual features were extracted from the fully connected layer consisting of 1000 nodes. The extracted features are further used to train ECOC classifier model built using three Support Vector Machines (SVM) binary learners. The ECOC model consists of a coding and decoding scheme as illustrated in Table 1.

Fig. 2 — Overview of ensemble of ResNet-50 and ECOC model.

Table 1.

Coding scheme of ECOC.

Class	SVM1	SVM2	SVM3
Covid-19(C1)	1	1	0
Viral Pneumonia (C2)	−1	0	1
Normal (C3)	0	−1	−1

Open in a new tab

The ECOC model consists of a coding and decoding scheme. The coding scheme determines the classes for which the SVM trains on, and the decoding scheme determines the aggregation of predictions determined by the SVM classifiers. Since the proposed model consists of three classes, there are three SVM learners used to build the design. The SVM 1 trains on the observations belonging to Class 1 (C1) and Class 2 (C2). SVM 2 trains on the observations belonging to C1 and Class 3 (C3). Similarly, SVM 3 trains on observations belonging to C2 and C3. During the testing stage, the majority voting scheme decides the class of the test image. The ResNet-50 architecture is applied to the testing data to extract the test features. Further, the extracted test features are classified using the ECOC model. The results of different kernels (polynomial, sigmoid, RBF (Gaussian)) was computed. However, the performance using linear SVM kernel with quadratic function as the binary loss was found to be maximum. The observation is assigned to the class that yields the smallest average binary loss. The procedure for the selection of design parameters is described in detail in [15]. The ECOC models have proved to improve the classification accuracy in multiclass mechanisms.

2.2.2. Optimization process using Grey Wolf optimizer

The proposed architecture is divided into two parts. The first part consists of the extraction of features from 80% of the data, while the second part consists of optimizing CNN hyper parameters using the GWO optimizer. 80% of the training data is fed to the ResNet-50 architecture wherein the last three layers comprise of fully connected, softmax and classification layers. The features are extracted from the fully connected layer comprising of 1000 nodes. Rather, than optimizing the parameters of deep neural network architecture as in [9], we propose a novel strategy by introducing a Multilayer Perceptron (MLP) based GWO optimization.

One of the greatest milestones in the era of computational intelligence is the introduction of neural network with the capability to mimic the human nervous system. One among type of neural network is the Feed Forward Neural Network (FNN), which has a unidirectional connection between the neurons. One of the classes of FNN is a MLP. It consists of at least one hidden layer. The output of the MLPs for a given set of inputs mainly relies on the biases and weights. For instance, consider $X_{i}$ as i $th$ input. The weighted sum of inputs is as given in (1).

s_{i} = \sum_{i = 1}^{n} (W_{i j} X_{i}) - θ_{j}, j = 1, 2 \dots h

(1)

where $W_{i j}$ is the connection weight from the i $th$ node to the j $th$ node and $θ_{j}$ is the bias of the j $th$ layer.

The main goal of effectively training a MLP mainly relies on the exact choice of the weights and bias to achieve good performance for a particular set of input feature vectors. Thus, our goal is to optimize the parameters of MLP for tuning CNN hyper parameters. Many optimization algorithms based on swarm intelligence have been proposed in recent years [16], [17], [18]. One such optimization algorithm proposed by Mirajalili et al. [19] is the GWO. The GWO algorithm follows the hunting pattern of the grey wolves. There are four groups of population termed as alpha, beta, delta and omega denoted as $\propto, β, δ, ω$ respectively. Here $\propto, β$ and $δ$ are considered as the fittest wolves in the preceding order, and $ω$ act as subordinates. The hunting nature of the wolves is described in a circular pattern as given in (2)–(3).

D = | C X_{p} (t) - X (t) |

(2)

X (t + 1) = X_{p} - A D

(3)

Here, D denotes the distance, A and C are the coefficients, and $X_{p}$ denotes the prey’s position, t denotes the iteration, X denotes the wolf location. The A and C coefficients are computed as given in (4).

A = 2 a r 1 - a, C = 2 r 2

(4)

$r 1$ and $r 2$ are random values between 0 and 1, whereas the value of $‘ a ‘$ changes from 2 to 0. The first three best solutions are saved as $\propto, β$ , and $δ$ , and the position of $ω$ is updated similar to the hunting behavior of the wolves as given in (5)–(8).

\vec{D_{α}} = | \vec{C_{1}} \vec{X_{α}} - \vec{X} |

(5)

\vec{D_{β}} = | \vec{C_{2}} \vec{X_{β}} - \vec{X} |

(6)

\vec{D_{δ}} = | \vec{C_{3}} \vec{X_{δ}} - \vec{X} |

(7)

\vec{X} (t + 1) = \vec{X_{1}} + \vec{X_{2}} + \vec{X_{3}} ∕ 3

(8)

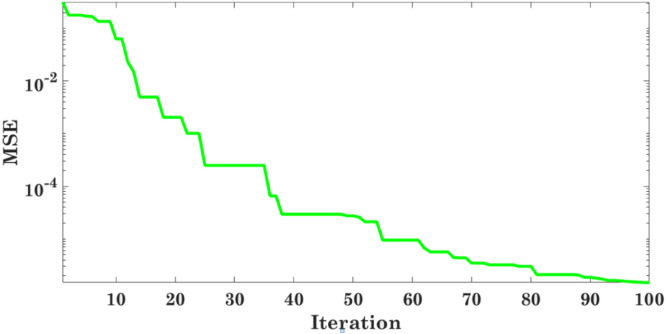
Here, $\vec{X_{1}}, \vec{X_{2}}$ and $\vec{X_{3}}$ are approximate distances as given in [19]. The position of the prey is estimated by $\propto, β$ , and $δ$ , whereas $ω$ updates its position randomly around the prey. The search process initially starts with the generation of random candidate solutions which are further updated over the course of iterations based on the probable prey positions as estimated by $\propto, β$ , and $δ$ . The divergence and convergence of the candidate solution relies on $\vec{A}$ $>$ 1 and $\vec{A}$ $<$ 1 condition respectively. As the total number of iterations are completed, the solution obtained by GWO at the last iteration is considered the best solution. Algorithm I describes sequential steps followed for obtaining the best parameters. One of the challenges involved in hyper parameter tuning is the careful selection of the learning rate, since a smaller value increases the number of epochs, resulting in the delay of the process, and a larger value results in a suboptimal solution. In the proposed method, the step size wherein the weights are updated also known as the learning rate of CNN is taken as the value of the best solution obtained by GWO. The minimization of Mean Square Error (MSE) of the MLP is the objective function of the aforementioned optimizer. The convergence curve for iteration versus MSE is given in Fig. 3.

Fig. 3 — The convergence curve for objective function versus iteration.

2.2.3. Optimization process using WOA-BAT algorithm

The WOA algorithm was proposed by Mirajalili et al. [20] by simulating the hunting behavior of the humpback whales by initially chasing the prey and simulating the bubble net strategy. The WOA algorithm consists of two main phases, encircling the prey and spiral updating known as the exploitation phase, wherein the prey is randomly searched. In this research work, the WOA algorithm initially starts with a set of random solution for $V = (W, B)$ , weights and bias for the MLP. At each iteration, the search agents are updated based on the randomly chosen search agent or the best solution that is obtained at the current iteration. The following equations (9)–(10) describe the behavior of hunting the prey.

\vec{X} (t + 1) = {\vec{X}}^{*} (t) - \vec{A} \vec{D}

(9)

\vec{D} = | \vec{C} {\vec{X}}^{*} (t) - \vec{X} (t) |

(10)

${\vec{X}}^{*} (t)$ is the whales best earlier position and $\vec{X} (t + 1)$ is the current position of the whale. $\vec{D}$ is the distance vector and $\vec{C}$ and $\vec{A}$ are the co-efficient vectors computed as (11).

\vec{C} = 2 r, \vec{A} = 2 a r + a

(11)

To speed up the convergence, the spiral updating mechanism of the bats is incorporated with certain modifications. A random value of p is generated considering if there is a 50% probability to choose between either the simulating encircling mechanism or the spiral model to update the position [21], [22]. If p $>$ 0.5, then the current iteration is updated as given in (12).

\vec{X} (t + 1) = \vec{D} e^{b k} cos (2 π k) + \vec{X} (t)

(12)

We consider $k = b = 1$ , hence (12) reduces to (13).

\vec{X} (t + 1) = 2.7 * \vec{D} + \vec{X} (t)

(13)

If p $<$ 0.5, then the current iteration is updated as given in (14)–(16).

f_{i} = f_{m i n} + (f_{m a x} - f_{m i n})

(14)

{v_{i}}^{t + 1} = {v_{i}}^{t} + ({x_{i}}^{t} - x_{*}) f_{i}

(15)

{x_{i}}^{t + 1} = ({x_{i}}^{t} + {v_{i}}^{t + 1})

(16)

Here, $x_{i}$ is the bat position and $v_{i}$ is the bat velocity. The frequency of the waves is the lower and upper bound taken as (−100,100). The new position of the bats is updated depending upon the new velocity because when the bat finds the food/prey, the loudness rate is inversely proportional to the emission rate. The CNN hyper parameters such as the learning rate and gradient decay factor are chosen as the values of the best positions which minimizes the MSE objective function. Algorithm II describes sequential steps followed for obtaining the best parameters using WOA-BAT.

2.2.4. CNN architecture design

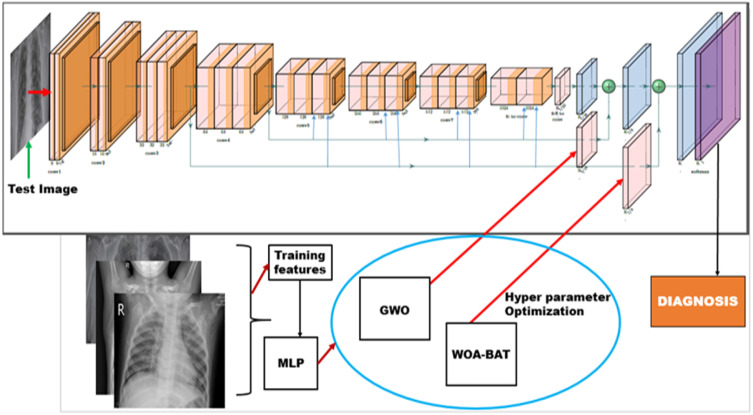
The CNN architecture is built using the input layer, Convolution Layer (CL), Max Pooling Layer (MPL), Batch Normalization Layer (BNL), Rectified Linear Unit (ReLu), fully connected layer, and the output layer. The structure of the CNN is illustrated in Fig. 4. The convolution layer extracts features at every offset of the input image. The hyper parameters of the layers are optimized using the GWO and the WOA-BAT optimization techniques. Output feature maps are sensitive to the location of features in the input image. One solution to address this sensitivity and achieve local translation variance is to perform pooling. After the non-linearity has been applied to the feature maps obtained from the convolutional layers, pooling is applied. The non-linear activation function used is ReLu, it maps the extracted features into the feature space. There are four types of pooling namely, (i) max pooling, (ii) average pooling, (iii) global max pooling, and, (iv) global average pooling. In our proposed study, max pooling is used, since it retains the most prominent features of the feature maps, thus retaining sharp features. The downsampling is performed using max-pooling of filter size 2 × 2, stride of [2 2], and padding of [1 1 1 1]. At the end of the structure, a global average pooling is applied to convert each feature map into one value. The batch normalization layer is responsible for normalizing the gradients and activations through the network. The values generated are further fed to the soft-max activation function to predict the multinomial probability distribution. Table 2 describes the details regarding the convolutional layers and filter size used in building the CNN.

Fig. 4 — The proposed classification set-up using optimization techniques.

Table 2.

Details of CNN architecture.

Layer	Type	Filter size	No. of filters	Stride
Input	448 × 448 × 1

Layer 1	CL $+$ BNL $+$ ReLU	7 × 7	8	1 × 1
	MPL	2 × 2		2 × 2

Layer 2	CL $+$ BNL $+$ ReLU	3 × 3	16	1 × 1
	MPL	2 × 2		2 × 2

Layer 3	CL $+$ BNL $+$ ReLU	3 × 3	32	1 × 1
	MPL	2 × 2		2 × 2

Layer 4	CL $+$ BNL $+$ ReLU	3 × 3	64	1 × 1
	MPL	2 × 2		2 × 2

Layer 5	CL $+$ BNL $+$ ReLU	3 × 3	128	1 × 1
	MPL	2 × 2		2 × 2

Layer 6	CL $+$ BNL $+$ ReLU	3 × 3	256	1 × 1
	MPL	2 × 2		2 × 2

Layer 7	CL $+$ BNL $+$ ReLU	3 × 3	512	1 × 1
	MPL	2 × 2		2 × 2

Layer 8	CL $+$ BNL $+$ ReLU	3 × 3	1024	1 × 1
	MPL	2 × 2		2 × 2

Output	Fully connected layer	Output size: 3
	Softmax
	classification layer

Open in a new tab

During training, the parameters of the convolutional kernels are adjusted based on the best values obtained during the optimization process. CNN usually use stochastic gradient or adam solver to tune the hyper parameters. The choice of the parameters is application dependent. However, appropriate choice of hyper parameters decide the convergence rate and accuracy of CNN in the classification task. If the initial learning rate is too low, then the training takes a longer time. The learning rate hyper parameter decides the change that is required each time, the model is updated depending on the error. Similarly, the L2 regularization parameter adds a regularization term to the cost function, to prevent the model from overfitting. The factor by which the learning rate changes every epoch is decided by the gradient decay factor. These hyper parameters are decided by the optimum best positions obtained by the two aforementioned optimization methodologies (GWO, WOA-BAT).

3. Results and discussion

3.1. Training and testing

The proposed set-up was implemented in MATLAB 2020a, on a 64-bit operating system. The data was divided into 80:20 ratio for training and testing respectively for optimization models. The training and testing image classes were randomly partitioned. For, the first ECOC model, from the fully connected layer, a set of 1000 features were obtained. The features were retained as it is and given as an input to the ECOC classifier to perform multiclass classification. The datasets consist of images of variable dimensions (R × C). The minimum dimension of the image available in the dataset was 448 × 448, thus, to maintain uniformity and reduce the processing time, all the images have been resized to 448 × 448 $\times$ 1. For, the optimized set-ups, an eight convolution layer architecture is designed to classify images into three categories (covid-19, normal and viral pneumonia). The adam solver hyper parameters are chosen based on the two optimization algorithms, optimized based on the training features extracted from the ResNet-50 CNN architecture. The training hyper parameters obtained from the optimization algorithms are given in Table 3. The test images are initially resized to 448 × 448 × 1 and fed as input to the trained CNN models optimized using GWO and WOA-BAT. Fig. 5(a), and (b), illustrates the training progress plot using WOA-BAT optimized CNN and un-optimized CNN. It can be observed that a decrease in the training performance is observed for the un-optimized CNN, in comparison to the WOA-BAT optimized CNN. Un-optimized CNN refers to training CNN using the default parameters used by the adam optimizer and then testing the performance using the test samples of the respective datasets. Since there are two datasets, optimization is performed using the first dataset and the same parameters are used for the second dataset. For both datasets, good performance is obtained.

Table 3.

Hyper parameters obtained from optimization.

Training solver	Initial learning rate	L2 regularization	Max epochs	Gradient decay factor	Validation frequency
GWO	0.0004	0.0005	10	0.8	10
WOA-BAT	0.0001	0.0004	10	0.7	10

Open in a new tab

Fig. 5 — Results of training progression (Blue and Red lines refer to the performance values during Training, the Black line refers to performance during Validation) (a) optimized WOA-CNN (b) Un-optimized CNN.

The performance of the proposed classification set-up is computed using sensitivity, specificity, accuracy, precision, and F1 score for predicted and annotated results as given in (17)–(21).

Accuracy = (T P + T N) ∕ (T P + T N + F P + F N)

(17)

Sensitivity = T P ∕ (T P + F N)

(18)

Specificity = T N ∕ (T N + F P)

(19)

Precision = T P ∕ (T P + F P)

(20)

F 1 score = 2 (\frac{Precision ∗ Recall}{Precision + Recall})

(21)

The accurate overall predictive ability of the classifier into the three classes is given by Accuracy (ACC). Sensitivity (SE) gives the rate of correctly classified positive instances into three classes. Specificity (SP) deals with the rate of correctly classified negative instances. Precision gives the rate of correctly classified true positives among the cumulative sum of true positives and false positives, it is an important evaluation parameter in multi-class problems. Similarly, the F1 score combines precision and recall, since, in contrast to precision, recall provides an indication of mixed positive predictions. For each class, the True Positives (TP), False Positives (FP), False Negatives (FN), and True Negatives (TN) are computed and summed up to determine the total TP, TN, FP, and FN obtained for all the three classes [23]. Further using the equations given in (17)–(21), the classifier performance is computed. The following subsections provide the confusion matrices and performance evaluation results.

3.2. Results of classification using ensemble of ResNet-50 and ECOC classifier

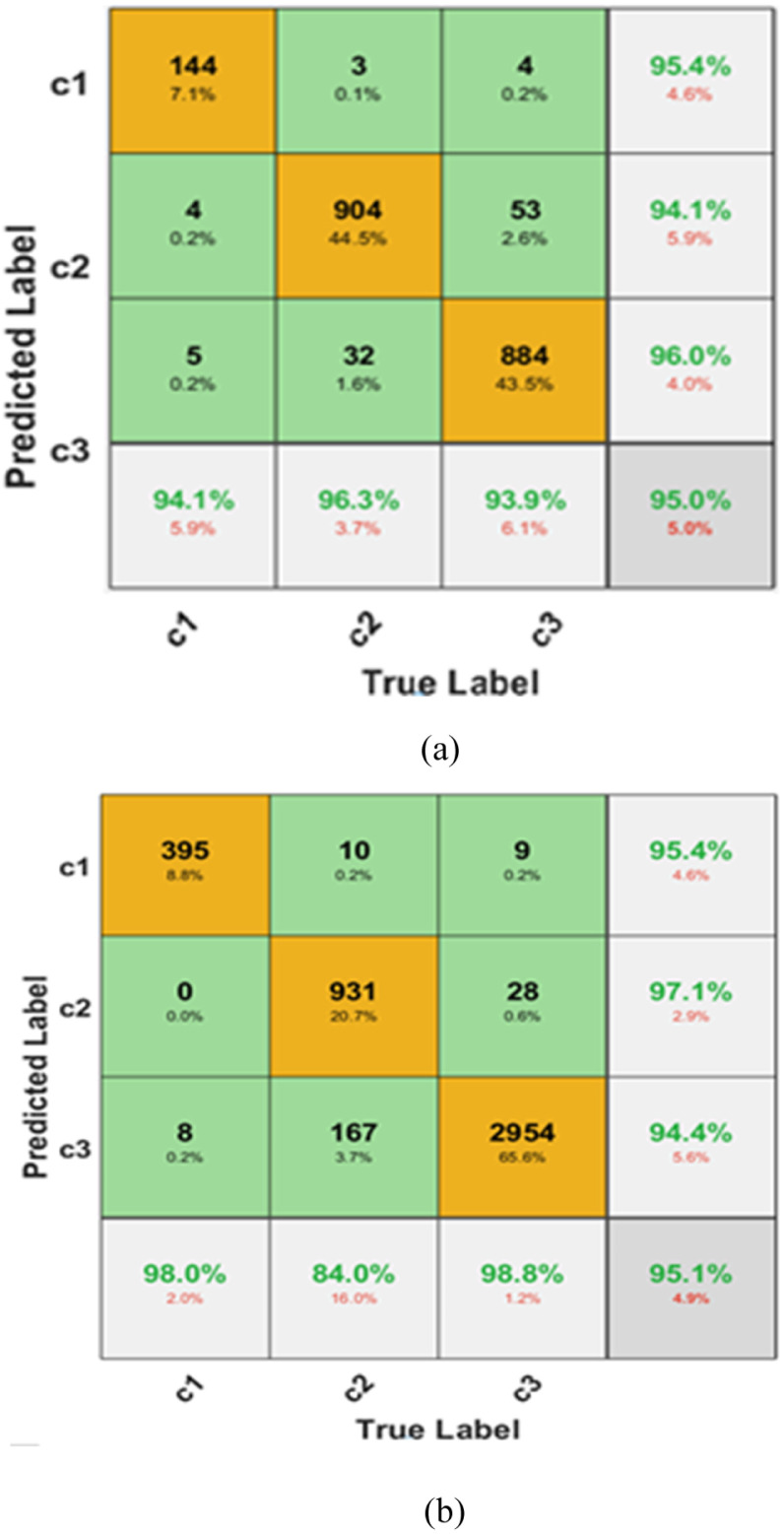
Dataset 1 was divided into a 30:70 ratio, wherein out of 2905 images, the number of images used for testing was 2033, and 872 images were used for training. Similarly, dataset 2 was also divided randomly into a 30:70 ratio, wherein out of 6432, the number of images used for testing was 4502, and 1930 images were used for training. Table 4 gives the results of classification for the two datasets and the corresponding confusion matrices in Fig. 6(a) and (b). In Fig. 6, c1, c2, and c3 belong to covid-19, normal, and viral pneumonia classes respectively.

Table 4.

Results of classification using ensemble of ECOC for 30:70 set-up.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.94	0.99	0.95	0.94	0.95
Dataset 2	0.98	0.99	0.95	0.96	0.95

Open in a new tab

Fig. 6 — Confusion matrices for multiclass ECOC (a) Dataset 1 (b) Dataset 2.

The ResNet-50 and ECOC classification set-up is performed on 50:50 training and test ratio, for the purpose of comparison for both the datasets. Further, five-fold cross-validation is also performed to validate the performance of the model on multiple folds. For dataset 1, each subset consists of 581 images, consisting of images from all the three classes selected using stratified sampling. In the case of dataset 2, there are 6432 images, three subsets consist of 1286 images, and two subsets consist of 1287 images since 6432 is not divisible by 5. The corresponding results of classification are given in Table 5, Table 6.

Table 5.

Results of classification using ensemble of ECOC for 50:50 set-up.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.93	0.99	0.94	0.94	0.96
Dataset 2	0.95	0.97	0.97	0.96	0.95

Open in a new tab

Table 6.

Results of classification using ensemble of ECOC for 5 fold cross-validation.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.94	0.99	0.94	0.93	0.93
Dataset 2	0.96	0.99	0.94	0.96	0.97

Open in a new tab

The main advantages of the ECOC-ResNet50 model are as follows:

1.
The proposed ResNet50-ECOC model is automated and performs well in the classification of covid-19 images from normal and viral pneumonia cases even under limited data conditions.
2.
Simple and avoids complex image pre-processing operations.

3.3. Results of classification using GWO and WOA optimized convolutional neural network

The dataset 1 was divided into 80:20 ratio, wherein out of 2905, the number of images used for training was 2324, and 581 images were used for testing. Similarly, dataset 2 was also divided randomly into 80:20 ratio, wherein out of 6432, the number of images used for training were 4502, and 1930 samples were used for testing. The Table 7, Table 8 give the results of classification for the two datasets using the two optimization techniques followed by un-optimized CNN classification results in Table 9.

Table 7.

Results of classification using GWO optimization for 80:20 classification set-up.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	1	0.99	0.98	0.99	0.98
Dataset 2	0.95	0.99	0.95	0.95	0.94

Open in a new tab

Table 8.

Results of classification using WOA-BAT optimization for 80:20 classification set-up.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	1	0.99	0.96	0.98	0.95
Dataset 2	1	0.99	0.96	0.98	0.96

Open in a new tab

Table 9.

Results of classification using un-optimized CNN.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.63	0.97	0.87	0.98	0.65
Dataset 2	0.44	1	0.88	0.61	1

Open in a new tab

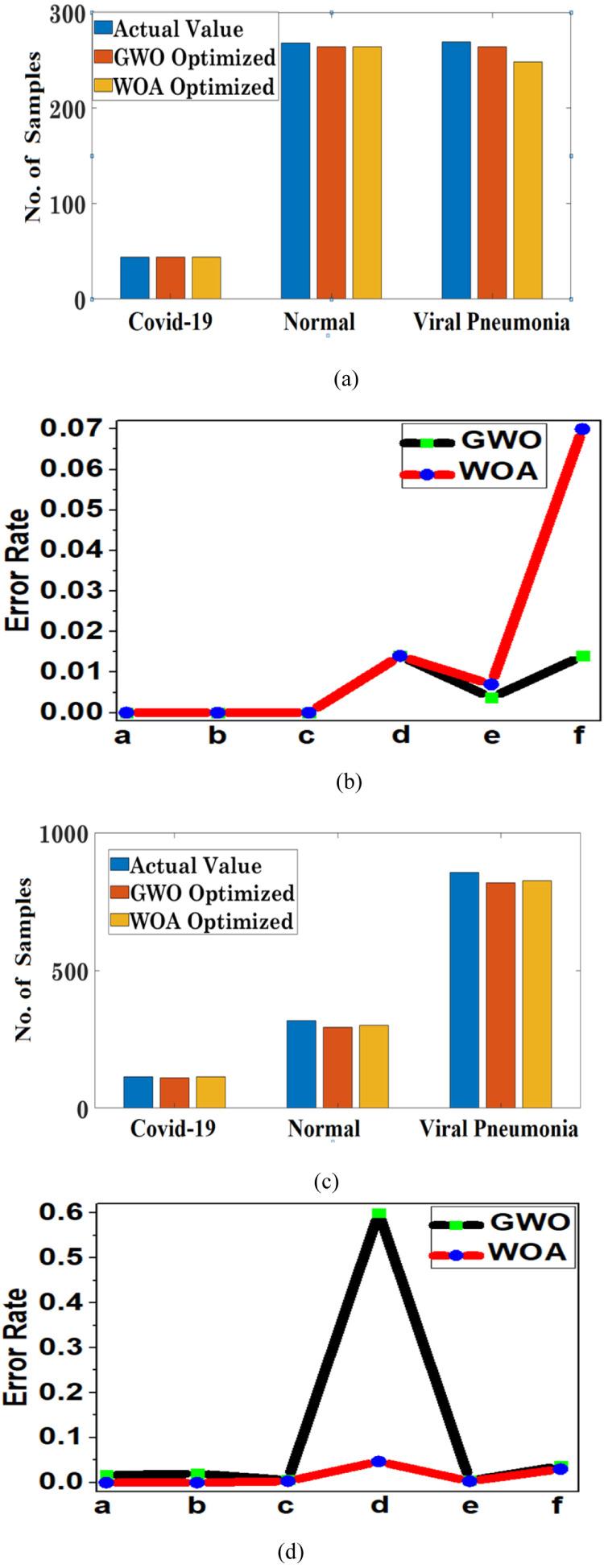
In Fig. 7, the actual values in the bar graph refer to the number of actual samples in the respective classes plotted against each of the predicted sample values for the respective methods. The resultant values are plotted as predicted by the two optimized CNN architectures. In Fig. 7b, the $x - a x i s$ corresponds to the frequency of one class samples belonging to the other class. The error rate on the $y - a x i s$ is computed for all the designed models as illustrated in Figs. 7b&d, 8b&d, and 9b&d. For instance, $a$ in error rate plot (Figs. 7b&d, 8b&d, and 9b&d), indicates $C 1 ϵ C 2$ , which correspondingly refers to the number of samples of $C 1$ incorrectly classified as $C 2$ , similarly $b$ indicates $C 1 ϵ C 3$ , $c$ indicates $C 2 ϵ C 1$ , $d$ indicates $C 2 ϵ C 3$ , $e$ indicates $C 3 ϵ C 1$ , and $f$ indicates $C 3 ϵ C 2$ . The error rate is reported on $y - a x i s$ , and it is computed as given in (22).

Error R a t e = \frac{N o . o f C 1 samples incorrectly classified a s C 2}{Total n o o f C 1 samples}

(22)

It can be observed from Figs. 8, and 9, that in comparison to un-optimized CNN architecture, the optimized CNN architectures (GWO and WOA-BAT) resulted in a good performance. However, when the two optimized architectures GWO and WOA-BAT are compared, GWO performs slightly better in contrast to WOA-BAT optimized CNN architecture as illustrated in Fig. 7.

Fig. 7 — Illustration of performance for the optimized CNN architecture using GWO and WOA-BAT, (a) Accuracy of correct classification in terms of the number of samples for dataset 1, (b) Error rate computed for different class samples for dataset 1, (c) Accuracy of correct classification in terms of the number of samples for dataset 2, (d) Error rate computed for different class samples for dataset 2.

Fig. 8 — Illustration of performance for the GWO optimized and unoptimized CNN architecture, (a) Accuracy of correct classification in terms of the number of samples for dataset 1, (b) Error rate computed for different class samples for dataset 1, (c) Accuracy of correct classification in terms of the number of samples for dataset 2, (d) Error rate computed for different class samples for dataset 2.

Fig. 9 — Illustration of performance for the WOA-BAT optimized and unoptimized CNN architecture, (a) Accuracy of correct classification in terms of the number of samples for dataset 1, (b) Error rate computed for different class samples for dataset 1, (c) Accuracy of correct classification in terms of the number of samples for dataset 2, (d) Error rate computed for different class samples for dataset 2.

Five-fold cross-validation is also performed to validate the performance of the model on multiple folds. For dataset 1, five subsets are created, each subset consists of 581 images, consisting of images from all three classes. For each iteration, four subsets are used for training, and one subset is used for testing. The average is computed by determining, the performance of the classifier at each iteration. In the case of dataset 2, there are 6432 images, three subsets consist of 1286 images, and two subsets consist of 1287 images since 6432 is not divisible by 5. Similarly, for each iteration, four subsets are used for training, and one subset is used for testing. The average performance values obtained for the five iterations for the respective datasets using the two optimization techniques are given in Table 10, Table 11.

Table 10.

Results of five-fold cross-validation using GWO based CNN.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.94	0.99	0.97	0.95	0.96
Dataset 2	0.94	0.99	0.96	0.95	0.98

Open in a new tab

Table 11.

Results of five-fold cross-validation using WOA-BAT based CNN.

Evaluation parameter	SE	SP	ACC	F1-score	Precision
Dataset 1	0.96	0.99	0.97	0.96	0.97
Dataset 2	0.98	0.99	0.97	0.97	0.96

Open in a new tab

A slightly better performance was observed using GWO optimized design in comparison to the WOA optimized design for dataset 1. However, a 100% classification accuracy can be observed in identifying covid-19 images for 80:20 classification set-up since the number of actual samples and the number of predicted samples are equal using WOA-BAT optimization algorithm for datasets 1 and 2.

3.4. Comparative analysis

A comparative analysis of the proposed CNN designs is performed by comparing with the state of art literature used for the classification of covid-19 chest X-ray images as illustrated in Table 12. Since there is a difference in the datasets used in the literature, a thorough comparative analysis cannot be carried out. However, a similarity exists between the image type (Chest X-ray). The purpose of the comparative study is not only to highlight the improvement in performance by the proposed design but also to provide an insight regarding the datasets used in the previous studies. The state of art methods reported in Table 12 is based on CNN. However, the choice of parameters is mainly standard. The optimization methodology adopted in [9], is somewhat similar to the proposed design, however, the hyper parameter optimization methodology of our proposed design is unique. In contrast to the methodology reported in [9], the proposed design has resulted in improved performance for both datasets. Further, in [9], the optimization was limited to a single dataset, whereas the universal acceptability of optimized parameters is proved by our proposed methodology since the same optimization parameters hold true for dataset 2 resulting in good classification performance. Additionally, most of the state of art methods have used a limited number of images and have not reported the other classification performance parameters. A SqueezeNet architecture with fewer parameters is investigated by providing the Chest X-ray images as the input [24]. The results obtained for the respective datasets are also reported in Table 12.

Table 12.

Comparative analysis of the proposed method with state of art methods.

Ref.	No. of images	SE	SP	ACC	F-score	Precision
Goel et al. 2020 [9]	2800	0.97	0.96	0.97	0.95	0.92
Sethy et al. 2020 [25]	–	–	–	95.3	91.4	–
Ozturk et al. 2020 [26]	1125	–	–	0.87	–	–
Abbas et al. 2020 [27]	196	0.97	–	0.95	0.93	–
Ioannis et al. 2020 [8]	1428	–	–	0.93	–	–
Narin et al. 2020 [11]	100	–	–	0.98	–	–
Oh et al. 2020 [28]	502	0.80	0.94	0.84	0.79	0.78
Shervin et al. 2020 [12]	3000	0.98	0.90	–	–	–
Nour et al. 2020 [29]	2905	0.89	0.99	0.98	0.96	–
Iandola et al. 2020 [24]	2905	0.85	0.91	0.90	0.86	0.87
	6432	0.87	0.92	0.91	0.87	0.87
Proposed	2905	1	0.99	0.98	0.99	0.98
	6432	1	0.99	0.96	0.98	0.96

Open in a new tab

4. Conclusion

In this study, an optimized deep learning-based model is proposed to detect and classify covid-19 cases from viral pneumonia and normal chest X-ray images. Since hyper parameters of CNN play an important role in classification accuracy, we have used GWO and ensemble of WOA-BAT techniques to optimize the parameters of CNN. One of the major challenges faced by researchers in developing a computer-aided automated diagnostic tool for detection of covid-19 using X-ray images is the limited availability of data. Creating a large database requires efforts from the radiologist, and also requires time to collect images from various parts of the globe. The proposed method aims to overcome such issues such as misclassification, poor classifier learning capability, and underfitting arising due to limited data. The classification results on the two datasets containing dataset 1 $=$ 2905 images and dataset 2 $=$ 6342 images are comparatively better than the state of art approaches. Although the number of covid-19 images is comparatively low (dataset 1 $=$ 219), (dataset 2 $=$ 576) in contrast to the normal and viral pneumonia cases, covid-19 classification accuracy is quite good, compared to the state of art approaches. The developed system hyper parameters were initially obtained using dataset 1 and the same parameters were kept constant for training and testing of dataset 2. Good classification accuracy of 98% and 96% was obtained for dataset 1 and dataset 2 respectively. Further, a 100% accuracy was achieved for classifying covid-19 images for both the optimization techniques. The proposed method can also be tested in big data situations (larger image database). In the future, we plan to build a robust dataset considering images from multiple diseases (viral pneumonia, bacterial pneumonia, other respiratory diseases, etc.,) and test the optimized CNN methodologies. Since, we plan to build a robust dataset considering images from various hospitals, and test the methodologies, the uncertainties in automatic detection could be handled by increasing the learning ability of the classifier to avoid misclassification of covid-19 cases. The proposed system can be used in covid-19 affected countries with a limited number of radiologists and can be deployed in remote areas to ease the task of covid-19 front line warriors.

CRediT authorship contribution statement

Sameena Pathan: Idea generation, Literature analysis, Interpretation of results, Software Simulation Analysis, Optimization and validation, Preparation of the manuscript. P.C. Siddalingaswamy: Interpretation of results, Preparation of the manuscript. Tanweer Ali: Literature analysis, Interpretation of results, Optimization and validation, Preparation of the manuscript.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1.Calvo C., López-Hortelano M.G., de Carlos Vicente J.C., Martínez J.L.V., de trabajo de la Asociación, G. Recommendations on the clinical management of the COVID-19 infection by the “new coronavirus” SARS-CoV2. Spanish Paediatric Association working group. Anal. Pediatr. (Engl. Ed.) 2020 doi: 10.1016/j.anpede.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. Coronavirus disease 2019 (COVID-19): a perspective from China. Radiology. 2020 doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Patel P. 2020. Chest X-ray (Covid-19 & Pneumonia) Retrieved October 02, 2020, from https://www.kaggle.com/prashant268/chest-xray-covid19-pneumonia. [Google Scholar]
4.Chan J.F.W., Yuan S., Kok K.H., To K.K.W., Chu H., Yang J., … L.J., Tsoi H.W. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395(10223):514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Zhao W., Zhong Z., Xie X., Yu Q., Liu J. Relation between chest CT findings and clinical conditions of coronavirus disease (COVID-19) pneumonia: a multicenter study. Amer. J. Roentgenol. 2020;214(5):1072–1077. doi: 10.2214/AJR.20.22976. [DOI] [PubMed] [Google Scholar]
6.Hemdan E.E.D., Shouman M.A., Karar M.E. 2020. Covidx-net: A framework of deep learning classifiers to diagnose covid-19 in x-ray images. arXiv preprint arXiv:2003.11055. [Google Scholar]
7.Wang L., Wong A. 2020. COVID-Net: A Tailored deep convolutional neural network design for detection of COVID-19 cases from Chest X-ray images. arXiv preprint arXiv:2003.09871. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020;1 doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Goel T., Murugan R., Mirjalili S., Chakrabartty D.K. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2020:1–16. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Apostolopoulos I., Aznaouridis S., Tzani M. Extracting possibly representative COVID-19 biomarkers from X-ray images with deep learning approach and image data related to pulmonary diseases. J. Med. Biol. Eng. 2020;14:1–8. doi: 10.1007/s40846-020-00529-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Narin A., Kaya C., Pamuk Z. 2020. Automatic detection of coronavirus disease (covid-19) using x-ray images and deep convolutional neural networks. arXiv preprint arXiv:2003.10849. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Minaee Shervin, et al. Deep-COVID: Predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020;65 doi: 10.1016/j.media.2020.101794. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Rahman T. 2020. COVID-19 Radiography Database. Retrieved October 02, 2020, https://www.kaggle.com/tawsifurrahman/covid19-radiography-database. [Google Scholar]
14.K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.
15.Allwein E.L., Schapire R.E., Singer Y. Reducing multiclass to binary: A unifying approach for margin classifiers. J. Mach. Learn. Res. 2000;1(Dec):113–141. [Google Scholar]
16.Eberhart R., Kennedy J. MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Ieee; 1995. A new optimizer using particle swarm theory; pp. 39–43. [Google Scholar]
17.Dorigo M., Birattari M., Stutzle T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006;1(4):28–39. [Google Scholar]
18.Kirkpatrick S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984;34(5–6):975–986. [Google Scholar]
19.Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl. Intell. 2015;43(1):150–161. [Google Scholar]
20.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]
21.Mohammed H.M., Umar S.U., Rashid T.A. A systematic and meta-analysis survey of whale optimization algorithm. Comput. Intell. Neurosci. 2019;2019 doi: 10.1155/2019/8718571. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Yang X.S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspired Comput. 2011;3(5):267–274. [Google Scholar]
23.Sokolova M., Lapalme G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manage. 2009;45(4):427–437. [Google Scholar]
24.Iandola F.N., Han S., Moskewicz M.W., Ashraf K., Dally W.J., Keutzer K. 2016. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv preprint arXiv:1602.07360. [Google Scholar]
25.Sethy P.K., Behera S.K. 2020. Detection of coronavirus disease (covid-19) based on deep features. Preprints, 2020030300, 2020. [Google Scholar]
26.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Acharya U.R. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Abbas A., Abdelsamea M.M., Gaber M.M. 2020. Classification of COVID-19 in chest X-ray images using detrac deep convolutional neural network. arXiv preprint arXiv:2003.13815. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Oh Y., Park S., Ye J.C. Deep learning covid-19 features on cxr using limited training data sets. IEEE Trans. Med. Imaging. 2020 doi: 10.1109/TMI.2020.2993291. [DOI] [PubMed] [Google Scholar]
29.Nour M., Cömert Z., Polat K. A novel medical diagnosis model for COVID-19 infection detection based on deep features and Bayesian optimization. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b1] 1.Calvo C., López-Hortelano M.G., de Carlos Vicente J.C., Martínez J.L.V., de trabajo de la Asociación, G. Recommendations on the clinical management of the COVID-19 infection by the “new coronavirus” SARS-CoV2. Spanish Paediatric Association working group. Anal. Pediatr. (Engl. Ed.) 2020 doi: 10.1016/j.anpede.2020.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b2] 2.Zu Z.Y., Jiang M.D., Xu P.P., Chen W., Ni Q.Q., Lu G.M., Zhang L.J. Coronavirus disease 2019 (COVID-19): a perspective from China. Radiology. 2020 doi: 10.1148/radiol.2020200490. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b3] 3.Patel P. 2020. Chest X-ray (Covid-19 & Pneumonia) Retrieved October 02, 2020, from https://www.kaggle.com/prashant268/chest-xray-covid19-pneumonia. [Google Scholar]

[b4] 4.Chan J.F.W., Yuan S., Kok K.H., To K.K.W., Chu H., Yang J., … L.J., Tsoi H.W. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: a study of a family cluster. Lancet. 2020;395(10223):514–523. doi: 10.1016/S0140-6736(20)30154-9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b5] 5.Zhao W., Zhong Z., Xie X., Yu Q., Liu J. Relation between chest CT findings and clinical conditions of coronavirus disease (COVID-19) pneumonia: a multicenter study. Amer. J. Roentgenol. 2020;214(5):1072–1077. doi: 10.2214/AJR.20.22976. [DOI] [PubMed] [Google Scholar]

[b6] 6.Hemdan E.E.D., Shouman M.A., Karar M.E. 2020. Covidx-net: A framework of deep learning classifiers to diagnose covid-19 in x-ray images. arXiv preprint arXiv:2003.11055. [Google Scholar]

[b7] 7.Wang L., Wong A. 2020. COVID-Net: A Tailored deep convolutional neural network design for detection of COVID-19 cases from Chest X-ray images. arXiv preprint arXiv:2003.09871. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b8] 8.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from x-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020;1 doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b9] 9.Goel T., Murugan R., Mirjalili S., Chakrabartty D.K. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl. Intell. 2020:1–16. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b10] 10.Apostolopoulos I., Aznaouridis S., Tzani M. Extracting possibly representative COVID-19 biomarkers from X-ray images with deep learning approach and image data related to pulmonary diseases. J. Med. Biol. Eng. 2020;14:1–8. doi: 10.1007/s40846-020-00529-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b11] 11.Narin A., Kaya C., Pamuk Z. 2020. Automatic detection of coronavirus disease (covid-19) using x-ray images and deep convolutional neural networks. arXiv preprint arXiv:2003.10849. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b12] 12.Minaee Shervin, et al. Deep-COVID: Predicting COVID-19 from chest X-ray images using deep transfer learning. Med. Image Anal. 2020;65 doi: 10.1016/j.media.2020.101794. Available: [DOI] [PMC free article] [PubMed] [Google Scholar]

[b13] 13.Rahman T. 2020. COVID-19 Radiography Database. Retrieved October 02, 2020, https://www.kaggle.com/tawsifurrahman/covid19-radiography-database. [Google Scholar]

[b14] 14.K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 770–778.

[b15] 15.Allwein E.L., Schapire R.E., Singer Y. Reducing multiclass to binary: A unifying approach for margin classifiers. J. Mach. Learn. Res. 2000;1(Dec):113–141. [Google Scholar]

[b16] 16.Eberhart R., Kennedy J. MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Ieee; 1995. A new optimizer using particle swarm theory; pp. 39–43. [Google Scholar]

[b17] 17.Dorigo M., Birattari M., Stutzle T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006;1(4):28–39. [Google Scholar]

[b18] 18.Kirkpatrick S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984;34(5–6):975–986. [Google Scholar]

[b19] 19.Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl. Intell. 2015;43(1):150–161. [Google Scholar]

[b20] 20.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]

[b21] 21.Mohammed H.M., Umar S.U., Rashid T.A. A systematic and meta-analysis survey of whale optimization algorithm. Comput. Intell. Neurosci. 2019;2019 doi: 10.1155/2019/8718571. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b22] 22.Yang X.S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspired Comput. 2011;3(5):267–274. [Google Scholar]

[b23] 23.Sokolova M., Lapalme G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manage. 2009;45(4):427–437. [Google Scholar]

[b24] 24.Iandola F.N., Han S., Moskewicz M.W., Ashraf K., Dally W.J., Keutzer K. 2016. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and< 0.5 MB model size. arXiv preprint arXiv:1602.07360. [Google Scholar]

[b25] 25.Sethy P.K., Behera S.K. 2020. Detection of coronavirus disease (covid-19) based on deep features. Preprints, 2020030300, 2020. [Google Scholar]

[b26] 26.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Acharya U.R. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b27] 27.Abbas A., Abdelsamea M.M., Gaber M.M. 2020. Classification of COVID-19 in chest X-ray images using detrac deep convolutional neural network. arXiv preprint arXiv:2003.13815. [DOI] [PMC free article] [PubMed] [Google Scholar]

[b28] 28.Oh Y., Park S., Ye J.C. Deep learning covid-19 features on cxr using limited training data sets. IEEE Trans. Med. Imaging. 2020 doi: 10.1109/TMI.2020.2993291. [DOI] [PubMed] [Google Scholar]

[b29] 29.Nour M., Cömert Z., Polat K. A novel medical diagnosis model for COVID-19 infection detection based on deep features and Bayesian optimization. Appl. Soft Comput. 2020 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Automated Detection of Covid-19 from Chest X-ray scans using an optimized CNN architecture

Sameena Pathan

PC Siddalingaswamy

Tanweer Ali

Abstract

1. Introduction

Fig. 1.

1.1. Novelty and contributions

2. Materials and methods

2.1. Dataset

2.2. Optimization and classification

2.2.1. Ensemble of ResNet-50 and ECOC classifier

Fig. 2.

Table 1.

2.2.2. Optimization process using Grey Wolf optimizer

Fig. 3.

2.2.3. Optimization process using WOA-BAT algorithm

2.2.4. CNN architecture design

Fig. 4.

Table 2.

3. Results and discussion

3.1. Training and testing

Table 3.

Fig. 5.

3.2. Results of classification using ensemble of ResNet-50 and ECOC classifier

Table 4.

Fig. 6.

Table 5.

Table 6.

3.3. Results of classification using GWO and WOA optimized convolutional neural network

Table 7.

Table 8.

Table 9.

Fig. 7.

Fig. 8.

Fig. 9.

Table 10.

Table 11.

3.4. Comparative analysis

Table 12.

4. Conclusion

CRediT authorship contribution statement

Declaration of Competing Interest

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases