Abstract
We consider learning from comparison labels generated as follows: given two samples in a dataset, a labeler produces a label indicating their relative order. Such comparison labels scale quadratically with the dataset size; most importantly, in practice, they often exhibit lower variance compared to class labels. We propose a new neural network architecture based on siamese networks to incorporate both class and comparison labels in the same training pipeline, using Bradley-Terry and Thurstone loss functions. Our architecture leads to a significant improvement in predicting both class and comparison labels, increasing classification AUC by as much as 35% and comparison AUC by as much as 6% on several real-life datasets. We further show that, by incorporating comparisons, training from few samples becomes possible: a deep neural network of 5.9 million parameters trained on 80 images attains a 0.92 AUC when incorporating comparisons.
Keywords: neural network, joint learning, comparison, classification, siamese network
1. Introduction
Neural networks have been tremendously successful in tackling supervised learning problems in a variety of domains, including speech recognition (Hinton et al., 2012), natural language processing (Collobert et al., 2011), and image classification (Krizhevsky et al., 2012; Simonyan & Zisserman, 2014; Szegedy et al., 2015), to name a few. Unfortunately, in many real-life applications of interest, including medicine (Reynolds et al., 2002; Chiang et al., 2007; Wallace et al., 2008) and recommender systems (Schultz & Joachims, 2004; Zheng et al., 2009; Koren & Sill, 2011), class labels are generated by humans and exhibit high variance. This is further exacerbated by the fact that in many domains, such as, e.g., medicine, datasets are often small. Training neural networks over noisy, small datasets is challenging, as high-dimensional parametric models are prone to overfitting in this setting (Srivastava et al., 2014; Schmidhuber, 2015).
We propose to overcome this limitation by incorporating comparisons in a neural network’s training process. In doing so, we exploit the fact that in many domains, beyond producing class labels, labelers can assess the relative order between two inputs. For example, in a medical diagnosis problem with two classes of images (e.g., diseased and normal), an expert can generate not only diagnostic labels but also order pairs of images w.r.t. disease severity. Similarly, in a recommender system, class labels (e.g., star ratings) are ordered, and labelers can produce relative preferences between any two data samples.
Incorporating comparison labels to the training process has two advantages. First, in the presence of a small dataset, soliciting comparisons in addition to class labels increases the training set size quadratically. Compared to class labels on the same data samples, such labels indeed reveal additional information: comparisons express both inter- and intra-class relationships; the latter are not revealed via class labels alone. Second, in practice, comparisons are often less noisy than (absolute) class labels. Indeed, human labelers disagreeing when generating class judgments often exhibit far less variability when asked to compare pairs of samples instead. This has been extensively documented in a broad array of domains, including medicine (Stewart et al., 2005; Kalpathy-Cramer et al., 2016), movie recommendations (Brun et al., 2010; Desarkar et al., 2010, 2012; Liu et al., 2014), travel recommendations (Zheng et al., 2009), music recommendations (Koren & Sill, 2011), and web page recommendations (Schultz & Joachims, 2004), to name a few. As a result, incorporating comparisons in training is advantageous even when datasets are large and class labels are abundant; we demonstrate this experimentally in Section 4.1.
We make the following contributions:
We propose a neural network architecture that is trained on (and can be used to estimate) both class and comparison labels. Our architecture is inspired by siamese networks (Bromley et al., 1994), using Bradley-Terry (Bradley & Terry, 1952) and Thurstone (Cattelan, 2012) models as loss functions.
We extensively evaluate our model w.r.t. several metrics on real-life datasets. We confirm that combining comparisons with class labels via this model consistently improves the classification performance w.r.t. Area Under the ROC Curve (AUC) by 8%–35%, w.r.t. accuracy by 14%–25%, w.r.t. F1 score by 12% – 40%, and w.r.t. Area Under the Precision-Recall Curve (PRAUC) by 14% – 55%.
We validate the benefit of training with comparisons in learning from small datasets. We establish that, by incorporating comparisons, we can train and optimize a neural network with 5,974,577 parameters on a dataset of only 80 samples. In this setting, our combined model attains a classification performance of 0.914 AUC, 0.883 accuracy, 0.64 F1 score, and 0.731 PRAUC, whereas training only on class labels can only achieve 0.835 AUC, 0.705 accuracy, 0.517 F1 score, and 0.177 PRAUC.
The remainder of this paper is organized as follows. Section 2 discusses related work. Section 3 describes our methodology and introduces our model combining class and comparison labels. Section 4 reports our experimental results, evaluated on several real-life datasets. Finally, Section 5 summarizes our contributions.
2. Related Work
Siamese networks were originally proposed to regress similarity between two samples (Bromley et al., 1994). Many subsequent works using siamese networks thus focus on learning low-dimensional representations to predict similarity, for applications such as multi-task learning (Xia et al., 2014; Zhang et al., 2016; Gordo et al., 2016; Simo-Serra & Ishikawa, 2016; Shen et al., 2017), drug discovery (Stephenson et al., 2018), protein structure prediction (Hou et al., 2019; Moritz et al., 2019), person identification (Chen et al., 2016; Wu et al., 2017), and image retrieval (Hadsell et al., 2006; Norouzi et al., 2012; Wang et al., 2014; Gordo et al., 2016). Both the problem we solve and the methodology we employ significantly depart from these works; crucially, the learning objectives used in regressing similarity are not suitable for regressing comparisons. For instance, similarities and respective penalties, such as contrastive loss (Hadsell et al., 2006) and triplet loss (Norouzi et al., 2012), are sensitive to scaling: inputs further apart are heavily penalized. In contrast, comparisons reflecting relative order and, consequently, penalties for regressing them ought to be scaling-invariant. Such differences lead us to consider altogether different penalties.
A significant body of research in the last decade has focused on comparison and ranking tasks. RankSVM (Joachims, 2002) learns a target ranking via a linear Support Vector Machine (SVM), with constraints imposed by all possible pairwise comparisons. Burges et al. (2005) estimate pairwise comparisons via a fully connected neural network called RankNet, using the Bradley-Terry generative model (Bradley & Terry, 1952) to construct a cross-entropy objective function. Following Burges et al. (2005), we also model comparison labels as the difference between functions applied to feature pairs. However, we regress both comparison and class labels, while Burges et al. (2005) regress rating scores of compared objects (not comparisons per se). We also depart from cross-entropy and SVM losses used by Burges et al. (2005) and Joachims (2002), respectively, by learning comparisons via maximum likelihood based on the Bradley-Terry (Bradley & Terry, 1952) and Thurstone models (Thurstone, 1927). As we demonstrate experimentally in Section 4.1, losses induced by these models are more suitable, since these models consider the order between compared input pairs, unlike cross-entropy and SVM losses.
Closer to our work, Chang et al. (2016), Dubey et al. (2016), and Doughty et al. (2017) adopt siamese networks for comparison and ranking tasks. Chang et al. (2016) examine the ranking among the burst mode shootings of a scene, using an objective (maximum likelihood based on the Bradley-Terry model) similar to one of the two we consider. Dubey et al. (2016) predict the pairwise comparisons of urban appearance images, via a loss function combining cross-entropy loss for pairwise comparison and hinge loss for ranking. Doughty et al. (2017) assess videos with respect to the skill level in their content, by learning similarities and comparisons of video pairs via hinge loss. We differ from these works in jointly learning class labels along with comparison labels within the same pipeline.
Similar to our setting, several works study joint regression and ranking, albeit in shallow learning models. Sculley (2010); Chen et al. (2015); Takamura & Tsujii (2015), and Wang et al. (2016) learn the rank of two inputs as the difference between their regression outputs, rather than via labeler rankings, and apply this to click prediction and document or image retrieval. Sculley (2010) trains a logistic regression model, where the loss function is a weighted combination of the same loss applied to class and ranking predictions. Takamura & Tsujii (2015) and Wang et al. (2016) employ a similar approach as Sculley (2010) and train linear regression models with different loss functions for regression and ranking (mean-square and hinge, respectively). Chen et al. (2015) consider joint classification and ranking via a similar approach as RankSVM (Joachims, 2002). We also minimize a weighted combination of different losses applied to class and comparison labels. However, we model pairwise comparison probabilities via two linear comparison models: Bradley-Terry and Thurstone. Crucially, we also differ by learning both class and comparison labels via a neural network, instead of shallow models such as logistic regression and SVMs.
To the best of our knowledge, Sun et al. (2017) is the only previous work incorporating class and comparison labels via a neural network architecture. Nevertheless, they do not incorporate ordered class labels and utilize joint learning only for improving comparison label predictions. Our neural network architecture is more generic and learns class and comparison labels individually or jointly. Finally, we show experimentally in Section 4.2 that our approach outperforms Sun et al. (2017) w.r.t. predicting both class and comparison labels on several real-life datasets.
Finally, several works propose methods to reduce overfitting, while training a deep learning model on a small dataset. Mao et al. (2006) augment the dataset by generating artificial data samples from a trained SVM classifier. Antoniou et al. (2017) and Zhang et al. (2018) use generative adversarial networks to produce new images for data augmentation. Hauberg et al. (2016) generate synthetic data by using diffeomorphism, which is learned from pairs of data samples within each class. Other works aim to cope with overfitting by means of dimension reduction. Liu et al. (2017) propose a method to jointly select features and train a deep learning model. Keshari et al. (2018) propose a dictionary based algorithm to learn a single weight for each filter of a Convolutional Neural Network (CNN). Singh & Kingsbury (2017) use a dual tree complex wavelet transform (DTCWT) based CNN to learn edge-based invariant representations in the first few layers of the CNN. We differ from these works by not generating artificial data samples but by augmenting the dataset by comparison labels. Moreover, our objective significantly departs from the ones used in these works.
3. Problem Formulation
We consider a dataset containing N items, indexed by i ∈ {1,…, N}. Every item i has a corresponding d-dimensional feature vector . A labeler generates two types of labels for this dataset: absolute labels and comparison labels. Absolute labels characterize the class of an item, while comparison labels show the outcome of a comparison between two items. We denote the absolute label set by Da, containing tuples of the form (i, yi), where yi ∈ {−1, +1} shows which class the item i belongs to. Similarly, we denote the comparison label set by Dc, containing tuples of the form (i, j, y(i,j)), where y(i,j) = +1 represents that item i is ranked higher than item j and y(i,j) = −1, o.w. Neither our model nor our datasets contain any ties: a labeler always selects a comparison label in {−1, +1} when presented with two items.
In practice, when class labels are ordered, absolute and comparison labels can be coupled in the following natural fashion: given items (i, j), y(i,j) = +1 indicates that i has a higher propensity to receive the absolute label yi = +1, compared to j. As discussed in Section 1, ordered absolute labels naturally occur in applications of interest, such as medicine and recommender systems. For example, in the medical scenario, items i ∈ {1,…, N} are images and the absolute label yi = +1 represents the existence of a disease. Given images (i, j), y(i,j) = +1 indicates that the labeler deems the presence of the disease to be more severe in i. We describe several additional real-life examples, both medical and non-medical, in Section 4.
Acknowledging the coupling between absolute and comparison labels, our goal is to provide a single probabilistic model that can learn both labels jointly. In particular, learning from both absolute and comparison labels via our model enhances prediction performance on both types. To do so, we propose a combined neural network architecture in the next section.
3.1. Proposed Solution: A Combined Neural Network Architecture
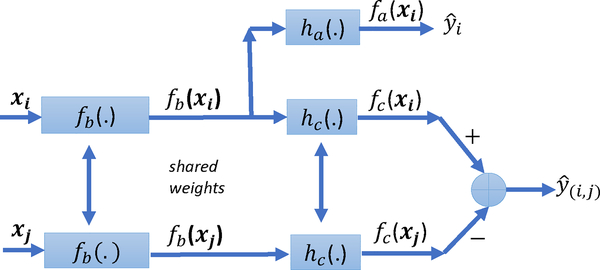
Our neural network architecture is inspired by siamese networks (Bromley et al., 1994), which are extensively used for regressing similarity between two inputs. A siamese network contains two identical base networks, followed by a module predicting the similarity between the inputs of the base networks. In this work, we extend the generic application of siamese networks to regress both absolute and comparison labels simultaneously. To do so, we adopt the combined neural network architecture given in Fig. 1.
Figure 1:
Our Combined Neural Network Architecture. Base network fb has the same structure and parameters for both types of labels. The absolute network receives xi as input, predicts the corresponding absolute label as , and consists of fb and ha. The comparison network is a siamese network. It receives xi and xj as inputs, predicts the corresponding comparison label as , and consists of fb and hc.
Our architecture is based on the assumption that absolute and comparison labels depend on the same latent variables. Formally, there exists a function representing the coupling between absolute and comparison labels. We interpret fb(xi) as a latent vector informative for both absolute and comparison label predictions involving i. Therefore, given items (i, j), the absolute label yi is regressed from fb(xi) and the associated comparison label y(i,j) is regressed from fb(xi) and fb(xj). We refer to fb as the base network, which has the same structure and parameters for all items i ∈ {1,…, N}.
Given fb, our combined neural network comprises two sub-networks: the absolute network fa and the comparison network fc. The absolute network receives xi as input and outputs , the absolute label prediction. Formally, for all (i,yi) ∈ Da:
| (1) |
where ∘ denotes function composition, is the base network, and is an additional network linking latent features to absolute labels. The comparison network is trained via a so-called siamese architecture. Given two inputs xi and xj, the corresponding comparison label prediction is given by:
| (2) |
where is again the base network and is an additional network linking latent features to a one-dimensional score fc = hc ∘ fb. We denote the parametrization of neural network functions fb, ha, and hc w.r.t. their weights as fb(·; Wb), ha(·; Wa), and hc(·; Wc), respectively. Note that, as a result, fa(·) = fa(·; Wa, Wb) and fc(·) = fc(·; Wc, Wb). Given both Da and Dc, we learn fb(·; Wb), ha(·; Wa), and hc(·; Wc) via a minimization of the form:
| (3) |
We train our combined neural network via stochastic gradient descent over Eq. (3). Here, La is a loss function for the absolute network and Lc is a loss function for the comparison network; we instantiate both below, in Section 3.2. The balance parameter α ∈ [0, 1] establishes a trade-off between the absolute label set Da and the comparison label set Dc. When α = 0, our model is restricted to the comparison/siamese network setting. When α =1, our model is restricted to the absolute/classical neural network setting.
This architecture is generic and flexible. In particular, the special case where ha = hc naturally captures the relationship between binary absolute and comparison labels described in the beginning of Section 3. Indeed, under this design, the event yi,j = +1 becomes more likely when i has a higher propensity to receive the absolute label yi = +1, compared to j. Nevertheless, we opt for the more generic scenario in which ha and hc may differ; joint prediction of absolute and comparison labels is thus more flexible. Finally, our design naturally extends to multi-class absolute labels, multiple labelers, and rankings. We present and apply an extension to multi-class absolute labels collected from multiple labelers in our experiments (c.f. ROP in Section 4). We discuss how to generalize to multi-class absolute labels in Appendix A, and how to generalize to rankings via the so-called Plackett-Luce model (Luce, 2012) in Appendix B.
3.2. Loss Functions
We train fa using classical loss functions La, such as cross-entropy, hinge loss, and mean-square loss. To train fc via Lc, we use two linear comparison models: Bradley-Terry and Thurstone. In contrast to cross-entropy and hinge losses, linear comparison models consider the order between compared items. The main advantage of these models is the capability of learning a score for each item, even though the labelers provide only binary comparative information, i.e., y(i,j) ϵ { − 1, +1} (Cattelan, 2012). This score is then used to predict not only the absolute label of the item, but also the rank of the item among all items in the dataset.
Formally, linear models for pairwise comparisons assert that every item i in a labeled comparison dataset Dc is parametrized by a (non-random) score si (Bradley & Terry, 1952; Imrey, 1998). Then, all labelling events in Dc are independent of each other, and their marginal probabilities are:
| (4) |
where F is a cumulative distribution function (c.d.f.). When F is the standard normal c.d.f., Eq. (4) becomes the Thurstone model, yet when F is the logistic c.d.f., Eq. (4) becomes the Bradley-Terry model (Cattelan, 2012). We extend the linear comparison model in Eq. (4) by introducing a generic representation of the score si. In particular, we assume that , where fc is the neural network described in Eq. (2). Then, given xi, xj, and y(i j) under the Bradley-Terry model, the (negative log-likelihood) comparison loss becomes:
| (5) |
where . Similarly, under the Thurstone model, the (negative log-likelihood) comparison loss becomes:
| (6) |
4. Experiments
Datasets
We evaluate our model on four real-life datasets, GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC, summarized in Table 1a.
Table 1:
(a) We evaluate our combined network on four real-life datasets: GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC (c.f. Section 4 for details). For each dataset, we allocate 60% of the total of N images for training, 20% for validation, and 20% for test. Here, Ntr, Nval, and Ntest denote training, validation, and test set sizes, respectively. For ROP, we augment the test set by adding the 5561 images in set H, which contains only absolute labels and no comparisons. (b) For each α, we tune the following on the validation set: absolute loss function La, comparison loss function Lc, regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T., given in Eq. (5)), and Thurstone (T., given in Eq. (6)) as loss functions.
| Dataset | Absolute Label |
Comparison Label |
||||
| Ntr | Nval | Ntest | Ntr | Nval | Ntest | |
| GIFGIF Happiness | 823 | 274 | 274 | 8830 | 390 | 390 |
| GIFGIF Pleasure | 675 | 225 | 225 | 5530 | 215 | 215 |
| ROP | 60 | 20 | 5561 | 10650 | 1140 | 1140 |
| FAC | 2112 | 704 | 704 | 4549 | 224 | 224 |
| (a) Datasets | ||||||
| Optimized on Validation Set | Values | |||||
| La | {C.E., H.} | |||||
| Lc | {B.T., T., C.E., H.} | |||||
| λ | [2 × 10−4, 2 × 10−2] | |||||
| L.R. | [10−4, 10−2] | |||||
| (b) Loss Functions and Hyperparameters | ||||||
GIFGIF is an MIT Media Lab project aiming to understand the emotional content of animated GIF images (MIT Media Lab). Labelers are provided with two images and are asked to identify which image better represents a given emotion. A labeler can choose either image, or use a third option: neither. We discard the outcomes that resulted in neither. This dataset does not contain absolute labels. We manually label N = 1371 GIF images within the category happiness, labeling image i with the absolute label yi = +1 if regarded as happy and yi = −1 if sad. There are 9617 pairwise comparisons among these 1371 images, where y(i,j) = +1 if image i is regarded as happier than j, and y(i,j) = −1, o.w. We repeat the same procedure for the emotion category pleasure and manually label N = 1125 GIF images within this category with yi = +1 if the subject of the image i is pleased and yi = −1 o.w. There are 5667 pairwise comparisons among these 1125 images.
Retinopathy of Prematurity (ROP) is a retinal disease occuring in premature infants; it is a leading cause of childhood blindness (Gole et al., 2005). The ROP dataset (Brown et al., 2018) contains two sets of images: a small set of N = 100 retinal images, which we denote by S, and a larger set of N = 5561 images that we denote by H. Images in both sets receive Reference Standard Diagnostic (RSD) labels (Ryan et al., 2014): To create an RSD label for a retinal image, a committee of three experts labels the image as ‘Plus’, ‘Pre-plus’, or ‘Normal’ based on the existence of ROP, indicating severe, intermediate level, and no ROP, respectively. These ordered categorical labels constitute our absolute labels. In addition, five experts independently label all 4950 pairwise comparisons of the images in set S only. Note that some pairs are labeled more than once by different experts. For each pair (i, j), the comparison label is y(i,j) = +1 if image i’s ROP severity is higher. Note that only images in S contain both absolute and comparison labels. We use S for training and reserve H for testing purposes.
The Filter Aesthetic Comparison (FAC) dataset (Sun et al., 2017) contains 1280 unfiltered images pertaining to 8 different categories. Twenty-two different image filters are applied to each image and resulting images are labelled by Amazon Mechanical Turk users. Filtered image pairs are labelled such that the comparison label y(i,j) = +1 if filtered image i has better quality than filtered image j, and y(i,j) = −1 o.w. Each filtered image appears in three comparison pairs. At the same time, absolute labels are generated by the creators of FAC dataset as follows. For each pair (i, j) such that y(i,j) = +1, i and j receive scores +1 and −1, respectively. Hence, each filtered image receives a score in [−3, +3]. Subsequently, image i receiving a +3 (−3) score is assigned the label yi = +1 (yi = −1); images that do not receive +3 or −3 score are discarded. Thus, the absolute label yi = +1 if the filtered image i has high quality and yi = −1, o.w. We choose one of the categories with N = 3520 filtered images as our dataset, since comparison labels only exist for filtered image pairs within the same category. All in all, there are 3520 binary absolute labels and 4964 pairwise comparison labels in this dataset.
Network Architectures
We use GoogLeNet (Szegedy et al., 2015) without the last two fully connected layers as our base network fb. We resize all images, so that . The corresponding base network output fb(xi) has p = 1024 dimensions ∀i ϵ {1,2, ⋯, N}. To leverage the well-known transfer learning properties of neural networks trained on images (Bengio et al., 2013), we initialize the layers from GoogLeNet with weights pre-trained on the ImageNet dataset (Deng et al., 2009). We choose ha and hc as single fully connected layers with sigmoid activations. We add L2 regularizers with a regularization parameter A to all layers and train our combined neural network end-to-end with stochastic gradient descent.1 We instantiate our loss functions and hyperparameters as shown in Table 1b. Specifically for ROP, we first pre-process retinal images with a pre-trained U-Net (Ronneberger et al., 2015) to convert the colorful images into black and white masks for retinal vessels (Brown et al., 2018). Recall that the special case where ha = hc, combining cross-entropy as La and Bradley-Terry loss as Lc, naturally captures the relationship between absolute and comparison labels (c.f. Section 3), at least in binary classification. In our experiments, we implement both ha ≠ hc and ha ≠ hc (c.f. Section 4.2).
Experiment Setup
We allocate 60% of the total of N images in the GIFGIF Happiness, GIFGIF Pleasure, ROP S, and FAC datasets for training, 20% for validation, and 20% for test. Thus, images in the training set are not paired with images in the validation or test sets for the generation of comparison labels. For ROP, we augment the test set by adding the 5561 images in set H and predict the existence of ROP during test time, i.e. if image i is predicted to be ‘Normal’ and , o.w. Recall that H contains only absolute labels and no comparisons (c.f. Table 1a).
Given α ϵ [0, 1], for each combination of the loss functions La, Lc, and hyperparameters λ, L.R. shown in Table 1b, we train our architecture over the training set. Then, we evaluate the resulting models on the validation set to determine the optimal loss functions and hyperparameters. We predict the absolute and comparison labels in the test set using the corresponding optimal models. When α ϵ (0, 1), functions fb, ha, and hc are trained (and tested) on both datasets Da and Dc. Note that when α ϵ = 0.0, by Eq. (3), we only learn fb and hc, as dataset Da is not used in training; in this case, we set ha = hc to predict the absolute labels on the validation and test sets. Similarly, when α = 1.0, we only learn fb and ha, and set hc = ha to predict comparisons.
Competing Methods
We implement four alternative methods which incorporate absolute and comparison labels: Sun et al. (2017)’s method, logistic regression, a support vector machine (SVM), and an ensemble method combining the predictions of logistic regression and SVM. We use Sun et al. (2017)’s norm-comparison loss function Lc, introduced in detail in Appendix C, combined with the best performing La for each dataset (c.f. Table 1b). In both logistic and SVM methods, we first use GoogLeNet pre-trained on the ImageNet dataset (Deng et al., 2009) to map input images to features. Then, we train a model via logistic regression and an SVM, respectively, on these features. Training procedures for these methods are reported in more detail in Appendix D. Finally, we implement a soft voting ensemble method combining logistic regression and SVM (Friedman et al., 2001). More precisely, we train another logistic classifier on the pairs of logistic regression and SVM predictions.
Metrics
To evaluate the performance of our model on validation and test sets, we use Area Under the ROC Curve (AUC), accuracy (Acc.), F1-score (F1), and Area Under the Precision-Recall Curve (PRAUC) on both absolute labels Da and comparison labels Dc. We report these metrics along with the 95% confidence interval, which we compute as 1.96 × σa, where is the variance. Variance for AUC and PRAUC are computed by:
| (7) |
where A is the AUC or PRAUC, Px = A/(2 − A), Py = 2A2/(1 + A), and m, n are the number of positive and negative samples, respectively (Hanley & McNeil, 1982). Variance for accuracy and F1-score are computed by:
| (8) |
for A being the accuracy or F1-score. Finally, when comparing the prediction performances of different methods, we assess the statistical significance of relative improvements. We do so via the p-value of one-sided Welch T-test for unequal variances (Sawilowsky, 2002), which is computed by:
| (9) |
where Φ is the standard normal cumulative distribution function (c.d.f.), and Al and As are the metric values with larger and smaller magnitudes, respectively.
4.1. Prediction Performance
Tables 2a and 2b show the prediction performance of our model trained on GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC datasets. For each a, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. For AUC, Acc., F1, and PRAUC on both Da and Dc, we evaluate all eight metrics on the test set, for α = 0.0 (comparison labels only), α =1.0 (absolute labels only), and best performing α ∈ [0, 1]. Optimal hyperparameters are reported in Appendix E (c.f. Tables E.4 to E.11).
Table 2:
Predictions on the GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC datasets. For each α, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. For AUC, Acc., F1, and PRAUC on both Da and Dc, we evaluate all eight metrics on the test set, for α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1]. Optimal hyperparameters are reported Appendix E (c.f. Tables E.4 to E.11). We use ha ≠ hc in these experiments.
| Dataset | α | Performance Metrics on Test Set of Absolute Labels |
|||
| AUC on Da | Acc. on Da | F1 on Da | PRAUC on Da | ||
| Happiness | 0.0 | 0.915 ± 0.041 | 0.85 ± 0.042 | 0.779 ± 0.049 | 0.824 ± 0.057 |
| 1.0 | 0.561 ± 0.072 | 0.664 ± 0.055 | 0.39 ± 0.057 | 0.401 ± 0.07 | |
| Best(α) | 0.915 ± 0.041(0.0)* | 0.85 ± 0.042(0.0)* | 0.791 ± 0.048(0.75) | 0.824 ± 0.057(0.0)* | |
| Pleasure | 0.0 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | 0.579 ± 0.075 | 0.56 ± 0.065 | 0.667 ± 0.062 | 0.591 ± 0.075 | |
| Best(α) | 0.887 ± 0.045(0.0)* | 0.814 ± 0.051(0.25) | 0.823 ± 0.05(0.5) | 0.88 ± 0.046(0.25) | |
| ROP | 0.0 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | 0.835 ± 0.017 | 0.705 ± 0.012 | 0.517 ± 0.014 | 0.177 ± 0.012 | |
| Best(α) | 0.914 ± 0.013(0.75) | 0.883 ± 0.009(0.75) | 0.64 ± 0.013(0.5) | 0.731 ± 0.019(0.0)* | |
| FAC | 0.0 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 |
| 1.0 | 0.746 ± 0.037 | 0.677 ± 0.035 | 0.684 ± 0.035 | 0.678 ± 0.041 | |
| Best(α) | 0.87 ± 0.028(0.0)* | 0.82 ± 0.029(0.0)* | 0.809 ± 0.03(0.0)* | 0.82 ± 0.033(0.0)* | |
| (a) Absolute label predictions | |||||
| Dataset | α | Performance Metrics on Test Set of Comparison Labels |
|||
| AUC on Dc | Acc. on Dc | F1 on Dc | PRAUC on Dc | ||
| Happiness | 0.0 | 0.898 ± 0.031 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.906 ± 0.031 |
| 1.0 | 0.419 ± 0.055 | 0.42 ± 0.047 | 0.397 ± 0.047 | 0.448 ± 0.056 | |
| Best(α) | 0.902 ± 0.03(0.5) | 0.83 ± 0.036(0.25) | 0.819 ± 0.037(0.0) | 0.906 ± 0.031(0.0) | |
| Pleasure | 0.0 | 0.836 ± 0.052 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.849 ± 0.05 |
| 1.0 | 0.531 ± 0.076 | 0.492 ± 0.065 | 0.662 ± 0.062 | 0.618 ± 0.073 | |
| Best(α) | 0.84 ± 0.052(0.25) | 0.755 ± 0.056(0.25) | 0.775 ± 0.055(0.25) | 0.855 ± 0.049(0.25) | |
| ROP | 0.0 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best(α) | 0.955 ± 0.013(0.0) | 0.883 ± 0.019(0.25) | 0.886 ± 0.019(0.25) | 0.963 ± 0.012(0.0) | |
| FAC | 0.0 | 0.751 ± 0.065 | 0.71 ± 0.06 | 0.706 ± 0.06 | 0.735 ± 0.066 |
| 1.0 | 0.809 ± 0.058 | 0.733 ± 0.058 | 0.72 ± 0.059 | 0.797 ± 0.06 | |
| Best(α) | 0.814 ± 0.057(0.5) | 0.759 ± 0.057(0.75) | 0.736 ± 0.058(0.5) | 0.797 ± 0.06(1.0) | |
| (b) Comparison label predictions | |||||
Tables 2a and 2b indicate that, on all datasets and metrics, comparisons significantly enhance the predictions of both label types. Compared to training on absolute labels alone (α = 1.0), combining absolute and comparison labels (α ∈ (0,1)) or training only on comparison labels (α = 0) considerably improves absolute label prediction, by 8% – 35% AUC, 14% – 25% Acc., 12% – 40% F1, and 14% – 55% PRAUC across all datasets. For all of these improvements over training with α = 1.0, we compute the p-value of Welch T-test. In all cases, p-values are above 0.99. Interestingly, in several cases indicated on Table 2a by *, comparisons lead to better predictions of absolute labels even when the latter are ignored during training. This indicates the relative advantage of incorporating comparison labels into training. Adding absolute labels to comparisons also improves comparison prediction performance, albeit modestly (by at most 6% AUC/0.923 p-value, 5% Acc./0.877 p-value, 3% F1/0.793 p-value, and 6% PRAUC/0.913 p-value).
Our performance over the ROP dataset is especially striking. Recall that its training set contains only 80 images and its test set contains 5561 images, unseen during training. Despite this extreme imbalance, by incorporating comparisons into training, we successfully train and optimize a neural network involving 5,974,577 parameters, on 80 images (60 for training, 20 for validation)! Specifically, our combined model attains an absolute label prediction performance of 0.914 AUC, 0.883 Acc., 0.64 F1, and 0.731 PRAUC. Training only on absolute labels, i.e. α = 1.0, can only achieve 0.835 AUC, 0.705 Acc., 0.517 F1, and 0.177 PRAUC (c.f. ROP rows in Table 2a). This further attests to the fact that comparisons are more informative than absolute labels and that our methodology is able to exploit this information even in the presence of a small dataset.
Our architecture is robust in the selection of a metric to optimize over the validation set. In Appendix E (c.f. Tables E.4 to E.11), we show that optimizing hyperparameters w.r.t. a metric (e.g., AUC) leads to good performance w.r.t. other metrics (e.g., Acc., and F1). Furthermore, for all metrics and datasets, comparison loss functions (Lc) induced by Bradley-Terry and Thurstone models (given in Eq. (5) and Eq. (6)) outperform cross-entropy and hinge losses. This further motivates the use of these linear comparison models for learning relative orders, compared to standard loss functions such as cross-entropy and hinge.
Learning with Fewer Samples
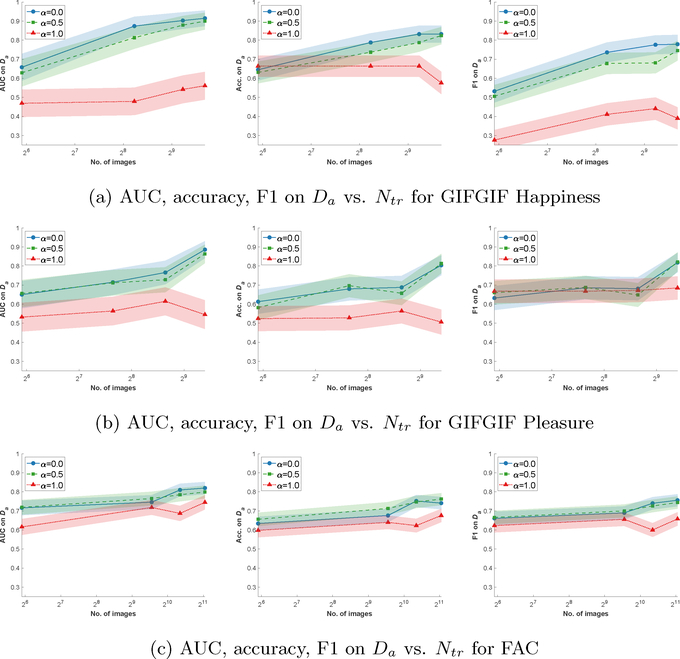
The striking performance of our model on ROP motivates us to study settings in which we learn from small datasets. To that end, we repeat our experiments, training our model on a subset of the training set containing both absolute and comparison labels, selected uniformly at random. The effect of the number of training images on AUC, Acc., and F1 for different values of α can be seen in Fig. 2, for GIFGIF Happiness, GIFGIF Pleasure, and FAC datasets. We illustrate that, despite the small number of images, learning from comparisons consistently improves absolute label predictions. In fact, e.g., in Fig. 2a, using comparisons (α ϵ {0.0,0.5}), we can reduce the training set size from 823 to 300 with a performance loss of only 4% on AUC, Acc., and F1. In contrast, using only absolute labels in training (α = 1.0) leads to a significant performance drop, by 12% – 39% AUC, 13% – 30% Acc., and 14% – 39% F1. These results confirm that, in the presence of a small dataset with few samples, soliciting comparisons along with training via our combined architecture significantly boosts prediction performance.
Figure 2:
Prediction performance on absolute labels (Da) vs. number of training images (Ntr) for the (a) GIFGIF Happiness, (b) GIFGIF Pleasure, and (c) FAC datasets. We train our model on the absolute labels Da and comparison labels Dc pertaining to Ntr images randomly sampled from the training set. For each Ntr ∈ {60, …} and α ϵ {0.0, 0.5, 1.0}, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. We evaluate AUC, Acc., and F1 on the test set w.r.t. Da.
Comparison Labels Exhibit Less Noise Than Absolute Labels
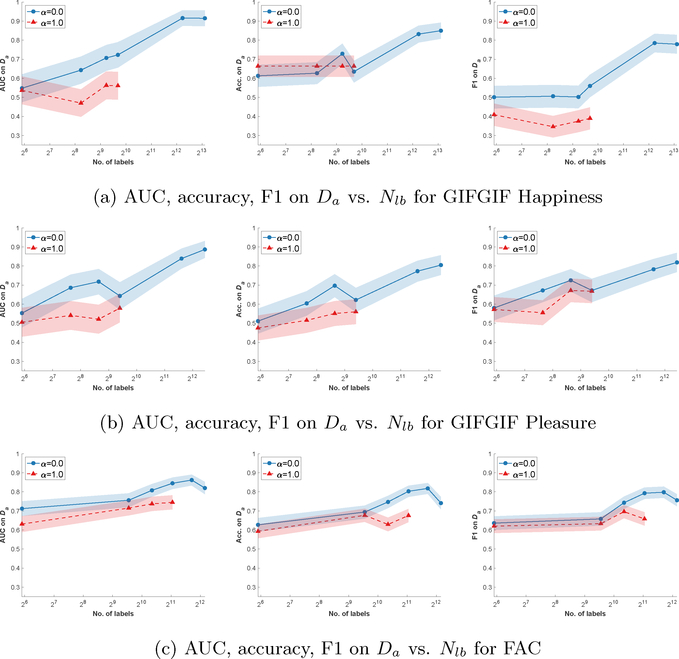
In the previous experiment, given the number of samples, the number of comparisons is significantly larger than the number of absolute labels. This raises the question of how training performs when the number of comparisons is equal to the number of absolute labels. To answer this question, we repeat the previous experiment by subsampling labels rather than images and train our model on the same number of absolute or comparison labels. In Fig. 3, we show AUC, Acc., and F1 as functions of the number of training labels for GIFGIF Happiness, GIFGIF Pleasure, and FAC datasets. We demonstrate that, for the same number of training labels, learning from comparisons (α = 0.0) instead of absolute labels (α = 1.0) boosts absolute label predictions by 11% – 30% AUC, 6% – 24% Acc., and 14% – 17% F1. This further corroborates our claim that comparisons are indeed less noisy and more informative than absolute labels. We note that this has been observed in other settings (Stewart et al., 2005; Kalpathy-Cramer et al., 2016; Brun et al., 2010).
Figure 3:
Prediction performance on absolute labels (Da) vs. number of labels (Nlb) in the training set for the (a) GIFGIF Happiness, (b) GIFGIF Pleasure, and (c) FAC datasets. We train our model on Nib absolute labels (Da) and Nib comparison labels (Dc) randomly sampled from the training set. For each Nlb ∈ {60, …} and α ∈ {0.0, 1.0}, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. We evaluate AUC, Acc., and F1 on the test set w.r.t. Da.
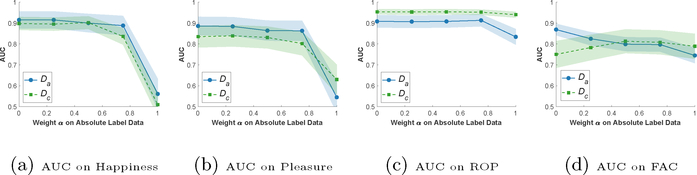
Impact of α
Fig. 4 shows the prediction AUC of our model vs. α on GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC datasets. For each a, we optimize the hyperparameters on the validation set following the procedure explained in Section 4.1 and evaluate AUC on the test set w.r.t. both Da and Dc. On all datasets, comparisons significantly boost the prediction performance on both Da and Dc. Our model achieves the peak prediction AUCs on both labels for learning from comparisons (α ∈ [0.0, 1.0)) and the lowest prediction AUCs for learning from absolute labels alone (α = 1.0), except for the FAC dataset. The FAC dataset differs from other datasets, since absolute labels are generated from comparisons instead of being independently produced by labelers (c.f. Datasets in Section 4).
Figure 4:
Prediction performance vs. a on GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC datasets. For each α ∈ {0.0, 0.25, 0.5, 0.75, 1.0}, we optimize the hyperparameters on the validation set following the procedure explained in Section 4.1. Finally, we evaluate the optimal models on the test set of both Da and Dc w.r.t. AUC.
4.2. Comparison with Competing Methods
In Tables 3a and 3b, we compare our combined neural network (CNN) with Sun et al. (2017)’s method (Norm), logistic regression (Log.), a support vector machine (SVM), and a soft voting ensemble method (Ensemble) linearly combining the predictions of logistic regression and SVM. We evaluate our CNN model both for ha = hc, and the special case where ha ≠ hc (CNN (ha = hc)), combining cross-entropy as La and Bradley-Terry loss as Lc. For each a, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. For the best performing α ∈ [0, 1], we evaluate AUC, Acc., and F1 on the test set w.r.t. both Da and Dc. We demonstrate that learning through the norm comparison loss (Norm) instead of maximum likelihood based on Bradley-Terry or Thurstone models (given in Eq. (5) and (6)) is not suitable for our architecture. Moreover, our method outperforms logistic, SVM, and ensemble methods, particularly in absolute label prediction, by 2% – 13% AUC, 5% – 13% Acc., and 3% – 15% F1 across all datasets. These improvements correspond to 0.772 – 1.0 p-value for AUC, 0.91 – 1.0 p-value for Acc., and 0.8 – 1.0 p-value for F1 under Welch T-test. Our method also outperforms other methods on comparison label prediction, specifically on ROP, by 11% AUC, 12% Acc., and 13% F1. For all of these improvements, p-values are 1.0.
Table 3:
As alternatives to our Combined Neural Network (CNN) method, we implement Sun et al. (2017)’s method (Norm), logistic regression (Log.), SVM, and a soft voting ensemble method (Ensemble) linearly combining the predictions of logistic regression and SVM using the objectives explained in Appendix C and Appendix D. We further evaluate our CNN method for the special case where ha = hc (CNN (ha = hc)), combining cross-entropy as La and Bradley-Terry loss as Lc. For each method and each α, we optimize the hyperparameters on the validation set following the procedure explained in Experiment Setup. Finally, for the best performing α ∈ [0, 1] on the test set, we evaluate AUC, Acc., and F1 on GIFGIF Pleasure, ROP, and FAC datasets w.r.t. both Da and Dc.
| Dataset | Method | Performance Metrics on Test Set of Absolute Labels |
||
| AUC on Da (α) | Acc. on Da (α) | F1 on Da (α) | ||
| Pleasure | CNN | 0.887 ± 0.045(0.0) | 0.814 ± 0.051(0.25) | 0.823 ± 0.05(0.5) |
| CNN(ha = hc) | 0.882 ± 0.046 | 0.823 ± 0.05 | 0.827 ± 0.05 | |
| Log. | 0.846 ± 0.051(0.25) | 0.773 ± 0.054(0.75) | 0.775 ± 0.054(0.75) | |
| SVM | 0.862 ± 0.048(0.75) | 0.768 ± 0.055(0.0) | 0.796 ± 0.052(0.0) | |
| Ensemble | 0.852 ± 0.051(0.25) | 0.787 ± 0.054(0.5) | 0.794 ± 0.053(0.5) | |
| Norm | 0.5 ± 0.07(0.5) | 0.5 ± 0.065(0.5) | 0.67 ± 0.061(0.5) | |
| ROP | CNN | 0.914 ± 0.013(0.75) | 0.883 ± 0.009(0.75) | 0.64 ± 0.013(0.5) |
| CNN(ha = hc) | 0.929 ± 0.012 | 0.876 ± 0.009 | 0.64 ± 0.013 | |
| Log. | 0.788 ± 0.017(0.0) | 0.823 ± 0.01(0.0) | 0.484 ± 0.013(1.0) | |
| SVM | 0.793 ± 0.017(0.5) | 0.822 ± 0.01(0.0) | 0.497 ± 0.013(0.5) | |
| Ensemble | 0.79 ± 0.018(0.0) | 0.823 ± 0.011(0.0) | 0.478 ± 0.014(1.0) | |
| Norm | 0.63 ± 0.04(0.0) | 0.82 ± 0.01(0.5) | 0.3 ± 0.012(0.0) | |
| FAC | CNN | 0.87 ± 0.028(0.0) | 0.82 ± 0.029(0.0) | 0.809 ± 0.03(0.0) |
| CNN(ha = hc) | 0.839 ± 0.031 | 0.817 ± 0.029 | 0.818 ± 0.029 | |
| Log. | 0.746 ± 0.036(0.5) | 0.681 ± 0.034(0.5) | 0.655 ± 0.035(0.0) | |
| SVM | 0.741 ± 0.037(0.5) | 0.684 ± 0.034(0.25) | 0.648 ± 0.035(0.5) | |
| Ensemble | 0.746 ± 0.037(0.5) | 0.692 ± 0.035(0.5) | 0.658 ± 0.036(0.5) | |
| Norm | 0.52 ± 0.04(0.5) | 0.55 ± 0.036(1.0) | 0.61 ± 0.036(0.5) | |
| (a) Absolute label predictions of competing methods. | ||||
| Dataset | Method | Performance Metrics on Test Set of Comparison Labels |
||
| AUC on Dc (α) | Acc. on Dc (α) | F1 on Dc (α) | ||
| Pleasure | CNN | 0.84 ± 0.052(0.25) | 0.755 ± 0.056(0.25) | 0.775 ± 0.055(0.25) |
| CNN(ha = hc) | 0.866 ± 0.048 | 0.764 ± 0.056 | 0.796 ± 0.053 | |
| Log. | 0.805 ± 0.056(0.0) | 0.741 ± 0.056(0.0) | 0.763 ± 0.055(0.0) | |
| SVM | 0.803 ± 0.056(0.75) | 0.736 ± 0.057(0.0) | 0.754 ± 0.055(0.0) | |
| Ensemble | 0.813 ± 0.056(0.25) | 0.75 ± 0.057(0.25) | 0.772 ± 0.055(0.25) | |
| Norm | 0.5 ± 0.07(0.5) | 0.46 ± 0.064(0.5) | 0 ± 0(0.5) | |
| ROP | CNN | 0.955 ± 0.013(0.0) | 0.883 ± 0.019(0.25) | 0.886 ± 0.019(0.25) |
| CNN(ha = hc) | 0.953 ± 0.013 | 0.874 ± 0.02 | 0.88 ± 0.019 | |
| Log. | 0.842 ± 0.023(0.5) | 0.762 ± 0.024(0.25) | 0.757 ± 0.024(0.75) | |
| SVM | 0.829 ± 0.024(0.0) | 0.732 ± 0.025(0.75) | 0.743 ± 0.025(0.5) | |
| Ensemble | 0.837 ± 0.024(0.5) | 0.758 ± 0.025(0.5) | 0.758 ± 0.025(0.5) | |
| Norm | 0.65 ± 0.03(1.0) | 0.47 ± 0.028(0.5) | 0.5 ± 0.028(1.0) | |
| FAC | CNN | 0.814 ± 0.057(0.5) | 0.759 ± 0.057(0.75) | 0.736 ± 0.058(0.5) |
| CNN(ha = hc) | 0.816 ± 0.057 | 0.755 ± 0.057 | 0.749 ± 0.057 | |
| Log. | 0.82 ± 0.055(0.0) | 0.75 ± 0.056(0.25) | 0.75 ± 0.056(0.25) | |
| SVM | 0.821 ± 0.055(0.25) | 0.75 ± 0.056(0.25) | 0.75 ± 0.056(0.25) | |
| Ensemble | 0.822 ± 0.056(0.25) | 0.755 ± 0.057(0.25) | 0.756 ± 0.057(0.25) | |
| Norm | 0.52 ± 0.07(0.5) | 0.54 ± 0.065(0.5) | 0.37 ± 0.063(0.5) | |
| (b) Comparison label predictions of competing methods. | ||||
Note that the performance of our architecture is robust to the design choice between single task learning with ha = hc vs. generic joint learning with ha ≠ hc. More precisely, our model balances the variance introduced by allowing ha and hc to differ by improving the bias.
5. Conclusion
In this paper, we tackle the problem of limited and noisy data that emerge in real-life applications. To do so, we propose a neural network architecture that can collectively learn from both absolute and comparison labels. We extensively evaluate our model on several real-life datasets and metrics, demonstrating that learning from both labels immensely improves predictive power on both label types. By incorporating comparisons into training, we successfully train an architecture containing 5.9 million parameters with only 80 images. All in all, we observe the benefit of learning from comparison labels.
Given the quadratic nature of pairwise comparisons, designing active learning algorithms that identify which comparisons to solicit from labelers is an interesting open problem. For example, generalizing active learning algorithms, as the ones proposed by Guo et al. (2018) for shallow models of comparisons to the neural network model we consider here, is a promising direction.
Acknowledgments
Our work is supported by NIH (R01EY019474, P30EY10572), NSF (SCH-1622542 at MGH; SCH-1622536 at Northeastern; SCH-1622679 at OHSU), and by unrestricted departmental funding from Research to Prevent Blindness (OHSU).
Appendix A. Multi-Class Absolute Labels
Our design naturally extends to multi-class absolute labels. In this setting, we consider one-hot encoded vectors yi ∈ [0,1]K ∀i as absolute labels, where K is the number of classes. When item i belongs to class k ∈ {1,…, K}, only the ith element of yi is 1, and the rest of its elements are 0. Recall that when class labels are ordered, absolute and comparison labels are coupled (c.f. Section 3). This implies for multi-class absolute labels, that given items (i, j) with absolute labels (ki, kj), y(i,j) = +1 indicates that ki > kj is more likely than kj > ki.
When trained on multi-class absolute labels, the absolute network takes the form . Thus, the additional network linking the base network output to absolute labels becomes (c.f.Fig. 1). In our experiments with multi-class absolute labels (c.f. ROP in Section 4), we choose ha as a single fully connected layer with softmax activation. We train fa using classical loss functions La, such as multi-class cross-entropy and multi-class hinge loss. Further details on multi-class classification can be found in Goodfellow et al. (2016).
Appendix B. Plackett-Luce Model
Rankings frequently occur in real-life applications, including, i.e. medicine and recommender systems. In top-1 ranking settings, given a subset of N alternative items, a labeler chooses the item they prefer the most. Formally, a labeler produces a top-1 ranking label of the form (w, A), where A ⊆ {1,…, N} is a set of alternative items and w ∈ A is the chosen item. Given a top-1 ranking dataset, the total order of N items can be learned through the Plackett-Luce (PL) model (Luce, 2012). PL model, being the generalization of the Bradley-Terry (BT) model to rankings, asserts that every item i in the ranking dataset is parametrized by a score si. Then, all labelling events are independent of each other, where the probability of choosing item w over the alternatives in set A is:
| (B.1) |
Another common setting is when labelers provide a total ranking over the alternatives, instead of a single choice. More precisely, a labeler produces a total ranking label of the form (σA, A), where σA is a permutation of the alternative items in A. In fact, a total ranking is equivalent to a sequence of |A| − 1 independent choices, where |A| is the size of set A: a labeler starts by choosing the first item σA(1) out of A, then chooses the second item σA(2) out of A \ {σA(1)}, then chooses the third item σA(3) out of A \ {σA(1), σA(2)}, and so on. Hence, under the PL model, probability of a total ranking over the alternatives in set A becomes:
| (B.2) |
Given {s1,⋯, sN}, all ranking events are fully determined by Eq.(B.2).
Recall that our architecture introduces a generic representation of the score s i through linear comparison models: we assume that , where fc is the comparison network. Hence, our formulation naturally generalizes to learning from rankings under PL model. To implement this generalization, given a total ranking (σa, A) with the corresponding feature vectors {xi}i∈A, we can train our architecture by adopting the (negative log-likelihood) loss function:
| (B.3) |
instead of Lc in our combined loss in Eq. (3).
Appendix C. Sun et.al. ‘s Method
Sun et al. (2017) leverage a siamese network to learn comparisons, where the base network architecture is either AlexNet (Krizhevsky et al., 2012) or RAPID net (Lu et al., 2014) with a fully-connected output layer. The base network receives an input image and generates the corresponding 128-dimensional feature vector. To regress the comparison labels from these features, Sun et al. (2017) employ a norm comparison loss function:
| (C.1) |
To evaluate the performance of their architecture, for each image i, they use as the quality score.
To compare the performance of our method with Sun et al. (2017)’s, we adapt our experimental setup as follows: we transfer the features extracted by our base network, i.e. GoogLeNet (Szegedy et al., 2015), to a fully-connected layer with 128-d output. We train the resulting architecture with our combined loss function (c.f. Eq. (3)), where La is the optimal absolute loss function for each dataset (c.f. Tables E.4 to E.11), and Lc is the norm comparison loss. For each a G {0.0,0.5,1.0}, we optimize the learning rate ranging from 10−6 to 10−2 and A ranging from 2 × 10−4 to 2 × 10−2 on the validation set. For this method, we also normalize the input images to aid convergence. Finally, we evaluate the test set predictions of the optimal models obtained through this setup, using as the quality score for each image i.
Appendix D. Logistic Regression and SVMs
For both logistic and SVM methods, we employ linear comparison models (c.f. Sec. 3.2) by assuming that the score of each item i, i.e. si, is parametrized by a common parameter vector and a common bias , such that si = βTfb(xi) + b. In other words, we assign hc(·) = ha(·) = βT +b in Eq.(1) and Eq.(2). Then, absolute and comparison label predictions become and , respectively. In the exposition below, as well as in our experiments in Sec. 4.2, fb is fixed, i.e. not trained, and given by GoogLeNet with weights pre-trained on the ImageNet dataset (Deng et al., 2009).
Under logistic method, maximum aposteriori (MAP) estimates of fl and b from absolute and comparison labels correspond to minimizing the negative log-likelihood functions and , respectively. Motivated by the combined loss function Eq.(3), we estimate β and b by solving:
| (D.1) |
where λ is the regularization parameter. Similarly, under SVM method, we estimate β and b by solving the convex program:
| (D.2) |
We optimize the regularization parameter A (ranging from 10−6 to 104) on the validation set of each dataset.
Appendix E. Robustness to Metric Selection
In this section, we illustrate that our model is robust in the selection of a metric to optimize over the validation set. We employ the experimental setup explained in Section 4.1 to train and evaluate our model on these datasets. Tables E.4 to E.11 report the test set performance of the models optimized on the validation set for each metric, over all eight metrics. These four tables correspond to GIFGIF Happiness, GIFGIF Pleasure, ROP, and FAC datasets, respectively. Note that the diagonals of each table correspond to the rows of Tables 2a and 2b. We conclude that optimizing hyperparameters w.r.t. a metric, e.g., AUC, still results in high performance w.r.t. other metrics, e.g., Acc., and F1.
Table E.4:
Absolute label prediction performance on the GIFGIF Happiness dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Da | Acc. on Da | F1 on Da | PRAUC on Da | ||
| AUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.915 ± 0.041 | 0.832 ± 0.044 | 0.783 ± 0.048 | 0.824 ± 0.057 |
| 1.0 | C.E. | B.T | 0.002 | 0.001 | 0.561 ± 0.072 | 0.638 ± 0.056 | 0.287 ± 0.053 | 0.401 ± 0.07 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.915 ± 0.041 | 0.832 ± 0.044 | 0.783 ± 0.048 | 0.824 ± 0.057 | |
| Acc. on Da | 0.0 | C.E. | B.T. | 0.002 | 0.001 | 0.883 ± 0.047 | 0.85 ± 0.042 | 0.789 ± 0.048 | 0.762 ± 0.064 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.504 ± 0.072 | 0.664 ± 0.055 | 0.0 ± 0.0 | 0.336 ± 0.066 | |
| Best (0.0) | C.E. | B.T. | 0.002 | 0.001 | 0.883 ± 0.047 | 0.85 ± 0.042 | 0.789 ± 0.048 | 0.762 ± 0.064 | |
| F1 on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.925 ± 0.038 | 0.824 ± 0.045 | 0.779 ± 0.049 | 0.848 ± 0.054 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.519 ± 0.072 | 0.613 ± 0.057 | 0.39 ± 0.057 | 0.383 ± 0.069 | |
| Best (0.75) | C.E. | T. | 0.0002 | 0.01 | 0.888 ± 0.046 | 0.85 ± 0.042 | 0.791 ± 0.048 | 0.764 ± 0.064 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.916 ± 0.042 | 0.833 ± 0.045 | 0.784 ± 0.049 | 0.824 ± 0.057 |
| 1.0 | C.E. | B.T. | 0.002 | 0.001 | 0.562 ± 0.073 | 0.639 ± 0.057 | 0.288 ± 0.054 | 0.401 ± 0.07 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.916 ± 0.042 | 0.833 ± 0.045 | 0.784 ± 0.049 | 0.824 ± 0.057 | |
| AUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.001 | 0.917 ± 0.04 | 0.835 ± 0.043 | 0.782 ± 0.048 | 0.803 ± 0.06 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.487 ± 0.072 | 0.565 ± 0.058 | 0.32 ± 0.055 | 0.383 ± 0.069 | |
| Best (0.5) | C.E. | T. | 0.002 | 0.001 | 0.9 ± 0.044 | 0.828 ± 0.044 | 0.77 ± 0.049 | 0.792 ± 0.061 | |
| Acc. on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.915 ± 0.041 | 0.832 ± 0.044 | 0.783 ± 0.048 | 0.824 ± 0.057 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.487 ± 0.072 | 0.565 ± 0.058 | 0.32 ± 0.055 | 0.401 ± 0.07 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.915 ± 0.041 | 0.843 ± 0.043 | 0.786 ± 0.048 | 0.815 ± 0.058 | |
| F1 on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.915 ± 0.041 | 0.832 ± 0.044 | 0.783 ± 0.048 | 0.824 ± 0.057 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.487 ± 0.072 | 0.565 ± 0.058 | 0.32 ± 0.055 | 0.383 ± 0.069 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.915 ± 0.041 | 0.832 ± 0.044 | 0.783 ± 0.048 | 0.824 ± 0.057 | |
| PRAUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.001 | 0.918 ± 0.041 | 0.836 ± 0.044 | 0.783 ± 0.049 | 0.803 ± 0.06 |
| 1.0 | H. | B.T. | 0.0002 | 0.01 | 0.466 ± 0.072 | 0.665 ± 0.056 | 0.0 ± 0.0 | 0.308 ± 0.063 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.001 | 0.918 ± 0.041 | 0.836 ± 0.044 | 0.783 ± 0.049 | 0.803 ± 0.06 | |
Table E.5:
Comparison label prediction performance on the GIFGIF Happiness dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Dc | Acc. on Dc | F1 on Dc | PRAUC on Dc | ||
| AUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.909 ± 0.029 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.917 ± 0.029 |
| 1.0 | C.E. | B.T | 0.002 | 0.001 | 0.461 ± 0.055 | 0.476 ± 0.048 | 0.443 ± 0.048 | 0.491 ± 0.057 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.909 ± 0.029 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.917 ± 0.029 | |
| Acc. on Da | 0.0 | C.E. | B.T. | 0.002 | 0.001 | 0.896 ± 0.031 | 0.805 ± 0.038 | 0.797 ± 0.039 | 0.895 ± 0.032 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.508 ± 0.056 | 0.496 ± 0.048 | 0.22 ± 0.04 | 0.499 ± 0.057 | |
| Best (0.0) | C.E. | B.T. | 0.002 | 0.001 | 0.896 ± 0.031 | 0.805 ± 0.038 | 0.797 ± 0.039 | 0.895 ± 0.032 | |
| F1 on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.913 ± 0.028 | 0.832 ± 0.036 | 0.83 ± 0.036 | 0.912 ± 0.03 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.51 ± 0.056 | 0.493 ± 0.048 | 0.477 ± 0.048 | 0.516 ± 0.057 | |
| Best (0.75) | C.E. | T. | 0.0002 | 0.01 | 0.892 ± 0.032 | 0.81 ± 0.038 | 0.807 ± 0.038 | 0.898 ± 0.032 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.91 ± 0.03 | 0.829 ± 0.037 | 0.82 ± 0.038 | 0.917 ± 0.029 |
| 1.0 | C.E. | B.T. | 0.002 | 0.001 | 0.462 ± 0.056 | 0.477 ± 0.049 | 0.444 ± 0.049 | 0.491 ± 0.057 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.91 ± 0.03 | 0.829 ± 0.037 | 0.82 ± 0.038 | 0.917 ± 0.029 | |
| AUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.001 | 0.898 ± 0.031 | 0.813 ± 0.037 | 0.808 ± 0.038 | 0.906 ± 0.031 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.419 ± 0.055 | 0.42 ± 0.047 | 0.397 ± 0.047 | 0.516 ± 0.057 | |
| Best (0.5) | C.E. | T. | 0.002 | 0.001 | 0.902 ± 0.03 | 0.813 ± 0.037 | 0.81 ± 0.038 | 0.893 ± 0.033 | |
| Acc. on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.909 ± 0.029 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.917 ± 0.029 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.419 ± 0.055 | 0.42 ± 0.047 | 0.397 ± 0.047 | 0.491 ± 0.057 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.911 ± 0.029 | 0.83 ± 0.036 | 0.828 ± 0.036 | 0.904 ± 0.031 | |
| F1 on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.909 ± 0.029 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.917 ± 0.029 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.419 ± 0.055 | 0.42 ± 0.047 | 0.397 ± 0.047 | 0.516 ± 0.057 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.909 ± 0.029 | 0.828 ± 0.036 | 0.819 ± 0.037 | 0.917 ± 0.029 | |
| PRAUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.001 | 0.899 ± 0.032 | 0.814 ± 0.038 | 0.809 ± 0.039 | 0.906 ± 0.031 |
| 1.0 | H. | B.T. | 0.0002 | 0.01 | 0.445 ± 0.056 | 0.465 ± 0.049 | 0.442 ± 0.049 | 0.448 ± 0.056 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.001 | 0.899 ± 0.032 | 0.814 ± 0.038 | 0.809 ± 0.039 | 0.906 ± 0.031 | |
Table E.6:
Absolute label prediction performance on the GIFGIF Pleasure dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Da | Acc. on Da | F1 on Da | PRAUC on Da | ||
| AUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | C.E. | B.T | 0.0002 | 0.001 | 0.579 ± 0.075 | 0.56 ± 0.065 | 0.557 ± 0.065 | 0.591 ± 0.075 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 | |
| Acc. on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | C.E. | B.T | 0.0002 | 0.001 | 0.579 ± 0.075 | 0.56 ± 0.065 | 0.557 ± 0.065 | 0.591 ± 0.075 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.865 ± 0.049 | 0.814 ± 0.051 | 0.813 ± 0.052 | 0.852 ± 0.051 | |
| F1 on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | C.E. | B.T | 0.002 | 0.001 | 0.616 ± 0.074 | 0.516 ± 0.066 | 0.667 ± 0.062 | 0.633 ± 0.073 | |
| Best (0.5) | H. | T. | 0.0002 | 0.001 | 0.853 ± 0.051 | 0.814 ± 0.051 | 0.823 ± 0.05 | 0.827 ± 0.055 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | C.E. | B.T | 0.0002 | 0.001 | 0.579 ± 0.075 | 0.56 ± 0.065 | 0.557 ± 0.065 | 0.591 ± 0.075 | |
| Best (0.25) | H. | T. | 0.0002 | 0.001 | 0.9 ± 0.042 | 0.832 ± 0.049 | 0.826 ± 0.05 | 0.88 ± 0.046 | |
| AUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.886 ± 0.045 | 0.809 ± 0.052 | 0.806 ± 0.052 | 0.874 ± 0.047 |
| 1.0 | H. | B.T | 0.0002 | 0.01 | 0.595 ± 0.074 | 0.507 ± 0.066 | 0.673 ± 0.062 | 0.599 ± 0.074 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.865 ± 0.049 | 0.814 ± 0.051 | 0.813 ± 0.052 | 0.852 ± 0.051 | |
| Acc. on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | H. | B.T | 0.0002 | 0.01 | 0.595 ± 0.074 | 0.507 ± 0.066 | 0.673 ± 0.062 | 0.599 ± 0.074 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.865 ± 0.049 | 0.814 ± 0.051 | 0.813 ± 0.052 | 0.852 ± 0.051 | |
| F1 on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.887 ± 0.045 | 0.805 ± 0.052 | 0.819 ± 0.051 | 0.873 ± 0.047 |
| 1.0 | H. | B.T | 0.002 | 0.001 | 0.615 ± 0.074 | 0.56 ± 0.065 | 0.686 ± 0.061 | 0.599 ± 0.074 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.865 ± 0.049 | 0.814 ± 0.051 | 0.813 ± 0.052 | 0.852 ± 0.051 | |
| PRAUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.886 ± 0.045 | 0.809 ± 0.052 | 0.806 ± 0.052 | 0.874 ± 0.047 |
| 1.0 | H. | B.T | 0.002 | 0.001 | 0.615 ± 0.074 | 0.56 ± 0.065 | 0.686 ± 0.061 | 0.599 ± 0.074 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.865 ± 0.049 | 0.814 ± 0.051 | 0.813 ± 0.052 | 0.852 ± 0.051 | |
Table E.7:
Comparison label prediction performance on the GIFGIF Pleasure dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Dc | Acc. on Dc | F1 on Dc | PRAUC on Dc | ||
| AUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | C.E. | B.T | 0.0002 | 0.001 | 0.53 ± 0.076 | 0.509 ± 0.065 | 0.538 ± 0.065 | 0.601 ± 0.074 | |
| Best (0.0) | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 | |
| Acc. on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.53 ± 0.076 | 0.509 ± 0.065 | 0.538 ± 0.065 | 0.601 ± 0.074 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.84 ± 0.052 | 0.755 ± 0.056 | 0.775 ± 0.055 | 0.855 ± 0.049 | |
| F1 on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | C.E. | B.T. | 0.002 | 0.001 | 0.597 ± 0.074 | 0.593 ± 0.064 | 0.627 ± 0.063 | 0.613 ± 0.073 | |
| Best (0.5) | H. | T. | 0.0002 | 0.001 | 0.832 ± 0.053 | 0.733 ± 0.058 | 0.754 ± 0.056 | 0.836 ± 0.052 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.001 | 0.53 ± 0.076 | 0.509 ± 0.065 | 0.538 ± 0.065 | 0.601 ± 0.074 | |
| Best (0.25) | H. | T. | 0.0002 | 0.001 | 0.828 ± 0.053 | 0.702 ± 0.06 | 0.715 ± 0.059 | 0.843 ± 0.051 | |
| AUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.836 ± 0.052 | 0.742 ± 0.057 | 0.764 ± 0.056 | 0.849 ± 0.05 |
| 1.0 | H. | B.T. | 0.0002 | 0.01 | 0.531 ± 0.076 | 0.492 ± 0.065 | 0.463 ± 0.065 | 0.618 ± 0.073 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.84 ± 0.052 | 0.755 ± 0.056 | 0.775 ± 0.055 | 0.855 ± 0.049 | |
| Acc. on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | H. | B.T. | 0.0002 | 0.01 | 0.531 ± 0.076 | 0.492 ± 0.065 | 0.463 ± 0.065 | 0.618 ± 0.073 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.84 ± 0.052 | 0.755 ± 0.056 | 0.775 ± 0.055 | 0.855 ± 0.049 | |
| F1 on Dc | 0.0 | C.E. | T. | 0.002 | 0.001 | 0.835 ± 0.053 | 0.729 ± 0.058 | 0.742 ± 0.057 | 0.856 ± 0.049 |
| 1.0 | H. | B.T. | 0.002 | 0.001 | 0.631 ± 0.072 | 0.615 ± 0.064 | 0.662 ± 0.062 | 0.618 ± 0.073 | |
| Best (0.25) | C.E. | T. | 0.0002 | 0.01 | 0.84 ± 0.052 | 0.755 ± 0.056 | 0.775 ± 0.055 | 0.855 ± 0.049 | |
| PRAUC on Dc | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.836 ± 0.052 | 0.742 ± 0.057 | 0.764 ± 0.056 | 0.849 ± 0.05 |
| 1.0 | H. | B.T. | 0.002 | 0.001 | 0.631 ± 0.072 | 0.615 ± 0.064 | 0.662 ± 0.062 | 0.618 ± 0.073 | |
| Best (0.25) | H. | T. | 0.0002 | 0.01 | 0.84 ± 0.052 | 0.755 ± 0.056 | 0.775 ± 0.055 | 0.855 ± 0.049 | |
Table E.8:
Absolute label prediction performance on the ROP dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Da | Acc. on Da | F1 on Da | PRAUC on Da | ||
| AUC on Da | 0.0 | C.E. | B.T | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T | 0.002 | 0.01 | 0.835 ± 0.017 | 0.824 ± 0.011 | 0.0 ± 0.0 | 0.528 ± 0.021 | |
| Best (0.75) | C.E. | B.T. | 0.02 | 0.001 | 0.914 ± 0.013 | 0.883 ± 0.009 | 0.622 ± 0.013 | 0.736 ± 0.019 | |
| Acc. on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.01 | 0.87 ± 0.015 | 0.705 ± 0.012 | 0.517 ± 0.014 | 0.549 ± 0.021 | |
| Best (0.75) | C.E. | B.T. | 0.02 | 0.001 | 0.914 ± 0.013 | 0.883 ± 0.009 | 0.622 ± 0.013 | 0.736 ± 0.019 | |
| F1 on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.01 | 0.87 ± 0.015 | 0.705 ± 0.012 | 0.517 ± 0.014 | 0.549 ± 0.021 | |
| Best (0.5) | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.87 ± 0.009 | 0.64 ± 0.013 | 0.731 ± 0.019 | |
| PRAUC on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.913 ± 0.013 | 0.822 ± 0.011 | 0.625 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.02 | 0.01 | 0.5 ± 0.02 | 0.177 ± 0.011 | 0.301 ± 0.013 | 0.177 ± 0.012 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.913 ± 0.013 | 0.822 ± 0.011 | 0.625 ± 0.013 | 0.731 ± 0.019 | |
| AUC on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.835 ± 0.017 | 0.824 ± 0.011 | 0.0 ± 0.0 | 0.528 ± 0.021 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 | |
| Acc. on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.835 ± 0.017 | 0.824 ± 0.011 | 0.0 ± 0.0 | 0.528 ± 0.021 | |
| Best (0.25) | C.E. | B.T. | 0.02 | 0.001 | 0.908 ± 0.013 | 0.882 ± 0.009 | 0.616 ± 0.013 | 0.731 ± 0.019 | |
| F1 on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.909 ± 0.013 | 0.824 ± 0.011 | 0.624 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.835 ± 0.017 | 0.824 ± 0.011 | 0.0 ± 0.0 | 0.528 ± 0.021 | |
| Best (0.25) | C.E. | B.T. | 0.02 | 0.001 | 0.908 ± 0.013 | 0.882 ± 0.009 | 0.616 ± 0.013 | 0.731 ± 0.019 | |
| PRAUC on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.913 ± 0.013 | 0.822 ± 0.011 | 0.625 ± 0.013 | 0.731 ± 0.019 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.835 ± 0.017 | 0.177 ± 0.011 | 0.301 ± 0.013 | 0.528 ± 0.021 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.913 ± 0.013 | 0.822 ± 0.011 | 0.625 ± 0.013 | 0.731 ± 0.019 | |
Table E.9:
Comparison label prediction performance on the ROP dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Dc | Acc. on Dc | F1 on Dc | PRAUC on Dc | ||
| AUC on Da | 0.0 | C.E. | B.T | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T | 0.002 | 0.01 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best (0.75) | C.E. | B.T. | 0.02 | 0.001 | 0.953 ± 0.013 | 0.869 ± 0.02 | 0.872 ± 0.02 | 0.957 ± 0.013 | |
| Acc. on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.01 | 0.89 ± 0.02 | 0.785 ± 0.024 | 0.785 ± 0.024 | 0.761 ± 0.028 | |
| Best (0.75) | C.E. | B.T. | 0.02 | 0.001 | 0.953 ± 0.013 | 0.869 ± 0.02 | 0.872 ± 0.02 | 0.957 ± 0.013 | |
| F1 on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.0002 | 0.01 | 0.89 ± 0.02 | 0.785 ± 0.024 | 0.785 ± 0.024 | 0.761 ± 0.028 | |
| Best (0.5) | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.872 ± 0.02 | 0.875 ± 0.02 | 0.963 ± 0.012 | |
| PRAUC on Da | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.959 ± 0.013 | 0.886 ± 0.019 | 0.89 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.02 | 0.01 | 0.5 ± 0.034 | 0.475 ± 0.029 | 0.0 ± 0.0 | 0.526 ± 0.034 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.959 ± 0.013 | 0.886 ± 0.019 | 0.89 ± 0.019 | 0.963 ± 0.012 | |
| AUC on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 | |
| Acc. on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best (0.25) | C.E. | B.T. | 0.02 | 0.001 | 0.954 ± 0.013 | 0.883 ± 0.019 | 0.886 ± 0.019 | 0.963 ± 0.012 | |
| F1 on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.955 ± 0.013 | 0.882 ± 0.019 | 0.885 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best (0.25) | C.E. | B.T. | 0.02 | 0.001 | 0.954 ± 0.013 | 0.883 ± 0.019 | 0.886 ± 0.019 | 0.963 ± 0.012 | |
| PRAUC on Dc | 0.0 | C.E. | B.T. | 0.02 | 0.001 | 0.959 ± 0.013 | 0.886 ± 0.019 | 0.89 ± 0.019 | 0.963 ± 0.012 |
| 1.0 | C.E. | B.T. | 0.002 | 0.01 | 0.941 ± 0.015 | 0.859 ± 0.021 | 0.865 ± 0.02 | 0.942 ± 0.015 | |
| Best (0.0) | C.E. | B.T. | 0.02 | 0.001 | 0.959 ± 0.013 | 0.886 ± 0.019 | 0.89 ± 0.019 | 0.963 ± 0.012 | |
Table E.10:
Absolute label prediction performance on the FAC dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Da | Acc. on Da | F1 on Da | PRAUC on Da | ||
| AUC on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 |
| 1.0 | H. | B.T | 0.002 | 0.01 | 0.746 ± 0.037 | 0.677 ± 0.035 | 0.659 ± 0.036 | 0.678 ± 0.041 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 | |
| Acc. on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 |
| 1.0 | H. | B.T. | 0.002 | 0.01 | 0.746 ± 0.037 | 0.677 ± 0.035 | 0.659 ± 0.036 | 0.678 ± 0.041 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 | |
| F1 on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.741 ± 0.038 | 0.618 ± 0.036 | 0.684 ± 0.035 | 0.66 ± 0.041 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 |
| 1.0 | H. | B.T. | 0.002 | 0.01 | 0.746 ± 0.037 | 0.677 ± 0.035 | 0.659 ± 0.036 | 0.678 ± 0.041 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.87 ± 0.028 | 0.82 ± 0.029 | 0.809 ± 0.03 | 0.82 ± 0.033 | |
| AUC on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.783 ± 0.035 | 0.733 ± 0.033 | 0.733 ± 0.033 | 0.698 ± 0.04 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.721 ± 0.039 | 0.554 ± 0.037 | 0.025 ± 0.012 | 0.638 ± 0.042 | |
| Best (0.5) | C.E. | H. | 0.02 | 0.001 | 0.764 ± 0.036 | 0.706 ± 0.034 | 0.679 ± 0.035 | 0.644 ± 0.042 | |
| Acc. on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.783 ± 0.035 | 0.733 ± 0.033 | 0.733 ± 0.033 | 0.698 ± 0.04 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.721 ± 0.039 | 0.554 ± 0.037 | 0.025 ± 0.012 | 0.638 ± 0.042 | |
| Best (0.75) | C.E. | H. | 0.02 | 0.001 | 0.758 ± 0.037 | 0.682 ± 0.035 | 0.633 ± 0.036 | 0.68 ± 0.04 | |
| F1 on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.783 ± 0.035 | 0.733 ± 0.033 | 0.733 ± 0.033 | 0.698 ± 0.04 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.721 ± 0.039 | 0.554 ± 0.037 | 0.025 ± 0.012 | 0.638 ± 0.042 | |
| Best (0.5) | H. | B.T. | 0.002 | 0.01 | 0.784 ± 0.035 | 0.718 ± 0.034 | 0.733 ± 0.033 | 0.674 ± 0.041 | |
| PRAUC on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.783 ± 0.035 | 0.733 ± 0.033 | 0.733 ± 0.033 | 0.698 ± 0.04 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.741 ± 0.038 | 0.618 ± 0.036 | 0.684 ± 0.035 | 0.66 ± 0.041 | |
| Best (1.0) | C.E. | B.T. | 0.02 | 0.001 | 0.741 ± 0.038 | 0.618 ± 0.036 | 0.684 ± 0.035 | 0.66 ± 0.041 | |
Table E.11:
Comparison label prediction performance on the FAC dataset. For each α, we find the optimal absolute loss function (La), comparison loss function (Lc), regularization parameter λ, and learning rate (L.R.). We consider cross-entropy (C.E), hinge (H.), Bradley-Terry (B.T.), and Thurstone (T.) as loss functions. We repeat this optimization for AUC, accuracy (Acc.), F1 score, and PRAUC metrics on the absolute (Da) and the comparison labels (Dc) of the validation set. Accordingly, each row triplet corresponds to the metric on which we optimize the hyperparameters. We then report all eight metrics on the test set, for training with α = 0.0 (comparison labels only), α = 1.0 (absolute labels only), and best performing α ∈ [0, 1].
| α | Hyperparameters Optimized on Validation Set | Performance Metrics on Test Set | |||||||
|---|---|---|---|---|---|---|---|---|---|
| La | Lc | λ | L.R. | AUC on Dc | Acc. on Dc | F1 on Dc | PRAUC on Dc | ||
| AUC on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 |
| 1.0 | H. | B.T | 0.002 | 0.01 | 0.792 ± 0.06 | 0.75 ± 0.057 | 0.746 ± 0.058 | 0.757 ± 0.064 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 | |
| Acc. on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 |
| 1.0 | H. | B.T. | 0.002 | 0.01 | 0.792 ± 0.06 | 0.75 ± 0.057 | 0.746 ± 0.058 | 0.757 ± 0.064 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 | |
| F1 on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.821 ± 0.057 | 0.75 ± 0.057 | 0.736 ± 0.058 | 0.797 ± 0.06 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 | |
| PRAUC on Da | 0.0 | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 |
| 1.0 | H. | B.T. | 0.002 | 0.01 | 0.792 ± 0.06 | 0.75 ± 0.057 | 0.746 ± 0.058 | 0.757 ± 0.064 | |
| Best (0.0) | C.E. | T. | 0.0002 | 0.01 | 0.72 ± 0.068 | 0.706 ± 0.06 | 0.716 ± 0.06 | 0.66 ± 0.072 | |
| AUC on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.751 ± 0.065 | 0.71 ± 0.06 | 0.706 ± 0.06 | 0.735 ± 0.066 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.809 ± 0.058 | 0.733 ± 0.058 | 0.72 ± 0.059 | 0.734 ± 0.066 | |
| Best (0.5) | C.E. | H. | 0.02 | 0.001 | 0.814 ± 0.057 | 0.755 ± 0.057 | 0.74 ± 0.058 | 0.749 ± 0.065 | |
| Acc. on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.751 ± 0.065 | 0.71 ± 0.06 | 0.706 ± 0.06 | 0.735 ± 0.066 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.809 ± 0.058 | 0.733 ± 0.058 | 0.72 ± 0.059 | 0.734 ± 0.066 | |
| Best (0.75) | C.E. | H. | 0.02 | 0.001 | 0.817 ± 0.057 | 0.759 ± 0.057 | 0.743 ± 0.058 | 0.774 ± 0.062 | |
| F1 on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.751 ± 0.065 | 0.71 ± 0.06 | 0.706 ± 0.06 | 0.735 ± 0.066 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.809 ± 0.058 | 0.733 ± 0.058 | 0.72 ± 0.059 | 0.734 ± 0.066 | |
| Best (0.5) | H. | B.T. | 0.002 | 0.01 | 0.785 ± 0.061 | 0.737 ± 0.058 | 0.736 ± 0.058 | 0.76 ± 0.064 | |
| PRAUC on Dc | 0.0 | C.E. | B.T. | 0.002 | 0.01 | 0.751 ± 0.065 | 0.71 ± 0.06 | 0.706 ± 0.06 | 0.735 ± 0.066 |
| 1.0 | C.E. | B.T. | 0.02 | 0.001 | 0.821 ± 0.057 | 0.75 ± 0.057 | 0.736 ± 0.058 | 0.797 ± 0.06 | |
| Best (1.0) | C.E. | B.T. | 0.02 | 0.001 | 0.821 ± 0.057 | 0.75 ± 0.057 | 0.736 ± 0.058 | 0.797 ± 0.06 | |
Footnotes
Our code is publicly available at https://github.com/neu-spiral/ClassificationAndComparisonViaNeuralNetworks.
References
- Antoniou A, Storkey A, & Edwards H (2017). Data augmentation generative adversarial networks. arXiv preprint arXiv:1711.0f3f0,.
- Bengio Y, Courville A, & Vincent P (2013). Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35, 1798–1828. [DOI] [PubMed] [Google Scholar]
- Bradley RA, & Terry ME (1952). Rank analysis of incomplete block designs: I. the method of paired comparisons. Biometrika, 39, 324–345. [Google Scholar]
- Bromley J, Guyon I, LeCun Y, Sackinger E, & Shah R (1994). Signature verification using a ”siamese” time delay neural network. In Advances in Neural Information Processing Systems (pp. 737–744). [Google Scholar]
- Brown JM, Campbell JP, Beers A, Chang K, Ostmo S, Chan RP, Dy J, Erdogmus D, Ioannidis S, & Kalpathy-Cramer J (2018). Automated diagnosis of plus disease in retinopathy of prematurity using deep convolutional neural networks. JAMA Ophthalmology,. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brun A, Hamad A, Buffet O, & Boyer A (2010). Towards preference relations in recommender systems. In Preference Learning (PL 2010) ECML/PKDD 2010 Workshop. [Google Scholar]
- Burges C, Shaked T, Renshaw E, Lazier A, Deeds M, Hamilton N, & Hullender G (2005). Learning to rank using gradient descent. In Proceedings of the International Conference on Machine Learning (pp. 89–96). ACM. [Google Scholar]
- Cattelan M (2012). Models for paired comparison data: A review with emphasis on dependent data. Statistical Science, (pp. 412–433). [Google Scholar]
- Chang H, Yu F, Wang J, Ashley D, & Finkelstein A (2016). Automatic triage for a photo series. ACM Transactions on Graphics (TOG), 35, 148. [Google Scholar]
- Chen L, Zhang P, & Li B (2015). Fusing pointwise and pairwise labels for supporting user-adaptive image retrieval. In Proceedings of the 5th ACM on International Conference on Multimedia Retrieval (pp. 67–74). ACM. [Google Scholar]
- Chen S-Z, Guo C-C, & Lai J-H (2016). Deep ranking for person reidentification via joint representation learning. IEEE Transactions on Image Processing, 25, 2353–2367. [DOI] [PubMed] [Google Scholar]
- Chiang MF, Jiang L, Gelman R, Du YE, & Flynn JT (2007). Interexpert agreement of plus disease diagnosis in retinopathy of prematurity. Archives of Ophthalmology, 125, 875–880. [DOI] [PubMed] [Google Scholar]
- Collobert R, Weston J, Bottou L, Karlen M, Kavukcuoglu K, & Kuksa P (2011). Natural language processing (almost) from scratch. Journal of Machine Learning Research, 12, 2493–2537. [Google Scholar]
- Deng J, Dong W, Socher R, Li L-J, Li K, & Fei-Fei L (2009). Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on (pp. 248–255). IEEE. [Google Scholar]
- Desarkar MS, Sarkar S, & Mitra P (2010). Aggregating preference graphs for collaborative rating prediction. In Proceedings of the fourth ACM Conference on Recommender Systems (pp. 21–28). ACM. [Google Scholar]
- Desarkar MS, Saxena R, & Sarkar S (2012). Preference relation based matrix factorization for recommender systems. In International conference on user modeling, adaptation, and personalization (pp. 63–75). Springer. [Google Scholar]
- Doughty H, Damen D, & Mayol-Cuevas W (2017). Who’s better? who’s best? pairwise deep ranking for skill determination. arXiv:1703.09913,.
- Dubey A, Naik N, Parikh D, Raskar R, & Hidalgo CA (2016). Deep learning the city: Quantifying urban perception at a global scale. In European Conference on Computer Vision (pp. 196–212). Springer. [Google Scholar]
- Friedman J, Hastie T, & Tibshirani R (2001). The elements of statistical learning volume 1 Springer series in statistics; New York. [Google Scholar]
- Gole GA, Ells AL, Katz X, Holmstrom G, Fielder AR, Capone A Jr, Flynn JT, Good WG, Holmes JM, McNamara J et al. (2005). The international classification of retinopathy of prematurity revisited. JAMA Ophthalmology, 123, 991–999. [DOI] [PubMed] [Google Scholar]
- Goodfellow I, Bengio Y, & Courville A (2016). Deep learning. MIT press. [Google Scholar]
- Gordo A, Almazan J, Revaud J, & Larlus D (2016). Deep image retrieval: Learning global representations for image search. In European Conference on Computer Vision (pp. 241–257). Springer. [Google Scholar]
- Guo Y, Tian P, Kalpathy-Cramer J, Ostmo S, Campbell JP, Chiang MF, Erdogmus D, Dy JG, & Ioannidis S (2018). Experimental design under the bradley-terry model. In IJCAI; (pp. 2198–2204). [Google Scholar]
- Hadsell R, Chopra S, & LeCun Y (2006). Dimensionality reduction by learning an invariant mapping In Computer Vision and Pattern Recognition (CVPR) (pp. 1735–1742). IEEE. [Google Scholar]
- Hanley JA, & McNeil BJ (1982). The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology, 1f3, 29–36. [DOI] [PubMed] [Google Scholar]
- Hauberg S, Freifeld O, Larsen ABL, Fisher J, & Hansen L (2016). Dreaming more data: Class-dependent distributions over diffeomorphisms for learned data augmentation. In Artificial Intelligence and Statistics (pp. 342–350). [Google Scholar]
- Hinton G, Deng L, Yu D, Dahl GE, Mohamed A.-r., Jaitly N, Senior A, Vanhoucke V, Nguyen P, Sainath TN et al. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal processing magazine, 29, 82–97. [Google Scholar]
- Hou J, Wu T, Cao R, & Cheng J (2019). Protein tertiary structure modeling driven by deep learning and contact distance prediction in casp13. bioRxiv, (p. 552422). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imrey PB (1998). Bradley-Terry model. Encyclopedia of Biostatistics,. [Google Scholar]
- Joachims T (2002). Optimizing search engines using clickthrough data. In Proceedings of the eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 133–142). ACM. [Google Scholar]
- Kalpathy-Cramer J, Campbell JP, Erdogmus D, Tian P, Kedarisetti D, Moleta C, Reynolds JD, Hutcheson K, Shapiro MJ, Repka MX et al. (2016). Plus disease in retinopathy of prematurity: Improving diagnosis by ranking disease severity and using quantitative image analysis. Ophthalmology, 123, 2345–2351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keshari R, Vatsa M, Singh R, & Noore A (2018). Learning structure and strength of cnn filters for small sample size training. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 9349–9358). [Google Scholar]
- Koren Y, & Sill J (2011). Ordrec: an ordinal model for predicting personalized item rating distributions. In Proceedings of the fifth ACM Conference on Recommender Systems (pp. 117–124). ACM. [Google Scholar]
- Krizhevsky A, Sutskever I, & Hinton GE (2012). Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems (pp. 1097–1105). [Google Scholar]
- Liu B, Wei Y, Zhang Y, & Yang Q (2017). Deep neural networks for high dimension, low sample size data. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI-17 (pp. 22872293). [Google Scholar]
- Liu S, Tran T, Li G, & Jiang Y (2014). Ordinal random fields for recommender systems. In ACML 2014: Proceedings of the Sixth Asian Conference on Machine Learning (pp. 283–298). JMLR Workshop and Conference Proceedings. [Google Scholar]
- Lu X, Lin Z, Jin H, Yang J, & Wang JZ (2014). Rapid: Rating pictorial aesthetics using deep learning. In Proceedings of the 22nd ACM International Conference on Multimedia (pp. 457–466). ACM. [Google Scholar]
- Luce RD (2012). Individual choice behavior: A theoretical analysis. Courier Corporation. [Google Scholar]
- Mao R, Zhu H, Zhang L, & Chen A (2006). A new method to assist small data set neural network learning. In Intelligent Systems Design and Applications, 2006. ISDA’06. Sixth International Conference on (pp. 17–22). IEEE volume 1. [Google Scholar]
- MIT Media Lab (). GIFGIF. http://gifgif.media.mit.edu. Accessed: 2018-12-01.
- Moritz S, Pfab J, Wu T, Hou J, Cheng J, Cao R, Wang L, & Si D (2019). Cascaded-cnn: Deep learning to predict protein backbone structure from high-resolution cryo-em density maps. BioRxiv, (p. 572990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norouzi M, Fleet DJ, & Salakhutdinov RR (2012). Hamming distance metric learning. In Advances in Neural Information Processing Systems (NIPS) (pp. 1061–1069). [Google Scholar]
- Reynolds JD, Dobson V, Quinn GE, Fielder AR, Palmer EA, Saunders RA, Hardy RJ, Phelps DL, Baker JD, Trese MT et al. (2002). Evidence-based screening criteria for retinopathy of prematurity: natural history data from the CRYO-ROP and LIGHT-ROP studies. Archives of Ophthalmology, 120, 1470–1476. [DOI] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, & Brox T (2015). U-Net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention (pp. 234–241). Springer. [Google Scholar]
- Ryan MC, Ostmo S, Jonas K, Berrocal A, Drenser K, Horowitz J, Lee TC, Simmons C, Martinez-Castellanos M-A, Chan RP et al. (2014). Development and evaluation of reference standards for image-based telemedicine diagnosis and clinical research studies in ophthalmology. In AMIA Annual Symposium Proceedings (p. 1902). American Medical Informatics Association volume 2014. [PMC free article] [PubMed] [Google Scholar]
- Sawilowsky SS (2002). Fermat, schubert, einstein, and behrens-fisher: The probable difference between two means when . Journal of Modern Applied Statistical Methods, 1, 55. [Google Scholar]
- Schmidhuber J (2015). Deep learning in neural networks: An overview. Neural networks, 61, 85–117. [DOI] [PubMed] [Google Scholar]
- Schultz M, & Joachims T (2004). Learning a distance metric from relative comparisons. In Advances in Neural Information Processing Systems (pp. 41–48). [Google Scholar]
- Sculley D (2010). Combined regression and ranking. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 979–988). ACM. [Google Scholar]
- Shen C, Jin Z, Zhao Y, Fu Z, Jiang R, Chen Y, & Hua X-S (2017). Deep siamese network with multi-level similarity perception for person reidentification. In Proceedings of the 2017 ACM on Multimedia Conference (pp. 1942–1950). ACM. [Google Scholar]
- Simo-Serra E, & Ishikawa H (2016). Fashion style in 128 floats: joint ranking and classification using weak data for feature extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 298–307). [Google Scholar]
- Simonyan K, & Zisserman A (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1f09.1556,.
- Singh A, & Kingsbury N (2017). Efficient convolutional network learning using parametric log based dual-tree wavelet scatternet. In Computer Vision Workshop (ICCVW), 2017 IEEE International Conference on (pp. 1140–1147). IEEE. [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, & Salakhutdinov R (2014). Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15, 1929–1958. [Google Scholar]
- Stephenson N, Shane E, Chase J, Rowland J, Ries D, Justice N, Zhang J, Chan L, & Cao R (2018). Survey of machine learning techniques in drug discovery. Current drug metabolism,. [DOI] [PubMed] [Google Scholar]
- Stewart N, Brown GD, & Chater N (2005). Absolute identification by relative judgment. Psychological Review, 112, 881. [DOI] [PubMed] [Google Scholar]
- Sun W-T, Chao T-H, Kuo Y-H, & Hsu WH (2017). Photo filter recommendation by category-aware aesthetic learning. IEEE Transactions on Multimedia, 19, 1870–1880. [Google Scholar]
- Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, Anguelov D, Erhan D, Vanhoucke V, Rabinovich A et al. (2015). Going deeper with convolutions. In Computer Vision and Pattern Recognition, 2015.. [Google Scholar]
- Takamura H, & Tsujii J (2015). Estimating numerical attributes by bringing together fragmentary clues. In HLT-NAACL (pp. 1305–1310). [Google Scholar]
- Thurstone LL (1927). A law of comparative judgment. Psychological review, 34, 273. [Google Scholar]
- Wallace DK, Quinn GE, Freedman SF, & Chiang MF (2008). Agreement among pediatric ophthalmologists in diagnosing plus and pre-plus disease in retinopathy of prematurity. Journal of American Association for Pediatric Ophthalmology and Strabismus, 12, 352–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Leung T, Rosenberg C, Wang J, Philbin J, Chen B, Wu Y et al. (2014). Learning fine-grained image similarity with deep ranking. arXiv preprint arXiv:1404.4661,.
- Wang Y, Wang S, Tang J, Liu H, & Li B (2016). PPP: Joint pointwise and pairwise image label prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 6005–6013). [Google Scholar]
- Wu H, Xu Z, Zhang J, Yan W, & Ma X (2017). Face recognition based on convolution Siamese networks. In Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), 2017 10th International Congress on (pp. 1–5). IEEE. [Google Scholar]
- Xia R, Pan Y, Lai H, Liu C, & Yan S (2014). Supervised hashing for image retrieval via image representation learning. In AAAI; (p. 2). [Google Scholar]
- Zhang K, Zhang Z, Li Z, & Qiao Y (2016). Joint face detection and alignment using multitask cascaded convolutional networks. IEEE Signal Processing Letters, 23, 1499–1503. [Google Scholar]
- Zhang X, Wang Z, Liu D, & Ling Q (2018). Dada: Deep adversarial data augmentation for extremely low data regime classification. arXiv preprint arXiv:1809.00981,.
- Zheng Y, Zhang L, Xie X, & Ma W-Y (2009). Mining interesting locations and travel sequences from gps trajectories. In Proceedings of the 18th International Conference on World Wide Web (pp. 791–800). ACM. [Google Scholar]