Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-30T23:35:50.142Z Has data issue: false hasContentIssue false
  • English
  • Français

WELL ORDERING PRINCIPLES AND 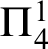${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY

Part of: General logic Proof theory and constructive mathematics Computability and recursion theory

Published online by Cambridge University Press:  16 February 2021

ANTON FREUND
ANTON FREUND*
Affiliation:
FACHBEREICH MATHEMATIK TECHNISCHE UNIVERSITÄT DARMSTADT SCHLOSSGARTENSTR. 7, 64289DARMSTADT, GERMANYE-mail:freund@mathematik.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

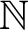In previous work, the author has shown that $\Pi ^1_1$ -induction along $\mathbb N$ is equivalent to a suitable formalization of the statement that every normal function on the ordinals has a fixed point. More precisely, this was proved for a representation of normal functions in terms of Girard’s dilators, which are particularly uniform transformations of well orders. The present paper works on the next type level and considers uniform transformations of dilators, which are called 2-ptykes. We show that $\Pi ^1_2$ -induction along $\mathbb N$ is equivalent to the existence of fixed points for all 2-ptykes that satisfy a certain normality condition. Beyond this specific result, the paper paves the way for the analysis of further $\Pi ^1_4$ -statements in terms of well ordering principles.

Keywords

well ordering principlesreverse mathematicsΠ14-statementsdilatorsptykesΠ12-induction

MSC classification

Primary: 03B30: Foundations of classical theories (including reverse mathematics)
Secondary: 03D65: Higher-type and set recursion theory 03F15: Recursive ordinals and ordinal notations 03F35: Second- and higher-order arithmetic and fragments
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 2 , June 2021 , pp. 709 - 745
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aczel, P., Mathematical problems in logic, Ph.D. thesis, University of Oxford, 1966.Google Scholar
Aczel, P., Normal functors on linear orderings, this Journal, vol. 32 (1967), p. 430, abstract to a paper presented at the annual meeting of the Association for Symbolic Logic, Houston, Texas, 1967.Google Scholar
Freund, A., Type-two well-ordering principles, admissible sets, and ${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$ -comprehension , Ph.D. thesis, University of Leeds, 2018, available at http://etheses.whiterose.ac.uk/20929/.Google Scholar
Freund, A., ${\varPi}_1^1$ -comprehension as a well-ordering principle. Advances in Mathematics, vol. 355 (2019), article no. 106767, 65 pp.CrossRefGoogle Scholar
Freund, A., A categorical construction of Bachmann-Howard fixed points. Bulletin of the London Mathematical Society, vol. 51 (2019), no. 5, pp. 801–814.CrossRefGoogle Scholar
Freund, A., Computable aspects of the Bachmann-Howard principle. Journal of Mathematical Logic, vol. 20 (2020), no. 2, article no. 2050006, 26 pp.CrossRefGoogle Scholar
Freund, A., A note on ordinal exponentiation and derivatives of normal functions. Mathematical Logic Quarterly, vol. 66 (2020), no. 3, 326–335.CrossRefGoogle Scholar
Freund, A., From Kruskal’s theorem to Friedman’s gap condition. Mathematical Structures in Computer Science, vol. 30 (2020), no. 8, pp. 952–975.CrossRefGoogle Scholar
Freund, A., How strong are single fixed points of normal functions? this Journal, vol. 85 (2020), no. 2, pp. 709–732.Google Scholar
Freund, A., What is effective transfinite recursion in reverse mathematics? Mathematical Logic Quarterly, vol. 66 (2020), no. 4, pp. 479–483.CrossRefGoogle Scholar
Freund, A. and Rathjen, M., Derivatives of normal functions in reverse mathematics. Annals of Pure and Applied Logic, vol. 172 (2021), no. 2, article no. 102890, 49 pp.CrossRefGoogle Scholar
Freund, A., Rathjen, M., and Weiermann, A., Minimal bad sequences are necessary for a uniform Kruskal theorem, preprint, 2020, arXiv:2001.06380.Google Scholar
Girard, J.-Y., ${\varPi}_2^1$ -logic, part 1: Dilators. Annals of Pure and Applied Logic, vol. 21 (1981), pp. 75–219.Google Scholar
Girard, J.-Y., Proof Theory and Logical Complexity, Studies in Proof Theory, vol. 1, Napoli, Bibliopolis, 1987.Google Scholar
Girard, J.-Y., Proof Theory and Logical Complexity , volume 2, 1982, unpublished manuscript. Available at http://girard.perso.math.cnrs.fr/Archives4.html (accessed 21 November 2017).Google Scholar
Girard, J.-Y. and Normann, D., Set recursion and ${\varPi}_2^1$ -logic. Annals of Pure and Applied Logic, vol. 28 (1985), pp. 255–286.CrossRefGoogle Scholar
Girard, J.-Y. and Normann, D., Embeddability of ptykes, this Journal, vol. 57 (1992), no. 2, pp. 659–676.Google Scholar
Hirst, J. L., Reverse mathematics and ordinal exponentiation. Annals of Pure and Applied Logic, vol. 66 (1994), pp. 1–18.CrossRefGoogle Scholar
Krombholz, M. and Rathjen, M., Upper bounds on the graph minor theorem, Well-Quasi Orders in Computation, Logic, Language and Reasoning (Schuster, P., Seisenberger, M., and Weiermann, A., editors), Trends in Logic (Studia Logica Library), vol. 53, Springer, Cham, 2020, pp. 145–159.CrossRefGoogle Scholar
Mac Lane, S., Categories for the Working Mathematician, vol. 5, second ed., Graduate Texts in Mathematics, Springer, New York, 1998.Google Scholar
Marcone, A. and Montalbán, A., The Veblen functions for computability theorists, this Journal, vol. 76 (2011), pp. 575–602.Google Scholar
Nash-Williams, C. S. J. A., On well-quasi-ordering finite trees. Proceedings of the Cambridge Philosophical Society, vol. 59 (1963), pp. 833–835.CrossRefGoogle Scholar
Rathjen, M., An ordinal analysis of parameter free ${\varPi}_2^1$ -comprehension. Archive for Mathematical Logic, vol. 44 (2005), pp. 263–362.CrossRefGoogle Scholar
Rathjen, M., ω-models and well-ordering principles, Foundational Adventures: Essays in Honor of Harvey M. Friedman (Tennant, N., editor), College Publications, London, 2014, pp. 179–212.Google Scholar
Rathjen, M. and Thomson, I. A., Well-ordering principles, $\omega$ -models and ${\varPi}_1^1$ -comprehension, The Legacy of Kurt Schütte (Kahle, R. and Rathjen, M., editors), Springer, Cham, 2020, pp. 171–215.CrossRefGoogle Scholar
Rathjen, M. and Vizcaíno, P. F. Valencia, Well ordering principles and bar induction, Gentzen’s Centenary: The Quest for Consistency (Kahle, R. and Rathjen, M., editors), Springer, Berlin, 2015, pp. 533–561.CrossRefGoogle Scholar
Rathjen, M. and Weiermann, A., Reverse mathematics and well-ordering principles, Computability in Context: Computation and Logic in the Real World (Cooper, S. B. and Sorbi, A., editors), Imperial College Press, 2011, pp. 351–370.CrossRefGoogle Scholar
Simpson, S. G., Nonprovability of certain combinatorial properties of finite trees, Harvey Friedman’s Research on the Foundations of Mathematics (Harrington, L. A., Morley, M. D., Sčědrov, A., and Simpson, S. G., editors), Studies in Logic and the Foundations of Mathematics, vol. 117, North-Holland, Amsterdam, 1985, pp. 87–117.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Thomson, I. A., Well-ordering principles and ${\boldsymbol{\varPi}}_{\mathbf{1}}^{\mathbf{1}}$ -comprehension $+$ Bar induction , Ph.D. thesis, University of Leeds, 2017, available at http://etheses.whiterose.ac.uk/22206/.Google Scholar