Abstract
The lead optimization phase of drug discovery refines an initial hit molecule for desired properties, especially potency. Synthesis and experimental testing of the small perturbations during this refinement can be quite costly and time consuming. Relative binding free energy (RBFE, also referred to as ΔΔG) methods allow the estimation of binding free energy changes after small changes to a ligand scaffold. Here we propose and evaluate a Convolutional Neural Network (CNN) Siamese network for the prediction of RBFE between two bound ligands. We show that our multi-task loss is able to improve on a previous state-of-the-art Siamese network for RBFE prediction via increased regularization of the latent space. The Siamese network architecture is well suited to the prediction of RBFE in comparison to a standard CNN trained on the same data (Pearson’s R of 0.553 and 0.5, respectively). When evaluated on a left-out protein family, our CNN Siamese network shows variability in its RBFE predictive performance depending on the protein family being evaluated (Pearson’s R ranging from −0.44 to 0.97). RBFE prediction performance can be improved during generalization by injecting only a few examples (few-shot learning) from the evaluation dataset during model training.
Graphical Abstract

Introduction
Lead optimization is an early phase of the drug discovery process that simultaneously optimizes a hit molecule for potency, solubility, and other toxicological and pharmaceutical properties. Small modifications are made to the chemical scaffold of the hit molecule and tested for their effect on the properties of interest. A collection of such molecules, along with the initial hit molecule, is termed a congeneric series. Congeneric series developed within a drug discovery campaign can contain tens to hundreds of compounds,1,2 with the synthesis and testing of each chemical modification taking considerable amounts of time and money. Relative binding free energy (RBFE, also called ΔΔG) methods provide an in silico alternative to the labor intensive synthesis and experimental testing of each compound in a congeneric series.
RBFE methods strike a balance between accuracy and throughput. Typical methods for RBFE determination utilize either molecular dynamics with alchemical perturbations or thorough sampling of the endpoints of the transformation. Alchemical methods, also called pathway methods, perturb the bound molecule from one ligand into another using chemical or alchemical means;3 Free Energy Perturbation4 (FEP) is one of the most popular alchemical methods. FEP utilizes explicitly solvated molecular dynamics or Monte Carlo simulations in which one ligand is alchemically transformed into another ligand. Recent advances in molecular mechanics force fields, sampling, and reductions in computational cost have encouraged the adoption of the FEP approach for the prediction of RBFE in both academia and industry. These advances have allowed for very high accuracy of FEP approaches, within about one kcal per mol. However, the current implementations only allow for the calculation of about four ligand perturbations per day with commonly available computing resources.5 FEP is somewhat limited to a maximum number of changes between ligands, about 10 heavy atoms, due to the high amount of sampling required for each change of a ligand. However, with careful consideration, more heavy atoms can be changed between the ligands while still achieving low errors in predictions.6,7 Endpoint sampling methods reduce the required amount of molecular dynamics needed to determine the free energy of the system.8 The most popular methods for determining RBFE with endpoint sampling are molecular mechanics Poisson-Boltzmann Surface Area (MMPBSA) and molecular mechanics generalized Borne surface area (MMGBSA). MMBPSA and MMGBSA, developed by Kollman et al.,9,10 evaluate the free energy through molecular dynamics simulations of the unbound ligands and the bound complexes. RBFE is computed via a simple difference of the energetics in each of the ligand binding modes.11 While these methods have reduced computational requirements in comparison to FEP, their free energy predictions are not as rigorous. This limited throughput of molecules and low allowance for changes between molecules can prevent medicinal chemists from fully exploring the optimization space of a lead molecule.
A number of scoring functions have been developed to simultaneously provide low error and high throughput for absolute binding affinity predictions.12–17 These are able to replace the more thorough and compute intensive simulation based methods for measuring the energy of the absolute binding affinity. More recently, these scoring functions utilize deep learning to infer absolute binding affinity directly from the bound protein-ligand complex.13–16 Using these deep learning absolute binding affinity methods as inspiration, Jiménez-Luna et al.18 utilize a Siamese Convolutional Neural Network (CNN) architecture to directly determine the RBFE between two bound protein-ligand complexes. This architecture removes the compounding error of determining the RBFE with the difference in absolute binding free energies of the two ligands. They showed the potential of their trained neural network in retrospective lead optimization campaigns with only a small amount of retraining required. Here we present further expansion on their Siamese network by introducing novel loss function components. We evaluate the impact of our loss components as well as the Siamese architecture on the predictive performance of our models. Generalizability of the RBFE predictions are examined through both external datasets and clustered protein family cross validation.
Methods
We describe the filtering and usage of the training and evaluation datasets for our RBFE models. The architecture and training hyperparameters of our CNN Siamese network are explained. Our CNN Siamese network is compared to state of the art methods for RBFE prediction on a retrospective lead optimization task and several benchmark datasets. Next, we investigate the relative importance of the components of our model on a small retrospective lead optimization task. Finally, we evaluate our model on novel protein families utilizing a leave-one-family-out cross validation to elucidate the generalizability of our model.
Data
Proper training of a deep learning model for RBFE in a lead optimization setting requires that we utilize congeneric series with experimentally validated binding affinity measurements. We therefore utilize the BindingDB 3D Structure Series dataset.19 This dataset was created by combing the literature for experimental binding affinities of many ligands bound to the same receptor and finding the crystal structure of at least one of those ligands bound to the same receptor. The ligands with no known bound structure were computationally docked to the protein using the Surflex docking software20 for template docking with the crystal ligand. The full dataset encompases 1038 unique receptor structures with an average of 9.61 ligands bound to each receptor structure. We filter the dataset to ensure the binding affinity measurements are high quality and to enforce comparisons between ligands with identical measures of potency: IC50, Kd, or Ki. First the dataset is split into three different groups, one for each of the measures of potency. A ligand can be in multiple groups if it has binding affinity measurements for multiple measures of potency. For each split, we strip any greater than (>) or less than (<) symbols from the binding affinity measurements of every ligand and use the remaining string as the exact binding affinity value. If a ligand has multiple measurements for a given measure of potency, we delete the ligand from that measure of potency split if the range of the measurements is greater than one order of magnitude. Otherwise we take the median of the multiple measurements. After this filtering, we remove any ligands that have binding affinity information for a PDBID that has no other ligands with binding affinity measurements. We then construct congeneric series by creating ordered pairs of ligands that have the same receptor structure and the same measure of potency (IC50, Kd,Ki). We utilize the log-converted measurements (− log10(value)), referred to as “pK”, for each measure of potency. We next define a reference ligand. The reference ligand is assigned as the ligand with the highest Tanimoto similarity (using the RDKFingerprint from RDKit21) to the ligand used for the template docking, usually the ligand in the crystal that was used for template docking. Our final filtered BindingDB dataset has 1082 congeneric series, encompassing 943 unique receptor structures with an average of 7.995 ligands per congeneric series. The average pK range of each congeneric series is 2.023 pK. Histograms of the number of ligands and the affinity ranges per congeneric series are shown in Figure S1.
We utilize the datasets provided by Mobley et al.,22 Wang et al.7, and Schindler et al.2 in order to evaluate the generalization performance of our model. Mobley et al.22 provide a series of benchmarks datasets for binding free energy prediction. One of their benchmark sets has experimentally determined ΔG values for a congeneric series of 8 ligands binding to the first bromodomain of the BRD4 protein. Wang et al.7 provides 8 congeneric series on different proteins with experimentally validated ΔG values for benchmarking RBFE predictions. They also released the evaluation statistics of FEP calculations when applied to each of the congeneric series. Schindler et al.2 provide 8 congeneric series with pharmaceutically relevant targets, all with experimentally measured binding affinities. The congeneric series in this set contain changes in net charge and the charge distribution of molecules as well as ring openings and core hopping; all of these are ligand changes that the Wang et al.7 dataset avoids.
The ligands in both the Mobley et al.22 and Wang et al.7 benchmark datasets are given experimental ΔG, so we must convert them to pK for proper evaluation with our model. We assume that the ligands bind in a non-competitive manner, generating the following equation for conversion:
where we set R = 1.98720425864083 × 10−3 and T = 297 K following the values utilized in Wang et al.7. The ligands in the Schindler et al.2 benchmark dataset are given associated IC50 values, so we simply log convert the values (− log10(value)) as we did for the BindingDB dataset.
The evaluation datasets are constructed from all possible pairs of ligands for each receptor.
Model Architecture
Similar to Jiménez-Luna et al.18 we utilize a Siamese network23 (Figure 1). Siamese networks utilize two arms that share weights and take in two inputs for determining distances between the inputs, often utilized in object matching or object tracking.24–26 Our network takes as input the bound structures of two ligands bound to the same protein, with each arm getting a different protein-ligand complex. We use CNNs as the arms of our Siamese network to learn directly from the 3D information of the bound protein-ligand structure. The bound protein-ligand 3D structures are voxelized utilizing the libmolgrid python library,27 using the default channels provided by the library. The inputs are then passed through the main convolutional architectures employed by Gnina, 28 Default2018 or Dense, as defined in Francoeur et al.13. The Default2018 convolutional architecture uses a series of convolutions and average pooling operations to discern information directly from bound protein-ligand complexes while minimizing computational cost. The Dense convolutional architecture uses a series of densely connected convolutional blocks 29 to enhance the propagation of information at the cost of increased computation. Both of these convolutional architectures demonstrate an ability to learn absolute binding affinity directly from the 3D bound structure of the protein-ligand complex. We remove the final linear layers from both architectures in order to access the final latent vector of the networks. The difference of the latent vectors of the two protein-ligand complexes is used to learn a linear mapping to the RBFE (ΔΔG) of the two inputs. We also utilize the latent vectors of each input before taking the difference to determine the absolute binding affinity of each input using a fully connected layer.
Figure 1:
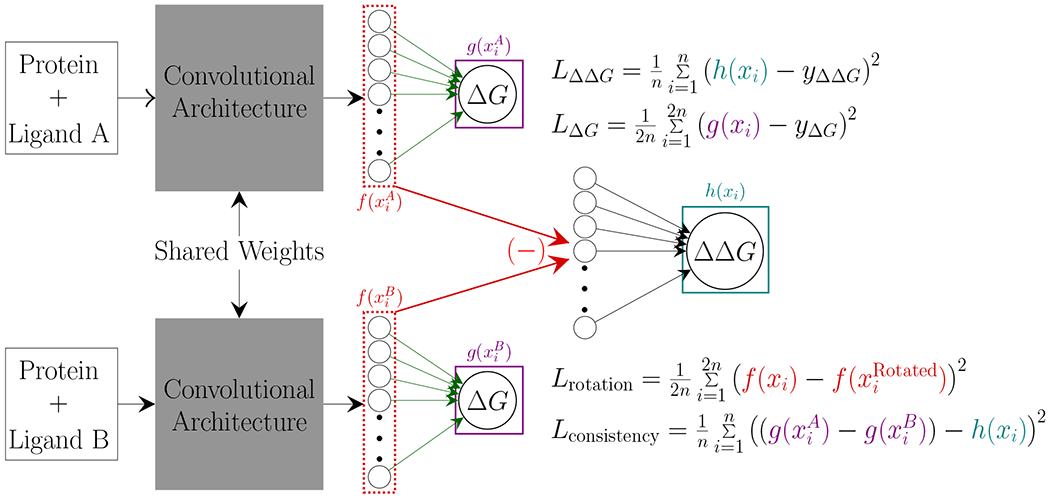
Siamese network simultaneously predicts both ΔΔG and ΔG using the latent vectors of each input as determined by the shared convolutional architecture. is a rotated view of the same protein-ligand complex as xi.
We train our model using a linear combination of loss components (Figure 1):
| (1) |
where . During the training of our model we set α = 10 and β, γ, δ = 1. is the mean square error (MSE) of the RBFE prediction. is the MSE of the absolute binding affinity prediction for both inputs. is the MSE of the latent vectors of two randomly rotated versions of each protein-ligand pair. This component encourages the latent space representation to ignore the rotation of the protein-ligand complex. is the MSE of the difference between the predicted absolute binding affinities and the predieted RBFE, to ensure that the model is providing consistent predictions. The Default2018 architecture’s weights are initialized with the Xavier uniform method30 and the biases are initialized to zero. The Dense model is initialized with weights and biases learned from its training described in Francoeur et al.13. All models are trained using the Adam stochastic gradient descent optimizer31 with the default parameters (β1 = 0.9, β2 = 0.999, ϵ = 1 × 10−8). Models are trained for 1000 epochs with a learning rate of 0.000367 and a scheduler that reduces the learning rate by a factor of 0.7 whenever the loss plateaus for more than 20 epochs. Data augmentation is achieved by randomly rotating and translating the inputs with a maximum translation of 2 Å from the center of mass of the ligand.
Retrospective lead optimization evaluation
In order to directly compare our trained model to the model developed by Jiménez-Luna et al.18, we utilize the additional ligands training set as described in their manuscript. We train our models on the reference ligand, as described in Data, and a given number of additional ligands. In the one additional ligands training set, we train on the two ordered pairs of the reference ligand and one additional ligand. Then, testing is carried out on the two-permutations between the ligands in the training set and ligands that the model has not seen, see Figure 2. We construct 25 versions of the training and testing datasets for each number of additional ligands to allow us to gather statistics about each number of additional ligands. In the case of the Dense convolutional architecture, we only use five versions of the training and testing datasets due to the architecture’s heavy computational cost. Each version of the dataset uses the same reference ligands and randomly chooses additional ligands to add to the training set for each congeneric series.
Figure 2:

The Siamese network model is evaluated in a number of different manners to allow us to compare to similar methods and investigate the generalizability of our predictions. The “Retrospective Lead Optimization” follows the evaluation described in Jiménez-Luna et al.18, where we incrementally add ligands from each congeneric series to the training set (filled in shapes) and test on ligand pairs that include one ligand in the training set. The “External Datasets Evaluation” utilizes a model trained on the entire BindingDB congeneric series dataset and evaluated on 17 congeneric series from our external datasets in both a no-shot and few-shot (3 epoch finetuning) manner. The “Leave One Protein Family Out CV” trains 60 different models, each with different training and testing datasets based on the left out protein family, in both a no-shot and few-shot manner, where ligand pairs from the left out protein family are added to the training set.
External Datasets Evaluation
We evaluate the generalizability of our model when applied to unseen data by training our Siamese CNN on all of the data available from the BindingDB Docked Congeneric Series dataset and evaluating on the datasets provided by Mobley et al.,22 Wang et al.7 and Schindler et al.2. Using the model trained on all of the BindingDB data, we can evaluate both the no-shot and few-shot performance of our model (Figure 2). No-shot performance refers to evaluations carried out on out-of-distribution examples with no prior knowledge about them, while the few-shot performance evaluates on out-of-distribution examples with a small amount of prior knowledge provided to the model about the evaluation distribution. The no-shot performance of our model is evaluated by training on the entire BindingDB dataset and predicting on the external test sets with no information about the test sets included during training. No-shot evaluation emulates the start of lead optimization for a given target, where no binding information is known about ligands in the congeneric series besides the lead molecule. The few-shot performance is evaluated utilizing increasing amounts of data from the test set during the training of the model. Few-shot evaluations show us how the model would perform later in lead optimization, when we have binding information for several ligands in our congeneric series. For all few-shot evaluations, the same model from the no-shot evaluation is used and finetuned. The smallest few-shot evaluation includes one ligand pair from the external test set included during the training of the model. We finetune our models by training for three epochs on the combined data of the BindingDB dataset and the included external test set examples with a learning rate of 0.000367. The data is stratified during training such that each batch contains equal amounts of data from the BindingDB set and the external dataset to most closely match the finetuning carried out in Jiménez-Luna et al.18. We evaluate performance when including the two-permutations of up to seven ligands from the external dataset in the finetuning dataset, see Figure 2. Identical test sets are used for both no-shot and few-shot learning for each congeneric series. The test set only includes pairs of ligands where at least one ligand in the pair was not utilized for the seven external ligands finetuning. We train and evaluate on both orderings of pairs of ligands.
Ablation Study
We probe the performance of our model in relation to the components of the loss function as well as the architecture of our model. Using the one additional ligand training and testing sets, we investigate the average performance of 25 models as we disable aspects of the model. Since our model utilizes a linear combination of several loss components we can investigate how each component contributes to test performance. During training, we evaluate RBFE performance when one of the loss hyperparameters (α, β, γ, and δ) is set to zero, keeping all other aspects of training the same. In order to accurately investigate the performance of the model when only trained for absolute binding free energy prediction, we set both α and δ to zero during training to disrupt the effects of the consistency loss encouraging the RBFE prediction to be the difference between the absolute binding free energies.
The contributions of the architecture to the performance of the model are also explored. The RBFE is dependent on the ordering of the ligands; if the ordering is swapped then the RBFE is multiplied by −1. Jiménez-Luna et al.18 claim that the latent space subtraction embeds this symmetry into the network architecture. We evaluate the utility of the latent space subtraction by concatenating rather than subtracting the latent spaces of the convolutional arms of the network. This requires that the fully connected layer of the network that predicts the RBFE doubles its input size. We further evaluate the importance of the Siamese network by instead training a CNN that takes in one protein-ligand pair and predicts the absolute binding free energy. RBFE is computed by subtracting the predicted absolute binding free energies of two ligands. When utilizing this architecture, we no longer enforce the LΔΔG and Lconsistency loss components. All other aspects of training are kept the same for all ablation studies.
We calculate the significance of the changes in Pearson’s R, RMSE, and MAE for both ΔΔG and ΔG values in relation to our default Siamese network via a two sided T-test. We account for multiple hypothesis testing by utilizing a p-value of 0.005 for all of our T-tests.
Protein Family Generalization Evaluation
Lead optimization requires precise predictions of the RBFE for all possible proteins and ligands. However, there is often very little experimental measurements of the protein of interest at the start of lead optimization. The worst case scenario is where there is no experimental measurements of the protein family of interest to train our RBFE prediction model. We perform a leave-one-family-out cross validation where we cluster by protein family to evaluate the model’s performance in the most challenging scenario on an entirely novel protein target. The Pfam database32 contains protein family annotations of all of the PDB accessible structures. The protein family annotations are used to label all of the proteins in the BindingDB dataset, where each protein can have more than one associated protein family. This provides us with 72 different protein families. Any protein family with fewer than seven ligands across all of the congeneric series is removed. This leaves us with 60 protein families. We create a test set for each of the protein families and its associated training set is the entire BindingDB dataset without that protein family. We evaluate the impact of including information about the left-out protein family by adding left-out ligand comparisons to the training data. The smallest finetuning includes two ligands from the left-out protein family; we continue adding two ligands to the training set and stop when six ligands from the left-out protein family have been added. Models are evaluated on the same test set regardless of how many ligands were included in training from the left-out protein family. Evaluations are carried out on all of the remaining ligands when we remove the six ligands used for the finetuning. Utilizing the trained model, we train for three epochs on the concatenation of the leave-one-out protein family training split and the added ligands from the left-out protein family, see Figure 2. No data stratification is used during training of the cross validation models as we determined that stratification hindered finetuning performance during our experiments. Only our Default2018 architecture is used for this cross validation evaluation due to computational constraints.
Results
Our convolutional Siamese network shows improved performance over the model developed by Jiménez-Luna et al.18 on the retrospective lead optimization dataset. However, we do not show the same increased performance over Jiménez-Luna et al.18 when evaluating on external datasets. Most of our loss components enhance the performance of our models for RBFE prediction, especially the Lconsistency component. Our models show reduced performance when evaluated on protein families that have never been seen in comparison to our retrospective lead optimization evaluation.
Enhanced Performance on Retrospective Lead Optimization
Both of our models predictions show higher correlation with the experimental RBFE (ΔΔG) and lower root mean square error (RMSE) on the RBFE predictions in comparison to the model developed by Jiménez-Luna et al.18 (Figure 3). The mean absolute error (MAE) of our models’ predictions show the same trend as the RMSE (Figure S2). Additionally, our models demonstrate a decreased variance across the 25 versions of the training and test splits. The models demonstrate a continual increase in performance as they are given more training information about the congeneric series. We find that the high parameter Dense model does better with lower amounts of congeneric series comparisons than the lower parameter, Default2018, model. The difference between the performance of the two CNN architectures decreases as more information is added to the training set of the models.
Figure 3:

Comparison of our models to Jiménez-Luna et al.18 on the additional ligands dataset. Error bars indicate ±1 standard deviation of 25 individual models (only 5 for Dense).
External Datasets Evaluation
The RBFE prediction of the model varies widely across the different test sets when no finetuning is performed. However, with increasing amounts of finetuning we see that the correlation with experimental affinity increases and the error decreases (Figure 4, S3, S4,5, S5, S6, S7, S8). Some congeneric series, especially those in the Schindler et al.2 dataset, show almost no improvement when adding more finetuning information. CDK2 shows nearly perfect correlation and zero error with no finetuning performed, likely due to the high ligand similarity to the BindingDB dataset (Table S3). A number of congeneric series (TYK2, PFKB3, SYK, and TNKS2) do not show monotonically increasing RBFE performance as more data is added to the finetuning dataset. Finetuning does not provide the same amount of RBFE prediction boost as demonstrated in Jiménez-Luna et al.18 on both the Mobley et al.22 and Wang et al.7 datasets (Figure 4).
Figure 4:

Pearson’s R on both the Mobley et al.22 (BRD4) and Wang et al.7 external datasets. We evaluate with and without finetuning (0). FEP performance as reported in Jiménez-Luna et al.18.
Figure 5:
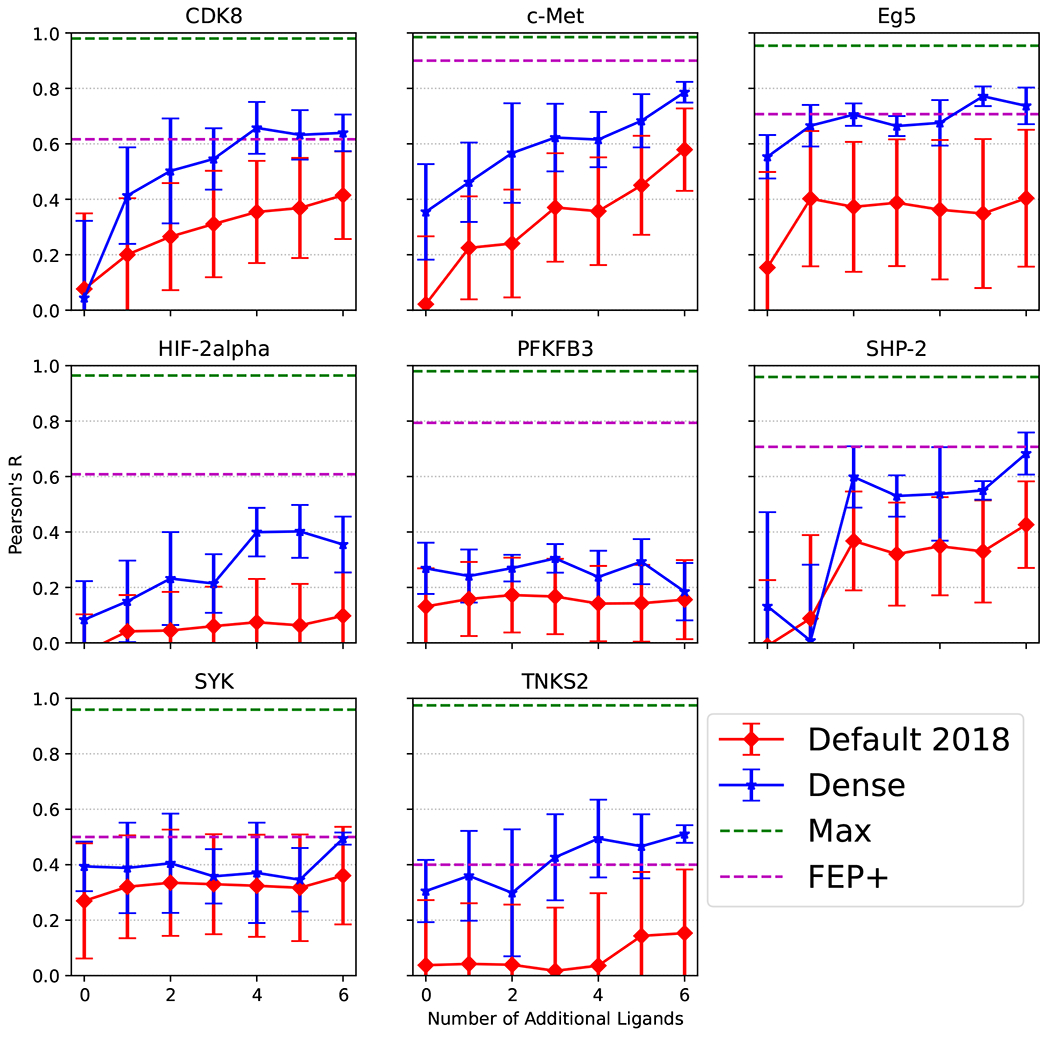
Pearson’s R on the Schindler et al.2 external dataset. We evaluate with and without finetuning (0). FEP+ performance given by Schindler et al.2. Max is the maximum possible correlation given the error in the experimental assay.
Ablation Study
Removing LΔΔG does not significantly decrease the performance of the RBFE predictions (Table 1), but increases the correlation and reduces the error of the absolute affinity prediction (Table S1). However, removing LΔG or Lconsistency drops the performance of the RBFE predictions by a considerable margin. The removal of Lrotation has little effect on the performance of the network, indicating that data augmentation may be all that is required to provide the necessary rotational invariance. When we remove LΔΔG and Lconsistency, the Siamese network no longer provides predictions that are correlated with the experimental affinity values, however, the errors of the predictions are only slightly increased from the baseline.
Table 1:
RBFE performance after ablating different components of the network on the 1 additional ligand set to determine their utility in the full network. Parentheses indicate the ±1 standard deviation of the 25 train/test versions. Bold indicates that it is not significantly different from the Standard model (p > 0.005).
| Ablation | Pearson’s R | RMSE (pK) | MAE (pK) |
|---|---|---|---|
| Standard | 0.553(±0.0233) | 1.11(±0.0309) | 0.82(±0.0187) |
| No LΔΔG | 0.551(±0.0202) | 1.12(±0.0248) | 0.829(±0.0179) |
| No LΔG | 0.459(±0.0238) | 1.27(±0.0289) | 0.945(±0.0182) |
| No LRotation | 0.556(±0.0188) | 1.11(±0.0233) | 0.819(±0.0162) |
| No LConsistency | 0.536(±0.021) | 1.14(±0.0356) | 0.842(±0.0186) |
| No LΔΔG, LConsistency | −0.0576(±0.136) | 1.24(±0.0143) | 0.908(±0.0144) |
| No LΔG, LConsistency | 0.456(±0.0231) | 1.28(±0.0319) | 0.95(±0.0233) |
| Concatenation | 0.554(±0.0134) | 1.11(±0.0223) | 0.821(±0.0174) |
| No Siamese Network | 0.5(±0.0347) | 1.15(±0.0362) | 0.854(±0.021) |
| Subtraction, Single-order | 0.512(±0.0213) | 1.17(±0.0213) | 0.877(±0.0151) |
| Concatentation, Single-order | 0.476(±0.023) | 1.21(±0.0253) | 0.907(±0.0182) |
Altering the Siamese network architecture does not affect performance as much as removing components of the loss function. If we exchange the latent space subtraction of the Siamese network for a concatenation, we do not see any change in performance of the model for RBFE prediction. However, we find that when training the Siamese network with latent space subtraction on only one ordering of each ligand pair, the network is better able to comprehend the negation of the ΔΔG when the ligand ordering is reversed (Table S2). This demonstrates that the latent space subtraction better embeds the symmetry of the ΔΔG prediction problem in comparison to latent space concatenation. We train a single-arm convolutional architecture to predict the absolute affinity values using the same training set (No Siamese Network in Table 1). The single-arm convolutional architecture’s absolute affinity predictions are subtracted for pairs of ligands to produce RBFE predictions. The single-arm convolutional architecture is worse than the CNN Siamese network at both absolute and relative binding affinity prediction.
Generalization to new Protein Families
When the Default2018 Siamese network is trained on all of the BindingDB dataset, excluding the left out protein family, and evaluated on the left out protein family, we find that the average RBFE prediction correlation across all of the protein families is nearly zero. (Figure 6). The variance across protein families is quite large, with some protein families having near perfect predictions and other protein families having extremely poor predictive performance.
Figure 6:
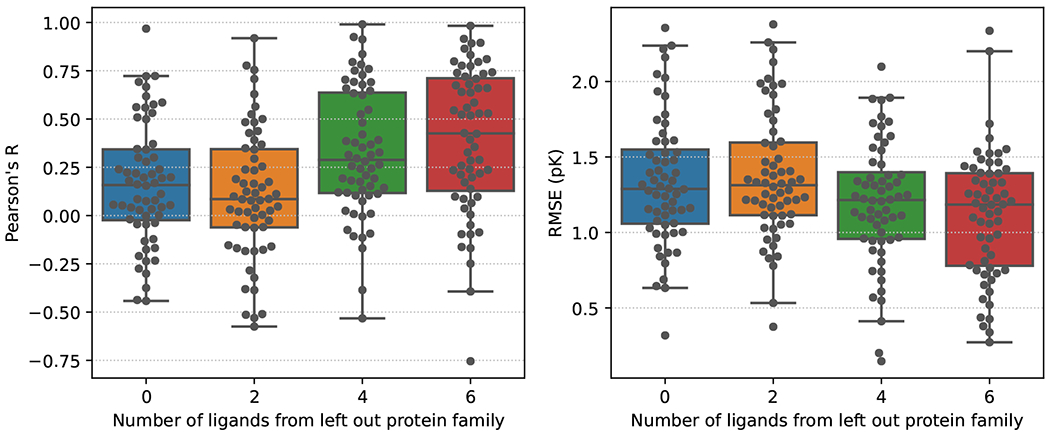
Average performance on left out protein family for the protein families in the BindingDB dataset. The predictive power of the model increases as we include information from the left out test set.
Adding information to the training set about the left out protein family tends to increase the average correlation and decrease the average error across protein families, (Figure 6 and S9). However, only adding one pair of ligands from the left out protein family does not seem to help the performance of the model. We need at least 4 ligands from the protein family that we are evaluating on to see an increase in our RBFE prediction performance. Adding ligands from the left out protein family to our training data seems to have a greater impact on the correlation of the RBFE predictions rather than the error.
Discussion
Our models show higher correlation with experimental RBFE and lower errors of prediction than the model developed by Jiménez-Luna et al.18 when evaluated on the additional ligands dataset. We see an increase in model performance as the amount of information about each congeneric series is increased. Our models do not show diminishing returns as more ligands are added to the training set, unlike the model developed by Jiménez-Luna et al.18. Our highest parameter CNN architecture, Dense, was able to outperform the lower parameter Default2018 architecture on the smallest training set. However, the Dense model is initialized with weights from an absolute binding affinity prediction task that provide the model with much greater initial knowledge of the problem than a randomly initialized network. When using the Dense architecture with random initialization, the model had lower RBFE prediction performance than the randomly initialized Default2018 model (results not shown). The Dense model was unable to train effectively without L2 regularization (weight decay), likely due to the small amount of data and the large amount of parameters in the model.
Only some components of the loss function are contributing to the models RBFE prediction performance. The removal of LΔΔG does not have a large impact on model performance indicating LΔG and Lconsistency contribute significantly to the RBFE prediction performance. However, it is important to note the Lconsistency encourages the model to make the ΔΔG prediction identical to the differences in absolute binding affinity predictions which will provide some notion of ΔΔG loss. The removal of the Lrotation component did not significantly change the performance of the model, which may indicate some isotropic properties of the network architecture. The latent space structure imposed by the subtraction operation did not result in improved performance when using both ligand orderings for training. However, training on only one ordering of ligand pairs demonstrates that latent space subtraction is able to embed the RBFE ligand ordering symmetry. This symmetry embedding can be learned by a network using latent space concatenation when using the freely available other orderings during training. The Siamese architecture enables understanding of ordering within congeneric series, which is ignored when only training for absolute affinity prediction. Without the Siamese architecture, the performance of the model suffers on both relative and absolute binding affinity prediction. This may be due to both the symmetry embedding of the network architecture and the increased regularization of the latent space that the Siamese architecture imposes.
The RBFE model has difficulty generalizing to new datasets. We find that our model does not perform as well as the Siamese network proposed by Jiménez-Luna et al.18 when evaluated on the external datasets from Mobley et al.22 and Wang et al.7, in most cases. We find high protein and ligand similarity between the BindingDB Congeneric Series set and the external datasets from Mobley et al.22 and Wang et al.7. We provide the minimum protein distance, determined via a global alignment with no parameters and no gap penalties (Biopython.align.globalxx), and highest ligand similarity, determined with RDKit’s FingerprintSimilarity function in Table S3. BACE has the minimum protein distance with a protein in the BindingDB dataset and both CDK2 and PTP1B have greater than 95% of their ligands in the BindingDB dataset. This is likely why the correlation and error on CDK2 are nearly perfect with no finetuning. We would expect similar results for PTP1B since it shares a nearly identical minimum protein distance and similar percentage of ligands found in the BindingDB set, but PTP1B has lower correlation and higher error than CDK2 in the no-shot evaluation. Our models do not show the same level of RBFE prediction correlation as Jiménez-Luna et al.18, however, the RMSE of the predictions is about the same or less. Correlation is a poor predictor of relative binding affinity performance, due to the low range of affinities in a congeneric series.7,33 If, for instance, each ligand in a congeneric series has an identical affinity value, then there is no way to measure a predictive Pearson’s R correlation. Therefore, it is difficult to determine if the model built by Jiménez-Luna et al.18 demonstrates more generalizability than our models. When we evaluate our Siamese network on the more difficult Schindler et al.2 dataset, we again see much variability in our models performance across the different targets. Our model is unable to match the performance of the FEP+ model in correlation of prediction (Figure 5, S5, and S6) without using the largest amount of finetuning we explored. Examining the RMSE of the RBFE predictions shows the Siamese network outperforming the FEP+ method on all of the targets, when all of the finetuning data is introduced. The lower correlation and lower error are due to our Siamese network predicting values around the mean of the data. FEP predictions are not dependent on the labels of the data, since there is no training necessary, and therefore would eliminate these sort of predictions.
Despite good intra-congeneric series performance, our Siamese network does not generalize well to new protein families suggesting the approach is best used later in the lead optimization process. We do show that adding information on the left out protein family to the training set improves the performance of the RBFE predictions. However, noticeable improvements would require the experimental binding affinity determination of at least four ligands for the new protein family.
Work still needs to be done on both absolute and relative binding affinity predictors to ensure that they are learning robust models of the intermolecular interactions. Future work should focus on including additional symmetries involved in RBFE in the predictive models, such as cycle closure.34,35 Including the Lconsistency term, focused on the symmetry of the relative and absolute binding affinity prediction, was able to increase the performance of our RBFE predictions, therefore including higher order symmetries of the RBFE problem may enhance the performance of future models. Rotational symmetries of the inputs can be addressed with SE(3)-equivariant convolutions,36 rather than a rotational loss. Adding uncertainty quantification37–39 to the predictive model could enable large performance improvements with fewer ligands during finetuning by focusing on the ligands with the greatest uncertainty according to the RBFE model.
Conclusion
Convolutional Siamese networks are capable of RBFE prediction (Figure 3). We find that higher capacity CNN models used in the arms of the Siamese network increases the predictive performance of the model. Our multitask loss is able to boost the performance of the RBFE prediction in comparison to only calculating a loss on the RBFE (Table 1). This indicates that RBFE prediction is aided by increased regularization of the CNN latent space. The latent space subtraction of the Siamese network is able to implicitly embed the reverse symmetry of the RBFE prediction. However, the reverse symmetry is learnable without the latent space subtraction when the model is trained on both orderings of ligands for RBFE prediction. We note that our convolutional Siamese network’s performance is less consistent when applied to out of distribution examples (Figures 4, 5, 6). The Siamese network can adapt to out of distribution examples via injection of training examples from the new distribution through either finetuning or baseline training. Our model can make RBFE predictions in significantly less time than FEP methods, but requires experimentally determined free energies of several ligands in a congeneric series to outperform the RBFE predictions of FEP methods. The convolutional Siamese network provides a faster alternative to more expensive FEP methods later in lead optimization when affinity information has been experimentally determined for more ligands in the congeneric series. Improvements to the RBFE prediction may be found by exploiting other symmetries of RBFE, like cycle consistency. We provide the source code and data for use at our github repo: www.github.com/drewnutt/DDG/
Supplementary Material
Acknowledgement
The authors thank Paul Francoeur and Jonathan King for their comments during the preparation of the manuscript.
This work is supported by the R35GM140753 from the National Institute of General Medical Sciences and CHE-2102474 from the National Science Foundation.
Data and Software Availability:
Our dataset filtering, models, and training procedure are open source and available under a BSD 3-Clause license. Everything is available at www.github.com/drewnutt/DDG/.
References
- (1).Williams-Noonan BJ; Yuriev E; Chalmers DK Free energy methods in drug design: Prospects of “alchemical perturbation” in medicinal chemistry: miniperspective. Journal of medicinal chemistry 2018, 61, 638–649. [DOI] [PubMed] [Google Scholar]
- (2).Schindler CE; Baumann H; Blum A; Böse D; Buchstaller H-P; Burgdorf L; Cappel D; Chekler E; Czodrowski P; Dorsch D, et al. Large-scale assessment of binding free energy calculations in active drug discovery projects. Journal of Chemical Information and Modeling 2020, 60, 5457–5474. [DOI] [PubMed] [Google Scholar]
- (3).Steinbrecher T; Labahn A Towards accurate free energy calculations in ligand protein-binding studies. Current medicinal chemistry 2010, 17, 767–785. [DOI] [PubMed] [Google Scholar]
- (4).Zwanzig RW High-temperature equation of state by a perturbation method. I. Nonpolar gases. The Journal of Chemical Physics 1954, 22, 1420–1426. [Google Scholar]
- (5).Wang L; Chambers J; Abel R Biomolecular Simulations; Springer, 2019; pp 201–232. [Google Scholar]
- (6).Abel R; Wang L; Harder ED; Berne B; Friesner RA Advancing drug discovery through enhanced free energy calculations. Accounts of chemical research 2017, 50, 1625–1632. [DOI] [PubMed] [Google Scholar]
- (7).Wang L; Wu Y; Deng Y; Kim B; Pierce L; Krilov G; Lupyan D; Robinson S; Dahlgren MK; Greenwood J, et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. Journal of the American Chemical Society 2015, 137, 2695–2703. [DOI] [PubMed] [Google Scholar]
- (8).Genheden S; Ryde U The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert opinion on drug discovery 2015, 10, 449–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Srinivasan J; Cheatham TE; Cieplak P; Kollman PA; Case DA Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate- DNA helices. Journal of the American Chemical Society 1998, 120, 9401–9409. [Google Scholar]
- (10).Kollman PA; Massova I; Reyes C; Kuhn B; Huo S; Chong L; Lee M; Lee T; Duan Y; Wang W, et al. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Accounts of chemical research 2000, 33, 889–897. [DOI] [PubMed] [Google Scholar]
- (11).Wang E; Sun H; Wang J; Wang Z; Liu H; Zhang JZ; Hou T End-point binding free energy calculation with MM/PBSA and MM/GBSA: strategies and applications in drug design. Chemical reviews 2019, 119, 9478–9508. [DOI] [PubMed] [Google Scholar]
- (12).Trott O; Olson AJ AutoDock Vina: improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. Journal of computational chemistry 2010, 31, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Francoeur PG; Masuda T; Sunseri J; Jia A; Iovanisci RB; Snyder I; Koes DR Three-dimensional convolutional neural networks and a cross-docked data set for structure-based drug design. Journal of Chemical Information and Modeling 2020, 60, 4200–4215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Feinberg EN; Sur D; Wu Z; Husic BE; Mai H; Li Y; Sun S; Yang J; Ramsundar B; Pande VS PotentialNet for molecular property prediction. ACS central science 2018, 4, 1520–1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Jiménez J; Skalic M; Martinez-Rosell G; De Fabritiis G K deep: protein–ligand absolute binding affinity prediction via 3d-convolutional neural networks. Journal of chemical information and modeling 2018, 58, 287–296. [DOI] [PubMed] [Google Scholar]
- (16).Stepniewska-Dziubinska MM; Zielenkiewicz P; Siedlecki P Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics 2018. , 34, 3666–3674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Ballester PJ; Mitchell JB A machine learning approach to predicting protein–ligand binding affinity with applications to molecular docking. Bioinformatics 2010, 26, 1169–1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Jiménez-Luna J; Pérez-Benito L; Martínez-Rosell G; Sciabola S; Torella R; Tresadern G; De Fabritiis G DeltaDelta neural networks for lead optimization of small molecule potency. Chemical science 2019, 10, 10911–10918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Liu T; Lin Y; Wen X; Jorissen RN; Gilson MK BindingDB: a web-accessible database of experimentally determined protein–ligand binding affinities. Nucleic acids research 2007, 35, D198–D201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Spitzer R; Jain AN Surflex-Dock: Docking benchmarks and real-world application. Journal of computer-aided molecular design 2012, 26, 687–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).RDKit: Open-source cheminformatics. http://www.rdkit.org, [Online; accessed 11-April-2013].
- (22).Mobley DL; Gilson MK Predicting binding free energies: frontiers and benchmarks. Annual review of biophysics 2017, 46, 531–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Bromley J; Bentz JW; Bottou L; Guyon I; LeCun Y; Moore C; Säckinger E; Shah R Signature verification using a “siamese” time delay neural network. International Journal of Pattern Recognition and Artificial Intelligence 1993, 7, 669–688. [Google Scholar]
- (24).Song L; Gong D; Li Z; Liu C; Liu W Occlusion robust face recognition based on mask learning with pairwise differential siamese network. Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019; pp 773–782. [Google Scholar]
- (25).Simonovsky M; Meyers J DeeplyTough: learning structural comparison of protein binding sites. Journal of chemical information and modeling 2020, 60, 2356–2366. [DOI] [PubMed] [Google Scholar]
- (26).Koch G; Zemel R; Salakhutdinov R, et al. Siamese neural networks for one-shot image recognition. ICML deep learning workshop. 2015. [Google Scholar]
- (27).Sunseri J; Koes DR libmolgrid: Graphics Processing Unit Accelerated Molecular Gridding for Deep Learning Applications. Journal of Chemical Information and Modeling 2020, 60, 1079–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).McNutt AT; Francoeur P; Aggarwal R; Masuda T; Meli R; Ragoza M; Sunseri J; Koes DR GNINA 1.0: molecular docking with deep learning. Journal of cheminformatics 2021, 13, 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Huang G; Liu Z; Van Der Maaten L; Weinberger KQ Densely connected convolutional networks. Proceedings of the IEEE conference on computer vision and pattern recognition. 2017; pp 4700–4708. [Google Scholar]
- (30).Glorot X; Bengio Y Understanding the difficulty of training deep feedforward neural networks. Proceedings of the thirteenth international conference on artificial intelligence and statistics. 2010; pp 249–256. [Google Scholar]
- (31).Kingma DP; Ba J Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 2014, [Google Scholar]
- (32).Mistry J; Chuguransky S; Williams L; Qureshi M; Salazar GA; Sonnhammer EL; Tosatto SC; Paladin L; Raj S; Richardson LJ, et al. Pfam: The protein families database in 2021. Nucleic Acids Research 2021, 49, D412–D419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Brown SP; Muchmore SW; Hajduk PJ Healthy skepticism: assessing realistic model performance. Drug discovery today 2009, 14, 420–427. [DOI] [PubMed] [Google Scholar]
- (34).Wang L; Deng Y; Knight JL; Wu Y; Kim B; Sherman W; Shelley JC; Lin T; Abel R Modeling local structural rearrangements using FEP/REST: application to relative binding affinity predictions of CDK2 inhibitors. Journal of chemical theory and computation 2013, 9, 1282–1293. [DOI] [PubMed] [Google Scholar]
- (35).Wang L; Lin T; Abel R Cycle closure estimation of relative binding affinities and errors. 2014.
- (36).Weiler M; Geiger M; Welling M; Boomsma W; Cohen T 3d steerable cnns: Learning rotationally equivariant features in volumetric data. arXiv preprint arXiv:1807.02547 2018, [Google Scholar]
- (37).Liu JZ; Lin Z; Padhy S; Tran D; Bedrax-Weiss T; Lakshminarayanan B Simple and principled uncertainty estimation with deterministic deep learning via distance awareness. arXiv preprint arXiv:2006.10108 2020, [Google Scholar]
- (38).Soleimany AP; Amini A; Goldman S; Rus D; Bhatia SN; Coley CW Evidential deep learning for guided molecular property prediction and discovery. ACS central science 2021, 7, 1356–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).van Amersfoort J; Smith L; Jesson A; Key O; Gal Y Improving deterministic uncertainty estimation in deep learning for classification and regression. arXiv preprint arXiv:2102.11409 2021, [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Our dataset filtering, models, and training procedure are open source and available under a BSD 3-Clause license. Everything is available at www.github.com/drewnutt/DDG/.


