Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2024 Jan 9.
Published in final edited form as: J Chem Inf Model. 2022 Dec 6;63(1):67–75. doi: 10.1021/acs.jcim.2c01213

LAST: Latent Space Assisted Adaptive Sampling for Protein Trajectories

Hao Tian †, Xi Jiang ‡, Sian Xiao †, Hunter La Force †, Eric C Larson , Peng Tao †
PMCID: PMC9904845  NIHMSID: NIHMS1863727  PMID: 36472885

Abstract

Molecular dynamics (MD) simulation is widely used to study protein conformations and dynamics. However, conventional simulation suffers from being trapped in some local energy minima that are hard to escape. Thus, most computational time is spent sampling in the already visited regions. This leads to an inefficient sampling process and further hinders the exploration of protein movements in affordable simulation time. The advancement of deep learning provides new opportunities for protein sampling. Variational autoencoders are a class of deep learning models to learn a low-dimensional representation (referred to as the latent space) that can capture the key features of the input data. Based on this characteristic, we proposed a new adaptive sampling method, latent space assisted adaptive sampling for protein trajectories (LAST), to accelerate the exploration of protein conformational space. This method comprises cycles of (i) variational autoencoders training, (ii) seed structure selection on the latent space and (iii) conformational sampling through additional MD simulations. The proposed approach is validated through the sampling of four structures of two protein systems: two metastable states of E. Coli adenosine kinase (ADK) and two native states of Vivid (VVD). In all four conformations, seed structures were shown to lie on the boundary of conformation distributions. Moreover, large conformational changes were observed in a shorter simulation time when being compared with structural dissimilarity sampling (SDS) and conventional MD (cMD) simulations in both systems. In metastable ADK simulations, LAST explored two transition paths toward two stable states while SDS explored only one and cMD neither. In VVD light state simulations, LAST was three times faster than cMD simulation with a similar conformational space. Overall, LAST is comparable to SDS and is a promising tool in adaptive sampling. The LAST method is publicly available at https://github.com/smu-tao-group/LAST to facilitate related research.

Graphical Abstract

graphic file with name nihms-1863727-f0001.jpg

1. Introduction

Molecular dynamics (MD) simulation has wide application on the study of protein conformations and dynamics.1–3 Recent developments in bio-computing, such as Anton,4 AMBER5 and OpenMM,6 have enabled the simulation time scale to milliseconds, which promotes the research in sampling protein motions and structure landscapes.7,8 However, the time scales of many protein functions exceed the time scales achievable through traditional MD simulations. Moreover, protein sampling suffers from being trapped within local energy minima, proving difficult to escape.9,10 As a result, most of the computational time is typically spent in sampling previously visited regions, which hinders efficient exploration of protein conformational space.

Many enhanced sampling methods have been developed to address this issue. These methods can be classified into two types. In the first type, biasing potentials are introduced to expand the sampling space, such as metadynamics11,12 and Gaussian-accelerated MD.13 In the second type, seed structures are selected as restarts for iterative MD simulations. This is referred to as adaptive sampling and numerous methods have been proposed that differ in seed selection methods. Markov state models have been applied to cluster conformations into microstates;14 parallel cascade selection MD (PaCS-MD)15 and nontargeted PaCS-MD16 calculates the root-mean-square deviation (RMSD) to select top snapshots; frontier expansion sampling17 conducts dimensionality reduction with principal component analysis and Gaussian mixture models to select frontier structures; structural dissimilarity sampling (SDS)18 selects new seeds based on principal component analysis.

Recent innovations in deep learning have provided new insights into sampling protein conformational space.19,20 Autoencoders (AEs) and variational autoencoders (VAEs) are a class of deep learning models that learn a representation (encoding) which can capture the key features of input data. Several studies have demonstrated the success of AEs and VAEs in their applications to protein conformations and functions.2,21–23 In our previous work,24 we showed that VAEs are capable of learning a low-dimensional representation (referred to as the latent space) of protein systems. Through a quantitative study, the learned latent space is shown to be able to represent conformational characteristics. This property indicates that the larger differences two protein conformations have, the farther their corresponding latent points are from each other.

In this study, we proposed a new adaptive sampling method, latent space assisted adaptive sampling for protein trajectories (LAST), to accelerate the exploration of protein conformational space. Initially, a short MD simulation is conducted starting from the crystal structure. Afterwards, the following steps are repeated iteratively until certain criteria are met. First, a VAE is trained using sampled protein conformations. Then, seed structures are selected in the learned latent space. Finally, starting from these selected seed structures, additional simulations are conducted to sample more protein conformations that will be used in the next round. To quantify the performance, we applied LAST on four conformations in two protein systems: two metastable states of E. Coli adenosine kinase (ADK) and two native states of Vivid (VVD). To better explore the protein conformational space, ADK conformations sampled from the simulation were projected onto its two intrinsic angles, and VVD conformations were projected onto the space using two RMSD values with reference to the two native structures in dark and light states, respectively. These collective variables are unrelated and unknown to the VAE models. Our results showed that seed structures were consistently located on the boundary of sampled conformational distributions in all four conformations regardless of protein projection methods. We further compared the sampling efficiency among LAST, SDS and conventional MD (cMD). In both systems, large conformational changes were observed in a shorter time in LAST simulations. To be specific, LAST explored two transition paths toward two stable states while SDS explored one and cMD neither in the metastable ADK simulations. In VVD simulations, LAST only took one third of cMD simulation time to discover a similar conformational space.

2. Methods

2.1. Variational Autoencoder

An autoencoder is a type of deep learning models that aims to encode a high-dimensional input to a low-dimensional latent space through an encoder module and decode it back to the original dimensions through a decoder module. By minimizing the differences between inputs and outputs, known as reconstruction loss, the latent space is expected to learn a low-dimensional representation of the input space. However, the latent space in an AE is not well-constrained and leads to unsatisfying results when sampling in the latent space.25 To overcome this issue, variational autoencoders add an optimization constraint on the latent space to follow a certain distribution.

The encoder module qϕ(z|x) is an inference model that transforms data x into output latent variable z, being parametrized with ϕ. In reverse, the decoder module pθ(x|z) is a generative model that transforms latent variable z into output data x^, being parametrized with θ. Both models are trained simultaneously with a joint distribution as p(x, z) = pθ(x|z)p(z). p(z) is the constraint distribution for latent space and typically is chosen as a normal distribution.26 The tractable variational Bayes approach is used to approximate the intractable posterior pθ(z∣x)=pθ(x∣z)p(z)/∫pθ(x∣z)p(z)dz by maximizing the Evidence Lower Bound (ELBO):

ℒ(ϕ,θ;x)=Eqϕ(z∣x)logpθ(x∣z)−KLqϕ(z∣x)∥p(z)≤logpθ(x) 1

where KL is the Kullback-Leibler divergence.

In our implementation, the VAE model is developed using Keras package27 with Tensorflow backend.28

2.2. Molecular Dynamics Simulations

The initial structures of four conformations in two protein systems: two metastable states (PDB ID 1DVR and 2AK3) of E. Coli adenosine kinase (ADK) and two native states (PDB ID 2PD7 and 3RH8) of Vivid (VVD) were taken from the Protein Data Bank (PDB)29 . For each conformation, ligands and crystal waters were removed and chain A was extracted as the starting structure. The system was further solvated in a box of TIP3P water molecules and neutralized using Na+ and Cl−. Simulation files were generated using tleap30 with the AMBER ff14SB force filed.31 100 ps NVT Langevin MD simulations were carried out, followed by 200 ps NPT simulations at 1 atm and 300 K. In each round of LAST method, one 100 ps MD simulation was conducted for each seed structure. Particle Mesh Ewald (PME) algorithm was used to calculate long-range electrostatic interactions. The simulation time step was set as 2 fs. All simulations were conducted with OpenMM 7.6

2.3. Latent Space Assisted Adaptive Sampling for Protein Trajectories

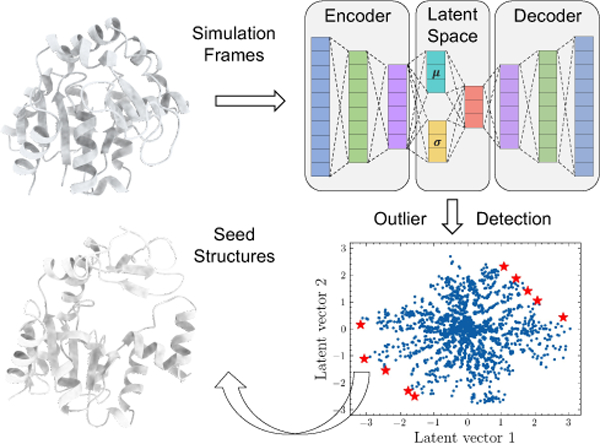
LAST method includes three steps, and its workflow is shown in Figure 1. First, a variational autoencoder is trained using all previous simulations. Second, the lowest-probability samples are selected on the latent space and their corresponding protein structures are treated as seeds. Third, additional MD simulations are conducted from seed structures.

Figure 1:

Figure 1:

Open in a new tab

The workflow of LAST method. To begin with, a short MD simulation is conducted from crystal structures. All sampled conformations are stored in a pool. In each round, if there is no increase of maximum RMSD of the new sampled conformations in a consecutive of 5 rounds, the workflow stops. Otherwise, a VAE model is trained using all conformations in the pool. Then, the seeds are selected on the latent space. For each of selected seed, new MD simulations are conducted, and the sampled conformations are stored in the pool.

VAE Training

In each iteration, some preprocessing procedures are needed. The simulation trajectories are firstly aligned to the first frame and heavy atoms are extracted with Cartesian coordinates being expanded as a feature vector (Figure 1A-B). Then, each feature is transformed to a range of 0 to 1 using min-max linear scaling, which is used to construct a dataset for VAE training.

The architecture of VAE model is shown in Figure 1C. In the current study, we design the encoder model being composed of three hidden layers with size of 512, 128 and 32 and decoder model with size of 32, 128 and 512. The number and size of hidden layers can be adjusted based on the size of proteins. The dimension of latent space is set as two for the simplicity and ease of visualization.

Seeds Selection

Appropriate seed selection method is needed to expedite the sampling of protein conformational space. In LAST, seeds are selected on the two-dimensional learned latent space of VAE, which has two important characteristics to enable an efficient seeds selection. First, as demonstrated in our previous work, the distance between two data points on the latent space is meaningful. Two structurally similar proteins have a shorter distance between their corresponding latent vectors. Second, the sampling distribution of latent space in the VAE is similar to, but not strictly follow a normal distribution. It is likely that the KL divergence term in the loss function contributes to the normal distribution, and the reconstruction loss component in the loss function may contribute to the deviation from the normal distribution. As for the distribution of the VAE latent space of protein conformations, the most common protein structures are encoded in the center of the latent space while structurally different proteins are encoded on the boundary. In a data distribution, samples with the lowest probabilities refer to those points that differ significantly from other data. Based on the above two points, it is reasonable to treat the lowest-probability samples on the latent space as seeds to accelerate conformational space exploration, as their conformations deviate the majority of the sampled ones.

To implement the seed selection method, we propose three improvements to make LAST computationally efficient.

  1. Latent space of VAE is not strictly normal after optimization even though the normality is incentivized in the loss function. Therefore, a non-parametric multivariate kernel density estimator, instead of multivariate normal density function, is used to fit the latent space. The estimator is developed in Python statsmodels library.32

  2. Latent space distribution might be skewed so that the top N lowest-probability samples with the smallest probability densities tend to gather on one side of distribution. To avoid the above issue, the cumulative distribution function (CDF) of the fitted non-parametric multivariate kernel density estimator on the latent space, instead of probability density, is applied to guarantee that samples from both sides of CDF (values close to 0 and 1) are equally selected. In this case, the first order of the density estimator was accumulated in the latent space.

  3. Protein conformations corresponding to the lowest-probability samples can be located and selected based on data index. These protein conformations might be similar to each other, resulting in sampling repeated conformational space from MD simulations starting from these conformations. Thus, to further boost sampling efficiency, we require new seed structures to have at least 1Å RMSD with all previously selected seeds.

One example of seeds selection result is shown in Figure 1D, where seeds are highlighted in red stars in the latent space visualization.

Additional MD Simulations

Short MD simulations are conducted in each round. In the current study, 10 seeds are selected in one round and 100ps simulation is done starting from each seed. Thus, the total simulation time in each round is 1ns. The detail of these simulations is described in section 2.2.

The above three steps are iteratively done until convergence. Here, we design the convergence criterion by calculating the mean RMSD of Cα atoms with regard to the starting protein structure. The iterative sampling process is terminated once the mean RMSD stops to increase for successive five rounds or reaches the maximum round number.

Algorithm 1 Latent space assisted adaptive sampling for protein trajectories                           ¯¯    Prepare simulation files.    Conduct 100 ps NVT and 200 ps NPT simulations.    while iteration is not reaching the maximum round do           Align trajectories and extract Cartesian coordinates.           Train a VAE model.           Fit latent space with a non-parametric multivariate kernel density estimator.           Select top 10 lowest-probability samples based on CDF and get seed structures.           Conduct 100 ps simulation for each seed.           if mean RMSD is converged then                  Stop iteration.       end if     end while                                                                                                                                                                  ¯

The LAST algorithm is summarized in Algorithm 1 with codes are freely available at the GitHub site of https://github.com/smu-tao-group/LAST.

2.4. Structural Dissimilarity Sampling

Structural dissimilarity sampling (SDS) is an efficient method to quickly expand protein conformational distributions toward unvisited conformational spaces. Similar to LAST, SDS iterates between (1) arrangement of seed structures for a diverse distribution in the frontiers of conformational regions and (2) conduction of additional MD simulations based on these selected structures. In this work, SDS was applied to each protein system and the sampled protein conformational spaces were compared with the LAST and cMD results under the same simulation time. The SDS was implemented using scripts from Zhang and Gong17 under https://github.com/Gonglab-THU-MD/Frontier-Expansion-Sampling.

3. Results

Four structures of two protein systems (ADK and VVD) were prepared for MD simulations as described in section 2.2. For each protein structure, 100 ps NVT and 200 ps NPT simulations were conducted. During the iterative process, all previous simulations were aligned to the first frame with Cartesian coordinates of heavy atoms being extracted as a feature vector to represent protein conformation. Afterwards, a variational autoencoder model was trained. 10 seed structures were selected with additional 100 ps simulation starting from each of them. Therefore, each iteration takes 1 ns simulation time.

ADK protein is composed of a rigid CORE domain, a lid-shaped ATP-binding domain (LID) and an AMP-binding domain (NMP). Many computational studies have shown ADK to carry out large conformational transitions between the closed state to the open state during the ATP-ADP catalyzation process.33,34 Four vectors that form NMP-CORE and LID-CORE angles, as shown in Figure S1, have been widely used to characterize ADK protein conformation. VVD is a light-oxygen-voltage domain that undergoes global conformational changes upon perturbation. VVD is shown to be flexible in the native light state and relatively stable in the native dark state.34 ADK and VVD structures are illustrated using ChimeraX35 (Figure 2).

Figure 2:

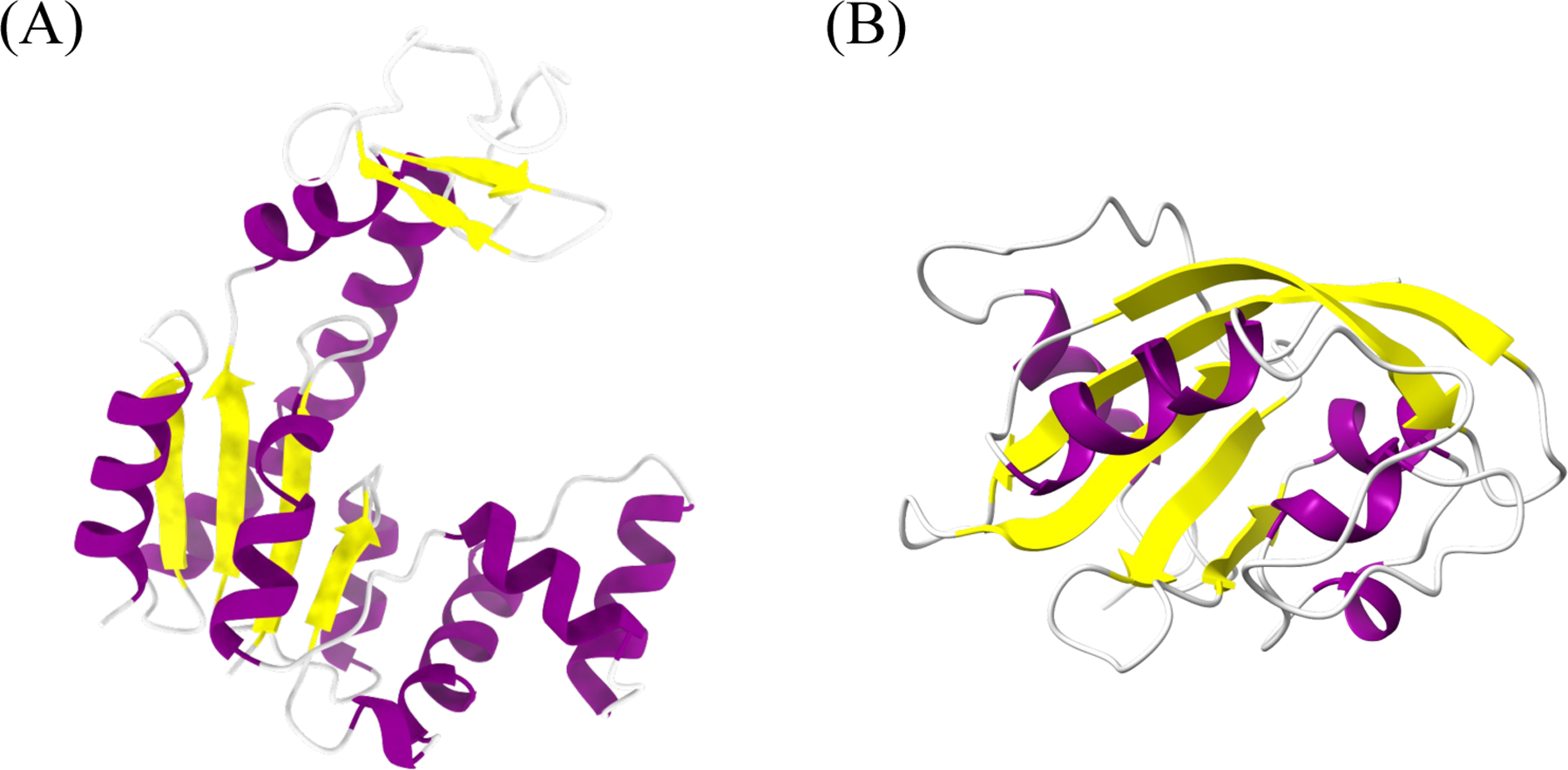
Figure 2:

Open in a new tab

Structures of (A) ADK and (B) VVD. ADK is composed of a CORE domain, a LID domain and a NMP domain. LID-CORE and NMP-CORE angles are calculated by four vectors to represent protein conformations. Both proteins are colored at secondary structure level using ChimeraX.

Proper low-dimensional protein representations are needed to evaluate the quality of seed selection. In the current study, ADK protein structure is projected to LID-CORE and NMP-CORE 2D angle plot. We followed the same reside selection rule to calculate vectors and angles.24 For VVD structure, 2D root-mean-square deviation (RMSD) with reference to the native dark and light structures was used to show the sampled protein conformational space.

Both the angle plot in ADK and RMSD plot in VVD were used to display the protein conformation of seed structures (Figure 3). In each subplot, seed structures are highlighted as red stars. In two metastable ADK conformations (Figure 3A-B), seed structures mainly locate in the less sampled regions with small or large LID/NMP angles. This indicates that the variational autoencoder can capture the structural differences of protein conformations within the learned latent space. In the native dark and native light VVD conformations (Figure 3C-D), seed structures are also shown to be evenly distributed in the boundary of protein conformational space defined by RMSD to two native VVD structures.

Figure 3:

Figure 3:

Open in a new tab

Seed structure distribution on the low-dimensional protein representations. (A-B) ADK protein conformations are represented in LID-CORE and NMP-CORE angle vectors. (C-D) VVD protein conformation are represented in RMSDs with regard to the native dark and native light states. Seed structures are represented in red stars. The analysis in these plots was carried out after 7 rounds of LAST simulations for illustration purpose.

To compare the effectiveness of LAST to conventional molecular dynamics simulations, the sampled protein conformational space in each round of LAST method is displayed together with cMD sampled conformations. Figure 4 shows the protein conformations in 1 ns, 5 ns, 10 ns and 15 ns for both LAST and cMD. It is shown that under the same simulation time, LAST can explore more protein conformations than cMD. Moreover, the trained variational autoencoder can consistently learn a low-dimensional protein representation in the latent space, regardless of the growing number of simulations and changing shape of conformational space, and guide MD simulations to explore less sampled regions. In contrast, there are limited new conformations being explored in cMD simulations from 10 ns to 15 ns, indicating that it might be trapped in a local energy minimum.

Figure 4:

Figure 4:

Open in a new tab

Comparison of ADK conformational spaces of LAST and cMD. Protein conformations are shown in blue at iteration 1, 5, 10 and 15 in LAST method. Protein conformations produced by cMD are shown in grey with the same simulation time. In each round LAST explored a larger conformational space compared with cMD.

We continued the LAST simulation of ADK until the convergence of LAST. For comparison, both SDS and cMD simulations were conducted under the same simulation time. The sampled protein conformational spaces are shown in Figure 5A. The LAST sampling method took 22 iterations (22 ns simulation time) and explored two paths from the metastable state to the two native states. This aligns with the computational finding that ADK protein undergoes conformational transitions between the open and the closed states.36 Moreover, the sampled conformational space in LAST spans in the intermediate regions between the closed and open states, with some coverage in the open state and no coverage in the closed state. Meanwhile, SDS only explored one path towards the open state, and cMD mostly sampled the overlap of LAST and SDS methods. The sampled two transition pathways align well with a previous study,33 in which a 200 ns AMBER simulation was conducted showing that the LID-open NMP-closed metastable ADK structure could visit both native open and closed states. The same experimental setting was applied to the open and closed states of ADK protein. While these two states are stable, LAST can still cover the majority of cMD results and sample more conformations when being compared with SDS simulations, as shown in Figure S2. The sampled conformations in the LID-open NMP-closed metastable ADK structure were also projected using the first two components in PCA (Figure S3). In contrast to Figure 5A, the SDS sampled conformations do not fully overlap with LAST. Instead, both methods sampled different conformational regions and are complementary to the cMD results.

Figure 5:

Figure 5:

Open in a new tab

Explored conformational spaces of (A) ADK and (B) SDS proteins using LAST (red dashed line), SDS (blue dotted line) and cMD (black solid line) methods. LAST took 22 and 30 iterations to complete for ADK and SDS proteins, respectively. In each system, SDS and cMD simulations were conducted under the same simulation time. In the ADK conformational space, LAST explored two paths to the open and closed states, while SDS explored one path towards the open state.

There are 120 ADK structures in the PDB. The minimum RMSDs in LAST and SDS produced trajectories were calculated with reference to each ADK structure and are listed in Table S2. More than two thirds (84 out of 120) of minimum RMSDs in LAST are less than those in SDS. On average, the minimum RMSD in LAST is 0.07 Å less than that in SDS. These indicate that LAST method is comparable to SDS and allows structural integrity of protein to be reasonably maintained.

For the VVD system, LAST simulation took 30 iterations (30 ns simulation time) to converge. The conformational space is illustrated in Figure 5B. SDS and LAST methods sampled similar conformational spaces and both covered a majority of cMD sample regions. To compare the efficiency of LAST and cMD methods, this cMD simulation was continued while this 2D RMSD map being monitored. It took 100 ns simulation time for cMD simulation to have a similar space shape with LAST. The initial 30 ns and 100 ns simulations are displayed in Figure S4B. In terms of MD simulation time, LAST was three times faster than cMD. Considering the VAE training time, the overall time cost for LAST was around 40% of cMD with all computations carried out on a Tesla P100 GPU node.

The mean RMSDs with regard to the starting protein structure in each iteration were calculated for both ADK and VVD systems and are shown in Figure 6. Mean RMSDs are presented with black lines and standard deviation shown in red lines for each round. The maximum and minimum RMSD values are shown as the upper and lower bound in the colored regions. Currently, we set the patience as 5: the iteration loop stops if the maximum mean RMSD does not increase in 5 consecutive rounds. For the simulation in ADK system, RMSD starts with 2Å, gradually increases to 3.5Å, and stops at iteration 22. In contrast, the RMSDs in VVD system are smaller and the total simulation lasts longer with a total of 30 iterations.

Figure 6:

Figure 6:

Open in a new tab

Mean RMSDs in (A) ADK and (B) VVD systems. Mean RMSD values are connected with black lines. Standard deviation in each iteration is plotted as vertical red lines. The gap between minimum and maximum RMSD values are colored as light grey background.

4. Discussion

In this study, we proposed a new adaptive sampling method to explore protein conformational space. LAST iteratively trains a VAE model using previous simulations, selects seeds that are structurally different to the sampled conformations, and uses them to initiate additional short MD simulations. LAST differs with previous methods in seed selection design, where the lowest-probability samples are selected and are treated as seeds on the latent space of VAE. VAE has been demonstrated to be effective in learning a low-dimensional protein representation in the latent space.20,37,38 The embeddings in the latent space are known to keep a distance similarity: if two protein structures are similar in structure, their embeddings in the latent space are close to each other. With this nature, the lowest-probability samples on the latent space are worth further exploration through MD simulations, as their corresponding protein structures deviate from the most common structures. In LAST, these low-probability samples are treated as seed structures to conduct additional MD simulations.

The normality of latent space provides new opportunity for seed selection. However, the latent space does not strictly follow a normal distribution, as shown in Table S1 and Figure S5. This is mainly because of the relatively strong emphasis on reconstruction loss and lesser emphasis on KL divergence during VAE training. The reconstruction loss term controls the quality of latent space data reconstruction (how well the VAE can reconstruct a protein structure) and KL divergence term constrains the distribution of the latent space (to what degree the latent space needs to follow a normal distribution). Therefore, in order to have a well-constructed and normal regularized latent space, appropriate weights are needed to be set for both terms. This is a challenging task with finetuning by hand, as the sample size keeps growing linearly with additional MD simulations in each round. Therefore, instead of trying to find weights to balance the reconstruction loss and KL divergence, we allow the latent space not strictly follow a normal distribution and use a non-parametric multivariate kernel density estimator to fit the latent space.

One potential problem is that the distribution of the latent space might be skewed or kurtotic. In such cases, one side of probability density function will have a long tail with low values. This could lead to the situation that all selected seed structures lie in the long tail side, and the corresponding protein structures of these seeds might be similar to each other. Seeds gathering on one side of latent space distribution decreases the chance to explore more structurally different conformations and thus leads to a less efficient protein sampling process. To partially overcome this issue, we used the cumulative distribution function to select the lowest-probability samples: data points on the two sides of the CDF are evenly selected. This improvement, as shown in Figure S6A and S6B, prevents sampling similar seeds on the boundary of protein conformational spaces.

Still, seed structures might be similar to each other. Nontargeted PaCS-MD proposed a nonredundant selection rule which calculates pairwise RMSDs between the current simulation cycle and seeds selected in all the past cycles.39 Protein configurations with large RMSD are then selected as new seeds in the current cycle. We took reference from this idea when selecting seeds. The lowest-probability samples from two ends of the estimated CDF are picked sequentially while the pairwise RMSDs to previously selected seeds are calculated. We set the RMSD threshold as 1 Å and require that the RMSD values of the newly selected seeds should be greater than the threshold. If not, LAST discards this outlier and moves to the next. The effect of this improvement can be seen through the comparison of Figure S6B and S6C. Moreover, LAST is a memory method: the selected seed structures are stored for RMSD calculation in future iterations, which avoids repeated sampling in the same conformational region and further improves the sampling efficiency.

For ADK, two angles with prior knowledge on its conformational dynamics were chosen to reveal the sampling efficiency. Similarly, RMSD values with reference to VVD native dark and light structures, respectively, were used for the same purpose. These pre-selected order parameters do not reduce the generality of LAST method, because they were not used to develop VAE models. In the other words, the VAE models are ”unaware” and do not require this information.

There are some tuning parameters in the LAST sampling scheme, including the dimensions of the latent space, the number of seed structures, the RMSD threshold in seed selection, the architecture of VAE model and the number of rounds in convergence. In LAST method, the seed structures need to be selected in the frontier regions of conformational space which has been sampled. These so-called frontier regions could not be easily identified in the Cartesian coordinates. On the contrary, after being projected onto a low dimensional latent space, the frontier regions of the conformational space representing existing simulations could be easily identified based on the distribution of exiting simulations. Consequently, the seed structures for further simulations could be chosen in these frontier regions in the low dimensional latent space. The latent space is one of the hidden layers in a VAE model. Typically, its dimension is much lower than the input dimension, and is considered as the bottleneck. In this study, the latent space was set as 2D to visualize, project and compare high-dimensional protein conformations. The performance of higher dimensions in the latent space is worth further study. For the number of seed structures, 10 seeds are selected in each round. This could be changed under different protein systems and is subjected to the available computing resources. Also, the MD simulation time starting from seeds, currently set as 100 ps, can be adjusted accordingly. However, it should be noted that this simulation time should match the RMSD threshold: the simulation time should not be too short with large RMSD threshold. Given that the conformational space of selected seeds is not likely to be visited again, it is expected to have a reasonable simulation time to fully explore the conformations in each additional MD run. Besides, the number of hidden layers in VAE model is important to learn a useful latent space. Our previous finding suggests that a VAE model with three hidden layers is sufficient to learn the ADK protein conformations. Larger model architectures do not have a significant improvement but instead will lead to longer training time. The proper architecture of VAE, in terms of the number of hidden layers and the number of dimensions in the latent space, is worth studying to provide general guidelines when dealing with different protein families. In general, LAST method is applicable in all protein systems. The implementation of LAST method is similar regardless of whether the protein systems contain non-protein components. However, the user needs to obtain appropriate force field parameters for the system under simulation. Lastly, it is worth noting that the convergence criterion used in this study does not represent the ”true” convergence of protein systems. The notion of ”true” convergence, as discussed in previous studies,40–42 is elusive in simulations. More appropriate criteria are needed for the convergence signal in adaptive sampling, through either numerical indicators or self-consistency checks.

5. Conclusion

In this study, we present an adaptive sampling method, latent space assisted adaptive sampling for protein trajectories, to accelerate the exploration of protein conformational spaces. LAST iterates through variational autoencoder training, seed selection and additional short MD simulations. LAST differs with previous methods in seed selection where the lowest-probability samples in the learned latent space are selected and treated as seed structures. LAST method is compared with SDS and cMD using ADK and VVD protein systems, each with different low-dimensional representations. In both systems, LAST can capture the key protein characteristics and select seeds that lie in the boundary of conformational space. For ADK simulations, LAST explored two transition paths that are in agreement with previous findings. For VVD simulations, LAST is three times faster than conventional MD for exploring the same conformational regions. To conclude, LAST provides an alternative method for efficient adaptive sampling.

Supplementary Material

SI

Acknowledgement

Research reported in this paper was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award No. R15GM122013. Computational time was generously provided by Southern Methodist University’s Center for Research Computing.

Footnotes

Data and Software Availability

The LAST algorithm is publicly available on GitHub at https://github.com/smu-tao-group/LAST. The SDS algorithm is available at https://github.com/Gonglab-THU-MD/Frontier-Expansion-Sampling. All simulation trajectories generated in this study are available from the corresponding author without restriction.

Supporting Information Available

Additional figures including ADK vectors, sampled conformational spaces in native ADK structures, PCA decomposition, sampled structures of VVD in LAST and cMD, Q-Q plots of the latent space, seed structure selection comparison, and tables including Henze-Zirkler tests and RMSDs of LAST and SDS to ADK structures.

References

  • (1).Allison JR Computational Methods for Exploring Protein Conformations. Biochem. Soc. Trans 2020, 48, 1707–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (2).Jin Y; Johannissen LO; Hay S Predicting New Protein Conformations from Molecular Dynamics Simulation Conformational Landscapes and Machine Learning. Proteins: Struct., Funct., Bioinf 2021, 89, 915–921. [DOI] [PubMed] [Google Scholar]
  • (3).Tian H; Trozzi F; Zoltowski BD; Tao P Deciphering the Allosteric Process of the Phaeodactylum Tricornutum Aureochrome 1a Lov Domain. The Journal of Physical Chemistry B 2020, 124, 8960–8972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (4).Shaw DE; Dror RO; Salmon JK; Grossman JP; Mackenzie KM; Bank JA; Young C; Deneroff MM; Batson B; Bowers KJ; Chow E; Eastwood MP; Ierardi DJ; Klepeis JL; Kuskin JS; Larson RH; Lindorff-Larsen K; Maragakis P; Moraes MA; Piana S; Shan Y; Towles B Millisecond-Scale Molecular Dynamics Simulations on Anton. Int. Conf. High Perform. Comput. Netw. Storage Anal 2009; pp 1–11. [Google Scholar]
  • (5).Salomon-Ferrer R; Gotz AW; Poole D; Le Grand S; Walker RC Routine Microsecond Molecular Dynamics Simulations with Amber on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput 2013, 9, 3878–3888. [DOI] [PubMed] [Google Scholar]
  • (6).Eastman P; Swails J; Chodera JD; McGibbon RT; Zhao Y; Beauchamp KA; Wang L-P; Simmonett AC; Harrigan MP; Stern CD; Wiewiora RP; Brooks BR; Pande VS OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol 2017, 13, e1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (7).Prinz J-H; Wu H; Sarich M; Keller B; Senne M; Held M; Chodera JD; Schütte C; Noe F Markov Models of Molecular Kinetics: Generation and Validation. J. Chem. Phys 2011, 134, 174105. [DOI] [PubMed] [Google Scholar]
  • (8).Lindert S; Bucher D; Eastman P; Pande V; McCammon JA Accelerated Molecular Dynamics Simulations with the Amoeba Polarizable Force Field on Graphics Processing Units. J. Chem. Theory Comput 2013, 9, 4684–4691. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (9).Krivov SV The Free Energy Landscape Analysis of Protein (FIP35) Folding Dynamics. J. Phys. Chem. B 2011, 115, 12315–12324. [DOI] [PubMed] [Google Scholar]
  • (10).Brotzakis ZF; Limongelli V; Parrinello M Accelerating the Calculation of Protein–Ligand Binding Free Energy and Residence Times Using Dynamically Optimized Collective Variables. J. Chem. Theory Comput 2018, 15, 743–750. [DOI] [PubMed] [Google Scholar]
  • (11).Barducci A; Bonomi M; Parrinello M Metadynamics. Wiley Interdiscip. Rev.: Comput. Mol. Sci 2011, 1, 826–843. [Google Scholar]
  • (12).Raiteri P; Laio A; Gervasio FL; Micheletti C; Parrinello M Efficient Reconstruction of Complex Free Energy Landscapes by Multiple Walkers Metadynamics. J. Phys. Chem. B 2006, 110, 3533–3539. [DOI] [PubMed] [Google Scholar]
  • (13).Hamelberg D; Mongan J; McCammon JA Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules. J. Chem. Phys 2004, 120, 11919–11929. [DOI] [PubMed] [Google Scholar]
  • (14).Bowman GR; Ensign DL; Pande VS Enhanced Modeling via Network Theory: Adaptive Sampling of Markov State Models. J. Chem. Theory Comput 2010, 6, 787–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (15).Harada R; Kitao A Parallel Cascade Selection Molecular Dynamics (PaCS-MD) To Generate Conformational Transition Pathway. J. Chem. Phys 2013, 139, 07B611_1. [DOI] [PubMed] [Google Scholar]
  • (16).Harada R; Kitao A Nontargeted Parallel Cascade Selection Molecular Dynamics for Enhancing the Conformational Sampling of Proteins. J. Chem. Theory Comput 2015, 11, 5493–5502. [DOI] [PubMed] [Google Scholar]
  • (17).Zhang J; Gong H Frontier Expansion Sampling: A Method to Accelerate Conformational Search by Identifying Novel Seed Structures for Restart. J. Chem. Theory Comput 2020, 16, 4813–4821. [DOI] [PubMed] [Google Scholar]
  • (18).Harada R; Shigeta Y Efficient Conformational Search Based on Structural Dissimilarity Sampling: Applications for Reproducing Structural Transitions of Proteins. J. Chem. Theory Comput 2017, 13, 1411–1423. [DOI] [PubMed] [Google Scholar]
  • (19).Chen W; Ferguson AL Molecular Enhanced Sampling with Autoencoders: On-the-Fly Collective Variable Discovery and Accelerated Free Energy Landscape Exploration. J. Comput. Chem 2018, 39, 2079–2102. [DOI] [PubMed] [Google Scholar]
  • (20).Hawkins-Hooker A; Depardieu F; Baur S; Couairon G; Chen A; Bikard D Generating Functional Protein Variants with Variational Autoencoders. PLoS Comput. Biol 2021, 17, e1008736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (21).Ramaswamy VK; Musson SC; Willcocks CG; Degiacomi MT Deep Learning Protein Conformational Space with Convolutions and Latent Interpolations. Phys. Rev. X 2021, 11, 011052. [Google Scholar]
  • (22).Bandyopadhyay S; Mondal J A Deep Autoencoder Framework for Discovery of Metastable Ensembles in Biomacromolecules. J. Chem. Phys 2021, 155, 114106. [DOI] [PubMed] [Google Scholar]
  • (23).Guo X; Du Y; Tadepalli S; Zhao L; Shehu A Generating Tertiary Protein Structures via Interpretable Graph Variational Autoencoders. Bioinform. Adv 2021, 1, vbab036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (24).Tian H; Jiang X; Trozzi F; Xiao S; Larson EC; Tao P Explore Protein Conformational Space with Variational Autoencoder. Front. Mol. Biosci 2021, 8 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (25).Wetzel SJ Unsupervised Learning of Phase Transitions: From Principal Component Analysis to Variational Autoencoders. Phys. Rev. E 2017, 96, 022140. [DOI] [PubMed] [Google Scholar]
  • (26).Doersch C Tutorial on Variational Autoencoders. arXiv preprint arXiv:1606.05908 2016, DOI: arXiv:1606.05908, Accessed on May 21, 2022. [Google Scholar]
  • (27).Chollet F Keras: The Python Deep Learning Library. Astrophys. Source Code Libr 2018, ascl–1806. [Google Scholar]
  • (28).Abadi M; Barham P; Chen J; Chen Z; Davis A; Dean J; Devin M; Ghemawat S; Irving G; Isard M; Kudlur M; Levenberg J; Monga R; Moore S; Murray DG; Steiner B; Tucker P; Vasudevan V; Warden P; Wicke M; Yu Y; Zheng X {TensorFlow}: A System for {Large-Scale} Machine Learning. 12th Proc. USENIX Symp. Oper. Syst. Des. Implement. (OSDI 16) 2016; pp 265–283. [Google Scholar]
  • (29).Berman HM; Bhat TN; Bourne PE; Feng Z; Gilliland G; Weissig H; West-brook J The Protein Data Bank and the Challenge of Structural Genomics. Nat. Struct. Biol 2000, 7, 957–959. [DOI] [PubMed] [Google Scholar]
  • (30).Case DA; Cheatham III TE; Darden T; Gohlke H; Luo R; Merz KM Jr; Onufriev A; Simmerling C; Wang B; Woods RJ The Amber Biomolecular Simulation Programs. J. Comput. Chem 2005, 26, 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (31).Maier JA; Martinez C; Kasavajhala K; Wickstrom L; Hauser KE; Simmerling C ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput 2015, 11, 3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (32).Seabold S; Perktold J Statsmodels: Econometric and Statistical Modeling with Python. Proc. 9th Python Sci. Conf 2010; p 61. [Google Scholar]
  • (33).Unan H; Yildirim A; Tekpinar M Opening Mechanism of Adenylate Kinase Can Vary According to Selected Molecular Dynamics Force Field. J. Comput.-Aided Mol. Des 2015, 29, 655–665. [DOI] [PubMed] [Google Scholar]
  • (34).Matsunaga Y; Fujisaki H; Terada T; Furuta T; Moritsugu K; Kidera A Minimum Free Energy Path of Ligand-Induced Transition in Adenylate Kinase. PLoS Comput. Biol 2012, 8, e1002555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (35).Goddard TD; Huang CC; Meng EC; Pettersen EF; Couch GS; Morris JH; Ferrin TE UCSF ChimeraX: Meeting Modern Challenges in Visualization and Analysis. Protein Sci 2018, 27, 14–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (36).Formoso E; Limongelli V; Parrinello M Energetics and Structural Characterization of the Large-Scale Functional Motion of Adenylate Kinase. Sci. Rep 2015, 5, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (37).Sultan MM; Wayment-Steele HK; Pande VS Transferable Neural Networks for Enhanced Sampling of Protein Dynamics. J. Chem. Theory Comput 2018, 14, 1887–1894. [DOI] [PubMed] [Google Scholar]
  • (38).Xiao S; Song Z; Tian H; Tao P Assessments of Variational Autoencoder in Protein Conformation Exploration. ChemRxiv 2022, DOI: 10.26434/chemrxiv-2022-g2c00, Accessed on Oct 28, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • (39).Harada R; Sladek V; Shigeta Y Nontargeted Parallel Cascade Selection Molecular Dynamics Based on a Nonredundant Selection Rule for Initial Structures Enhances Conformational Sampling of Proteins. J. Chem. Inf. Model 2019, 59, 5198–5206. [DOI] [PubMed] [Google Scholar]
  • (40).Romo TD; Grossfield A Block Covariance Overlap Method and Convergence in Molecular Dynamics Simulation. J. Chem. Theory Comput 2011, 7, 2464–2472. [DOI] [PubMed] [Google Scholar]
  • (41).Sawle L; Ghosh K Convergence of Molecular Dynamics Simulation of Protein Native States: Feasibility vs Self-Consistency Dilemma. J. Chem. Theory Comput 2016, 12, 861–869. [DOI] [PubMed] [Google Scholar]
  • (42).Knapp B; Frantal S; Cibena M; Schreiner W; Bauer P Is an Intuitive Convergence Definition of Molecular Dynamics Simulations Solely Based on the Root Mean Square Deviation Possible? J. Comput. Biol 2011, 18, 997–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SI
NIHMS1863727-supplement-SI.pdf (2.3MB, pdf)

RESOURCES