We have recently published a clustering method, namely CSMR, based on mixture regression in the context of high-dimensional predictors [1]. The motivation of our work was to provide a scalable method to deal with high-dimensional molecular features when there exist heterogeneous relationships between the molecular features and a disease phenotype of interest. In our original work, we simulated different data environments, including sample size 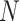 , number of cluster-differentiating and cluster-specific predictors
, number of cluster-differentiating and cluster-specific predictors  , number of clusters
, number of clusters 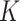 , and noise level
, and noise level  . We evaluated CSMR on the simulation datasets, based on its accuracy of clustering using Rand index, and feature selection using true positive/negative rate, as well as the consistency of predicted and observed response values using Pearson correlation. In a real-world Cancer Cell Line Encyclopedia (CCLE) dataset [2], we evaluated CSMR based on the consistency of predicted and observed response values using cross-validation.
. We evaluated CSMR on the simulation datasets, based on its accuracy of clustering using Rand index, and feature selection using true positive/negative rate, as well as the consistency of predicted and observed response values using Pearson correlation. In a real-world Cancer Cell Line Encyclopedia (CCLE) dataset [2], we evaluated CSMR based on the consistency of predicted and observed response values using cross-validation.
The letter by Zhang et al. raised the concerns that the performance of CSMR drops significantly when the number of cluster-differentiating predictors 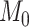 increases from 5 to 20, as demonstrated by evaluation metrics including the adjusted Rand index (ARI) and the clustering internal consistency (IC), both of which are advocated by Zhang et al. to be used for evaluating clustering methods. We appreciate Zhang et al.’s interests in our method and agree that their observations of the performance drop in the large
increases from 5 to 20, as demonstrated by evaluation metrics including the adjusted Rand index (ARI) and the clustering internal consistency (IC), both of which are advocated by Zhang et al. to be used for evaluating clustering methods. We appreciate Zhang et al.’s interests in our method and agree that their observations of the performance drop in the large 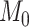 case are indeed true. We would like to mention that mixture regression models, with the presence of both low- and high-dimensional features, rely on Expectation–Maximization (EM) algorithm or its variants for a solution. However, EM algorithm often converges to the maximum likelihood estimate of the mixture parameters locally [3], and using EM algorithm to solve mixture regression problem might yield poor clustering performance if the parameters are not initialized properly, and finding a good initial value is always a challenge. In other words, EM algorithm is highly sensitive to initialization, and different initial values may lead to different solutions and hence the instability. Many works have been published on establishing the convergence and stability criterion for EM algorithm [4–7]. For example, a guarantee for the EM algorithm to converge to the unique global optimum is when the likelihood is unimodal with certain regularity conditions [4]. However, the likelihood function could be multi-modal in many cases, for which only local optimum could be guaranteed; and what’s worse, sometimes the local optimum is a poor one that is far away from any global optimum of the likelihood [7]. In all, while EM algorithm has enjoyed popular use in solving mixture model, there is still space for improved theoretical understanding.
case are indeed true. We would like to mention that mixture regression models, with the presence of both low- and high-dimensional features, rely on Expectation–Maximization (EM) algorithm or its variants for a solution. However, EM algorithm often converges to the maximum likelihood estimate of the mixture parameters locally [3], and using EM algorithm to solve mixture regression problem might yield poor clustering performance if the parameters are not initialized properly, and finding a good initial value is always a challenge. In other words, EM algorithm is highly sensitive to initialization, and different initial values may lead to different solutions and hence the instability. Many works have been published on establishing the convergence and stability criterion for EM algorithm [4–7]. For example, a guarantee for the EM algorithm to converge to the unique global optimum is when the likelihood is unimodal with certain regularity conditions [4]. However, the likelihood function could be multi-modal in many cases, for which only local optimum could be guaranteed; and what’s worse, sometimes the local optimum is a poor one that is far away from any global optimum of the likelihood [7]. In all, while EM algorithm has enjoyed popular use in solving mixture model, there is still space for improved theoretical understanding.
Here, we must clarify that in our setup, the total number of features, 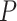 , is equal to
, is equal to 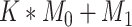 . Here
. Here 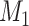 is the number of features that have no power to differentiate the different clusters, called the noise features. In our simulation data,
is the number of features that have no power to differentiate the different clusters, called the noise features. In our simulation data, 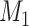 is usually much larger than
is usually much larger than 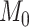 , to mimic the high-dimensional feature space setting. Obviously, there are only
, to mimic the high-dimensional feature space setting. Obviously, there are only 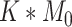 features that truly define the
features that truly define the 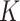 clusters. When there is no noise features, i.e.
clusters. When there is no noise features, i.e. 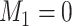 , under the case of
, under the case of 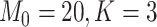 , which is the case the authors pointed out to be least stable, we have
, which is the case the authors pointed out to be least stable, we have 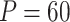 , which is relatively large. While there is no direct empirical or theoretical study on how the number of features might impact the stability of the EM algorithm, a recent study investigated the effect of sample size on the estimation efficiency of mixture regression model using EM algorithm [8]. Their simulation studies suggest that the stability of the results will be reduced with low class separation and small sample size. We argue that for a fixed sample size 400, and cluster number
, which is relatively large. While there is no direct empirical or theoretical study on how the number of features might impact the stability of the EM algorithm, a recent study investigated the effect of sample size on the estimation efficiency of mixture regression model using EM algorithm [8]. Their simulation studies suggest that the stability of the results will be reduced with low class separation and small sample size. We argue that for a fixed sample size 400, and cluster number  ,
, 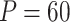 is a relatively large feature space, making a sample size of 400 a relatively small sample size. Hence, according to Jaki et al. [8], the stability of the mixture regression results will be impacted. We believe this is the root reason for the instability of CSMR.
is a relatively large feature space, making a sample size of 400 a relatively small sample size. Hence, according to Jaki et al. [8], the stability of the mixture regression results will be impacted. We believe this is the root reason for the instability of CSMR.
At the initialized clustering assignment, as well as at the end of each of the iteration of CSMR, after a noise feature filtering step, CSMR will call an external mixture regression solver to fit the ‘low-dimensional’ model to update the posterior probability. We observe that for  , N = 400, when the number of predictors increases to 60, the low-dimensional version of mixture regression fails to stably produce clustering results, even for the same dataset, under the same parameter setting, as evidenced by the low pair-wise ARI for repeated runs of (low-d) mixture regression on the same dataset using the same parameter setting (Figure 1). Here, we used flexmix function from the ‘flexmix’ R package as the low-d mixture regression solver, as it is currently the most popular and widely used implementation of mixture regression. Such instability is caused by the existence of many local optima, and the clustering results differ due to different starting values. Figure 1 suggests that the clustering performance deteriorates drastically with the increase of the size of the feature space,
, N = 400, when the number of predictors increases to 60, the low-dimensional version of mixture regression fails to stably produce clustering results, even for the same dataset, under the same parameter setting, as evidenced by the low pair-wise ARI for repeated runs of (low-d) mixture regression on the same dataset using the same parameter setting (Figure 1). Here, we used flexmix function from the ‘flexmix’ R package as the low-d mixture regression solver, as it is currently the most popular and widely used implementation of mixture regression. Such instability is caused by the existence of many local optima, and the clustering results differ due to different starting values. Figure 1 suggests that the clustering performance deteriorates drastically with the increase of the size of the feature space,  . The increase of
. The increase of 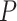 in some sense makes the sample size relatively smaller. On the CCLE real dataset, the number of molecular features is large, and they are strongly collinear as many genes perform similar or related functions. In addition, it is unclear how well-separated the hidden clusters are, which depends on the level of heterogeneity of the different cell lines. In this case, it is very likely that the feature filtering step in CSMR would retain a large number of features, making the low-d mixture regression model fail to perform stably, and hence resulting in the unstable clustering results as demonstrated by Zhang et al. And the multi-collinearity problem among the features makes the coefficient estimation efficiency even worse. We are working to improve the algorithm of CSMR by limiting the retained molecular features that is fed into the low-d mixture regression solver, such that the solver will be stable even with relatively larger number of predictor space. Currently, we have taken a simple but effective approach, by setting a limit on the maximum number of features entering into the low-d mixture model to be 40 or
in some sense makes the sample size relatively smaller. On the CCLE real dataset, the number of molecular features is large, and they are strongly collinear as many genes perform similar or related functions. In addition, it is unclear how well-separated the hidden clusters are, which depends on the level of heterogeneity of the different cell lines. In this case, it is very likely that the feature filtering step in CSMR would retain a large number of features, making the low-d mixture regression model fail to perform stably, and hence resulting in the unstable clustering results as demonstrated by Zhang et al. And the multi-collinearity problem among the features makes the coefficient estimation efficiency even worse. We are working to improve the algorithm of CSMR by limiting the retained molecular features that is fed into the low-d mixture regression solver, such that the solver will be stable even with relatively larger number of predictor space. Currently, we have taken a simple but effective approach, by setting a limit on the maximum number of features entering into the low-d mixture model to be 40 or 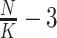 , whichever is smaller. The retained features are selected to be the ones with top Pearson correlation strengths with the response variable. While the Pearson correlation seems to go against the mixture relations, it is only needed at the initialization step. The users could certainly set up different criterion for feature filtering. Overall, with this simple step, we will not allow a large number of features to enter into the low-d mixture model, avoiding the possible instability of the low-d mixture regression solver. As shown in Figure 2, the clustering performance significantly improved with such a feature number limiting step. However, we must argue that the instability issue may persist with increased (cluster-differentiating) predictor size, which violates the sparsity assumption of CSMR.
, whichever is smaller. The retained features are selected to be the ones with top Pearson correlation strengths with the response variable. While the Pearson correlation seems to go against the mixture relations, it is only needed at the initialization step. The users could certainly set up different criterion for feature filtering. Overall, with this simple step, we will not allow a large number of features to enter into the low-d mixture model, avoiding the possible instability of the low-d mixture regression solver. As shown in Figure 2, the clustering performance significantly improved with such a feature number limiting step. However, we must argue that the instability issue may persist with increased (cluster-differentiating) predictor size, which violates the sparsity assumption of CSMR.
Figure 1.
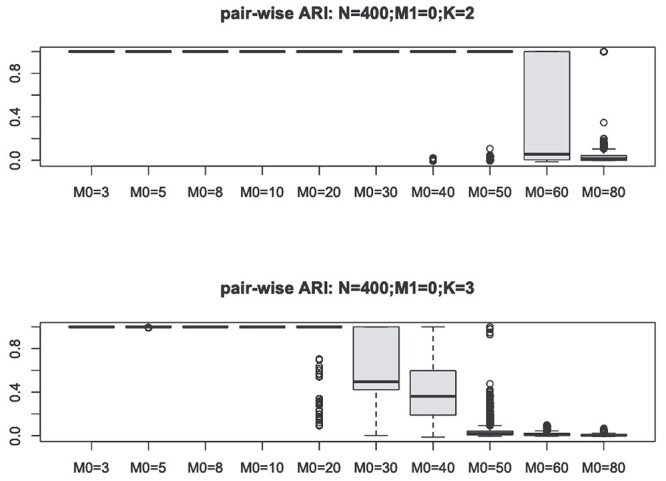
We show the instability issue of low-dimensional mixture regression solver on simulated datasets with no noise features, i.e. 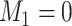 , for a sample size of 400, and cluster number
, for a sample size of 400, and cluster number 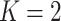 (top panel) and
(top panel) and 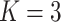 (bottom panel). The y-axis shows the distribution of the pair-wise ARI, and x-axis for different cluster-specific predictor
(bottom panel). The y-axis shows the distribution of the pair-wise ARI, and x-axis for different cluster-specific predictor  . Basically, for the same simulated dataset using the same parameter, we show the ARI of clustering results for any pair of runs among 100 repetitions of running flexmix function in the ‘flexmix’ R package, which is the most popular implementation of low-dimensional mixture regression solver.
. Basically, for the same simulated dataset using the same parameter, we show the ARI of clustering results for any pair of runs among 100 repetitions of running flexmix function in the ‘flexmix’ R package, which is the most popular implementation of low-dimensional mixture regression solver.
Figure 2.
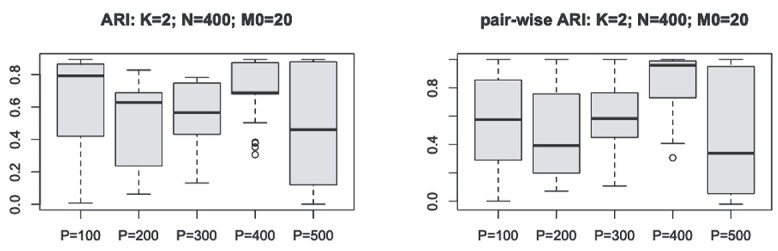
We show that the clustering instability and accuracy issue could be alleviated by slightly modifying the initialization step in CSMR by allowing only a smaller number of features to enter into the model, such that the low-d mixture regression solver will not fail. For clustering number  , sample size
, sample size 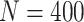 , and cluster-differentiating predictor number
, and cluster-differentiating predictor number 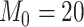 , we demonstrated the ARI (y-axis) with respect to the true cluster assignment (left panel), and the pair-wise ARI (y-axis) with respect to each other among 100 repetition runs on the same simulated dataset (right panel), for different number of total feature size,
, we demonstrated the ARI (y-axis) with respect to the true cluster assignment (left panel), and the pair-wise ARI (y-axis) with respect to each other among 100 repetition runs on the same simulated dataset (right panel), for different number of total feature size, 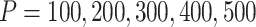 , are much improved in the modified version of CSMR. Further investigation is warranted.
, are much improved in the modified version of CSMR. Further investigation is warranted.
In summary, the instability issue of CSMR is caused by the instability of the EM-algorithm-based low-d mixture regression solver when facing with relatively large number of predictors, which is common to all EM algorithm-based mixture regression solver due to the existence of many local optima. In application of the CSMR algorithm, one underlying assumption is the sparsity of the differentiating predictors. Clearly, 60 true predictors with respect to sample size of 400 are not very sparse. However, in real-world biomedical data, no one could foresee how many differentiating genomic predictors there is, that is hidden in the large amount of feature space. It warrants further investigation using more comprehensive simulation data settings to explore the impact of multicollinearity, cluster separation and predictor dimensions on the performance of EM algorithm in solving mixture regression model.
Key Points
We agree with the observation made by Zhang et al on the instability and accuracy issue of CSMR with large number of differentiating predictors or total predictors, especially when there exists a large number of clusters (
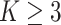 ). We, however, point out that the large differentiating predictor size violates the underlying sparsity assumption of CSMR.
). We, however, point out that the large differentiating predictor size violates the underlying sparsity assumption of CSMR.We would like to clarify that the clustering instability is a common issue for mixture regression-based clustering when there exists a relatively large number of predictors, regardless of whether there are other high-dimensional noise features present or not.
We demonstrated that the instability and accuracy issue could be alleviated by slightly changing the clustering initialization step, where we enforce limits on the number of retained features, such that the low-d mixture regression solver will not become unstable.
Author Biographies
Wennan Chang is a PhD student in the Department of Electrical and Computer Engineering, Purdue University.
Chi Zhang is an assistant professor in the Department of Medical and Molecular Genetics and a member of the Center for Computational Biology and Bioinformatics, Indiana University School of Medicine.
Sha Cao is an assistant professor in the Department of Biostatistics and Health Data Science and a member of the Center for Computational Biology and Bioinformatics, Indiana University School of Medicine.
Contributor Information
Wennan Chang, Department of Electrical and Computer Engineering, Purdue University, Indianapolis, 46202, USA; Department of Medical and Molecular Genetics, Center for Computational Biology and Bioinformatics, School of Medicine, Indiana University, Indianapolis, 46202, USA.
Chi Zhang, Department of Electrical and Computer Engineering, Purdue University, Indianapolis, 46202, USA; Department of Medical and Molecular Genetics, Center for Computational Biology and Bioinformatics, School of Medicine, Indiana University, Indianapolis, 46202, USA.
Sha Cao, Department of Biostatistics and Health Data Science, Indiana University, Indianapolis, 46202, USA; Department of Medical and Molecular Genetics, Center for Computational Biology and Bioinformatics, School of Medicine, Indiana University, Indianapolis, 46202, USA.
Funding
This work is supported by National Science Foundation (IIS-2145314), National Institute of Aging (1P30AG072976-01), and National Cancer Institute (5P30CA082709-22).
References
- 1. Chang W, Wan C, Zang Y, et al. Supervised clustering of high-dimensional data using regularized mixture modeling. Brief Bioinform 2021;22(4). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Barretina J, Caponigro G, Stransky N, et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 2012;483(7391):603–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc B Methodol 1977;39(1):1–22. [Google Scholar]
- 4. Wu CFJ. On the convergence properties of the EM algorithm. Ann Stat 1983;11(1):95–103. [Google Scholar]
- 5. Tseng P. An analysis of the EM algorithm and entropy-like proximal point methods. Math Oper Res 2004;29(1):27–44. [Google Scholar]
- 6. Chrétien S, Hero AO. On EM algorithms and their proximal generalizations. ESAIM PS 2008;12:308–26. [Google Scholar]
- 7. Balakrishnan S, Wainwright MJ, Yu B. Statistical guarantees for the EM algorithm: from population to sample-based analysis. Ann Stat 2017;45(1):77–120. [Google Scholar]
- 8. Jaki T, Kim M, Lamont A, et al. The effects of sample size on the estimation of regression mixture models. Educ Psychol Meas 2019;79(2):358–84. [DOI] [PMC free article] [PubMed] [Google Scholar]


