Abstract
Identifying the closest of a set of locations typically requires computing the distance to each of these locations, given a current position. However, Voronoi Diagrams precompute the geometric areas that each of these locations is closest to in order to ameliorate the cost of computing distances later on. Problematically, the initial computations required to generate a Voronoi Diagram can be computationally expensive. Naive approaches to generating discretized Voronoi Diagrams require every discretized position to be analyzed with the set of locations. This paper introduces a new algorithm to compute discretized Voronoi Diagrams using a divide-and-conquer approach. Rather than calculate every position, our approach calculates the positions at the four corners of a quadrant. If the corners belong to the same region, there is no need to subdivide this quadrant anymore; but if they are different than the original quadrant is subdivided into smaller quadrants. The process is repeated recursively until the entire diagram has been calculated appropriately.
Keywords: Voronoi Diagram, Divide-and-Conquer
I. Introduction
Voronoi diagrams [1] divide a two dimensional space into regions. The starting point for calculating a Voronoi diagram is a set of n seeds, points that are located in the two dimensional space. Each region contains the set of points that are closest to a particular seed. A Voronoi diagram will contain n regions. Voronoi diagrams are considered “one of the most fundamental data structures in computational geometry” [1]. Voronoi diagrams are used in a variety of fields from finite difference methods and image compression [2] in engineering and computer science to representations of cell biology and territorial animal behavior in the natural sciences and any other field or problem requiring the identification of the nearest in a set of seeds. However, as useful as Voronoi diagrams are, it is necessary to create them before benefiting from them.
The creation of Voronoi diagrams from a set of seeds may be calculated on a space with an infinite number of points [1] or on a discretized range of finite points [3]. In algorithms applied to a range of finite points, a naive method of Voronoi diagram generation [3] finds the closest seed for each point in the range of finite points. Every seed is associated with a particular color (or shade of grey). All the points that are closest to a particular seed are assigned the same color (or shade of grey) as their closest seed. For example, Figure 1 shows different regions with different shades of grey representing the points in a two-dimensional plane closest to one of ten seeds, scaled from the original for display. The original grid is of size 2048 × 2048 and the seeds are located at coordinates: (512, 512), (512, 1024), (512, 1536), (1024, 512), (1024, 1024), (1024, 1536), (1536, 512), (1536, 1024), (1536, 1536), and (2000, 2000). Point (0, 0) in the grid is in the upper left corner. However, given a plane discretized into an m by m square with n seeds, the computational cost is in . Therefore, faster methods are necessary. The naive algorithm can be parallelized easily on machines with several processors (cores) or Graphical Processing Units (GPUs) [3], but parallel resources are not available to every user. The Jump Flow Algorithm (JFA) [4] is faster than the naive method described previously. JFA is described briefly in the related work section.
Fig. 1. A Voronoi Diagram with 10 Seeds.
This paper describes a divide-and-conquer algorithm to reduce the computational cost of generating a Voronoi diagram without necessitating specialized hardware or reductions in accuracy beyond the discretization. While a naive approach treats each discretized point without relation to the others, the divide-and-conquer approach exploits inferred information based on similarities between points within the same region of the diagram in order to reduce the number of computations. For example, if a single point is entirely surrounded by points from a single region then the enclosed point must be in that region. The algorithm presented here recursively computes boundary points within the discretized range of finite points until the points within the boundary points can be inferred without additional calculation, reducing the computational cost of generating a Voronoi diagram.
The contributions of this paper are as follows:
We introduce a divide-and-conquer algorithm to generate Voronoi diagrams,
We compare the naive approach with the introduced divide-and-conquer approach, and
We provide a proof sketch the correctness of the additional assumptions necessary for the divide-and-conquer approach to generate correct Voronoi diagrams.
The remainder of the paper is organized into the following sections. Section II provides and overview of the background information, including Voronoi diagrams and divide-and-conquer algorithms. Section III presents our approach, proof sketch, and concrete example. Section IV details our results, while Sections V and VI describes related work and our conclusions, respectively.
II. Background
This section covers background in Voronoi diagrams and divide-and-conquer algorithms.
A. Voronoi Diagrams
The Voronoi diagram for a set of n seeds in a plane partitions the plane into n Voronoi regions such that each region contains only one seeds (also referred to as a site). For every seed, s, the Voronoi region, or tile, enclosing it contains all the points in the plane that are closer to s than to any other seed. In two-dimensional diagrams, Voronoi regions are usually depicted as a set of polygons, each enclosing a single black dot (i.e., the seed) and filled with a unique color. The goal for computing the Voronoi diagram for a set of n seeds, which can be thought of a scattering of black dots on a white background, is to determine the regions of the plane that are closest to each individual seed. Each of these regions closest to a single individual seed are recorded (e.g., via unique colors) so that all points in the plane are associated with their closest seed. In this paper we use Euclidean distance [5].
B. Divide-And-Conquer Algorithms
Divide-and-conquer algorithms use the strategy of dividing a large problem into smaller pieces, solving the problem for the smaller pieces, and then to using the solutions for the smaller pieces to assemble a solution for the original problem. The division of the problem might take several stages, that is, the sub-problems may need to be subdivided several times into smaller and smaller pieces. Divide-and-conquer algorithms rely on the fact that solutions for very small problems are easy to compute or they may rely on certain sub-problems having a trivial solution. Hence the original problem is subdivided into pieces until the solution to a particular piece is easy to compute. Once the solutions to the sub-problems have been found, a second state of the algorithm may require combining the solutions of the sub-problems into a solution for the original problem.
A classical example of a divide-and-conquer algorithm is the merge-sort algorithm [6]. The original list (or array) is subdivided, recursively, into smaller and smaller segments. Once a list is of size 2 or 1, solving the sorting problem for that very small list is trivial. If the list contains a single element, it is in order. If the list contains two elements, then either the elements are in order, or they are out of order. If the elements are in order, no further action is required. If they are out of order, a swap of the elements suffices to obtain a sorted list. Those small sub-lists are merged, recursively, until the original list is sorted.
III. Approach
The naive approach to computing Voronoi diagrams is, for every discretized point in a plane (on GPUs this could be a pixel), calculate the distance between that discretized point and every seed in the plane. Whichever seed is closest indicates which region that discretized point belongs in. Often, every one of these seeds has a different color (or shade of grey) associated with it that is associated with the discretized point. While this method is accurate and easily understood, its benefits are offset by the growth in computation time as diagram size increases.
We propose a method that does not require every discretized point to be individually calculated, but instead relies on geometric relationships to identify areas that all must be within the same region.
In the remainder of this section we will cover an overview of our proposed algorithm. Following our overview, we will present a proof sketch of the assumptions necessary for our algorithm to correctly function. Finally, we will provide a concrete example of our algorithm on a small discretized grid as well as limitations of our algorithm.
A. Divide-And-Conquer Algorithm Overview
The divide-and-conquer approach can be described as follows via the following steps:
Step 1: Calculate Points:
Assuming that the plane on which the diagram will be computed is rectangular, find the seeds closest to each of the four corners of that rectangle using Euclidean distance. In other words, for every one of the corner points, calculate the distance to all seeds and select the closest seed to each of those corner points.
Step 2: Base Case:
If all the corner points are closest to the same seed, then assign all points within the rectangle bounded by the four corner points to the region associated with the corners’ closest seed.
Step 3: Subdivide Case:
If all the corner points are not closest to the same seed, subdivide the rectangle enclosed by the four corner points into four smaller rectangular fragments consisting of the top-left, top-right, bottom-left, and bottom-right sub-rectangles of the original plane. Each of these 4 fragments of the original rectangle is then recursively processed by Step 1: Calculate Points.
This recursive process will continue until all subdivided rectangles cover a single seed closest to their four corner points. It is possible that the algorithm may have to keep subdividing into smaller and smaller rectangles until a single discretized point is obtained that must be closest to only one seed. In the event of a tie, the first seed processed is considered closest.
B. Proof Sketch
The presented divide-and-conquer algorithm depends on the observation that if the four corners of a rectangular area are all closest to the same seed, then the entirety of the enclosed rectangular area must also be closest to that same seed when using Euclidean distance. A proof sketch for this dependency is provided below.
If the Euclidean distance is used to calculate the distances in a Voronoi Diagram, all regions in that Voronoi Diagram are convex polygons [1].
Our proposition is that any line that connects two points inside a convex polygon is completely contained by the polygon. Given that a rectangle is composed of four connected lines, and any line that connects two points inside a convex polygon is, based on our proposition, completely contained by the polygon, we can also say that any rectangle that connects four points inside a convex polygon is completely contained by the polygon.
Proof.
We will use a proof by contradiction. We assume that on a plane, 4 points: C1, C2, C3, and C4, form the corners of a rectangle that encloses point P. Measuring with Euclidean distance, C1 through C4 are all closer to seed X than any other, but P is closest to seed Y.
Since C1-C4 are all closest to X, we know that C1-C4 and X are both within the X-Voronoi region.
Since P is closest to Y, we know that P and Y are both within the Y-Voronoi region. Therefore the Y-Voronoi region must be completely or partially contained within the X-Voronoi region.
Since Voronoi regions are convex polygons by definition, so we can conclude the X-Voronoi region must be a convex polygon and any line that connects two points inside the polygon is completely contained by the polygon.
However, because the X-region must partially or fully enclose the Y-region if P is closest to seed Y and P is enclosed by the rectangle defined by C1-C4, there are inevitably lines connecting two points (i.e., two from C1-C4) within the X-region that exit the boundaries of the convex polygon region despite connecting two points existing within the region. This is a contradiction. □
Now that our assumptions have been validated, it is accurate to assume the Voronoi region of a rectangle is entirely from one seed if the closest seed to each corner of the rectangle, using Euclidean distance, is the same.
C. Example
To illustrate this method, we used a grid of integers to represent the empty “plane” that will be partitioned. Empty spaces represent grid points that have not been assigned to any region yet, and integers represent the location of seeds. In this form, the Voronoi diagram for a set of seeds can be determined by hand and used to illustrate the computer-generated solutions.
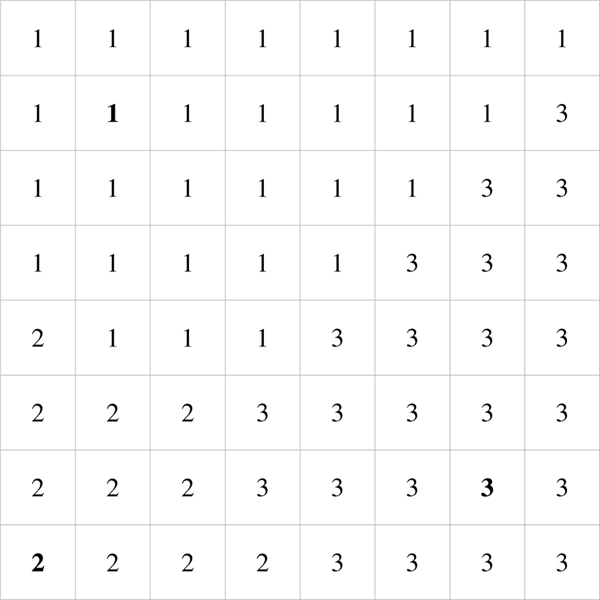
In Figure 2 we use an 8 × 8 grid to illustrate how the algorithm works. The upper left coordinate has coordinates (0, 0) and the lower right hand corner has coordinates (7, 7). There are three seed points: 1, 2 and 3 at coordinates (1, 1), (0, 7) and (6, 6). The seeds are represented using numbers in boldface.
Fig. 2.
Initial state: A Voronoi Diagram with 3 seeds.
The initial step of the algorithm calls for calculating the closest seeds for the four corners of the grid: Points with coordinates (0, 0), (0, 7), (7, 7) and (7, 0). Clearly, the closest seeds for those points are not the same. Hence, the algorithm calls for dividing the original grid into four smaller sub-grids, as illustrated in Figure 3 by the thick red lines.
Fig. 3.
Initial subdivision.
The algorithm is applied recursively to each of the four quadrants. Figure 4 illustrates that the upper left quadrant and the lower right quadrant can be filled at this stage, but further subdivisions (shown in thick blue lines) are required for the lower left quadrant and the upper right quadrant.
Fig. 4.
Second subdivision.
The process continues until the final result is calculated, as shown in Figure 5.
Fig. 5.
Final result.
A grid of size 8 × 8 can be represented in the computer using a 2D dimensional integer array of length 8 and width 8. The indices of the array act as coordinates to their respective locations in the grid. For example: the integer present in the first row and second column of integer grid numbers, represented by integer array numArray, can be returned through numArray[0][1]. To turn an incomplete grid into a complete one, every zero in the grid must be replaced by the integer that represents the seed closest to this grid location. If the top right “0” is closest to the seed labeled “2”, then it is changed to a “2”.
D. Limitations
The divide-and-conquer algorithm presented here is limited to Euclidean distance, as other distances do not result in Voronoi regions that are convex polygons (e.g., Manhattan Distance often used in k-means clustering [7]). Additionally, we have provided a proof sketch for rectangular division only, though other divisions of the space may also hold the same properties.
IV. Results
To test the speed of our new method, we created a Java program that auto-generated two identical copies of a random incomplete integer-grid Voronoi diagram like has been described in the approach (Section III). The Java program then computes one copy with the naive method and one with the divide-and-conquer method, recording the total computation time for both. We performed tests with grids of different sizes, including 32 × 32, 64 × 64, 128 × 128, 256 × 256, 512 × 512, 1024 × 1024, and 2048 × 2048.
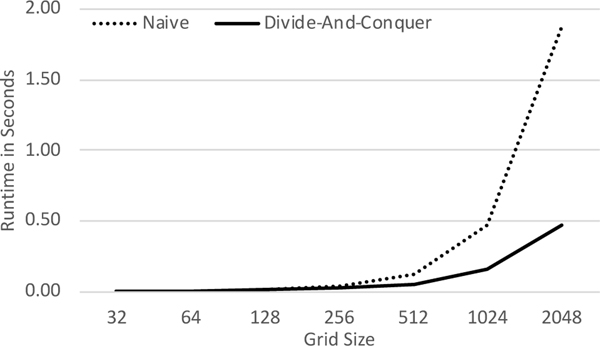
In Figure 6, we graph the time (in seconds) taken for both the naive and divide-and-conquer algorithms to generate the Voronoi diagrams for 50 randomly selected seeds. The values graphed for each grid size were executed with a different set of randomly selected seeds 50 times, though there is no appreciable difference in their distribution. For small grids, of size 32 × 32 or 64 × 64, the naive algorithm was faster than the proposed divide-and-conquer algorithm. However, for grids of sizes 128 × 128 or larger, the divide-and-conquer algorithm was faster and the difference between the two algorithms increased as the size of the grid increased.
Fig. 6.
Execution Times with 50 Seeds
In Figure 7 we graph the time (in seconds) taken for both the naive and divide-and-conquer algorithms to generate the Voronoi diagram for a grid of size 2048 × 2048 with increasing numbers of seeds. It can be observed that the divide-and-conquer algorithm is faster than the naive algorithm regardless of the numbers of seeds, though the difference becomes more pronounced as the number of seeds increases. As before, each grid with a number of seeds was executed with a different set of randomly selected seeds 50 times, though there is no appreciable difference in their distribution.
Fig. 7.
Execution Times with a 2048 × 2048 Grid
The proposed divide-and-conquer algorithm presented in this paper takes less time than the naive approach given an increasing number of seeds or an increasing grid size.
V. Related Work
The best algorithm for calculating the original Voronoi Diagram is the sweep line algorithm by Steven Fortune [8]. This algorithm will work with sites (i.e., seeds) with real coordinates. It produces the line segments that surround the tiles. Its time complexity is , where n is the number of seeds. This algorithm has the limitation of requiring special handling for seeds that are located co-linearly, seeds that will be reached simultaneously by the sweep line. This algorithm will require an additional stage to visualize the results on a computer screen. It is also an algorithm that is difficult to parallelize. In contrast, our divide-and-conquer algorithm works with discretized points in a grid that is immediately visualizable and provides direct lookup within the grid after the Voronoi diagram has been generated.
Since there are many data sets that are the results of ”rasterizing” information, in which each point is represented with integer coordinates, and which will be used frequently to be displayed on computer screens, the naive algorithm described previously has been proposed. This algorithm can be parallelized efficiently using Graphical Processing Units (GPUs) [3]. However, in embedded or resource constrained applications where a GPU is not available the divide-and-conquer method reduces cost without requiring special hardware.
The Jump Flow Algorithm [4] was devised expressly for Graphical Processing Units. In a first stage, the points adjacent to each individual seed are colored with the color of the seed their surround. In the second stage the points that do not have a color yet and are at a distance of 2 from a seed acquire the color of that (closest) seed. In stage 3, the points that are a distant of 4 from a seed acquire the color of that seed. The process continues until points in the plane have been colored. The jump flood algorithm occasionally assigns incorrect colors to certain points in the grid. While the presented divide-and-conquer method is not specifically designed for GPUs, it is guaranteed to provide the correct discretized Voronoi diagram.
VI. Conclusion
In this paper, we have presented a divide-and-conquer approach to generate discretized Voronoi diagrams in two dimensions. We have compared our approach to the naive approach over an increasing number of seeds and an increasing grid size. In each case, the proposed divide-and-conquer approach presented outperformed the naive approach as the number of seeds or grid size increased.
Given the increased performance and lower computation cost of the divide-and-conquer approach, we believe that our proposed method is well suited to applications within embedded or resource constrained systems.
Future research directions include exploration into how our approach can be extended to different geometric divisions within our divide-and-conquer algorithm, non-Euclidean spaces, higher dimensions (e.g., three dimensional Voronoi diagrams), and parallelization.
Acknowledgment
This work partially funded by Michigan Space Grant Consortium, NASA grant #NNX15AJ20H. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Michigan Space Grant Consortium (MSGC), National Aeronautics and Space Administration (NASA), Grand Valley State University (GVSU), or other research sponsors.
References
- [1].Aurenhammer F, “Voronoi diagrams—a Survey of a Fundamental Geometric Data Structure,” ACM Computing Surveys (CSUR), vol. 23, no. 3, pp. 345–405, 1991. [Google Scholar]
- [2].Erwig M, “The graph Voronoi diagram with applications,” Networks: An International Journal, vol. 36, no. 3, pp. 156–163, 2000. [Google Scholar]
- [3].Majdandzic I, Trefftz C, and Wolffe G, “Computation of Voronoi diagrams using a graphics processing unit,” in 2008 IEEE International Conference on Electro/Information Technology IEEE, 2008, pp. 437–441. [Google Scholar]
- [4].Rong G. and Tan T-S, “Jump flooding in GPU with applications to Voronoi diagram and distance transform,” in Proceedings of the 2006 symposium on Interactive 3D graphics and games, 2006, pp. 109–116. [Google Scholar]
- [5].Danielsson P-E, “Euclidean distance mapping,” Computer Graphics and image processing, vol. 14, no. 3, pp. 227–248, 1980. [Google Scholar]
- [6].Knuth D, “Section 5.2. 4: Sorting by merging,” The Art of Computer Programming, vol. 3, pp. 158–168, 1998. [Google Scholar]
- [7].Singh A, Yadav A, and Rana A, “K-means with three different distance metrics,” International Journal of Computer Applications, vol. 67, no. 10, 2013. [Google Scholar]
- [8].Fortune S, “A sweepline algorithm for voronoi diagrams,” Algorithmica, vol. 2, no. 1–4, p. 153, 1987. [Google Scholar]