MOSAICING OF DYNAMIC MESENTERY VIDEO WITH GRADIENT BLENDING

Rumana Aktar; V H Huxley; G Guidoboni; H AliAkbarpour; F Bunyak; K Palaniappan

doi:10.1109/icip40778.2020.9191045

. Author manuscript; available in PMC: 2022 Jun 1.

Published in final edited form as: Proc Int Conf Image Proc. 2020 Sep 30;2020:563–567. doi: 10.1109/icip40778.2020.9191045

MOSAICING OF DYNAMIC MESENTERY VIDEO WITH GRADIENT BLENDING

Rumana Aktar ¹, V H Huxley ², G Guidoboni ¹, H AliAkbarpour ¹, F Bunyak ¹, K Palaniappan ¹

PMCID: PMC9159528 NIHMSID: NIHMS1685785 PMID: 35656332

Abstract

In biomedical imaging using video microscopy, understanding large tissue structures at cellular and finer resolution poses many image acquisition challenges including limited field-of-view and tissue dynamics during imaging. Automated mosaicing or stitching of live tissue video microscopy enables the visualization and analysis of subtle morphological structures and large scale vessel network architecture in tissues like the mesentery. But mosacing can be challenging if there are deformable, motion-blurred, textureless, feature-poor frames. Feature-based methods perform poorly in such cases for the lack of distinctive keypoints. Standard single block correlation matching strategies might not provide robust registration due to deformable content. In addition, the panorama suffers if there is motion blur present in a sequence. To handle these challenges, we propose a novel algorithm, Deformable Normalized Cross Correlation (DNCC) image matching with RANSAC to establish robust registration. Besides, to produce seamless panorama from motion-blurred frames we present gradient blending method based on image edge information. The DNCC algorithm is applied on Frog Mesentery sequences. Our result is compared with PSS/AutoStitch [1, 2] to establish the efficiency and robustness of the proposed DNCC method.

Index Terms—: Biomedical, Mesentery, Cross Correlation, Registration, Mosaicing, Gradient blending

1. INTRODUCTION

Due to wide applications of biomedical imagery mosaicing, lots of research has been done on this field. Correlation based image registration and mosaicing has been explored for stitching of high-resolution microendoscope (HRME) [3], multispectral and hyperspectral data [4], chicken breast [5], etc. Some applications include Lukas Canady Tracker for feature selection for mosaicing of colon [6], bone, blood and lung [7]. In addition, structure propagation for mouse brain [8], phase correlation for breast tissue [9], SIFT for confocal microscopy in the oral cavity [10], etc. have also shown promising results. Lots of research has been reported on retinal images with different features such as covariance [11], Y-feature: where 3 vessels converge [12], mSIFT [13], UR-SIFT [14], etc.

In biomedical data, two main concerns are deformable tissues and moving cells. In addition, Mesentery images suffer from high motion blur, irregular motion, large illumination change, low contrast and low textured region. Thus, we avoid feature-based registration and choose to proceed with correlation based matching which performs comparatively better in poorly-featured images. Single block correlation matching based mosaicing has been explored in many mosaicing applications including biomedical and aerial imagery [3, 4, 5, 15, 16, 17, 18]. What makes our approach distinctive from others is that DNCC establishes 3×3 block matching between two images followed by RANSAC [19] to ensure robust registration. In addition, we propose image gradient or edge based blending algorithm for seamless blending of motion-blurred frames which is difficult to achieve from other traditional blending methods.

2. METHODS

Mesentery images were captured on an Olympus Inverted Microscope (IX70) using a 10x (numerical aperture 0.22) lens. Basically the image was projected on to a black and white CCD camera (Dage-MTI 72) projecting a field of view of 0.65mm × 0.78 mm. After observing the Mesentery sequences, we assume that the motion between any two consecutive frames is translation.

2.1. Correlation-Based Registration and Mosaicing

The block diagram for the proposed Deformable Normalized Cross Correlation (DNCC) based method is shown in Fig. 1 where two frames are registered by image correlation as shown in row C. For a block, B_x in F_i and search window, B_x+Δ in frame F_i−1, NCC is defined as below:

γ_{i} (B_{x}) = \frac{\sum_{x} (F_{i - 1} (B_{x}) - {\bar{F}}_{i - 1}) \cdot (F_{i} (B_{x + Δ}) - {\bar{F}}_{i})}{\sqrt{\sum_{x} {(F_{i - 1} (B_{x}) - {\bar{F}}_{i - 1})}^{2} \sum_{x} {(F_{i} (B_{x + Δ}) - {\bar{F}}_{i})}^{2}}}

(1)

where, ${\bar{F}}_{i - 1}$ is the local mean of F_i−1(B_x). The three main steps in our DNCC approach as seen in Fig. 1. The translation between two consecutive frames is estimated using NCC as illustrated in Row C of Fig. 1. Let the top-left corner of the template be (p_x, p_y) on frame, F_i. Similarity score or correlation coefficient matrix is computed between the template and frame, F_i−1 using normxcorr2 (Matlab function). The maximum value of correlation matrix corresponds for best matching or similarity between the frames. Let (P_x, P_y) be the position of maximum correlation score as shown in Fig. 1. Finally, the target translation parameters (t_x, t_y) are calculated using the equations shown in row, C.

We define the position (x_i, y_i) of i^th frame, F_i on canvas as the coordinate of the top-left corner. Once translation (t_x, t_y) between the previous F_i−1 and current F_i frames is estimated, then using the previous frame translation, (x_i−1, y_i−1), the position of F_i on the canvas under a rigid translation model can be calculated as:

{(x_{i}, y_{i})}_{R} = (x_{i - 1} + t_{x}, y_{i - 1} + t_{y})

(2)

2.2. Deformable Normalized Cross Correlation (DNCC)

Initially, we use a single template of size 150×100 from F_i and search for similarity in the whole image, F_i−1. The mosaic generated from this approach is greatly influenced by the templates. As template position, (p_x, p_y) is fixed along the sequence, the characteristics such as image contrast, deformability, illumination, motion blur, texture, etc., of the template is varied for each frame. Thus, the content of the template for some of the frames might not be informative enough for a robust NCC matching. This can be shown by the examples in Fig. 3 for two sets of templates, i.e., (p_x, p_y): (200, 100), and (100, 60). It is noticeable that for $M_{3}, (p_{x}, p_{y}) = (200, 100)$ works well where for other sequences, (p_x, p_y) = (100, 60) provide accurate registration. This observation holds even if the size of template is varied.

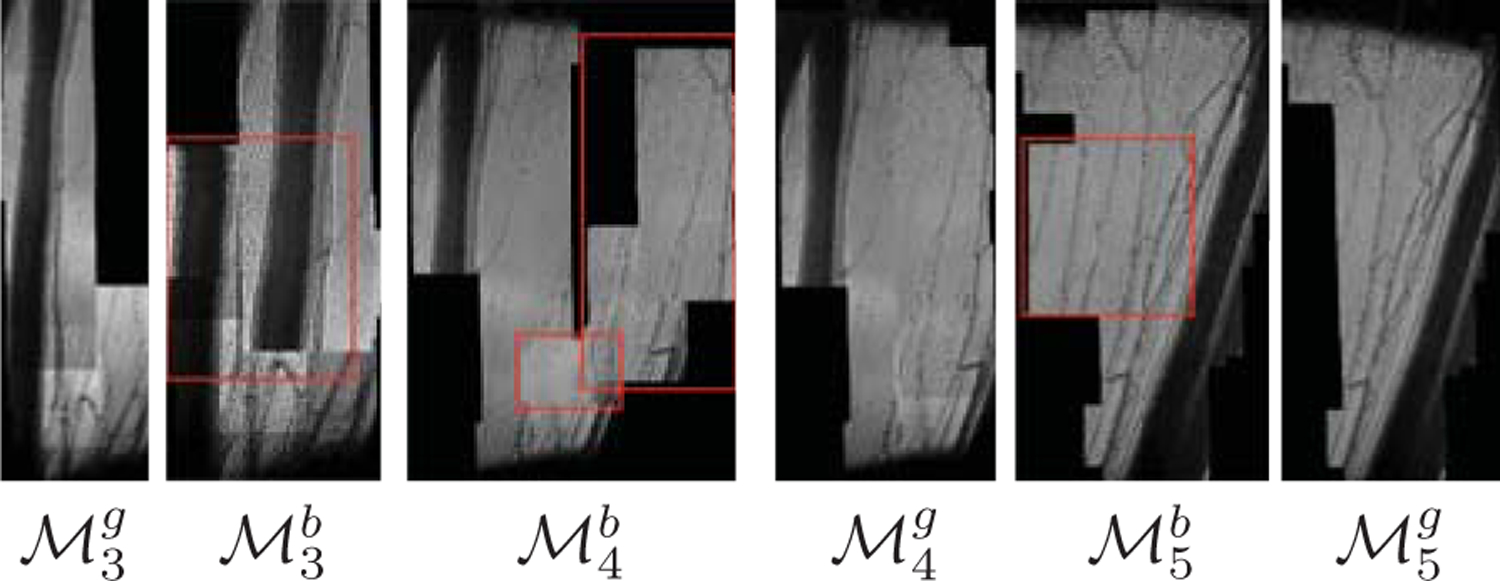
Fig. 3. — Examples of failure of single template (instead of 3×3 blocks) method with effect of template position (p_x, p_y) across the sequences where superscript g and b stands for *good* and *bad* registration. For template position, (p_x, p)=(200, 100), mosaics $M_{3}^{g}$ , $M_{4}^{b}$ and $M_{5}^{b}$ is generated from 3 sequences. On the other hand, for (p_x, p_y)=(100, 60), mosaics $M_{3}^{b}$ , $M_{4}^{g}$ and $M_{5}^{g}$ are found. The misregistered parts $M_{3}^{b}$ , $M_{4}^{b}$ and $M_{5}^{b}$ are highlighted in red rectangles.

Thus, to get robust matching, we propose to use 3×3 non-overlapping templates from frame, F_i as shown in Fig. 2. Each template block, B_k is matched within its corresponding search window in the previous frame, F_i−1 where k=1, 2, …, 9 for the nine blocks (3 × 3 group of blocks as shown in Fig. 2). Consequently, 9-sets of translation parameters, (t_x(B_k), t_y(B_k)) are returned. Some of (t_x(B_k), t_y(B_k)) pairs might be false matching due to deformability and motion of cells in Mesentery. Thus, RANSAC [19] is introduced to remove false matches. After the RANSAC outlier block elimination, K remaining pairs of translation parameters, (t_x(B_k), t_y(B_k)) are used to update the non-rigid local translations,

{(x_{i}, y_{i})}_{D} = (x_{i - 1} + {〈t_{x}〉}_{K}, y_{i - 1} + {〈t_{y}〉}_{K}), K \leq 9

(3)

where 〈·〉 is the averaging operator, t_x is averaged over K blocks B_k. If K < 2, we do not consider it as a robust match and discard the frame, F_i and continue for the next iteration. Otherwise, the mean of t_x(j) and t_y(j) become the target translation values: ${\bar{t}}_{x}$ and ${\bar{t}}_{y}$ as demonstrated in Fig. 2. This method is defined as Deformable NCC (DNCC) as it can filter out incorrect matches due to deformable objects and motion blur with the application of RANSAC.

Fig. 2. — Proposed multiple templates matching registration between two frames: 9 non-overlapping templates/blocks are used in order to ensure robust matching. True matches are found after RANSAC outlier removal and their mean is considered as the target translation parameters, ( ${\bar{t}}_{x}$ , ${\bar{t}}_{y}$ ).

2.3. Gradient Blending of frame, F_i With Mosaic, $M_{i - 1}$

Though widely used, alpha blending (Eq. 4) does not perform well for Mesentery sequences. We have tested for different values of α such as α =1 (pixel filling), α =0 (replacement) and α =0.5 (averaging). None of these can overcome the blurriness present in the sequences. Thus, to obtain seamless blending in presence of highly motion-blurred frames, the gradient or edge information of two frames are compared as shown in Fig. 4. Gradient Response Ratio (GRR) is defined as the ratio of edge pixels in $M_{i - 1}$ and F_i. For this purpose, we use canny edge which is computed from Matlab edge function. Finally, α in Eq. 4 becomes a function of GRR as presented in Eq. 5.

Fig. 4. — Gradient (canny edge) response (left-to-right): regular frame and edge, motion blurred frame and edge. GRR=0.845.

M_{i} = α M_{i - 1} + (1 - α) F_{i}

(4)

α = {\begin{array}{l} 1 & if G R R_{i} \geq 1 \\ 0 & otherwise \end{array}

(5)

3. RESULTS

As no ground truth is known for Mesentery sequences, we generated 4 synthetic datasets (D1, D2, D3 and D4) each with 50 frames. To establish similar characteristics of Mesentery data, we added low, medium and high level of motion blur in 12 images of D2, D3 and D4. The performance of DNCC method is compared with Panoramic Stitching using SURF (PSS/AutoStitch) [1, 2]. We manually identified 10 strong keypoints in groundtruth mosaic and checked Distance Error (DE) in DNCC and PSS mosaic. DE is defined as the euclidean distance between a keypoint, gp(x, y) on groundtruth mosaic and corresponding keypoint on candidate mosaic cp(x, y). We found that DE always smaller in DNCC compared to PSS. Due to space limitation, DE values of 4 points are presented in Table 1. It is also notable that with the increase of motion blur, DE values increase exponentially in PSS where it remains linear (and really small) in DNCC which proves the robustness of our 3×3 block matching method with RANSAC. More importantly, for D4 dataset, PSS algorithm fails to detect and match feature for the lack of strong keypoints due to high motion blur where DNCC performs very well. Structural Similarity (SSIM) also proves the superiority of DNCC over PSS for the sythetic datasets. We compared Gradient blending with other blending methods: averaging, averaging with deblurring (ADB) and replacement or overlay. From Table 2, it can be concluded that Gradient blending outperforms others in comparing SSIM, Root Mean Square Error (RMSE) and Peak Signal to Noise Ratio (PSNR).

Table 1.

Comparison between DNCC and PSS/AutoStitch [1, 2] algorithm for 4 synthetic datasets each with 50 frames.

Data	Blur	SSIM		DE 1		DE 2		DE 3		DE 4		Time(s)/fr
Data	Blur	DNCC	PSS	DNCC	PSS	DNCC	PSS	DNCC	PSS	DNCC	PSS	DNCC	PSS
D1	-	1	0.96	0	3.5	0.22	0.42	0.56	0.47	0.56	46.8	0.27	0.35
D2	low	1	0.97	0.71	13.5	0.71	40.5	0.44	58.3	0.56	68.3	0.27	0.38
D3	med.	0.99	0.93	2.54	59.54	0.71	172	0.56	271	2.78	288	0.28	0.72
D4	high	0.99	-	2.54	-	1.58	-	0.57	-	2.78	-	0.28	-

Open in a new tab

Table 2.

Comparison of Gradient (Grad.) bl., averaging (Avg.), replacement (Rep.), and averaging with deblurring (ADB).

Data	Blur	SSIM				RMSE				PSNR
Data	Blur	Grad.	Avg.	ADB	Rep.	Grad.	Avg.	ADB	Rep.	Grad.	Avg.	ADB	Rep.
D2	low	0.991	0.987	0.985	0.983	1.32	1.47	1.50	1.62	45.58	44.68	44.5	43.84
D3	medium	0.985	0.979	0.977	0.971	1.81	1.91	1.98	2.18	42.85	42.38	42.0	41.23
D4	high	0.971	0.960	0.953	0.931	2.46	2.89	3.07	3.84	40.14	38.73	38.2	36.25

Open in a new tab

Finally, our algorithm is tested on 3 sequences of Mesentery images. The stitching results is presented in Fig. 6. Average time per frame for these sequences are: 0.4029, 0.3526 and 0.3830 seconds. We tried to mosaic these sequences with PSS [1, 2]. PSS method fails (crashes) to match motion blurred frames at some point due to lack of strong keypoints as explained in Fig. 7. Additionally, we also implemented SURF-based Translation (ST) model which requires only 1 feature match between two frames. Though this method can mosaic a whole sequence, unfortunately, it comes with lots of misregistration as shown in Fig. 7. The summary of the experiments are presented in Table 3.

Fig. 7. — Failure of SURF-based methods for *Sequence*₅. (a) feature detection and matching failure in (PSS)/AutoStitch [1, 2], only 2 matches are found, at least 4 is required for projective transformation in PSS. (b) PSS can mosaic only 47 frames (out of 956). (c) SURF with Translation (ST) model implemented by us; it can mosaic all frames as it requires 1 feature point match only but misregisters lot of frames as highlighted. (d) ST result in zoomed-in scale.

Table 3.

Comparison of the proposed DNCC, SURF-based Translation (ST) and PSS [1, 2] for Mesentery sequences.

Data (#fr.)	Frames Processed			Reason for Failure
Data (#fr.)	DNCC	ST	PSS	ST	PSS
$M_{3}$ (491)	491	491	22	matching	feature
$M_{4}$ (770)	770	770	81	matching	feature
$M_{5}$ (956)	956	956	47	matching	feature

Open in a new tab

Fig. 5 compares Gradient blending with average blending with raw frames and deblurred frames. From this example, it is comprehensible that proposed Gradient blending outperforms alpha-blending even after the attempt of restoration of original image structure by deblurring [20, 21].

4. DISCUSSION

In this paper we present a mosaicing algorithm for stitching motion-blurred, low-textured and feature-poor Frog Mesentery sequences. The novelty of our algorithm is the introduction of 3×3 non-overlapping block matching with RANSAC for filtering out false correspondences. We also propose a gradient-based blending method that offers high quality blending in presence of motion-blurred frames.

Currently the algorithm uses fixed size search window for NCC which is unnecessary when motion is slow. For efficiency, we want to introduce adaptive search window according to pairwise image motion. In addition, we plan to introduce deep learning based correlation matching for deep registration. Beside, we would like to apply histogram matching for more color-uniform blending.

5. ACKNOWLEDGMENTS

We gratefully acknowledge the support of the U. S. National Institute of Neurological Disorders and Stroke award R01-NS110915, the U.S. Army Research Laboratory project W911NF-18-2-0285, the U. S. National Science Foundation grant MCB-1122130, and the Executive Womens Forum.

6. REFERENCES

[1].Brown M and Lowe DG, “Automatic panoramic image stitching using invariant features,” International journal of computer vision, vol. 74, no. 1, pp. 59–73, 2007. [Google Scholar]
[2].Matlab Feature Based Panoramic Image Stitching, 2019. (accessed February 3, 2020). [Google Scholar]
[3].Bedard N, Quang T, Schmeler K, Richards-Kortum R, and Tkaczyk TS, “Real-time video mosaicing with a high-resolution microendoscope,” Biomedical optics express, vol. 3, no. 10, pp. 2428–2435, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
[4].Lang RT, Tatz J, Kercher EM, Palanisami A, Brooks DH, and Spring BQ, “Multichannel correlation improves the noise tolerance of real-time hyperspectral microimage mosaicking,” Journal of Biomedical Optics, vol. 24, no. 12, pp. 126002, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
[5].Rosa B, Erden MS, Vercauteren T, Herman B, Szewczyk J, and Morel G, “Building large mosaics of confocal edomicroscopic images using visual servoing,” IEEE Transactions on Biomedical Egineering, vol. 60, no. 4, pp. 1041–1049, 2012. [DOI] [PubMed] [Google Scholar]
[6].Loewke KE, Camarillo DB, Piyawattanametha W, Mandella MJ, Contag CH, Thrun S, and Salisbury JK, “In vivo micro-image mosaicing,” IEEE Transactions on Biomedical Engineering, vol. 58, no. 1, pp. 159–171, 2010. [DOI] [PubMed] [Google Scholar]
[7].Piccinini F, Bevilacqua A, and Lucarelli E, “Automated image mosaics by non-automated light microscopes: the micromos software tool,” Journal of Microscopy, vol. 252, no. 3, pp. 226–250, 2013. [DOI] [PubMed] [Google Scholar]
[8].Yigitsoy M and Navab N, “Structure propagation for image registration,” IEEE Transactions on Medical Imaging, vol. 32, no. 9, pp. 1657–1670, 2013. [DOI] [PubMed] [Google Scholar]
[9].Abeytunge S, Li Y, Larson BA, Peterson G, Seltzer E, Toledo-Crow R, and Rajadhyaksha M, “Confocal microscopy with strip mosaicing for rapid imaging over large areas of excised tissue,” Journal of Biomedical Optics, vol. 18, no. 6, pp. 061227, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
[10].Peterson G, Zanoni DK, Ardigo M, Migliacci JC, Patel SG, and Rajadhyaksha M, “Feasibility of a video-mosaicking approach to extend the field-of-view for reflectance confocal microscopy in the oral cavity in vivo,” Lasers in Surgery and Medicine, vol. 51, no. 5, pp. 439–451, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
[11].Yang G and Stewart CV, “Covariance-driven mosaic formation from sparsely-overlapping image sets with application to retinal image mosaicing,” in IEEE Computer Vision and Pattern Recognition, 2004, vol. 1. [Google Scholar]
[12].Choe TE, Cohen I, Lee M, and Medioni G, “Optimal global mosaic generation from retinal images,” in Int. Con. on Pattern Recognition, 2006, vol. 3, pp. 681–684. [Google Scholar]
[13].Li J, Chen H, Yao C, and Zhang X, “A robust feature-based method for mosaic of the curved human color retinal images,” in Int. Conf. on BioMedical Engineering and Informatics, 2008, vol. 1, pp. 845–849. [Google Scholar]
[14].Ghassabi Z, Shanbehzadeh J, Sedaghat A, and Fatemizadeh E, “An efficient approach for robust multi-modal retinal image registration based on ur-sift features and piifd descriptors,” Journal on Image and Video Processing, vol. 2013, no. 1, pp. 25, 2013. [Google Scholar]
[15].Aktar R, Aliakbarpour H, Bunyak F, Seetharaman G, and Palaniappan K, “Performance evaluation of feature descriptors for aerial imagery mosaicking,” in IEEE Applied Imagery Pattern Recognition Workshop, 2018. [Google Scholar]
[16].Aktar R, Prasath VBS, Aliakbarpour H, Sampathkumar U, Seetharaman G, and Palaniappan K, “Video haze removal and poisson blending based mini-mosaics for wide area motion imagery,” in IEEE Applied Imagery Pattern Recognition Workshop, 2016. [Google Scholar]
[17].Aktar R, “Automatic geospatial content summarization and visibility enhancement by dehazing in aerial imagery,” in MS Thesis. 2017, University of Missouri-Columbia. [Google Scholar]
[18].Hafiane A, Palaniappan K, and Seetharaman G, “Uav-video registration using block-based features,” in IEEE International Geoscience and Remote Sensing Symposium, 2008, vol. 2, pp. 1104–1107. [Google Scholar]
[19].Fischler MA and Bolles RC, “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography,” Communications of the ACM, vol. 24, no. 6, pp. 381–395, 1981. [Google Scholar]
[20].Matlab, Deblurring of Image, 2019. (accessed February 6, 2020). [Google Scholar]
[21].Holmes TJ, Bhattacharyya S, Cooper JA, Hanzel D, Krishnamurthi V, Lin W, Roysam B, Szarowski DH, and Turner JN, “Light microscopic images reconstructed by maximum likelihood deconvolution,” in Handbook of Biological Confocal Microscopy, pp. 389–402. Springer, 1995. [Google Scholar]

[R1] [1].Brown M and Lowe DG, “Automatic panoramic image stitching using invariant features,” International journal of computer vision, vol. 74, no. 1, pp. 59–73, 2007. [Google Scholar]

[R2] [2].Matlab Feature Based Panoramic Image Stitching, 2019. (accessed February 3, 2020). [Google Scholar]

[R3] [3].Bedard N, Quang T, Schmeler K, Richards-Kortum R, and Tkaczyk TS, “Real-time video mosaicing with a high-resolution microendoscope,” Biomedical optics express, vol. 3, no. 10, pp. 2428–2435, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] [4].Lang RT, Tatz J, Kercher EM, Palanisami A, Brooks DH, and Spring BQ, “Multichannel correlation improves the noise tolerance of real-time hyperspectral microimage mosaicking,” Journal of Biomedical Optics, vol. 24, no. 12, pp. 126002, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] [5].Rosa B, Erden MS, Vercauteren T, Herman B, Szewczyk J, and Morel G, “Building large mosaics of confocal edomicroscopic images using visual servoing,” IEEE Transactions on Biomedical Egineering, vol. 60, no. 4, pp. 1041–1049, 2012. [DOI] [PubMed] [Google Scholar]

[R6] [6].Loewke KE, Camarillo DB, Piyawattanametha W, Mandella MJ, Contag CH, Thrun S, and Salisbury JK, “In vivo micro-image mosaicing,” IEEE Transactions on Biomedical Engineering, vol. 58, no. 1, pp. 159–171, 2010. [DOI] [PubMed] [Google Scholar]

[R7] [7].Piccinini F, Bevilacqua A, and Lucarelli E, “Automated image mosaics by non-automated light microscopes: the micromos software tool,” Journal of Microscopy, vol. 252, no. 3, pp. 226–250, 2013. [DOI] [PubMed] [Google Scholar]

[R8] [8].Yigitsoy M and Navab N, “Structure propagation for image registration,” IEEE Transactions on Medical Imaging, vol. 32, no. 9, pp. 1657–1670, 2013. [DOI] [PubMed] [Google Scholar]

[R9] [9].Abeytunge S, Li Y, Larson BA, Peterson G, Seltzer E, Toledo-Crow R, and Rajadhyaksha M, “Confocal microscopy with strip mosaicing for rapid imaging over large areas of excised tissue,” Journal of Biomedical Optics, vol. 18, no. 6, pp. 061227, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] [10].Peterson G, Zanoni DK, Ardigo M, Migliacci JC, Patel SG, and Rajadhyaksha M, “Feasibility of a video-mosaicking approach to extend the field-of-view for reflectance confocal microscopy in the oral cavity in vivo,” Lasers in Surgery and Medicine, vol. 51, no. 5, pp. 439–451, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] [11].Yang G and Stewart CV, “Covariance-driven mosaic formation from sparsely-overlapping image sets with application to retinal image mosaicing,” in IEEE Computer Vision and Pattern Recognition, 2004, vol. 1. [Google Scholar]

[R12] [12].Choe TE, Cohen I, Lee M, and Medioni G, “Optimal global mosaic generation from retinal images,” in Int. Con. on Pattern Recognition, 2006, vol. 3, pp. 681–684. [Google Scholar]

[R13] [13].Li J, Chen H, Yao C, and Zhang X, “A robust feature-based method for mosaic of the curved human color retinal images,” in Int. Conf. on BioMedical Engineering and Informatics, 2008, vol. 1, pp. 845–849. [Google Scholar]

[R14] [14].Ghassabi Z, Shanbehzadeh J, Sedaghat A, and Fatemizadeh E, “An efficient approach for robust multi-modal retinal image registration based on ur-sift features and piifd descriptors,” Journal on Image and Video Processing, vol. 2013, no. 1, pp. 25, 2013. [Google Scholar]

[R15] [15].Aktar R, Aliakbarpour H, Bunyak F, Seetharaman G, and Palaniappan K, “Performance evaluation of feature descriptors for aerial imagery mosaicking,” in IEEE Applied Imagery Pattern Recognition Workshop, 2018. [Google Scholar]

[R16] [16].Aktar R, Prasath VBS, Aliakbarpour H, Sampathkumar U, Seetharaman G, and Palaniappan K, “Video haze removal and poisson blending based mini-mosaics for wide area motion imagery,” in IEEE Applied Imagery Pattern Recognition Workshop, 2016. [Google Scholar]

[R17] [17].Aktar R, “Automatic geospatial content summarization and visibility enhancement by dehazing in aerial imagery,” in MS Thesis. 2017, University of Missouri-Columbia. [Google Scholar]

[R18] [18].Hafiane A, Palaniappan K, and Seetharaman G, “Uav-video registration using block-based features,” in IEEE International Geoscience and Remote Sensing Symposium, 2008, vol. 2, pp. 1104–1107. [Google Scholar]

[R19] [19].Fischler MA and Bolles RC, “Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography,” Communications of the ACM, vol. 24, no. 6, pp. 381–395, 1981. [Google Scholar]

[R20] [20].Matlab, Deblurring of Image, 2019. (accessed February 6, 2020). [Google Scholar]

[R21] [21].Holmes TJ, Bhattacharyya S, Cooper JA, Hanzel D, Krishnamurthi V, Lin W, Roysam B, Szarowski DH, and Turner JN, “Light microscopic images reconstructed by maximum likelihood deconvolution,” in Handbook of Biological Confocal Microscopy, pp. 389–402. Springer, 1995. [Google Scholar]

PERMALINK

MOSAICING OF DYNAMIC MESENTERY VIDEO WITH GRADIENT BLENDING

Rumana Aktar

V H Huxley

G Guidoboni

H AliAkbarpour

F Bunyak

K Palaniappan

Abstract

1. INTRODUCTION

2. METHODS

2.1. Correlation-Based Registration and Mosaicing

Fig. 1.

2.2. Deformable Normalized Cross Correlation (DNCC)

Fig. 3.

Fig. 2.

2.3. Gradient Blending of frame, F_i With Mosaic, $M_{i - 1}$

Fig. 4.