Abstract
Under the ceaseless global COVID-19 pandemic, lung ultrasound (LUS) is the emerging way for effective diagnosis and severeness evaluation of respiratory diseases. However, close physical contact is unavoidable in conventional clinical ultrasound, increasing the infection risk for health-care workers. Hence, a scanning approach involving minimal physical contact between an operator and a patient is vital to maximize the safety of clinical ultrasound procedures. A robotic ultrasound platform can satisfy this need by remotely manipulating the ultrasound probe with a robotic arm. This paper proposes a robotic LUS system that incorporates the automatic identification and execution of the ultrasound probe placement pose without manual input. An RGB-D camera is utilized to recognize the scanning targets on the patient through a learning-based human pose estimation algorithm and solve for the landing pose to attach the probe vertically to the tissue surface; A position/force controller is designed to handle intraoperative probe pose adjustment for maintaining the contact force. We evaluated the scanning area localization accuracy, motion execution accuracy, and ultrasound image acquisition capability using an upper torso mannequin and a realistic lung ultrasound phantom with healthy and COVID-19-infected lung anatomy. Results demonstrated the overall scanning target localization accuracy of 19.67 ± 4.92 mm and the probe landing pose estimation accuracy of 6.92 ± 2.75 mm in translation, 10.35 ± 2.97 deg in rotation. The contact force-controlled robotic scanning allowed the successful ultrasound image collection, capturing pathological landmarks.
I. Introduction
As the Coronavirus Disease 2019 (COVID-19) continues to overwhelm global medical resources, a cost-effective diagnostic approach capable of monitoring the severeness of infection on COVID-19 patients is highly desirable. Computed tomography (CT) and X-ray are considered the gold-standard diagnostic imaging for lung-related diseases [1]. However, their accessibility is growingly limited due to the overwhelming amount of COVID-19 patients around the globe [2]. Ultrasound (US) imaging, in comparison, is easier to access, more affordable, radiation-free, highly sensitive to pneumonia, and has the real-time capability [3]. Therefore lung ultrasound (LUS) becomes an alternative accessible approach to diagnose COVID-19 and other contagious lung pathology (e.g., in medical equipment restricted places) [4]. An effective LUS scans a wide area of the chest. Several protocols are introduced to standardize the LUS procedure. Bedside LUS in an emergency modified (BLUE) protocol [5] is an accepted standard in which the anterior chest area is divided into a few regions, and the centroid of each region is considered the scanning target. The operator places the US probe perpendicularly on each target with an appropriate amount of force applied, followed by fine-tuning movements to search for pathological features, and all the targets are to be covered sequentially. However, the LUS procedure is highly operator-dependent and requires physical contact between the operator and patient for a substantial amount of time, increasing the operator’s vulnerability. A less contact-intensive LUS procedure could significantly reduce transmission risk when handling patients with infective respiratory diseases but is difficult to achieve with conventional freehand US. The robotic US (RUS), which uses a robot manipulator equipped with an US transducer to perform an US scan, on the other hand, is a feasible solution to address the clinical need by isolating patients from operators [6]. In recent years, RUS has been actively studied to augment human-operated US [7], [8] for various clinical applications, including thyroid [9], [10], spine [11], vascular [12], [13] and joint [14] imaging. To assure the safety and efficacy of the RUS system, the scanning procedure should be close to the real clinical practice and should avoid excessive pressure being applied on the patient [15].
A. Related Works
Attempts have been made to develop tele-operative RUS systems for LUS applications. Tsumura et al. proposed a gantry-based platform for LUS using a novel passive-actuated force control mechanism that maintains constant contact force with the patient while achieving a large workspace [16]. Ye et al. implemented a remote teleoperated RUS system communicating via 5G network which was deployed to Wuhan, China, for COVID-19 patient diagnosis [17].
Though tele-operative systems allow remote and contact-less US imaging, the procedure is still heavily operator-dependent and may require special training on the user. In this sense, RUS systems with higher-level autonomy could be more clinically valuable. Huang et al. demonstrated a framework using an RGB-D camera to segment the scanning target via color thresholding, meanwhile computing the desired probe position and orientation from the point cloud data [18]. Virga et al. and Hennersperger et al. adopted the patient-to-MRI registration to solve for the probe pose that covers the organ to be examined [19], [20], Yorozu et al. and Jiang et al. implemented US confidence map [21] to find the optimal probe in-plane orientation for maximizing the US signal quality [22], [23]. Similarly, Visual-servoing is applied to adjust the probe’s rotation so that the artifact of interest is centered in the field of view (FOV) in the US image [24], [26], [27].
The workflow of a RUS system can be decomposed into two phases. In the first phase, the scanning target is identified in 3D space. A rough probe landing pose is estimated and converted into robot motion. The second phase further optimizes the probe placement, aiming to obtain a high-quality US image while assuring patient’s safety. While several previous studies have investigated the US probe placement optimization [18] – [27], few works explicitly tackle the first phase. Many of them (e.g. [19], [20]) require pre-operative inputs such as CT/MRI scan for each patient, compromising cost-effectiveness and accessibility. Some adopt patient recognition methods such as color thresholding (e.g. [18]), which involves environmental constraints, requiring further generalization. Without first automating the first phase, the second phase can hardly eliminate manual assistance for initial positioning, therefore downgrading the autonomous RUS approach.
B. Contribution
This work focuses on the scanning target localization, highlighted as the first phase in the previous section, to bring the autonomous RUS a step forward. The scanning targets are designed based on the BLUE protocol that has been used for LUS. For the purpose of recognizing scanning targets automatically and dynamically and being less subject to an individual patient, we implement a learning-based human pose estimation algorithm using an RGB-D camera in real-time. RGB images are used to localize targets first in 2D, and then the detected 2D targets are extended to 3D by combining with depth sensing. We also develop the pipeline of implementing the target localization with the RUS execution. A serial manipulator places the US probe vertical to each target based on the previous-step localization with the desired contact force. Once the probe is placed automatically, the operator can perform the further pose refinement manually by observing real-time US images displayed, as semi-autonomous scanning. The contributions of this work fold under two aspects. i) We introduce the novel framework for autonomous robotic US probe placement based on scanning target localization without requiring manual input. The pipeline combines human segmentation in 2D and vertical landing pose calculation in 3D for robotic US probe placement. ii) We implement and evaluate the safety and efficacy of the semi-autonomous RUS system for LUS diagnosis by imaging an upper torso mannequin and a lung ultrasound phantom.
II. Materials and Methods
This section introduces the implementation detail of the proposed system. The proposed system will automatically recognize the pre-assigned scanning region through visual sensing and determine the position and orientation for the US probe placement at the right spot with desired contact force using a robotic arm. The workflow can be presented in three major tasks: Task 1) RGB image-based perception that segments the patient torso from the background and localizes the desired scanning targets on the patient’s body in 2D; Task 2) US probe pose identification in 3D by converting the target localized in 2D to 3D transformation describing the robot’s end-effector pose through depth sensing. The probe is set perpendicular to the tissue surface, given that such placement grants the maximum echo signals for collecting good US image quality [25]; Task 3) Robot position/force control scheme that determines the trajectory generation and path planning and controls the US probe placement with desired contacting force applied for safety and compliance.
As the implementation overview, the state-of-art 3D human dense pose estimation pipeline, DensePose, is applied to segment the human body from the background and map human anatomical locations as pixels in the image frame to vertices on the 3D skinned multi-person linear (SMPL) mesh model [28] (for Task 1). An RGB-D camera (D435i, RealSense, Intel, USA) is used to implement Task 2. The RGB image is used to infer the scanning targets with DensePose, and the depth image is used for solving the 3D normal pose of the probe. For Task 3, a velocity-based controller with position/force feedback is implemented on the 7 degree-of-freedom (DoF) robotic arm (Panda, Franka Emika, Germany), which holds an US transducer. Finally, the above components are integrated and can be executed as an interconnected system.
A. Scanning Target Recognition with DensePose
DensePose uses the Mask R-CNN for instance segmentation and regresses the 2D coordinates representing anatomical locations as vertices on the SMPL model. It outputs a 3-channel matrix with the same dimension as the input image (see Fig. 1a). The first channel is the classification for each pixel (the class ID ranges from 0 to 24, where 0 refers to the background, 1 to 24 each corresponds to a part of the body, e.g., head, arm, leg, etc.). The second and third dimensions, denoted as set U and V, are the mapped 2D human mesh coordinates consisting of u (vertical) and v (horizontal) coordinates for all body parts. A 2D pixel [r, c]⊤ can be one-to-one mapped into human mesh coordinates as [u = U(r, c), v = V (r, c)]⊤. To map from mesh coordinates [u, v]⊤ to a pixel [r, c]⊤, which is not guaranteed to be one-to-one, (1) is adopted, where n is the number of possible [ri, ci]⊤ pairs.
Fig. 1.
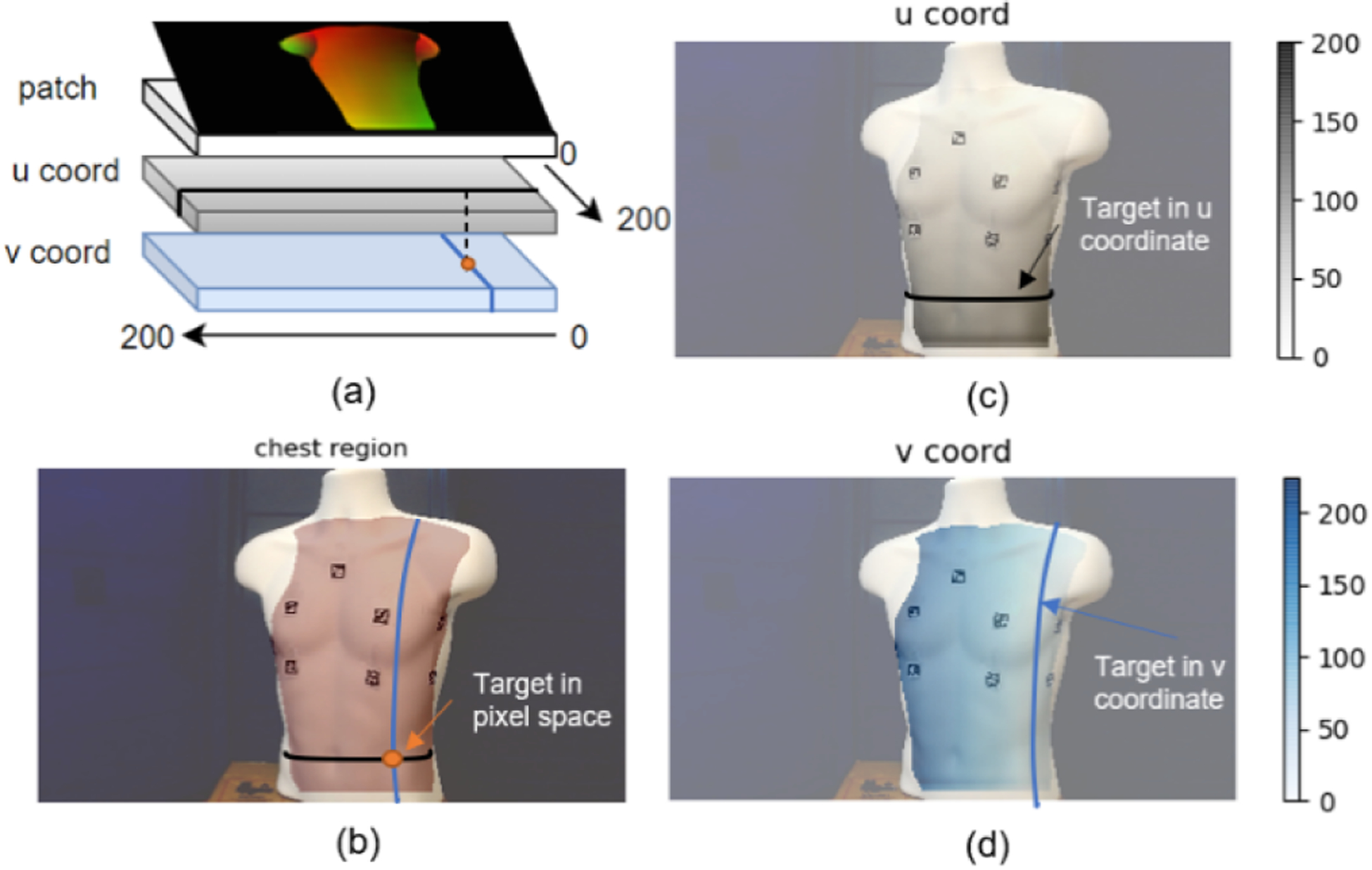
An example visualization of extracting chest region using Dense-Pose. a) shows DensePose output format. b) shows the anterior chest region mask overlaid on the input image. c) shows the vertical u coordinate of the mapping from each pixel on chest region to the SMPL model. d) shows the horizontal v coordinate of the same mapping. b)-d) are from our previous work in [29].
| (1) |
A graphical interpretation of the above workflow can be seen in Fig. 1b–d. The desired targets to be automatically detected must first be specified in [u, v]⊤. Then, these targets in the pixel [r, c]⊤ can be solved from arbitrary camera pose relative to the patient using (1) but referring to the same position on the chest ideally. The detailed implementation to define the reference target locations [u, v]⊤ will be covered in Section III.
B. 3D Probe Pose Computation
Based on the recognized 2D scanning targets in the image space, we need to compute the end-effector pose of the robot under the camera frame normal to the scanning surface, expressed as a transformation matrix (3). Depth information is used to bridge 2D to 3D. We first align the depth frame to the color frame to ensure the 2D targets in the color image remain unchanged in the depth image before applying spatial filtering and hole filling techniques to smoothen the depth data. The deprojection operation , which maps a pixel in the depth image to a 3D point in the point cloud, is provided as an API in RealSense SDK. Therefore, a general 2D target P0 can correspond to the 3D point in the point cloud through .
The calculation of the surface normal originated at is illustrated in Fig. 2. 3 unique points on a surface are required to determine the normal vector of a given surface. However, the depth measure introduces a significant amount of noise that leads to fluctuating 3D coordinates reading. Our solution is to find supplementary points neighboring to the target, providing additional normal vectors that can be averaged into a steady one. After specifying P0, 8 more points (P1 to P8 in Fig. 2b) are indexed from the depth image such that they form a square patch with edge length L. Inside the patch, 8 sub-planes, each consisting of 3 points, can be found (S1 to S8 in Fig. 2b). Deprojection of P0 to P8 results in a surface where each sub-plane contributes a normal vector. Averaging and normalizing all 8 normal gives the estimated surface normal Vavg (see Figs. 3c–d).
Fig. 2.

Mapping of a 2D target to a 3D pose. a) DensePose output from an input image. The red mask is the segmented chest area, R1 to R4 are the scanning regions in [5], the center of the white circles marked with 1 to 4 corresponds to the 2D scanning targets. b) The generated patch in image space. c) The deprojected patch in 3D and the calculation of one sub-plane normal vector V12 given by . d) The averaged normal vector Vsum (dashed orange line) by summing all sub-plane normal (solid orange line) and its normalized unite vector Vavg (solid blue line).
Fig. 3.
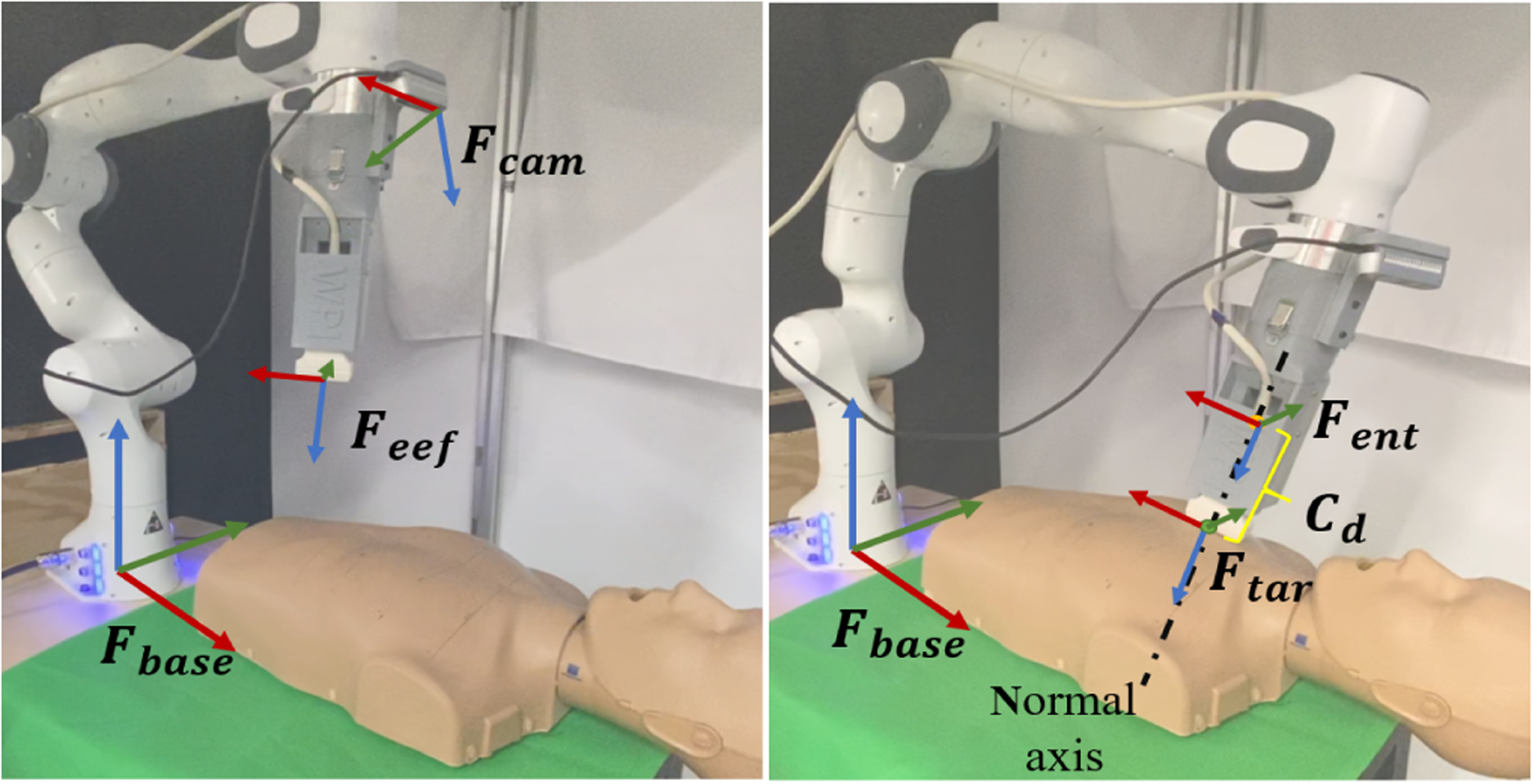
Robot setup and coordinate frame convention. The left figure shows the robot’s home configuration and its coordinate frame definitions. The right figure shows the robot working under contact mode. Cd is the displacement along the normal. (red arrow represents x-aixs, green represents y-axis, blue represents z-axis)
The desired end-effector pose under the camera frame can be decomposed into the rotational part Rtar ∈ SO(3) and the translational part . The approach vector Vz in the rotation matrix should be −Vavg so that it points out-wards from the end-effector tip, leaving only the orientation vector Vx of the probe’s long axis undetermined. In lung examination, the long axis is usually parallel to the body’s midsagittal plane to visualize the ribs. In our case, Vx should be parallel to the x-axis of the robot base frame, then Vy can be calculated according to the right-hand rule. The final target pose is given in (2).
| (2) |
C. Position and Force Control of the Robot
The Franka Emika 7-DoF manipulator provides a direct Cartesian space control interface and is equipped with joint torque sensors in all 7 joints, making task space wrench estimation possible. The hardware setup of the robot can be seen in Fig. 3: we designed an end-effector in [10] that holds a linear ultrasound probe and the RealSense camera, mounted to the flange of the manipulator. Based on the mechanical data of the end-effector, the transformation from the end-effector frame Feef to the camera frame Fcam is obtained. Further, the transformation from the target frame Ftar to the robot base frame Fbase can be solved from (3).
| (3) |
The robot operates under two different modes: non-contact mode for executing non-collision motion and contact mode for maintaining constant contact force with the tissue surface. For safety considerations, an entry pose Fent above the target pose Ftar along Vavg with displacement Cd is set as the goal under non-contact mode instead of Ftar. Once the entry pose Fent is reached, the robot enters contact mode where force is exerted by reducing Cd (see Fig. 3). The equation to set Cd is given below:
| (4) |
where kp is the proportional gain, is the desired contact force along the end-effector’s z-axis, which in our case is set to 5 N, Fz is the estimated force along the end-effector’s z-axis read directly from the robot. With the orientation unchanged, the new translational component after applying Cd is:
| (5) |
The control to the robot is a task space twist defined as [vx, vy, vz, wx, wy, wz], representing linear velocities along x, y, z axes and angular velocities along the three axes. The rotation part of is converted to roll pitch and yaw angles to ease angular velocity calculation. A PD controller is implemented to command end-effector velocity using errors of translational components and roll pitch yaw angles, as well as derivative of the errors. The elbow joint angle is limited to 180 degrees to avoid singularities.
D. System Integration
The overall system diagram and a flowchart of the LUS procedure using the developed system are shown in Fig. 4. The software architecture in Fig. 4a is built upon ROS (Robot Operating System). DensePose runs at 2fps on 480 by 480 image input to infer the scanning targets, which are later converted to end-effector poses in terms of translational goal and rotational goal relative to the robot base by incorporating with depth sensing and robot pose measurement. Motion errors are then calculated to be fed into the PD controller, which gives the velocity twist command to the robot. Mean-while, a state machine is designed to determine a Boolean variable isContact that controls the switch between contact mode and non-contact mode. isContact is assigned to 1 if the robot’s motion error is within the sufficiently small threshold (2 mm in translation, 0.03 rad in rotation) and 0 elsewhere.
Fig. 4.

System Integration. a) The hardware & software integration of the proposed RUS system. b) The workflow of the system to perform the LUS scanning. c) The robot configuration when scanning each of the four anterior targets.
Fig. 4b presents the implemented workflow of the LUS procedure: 4 targets are computed and queued at the beginning of the procedure. The robot reaches the targets sequentially and stays on each target for 20 seconds for US image acquisition.
III. Experimental Setup
In this section, experiments are designed to validate the proposed RUS system. The experimental evaluations of the system are formulated as: i) 2D scanning target localization, ii) 3D probe pose calculation, iii) Robot motion control, and iv) US image acquisition. i) is the foundational step for accurately localizing scanning targets from a 2D image before ii) can be built upon i) to determine the correct probe placement. iii) guarantees i) and ii) to be precisely translated into actual robot motion. Lastly, iv) using the proposed RUS system serves the evaluation of the entire procedure.
A. Validation of 2D Scanning Targets Localization
We aim to localize four scanning targets on the anterior chest using the DensePose based framework and quantitatively evaluate the influence of subject positioning on the localization accuracy. A mannequin (CPR-AED Training Manikin, Prestan, USA) with human-mimicking anterior anatomy is used as the experiment subject. As stated in section II, the targets need to be specified in [u, v]⊤. We place four ArUco markers empirically on the mannequin and read their centroid positions in the image while simultaneously running DensePose to acquire U and V data. The robot is configured at the home position during this process because DensePose achieves the best accuracy and stability when the input image captures the front view of the mannequin. The scanning targets in [u, v]⊤ can be obtained by plugging the markers’ centroid positions into U and V, The targets in image coordinates are then localized using (1). To quantify the localization accuracy, we keep the markers on the mannequin and use their centroid position as the ground truth, then place the mannequin at different locations. The mannequin is translated horizontally and vertically on the test table plane, altogether covering 15 locations starting from the default location. The 2D targets are calculated using DensePose at each location and sampled 100 times before being compared with the ground truth.
B. Validation of 3D Probe Pose Calculation
The 3D probe pose calculation is evaluated through the preciseness of 3D target point localization and normal vector calculation. Without loss of generality, a 3 by 4 virtual grid (see Fig. 6a) covering a whole anterior chest area, including the four anterior targets, is overlaid on the same mannequin. We place the ArUco marker at the center of each cell and estimate its 3D pose with OpenCV, knowing the camera intrinsic. The translational component and the approach vector of the marker’s pose are used as the 3D target ground truth and normal vector ground truth, respectively. We then deproject the 2D target at the center of the marker to 3D using the depth camera and calculate the normal vector using our patch-based method to get an estimation of the same variables and calculate the error accordingly. Similar to the validation in A., the error contains 100 samples to exhibit the stability of the calculation.
Fig. 6.

Validation of 3D probe pose. a) The virtual gird overlay placed on top of the mannequin, where cell (1,2), (1,3), (2,2), (2,3) cover the four anterior targets respectively. b) The error of the targets’ 3D position (top) and the error of their normal vectors (bottom). The error bar reflects the standard deviation.
C. Validation of Robot Motion
Based on the defined target, we examine the robot’s motion when moving to the designated pose using the mannequin above. The system runs in a complete loop as depicted in Fig. 4b, covering all four anterior targets. The robot motion data is logged at a frequency of 10 Hz.
D. Validation of US Image Acquisition and Force Control
To evaluate the imaging capability of the proposed semi-autonomous RUS system, a lung phantom (COVID-19 Live Lung Ultrasound Simulator, CAE Blue Phantom™, USA) simulating healthy lung and pathological landmarks (thickened pleural lining, diffused bilateral B-lines, sub-pleural consolidation) is used as the testing subject. The phantom simulates the respiratory motion of the lung during breathing as well. Since the phantom geometry is limited to the left anterior chest and does not have any external body feature for DensePose to recognize, the 2D scanning targets are assigned manually. Diagnostic landmarks are supposed to be observable in the US image if the system is effective. Comparing with the mannequin, the rigidity of the phantom is closer to the actual human chest; hence we recorded the end-effector force at 10 Hz during scanning to validate the force control.
IV. Results
A. Evaluation of 2D Scanning Targets
Fig. 2a shows the inferred 2D scanning targets on the mannequin when placed at the default location with 0 horizontal and vertical offset. Fig. 5 shows the error, defined as the Euclidean distance between the averaged pixel position of the inferred targets and the ground truth with respect to varied mannequin locations. The averaged errors for the four targets in pixels are 20.97 ± 5.40, 26.59 ± 6.36, 21.95 ± 6.28 and 25.31 ± 5.67, approximately corresponding to 17.41 ± 4.48 mm, 22.07 ± 5.28 mm, 18.22 ± 5.21 mm, and 21.00 ± 4.71 mm, respectively, showing good reproducible 2D localization precision. The bounding region (see Fig. 2a) of each scanning target is roughly 70 mm by 70 mm in size; hence the errors account for 21% to 34% of the region’s diagonal length, which is considered satisfactory for a rough landing. Such rough landing can be corrected through the following manual refinement of the probe placement.
Fig. 5.

Validation of 2D scanning targets. VERT and HORIZ correspond to vertical and horizontal direction of the test table respectively. 0 offset is the default location to place the mannequin. The error bar reflects the standard deviation.
B. Evaluation of 3D Probe Pose
The distribution of the errors on the virtual grid is shown in Fig. 6b, where the rotational error is defined as the absolute angle difference between the estimated and ground truth normal vectors, the translational error is defined as the Euclidean distance between the 3D target point measured using the depth camera and the ground truth. In terms of translation, the mean error for all the cells is 7.76 ± 2.71 mm, among which around 59% are along the z direction of the camera frame, whereas errors along x and y direction are mostly ignorable. The rotation error for all the cells is 12.61 ± 3.32 deg. In cells containing the anterior scanning targets, the mean translational error is 6.92 ± 2.75 mm, and the mean rotational error is 10.35 ± 2.97 deg, both of which are lower than the all-inclusive mean and meet our rough landing requirement. Nonetheless, the unbalanced scattering of errors suggests the necessity to improve consistency.
C. Evaluation of Robot Motion
The recorded robot motion is shown in Fig. 7. The errors when moving to entry poses are calculated by subtracting the current end-effector pose from the entry pose (defined as Fent in Fig. 3) of each target; the errors when moving to target poses are calculated by subtracting the current end-effector pose from the target pose (defined as Ftar in Fig. 3). From the plot, both translational and rotational errors converge when moving to the entry poses, proving the effectiveness of the PD controller. While rotational error continues to stay low when reaching the target poses, the steady-state error is noticed in the z direction in translation.
Fig. 7.
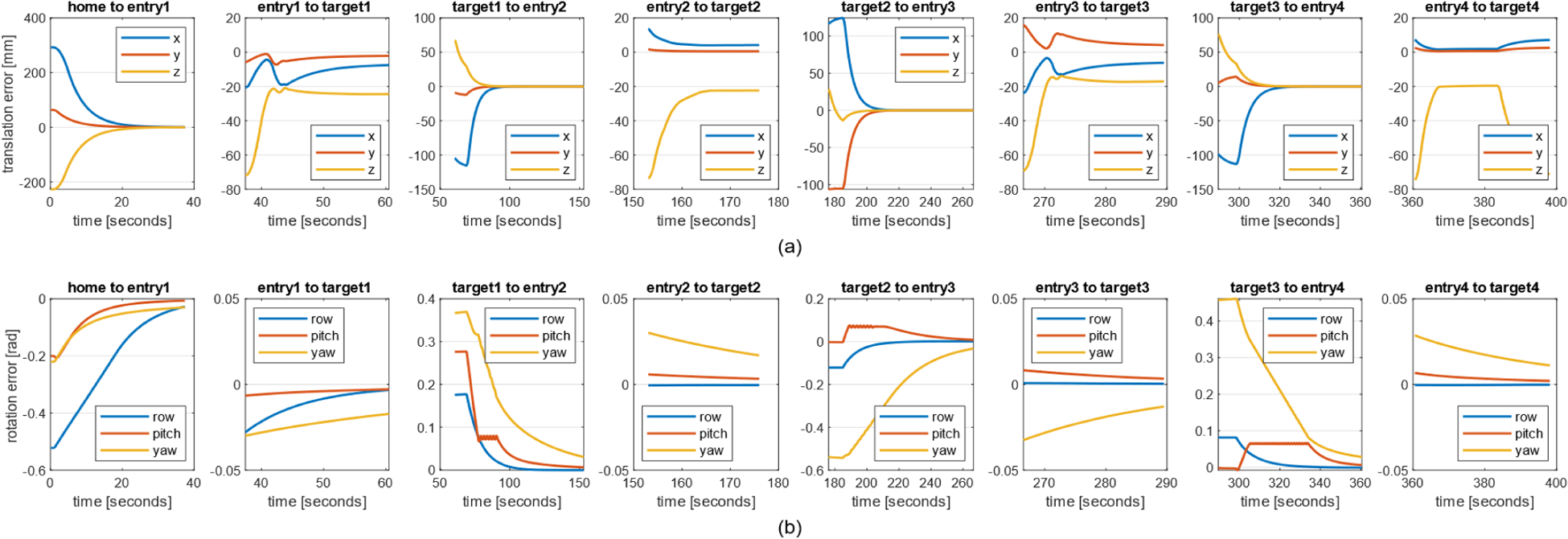
Recorded robot motion when executing the trajectory for targets 1 to 4 a) The translational error relative to the robot base. b) The rotational error relative to the robot base.
D. Evaluation of US Imaging and Force Control
Representative US images when setting the desired constant contact force at 5 N are shown in Fig. 8c. The healthy part of the phantom (target A) presented no respiratory abnormality where the rib and pleural lines are clearly visible. The thickened plural lines were imaged in the other part of the phantom (target B), simulating typical pathological abnormalities that appear in COVID-19 patients. Capturing these features supports the effectiveness of the proposed probe placement approach, including the probe orientation control and desired contact force selection. The appearance of air gaps on the top-left corner suggests further image quality improvement through manual fine adjustment. The recorded force while turning on the breathing motion is shown in Fig. 8b. The error was stabilized at around 70% of the desired force with limited oscillation even during breathing. However, zero-drifting can be observed before landing, along with an overshoot of 1 N when scanning target B, indicating room for further optimization.
Fig. 8.

Results scanning the lung phantom. a) The lung phantom picture with the two manually selected scanning targets labeled as A and B, respectively. The target A simulates the lung of healthy patients and the target B simulates that of the COVID-19 patients. b) The logged end-effector force when scanning targets A and B during the presence of respiratory motion. c) Example US images collected at target A and target B, respectively.
V. Discussion and Conclusions
This manuscript presents a feasibility study of the scanning target localization based on a neural network-driven architecture to support its extension toward autonomous RUS scanning. It is worth noticing that our system has considerable extensibility: the scanning protocol adopted is applicable to not only COVID-19 patients but also general LUS procedures. Moreover, DensePose can classify the human body into 23 parts, and these classes can potentially be used for automating US scans on other anatomical regions based on a similar implementation pipeline.
Evaluations on 2D target localization and 3D pose calculation accuracy imply an overall 2D scanning target localization accuracy of 19.67 ± 4.92 mm and 3D pose solver accuracy of 6.92 ± 2.75 mm in translation, 10.35 ± 2.97 deg in rotation. The pose solver performance using an RGB-D camera can be subject primarily to the physical environment which is indicated by the notable difference in the distribution of errors on the virtual grid caused by the unevenly lighted scan surface. The performance may be improved with a better light condition in the real-world clinical environment.
The robot motion accuracy is high, with translational error under 2 mm and rotational error under 0.03 rad. When contacting the tissue, the translation along x and y direction aligns with the pre-calculated 3D target position, evidencing good localizing of the 3D target point on the x-y plane. In Fig. 8b, the contact force is observed to stabilize at around 1.5 N below the desired value. Distinct initial force reading at time 0 and the amount of overshoot when the probe lands from different poses are also noticed. Usually, the deviation from the desired value can be alleviated by increasing the control gain, yet an overly large value will lead to a robot collision-protective behavior. A damping term in the force control law in (4) may mitigate this problem. The inconsistent initial force reading and overshoot amount imply the force sensing to be a function of the end-effector pose, which suggests our parameterization of the custom end-effector based on the CAD model is not accurate enough for the built-in gravity compensation to work properly. More advanced payload identification methods can be investigated to address the issue. Nevertheless, landmarks are visible in the collected US images and could be used for diagnosis purposes. This signifies the importance of including more US image-based evaluation over straightforward force reading when assessing the system efficacy.
Some limitations exist in this study. First, this study targets the anterior chest for detection and assumes no patient movement based on the nature of the experimental conditions. Including additional cameras in addition to the one mounted on the robot end-effector can enlarge the field of view and continuously update the patient pose, allowing the scans in the lateral and posterior chests to fully cover the modified BLUE protocol [5]; Second, the landing motion is purely force-based. Yet, ideally, US image should be incorporated as another feedback (e.g., the work in [23] uses both force and US image to adjust the probe orientation) to grant high-quality diagnostic ability; Third, the custom end-effector design has room to improve. The total length of the end-effector needs to be optimized for better dexterity. The current design requires US gel to be manually applied in advance to enhance image quality. A more compact design embedded with an automatic gel dispensing mechanism is desired; Fourth, restricted by the experiment subject, there is no evaluation of how well the 2D targets regressed from DensePose accommodate the variation of body shapes. Including human subjects in future study will allow us to assess the adaptability of the scanning target localization approach; Fifth, the patient transverse direction is assumed to be parallel to the robot base’s x axis for simplicity. The final probe alignment and adjustment are performed manually through a teleoperative control.
For future work, we will adopt a more clinically practical hardware setup (e.g., place the robot at the bedside) and incorporate scanning direction alignment based on the patient orientation and posture.
ACKNOWLEDGMENT
This research is supported by the National Institute of Health (DP5 OD028162) and the National Science Foundation (CCF 2006738).
References
- [1].Fang Y et al. , “Sensitivity of Chest CT for COVID-19: Comparison to RT-PCR,” Radiology vol. 296 (2), pp. E115–E117, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Ayebare RR, Flick R, Okware S, Bodo B, and Lamorde M, “Adoption of COVID-19 triage strategies for low-income settings,” Lancet Respir. Med, vol. 8 (4), p. e22, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Xia Y, Ying Y, Wang S, Li W, and Shen H, “Effectiveness of lung ultrasonography for diagnosis of pneumonia in adults: A systematic review and meta-analysis,” J. Thorac. Dis, vol. 8, pp. 2822–2831, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Smith MJ, Hayward SA, Innes SM, and Miller ASC, “Point-of-care lung ultrasound in patients with COVID -19 – a narrative review,” Anaesthesia, vol. 75, no. 8, pp. 1096–1104, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Lichtenstein DA, “BLUE-Protocol and FALLS-Protocol: Two applications of lung ultrasound in the critically ill,” Chest, vol. 147, no. 6, pp. 1659–1670, 2015. [DOI] [PubMed] [Google Scholar]
- [6].Priester AM, Natarajan S and Culjat MO, “Robotic Ultrasound Systems in Medicine,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 60, no. 3, pp. 507–523, 2013. [DOI] [PubMed] [Google Scholar]
- [7].Zhang HK, Finocchi R, Apkarian K and Boctor EM, “Co-robotic synthetic tracked aperture ultrasound imaging with cross-correlation based dynamic error compensation and virtual fixture control,” IEEE International Ultrasonics Symposium (IUS), 2016. [Google Scholar]
- [8].Fang TY, Zhang HK, Finocchi R, Taylor RH, and Boctor EM, “Force-assisted ultrasound imaging system through dual force sensing and admittance robot control,” Int. J. Comput. Assist. Radiol. Surg, vol. 12, no. 6, pp. 983–991, 2017. [DOI] [PubMed] [Google Scholar]
- [9].Kojcev R et al. , “On the reproducibility of expert-operated and robotic ultrasound acquisitions,” International Journal of Computer Assisted Radiology and Surgery, vol. 12, no. 6, pp. 1003–1011, 2017. [DOI] [PubMed] [Google Scholar]
- [10].Kaminski JT, Rafatzand K, and Zhang H, “Feasibilit of robot-assisted ultrasound imaging with force feedback for assessment of thyroid diseases,” Medical Imaging 2020: Image-Guided Procedures, Robotic Interventions, and Modeling, vol. 11315, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Tirindelli M et al. , “Force-Ultrasound Fusion: Bringing Spine Robotic-US to the Next “Level”,” IEEE Robotics and Automation Letters, vol. 5, no. 4, pp. 5661–5668, 2020. [Google Scholar]
- [12].Jiang Z et al. , “Autonomous Robotic Screening of Tubular Structures based only on Real-Time Ultrasound Imaging Feedback,” IEEE Transactions on Industrial Electronics, 2021. [Google Scholar]
- [13].Langsch F, Virga S, Esteban J, Göbl R and Navab N, “Robotic Ultrasound for Catheter Navigation in Endovascular Procedures,” IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 5404–5410, 2019. [Google Scholar]
- [14].Antico M et al. , “4D Ultrasound-Based Knee Joint Atlas for Robotic Knee Arthroscopy: A Feasibility Study,” IEEE Access, vol. 8, pp. 146331–146341, 2020. [Google Scholar]
- [15].Swerdlow DR, Cleary K, Wilson E, Azizi-Koutenaei B, and Monfaredi R, “Robotic arm-assisted sonography: Review of technical developments and potential clinical applications,” Am. J. Roentgenol, vol. 208 (4), pp. 733–738, 2017. [DOI] [PubMed] [Google Scholar]
- [16].Tsumura R et al. , “Tele-Operative Low-Cost Robotic Lung Ultrasound Scanning Platform for Triage of COVID-19 Patients,” IEEE Robotics and Automation Letters, vol. 6, no. 3, pp. 4664–4671, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Ye R et al. , “Feasibility of a 5G-based robot-assisted remote ultrasound system for cardiopulmonary assessment of patients with COVID-19,” Chest, vol. 1, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Huang Q, Lan J, and Li X, “Robotic arm based automatic ultrasound scanning for three-dimensional imaging,” IEEE Trans. Ind. Inform, vol. 15, no. 2, pp. 1173–1182, 2019. [Google Scholar]
- [19].Virga S et al. , “Automatic Force-Compliant Robotic Ultrasound Screening of Abdominal Aortic Aneurysms,” Proc. of IEEE/RSJ Int. Conf. Intelligent Robots and Systems, pp. 508–513, 2016. [Google Scholar]
- [20].Hennersperger C et al. , “Towards MRI-Based Autonomous Robotic US Acquisitions: A First Feasibility Study,” IEEE Transactions on Medical Imaging, vol. 36, no. 2, pp. 538–548, 2017. [DOI] [PubMed] [Google Scholar]
- [21].Nicole R, Karamalis A, Wein W, Klein T, and Navab N, “Ultrasound confidence maps using random walks,” Med. Image Anal, vol. 16, no. 6, pp. 1101–1112, 2012. [DOI] [PubMed] [Google Scholar]
- [22].Yorozu Y, Chatelain P, Krupa A, and Navab N, “Confidence-driven control of an ultrasound probe,” IEEE Transactions on Robotics, vol. 33, no. 6, pp. 1410–1424, 2017. [Google Scholar]
- [23].Jiang Z et al. , “Automatic Normal Positioning of Robotic Ultrasound Probe Based Only on Confidence Map Optimization and Force Measurement,” IEEE Robotics and Automation Letters, vol. 5, no. 2, pp. 1342–1349, 2020. [Google Scholar]
- [24].Young M, Graumann C, Fuerst B, Hennersperger C, Bork F, and Navab N, “Robotic ultrasound trajectory planning for volume of interest coverage,” IEEE International Conference on Robotics and Automation (ICRA), pp. 736–741, 2016. [Google Scholar]
- [25].Scorza A, Conforto S, d’Anna C and Sciuto S, “A comparative study on the influence of probe placement on quality assurance measurements in B-mode ultrasound by means of ultrasound phantoms,” Open Biomed. Eng. J, vol. 9, pp. 164, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Patlan-Rosales PA and Krupa A, “Strain estimation of moving tissue based on automatic motion compensation by ultrasound visual servoing,” 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 2941–2946, 2017. [Google Scholar]
- [27].Patlan-Rosales PA and Krupa A, “A robotic control framework for 3-D quantitative ultrasound elastography,” 2017 IEEE International Conference on Robotics and Automation (ICRA), pp. 3805–3810, 2017. [Google Scholar]
- [28].Güler RA, Neverova N and Kokkinos I, “DensePose: Dense Human Pose Estimation in the Wild,” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 7297–7306, 2018. [Google Scholar]
- [29].Bimbraw K, Ma X, Zhang Z, and Zhang H, “Augmented Reality-Based Lung Ultrasound Scanning Guidance,” Medical Ultrasound, and Preterm, Perinatal and Paediatric Image Analysis, vol. 12437, pp. 106–115, 2020. [Google Scholar]


