Abstract
Accelerating data acquisition in magnetic resonance imaging (MRI) has been of perennial interest due to its prohibitively slow data acquisition process. Recent trends in accelerating MRI employ data-centric deep learning frameworks due to its fast inference time and ‘one-parameter-fit-all’ principle unlike in traditional model-based acceleration techniques. Unrolled deep learning framework that combines the deep priors and model knowledge are robust compared to naive deep learning based framework. In this paper, we propose a novel multi-scale unrolled deep learning framework which learns deep image priors through multi-scale CNN and is combined with unrolled framework to enforce data-consistency and model knowledge. Essentially, this framework combines the best of both learning paradigms:model-based and data-centric learning paradigms. Proposed method is verified using several experiments on numerous data sets.
Keywords: Magnetic resonance imaging, deep learning, unrolled network, multi-scale CNN
I. Introduction
Magnetic Resonance Imaging (MRI) is one of the most preferred imaging modality in radiology because of its non-ionizing characteristics and superior tissue contrast. However, due to inherent underlying physics and sequential data acquisition fashion in the Fourier space, so called k-space, acquiring MR scans are prohibitively slow [1] , [2]. For this reason, accelerating data acquisition in MR imaging has been of perennial interest. Several image and signal processing techniques such as parallel imaging [3], low-rank and compressed sensing [1], [2], dictionary learning [4] and most recently non-linear low-rank and sparse frameworks [5]-[10] have remarkably improved data acquisition speed, enabling MR imaging in several challenging imaging protocols.
While all these methods are significantly different in terms of exploiting several signal processing tools and understanding different signal properties in MR images, most of these methods rely on exploiting signal and system prior information, making them model-based MR accelerating and reconstruction techniques. With recent advent of fast computing capabilities and access to massive data, a new class of data-centric framework, so-called deep learning (DL) techniques have drawn massive interest in MR acceleration community. Convolutional neural networks (CNN) [11], [12] based DL frameworks [13] have shown promising results in MR acceleration and image reconstruction. CNN based DL frameworks [13] pose MR acceleration and reconstruction problem as a task of finding an appropriate mapping function f (·) parameterized by some neural network parameters θ that maps undersampled corrupted MR images to clean fully sampled images xi such that given a set of undersampled and fully sampled training image data pairs . While these methods focus on learning a parameterized mapping function f (·) based on given training data pairs for some sort of loss function, typically ℓ1, ℓ2 minimization and have shown promising results, they essentially ignore data consistency and system priors [14]-[16]. Another class of DL frameworks [14]-[20] combine data consistency and system priors with image features learned from data-centric DL architectures resulting in a more robust and efficient hybrid data-centric and model-based DL framework for MR acceleration and reconstruction. It is important to note here that at the current stage DL based framework have substantially similar or slightly better reconstruction quality compared to traditional model-based acceleration frameworks. However, DL frameworks are still preferred for two particular reasons: i) They have very short reconstruction (inference) time compared to traditional model-based iterative techniques once the framework is trained on training data, and ii) DL training advocates, ‘One-model-fit-all’ principle, i.e once the DL framework is trained, it eliminates the necessity to tune parameters for each reconstruction unlike in model-based iterative techniques. Both these features typical to DL models are essential for realizing new reconstruction techniques into large scale applications and clinical practices.
In this paper, motivated by the fact that different regions of k-space of MR images capture image features at different scales; for example, lower frequency components of k-space capture image features at coarse scale such as structure, anatomy and smoothness, and higher frequency components capture more detail image features at finer scale, we propose to use multi-scale CNN [11], [21] that captures image features at different scales. Moreover, we combine multi-scale CNN with unrolled DL architecture [14], [15] that incorporates data consistency and parallel imaging to build a robust Multi-scale Unrolled DL architecture for MR image acceleration. We also investigate the consequence of unrolled architecture and multi-scale CNN on reconstructed image quality and compare to architectures without such provisions. The rest of the paper is organized as follows. Section II describes the basic principle behind accelerated MRI with undersampled data, Section III presents the proposed method, and section IV validates the advocated approach using extensive numerical tests on data. Finally, section V concludes the paper.
II. Background
In accelerated MRI, the data acquisition process is characterized by systems of equations such that y = ϕ(x) where ϕ is a forward operator that characterize partial Fourier operation and coil sensitivities [3], is acquired partial(undersampled) k-space data, and is the desired image. Clearly, because ϕ is a partial Fourier operator, M << N, hence this system of equations is ill-posed. To solve for x from such ill-posed system, MR image reconstruction problem is formulated as a constrained optimization problem,
| (1) |
Essentially, in traditional model-based methods, the data regualizer is enforced via known signal/image priors such as smoothness, low-rank [1], sparsity [2]. Whereas, in data-centric DL models [13], [15], data regularizers/priors are learned and enforced from given training data. Typically, CNNs are known to be very efficient in learning such data priors in case of images, and have shown very promising results [13], [15], [16].
III. Proposed Framework
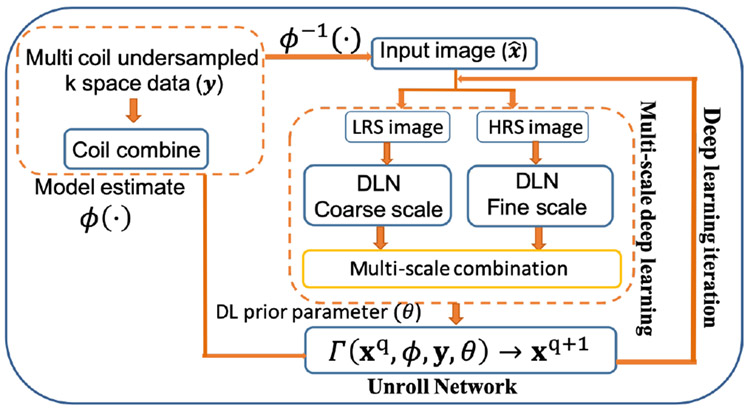
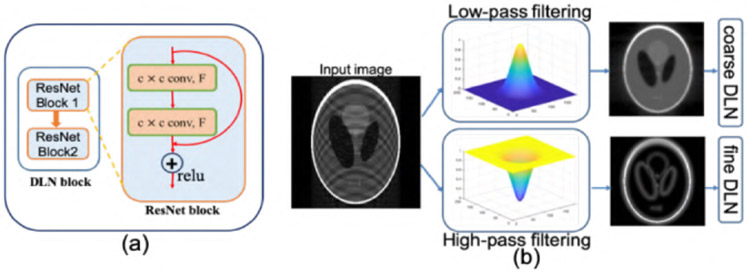
CNNs have shown to have an immense ability to capture underlying image features. Different kernel sizes in CNNs capture image features at different scales [11], [21]. Such multi-scale CNNs have shown potential on image recognition, classification and image de-hazing [22]. In MRI, different regions of k-space captures image features at different scales. For example, the lower frequency components of k-space capture coarse features such as anatomical structures, contrast and intensity whereas high frequency components capture finer details. Motivated by this fact we develop a multi-scale CNN for MR image reconstruction and integrate it to unrolled DL architecture to enforce data consistency and coil sensitivity maps, resulting in a robust DL framework for accelerated MRI. Such model captures the best of both learning paradigms: model-based and data-centric deep learning paradigm. Essentially, our framework consists of two important constituents i) Multi-scale CNN block and ii) Unroll Network block as shown in the Fig 1. Two deep learning network (DLN) blocks capture image features at different scale. Each DLN blocks consists of two ResNet [12] blocks. Each ResNet block is a 2 layer convolution neural network with a relu activation as shown in the Fig. 2(a). Different convolution filters with different kernel sizes are used in each DLN block to learn image features at Coarse and Fine scale. These different features are combined through a single layer CNN layer as shown in the Fig. 1. At every DL iteration an Unroll Network block enforces coil-sensitivities and data consistency to ensure robust reconstruction.
Fig. 1.
Schematic of multi-scale unrolled deep learning framework. Each DLN blocks 1 and 2 consists of ResNet blocks with different kernel size and feature maps size as shown in 2(a). Multi-scale deep learning block learns image features at different scales and unroll block integrates data model prior and multi-scale deep features.
Fig. 2.
(a)Schematic of DL blocks that consist of two ResNet blocks. (b) Illustration of filtering technique to produce coarse scale image and fine scale image.
A. Multi-scale CNN
Kernel size and feature maps of convolution filters in deep convolutional neural networks(CNN) [11], [21] correspond to feature scales. For example, small kernel filters are known to capture finer details such as edges and details whereas bigger kernel filters capture coarse features such as structures in images. In MRI, low-frequency components (central k-space) capture anatomical structures and higher frequency components capture edges and details. Motivated by this fact and recent development in multigrid CNN [11] we divide the undersampled MR input image into two different images: Low-resolution scale (LRS image) and high-resolution scale (HRS image) images from corresponding lower and higher frequency components of k-space. Essentially, an undersampled aliased input MR image is passed through a low-pass filter and a high-pass filter that gives coarse scale and fine scale version of input image as shown in Fig. 2(b). Here, we use Gaussian kernel based filter so that the Gibb’s ringings are removed from filtered LR and HR image. Typically, a bigger convolution kernel filters with with kernel size (k1) and a smaller activation map for coarse scale block, and a smaller convolution kernel filters with kernel size (k2) and larger activation map for Fine scale DLN is used. Filtered LRS image and HRS image are passed through coarse scale DLN and fine scale DLN, respectively. Finally, similarly as in [11], multi-scale features from two different DLNs combined through a single CNN layer.
B. Unrolled Network
Several works [15], [19], [20] have advocated use of unrolled frameworks [14], [16] to enforce the data consistency in DL based MR image reconstruction for robust reconstruction. In unrolled framework, unlike in typical DL regression problem where the goal is to estimate a mapping function for T training pairs of undersampled and fully sampled images over some loss function such that , instead, solving a joint problem of form (1) is advocated. In such frameworks, data regularizer is learned through some DL techniques such as a CNN or multi-scale CNN as discussed in III-A and a joint optimization between learning deep image regulaizier and data consistency is performed. Typically, two kinds of frameworks are popular. i) The framework that alternates between DL optimization step and data consistency step through direct substitution of k-space measurements from acquired location [13], [23] and ii) the framework where data consistency step involves iterative soft threshold algorithms such as ISTA [24], FISTA [25], to make an estimate of desired image x at each iteration, and alternates between data consistency and DL iteration. In this paper, we employ a FISTA [25] based joint iterative optimization approach. Specifically, at each iteration in deep learning training phase, a proximal based FISTA [25] algorithm with Q iterations is solved with current image estimate xq, current deep learning network parameters, and data model to obtain new estimate xq+1 of an image such that xq+1 = Γ (xq, ϕ, y, θ) as shown in Fig. 1, where Γ(·) is a proximal operator. For details of FISTA based unroll network please refer to [14], [15], [25].
IV. Experiments and Results
Our framework is implemented on TensorFlow 1.10.1. Adam optimizer with β1 = 0.99, β2 = 0.99, learning rate α = 0.001 is used and the loss function is defined to minimize the ℓ1 norm between the output and the ground truth image during training phase. Coarse scale DLN consists of F = 64 convolution kernel filters of size k1 = 8 × 8 at each convolution layer whereas, fine scale DLN consists of F = 64 convolution kernel filters of size k2 = 2 × 2 at each convolution layer. For unroll network, Q = 2 numbers of proximal iterations are carried out. In this paper we present our results on two different data sets from knee and body imaging. Both data sets were 32 coil, 3D volume data. 3D volumetric k-space data were first converted to 2D k-space by taking inverse Fourier transform along z-direction and coil compressed [3] to give 8 coil x − y 2D k-space. As a result, 6400, 8-coil knee MR images and 5200, 8-coil body MR images were obtained. Data were collected at Stanford University and Stanford Hospital with full patient consent and approved by the hospital ethics committee. Both data sets were divided into 60%, 5%, and 35% train, validation and test sets, respectively. For training purpose, a total of 35, 2D variable density undersampling masks with different undersampling rates of 2, 3, 4, 6, and 9 were used. We compare our multi-scale unrolled CNN results with two other frameworks, a naive CNN network without unrolling/data-consistency, and a single-scale unrolled CNN. For both competing networks convolution kernels of 4 × 4 and F = 128 at each layer, i.e double the numbers of filters in multi-scale framework were used, keeping all other common parameters the same.
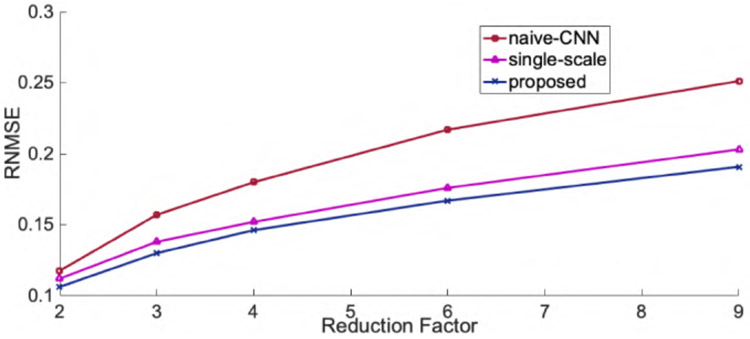
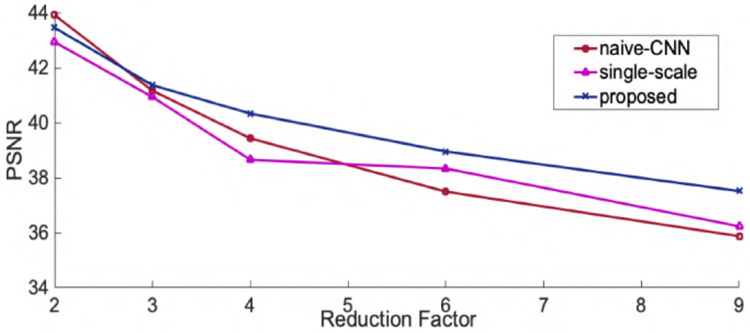
Fig.3 and Fig.4 show the representative axial knee image reconstructions at undersampling factor of 6 and 9, respectively. It can be clearly seen that the proposed multi-scale framework gives cleaner and sharper reconstructed images typically at higher undersampling rate of 9. We believe, this is particularly because our coarse scale DL network is able to capture smoothness of MR images more efficiently. However, some finer details are lost on both single-scale and multi-scale framework. It is observed that, a naive-CNN framework without data consistency results in noisy reconstruction compared to other methods. However, it is worth to mention here that few reports have been made that deeper naive-CNN frameworks are able to give comparable results [13], [23]. However, for our case where our network has only 2 ResNet blocks the naive-CNN performs substantially poor. Figs 5, 6 show quantitative performance metrics root normalized mean square error (RNMSE), and peak signal to noise ratio (PSNR), respectively on the test data set at different reduction factors(SSIM metric isn’t included here due to space limit). It is clear that, the proposed framework outperforms all other methods in both quantitative metrics. We also reconstructed coronal view knee image slices from the network trained on axial slices to test the generality and transferable potential of the model for multi-view reconstruction. In Fig. 7, we see both single-scale and multi-scale reconstruction are able to infer meaningful coronal view knee image reconstruction from a model trained on axial view, but clearly, multi-scale reconstructions look cleaner and sharper advocating the fact that our proposed framework is able to capture more low-level coarse image features such as smoothness and intensity and enables it into translating multi-view reconstruction from slice training data sets.
Fig. 3.
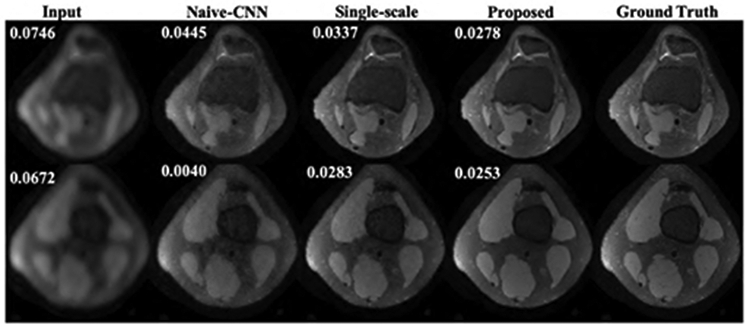
Representative image reconstructions of axial view knee images at reduction factor of 6. Numbers on top left represent RNMSE values.
Fig. 4.
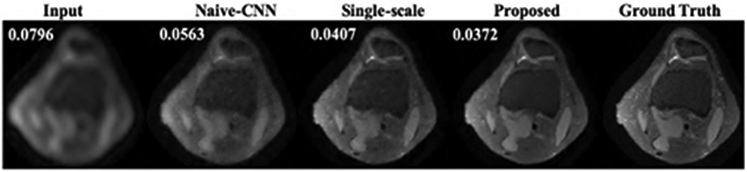
Representative image reconstructions of axial view knee images at reduction factor of 9. Numbers on top left represent RNMSE values.
Fig. 5.
Root normalized mean squared error for axial view knee image reconstructions.
Fig. 6.
Peak signal to noise ratio for axial view knee image reconstructions.
Fig. 7.
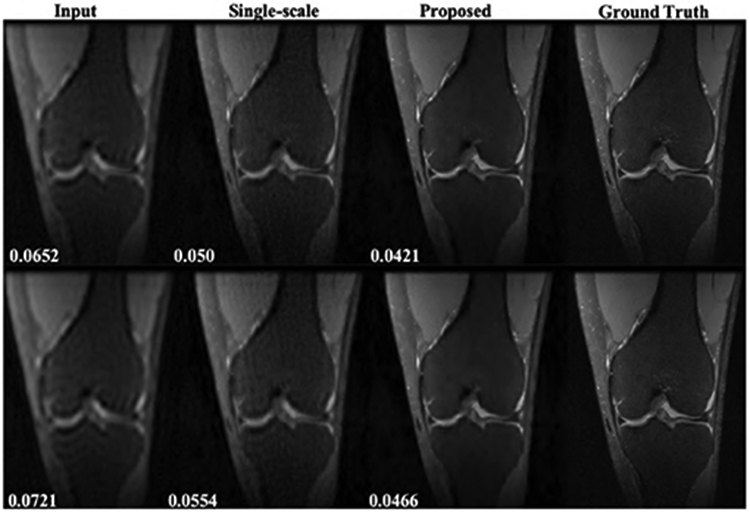
Representative results for coronal view knee image reconstruction from model trained on axial view. Top row: reduction factor = 6, bottom row: reduction factor = 9. Numbers on bottom left represent RNMSE values.
Finally, Fig. 8 shows representative body MR image reconstructions from single-scale and multi-scale framework at reduction factor of 4. It is worth to note here that, both reconstructions seem to give comparable results in this case. This is possibly because, the MR images in this case are high-resolution images with many finer details and consisted images of different anatomical regions as well as several noisy images in the training and test case. This possibly affects the behaviour of network, so the ability of multi-scale framework to capture low-level image features such as smoothness could not significantly contribute in the reconstruction. It is desired to further investigate such consequences in future works. Nonetheless, our proposed framework showed substantially improved results in knee imaging both qualitatively and quantitatively as shown in Fig. 3 through Fig. 7.
Fig. 8.
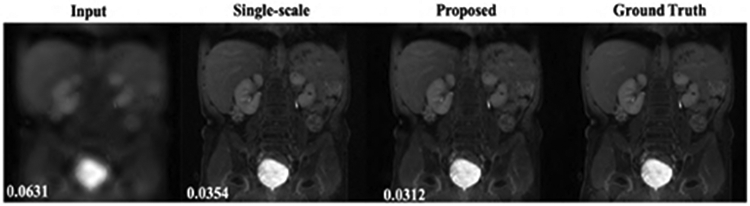
Representative results for body MRI at reduction factor = 4. Numbers on bottom left represent RNMSE values.
V. Conclusion
In this paper, we proposed a robust multi-scale unrolled deep learning framework for accelerating magnetic resonance imaging. our proposed method combines the best of two different learning paradigms: model-based learning and data-centric learning by using multi-scale CNN and proximal operator based unrolled deep learning framework. our proposed method have shown to be better in both qualitative and quantitative metrics compared to naive-CNN framework and single-scale unrolled CNN. Superiority of the proposed method is verified through several numerical experiments on different data sets. A detailed further study and experimentation on behaviour of such multi-scale framework is sought for in future endeavors.
Acknowledgment
This work is supported in part by the NIH R01EB009690, NIH R01 EB026136 grants, and GE Healthcare.
References
- [1].Liang Z-P and Lauterbur PC, “An efficient method for dynamic magnetic resonance imaging,” Medical Imaging, IEEE Transactions on, vol. 13, no. 4, pp. 677–686, 1994. [DOI] [PubMed] [Google Scholar]
- [2].Lustig M, Donoho D, and Pauly JM, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007. [DOI] [PubMed] [Google Scholar]
- [3].Zhang T, Pauly JM, Vasanawala SS, and Lustig M, “Coil compression for accelerated imaging with cartesian sampling,” Magnetic Resonance in Medicine, vol. 69, no. 2, pp. 571–582, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ravishankar S and Bresler Y, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” Medical Imaging, IEEE Transactions on, vol. 30, no. 5, pp. 1028–1041, 2011. [DOI] [PubMed] [Google Scholar]
- [5].Poddar S and Jacob M, “Dynamic MRI using smoothness regularization on manifolds (SToRM),” Medical Imaging, IEEE Transactions on, vol. 35, no. 4, pp. 1106–1115, April 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Usman M, Atkinson D, Kolbitsch C, Schaeffter T, and Prieto C, “Manifold learning based ECG-free free-breathing cardiac cine MRI,” Journal of Magnetic Resonance Imaging, vol. 41, no. 6, pp. 1521–1527, 2015. [DOI] [PubMed] [Google Scholar]
- [7].Nakarmi U, Zhou Y, Lyu J, Slavakis K, and Ying L, “Accelerating dynamic magnetic resonance imaging by nonlinear sparse coding,” Biomedical Imaging (ISBI), IEEE International Symposium on, pp. 510–513, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Nakarmi U, Slavakis K, Lyu J, and Ying L, “M-MRI: A manifold-based framework to highly accelerated dynamic magnetic resonance imaging,” In proceedings, Biomedical Imaging (ISBI), IEEE International Symposium on, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Nakarmi U, Wang Y, Lyu J, Liang D, and Ying L, “A kernel-based low-rank (KLR) model for low-dimensional manifold recovery in highly accelerated dynamic mri,” IEEE Transactions on Medical Imaging, vol. 36, no. 11, pp. 2297–2307, November 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Nakarmi U, Slavakis K, and Ying L, “MLS: Joint manifold-learning and sparsity-aware framework for highly accelerated dynamic magnetic resonance imaging,” in 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), April 2018, pp. 1213–1216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Ke T, Maire M, and Yu SX, “Neural multigrid,” CoRR, vol. abs/1611.07661, 2016. [Google Scholar]
- [12].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” CoRR, vol. abs/1512.03385, 2015. [Google Scholar]
- [13].Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, and Liang D, “Accelerating magnetic resonance imaging via deep learning,” in 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), April 2016, pp. 514–517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Diamond S, Sitzmann V, Heide F, and Wetzstein G, “Unrolled optimization with deep priors,” CoRR, vol. abs/1705.08041, 2017. [Google Scholar]
- [15].Cheng JY, Chen F, Alley MT, Pauly JM, and Vasanawala SS, “Highly scalable image reconstruction using deep neural networks with bandpass filtering,” CoRR, vol. abs/1805.03300, 2018. [Google Scholar]
- [16].Jin KH, McCann MT, Froustey E, and Unser M, “Deep convolutional neural network for inverse problems in imaging,” IEEE Transactions on Image Processing, vol. 26, no. 9, pp. 4509–4522, September 2017. [DOI] [PubMed] [Google Scholar]
- [17].Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, and Knoll F, “Learning a variational network for reconstruction of accelerated mri data,” Magnetic Resonance in Medicine, vol. 79, no. 6, pp. 3055–3071, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Quan TM, Nguyen-Duc T, and Jeong W, “Compressed sensing MRI reconstruction with cyclic loss in generative adversarial networks,” CoRR, vol. abs/1709.00753, 2017. [DOI] [PubMed] [Google Scholar]
- [19].Mardani M, Gong E, Cheng JY, Vasanawala S, Zaharchuk G, Alley MT, Thakur N, Han S, Dally WJ, Pauly JM, and Xing L, “Deep generative adversarial networks for compressed sensing automates MRI,” CoRR, vol. abs/1706.00051, 2017. [Google Scholar]
- [20].Biswas S, Aggarwal HK, and Jacob M, “Dynamic mri using model-based deep learning and storm priors: Modl-storm,” Magnetic Resonance in Medicine, vol. 82, no. 1, pp. 485–494, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Chen Y, Fan H, Xu B, Yan Z, Kalantidis Y, Rohrbach M, Yan S, and Feng J, “Drop an octave: Reducing spatial redundancy in convolutional neural networks with octave convolution,” CoRR, vol. abs/1904.05049, 2019. [Online]. Available: http://arxiv.org/abs/1904.05049 [Google Scholar]
- [22].Zhang H, Sindagi V, and Patel VM, “Multi-scale single image dehazing using perceptual pyramid deep network,” in 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), June 2018, pp. 1015–101 509. [Google Scholar]
- [23].Li H, Zhang C, Nakarmi U, Huang P, Liu R, and et al. , “Effect of cnn layers on mr image reconstruction with deep learning,” ISMRM workshop on machine learning, 2018. [Google Scholar]
- [24].Daubechies I, Defrise M, and Mol CD, “An iterative thresholding algorithm for linear inverse problems with a sparsity constraint,” CoRR, 2003. [Google Scholar]
- [25].Beck A and Teboulle M, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009. [Google Scholar]