Abstract
Functional brain network (FBN) is becoming an increasingly important measurement for exploring cerebral mechanisms and mining informative biomarkers that assist diagnosis of some neurodegenerative disorders. Despite its effectiveness to discover valuable hidden patterns in the human brain, the estimated FBNs are often heavily influenced by the quality of the observed data (e.g. blood oxygen level dependent signal series). In practice, a preprocessing pipeline is usually employed for improving data quality. With this in mind, some data points (volumes or time course in the time series) are still not clean enough, due to artifacts including spurious resting-state processes (head movement, mind-wandering). Therefore, not all volumes in the fMRI time series can contribute to the subsequent FBN estimation. To address this issue, we propose a novel FBN estimation method by introducing a latent variable as an indicator of the data quality, and develop an alternating optimization algorithm for jointly scrubbing the data and estimating FBN simultaneously. To further illustrate the effectiveness of the proposed method, we conduct experiments on two publicly datasets to identify subjects with mild cognitive impairment (MCI) from normal controls (NCs) based on the estimated FBNs, and achieve improved accuracies than the baseline methods.
Keywords: Functional Brain Network, Resting-state Functional Magnetic Resonance Imaging (rs-fMRI), Mild Cognitive Impairment (MCI)
I. Introduction
FUNCTIONAL brain network (FBN) provides an increasingly important way of quantifying brain activity [1,2] and mining sensitive biomarkers for neurological disease diagnosis such as autism spectrum disorder [3–5]. Alzheimer’s disease [6,7] and Parkinson’s disease [8]. All of these examples rely heavily on the quality of the final FBNs, and therefore it is imperative to estimate FBNs more accurately [9].
Currently, several researchers have proposed many different methods towards better FBN estimation, most of which can be explained under a regularized framework, that require a reliable FBN estimation model to not only fits the data well, but also effectively encodes priors of the brain organization [10]. In practice, the commonly-used priors include sparsity [11], modularity [10], group-sparsity [12–13], low-rank [14] and scale-free [15], which can all be transformed into their corresponding regularization terms in FBN estimation models and can often improve the performance of the acquired FBNs.
Besides regularizers, the data-fitting terms also have a high influence on FBN estimation, which provides an effective way of capturing statistical information in data (e.g., Pearson’s correlation [15] and partial correlation [10]). However, the artifacts, noises or some “abnormal” resting states involved in the observed data (or time series) usually lead to poor results. Therefore, a preprocessing pipeline comprising motion correction, spatial smoothing and temporal filtering, is typically employed to improve the quality of data before FBN estimation [16]. Even when using this data preprocessing, it is still difficult to eliminate all the potential artifacts or some “abnormal” resting-state processes within the data due to the weak functional magnetic resonance imaging (fMRI) signals and complex disturbing sources. Moreover, some steps in the preprocessing pipeline may also cause erroneous volumes in the time series [17].
As a recently developed preprocessing step, the scrubbing operation has been investigated to further clean the data by removing some potentially “bad” volumes from the fMRI series [18]. Despite its seeming appeal, there are debates on the scrubbing operations [19–20]. Some researchers believed that head micromovements have a neurobiological basis and can still provide useful information [21–22]. On the other hand, resting state is an unconstrained condition that involves heterogeneous levels of mind-wandering, arousal, attention and vigilance [23–24]. Thus, these “abnormal” resting-state processes may result in “noisy” volumes mixed in the fMRI data which cannot be detected by the traditional scrubbing technique.
More notably, the scrubbing operation is independent of the FBN estimation model, and thus cannot guarantee that the preserved volumes necessarily benefit for the subsequent FBN estimation, while the removed volumes are not necessarily helpful. In addition, the amount of removed volumes in the scrubbing operation is often relatively high (between 20% and 60% of all volumes [23]), which may lead to unreliable FBN estimation [10,25].
To address these issues, we propose a novel FBN estimation method by introducing a latent indicator variable into the FBN optimization model. The latent variable indicates the quality or the state of each time point in fMRI series. Based on the latent variable model [26], we develop an alternating optimization algorithm for jointly estimating the indicator variables and FBNs in a single framework. Consequently, the proposed method can automatically identify and remove the “bad” volumes from the fMRI series; that is, it can make a self-scrubbing operation at the FBN estimation procedure. In brief, we summarize the main contributions of our proposed framework as follows:
Different from traditional methods that often conduct data scrubbing and FBN estimation in two separate sequential steps, our proposed framework combines them into a single model. By a joint optimization (or targeted scrubbing), we can obtain clearer FBNs with potentially higher reliability and discriminability.
Technically, we introduce a latent variable as an indicator of the data quality into the FBN estimation model, and design an alternating optimization algorithm, by which we can scrub the time points that are potentially not helpful for FBN estimation.
Compared with the traditional scrubbing operation that only scrubs the motion artifact and often removes too many data points, our proposed framework is capable of further scrubbing some “abnormal” resting-state processes and controlling the size of scrubbed data by an optimized hyper-parameter.
The proposed scheme is adopted on the MCI classification task, and significantly improves the performance of the baseline methods.
To verify the effectiveness of the proposed method, we apply it to estimate FBNs based on the resting-state functional magnetic resonance imaging (rs-fMRI), and then identify subjects with mild cognitive impairment (MCI) from normal control (NC) via the estimated FBNs. Experiments are conducted on two publicly available datasets, and the experimental results illustrate that our proposed method works well on both scrubbed and non-scrubbed rs-fMRI data. It results in the improved classification accuracy for MCI identification. For facilitating efforts to replicate our results, we also share the source codes in https://github.com/Cavin-Lee/self-scrubbing/.
II. Materials and Method
A. Data Preparation
MCI is often regarded as a prodromal stage of AD. Early detection of MCI with timely intervention is believed to be the most effective measures for delaying the transition from MCI to AD. Therefore, in this study, we focus on MCI and NC classification. Our analysis is based on two publicly available datasets. One is from Alzheimer’s Disease Neuroimaging Initiative (ADNI)1, and the other is from Neuroimaging Informatics Tools and Resources Clearinghouse (NITRC)2 shared by a recent study [10].
For ADNI dataset, 110 participants, including 51 MCIs and 59 NCs, are adopted in this experiment. The fMRIs are obtained by 3.0T Philips scanners with the following parameters: TR/TE = 3000/30mm, flip angle = 80, imaging matrix=64×64, 48 slices, 140 volumes, and voxel thickness = 3.3mm. SPM8 toolbox3 and DPARSFA (version 2.2) [27] are used to preprocess the fMRI data according to the well-accepted preprocessing pipeline. The first 10 rs-fMRI volumes of each subject are discarded to avoid signal shaking. The remaining images are first corrected for different slice acquisition timing and head motion [28]. Then, regression of ventricular and WM signals as well as six head-motion profiles are conducted to further reduce the effects of nuisance signals. For spatial normalization, the T1-image is first co-registered to the averaged motion corrected fMRI data, and then segmented using DARTEL [29], which produces a deformation field projecting each subject from the original individual space to MNI space [30]. The fMRI series is band-pass filtered (0.01-0.08Hz). Depending on the automated anatomical labeling (AAL) atlas [31], the pre-processed blood oxygen level dependent (BOLD) time series signals are partitioned into 116 ROIs.
For NITRC dataset, it includes 46 MCIs and 45 NCs that come from the participants recruited via advertisements in local newspapers and media. A similar preprocessing pipeline is employed as in the ADNI dataset. For detailed discussion on the preprocessing pipelines on NITRC data, please refer to [10].
B. Related works
According to a recent review [1], the FBN estimation methods, from simple to complex, include Pearson’s Correlation (PC), partial correlation [32], regularized partial correlation [11]. Bayesian network [33], structural equation modeling [34], and dynamic casual modeling [35]. Each of these methods, in our view, can be considered as a trade-off among biological interpretability, computational efficiency, and statistical robustness. In this paper, we mainly focus on the correlation-based methods, since they are currently the most popular ways of FBN estimation and have been empirically demonstrated to be more sensitive than the complex or higher-order methods [9]. In this section, we first review several representative correlation-based methods that provide a platform for developing our model. Then, we briefly introduce the traditional scrubbing scheme as it is related to the proposed method.
1). Pearson’s Correlation
As pointed out previously, PC lies on the simplest extreme of the existing FBN methods. We suppose that each brain has been parcellated into N regions of interest (ROIs) based on a certain atlas, and the fMRI time series associated with the ith ROI is represented by xi ∈ RT, i = 1, …, N, where T is the number of volumes in each series. Then, the edge weights of the FBN based on PC can be calculated as follows:
| (1) |
By re-defining , a centralized and normalized counterpart of the original xi, we can simplify PC as Wij = xiTxj, which corresponds to the solution of the following optimization problem:
| (2) |
Here, X = [x1, x2, ⋯, xN] ∈ RT×N is the data matrix, W is the edge weight matrix, and ‖∙‖F denotes the F-norm of a matrix. Since the BOLD signals commonly contain noises, the original PC tends to result in a FBN with dense connections. In practice, a threshold scheme is generally used to sparsify the PC-based FBN by filtering out the noisy or weak connections. For detailed discussion on the thresholding strategy, please refer to Section 3.2.1 in [36].
2). Partial Correlation
Partial correlation is used in FBN estimation for treating the confounding problem involved in the full correlation methods such as PC. A general approach to calculate partial correlation is based on the estimation of inverse covariance matrix [37]. However, this approach may be ill-posed due to the singularity of the estimated sample covariance matrix Σ = XTX. Therefore, a regularization term R(W) is generally introduced into the FBN estimation model as follows.
| (3) |
Equivalently, it can be further simplified to the following matrix form:
| (4) |
In Eq. (3) or (4), the first term implies to invert the covariance matrix Σ, and λ is a regularized parameter to control the balance between the first (data-fitting) term and the second (regularization) term. The most popular regularizer is l1-norm, i.e., , which corresponds to the sparsity prior of FBN, and leads to LASSO or sparse representation (SR) model [11]. As discussed earlier, some other regularizers have been investigated in recent years to encode different priors, which is beyond the scope of this paper.
3). A Regularized FBN Estimation Framework
According to a recent study [10], a large family of FBN estimation models can be summarized by the following regularized framework:
| (5) |
where f(X, W) is the data-fitting term, aiming to capture some statistics of the data (e.g., the covariance or inverse covariance structure), and R(W) is the regularization term, aiming to encode the biological/physical priors of the FBN. Sometimes, specific constraints (e.g., symmetry or positive semi-definite) are included in Δ for shrinking the search space of W towards better FBNs.
Note that, such a regularized framework can not only stabilize the statistical estimation, but also, and more importantly, provide a general platform for designing the new FBN estimation method in this paper.
4). Scrubbing Metric
Despite a sophisticated preprocessing pipeline, the fMRI series may be not clean enough due to, for example, head micromovements [16]. In order to eliminate the influence of the instantaneous head motion, a scrubbing operation is typically implemented to remove some volumes according to the frame-wise displacement (FD) [18] or DVARS [38]. In particular, FD of the tth time point is defined as follows.
| (6) |
where x, y, z, α, β, γ are six head motion parameters, and 50 (with the unit of mm) denotes the assumed radius of the head [39]. In general, the volume would be scrubbed if FD exceeds 0.5 mm.
In contrast, the DVARS metric is defined in Eq. (7).
| (7) |
where Yi,t is the value of the fMRI data at voxel i and time point t. The parameter I is the number of the voxels. The DVARS metric can be nonnalized as follows:
| (8) |
where is the variance of Yi,t and ρi is the correlation coefficient between Yi,t and Yi,t−1. Then, the “bad” volumes can be removed according to the p-value of DVARS2.
C. The Proposed Method
As mentioned, both prior information and data quality have a significant influence on the reliability of the estimated FBNs. The priors can be generally encoded by regularization terms. In contrast, the quality of time points in fMRI series cannot be easily measured without the guidance of a specific learning or estimation task. Therefore, we propose a novel solution for identifying the quality of time points with FBN estimation (task) together, by which we expect to achieve cleaner data, and, in turn, more accurate and discriminative FBNs.
1). Motivation
Before presenting the novel FBN estimation model, we first introduce the motivation and the basic idea behind it by a toy example. As shown in Fig. 1, we have a set of rs-fMRI series from N = 5 ROIs, each of which includes T = 30 volumes. According to the previous discussion, we cannot guarantee all volumes in the fMRI series are clean. To illustrate this more clearly, some data points in Fig. 1 are labelled as “clean”, while the others are labelled as “dirty”. Equivalently, a binary indicator can also be used to denote the quality of the data, with “0” corresponding to “dirty”, and “1” to “clean”.
Fig. 1.
A toy example for illustrating the motivation of the proposed method.
However, the indicator cannot be observed directly in practice. Traditionally, a data-scrubbing operation (e.g., based on FD or DVARS) is used to identify the quality of the data points (or, equivalently, determine the value of the indicator) by detecting head motion [16]. Despite its potential effectiveness, such a scheme (1) cannot remove all the “dirty” data points caused by different factors [23]; (2) tends to scrub too many time points due to the lack of a control mechanism [19]; and (3) is independent on the specific task, and thus will not necessarily benefit the ensuing FBN estimation.
2). Model
To address the above problems, in this paper, we propose a task-dependent data scrubbing method for FBN estimation. In particular, we consider the binary indicator as a latent variable vt for denoting the quality of the tth time point (vt = 0 for “dirty”, and vt = 1 for “clean”), and thus the regularized FBN estimation framework in Eq. (5) can be extended to the following form with an latent indicator variable.
| (9) |
where X(t) is tth row of the data matrix X. Note that, when the indicator variable vt = 0, the tth time point in fMRI series will be removed, meaning that it has no contribution to FBN estimation; when vt = 1 for all t = 1, 2, ⋯, T, Eq. (9) will reduce to the original FBN estimation framework given in Eq. (5).
In practice, however, Eq. (9) will always return a trivial solution that vt = 0 for all t = 1, 2, ⋯, T. Therefore, we introduce a negative l1-norm regularization term into Eq. (9) for avoiding an exceedingly sparse solution. Additionally, we relax4 the binary indicator variable vt ∈ {0,1} to a real range [0,1], for simplifying the solving of the optimization problem. Them we get the following model:
| (10) |
where λ and γ are two regularized parameters for controlling the balance of three terms in the objective function. Especially for γ, it plays a role to determine the number of removed time points from the whole series. When the value of γ approaches 0, most of the time points will be removed. On the other hand, when γ has a large value, all the time points in the series will be kept for FBN estimation. In other words, the proposed model can scrub the data adaptively in the process of FBN estimation, by controlling the hyper-parameter γ and learning the indicator variable vt from the data. Therefore, we name our proposed scheme as FBN estimation with self-scrubbing (SS for short).
In principle, any data-fitting/regularization term can all be adopted to realize the SS model, but, in this paper, we select the partial correlation strategy shown in Eq. (3) or (4), since it overcomes the confounding effect and is empirically verified to more effective than the full correlation [9]. Consequently, the partial correlation based self-scrubbing FBN estimation model is given as follows:
| (11) |
where is the tth time point of the series associated with the ith node (e.g. ROI). For simplicity, we rewrite Eq. (11) into the following matrix form:
| (12) |
where V = diag(v1, v2, ⋯, vT) ∈ RT×T is a diagonal matrix containing the indicator variables on its principal diagonal. The constraint, Wii = 0, is employed only to avoid the trivial solution that leads to W being an identity matrix. For R(W), we can, in principle, use any off-the-shelf regularizers such as l1-norm [11], l2,1-norm [13], trace norm and their combination [10]. However, this problem goes beyond the main focus in this paper. Therefore, we only attempt l1-norm (sparsity prior) due to its simplicity and effectiveness [11] and get the specific FBN estimation model (named SR+SS) as follows.
| (13) |
3). Optimization Algorithm
Considering that there are two variables V and W involved in Eq. (12), in this paper, we employ alternative convex search (ACS) [40] method to solve them alternately, by two following steps. Note that, we first initialize indicator V as an identity matrix, meaning that all time points are retained in first iteration.
Step 1: With a fixed V, Eq. (13) reduces to a traditional FBN estimation problem that can be solved by many convex optimization methods. Here, we use the proximal method [41] due to its efficiency and simplicity. Two main steps are involved in the proximal method, including gradient descent and proximal operation. First, for the data-fitting term , whose gradient w.r.t W is ∇Wf(X, W) = 2XTVTVXW − XTVTVX, we have the following update formula according to the gradient descent criterion:
| (14) |
where αk denotes the step size of the gradient descent5 [42]. Then, the proximal operator is imposed on the current W. For the sparsity regularizer λ‖W‖1, the proximal operator is defined as follows.
| (15) |
where sgn(Wij) and abs(Wij) return the sign and absolute value of Wij respectively.
Step 2: With a fixed W, we then update V. Now, Eq. (13) reduces to the following optimization problem,
| (16) |
or
| (17) |
Eq. (17) can be further simplified to the following problem.
| (18) |
where (i.e., loss value of the data-fitting term) is a constant. Note that Eq. (18) is a linear programming problem, and thus we can easily get its optimal solution as follows.
| (19) |
This means that 1) if ‖X(t) − X(t)W‖2 > γ, the tth time point is more likely to be removed by labelling it with 0; on the contrary, 2) if ‖X(t) − X(t)W‖2 < γ, the tth time point will be kept by labelling it with 1. Such a formula for updating vt coincides well with the intuition that the “dirty” time points (labelled as 0) can cause a poor fitting with high bias/residual (i.e., ‖X(t) − X(t)W‖2 > γ ). In fact, in the experimental section, we will further illustrate this problem based on a toy dataset, and empirically verify that the proposed method can automatically detect “dirty” time points. Finally, we summarize the algorithm for solving Eq. (13) in ALGORITHM I.
ALGORITHM I.
Estimating FBN with self-scrubbing
III. Experiment
In Section A, we first give a simple toy example for illustrating how the proposed model/algorithm works. Then, in Section B, we provide both quantitative and qualitative results for evaluating the FBNs estimated by the proposed method.
A. A Toy Example
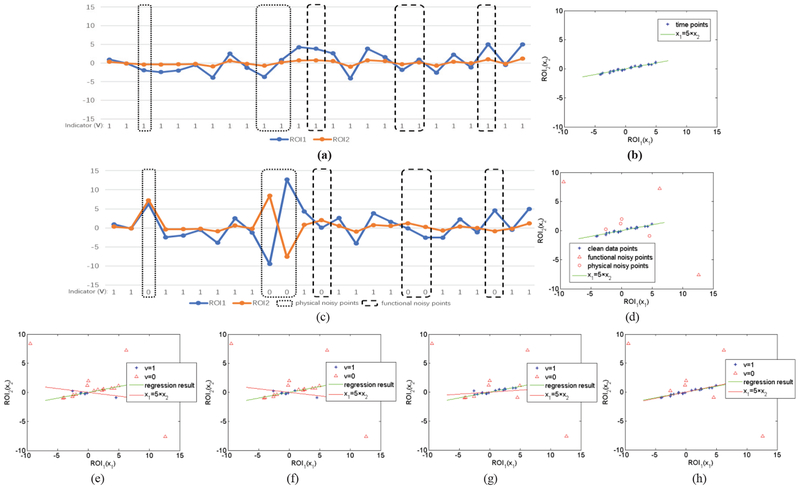
For the convenience of interpretation and visualization, we only consider the simplest case where N = 2. Thus, we have two series, x1 and x2, associated with ROI1 and ROI2, respectively. Without loss of generality, we suppose that there is a strong connection between ROI1 and ROI2. In particular, we generate the data by an approximately linear relationship that x1 ≈ 5 × x2, as shown in Fig. 2 (a) and (b). Based on the generated data, we can easily calculate the Pearson’s correlation coefficient between ROI1 and ROI2, and the result is 0.985.
Fig. 2.
A toy example for illustrating how the proposed method works, (a) Original toy signals without noises; (b) scatter plot corresponding to (a); (c) introducing 7 noisy points into the original signals in (a); (d) scatter plot corresponding to (c); (e)-(h) the first, second, fifth and final iterative results of the proposed algorithm. Note that the proposed method can effectively remove the noisy points gradually with the iterations.
However, as discussed previously, the correlation can be significantly affected by the data quality. To illustrate this situation, we change several time points randomly in the generated data for simulating the possible artifacts, noises or “abnormal” resting-state processes. In particular, as shown in Fig. 2 (c) and (d), we first introduce three “dirty” points to simulate the physical noises (e.g., motion artifacts) that generally lead to large-amplitude changes in signals [18], and then we introduce four “dirty” points to simulate the possible functional “noises”, by setting them off the main direction (i.e., x1, = 5 × x2). Here, we simply suppose the special signals that cannot fit the data well as functional “noises”, according to a recent study [43].
Now, the Pearson’s correlation between ROI1 and ROI2 is −0.399, meaning that even limited change of data points can have a big effect on the estimation of functional connections. Based on the toy data with “dirty” time points, we run the proposed algorithm, and find that it can remove the “dirty” points gradually with iterations, as shown in Fig. 2 (e) – (h). As a result, the Pearson’s correlation between ROI1 and ROI2 based on our SR+SS scheme6 is 0.980. In contrast, the traditional DVARS scheme (based on p-value<0.05) returns a final correlation of 0.492. This means that the proposed method leads to a more accurate estimation, since the true correlation is 0.985 on the toy data.
B. MCI Identification
1). FBN estimation
After obtaining the preprocessed fMRI data, we estimate FBNs based on three different methods, PC, SR, and the proposed SR+SS. In our experiments, the average convergence times of SR and SR+SS are 0.0861s and 0.0916s per network, respectively, based on Win 10 OS, core i7 and MATLAB 2016a. The convergence time is calculated by tic and toc tool in MATLAB. This means that the proposed method does not spend much more running time than the baseline method.
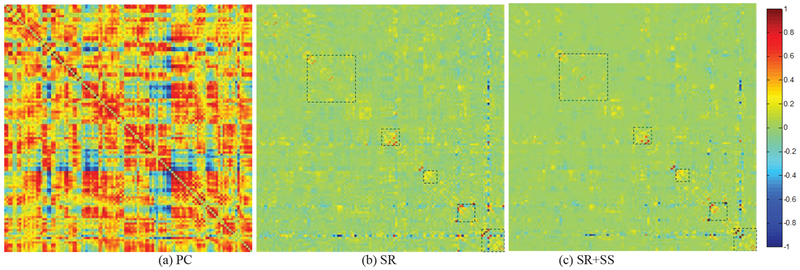
In Fig. 3, we visualize the adjacency matrices7 of the FBN estimated by these methods on ADNI dataset. For SR, we simply set the regularized parameter λ = 1 and for SR+SS, λ = 1 and λ = 0.5. As shown in Fig. 3, the FBN estimated by PC has a highly different topology from that of the partial correlation-based methods (i.e., SR and SR+SS), since they use different data fitting term. In contrast, SR and SR+SS lead to a similar FBN structure by using the same kind of data fitting term. The differences of the FBNs estimated by SR and SR+SS methods lie mainly in several specific brain regions.
Fig. 3.
The FBN adjacency matrices estimated by 3 different methods. The rectangles in (b) and (c) help for distinguishing the differences between two FBNs.
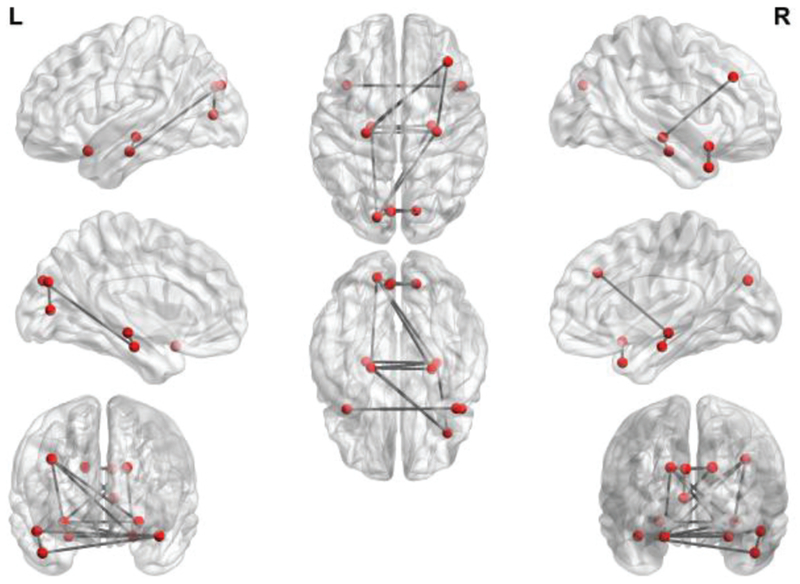
For investigating the effect of SS on the estimated FBN, in Fig. 4, we map the most significantly changed connections between SR and SR+SS onto the International Consortium for Brain Mapping (ICBM) 152 surface template. For a better visualization, we do not provide the cerebellum part. It can be observed, in Fig. 4, that the changed connections mainly concentrate on the hippocampus, parahippocampus, cuneus and temporal lobe regions. In Part 4), we will give a further discussion on the self-scrubbing scheme.
Fig. 4.
The most significantly changed connections between SR and SR+SS. We first estimate FBNs based on the data with and without SS. Then, we investigate the statistical differences in functional connectivity with and without SS by pair-wise t-test. The most significantly changed connections are mapped onto the ICBM 152 surface template. We note that the changed connections mainly concentrate on the hippocampus, parahippocampus, cuneus and temporal lobe regions. This figure is drawn by BrainNetViewer toolbox (https://www.nitrc.org/projects/bnv/).
2). Experimental Settings
Once we obtain the FBNs of all subjects, the subsequent task is to identify the subjects with MCI from NCs based on the estimated FBNs. Then, the problem turns to determine which features and classifiers should be used for identification. Considering the big influence of different steps in the classification pipeline on the final accuracy, it is difficult to conclude whether the FBN estimation methods or the ensuing feature selection and classification methods contribute to the ultimate result. Therefore, we only adopt the simplest feature selection method (t-test with p<0.01) and the most popular SVM [44] classifier (linear SVM with default parameter C=1) in our experiment.
Note that, for comparing the proposed method with the traditional FD-based scrubbing method, we conducted experiments on both scrubbed and non-scrubbed data. The scrubbing criterion is based on the commonly used scheme with FD > 0.5mm.
Due to limited samples, we test the involved methods using the leave one out cross validation (LOOCV), in which only one subject is kept out for testing while the remaining are used for training the models. This is repeated until each fold has been used once for testing. For obtaining optimal values of the regularized parameters, an inner LOOCV is further conducted on the training data by a grid-search. For the parameter λ, the candidate value is ranged in [2−5, 2−4, ⋯, 20, ⋯, 24, 25]; for the parameter γ , the candidate value is ranged in [0.1,0.2,⋯,0.9,1]; for the threshold in PC, we use 20 sparsity levels from [5%, 10%, ⋯, 95%, 100%], where, for example, 90% means that 10% of the weak edges are filtered out from the FBN.
In addition, we evaluate the classification performance of different methods by a set of quantitative measures, including accuracy, sensitivity and specificity, which are defined as follows:
| (21) |
| (22) |
| (23) |
where TP, TN, FP and FN denote the number of True Positive, True Negative, False Positive and False Negative, respectively.
3). Results
The classification results on ADNI dataset (with and without traditional scrubbing8) are reported in TABLE I. The corresponding classification results on NITRC dataset are given in TABLE II. Based on the results, we can observe that the proposed SR+SS method achieves the best discriminability on both scrubbed and non-scrubbed datasets. The proposed methods significantly out perform the baseline under the 95% confidence interval based on the DeLong’s non-parametric statistical test [45]. The p-value of the DeLong test is summarized in TABLE III. The receiver operating characteristic (ROC) is given in Fig. 5. It can be clearly found that the proposed method performs better than the traditional scrubbing method and can further improve the performance on the scrubbed data.
TABLE I.
Classification Performance Corresponding to Different FBN Estimation Methods on ADNI Dataset.
| Data | Method | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|
| Non-scrubbed | PC | 77.27% | 74.58% | 80.39% |
| SR | 78.18% | 76.27% | 80.39% | |
| SR+SS | 81.81% | 79.66% | 84.31% | |
| Scrubbed | PC | 79.09% | 76.27% | 82.35% |
| SR | 80.91% | 79.66% | 82.35% | |
| SR+SS | 82.73% | 81.35% | 84.31% | |
TABLE II.
Classification Performance Corresponding to Different FBN Estimation Methods on NITRC Dataset.
| Data | Method | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|
| Non-scrubbed | PC | 61.54% | 60.87% | 62.22% |
| SR | 72.52% | 67.39% | 77.78% | |
| SR+SS | 80.21% | 78.26% | 82.22% | |
| Scrubbed | PC | 60.44% | 57.78% | 63.04% |
| SR | 76.92% | 73.33% | 80.43% | |
| SR+SS | 83.52% | 82.22% | 84.78% | |
“scrubbed” represents that the data are scrubbed by FD
TABLE III.
The P-value of SR+SS Methods Outperforms SR and PC Under the Delong Test
| Data | ADNI | ADNI-S | NITRC | NITRC-S |
|---|---|---|---|---|
| PC | 0.0043 | 0.0110 | 0.0416 | 0.0321 |
| SR | 0.0391 | 0.0481 | 0.0000 | 0.0000 |
-S represents the data has been scrubbed based on traditional method.
Fig. 5.
The ROC curve of the classification performance for PC, SR and SR+SS methods on the (a) unscrubbed ADNI dataset (b) scrubbed ADNI dataset (c) unscrubbed NITRC dataset and (d) scrubbed NITRC dataset.
It is worth noting that compared to PC and SR, the proposed SS scheme has an extra hyper-parameter γ for controlling the number of the removed volumes. In Fig. 6, we count the removed volumes across subjects for different values of the hyper-parameter and find no significant differences between two groups (i.e., MCI and NC). This means that the self-scrubbing operation itself does not introduce bias into MCI and NC data. In other words, the improvement of the discriminability may mainly benefit from the proposed FBN estimation method.
Fig. 6.
The average number of the scrubbed volumes on MCI, NC, or both, with each bar denoting the standard deviation. The volumes are scrubbed by the proposed method with fixed γ = 0.3, 0.5, 0.7 or optimized γ, respectively. The optimized γ is obtained by LOOCV for each subject. Based on t-test, we note that the numbers of removed volumes have no statistical differences between MCI and NC groups, since all p-values (0.3621 for γ =0.3, 0.5729 for γ =0.5, 0.4764 for γ =0.7, and 0.1473 for optimized γ) are greater than 0.05. Therefore, the self-scrubbing operation itself does not introduce bias into MCI and NC data.
4). Further Discussion on the Self-Scrubbing Scheme
In this section, we designed two experiments for investigating the scrubbed volumes by our proposed method. First, we conduct an experiment to investigate the removed volumes by the traditional scrubbing (DVARS) and our proposed self-scrubbing scheme. Based on the result shown in Fig. 7, we note that they can remove some common volumes with higher possibility than the random case. For example, if 30 volumes were removed from the time series with totally 137 volumes, nearly 13 volumes are common, on the average, by DVARS and the proposed method. However, the number of common volumes is only 5 for the random case. This result illustrates that the scrubbed volumes by the proposed criterion contain a part of stereotyped structured noisy points such as head motion.
Fig. 7.
The average number of common volumes removed by two methods, with each bar denoting the margin of error. We use the p-value of DVARS2 and the (fitting) loss value in our method (γ = 0.5) to scrub the same number of volumes, and then count the common volumes. The result shows that the number of common volumes removed by DVARS and our proposed method is significantly larger than that by two random scrubbing operations.
Second, in order to further explore the removed volumes by our scheme, we estimate FBNs by the time series with and without SS9, and then determine the brain regions (ROIs) with connections influenced significantly by SS. For each brain region, we add up their corresponding connection weights, and the sum for the ith brain region is calculated as follows:
| (20) |
where N is the number of ROIs, R is the number of subjects, Wij is the connection weight value between ROIs i and j in the estimated FBN and k is the k-th subject. For each brain region, we have a series with R elements.
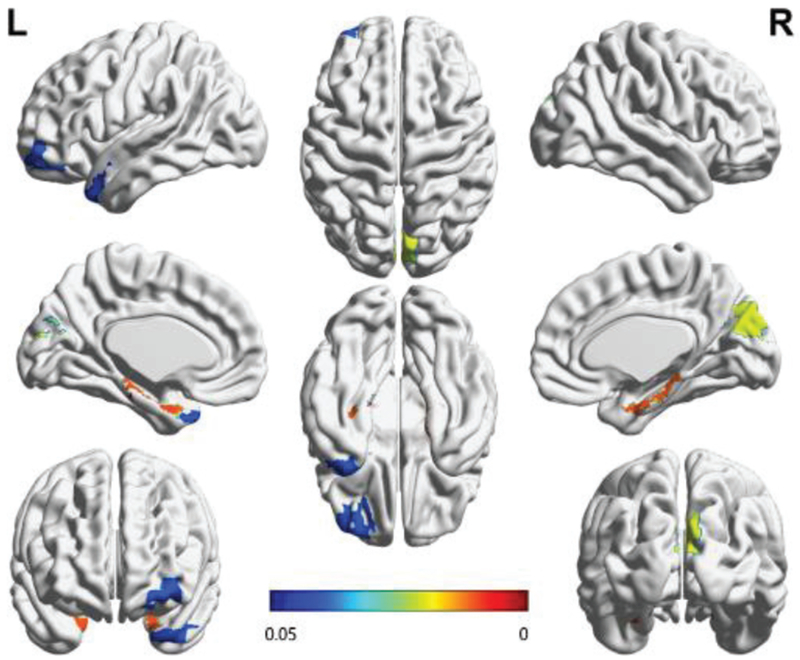
Then, we investigate the statistical differences of brain regions with and without SS by pair-wise t-test. The result is mapped onto the ICBM 152 template as shown in Fig. 8, where the color bar represents the p-value of t-test. In particular, under the ICBM 152 template and AAL atlas, we simply set the value of corresponding ROI as the p-value (p<0.05). In Fig.8, we note that the differences of the estimated FBNs mainly concentrate on hippocampus, temporal lobe, cuneus and frontal regions. These brain regions have been shown to be closely related to memory, emotion and auditory sense [46–49]. Therefore, we assume that those removed points may be related to some abnormal resting-state processes such as mind-wandering (memory), worrying (emotion), or distraction due to scanner sounds [23]. In other words, the time points that do not fit the FBN estimation may be related to some “disturbances” from the scanning conditions, memory, emotion or mind wandering. That is, compared with the traditional motion-based scrubbing methods, the proposed method can further scrub some “abnormal resting-states” points.
Fig. 8.
The brain regions with their connections significantly influenced by SS. We first estimate FBNs based on time series with and without SS, and then calculate the sum of connection weights for each brain region by Eq. (20). Finally, we investigate the statistical differences of brain regions with and without SS by t-test. The p-value of t-test for each brain region (p<0.05) is mapped onto the ICBM 152 surface template. The color bar represents the p-value of t-test. As we can see, the changes mainly take place in the hippocampus, cuneus and temporal lobe regions. This figure is drawn by BrainNet Viewer toolbox (https://www.nitrc.org/projects/bnv/).
5). Discriminative Connection
For FBNs based on SR+SS, we investigate the most discriminative connections for identifying subjects with MCI from NCs. Specifically, we select 64 connections whose p-value are less than 0.01. As visualized in Fig. 9, the thickness of the arc is inversely proportional to the p-value, indicating the discriminative power of the corresponding edge. It is worth pointing out that the significantly changed connections or regions, as shown in Fig. 4 and 8, are contained in these discriminative connections. Therefore, it can support the classification accuracy improvement of the proposed method to some extent. Additionally, we note that several regions, including superior-medial frontal gyrus, medial orbitofrontal gyrus, hippocampus, para-hippocampus and precuneus, are selected in our proposed method. These regions are generally involved in the default mode network [50], and believed to be biologically associated with MCI identification, according to previous studies [51,52].
Fig. 9.
The most frequently selected connections for the 90 AAL ROIs. The figure is created by circularGraph tool, shared by Paul Kassebaum. http://www.mathworks.com/matlabcentral/fileexchange/48576-circulargraph
IV. Conclusion
The observed fMRI time series commonly contain various artifacts, noises or some “abnormal” resting-state processes, thus leading to a poor estimation of the FBN. In this paper, we propose a novel FBN estimation method by incorporating a latent variable into the regularized FBN estimation model as an indicator of the data quality. Then, we design an alternating optimization algorithm to solve the proposed model. As a result, the proposed method estimates FBN and scrubs the fMRI series adaptively in a single framework. In particular, we adopt the SR scheme as a simple test platform in this paper for developing our method that is then validated on two real-world (both scrubbed and non-scrubbed) datasets. The experimental results show that the proposed method can consistently improve the final performance in all cases. Moreover, compared with traditional scrubbing methods, our proposed method can work with a clearer goal by estimating FBN and detecting “noisy” volumes jointly in a unified optimization framework. Also, compared with the traditional scrubbing methods that only scrub the physical or structured noises, the proposed method can further scrub the “abnormal resting-states” time points.
In order to examine how FBN changes following the self-scrubbing, we compare the FBNs estimated by SR and SR+SS methods. The result shows that the removed volumes are highly related to some “abnormal” resting-state processes. However, that is only a conjecture based on an initial and indirect experiment. A task-oriented experimental design is necessary for providing more evidence, which is beyond the scope of this paper. In the future, we plan to investigate this interesting problem by well-designed task-state experiments.
Again, we would like to emphasize that the proposed method is the first to attempt a joint optimization of FBN with scrubbing based on a latent variable model. But, it still has several limitations that need to be improved. For example, (1) the proposed method selects all time points in the first iteration, which may lead to a bad regression result (local minimum) when a large number of “bad” volumes exists; and (2) the possibly useful information from the removed points can be lost, since the proposed method simply discards them based on the hard indicator. Therefore, in the future we plan to design a soft indicator variable for further improving the flexibility of the proposed method.
Acknowledgments
This work was partly supported by National Natural Science Foundation of China (61300154, 61402215), Natural Science Foundation of Shandong Province (ZR2018MF020), Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJQN201800716, KJ175492), Natural Science Foundation Project of CQCSTC (2018jcyjAX0398), Shanghai Municipal Planning Commission of Science and Research Fund (201740010) and NIH grants (EB022880, AG049371, AG042599).
Footnotes
In Section 3 (Optimization Algorithm), we will find that such a relaxation is tight, thus resulting in a binary solution for vt.
In our experiments, the initial value of the step size is 0.001, and then it is adaptively updated step by step according to the used SLEP toolbox (http://www.yelab.net/software/SLEP).
Note that, the SR model reduces to Pearson’s correlation, since only two ROIs are involved in this toy problem.
The elements of the adjacency matrix indicate the connection strengths of the node pairs in the network. Here, for the convenience of comparison among different methods, all the weights are normalized to the interval [−1 1].
Since the data scrubbing by FD may remove large proportion of frames for some subjects, we exclude subjects with the remaining time points < 80.
For reducing the confounding effect of the physical/structured noisy points, we exclude the common removed volumes shared with the traditional scrubbing method.
Contributor Information
Weikai Li, School of Mathematics Science, Liaocheng University, Liaocheng 252000, China; College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, MIIT Key Laboratory of Pattern Analysis and Machine Intelligence, Nanjing 211106 China.
Lishan Qiao, School of Mathematics Science, Liaocheng University, Liaocheng 252000, China.
Limei Zhang, School of Mathematics Science, Liaocheng University, Liaocheng 252000, China.
Zhengxia Wang, College of Information Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, China.
Dinggang Shen, Department of Radiology and BRIC, University of North Carolina at Chapel Hill, NC 27599, USA; Department of Brain and Cognitive Engineering, Korea University, Seoul 02841, Republic of Korea.
References
- [1].Smith SM, Vidaurre D, Beckmann CF, Glasser MF, Jenkinson M, Miller KL, Nichols TE, Robinson EC, Salimi-Khorshidi G, and Woolrich MW, “Functional connectomics from resting-state fMRI,” Trends in Cognitive Sciences, vol. 17, no. 12, pp. 666–682, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Greicius MD, Krasnow B, Reiss AL, and Menon V, “Functional connectivity in the resting brain: a network analysis of the default mode hypothesis,” Proceedings of the National Academy of Sciences of the United States of America, vol. 100, no. 1, pp. 253–258, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Wee CY, Yap PT, and Shen D, “Diagnosis of Autism Spectrum Disorders Using Temporally Distinct Resting-State Functional Connectivity Networks,” Cns Neuroscience & Therapeutics, vol. 22, no. 3 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wee CY, Wang L, Shi F, Yap PT, and Shen D, “Diagnosis of autism spectrum disorders using regional and interregional morphological features,” Human Brain Mapping, vol. 35, no. 7, pp. 3414–30, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Delmonte S, Gallagher L, O’Hanlon E, Mcgrath J, and Balsters JH, “Functional and structural connectivity of frontostriatal circuitry in Autism Spectrum Disorder,” Frontiers in Human Neuroscience, vol. 7, no. 7, pp. 233–242. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Huang S, Li J, Sun L, Liu J, Wu T, Chen K, Fleisher A, Reiman E, and Ye J, “Learning Brain Connectivity of Alzheimer’s Disease from Neuroimaging Data,” Conference on Neural Information Processing Systems, pp. 808–816, 2009. [Google Scholar]
- [7].Supekar K, Menon V, Rubin D, Musen M, and Greicius MD, “Network Analysis of Intrinsic Functional Brain Connectivity in Alzheimer’s Disease,” Plos Computational Biology, vol. 4, no. 6, pp. 1–11, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Duval C, Daneault JF, Hutchison WD, and Sadikot AF, “A brain network model explaining tremor in Parkinson’s disease,” Neurobiology of Disease, vol. 85, 2015. [DOI] [PubMed] [Google Scholar]
- [9].Smith SM. Miller KL. Salimi-Khorshidi G. Webster M. Beckmann CF, Nichols TE, Ramsey JD, and Woolrich MW, “Network modelling methods for FMRI,” Neuroimage, vol. 54, no. 2, pp. 875–91, 2011. [DOI] [PubMed] [Google Scholar]
- [10].Qiao L, Han Z, Kim M, Teng S, Zhang L, and Shen D, “Estimating functional brain networks by incorporating a modularity prior,” Neuroimage, vol. 141, pp. 399–407, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Lee H, Lee DS, Kang H, Kim BN, and Chung MK, “Sparse brain network recovery under compressed sensing,” IEEE Transactions on Medical Imaging, vol. 30, no. 5, pp. 1154–65, 2011. [DOI] [PubMed] [Google Scholar]
- [12].Yu R. Zhang H. An L. Chen X. Wei Z. and Shen D. “Correlation-Weighted Sparse Group Representation for Brain Network Construction in MCI Classification,” International Conference on Medical Image Computing & Computer-assisted Intervention, vol. 9900, pp. 37–45, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Wee CY, Yap PT, Zhang D. Wang L, and Shen D, “Group-constrained sparse fMRI connectivity modeling for mild cognitive impairment identification,” Brain Structure & Function, vol. 219, no. 2, pp. 641–656, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Zhu X, Suk HI, Huang H, & Shen D, “Structured Sparse Low-Rank Regression Model for Brain-Wide and Genome-Wide Associations,” International Conference on Medical Image Computing & Computer-assisted Intervention, vol. 9900, pp.344, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Li W, Wang Z, Zhang L, Qiao L, and Shen D, “Remodeling Pearson’s Correlation for Functional Brain Network Estimation and Autism Spectrum Disorder Identification,” Frontiers in Neuroinformatics, vol. 11, pp. 55, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Poldrack RA, Mumford JA, and Nichols TE, “Handbook of functional MRI data analysis,” London: Cambridge University Press, 2011. [Google Scholar]
- [17].Freire L, and Mangin JF, “Motion correction algorithms may create spurious brain activations in the absence of subject motion,” Neuroimage, vol. 14, no. 3, pp. 709–22, 2001. [DOI] [PubMed] [Google Scholar]
- [18].Power JD, Barnes KA, Snyder AZ, Schlaggar BL, and Petersen SE, “Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion,” Neuroimage, vol. 59, no. 3, pp. 2142, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Yan CG. Cheung B. Kelly C. Colcombe S, Craddock RC, Martino AD, Li Q, Zuo XN, Castellanos FX, and Milham MP, “A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics,” Neuroimage, vol. 76, no. 1, pp. 183–201, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Chen X, Zhang H, Zhang L, Shen C, Lee SW, and Shen D, “Extraction of dynamic functional connectivity from brain grey matter and white matter for mci classification,” Human Brain Mapping, vol. 38, no. 10, pp. 5019, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Van Dijk KR, Sabuncu MR, and Buckner RL, “The influence of head motion on intrinsic functional connectivity MRI,” Neuroimage, vol. 59, no. 1, pp. 431–438, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Yang S, Ross TJ, Zhang Y, Stein EA, and Yang Y, “Head motion suppression using real-time feedback of motion information and its effects on task performance in fMRI,” Neuroimage, vol. 27, no. 1, pp. 153, 2005. [DOI] [PubMed] [Google Scholar]
- [23].Bijsterbosch J, Smith S and Beckmann C, “Introduction to Resting State fMRI Functional Connectivity,” London: Oxford University Press, 2017 [Google Scholar]
- [24].Chang C, and Glover GH, “Time-frequency dynamics of resting-state brain connectivity measured with fMRI,” Neuroimage, vol. 50, no. 1, pp. 81, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, Wolf DH, “An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data,” Neuroimage, vol. 64, pp. 240–256, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Kumar MP, Packer B, and Koller D, “Self-Paced Learning for Latent Variable Models.” pp. 1189–1197. [Google Scholar]
- [27].Chao-Gan Y. and Yu-Feng Z. “DPARSF: a MATLAB toolbox for “pipeline” data analysis of resting-state fMRI,” Frontiers in Systems Neuroscience, vol. 4, no. 13, pp. 13, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Friston KJ, Williams S, Howard R, Frackowiak RSJ, and Turner R, “Movement-Related effects in fMRI time-series,” Magnetic Resonance in Medicine, vol. 35, no. 3, pp. 346–355, 1996. [DOI] [PubMed] [Google Scholar]
- [29].Ashburner J, “A fast diffeomorphic image registration algorithm,” Neuroimage, vol. 38, no. 1, pp. 95–113, 2007. [DOI] [PubMed] [Google Scholar]
- [30].Brett M, Christoff K, Cusack R, and Lancaster J, “Using the talairach atlas with the mni template,” Neuroimage, vol. 13, No. 6, pp: 85–85,2011. [Google Scholar]
- [31].Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, and Joliot M, “Automated Anatomical Labeling of Activations in SPM Using a Macroscopic Anatomical Parcellation of the MNI MRI Single-Subject Brain,” Neuroimage, vol. 15, no. 1 pp. 273–289, 2002. [DOI] [PubMed] [Google Scholar]
- [32].Marrelec G, Krainik A, Duffau H, Pélégriniissac M, Lehéricy S, Doyon J, and Benali H, “Partial correlation for functional brain interactivity investigation in functional MRI,” Neuroimage, vol. 32, no. 1, pp. 228–37, 2006. [DOI] [PubMed] [Google Scholar]
- [33].Ramsey JD, Hanson SJ, Hanson C, Halchenko YO, Poldrack RA, and Glymour C, “Six problems for causal inference from fMRI,” Neuroimage., vol. 49, no. 2, pp. 1545–1558, 2010. [DOI] [PubMed] [Google Scholar]
- [34].Mcıntosh AR, and Gonzalez-Lima F, “Structural equation modeling and its application to network analysis in functional brain imaging,” Human Brain Mapping, vol. 2, no. 1-2, pp. 2–22, 1994. [Google Scholar]
- [35].Friston KJ, Harrison L, and Penny W, “Dynamic causal modelling,” Neuroimage, vol. 19, no. 4, pp. 1273, 2003. [DOI] [PubMed] [Google Scholar]
- [36].Fomito A, Zalesky A, and Bullmore E, “Fundamentals of brain network analysis” USA: Academic Press, 2016. [Google Scholar]
- [37].Mardia KV, Kent JT, and Bibby JM, “Multivariate analysis,” Mathematical Gazette, vol. 37, no. 1, pp. 123–131, 1979. [Google Scholar]
- [38].Nichols TE, “Notes on Creating a Standardized Version of DVARS,” Arxiv, 2017. [Google Scholar]
- [39].Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, and Petersen SE, “Methods to detect, characterize, and remove motion artifact in resting state fMRI,” Neuroimage, vol. 84, no. 1, pp. 320, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Bazaraa MS, Sherali HD, and Shetty CM, Nonlinear Programming: Theory and Algorithms, 3rd Edition: Wiley, 2013. [Google Scholar]
- [41].Combettes PL, and Pesquet JC, “Proximal Splitting Methods in Signal Processing,” Bauschke Heinz H, vol. 49, pp. 185–212, 2015. [Google Scholar]
- [42].Liu Jun, and Ye J. “Efficient Euclidean projections in linear time.” International Conference on Machine Learning ACM, vol.12, pp.657–664, 2009. [Google Scholar]
- [43].Jie Z, Wei C. Liu Z. Kai Z. Xu L. Ye Y. Becker B. Liu Y. Kendrick KM, and Lu G, “Neural, electrophysiological and anatomical basis of brain-network variability and its characteristic changes in mental disorders,” Brain, vol. 139, no. 8, 2016. [DOI] [PubMed] [Google Scholar]
- [44].Chang CC, and Lin CJ, “LIBSVM: A library for support vector machines,” Acm Transactions on Intelligent Systems & Technology, vol. 2, no. 3, article 27, pp. 389–396, 2007. [Google Scholar]
- [45].Delong ER, Delong DM, and Clarkepearson DL, “Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach,” Biometrics, vol. 44, no. 3, pp. 837–845, 1988. [PubMed] [Google Scholar]
- [46].Immordinoyang MH, and Singh V, “Hippocampal contributions to the processing of social emotions,” Human Brain Mapping, vol. 34, no. 4, pp. 945, 2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].D J, and MA W, “Coordinated memory replay in the visual cortex and hippocampus during sleep,” Nature Neuroscience, vol. 10, no. 1, pp. 100–107, 2006. [DOI] [PubMed] [Google Scholar]
- [48].Strouse A, Ashmead DH, Ohde RN, and Grantham DW “Temporal processing in the aging auditory system,” Journal of the Acoustical Society of America, vol. 104, no. 4, pp. 2385–99, 1998. [DOI] [PubMed] [Google Scholar]
- [49].Fletcher PC, and Henson RNA, “Frontal lobes and human memory,” Brain, vol. 124, no. 5, pp. 849–881, 2001 [DOI] [PubMed] [Google Scholar]
- [50].Greicius MD, Krasnow B, Reiss AL, & Menon V “Functional connectivity in the resting brain: a network analysis of the default mode hypothesis”. Proceedings of the National Academy of Sciences, vol. 100, no. 1 pp. 253–258, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Greicius M, “Resting-state functional connectivity in neuropsychiatric disorders,” Current Opinion in Neurology, vol. 21, no. 4, pp. 424–430, 2008. [DOI] [PubMed] [Google Scholar]
- [52].Albert MS, DeKosky ST, Dickson D, Dubois B, Feldman HH, Fox NC, et al. , “The diagnosis of mild cognitive impairment due to Alzheimer’s disease: recommendations from the National Institute on Aging-Alzheimer’s Association Workgroups on Diagnostic Guidelines for Alzheimer’s disease.” Alzheimers Dement vol. 7, no. 3, pp. 270–279,2011 [DOI] [PMC free article] [PubMed] [Google Scholar]