Abstract
State-of-the-art exoskeletons are typically limited by low control bandwidth and small range stiffness of actuators which are based on high gear ratios and elastic components (e.g., series elastic actuators). Furthermore, most exoskeletons are based on discrete gait phase detection and/or discrete stiffness control resulting in discontinuous torque profiles. To fill these two gaps, we developed a portable lightweight knee exoskeleton using quasi-direct drive (QDD) actuation that provides 14 Nm torque (36.8% biological joint moment for overground walking). This paper presents 1) stiffness modeling of torque-controlled QDD exoskeletons and 2) stiffness-based continuous torque controller that estimates knee joint moment in real-time. Experimental tests found the exoskeleton had high bandwidth of stiffness control (16 Hz under 100 Nm/rad) and high torque tracking accuracy with 0.34 Nm Root Mean Square (RMS) error (6.22%) across 0–350 Nm/rad large range stiffness. The continuous controller was able to estimate knee moments accurately and smoothly for three walking speeds and their transitions. Experimental results with 8 able-bodied subjects demonstrated that our exoskeleton was able to reduce the muscle activities of all 8 measured knee and ankle muscles by 8.60%−15.22% relative to unpowered condition, and two knee flexors and one ankle plantar flexor by 1.92%−10.24% relative to baseline (no exoskeleton) condition.
Index Terms—: Knee exoskeleton, quasi-direct drive actuation, stiffness control, force/torque control
I. Introduction
Portable lower-limb exoskeletons have great potential for mobility restoration and human augmentation [1–3]. Compliance, low mass, and the ability to assist a diverse array of movements are key requirements for an exoskeleton to be viable in daily life. There is a wealth of literature on ankle exoskeletons to augment human walking [4–7] and a substantial amount of literature on hip or ankle exoskeletons for walking augmentation [8–13]. Comparably, there is little research on knee exoskeletons for augmentation [14, 15], likely because the positive work done at the knee in level walking is less than that at the ankle or hip [16]. However, the knee is crucial in locomotion, and there is a compelling need to investigate the benefits of a knee exoskeleton on human performance and understand the human-robot interaction.
The challenges of exoskeleton design stem from the need to balance multiple attributes of the mechatronic system, including weight, power, and compliance while being able to replicate near biological levels of assistance [1, 17]. Tethered actuation can circumvent the exoskeleton design challenges in a research environment, but tethered exoskeletons are not directly transferable to real-world applications. Untethered (or portable) exoskeletons are suitable for non-controlled environments and have a wide potential for mobility assistance [18] and human augmentation [11]. But the mass of the actuators, power supply, and wearable structure imposes a penalty on energetics and biomechanics that some state-of-the-art exoskeletons have not managed to overcome [19, 20]. Furthermore, these exoskeletons are not very compliant, which can inhibit natural movements [19]. The most prevalent method of enhancing compliance is to use a series elastic actuator (SEA), which introduces spring, an elastic element of fixed stiffness [21]. In addition, variable stiffness actuators (VSA) can vary stiffness throughout gait but typically require a second motor [22]. Both SEA and VSA bring extra weight and make the exoskeleton heavy and bulky. A further difficulty in using series elastic or variable stiffness actuators in exoskeletons is their low bandwidth, making it challenging to adapt the assistance to human locomotion or unexpected perturbations [23, 24]. Thus, SEA actuators are not able to realize both high compliance and high bandwidth, and there is a solid need to overcome this limitation. Except for electric motors, a compliant exoskeleton with pneumatic artificial muscles was studied in [25, 26], but both the bandwidth and stiffness range is minimal, and the artificial muscles must be tethered to a large and heavy air compressor.
To address multifaceted mechatronic design challenges of exoskeletons, we proposed a quasi-direct drive (QDD) actuator with electrically adjustable stiffness in this paper. QDD actuators, comprised of high torque density motors and low gear ratio transmission, were popularized in legged robots [27, 28] before they gained traction in the wearable robotics community [23, 29, 30]. Our prior work [23] focused on the mechatronics design of a hip exoskeleton, but this work is primarily about novel control algorithms for knee exoskeletons. Compared with the QDD actuator used in the legged robot [28], our actuator contains a customized motor with a high torque constant. Therefore, our actuator has a high torque density, and it meets the high torque and lightweight requirements of knee exoskeleton applications. As shown in Fig. 1, by leveraging our high-torque density actuator and simple mechanical design (e.g., no spring mechanism and associated structures), we developed the most lightweight portable powered knee exoskeleton (Table I), which is the platform to study stiffness modeling and continuous torque control in this paper. To the best of our knowledge, there is no investigation into stiffness control of quasi-direct-drive actuators for wearable robots to understand the performance through modeling and experiments. The low inertia and high stiffness transmission of QDD actuators can be designed with a high stiffness control bandwidth with a large range of stiffness, making them uniquely suitable for exoskeletons.
Fig. 1.
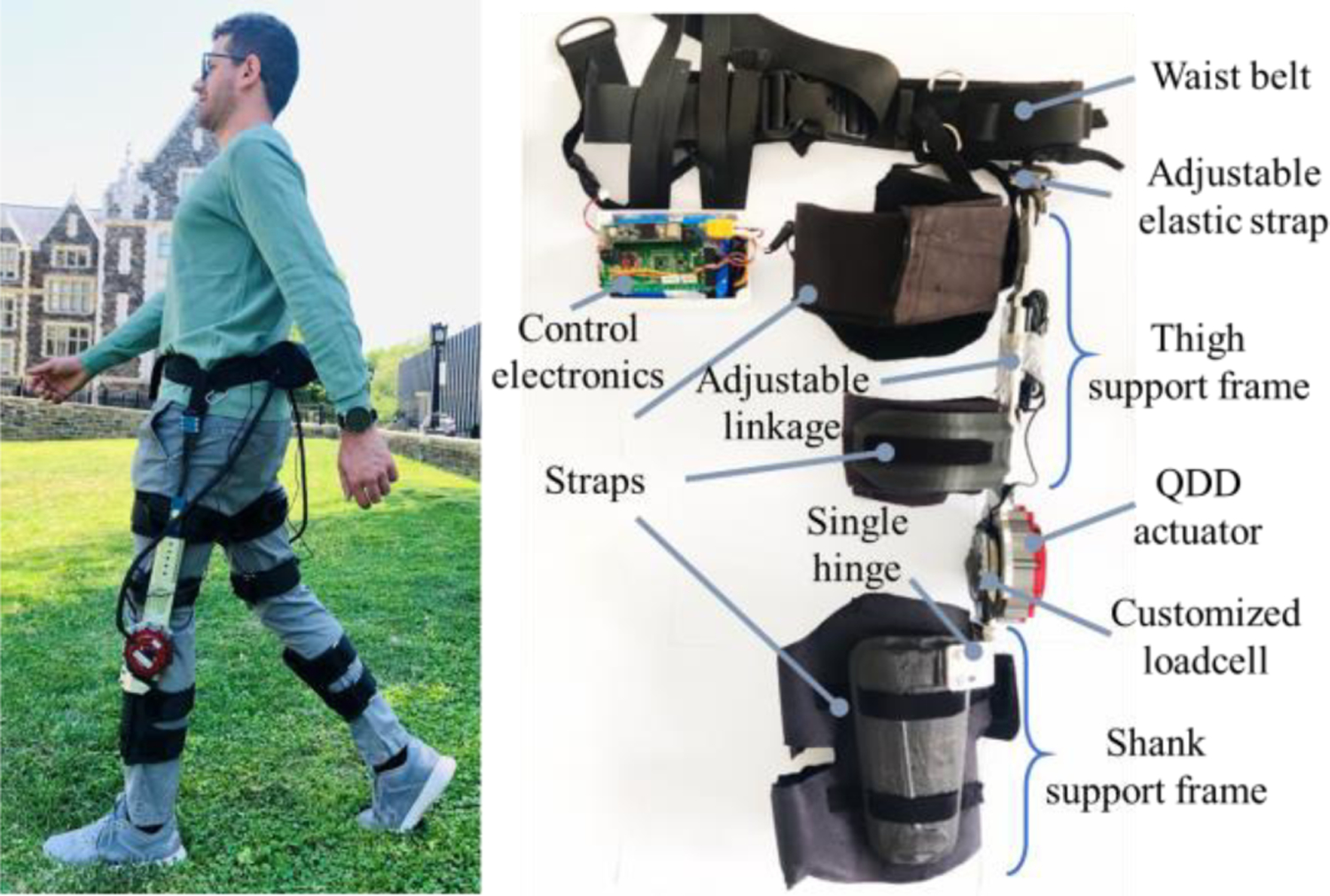
The lightweight and compact powered portable knee exoskeleton is based on quasi-direct drive (QDD) actuation. The knee exoskeleton comprises a waist belt, adjustable elastic strap, thigh support frame, knee joint actuation system, and shank support frame. The total weight of a middle-size unilateral (bilateral) knee exoskeleton is 2.1 (3.5) kg, including control electronics and battery (0.7 kg).
TABLE I.
Comparison of Portable Knee Exoskeletons
| Unilateral Knee Exoskeleton | Weight (kg) | Actuation Paradigm | Gear Ratio | Actuation Torque (Nm) | Actuation Reflected Inertia (kg-cm2) | Torque Density (Nm/kg) | Backdrive Torque (Nm) | Torque Control Bandwidth (Hz) | Control Method |
|---|---|---|---|---|---|---|---|---|---|
| This work | 2.1 | QDD | 6:1 | 14 | 32.22 | 6.66 | Low (0.22) | High (40.7) | State-based |
| Zhu [29] | 2.69 | QDD | 7:1 | 10.5 | 200.90 | 3.90 | Low (1.32) | High (55.1) | Phase angle |
| Lee [20] | 2.7 | Conventional | 113:1 | 15.14 | 2311.19 | 5.61 | Medium | Medium | Time-based |
| Chen [40] | 2.59 | Conventional | 153:1 | 14.63 | 772.50 | 5.65 | Medium | Medium (9.6) | Time-based |
| Karavas [19] | >41 | SEA | 100:1 | 81.3 | 39320.00 | N/A | High | Low | EMG-based |
| Liu [41] | >51 | SEA (VSA) | 100:1 | 45.8 | 31700.00 | N/A | High | Low | N/A |
Traditional high-level exoskeleton controllers cannot accurately produce biological joint moment patterns and adapt to changes in walking patterns [20, 31]. Existing exoskeleton controls are typically based on time (gait cycle) [32] or kinematics (e.g., joint angle) [33]. Those controllers typically implement the assistive torque profile for discrete phases of the gait cycle and have difficulty in adapting to varying walking patterns (e.g., speed changes and sudden stops), because the assistive torque profile can only be changed at the start of the following discrete segment.
Therefore, continuous gait detection and controllers are gaining popularity in wearable robotics. They can instantaneously update the assistance profile in response to the input signal (e.g., joint angle), which allows quick adaptations to change in the walking pattern [34–37]. Martinez et al. [34] used hip and knee joint angles to map joint kinematics to drive torque control for a lower limb exoskeleton in the swing phase and allow the user to change step length and step time. Lim et al. [35] used hip joint angle to provide continuous sinusoidal torque assistance at the hip exoskeleton. Quintero et al. [36] used gait phase to map kinematics constraint to continuously provide periodic (sine and cosine) wave-based torque assistance for a knee-ankle prosthesis. However, none of them can generate continuous biological torque profiles. Thatte et al. [37] developed a continuous torque profile to assist knee-ankle prosthesis by utilizing joint angle, angular velocity, and feedforward torque. However, this method is computationally expensive, and the angular velocity data from differential calculation makes the controller sensitive to noise from ground contacts [36].
To continuously provide proportional biological torque assistance, we developed a stiffness-based continuous torque controller in this paper. As one type of impedance control, stiffness control (no inertia and damper terms, no acceleration and angular velocity data required) can be a simple yet robust control method to produce mechanical compliance for assistive wearable robots. The biomechanics of human walking involves the coordination of lower limb joints with complicated stiffness dynamics [15, 38]. It is of great significance if the wearable robot can provide sufficient stiffness dynamics for handling various human movement patterns. However, reported stiffness control methods for the assistive wearable robot are generally either discrete or discontinuous [39]. Inspired by the gait biomechanics, we propose a simple stiffness-torque model for our stiffness-based continuous torque controller to estimate biological moment in real-time using only a few measurements (i.e., knee joint angles). There are several advantages of this work. perspective ensures that our controller is not too sensitive to errors in timing. Second, a controller based on the estimated biological knee moment provides a broadly applicable assistance model that does not depend on a particular angle/trajectory but instead allows the assistance to be scaled as a percentage of user effort (i.e., volitional moment). This approach can be used for augmentation (the focus of this paper), whereby the amount of assistance can be proportional to the effort exerted by the user. Likewise, the same approach can be beneficial for rehabilitation by ensuring that a targeted amount of volitional effort (or muscle activity) is maintained.
This work focuses on two major contributions by leveraging our lightweight exoskeleton platform. First, we developed a stiffness modeling of quasi-direct drive (QDD) exoskeleton and benchmarked it with the series elastic actuation-based exoskeletons. The results showed that our exoskeleton (Fig. 1) has a high stiffness control bandwidth (16 Hz under 100 Nm/rad) with a large range of stiffness (our robot provides 0–350 Nm/rad stiffness compared to the human knee joint stiffness of 0–176 Nm/rad) and high torque tracking accuracy (0.34 Nm root mean square error, 6.22% of the desired peak torque). Second, we proposed a continuous torque controller that uses the stiffness model to estimate the biological torque in real-time and is computationally efficient and adaptable to different overground walking speeds to overcome the limitations of discrete controllers (e.g., finite state machine methods). The results of eight able-bodied subjects indicated that our proposed exoskeleton could reduce the root mean square muscle activation of all the eight measured knee and ankle muscles by 8.60%~15.22% compared to the unpowered condition. A reduction of 1.92%~10.24% in root means square muscle activities of two knee flexors and one ankle plantar flexor in 8 able-bodied subjects compared with the baseline condition.
II. Biomechanics of Human Knee During Walking And Requirements for Design And Control
Understanding the biomechanics of human knees is crucial to enabling symbiotic human-robot collaboration. Specifically, it involves creating high-performance mechatronics, deriving models of human-robot interaction, and developing bio-inspired control.
A. Biomechanics of the Human Knee during Walking
The knee is essential for efficient locomotion, supporting body weight, absorbing shock, and providing foot clearance. Angle, moment, and power of the joint describe the action and function of the knee. The piecewise linear moment-angle relationship (also called quasi-stiffness) of the knee is a measure that characterizes knee stiffness and essentially models the knee joint as a torsional spring in distinct phases of stride [42]. Fukuchi et al. [43] collected biomechanics data from 23 subjects walking on a level treadmill at 1.24 ± 0.05 m/s and found an average peak torque of 31 Nm (0.46 Nm/kg) and the quasi-stiffness ranging from 0 to 176 Nm/rad.
Each stride can be split into 4 phases: 1) initial double First, looking at the torque assistive control from a state-space support, 2) single support, 3) second double support, and 4) swing phase, as illustrated in Fig. 2.
Fig. 2.
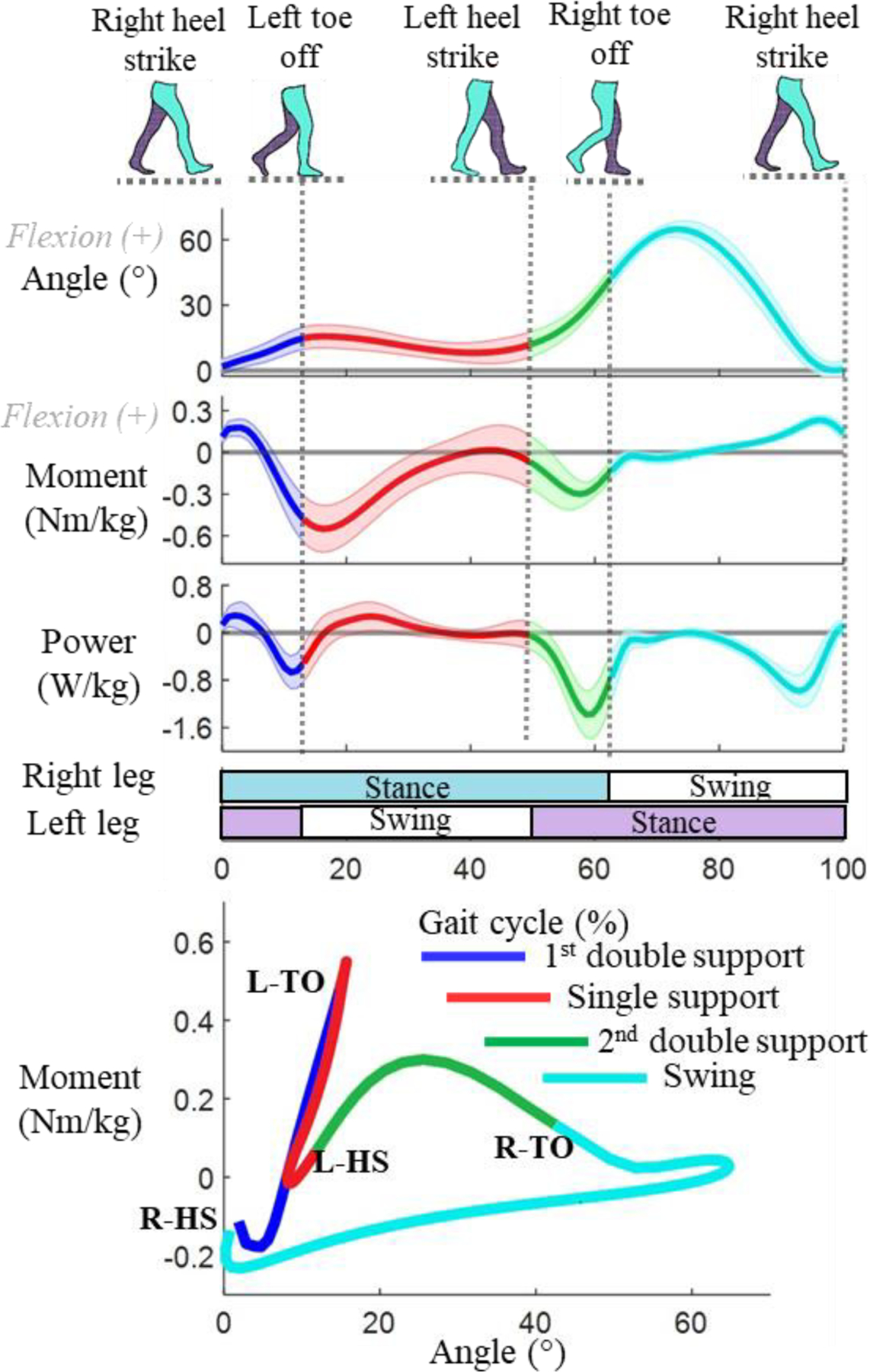
Knee biomechanics over a stride. Shaded areas represent the standard deviation. Different colors indicate the 4 phases: initial double support, single support, second double support, and swing.
Initial double support: The body weight is transferred from the trailing limb (left) to the leading limb. The knee joint moment-angle relationship is very linear in this phase, and the quasi-stiffness is high.
Single support: The right leg supports the entire body weight in this phase. The moment-angle relationship is linear in this phase, with a similar quasi-stiffness to initial double support.
Second double support: The body weight is shifted from the right leg to the left leg in this phase. The knee moment-angle relationship is somewhat linear in this phase, although the quasi-stiffness is substantially lower than in the previous phases.
Swing phase: The knee flexes to assist with foot clearance, then extends in preparation for ground contact. Overall, the moment magnitude in the swing phase is lower than in the stance phase. Although the relationship is non-linear (especially around the transition from flexion to extension), most of the phase can be represented as linear with relatively small error due to the low moment magnitude.
The benefits of powered assistance to the knee joint are not well understood. One reason is that state-of-the-art powered knee exoskeletons are heavy, and the mass penalty affects natural movements [41]. There is no prior work to systematically investigate the effect of a powered portable knee exoskeleton in three conditions (powered, unpowered, and baseline without exoskeleton). Although the knee contributes less positive power than the ankle and hip joints in level walking [16, 44], the knee is vital for effectual walking. And it is beneficial for the knee to have external assistance. First, some of the muscles that actuate the knee joint are multi-articular, meaning the muscle crosses and actuates multiple joints simultaneously [45–47]. Augmenting the knee joint will affect the muscle biomechanics of the bi- and tri-articular muscles, which could improve muscle efficiency or network efficiency done at the joint. Second, studies have found that altering dynamics at one lower limb joint can modify the dynamics of the non-assisted joints, such that a knee exoskeleton may be able to improve walking or muscle efficiency not only at the knee joint but also at the ankle and hip joints [15, 48, 49]. Third, modern inverse dynamics techniques (using six degrees of freedom) found that traditional inverse dynamics (with three degrees of freedom) underestimated the positive work done at the knee. Thus, more positive work was done at the knee than reported in the biomechanical study [50]. The powered knee exoskeleton could potentially benefit the wearer by increasing the amount of positive work done at the knee. In addition to these energetic considerations, a knee exoskeleton that reduces load through the knee has the potential to prevent injury, reduce chronic pain, or improve the walking ability of people with musculoskeletal impairments [51–55].
B. Requirements for Design and Control
Portable exoskeletons should be lightweight to reduce the energetic penalty of wearing the exoskeleton and diminish impacts on the inertial properties of legs [56]. For our design, we set desired parameters such that it exceeds the performance defined by knee biomechanics at 1.25 m/s walking speed to ensure the versatility of the exoskeleton, e.g., providing assistance across different walking speeds and not impeding natural movements (e.g., squatting and stair climbing). The requirements are summarized in Table II. Exoskeleton joint stiffness is required to span the range of biological stiffness (0~176 Nm/rad). It is unnecessary to provide assistive torque equivalent to 100% biological torque because well-timed assistive torques (e.g., 30%) can impart substantial biomechanical benefits to able-bodied individuals [30, 57]. Prior art on knee exoskeletons has predominantly focused on assisting only during the stance phase [15, 18, 20], as most mechanical work of a knee occurs in this phase. Swing phase knee assistance is primarily used for rehabilitation or assistance to users with limited mobility [52, 53]. Lockheed Martin’s Onyx is one of the few knee exoskeletons for able-bodied augmentation that provides assistance in both the stance and swing phases for level ground walking [14]. Augmenting the knee during the swing phase would help compensate for the added mass on the leg, which needs to be carried through the swing phase. Furthermore, assisting the knee during the swing phase may also improve dynamics at the ankle or hip joint. Therefore, we chose to assist the entire stride.
TABLE II.
Design Parameters of The Knee Exoskeleton
| Parameters | Human Walking | Desired | This work |
|---|---|---|---|
| Knee flexion (°) | 65 | 130 | 130 |
| Range of knee joint stiffness (Nm/rad) | 0 − 176 | 0 − 200 | 0 − 350 |
| Max knee joint moment (Nm/kg) | 0.4 | 0.12 | 0.25 |
| Max knee joint speed (rad/s) | 6.63 | 10 | 25 |
| Exoskeleton weight (kg) | —— | 5 | 3.5 |
For stiffness control of knee exoskeletons, state-of-the-art robots typically use discrete quasi-stiffness models [21], usually facilitated by finite state machines [39]. Aguirre-Ollinger et al. [21] recently developed a SEA actuation that operated between two discrete stiffness levels. However, discrete stiffness controllers tend to have large torque jerks between different stiffness modes, resulting in disruptive discontinuities in the assistance profile. One novelty of our work is a continuous stiffness controller based on the quasi-stiffness model of the knee joint, which provided a smoother and more natural assistance profile than switching among discrete stiffness values.
III. Mechatronic Design of A Portable Knee Exoskeleton With QDD Actuation
In this section, we present the mechatronic design of a portable knee exoskeleton by leveraging our custom high-torque density motor and low transmission ratio gear for QDD actuation. This platform is the foundation for the two contributions of this work, namely stiffness modeling of a torque-controlled QDD exoskeleton and continuous torque control.
A. Quasi-Direct Drive (QDD) Actuation
To meet the design and control requirements, our actuator is designed to be lightweight, compliant, and with high bandwidth. Leveraging our high torque density motor [23, 24] and gear-embedded actuator design method [28], we customize a compact QDD actuator with fully integrated control electronics components (Fig. 3). The actuator is lightweight (485 g), compact (Φ100 mm × 37 mm height), and can generate 20 Nm peak torque. The actuator includes a custom high torque density brushless direct current (BLDC) motor with 3.3 Nm peak torque output capability, an embedded 6:1 ratio planetary gear, 14-bit magnetic encoder (AS5048A, AMS, USA), and a microcontroller (STM32F407, STMicroelectronics, France). Unlike SEA actuators that use a high gear ratio mechanism (e.g., harmonic driver) and spring mechanism, QDD actuators are based on low ratio gear without spring components. Thus, QDD actuators are generally simpler and more affordable in terms of mechatronics design.
Fig. 3.
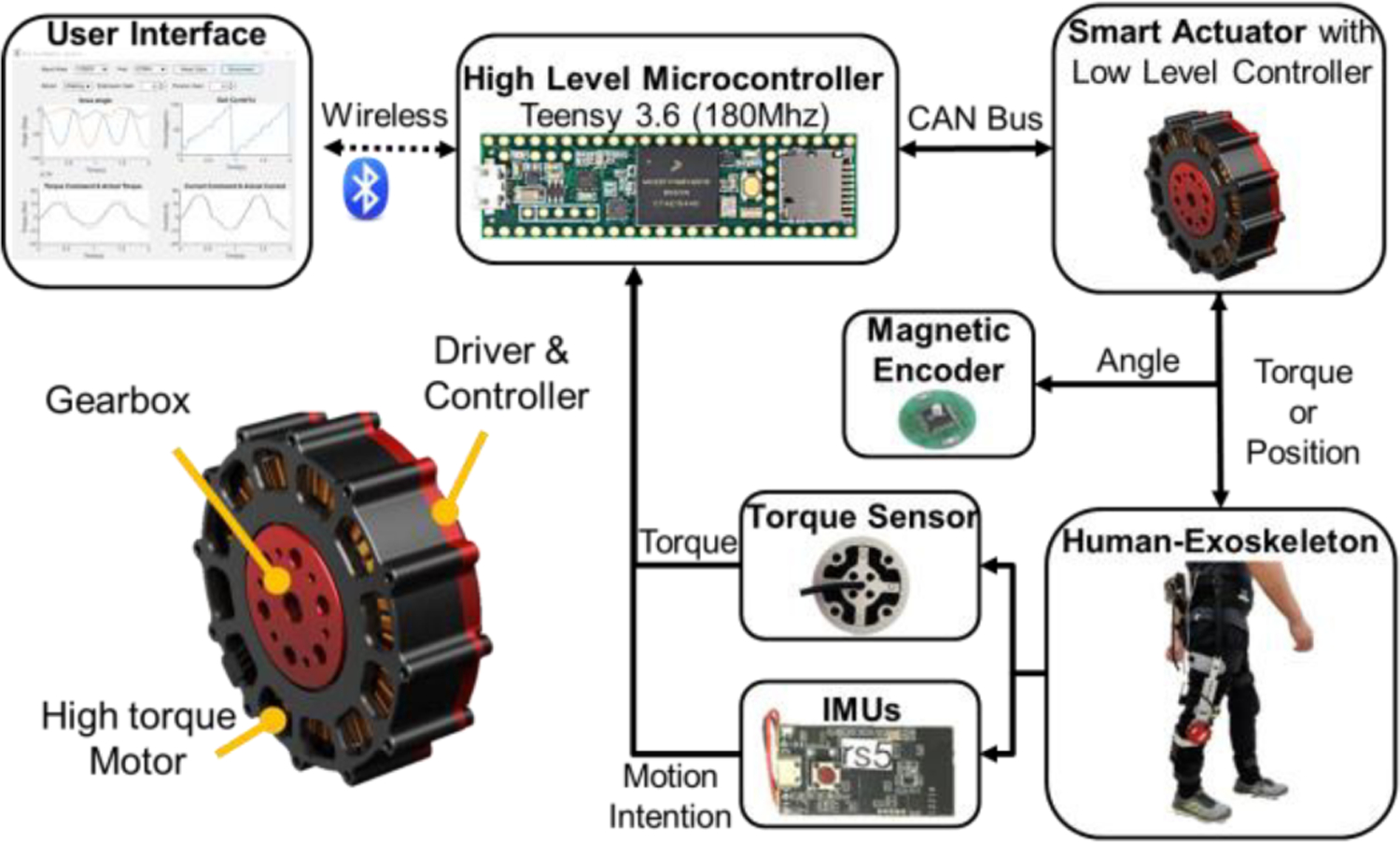
The electronic hardware architecture and QDD actuator (6:1 planetary gear) of the knee exoskeleton. The fully integrated architecture of the actuator includes a motor, a gearbox, and control electronics. We implement high-level control with a Teensy microcontroller. The robot could wirelessly communicate with a remote PC for data logging.
We implement a low-level control loop in the motor microcontroller to realize position, velocity, and current control. Real-time communication with a high-level control device is executed through the Controller Area Network (CAN) bus protocol. Powered by a nominal voltage of 42 V, the actuator reaches a nominal speed of 250 RPM (26.17 rad/s). Moreover, thanks to the low gear ratio transmission of the QDD design, the actuator has low output inertia (32.2 kg·cm2, see Table I for benchmark comparison with other exoskeletons), which is crucial to achieving low impedance that minimizes the resistance to human natural movements.
B. Mechatronic Design of Knee Exoskeleton
The design principle of this knee exoskeleton is to ensure a natural range of motion for multiple locomotion activities, e.g., walking, squatting, and stair ascent (lightweight and compliant features), and to minimize interference with external environments (compact feature). Thus the design avoids complicated mechanisms (e.g., our early work [58] that used a double rolling mechanism for knee exoskeleton). The main components of the exoskeleton include a waist belt, actuation system, thigh and shank support frames, and an adjustable elastic strap (Fig. 1). The knee joint actuation system includes a QDD actuator and a custom torque sensor (± 40 Nm full scale and ± 0.1 Nm resolution). The QDD actuator is connected to the thigh support frame, and the load cell is connected to the shank support frame. The design of the cuffs and straps ensure the assistive force on the wearer’s thigh and shank to be perpendicular to the surface of the respective segment, which reduces shear forces and discomfort.
We design the knee exoskeleton with the potential to assist multiple movements and for people with different body shapes. The wearable structures of the anterior lower thigh and shank do not interfere at maximum flexion (e.g., deep squatting). The range of motion of the knee exoskeleton is 0–160° (flexion), which is compatible with activities that require a wide range of motion, like stair ascent, sit-to-stand, and squatting. Additionally, different sizes of wearable structures are available. When combined with the adjustable linkage and single hinge structure, the design ensures the knee exoskeleton could fit a wide range of body sizes. The unilateral knee exoskeleton (without waist belt and battery) weighed 1.4 kg. The total weight of the bilateral knee exoskeleton (including all components) is 3.5 kg.
The electronic architecture of the knee exoskeleton facilitated high-level torque control, motor control, sensor signal conditioning, data communication, and power management, as shown in Fig. 3. The low-level controller embedded in the smart actuator measures the motor motion to realize motor current, velocity, and position control. The high-level microcontroller runs on Teensy 3.6 and implements continuous torque control (Section V). The microcontroller acquires knee joint angles from two wireless IMU sensors of each limb and conditioned torque signals from the custom loadcells in real-time. A Bluetooth microcontroller (nRF52840 Express, Adafruit, USA) connected to the main controller acts like a transceiver to communicate with a remote desktop computer for real-time data logging and monitoring.
IV. Stiffness Modeling And Benchmark Of Torque-Controlled Qdd Exoskeleton
To demonstrate the QDD knee exoskeleton has the potential to achieve human walking stiffness, we proposed a stiffness control model of the torque-controlled exoskeleton to benchmark QDD actuation exoskeletons. The effect of design parameters on the stiffness control bandwidth and range is then analyzed.
The model of the human-knee exoskeleton system (Fig. 4) incorporates the electro-mechanical model of the QDD actuator, the impedance model of the human-exoskeleton interface, and the biomechanical model of human walking [23]. V, L, R, i, Jm, θ m, τ m, b m, τ1, θ1, n, τ2, θ2, kc, bc, τa, τh, Jh, and θh denotes the winding voltage, winding inductance, winding resistance, motor current, motor rotor inertia, motor angle, motor input torque, motor damping, motor output torque, gear input angle, gear ratio, gear output torque, gear output angle, human-exoskeleton transmission stiffness, human-exoskeleton transmission damping, exoskeleton output assistive torque, knee muscle torque, human shank inertia, and knee angle, respectively.
Fig. 4.
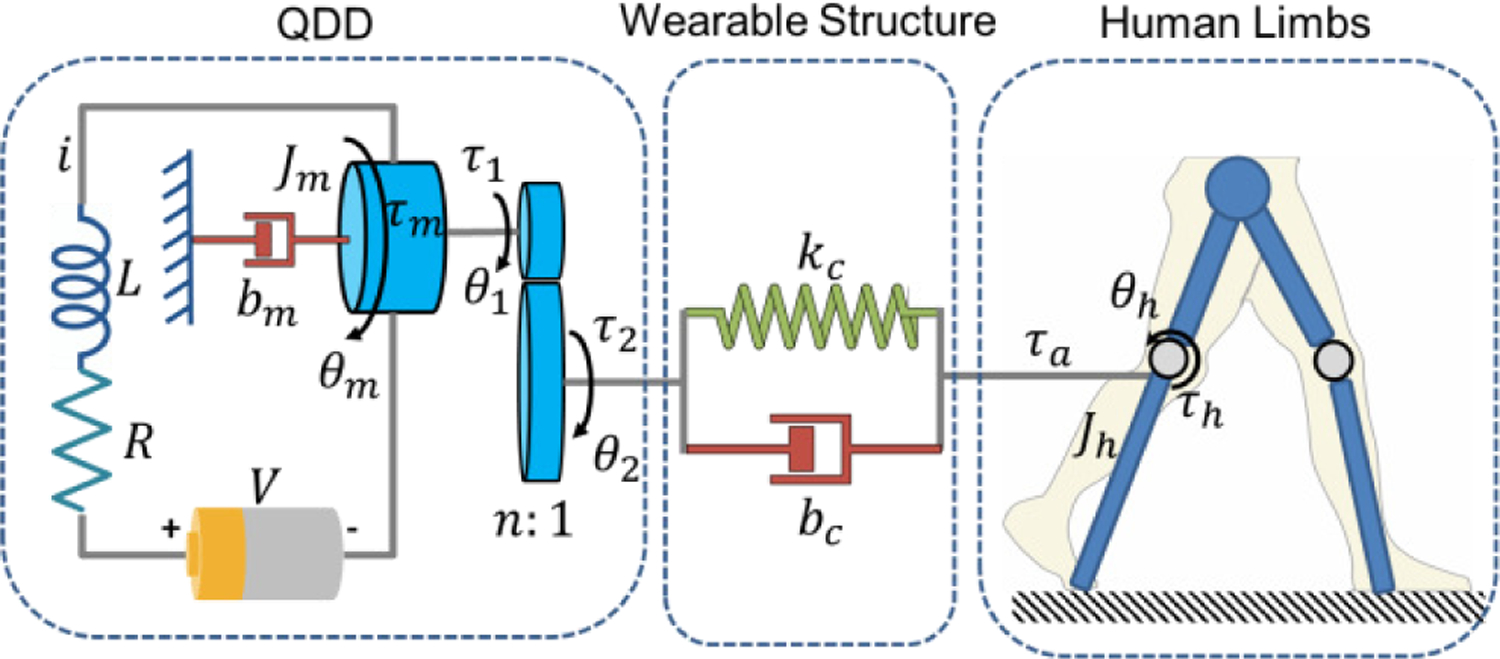
Model of the coupled human-knee exoskeleton system. It includes a QDD actuator, wearable structures, and human limbs (represented by the blue bars).
We hypothesize that the QDD actuation paradigm has higher control bandwidth and a larger range of stiffness than conventional and SEA actuation because of the high torque density motor, low gear ratio, and high stiffness transmission. To test our hypothesis, we use a human-exoskeleton model to derive the continuous stiffness control model and characterize the performance of knee exoskeletons with conventional, SEA, and QDD actuation paradigms.
A. Torque Control Modeling of Human-Exoskeleton Interaction
As discussed in Section II, a variable stiffness model can capture the dynamics of the human knee joint during walking. Here, we propose stiffness control to generate the torque for knee assistance with the QDD actuation paradigm. As shown in Fig. 5, the inner loop is the torque control, in which the input is the torque reference τr and the output is the actual torque applied to the human shank. In the model, the transmission damping coefficient bc is small and sets to zero; kp and ki are the proportional and integral gain, respectively. In this work, we derive the stiffness model and investigate stiffness dynamics by analysis (section IV.B) and experiments (section VI. A).
Fig. 5.

The block diagram of the stiffness controller. The input is the human knee angle θh and the output is the assistive torque τa at the knee joint. The controller aims to achieve the desired stiffess value of the exoskeleton by generating the corresponding torque reference τr. Here, the I gain is set to zero to simplify the benchmark comparison.
B. Stiffness Model of Torque-Controlled Exoskeletons and Benchmark of Three Actuation Paradigms
To establish the stiffness model, the input torque reference is given by
| (1) |
where the torque reference τr is generated proportionally to the knee angle θh via the reference stiffness kr. The transfer function for joint stiffness is modeled by
| (2) |
If we consider the motor inductance L approximate zero, then (2) is reduced to
| (3) |
To investigate the bandwidth of the stiffness control, the first and second corner frequencies (the corner frequency is defined as the boundary where frequency response begins to be attenuated or amplified) of the closed-loop stiffness control are found in Equation (4). Because the transmission stiffness kc and torque constant kt of the QDD system are larger and the gear ratio n is smaller than SEA system (see Table IX), the corner frequency of the stiffness control will be larger with the QDD system than in SEA and conventional high gear ratio actuation (CON).
| (4) |
To investigate the stiffness tracking performance in the frequency domain, the transfer function is given by
| (5) |
Considering that human motion is characterized by low frequency (ω → 0), the system stiffness is represented as
| (6) |
Additionally, when kp is large enough, such that kp → ∞, the system stiffness can be approximated by kr, i.e.,
| (7) |
which indicates that the stiffness controller can accurately track the reference stiffness kr for low-frequency human motion.
Conversely, when the motion frequency is high (ω → ∞), the transfer function approximates the transmission stiffness kc, i.e.,
| (8) |
Therefore, the stiffness controller cannot track the reference stiffness kr in high-frequency motion. Our QDD exoskeleton can provide sufficient bandwidth for dynamic stiffness tracking.
To illustrate the performance of stiffness control, the transfer function in Equation (2) is depicted in the Bode diagram in Fig. 6. We use the derived stiffness control model Equation (8) to benchmark the three actuation methods 1) a conventional (CON) high gear ratio knee exoskeleton [59]; 2) a SEA-based knee exoskeleton [60]; 3) our QDD knee exoskeleton. The SEA and CON have a higher ratio gear than the QDD actuation, and the SEA has a low stiffness constant due to the mechanical spring. For simplicity of the benchmark comparison, we set a large transmission stiffness of 500 Nm/rad for the CON and QDD actuators and set a small transmission stiffness of 200 Nm/rad for the SEA. The parameters from these three representative knee exoskeletons are listed in Appendix Table IX.
Fig. 6.
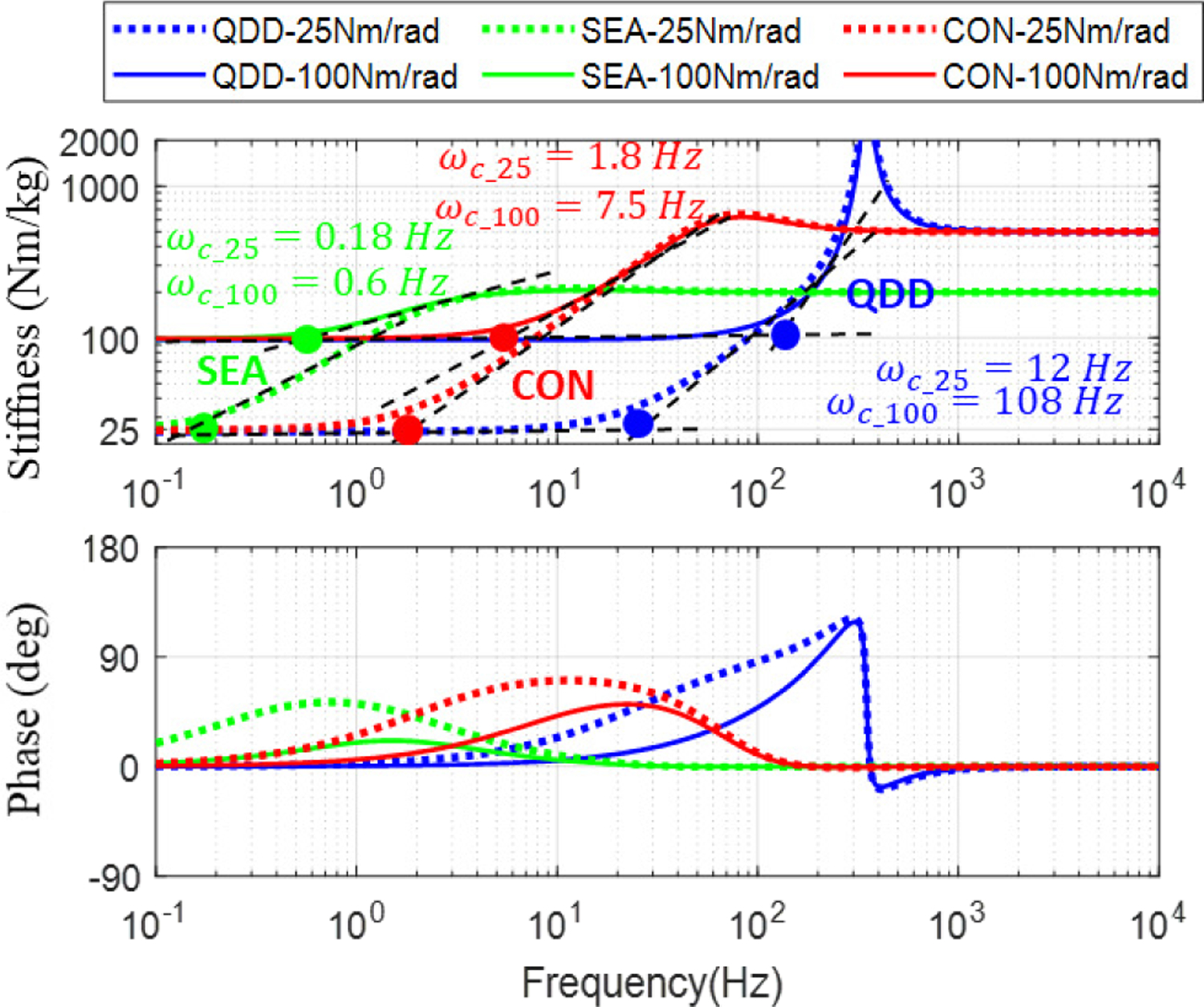
The Bode diagram of stiffness control for three actuation methods through the model derived in Equations (2–8). The input is human knee angle θh and the output is the calculated torque τa (negative value, opposite to rotation direction). The magnitude of the Bode diagram is the calculated joint stiffness. The QDD has the highest bandwidth compared to SEA and conventional actuators because of the high transmission stiffness and low gear ratio. Since human motion is low frequency, our QDD exoskeleton could have sufficient bandwidth for dynamic stiffness tracking in both low and high stiffness.
The bandwidths of the stiffness control for the QDD, SEA, and CON actuation with 25 Nm/rad reference stiffness are approximately 12 Hz, 0.18 Hz, and 1.8 Hz, respectively. The bandwidth of the stiffness control with 100Nm/rad reference stiffness for the QDD, SEA, and CON are approximately 80 Hz, 0.6 Hz, and 7.5 Hz, respectively. These results show that the QDD has the highest stiffness bandwidth in both 25 Nm/rad and 100 Nm/rad. At high frequencies, the actuator stiffness is dominated by the transmission spring stiffness kc. Therefore, the actual stiffness of the SEA, CON, and QDD at high frequency (see the stiffness in Fig. 6 as the frequency approaches 104 Hz) is approximated as kc.
V. Stiffness-Based Continuous Torque Control
A. Architecture of High-Level and Low-Level Controller
The main objective of the control law is to estimate the biological knee moment continuously during walking and assist the subject with a torque profile proportional to the estimated biological moment. Traditional finite state machine control methods, such as [42, 56, 61], are composed of two steps: 1) the gait cycle or phase-detection algorithm, and 2) assistive torque generation in terms of the gait phase of the gait cycle. Therefore, for different gait phases [40], the generated torque profiles are discontinuous, and the accuracy of assistive torque is dependent on the accuracy of gait phase detection. To overcome the problem of inaccurate gait phase estimation and discontinuous stiffness-based torque assistance (e.g., piecewise quasi-stiffness torque profiles), we develop a continuous stiffness model to estimate the knee joint moment. Our real-time control method combines gait phase detection and knee joint moment estimation into a unique estimation model, which identifies both the instantaneous gait phase and the required stiffness through an optimization process.
In Section II, we note that the knee joint quasi-stiffness transitioned between a high stiffness in the stance phase and low stiffness in the swing phase. The proposed control scheme is shown in Fig. 7. The variable stiffness control generated by the continuous phase stiffness model is employed as the high-level controller, which is given by
| (9) |
where, τr is the reference torque of the variable stiffness control, is the normalized estimated knee moment (described in Section IV. B), kw is the user’s body weight (in kg), and ka is the assistive proportional gain. The inputs of the variable stiffness control are the right knee angle θk,r, and left knee angle θk,l. The output is the torque reference τr. The control law for knee assistance can be calculated from Equation (9). Assistive control is achieved with a ka in the range [0,1]. We use IMUs on each shank and thigh (2 IMUs of each leg) to calculate the right and left knee angles (θk,r, and θk,l, respectively). The inner-loop controller implements torque control, and the feedback signal is the measured assistive torque τa (measured from the torque sensor of the knee exoskeleton).
Fig. 7.
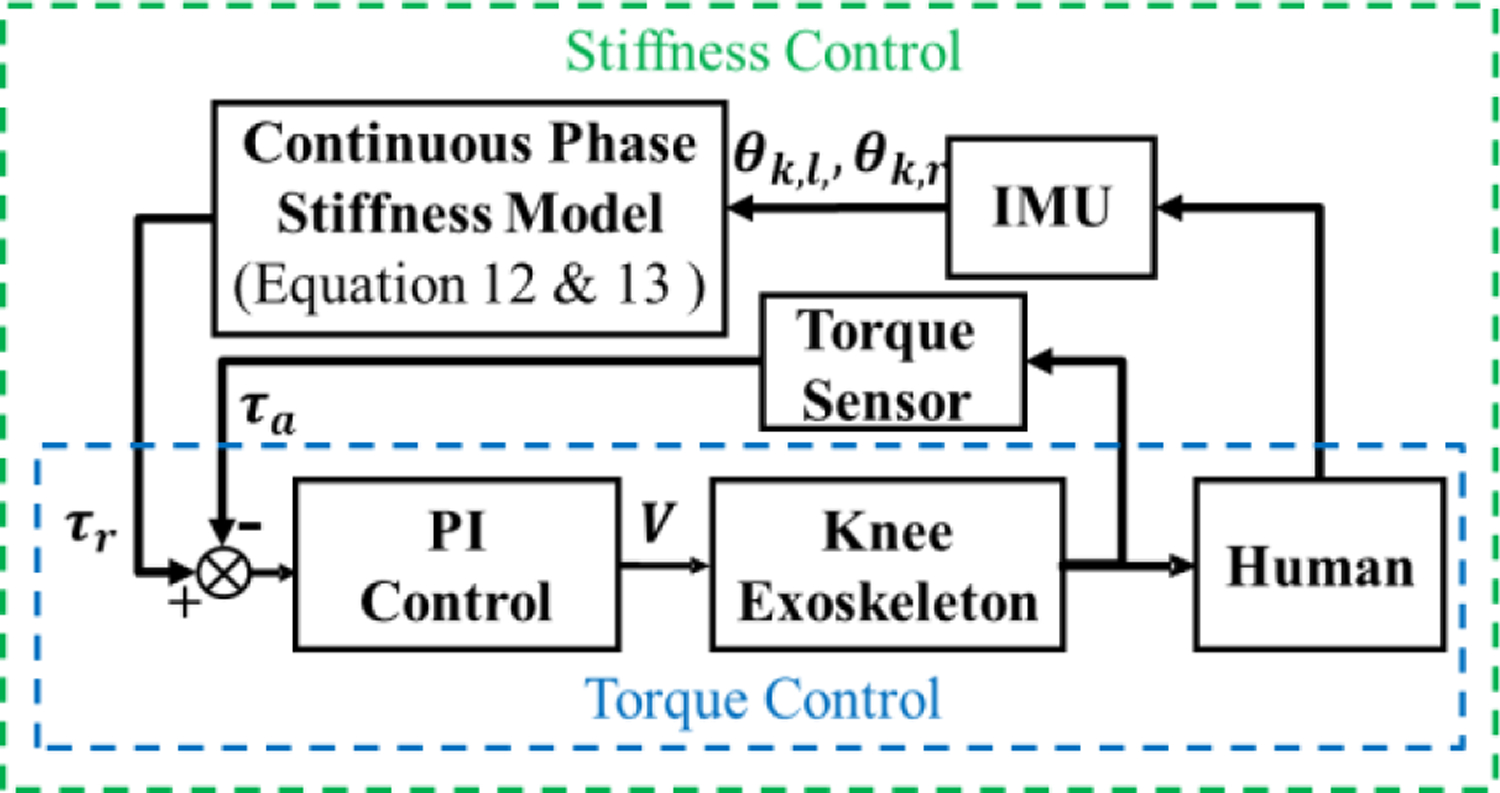
The architecture of the stiffness-based continuous torque control. It consists of two levels: 1) The stiffness control is the outer loop and 2) The torque control is the inner loop. θk,l,, and θk,r represents the right and left knee angles, τr is the reference torque estimated by the continuous phase stiffness model and τa is the measured torque from the torque sensor.
B. Stiffness-based Continuous Torque Controller with Biological Torque Estimation
We propose a simple and analytical model that uses a smooth function (e.g., sigmoid function) to generate a continuous output between 0 and 1, which is given by
| (10) |
The parameters a could regulate the width of the transition area of the sigmoid function. The function S(θk,r,θk,l) is the likelihood to apply the swing phase stiffness model. The function [1 − S(θk,r,θk,l)] is the likelihood to apply the stance phase stiffness model. The continuous nature of the gait phase detection output ensures that the estimation of the knee moment is also a continuous signal. An additional benefit of continuous gait phase detection is that transitions between gait phases can be easily and automatically processed instead of rule-based methods like a finite state machine. The proposed estimation function is given by
| (11) |
where S(θk,r,θk,l) is the sigmoid function given by Equation (10), is the estimation of right knee moment, kst is the joint stiffness of stance phase, ksw is the joint stiffness of the swing phase, θk,r is the right limb knee angle, θk,l is the left limb knee angle, θk,r,0 is the equilibrium angle for stiffness model of stance phase, θk,st,0 is the equilibrium angle for stiffness model of stance phase, and θk,sw,0 is the equilibrium angle for the stiffness model of the swing phase. Here, we propose to use two stiffness modes (high stiffness and low stiffness) to estimate the knee moments τk,r, and τk,l. In addition, the proposed method is not limited to stiffness control. It can be extended to a higher-order model of generic impedance controller with mass, spring, and damper terms, which needs angular velocity and angular acceleration (the derivatives of the knee angle and angular velocity, respectively). When implemented, the differential operation for the angular acceleration and angular velocity generates a non-causal system and introduces noise. Therefore, we choose to use stiffness control (without angular velocity and angular acceleration) that requires only joint angle feedback to approximate the knee moments τk,r, and τk,l.
The estimated optimal hyperplane is given by
| (12) |
| (13) |
Equation (12) separates the gait cycle into two gait phases by minimizing the torque estimation error. The parameters b could regulate the center of the transition area of the sigmoid function, respectively. The only input variables required to estimate the gait phase are right and left limb knee angles (θk,r, and θk,l, respectively). Hence, this control law is more stable compared to gait estimation methods that use angular velocity and/or acceleration. The output of the estimation function Equation (11) is the estimated right knee moment .
To find the optimal parameters (kst, ksw, θk,st,0, θk,sw,0, a, b) of the continuous phase stiffness model (Fig. 7), we solve an offline optimization problem over a collection of training data from 23 subjects walking overground [43]. Each subject was asked to perform overground walking trials at three speeds (a self-selected comfortable speed, a fast speed which is 30% faster than the self-selected speed, and slow speed which is 30% slower than the self-selected speed and the dataset for each speed include the averaged knee joint angles and moments from multiple trials. The dataset for each speed includes the averaged knee joint angles and moments from multiple trials. The time series of the data is converted to the percentage of the gait cycle and the joint moment is normalized to body mass (Nm/kg). We use the data at all three walking speeds to optimize the stiffness model parameters. Specifically, nonlinear regression is used to minimize the sum of the squared error between estimated and actual knee moment, employing the cost function in Equation (13). Here, and τk,r i are the estimated and actual knee moment at data point i, respectively, while the parameter m is the total number of data points in the training data. In this way, a nonlinear regression method is able to optimize parameters, including the width of the transition area (parameter a), the stiffness (kst & ksw ), and the equilibrium angles (θk,st,0 & θk,sw,0 ) of the two-phase stiffness models. The optimal hyperplane separates the gait cycle into two gait phases (corresponding to ) to minimize the error between estimated biological moment and actual biological moment.
C. Optimization of Biological Torque Estimation for Continuous Stiffness Torque Control
Optimal parameters of the continuous phase stiffness model are shown in TABLE III. The hyperplane (in the space of the angle difference between the right and left knee joint) is close to zero degrees.
TABLE III.
The Optimal Parameters for The Continuous Phase Stiffness Model.
| Parameter | K st | θ k,st,0 | k sw | θ k,sw,0 | a | b |
| Coefficient | 0.0379 | 5.322 | 0.0046 | 57.520 | 0.099 | 2.619 |
In our exoskeleton control law, the assistive torque is proportional to the estimated knee moment. We evaluate the accuracy of the estimated torque with respect to the actual knee moment using the correlation between the actual knee joint moment and moment estimated by the continuous stiffness model at the three different walking speeds (TABLE IV). The average correlation is 90%. The highest correlation (about 94.5%) is found in the comfortable walking condition, while the slow walking speed data has the lowest correlation (80.9%). These results indicate that the proposed joint moment estimation method is more suitable for self-selected and fast walking speeds than slow walking speeds.
TABLE IV.
The correlation results of the continuous phase stiffness model
| Dataset | Dataset Slow | Dataset Self-selected | Dataset Fast | Average |
|---|---|---|---|---|
| Correlation | 80.9% | 96.1% | 94.5% | 90.0% |
The trained continuous phase stiffness model and the corresponding training dataset are visualized in Fig. 8. Notably, the transition between stance and swing phase stiffness models is smooth, as intended by the continuous stiffness design.
Fig. 8.
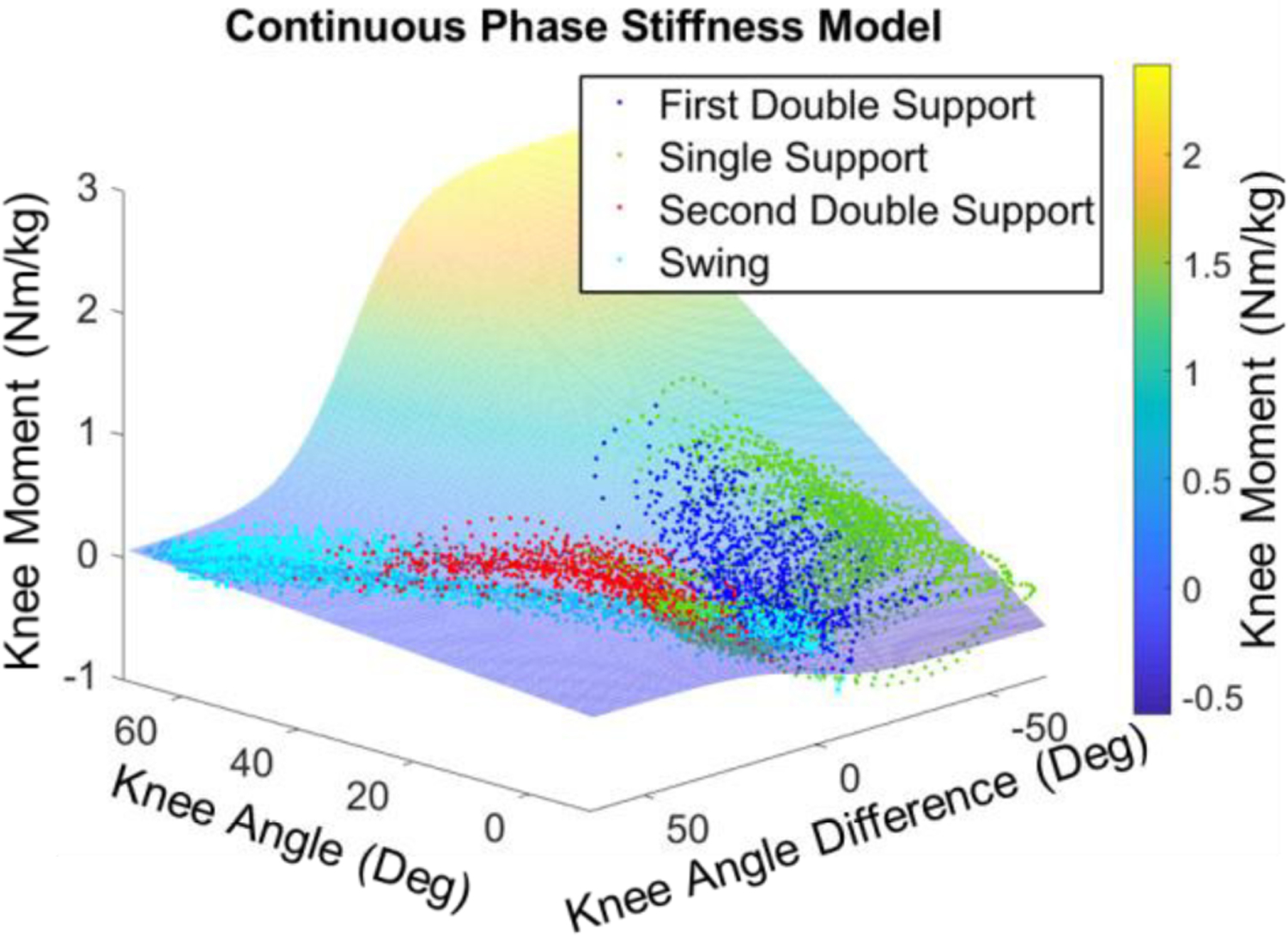
The estimated biological torque (colored 3D surface) by the continuous phase stiffness model matches well with respect to the training dataset of 23 able-bodied subjects (colored dots indicates four phases of each gait cycle).
D. Evaluation of the Continuous Phase Stiffness Model
We tested the generalization of our model by training with data from 22 subjects and then testing it on a new subject (not from the training set) to evaluate the knee moment estimation. The estimated knee moment for this subject walking at three speeds is shown in Fig. 9. The root mean square errors (and percentage) of the torque tracking at slow speed, self-selected speed, and fast speed is 0.0583 Nm/kg (13.68%), 0.0585 Nm/kg (8.27%), and 0.0874 Nm/kg (8.40%), respectively. The results demonstrate that the estimated knee moments were close to the actual knee moments, and the generated moment profiles were continuous and smooth. The black dashed line in the right column of Fig. 9 depicts the value of the sigmoid function S(θk,r, θk,l) ∈ [0,1] in Equation (11) across the entire gait cycle. It shows that the stiffness model is more inclined to the stance phase model (S(θk,r, θk,l) = 0) during the first double support and single support phase, while the swing phase stiffness model has a higher weight during the second double support and swing phase (S (θk,r, θk,l) = 1).
Fig. 9.

Demonstration of the continuous phase stiffness model (Fig. 7) in one subject. The left column depicted the knee angle vs. estimated knee moment and the right column depicted the gait cycle vs. estimated knee moment. The blue color indicates the single support phase, the red color indicates the second double support phase, and the cyan color indicates the swing phase. The solid line is the biological knee moment, while the dashed line is the estimated knee moment. The top, middle, and bottom rows showed the slow, self-selected, and fast walking speed results respectively. The black dashed line in the right column of Fig. 9 depicts the value of the sigmoid function S(θk,r, θk,l) ∈ [0,1] in Equation (11) across the entire gait cycle. It shows that the stiffness model is more inclined to the stance phase model during the first double support and single support phase, while the swing phase stiffness model has a higher weight during the second double support and swing phase.
VI. Experiments
To characterize the knee exoskeleton and evaluate controller performance, we conducted both benchtop and human subject experiments. Benchtop experiments aimed to evaluate the performance of the robot and its controller. The experiment with eight able-bodied subjects aimed to evaluate the tracking performance of the torque controller during walking at different speeds and muscle activity responses to exoskeleton assistance. Our protocol was approved by the City University of New York Institutional Review Board (CCNY IRB, application No. 2018–0885) and NC State University (eIRB # 24675). Our study was performed in line with the CCNY IRB and NC State IRB Guidance.
A. Benchtop Experiments
1). High Backdrivability Demonstration
We conducted a dynamic backdrivability test to characterize backdrivability. The actuator’s output shaft was manually rotated between −30° and 20° at frequencies between 0.5 Hz and 2 Hz. A loadcell measured the backdrive torque in unpowered mode, which was filtered (first-order, 1 Hz cutoff low-pass Butterworth filter) to eliminate sensor noise. The measured rotation angle and backdrive torque were presented in Fig. 10. The results indicated that our exoskeleton exhibited a very low backdrive torque (~0.22 Nm), indicating significantly better backdrivability than advanced SEA (8.5 Nm) [10] and other QDD based exoskeleton (1.32 Nm) [29].
Fig. 10.

Backdrivability test of the knee exoskeleton in unpowered condition. The maximum backdrive torque was approximately 0.22 Nm, less than state-of-the-art results in 8.5 Nm [10] (SEA actuator) and 1.32 Nm [29] (QDD actuator).
2). Stiffness Modulation with Torque Tracking Accuracy
The exoskeleton is required to provide both high stiffness and low stiffness control as the human knee joint exhibits high stiffness in the stance phase and low stiffness in the swing phase. In this experiment, a constant stiffness was set, and the output shaft was manually rotated, while the desired and actual torque were recorded. As shown in Fig. 11, we tested the torque tracking accuracy under low (1 Nm/rad), medium (100 Nm/rad), and high (350 Nm/rad) stiffness control conditions. The root mean square errors (and percentage of the desired peak torque) of the torque tracking were 0.08 Nm (8.06%), 0.31 Nm (5.24%), 0.64 Nm (5.36%) at low, medium, and high stiffness control, respectively. The tracking accuracy was superior to the stiffness control results (SEA actuators) reported in [10].
Fig. 11.

Torque tracking performance under relatively low (1 Nm/rad), medium (100 Nm/rad), and high (350 Nm/rad) stiffness control conditions. The measured torque (orange) tracked well the desired torque (black dashed line). The root mean square errors (and percentage of the desired peak torque) of the torque tracking were 0.08 Nm (8.06%), 0.31 Nm (5.24%), 0.64 Nm (0.987), respectively.
3). Exoskeleton Torque Control Bandwidth Evaluation
For the torque control bandwidth test, a chirp signal was used as the reference torque, whose magnitude was set to 5 Nm, 10 Nm, and 15 Nm. The Bode plot (Fig. 12) showed the bandwidth was 38.3 Hz, 39.3 Hz, and 40.7 Hz, for chirp magnitudes of 5 Nm, 10 Nm, and 15 Nm, respectively. The control bandwidth satisfied the design specification, being much higher than the requirement for human walking. The high control bandwidth can be helpful in more dynamic human activities like running and balance control in response to unexpected external disturbances. Compared with the 5 Hz bandwidth of one advanced exoskeleton using SEA [10], our exoskeleton had higher control bandwidth, making it more robust to uncertainties.
Fig. 12.

Bode plot for torque control for reference torque with 5 Nm, 10 Nm, and 15 Nm chirp signal. The high bandwidth (highest value was 40.7 Hz) demonstrates the ability to handle more dynamic human movements in comparison with state-of-the-art results (5 Hz bandwidth in [10]).
4). Exoskeleton Stiffness Control Bandwidth Evaluation
To evaluate the stiffness control bandwidth in a benchtop test we used step response with a 5-degree step function of human knee angle θh(t) as the input. We collected data with two reference stiffness (25 Nm/rad and 100 Nm/rad) and the frequency response of the actual stiffness transfer function, see Equation (2) was analyzed in Fig. 13. We identified the transfer function containing 2 poles and 2 zeros by the function tfest of MATLAB R2019b for both reference stiffness conditions. The results were shown in Fig. 13. We found the first corner frequency was 10.5 Hz for 25 Nm/rad reference stiffness and 16 Hz for 100 Nm/rad reference stiffness. Since the frequency of the human lower limb movement is typically less than 10.5 Hz, the stiffness control bandwidth demonstrated our proposed stiffness-based continuous torque controller was able to track reference stiffness accurately with the exoskeleton.
Fig. 13.
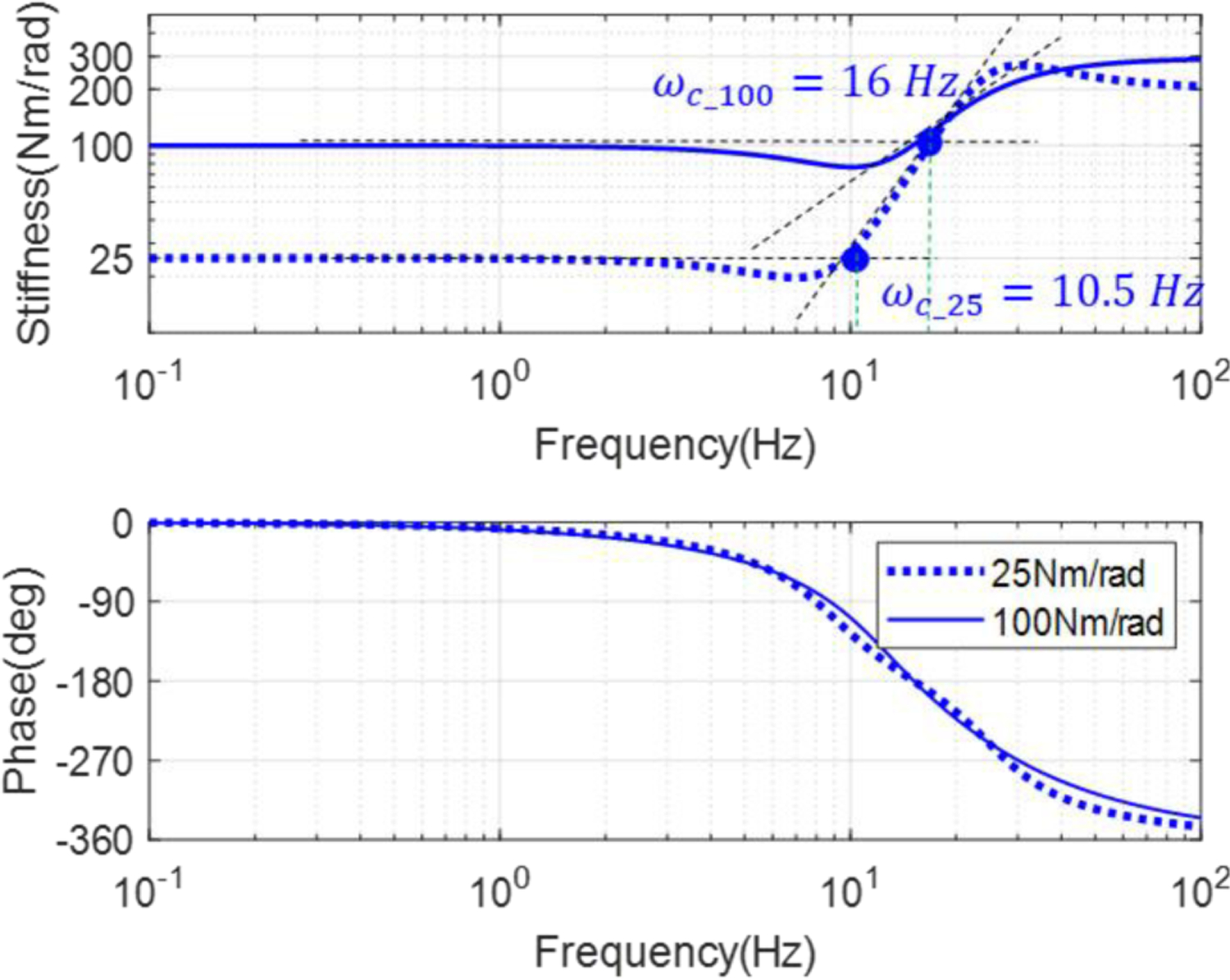
The Bode diagram of exoskeleton stiffness transfer function from the experiment. The input was human knee angle θh(t) with a 5-degree step function. The first corner frequency values showed the bandwidth of the stiffness control was 10.5 Hz for 25 Nm/rad reference stiffness and 16 Hz for 100 Nm/rad reference stiffness, which was higher than human lower-limb movement frequency and was able to track reference stiffness accurately with the exoskeleton.
B. Human Subject Experiments
The objective of the human experiments is 1) to evaluate the movement synergy of our continuous torque controller with humans at different walking speeds 2) to evaluate the capability of the system to track the desired torque and show that our exoskeleton with the proposed controller does not cause a significant change of knee kinematics 3) to understand the effect on lower limb muscle activities.
1). Accurate Biological Torque Estimation with Our Stiffness Model
To illustrate the benefit of our proposed controller, the knee moment estimation from the continuous torque controller is shown in Fig. 14 (a). As the treadmill velocity changed from 0.8 to 1.5 m/s, the gait cycle shrank, our proposed method automatically adapted to the changing speed and generated a continuous knee moment because it only required the current knee joint angle to estimate the knee moment and thus did not explicitly rely on the gait phase estimation.
Fig. 14.
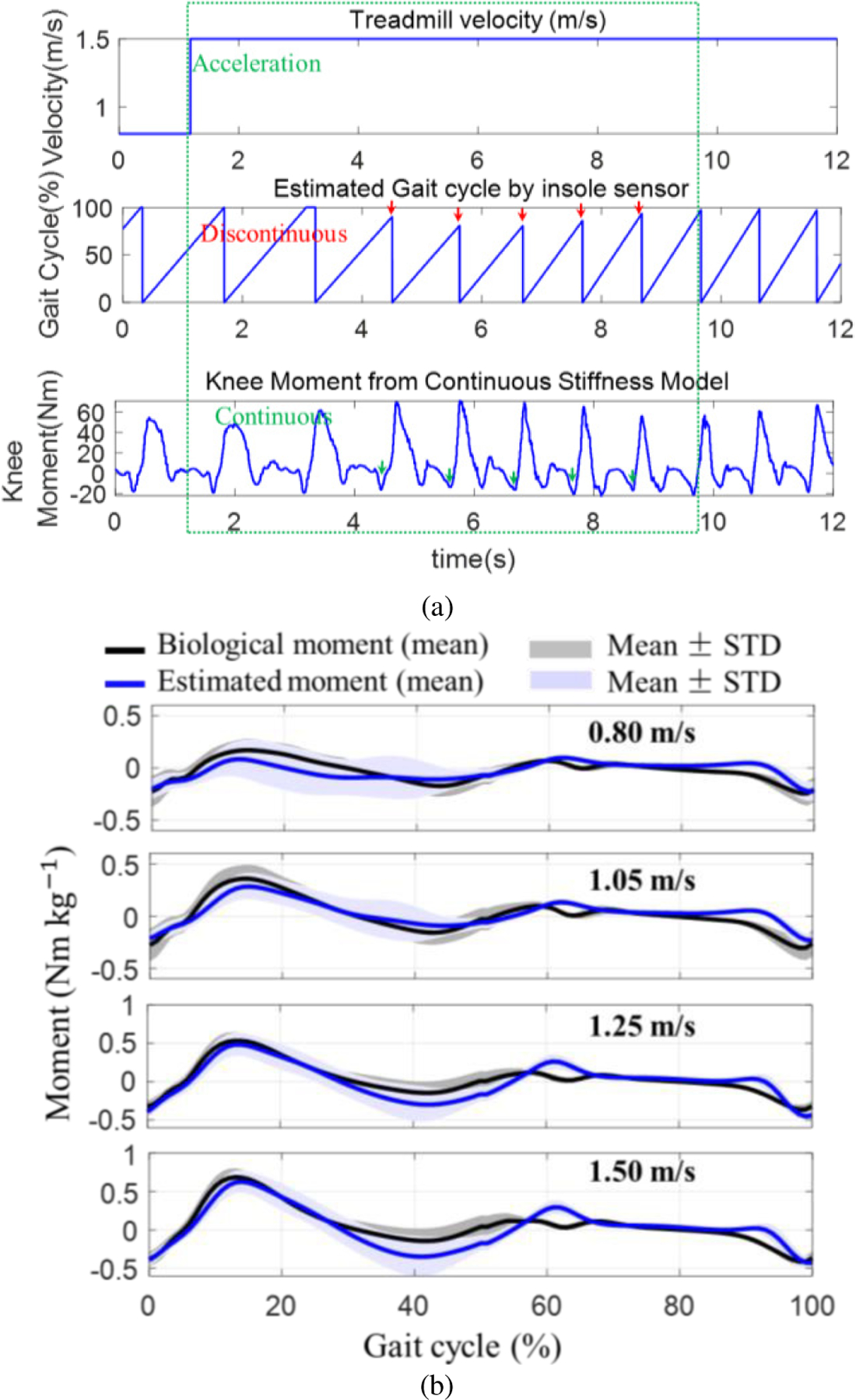
(a) Comparison between the knee moment estimation based on the gait cycle and the proposed continuous torque controller (Fig. 7). The proposed controller can adapt to walking speed from 0.8 m/s to 1.5 m/s and the estimated knee moment is continuous, in contrast to the discontinuous profile generated from the gait cycle-based method. (b) Estimated moment vs. actual biological knee moment for 4 speeds (mean ± std of 8 subjects’ data). We recorded 10 strides data for each subject/speed.
To evaluate the accuracy of the estimated biological knee moment by our stiffness model, we compared the estimated knee moment and biological moment for 8 subjects at four speeds (0.80 m/s, 1.05 m/s, 1.25 m/s, and 1.50 m/s). Fig. 14 (b) shows the comparison results between the estimated moment and actual biological knee moment for 8 subjects. To analyze the prediction accuracy and correlation, we calculated RMS error and correlation percentage for different speeds (8 subjects). As shown in Table V, the group average RMS error is 0.079 Nm/kg, and the group average correlation is 90.2%. The results demonstrate the proposed stiffness model can estimate knee joint moment under all three speeds of walking. Especially, the estimated moment of 1.25 m/s walking speed (normal walking speed) has the best accuracy and correlation.
TABLE V.
The RMSE and Correlation Between the Estimated Moment and Biological Moment for Different Speeds
| Speed (m/s) | 0.80 | 1.05 | 1.25 | 1.50 | Average |
|---|---|---|---|---|---|
| RMSE (Nm/kg) | 0.079 | 0.077 | 0.073 | 0.086 | 0.079 |
| Correlation | 84.3% | 90.3% | 93.3% | 92.9% | 90.2% |
2). Performance of Stiffness-based Continuous Torque Controller
This subsection evaluates the continuous torque control feature of the proposed controller. Fig. 15 shows the torque-angle behavior of our knee exoskeleton over 10 gait cycles collected from 8 subjects walking at 1.25 m/s on the treadmill.
Fig. 15.
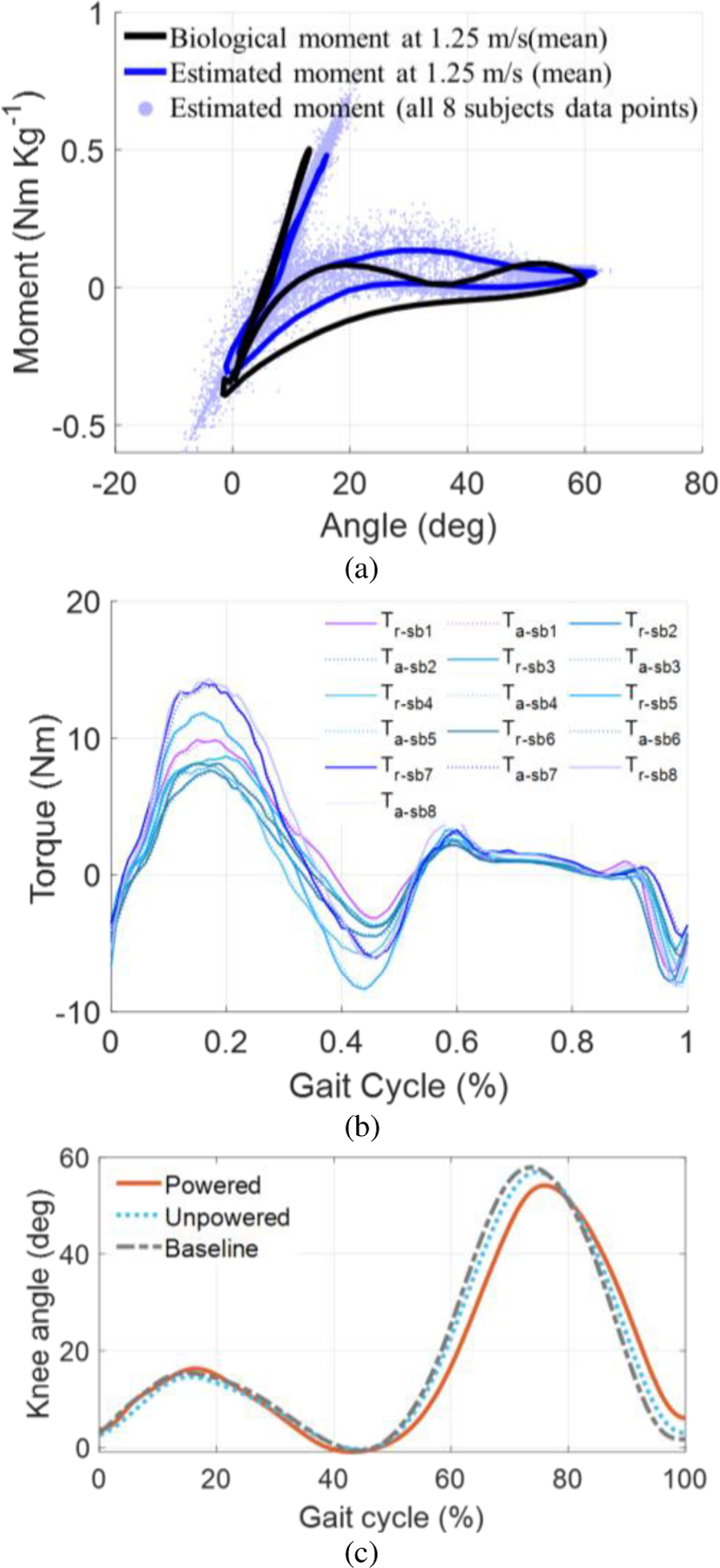
The experiment results of the powered exoskeleton over 10 gait cycles at 1.25 m/s treadmill walking with 30% biological torque assistance. (a) Knee angle vs. joint moment from 8 able-bodied subjects. The light blue dots show the 8 subjects’ data points that are the averaged curve of normalized estimated knee moment and knee angle, the blue line is the averaged curve of normalized estimated knee moment and knee angle curve from the continuous stiffness model, and the black line is the averaged curve of the normalized biological knee moment and knee angle. The torque profile generated by the stiffness-based continuous torque controller was similar to the biological knee joint moment. (b) Torque reference τr and actual assistive torque τa of 8 subjects. The torque tracking RMS error (and percentage) is 0.23 Nm (5.39%). It demonstrated the controller was able to track the torque reference accurately. (c) Knee angle vs. gait cycle averaged across 8 subjects. Mean knee angle vs. gait cycle averaged across 8 subjects. It demonstrated that the kinematics did not significantly change between unpowered and baseline conditions (p<0.001). The maximum knee flexion angle in the powered condition decreased about 2.8 degrees relative to the baseline condition.
In Fig.15 (a), the light blue dots are the estimated moment-angle data points for the 8 subjects, the blue line is the averaged curve of normalized estimated knee moment and knee angle from the continuous stiffness model of the 8 subjects, and the black line is the averaged curve of the normalized biological knee moment and knee angle. We observed that the tendency of the two curves in Fig.15 (a) are similar, especially in the stance phase.
As shown in Table VI, the largest RMS error (0.087 Nm/kg) between the estimated moment and the biological moment is found in subject 1, while subject 5’s data has the smallest RMS error (0.061 Nm/kg). The mean ± SD for the group RMS error is 0.073 ± 0.009 Nm/kg. The largest correlation (96.1%) is found in subject 1, while subject 5’s data has the smallest correlation (87.1%). The average correlation is 93.3%. These results indicate that the proposed joint moment estimation method can accurately estimate knee moment during walking with 1.25 m/s speed.
TABLE VI.
The RMSE and Correlation Between the Estimated Moment and Biological Moment under 1.25 m/s Walking Speed
| Subject | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| RMSE (Nm/kg) | 0.087 | 0.069 | 0.079 | 0.083 | 0.061 |
| Correlation | 87.1% | 95.0% | 89.3% | 88.7% | 96.1% |
| Subject | 6 | 7 | 8 | Average | |
| RMSE (Nm/kg) | 0.066 | 0.073 | 0.066 | 0.073±0.009 (mean ± SD) |
|
| Correlation | 95.8% | 95.3% | 94.7% | 93.3% | |
To evaluate the torque tracking performance of the stiffness based continuous control, the average torque reference, and the average actual assistive torque from 8 subjects are shown in Fig.15 (b). The torque (percentage) RMS error across the 8 subjects is 0.25 Nm (5.40% of peak torque). The experimental results demonstrated the capability of the system to track the desired torque at corresponding joint angles using our controller. Another feature is that the controller does not cause a significant difference in knee kinematics (in terms of knee angles) between unpowered and baseline conditions across all 8 subjects as shown in Fig. 15 (c) (prediction correlation coefficient = 0.983±0.008, p<0.001). The knee angle profile between the powered and baseline conditions was also similar (prediction correlation coefficient = 0.936±0.047, p<0.001), with only about a 2.8-degree decrease in the maximum flexion angle.
3). EMG Experimental Protocol
We designed and implemented a 2-session protocol to evaluate the presented controller design (Fig. 16). Session 1 was for a fitting, parameter tuning, and neuromuscular adaptation to the exoskeleton. A rest period of between 2–5 days occurred before session 2 to limit the effect of muscle fatigue. In visit 2 we collected experimental data. Following similar human evaluation studies [30, 48, 57, 62], 8 able-bodied subjects (6 males, 2 female, as shown in Table VII) with a mean age of 29.5 (±4.8) years, mean height of 1.76 (±0.04) m and mean weight of 76.1 (±10.1) kg were enrolled with approval from the Institutional Review Board.
Fig. 16.
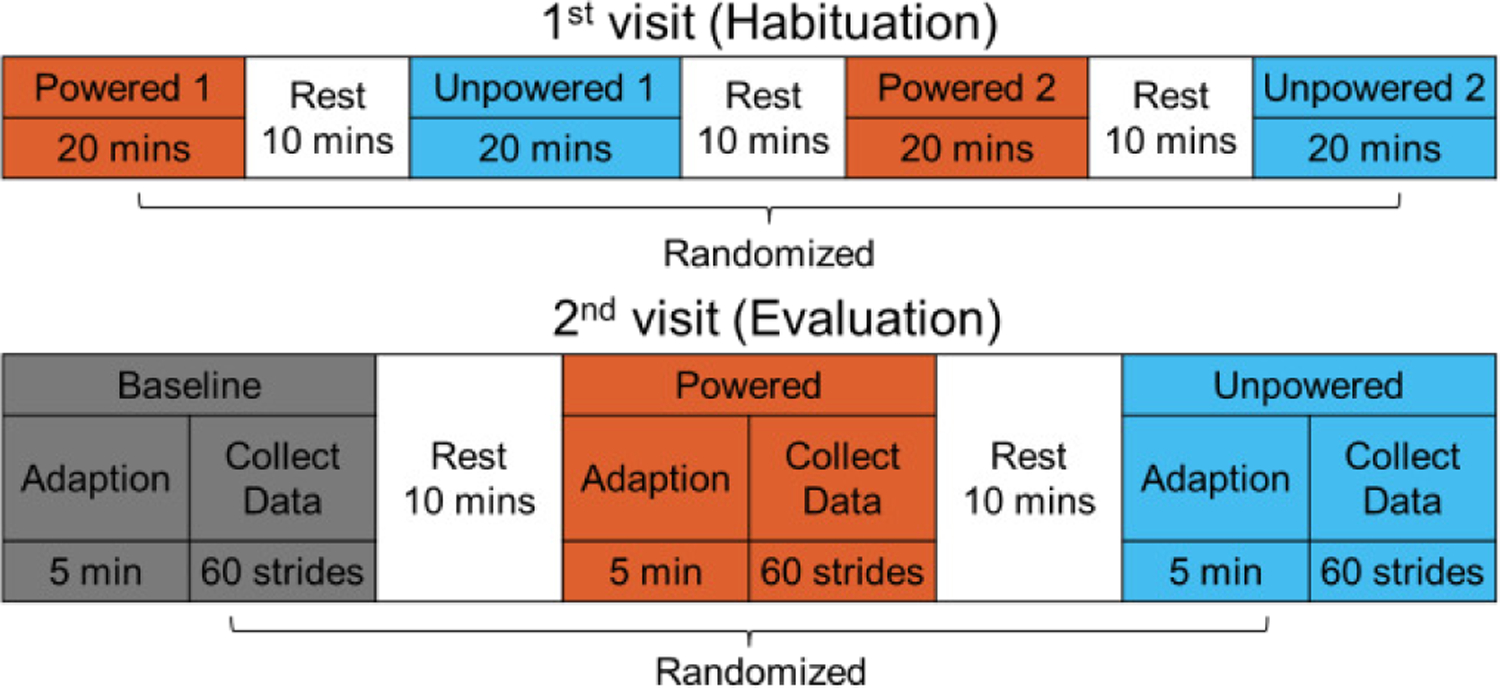
The protocol of human testing included two visits for habituation and evaluation, respectively. The second visit was scheduled two days after the first visit so that the subject could have sufficient rest. In both the visits, the conditions were randomly alternated to reduce bias.
TABLE VII.
Eight Able-bodied Subjects Information
| Subject No. | Gender | Age | Height (m) | Weight (kg) |
|---|---|---|---|---|
| 1 | Male | 31 | 1.76 | 70 |
| 2 | Male | 26 | 1.84 | 68 |
| 3 | Male | 27 | 1.74 | 75 |
| 4 | Male | 40 | 1.75 | 80 |
| 5 | Female | 29 | 1.74 | 70 |
| 6 | Male | 30 | 1.73 | 72 |
| 7 | Male | 29 | 1.81 | 100 |
| 8 | Female | 24 | 1.72 | 80 |
In the first visit, we tuned and adjusted the exoskeleton to best fit the subject. The subject then walked with the exoskeleton on a treadmill at 1.25 m/s in 2 conditions (powered and unpowered) with a total of 4 walking bouts. Each walking bout lasted 20 minutes and was interspaced with 10-minute rest periods. We randomized the order of conditions to minimize the learning effect. In the powered condition, the exoskeleton provided assistance torque equivalent to 30% of the biological torque at the knee. In the unpowered condition, the participant wore the exoskeleton while it was turned off and provided no active torque. An adaptation time of 40 minutes allowed the neuromuscular activity to adapt sufficiently to wearing the exoskeleton [14].
In session 2, the participant walked in 3 conditions (powered, unpowered, baseline) while we recorded data. The powered and unpowered conditions were the same as in session 1 and the baseline condition was walking without the exoskeleton. We randomized the order of the conditions to prevent the influence of order and reduce bias on the data collected. For each condition, the participant walked on the treadmill at 1.25 m/s for 5 minutes before data were collected over the next 60 strides. The participant rested for 10-minutes between two consecutive tests. Fig. 16 shows the detailed protocol of the 2-visit study.
The collected data included gait phase, knee joint angles, exoskeleton torques (estimated and measured), and electromyography (EMG) measurements. We used footswitches (B&L Engineering, USA) worn inside the subject’s shoes to identify ground contact times and then segmented all data into strides in post-processing. Knee joint angles in the sagittal plane were calculated using 4 inertial measurement units (IMUs) strapped to the thigh and shank segments on both legs of the subject. Eight wireless EMG sensors (Noraxon, Scottsdale, AZ, USA) recorded muscle activity of the 8 muscles on the right leg of the subject at 2000 Hz: rectus femoris (RF), vastus lateralis (VL), vastus medialis (VM), biceps femoris (BF), semitendinosus (SEM), tibialis anterior (TA), lateral gastrocnemius (LG) and medial gastrocnemius (MG). EMG data were notch filtered with a band stop filter (58–62 Hz, 4th-order, zero-phase Butterworth filter) and bandpass filtered (30–500 Hz, 4th-order, zero-phase Butterworth filter), and rectified. For each muscle, root-mean-square (RMS) and peak values of the EMG signal were extracted for 10 strides and averaged, then normalized to the RMS or peak (respectively) in baseline averaged condition. We normalized the RMS and peak values across participants. For visualization, the time series data were filtered by a low-pass filter (20 Hz, 4th-order, zero-phase Butterworth filter), normalized to 1001 data points, and averaged across 10 strides.
4). EMG Results
To evaluate the performance of the exoskeleton assistance and the proposed controller, Fig. 17 depicts the normalized EMG of the 8 muscles for one representative subject. The results showed the peak EMG signal of the 8 muscles in the unpowered condition was the highest compared with baseline and powered condition, which was due to the extra weight and friction introduced by the exoskeleton. The peak EMG signal of ankle extensors and flexors (TA, LG, and MG) were the lowest in the baseline condition, suggesting that the knee exoskeleton (both powered and unpowered conditions) increased the muscle activity for ankle muscle groups.
Fig. 17.
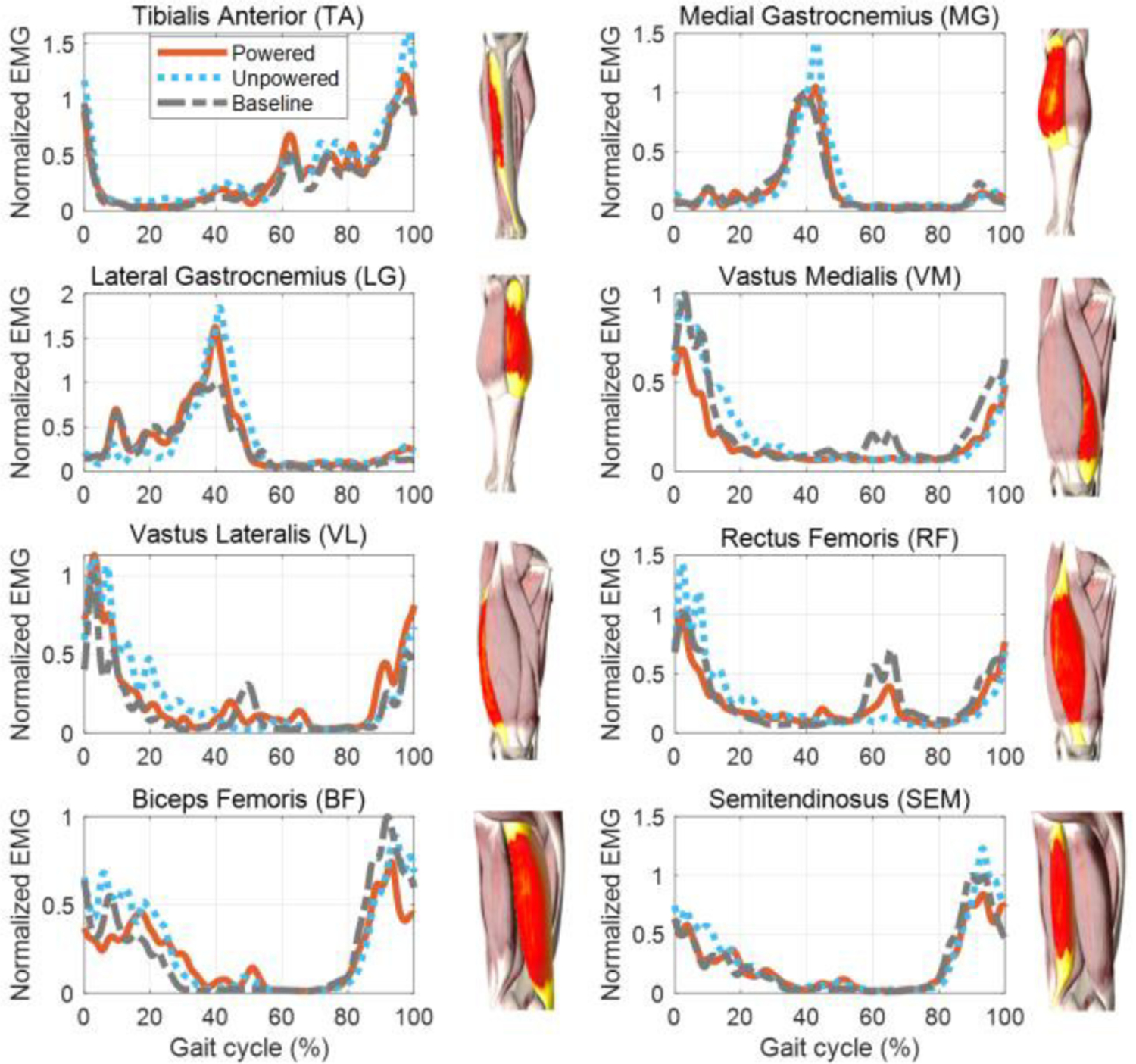
Normalized (baseline maximum =1) EMG vs. gait cycle for 8 muscles (TA, MG, LG, VM, VL, RF, BF, SEM) of a single subject. The blue dotted, gray dashed, and orange solid lines represent the time-normalized ensemble averages across all gait cycles in baseline, unpowered and powered conditions, respectively.
RMS EMG and maximum EMG averaged across 10 gait cycles and 8 subjects under the three test conditions are shown in Fig. 18 and Table VIII. Paired t-tests with Bonferroni correction (p=0.0031) was used to determine if the reduction of the muscle activity between powered and unpowered condition, and between powered and baseline condition was statistically significant. Changes in peak and RMS muscle activity are reported in Table VIII and Figure 18. Muscle activities of all 8 muscles were highest in the unpowered condition.
Fig. 18.
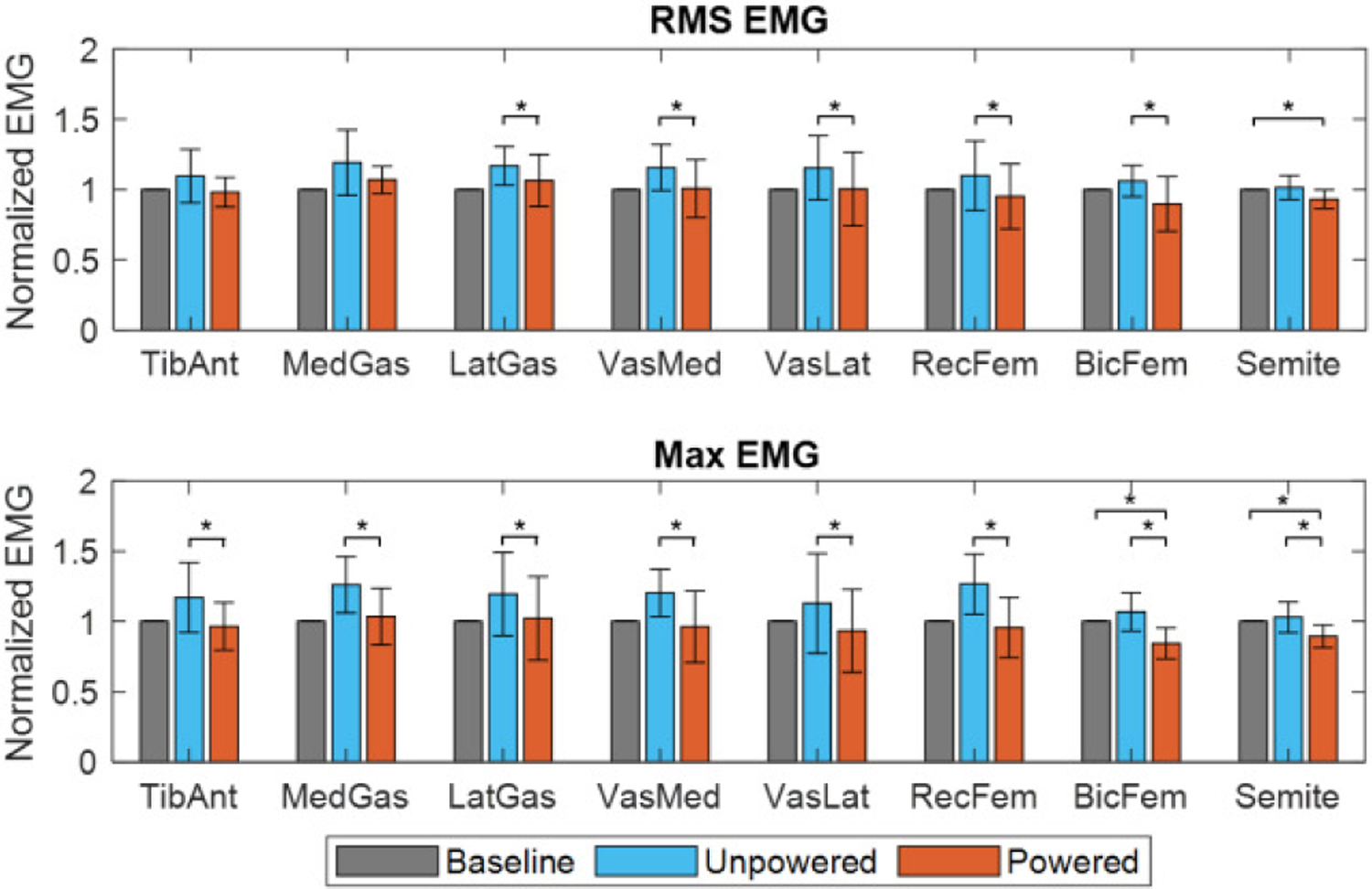
Normalized RMS and maximum EMG averaged across 10 gait cycles and multiple subjects under three conditions (baseline, unpowered, and powered) for TA (n=7), MG (n=4), LG (n=7), VM (n=8), VL (n=7), RF (n=6), BF (n=7), SEM (n=7), where n is the number of subjects whose EMG data were used for analysis for each muscle. The EMG signal of some muscles of some subjects was discarded due to signal artifacts. Asterisks indicate the reduction of the muscle activity between powered and unpowered conditions, and between powered and baseline conditions was statistically significant (paired t-test with Bonferroni correction, p = 0.0031 ). Compared with the unpowered condition, the powered result showed an overall RMS EMG reduction of 8.60%−15.22% and maximum EMG reduction of 12.36%−24.89%. The error bars represent ±1 standard deviation.
TABLE VIII:
Comparison of The RMS and Max EMG Among The Different Conditions – 8 Subjects Group Results
| RMS | Maximum | RMS | Maximum | RMS | Maximum | |
|---|---|---|---|---|---|---|
| TA | −8.60% | −16.04% | 9.55% | 17.07% | −1.92% | −3.52% |
| BF | −15.22% | −20.49% | 6.04% | 6.76% | −10.24% | −15.68% |
| SEM | −7.45% | −12.36% | 1.44% | 3.01% | −6.85% | −10.58% |
| MG | −8.97% | −17.94% | 19.11% | 26.08% | 6.88% | 3.55% |
| LG | −9.34% | −14.61% | 16.89% | 19.50% | 6.44% | 2.18% |
| VM | −12.99% | −19.64% | 15.63% | 20.29% | 0.72% | −3.73% |
| VL | −13.52% | −16.38% | 15.45% | 12.88% | 0.32% | −6.67% |
| RF | −13.68% | −24.89% | 9.91% | 26.65% | −4.95% | −4.39% |
VII. Discussion and Conclusion
The overarching goal of this work was to understand the benefits of a high-performance knee exoskeleton through stiffness modeling and advanced control methods for continuous torque assistance during overground walking. The proposed design and control methods result in a lightweight and compliant portable exoskeleton with high bandwidth of stiffness control and high torque tracking accuracy. The results of this research are significant because 1) it derives both modeling and continuous torque control for QDD exoskeletons. Presented theory and simulation delineate the advantages of QDD actuation in comparison with the SEA actuation method; 2) it proposes a stiffness-based continuous torque controller that estimates the biological torque in real-time and is adaptable to different overground walking speeds; 3) it comprehensively evaluates and demonstrates the feasibility of a portable knee exoskeleton to reduce muscular activities during level-ground walking in able-bodied individuals.
A. Advantages of Stiffness Modeling and Stiffness-Based Continuous Torque Control
Leveraging the analytical stiffness model, theoretical and experimental benchmark results demonstrate that the QDD actuator outperforms SEA in terms of both torque control and stiffness control. We showed that our QDD actuator has large stiffness bandwidth that covers the frequency of normal human walking and running. It also achieved a small torque tracking error under a wide range of stiffnesses.
We also proposed a control framework to generate a stiffness-based continuous torque assistance profile while ensuring a smooth transition during speed changes. Previous studies [26, 33] involving stiffness models were not able to adapt to speed changes and would generate a discontinuous torque profile. Since they depend on gait phase estimations, the sudden jump will appear at these points.
B. Neuromuscular Response and Interpretations
We investigated the effect of a portable high-performance knee exoskeleton on able-bodied subjects during level-ground walking. Previous studies demonstrated that it is possible to reduce muscle activities with a portable knee exoskeleton or exosuit. However, such benefits have only been shown in more torque demanding conditions, e.g., incline/decline walking [20, 30], or in particular, pre-swing and swing gait phases for inflatable exosuits pressure control [26]. This work comprehensively evaluates the effect of a portable knee exoskeleton on able-bodied subjects for level-ground walking. The results suggest that a powered lightweight portable knee exoskeleton has the potential to reduce several lower-limb muscle activations for level-ground walking.
Compared with the unpowered condition, the RMS and maximum EMG of all 8 muscles decreased in the powered condition. This reduction is remarkable in terms of RMS EMG for all 3 knee extensors examined (VM, VL, RF) and 2 knee flexors (LG, BF), and for all 8 muscles in terms of maximum EMG (Fig. 18, Table VIII). This result illustrates that our controller can effectively assist level-ground walking when compared with the unpowered case. Further improvement may be possible by separately optimizing the assistance profile in the stance and swing phase.
Interestingly, although the torque assistance is applied to the knee joint, a reduction in peak ankle extensor (TA) muscle activation is also observed. This agrees with the finding reported in [15, 48, 49] that altering the dynamics of the assisted joint may affect the dynamics of other joints. Therefore, although the knee joint primarily dissipates energy during the gait cycle [63], benefits to the overall level-ground walking performance may still be possible thanks to a corresponding reduction in muscle activity at other joints.
The reduction in muscle activation between powered exoskeleton and baseline is lower than that between powered and unpowered, with two muscles (SEM and BF) showing significant differences in peak EMG across the entire gait cycle. The two main factors limiting the reduction in muscle activity between baseline and powered conditions were device weight and standardized assistance profiles. Although we optimized the design of our exoskeleton to be lightweight (3.5 kg bilateral weight) and compliant (0.22 Nm backdrive torque), the increase in muscle activity between baseline and unpowered demonstrates that mass and/or friction had an effect. The torque assistance essentially mitigates the impact of mass/friction, but the benefit does not yet substantially exceed the imposed mass penalty. Further improvement of hardware design might alleviate the impact of mass on muscle activity during walking. Second, the torque assistance profile is based on a pre-trained population-averaged dataset and is not tailored to each participant. Individualized torque assistance profiles could provide further reduction of muscle activity between powered and baseline conditions. We discuss this limitation in Section VII.C.
C. Limitations of the Study
Here, we note some limitations of our study. First, we chose an assistive torque that mimics biological torque. Although it is an intuitive control approach in wearable robotics, some literature reports that the optimal exoskeleton torque profile for human performance augmentation may not be proportional to the biological torque [56]. Determining the optimal exoskeleton torque profile is challenging as the human-exoskeleton interaction must be fully understood, including how assistive torque impacts the dynamics of human muscles. Nonetheless, a proportional biological torque profile was worth investigating since it is unlikely to have a negative impact on human performance and is viable and simple for assisting wearers.
A second limitation is the misalignment of the exoskeleton and the human knee joint. While this is a common issue for a rigid powered exoskeleton, the misalignment may induce undesired interaction force that affects the comfortable operation of the exoskeleton [64]. Our previous work [55] developed a novel mechanism that used a rolling knee joint and double-hinge structure to reduce 74% of the joint misalignment at maximum knee flexion. However, due to the complexity of the mechanical structure, our previous design increases the total weight of the exoskeleton. It thus induces an undesired mass penalty to the overall human performance. Another approach to solving this problem is to use a jointless actuator design that eliminates the need for joint alignment in the first place. An example is the soft inflatable pneumatic knee exosuit developed by Sridar et al. [26]. Although the exosuit does not have joint alignment issues thanks to its soft nature, its actuator is powered by an external pneumatic source. Thus the tethered pneumatic design limits its portability and bandwidth.
D. Conclusion And Future Work
In this work, a continuous-phase stiffness model and the corresponding stiffness-based continuous torque controller are proposed and evaluated on a portable knee exoskeleton with 8 able-bodied subjects during treadmill walking. This stiffness model can achieeve a large and sufficient stiffness bandwidth (16 Hz) to cover normal human walking frequency rang, and the controller achieves a small torque tracking error (0.23 Nm) under different stiffness. Our continuous torque controller requires no gait phase estimation but can adapt to varying speeds and generate a continuous torque profile. Reducing the muscle activity of able-bodied subjects for level-ground walking using a portable knee exoskeleton has traditionally been considered a difficult task [65]. However, by leveraging our lightweight portable knee exoskeleton and our proposed continuous stiffness based torque controller, our neuromuscular walking experiments demonstrate that both the RMS and maximum EMG of all 8 muscles decreased (remarkable for 3 extensors and 2 flexors) in the powered condition relative to the unpowered condition and 2 out of 8 lower extremity muscles have a significant reduction in muscle activation in the powered condition relative to the baseline (no-exoskeleton) condition. Compared with the result of the baseline condition in Table VIII, the results showed the powered exoskeleton could reduce the maximum EMG of knee extensors (VM, VL, RF), knee flexors (BF, SEM), and ankle muscle (TA) and reduce the RMS of knee extensor (RF), knee flexors (BF, SEM), and ankle muscle (TA). But the RMS and maximum EMG of the ankle plantar flexors (MG, LG) were increased by 3.55% and 2.18%, respectively. Therefore, it can be concluded that the knee exoskeleton can reduce the EMG signal of the knee flexor and extensor muscles. In contrast, the weight of the exoskeleton might cause a slight increase in the EMG signal of the ankle plantar flexors, and it cannot be mitigated by knee joint torque assistance.
A recent study [49] demonstrated that a portable knee exoskeleton could only improve mobility for stroke subjects with a moderate level of neurological impairments because the device was too heavy and stiff. Since our knee exoskeleton is more lightweight and compliant (3.5 Kg vs. 5.4 Kg Keeogo), we will study whether the robot and associated stiffness-based continuous torque controller can benefit broader populations with mild, moderate, and severe levels of neurological impairments.
It may be worthwhile in future work to use an assistive torque profile other than the proportional biological torque profile or optimize the torque profile using human-in-the-loop methods [56, 66]. In addition, the adaptability of the controller to different terrains such as incline/decline walking and stair climbing will be thoroughly studied and evaluated. We are investigating the quasi-stiffness profiles during level-ground walking, incline walking [14] and loaded walking [38]. In future work, we will investigate the hypothesis that the continuous stiffness model (two modes) from this work can be generalized to multiple stiffness modes to produce assistive torque for different terrain conditions.
Supplementary Material
Acknowledgments
This work is in part supported by the National Science Foundation CAREER award CMMI 1944655, NIH R01EB029765, NIDILRR 90DPGE0011. T.C. Bulea was supported by the intramural research program of the NIH Clinical Center. Any opinions, findings, and conclusions, or recommendations expressed in this material are those of the author (s) and do not necessarily reflect the views of the funding organizations.
Biographies

Tzu-Hao Huang received the B.S. degree in Occupational Therapy from National Cheng Kung University, Tainan, Taiwan, in 2004, the M.S. degree in the Institute of Rehabilitation Science and Technology from National Yang Ming University, Taipei, Taiwan, in 2006, and the Ph.D. degree in Mechanical Engineering from National Taiwan University, Taipei, Taiwan, in 2013. He is currently an Assistant Professor in the Department of Mechanical Engineering at the City College of New York and an research assistant in the Department of Mechanical and Aerospace Engineering at the North Carolina State University. His major research area is control and design of the rehabilitation and assistive devices, human-machine interface for assistive and rehabilitation device, brain-machine interface for subjects with movement disability, and the smart textile for physiological sensing in firefight, sport, and medical application.

Sainan Zhang received the B.S. degree in Automation from Xi’an University of Posts and Telecommunications, in 2015, the M.S. degree in Control Science of Engineering from the University of Electronic Science and Technology of China, Sichuan, China, in 2018. She is currently working towards the Ph.D. degree supervised by Dr. Hao Su at the Department of Mechanical Engineering at the City University of New York, New York, USA. She is aslo a visiting scholar in the Department of Mechanical and Aerospace Engineering at the North Carolina State University. Her current research interests include the control and optimization of lower-limb wearable robots.

Shuangyue Yu received the B.S. and M.S. degree from the Beijing University of Technology, Beijing, China. He is currently working towards the Ph.D. degree supervised by Dr. Hao Su at the Department of Mechanical Engineering at the City University of New York, New York, USA. He is aslo a visiting scholar in the Department of Mechanical and Aerospace Engineering at the North Carolina State University. His current research interests include lower-limb wearable robots.

Mhairi K MacLean received the M.Eng degree in Biomedical Engineering from the University of Glasgow, Glasgow, UK and the M.S in Kinesiology from the University of Michigan, Ann Arbor, MI, USA. She received her PhD in Biomedical Engineering from the University of Florida, Gainesville, FL, USA. Mhairi was a postdoc in Hao Su’s laboratory at the City University of New York. Her current research interests include wearable robots and human biomechanics. She is currently an Assistant Professor in the Department of Mechanical Engineering at the University of Twente, Netherlands.

Junxi Zhu received the B.S. from Shanghai Jiao Tong University and M.S. degree from the University of Maryland, College Park both in Mechanical Engineering. He is currently working towards the Ph.D. degree in the Department of Mechanical and Aerospace Engineering at the North Carolina State University, under the supervision of Dr. Hao Su. His current research interest includes controller design and implementation of the exoskeleton system.

Antonio Di Lallo received the B.S., M.S., and Ph.D. degrees in Mechanical Engineering from the University of Pisa, Pisa, Italy, in 2012, 2015, and 2019, respectively. He is currently a postdoctoral fellow in the Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, USA. His research interests include soft robots and wearable robots.

Chunhai Jiao received the B.S. degree from Northwest A&F University, China, and the M.S. degree from the City College of New York, New York, USA. He has been committed to the mechanical design for 16 years in the field of the machine tool, planetary gear transmission and Automation equipment. His current research interests include mechanical design of the lower-limb, upper limb exoskeleton and other experimental devices to support biomechanic robotic projects.

Thomas C. Bulea (Member, IEEE) received the B.S. degree in Mechanical Engineering from the Ohio State University, Columbus, OH and the M.S. and Ph.D. degrees in Biomedical Engineering from Case Western Reserve University, Cleveland, OH. He is currently a Staff Scientist in the Functional & Applied Biomechanics Section of the Rehabilitation Medicine Department at the National Institutes of Health Clinical Center, Bethesda, MD. His research focuses on integration of neural interfacing and functional neuroimaging with rehabilitation robotics for evaluation and treatment of movement disorders. A recent emphasis has been on development of pediatric exoskeletons and their evaluation in children with cerebral palsy. He currently serves as an associate editor of IEEE Transactions on Neural Systems and Rehabilitation Engineering (TNSRE).

Minghui Zheng (Member, IEEE) received the B.E. and M.E. degrees, in 2008 and 2011 respectively, from Beihang University, Beijing, China, and the Ph.D. degree in Mechanical Engineering, in 2017, from University of California, Berkeley, USA. She joined University of Buffalo, NY, USA, in 2017, where she is currently an assistant professor in Mechanical and Aerospace Engineering. Her research interests include learning, planning, and control for multiple robotic systems such as collaborative manipulators for remanufacturing and drones for disaster resilience. She was the recipient of the NSF CAREER Award in 2021.

Hao Su (Member, IEEE) is an Associate Professor in the Department of Mechanical and Aerospace Engineering at the North Carolina State University. He was Irwin Zahn Endowed Assistant Professor at the City University of New York. He was a Research Scientist at Philips Research North America, and then a postdoctoral fellow at Harvard University and Wyss Institute for Biologically Inspired Engineering. Hao Su received B.S. degree from Harbin Institute of Technology, China, M.S. degree from State University of New York University at Buffalo, and Ph.D. degree from Worcester Polytechnic Institute.
He is a recipient of National Science Foundation CAREER Award, National Institutes of Health (NIH) R01 award, Best Student Paper Award of ASME Dynamic Systems Control Division Mechatronics Technical Committee, Toyota Mobility Challenge Discover Award, Best Medical Robotics Paper Runner-up Award in the IEEE International Conference on Robotics and Automation (ICRA) and Philips Innovation Transfer Award. He received the Advanced Simulation & Training Award from the Link Foundation and Dr. Richard Schlesinger Award from the American Society for Quality. He holds patents on surgical robotics and socially assistive robots. He serves as an associate editor of IEEE Robotics and Automation Letters (RAL), ASME Journal of Mechanisms and Robotics, IEEE International Conference on Robotics and Automation (ICRA), and IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).
APPENDIX
TABLE IX.
Parameters in the human-exoskeleton coupled model
| Parameter | Unit | Conventional Actuator | SEA | QDD |
|---|---|---|---|---|
| Motor | - | Maxon EC flat 45 651618 [20] | Kollmorgen T-2950 [19] | Ours |
| Nominal voltage | V | 24 | 38.4 | 42 |
| Nominal current | A | 3.29 | 1 | 7.5 |
| Nominal Torque | Nm | 0.134 | 0.813 | 2.165 |
| Motor resistance | Ω | 0.573 | 19.2 | 0.58 |
| Motor inductance | mH | 0.301 | 41 | 0.21 |
| Motor friction coefficient | Nm·s/rad | 0.01 | 0.034 | 0.08 |
| Torque constant | Nm/A | 0.0404 | 0.813 | 0.2886 |
| Motor inertia | g·cm2 | 181 | 3932 | 895 |
| Gear ratio | - | 113:1 | 100:1 | 6:1 |
| Transmission stiffness | Nm /rad | 500 | 200 | 500 |
Contributor Information
Tzu-Hao Huang, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Sainan Zhang, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Shuangyue Yu, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Mhairi K. MacLean, Lab of Biomechatronics and Intelligent Robotics; Department of Mechanical Engineering at the University of Twente, Netherlands.
Junxi Zhu, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Antonio Di Lallo, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Chunhai Jiao, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
Thomas C. Bulea, Functional and Applied Biomechanics Section, Rehabilitation Medicine Department, Clinical Center, National Institutes of Health, Bethesda, MD, 20892, US..
Minghui Zheng, Department of Mechanical and Aerospace Engineering, the University at Buffalo, The State University of New York, New York, 14260, US..
Hao Su, Lab of Biomechatronics and Intelligent Robotics (BIRO), Department of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, US..
References
- [1].Young AJ and Ferris DP, “State of the art and future directions for lower limb robotic exoskeletons,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 25, no. 2, pp. 171–182, 2016. [DOI] [PubMed] [Google Scholar]
- [2].Sawicki GS, Beck ON, Kang I, and Young AJ, “The exoskeleton expansion: improving walking and running economy,” Journal of NeuroEngineering and Rehabilitation, vol. 17, no. 1, pp. 1–9, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Yandell MB, Quinlivan BT, Popov D, Walsh C, and Zelik KE, “Physical interface dynamics alter how robotic exosuits augment human movement: implications for optimizing wearable assistive devices,” Journal of neuroengineering and rehabilitation, vol. 14, no. 1, p. 40, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gordon KE and Ferris DP, “Learning to walk with a robotic ankle exoskeleton,” Journal of biomechanics, vol. 40, no. 12, pp. 2636–2644, 2007. [DOI] [PubMed] [Google Scholar]
- [5].Mooney LM, Rouse EJ, and Herr HM, “Autonomous exoskeleton reduces metabolic cost of human walking during load carriage,” Journal of neuroengineering and rehabilitation, vol. 11, no. 1, pp. 1–11, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Wiggin MB, Sawicki GS, and Collins SH, “An exoskeleton using controlled energy storage and release to aid ankle propulsion,” in 2011 IEEE International Conference on Rehabilitation Robotics, 2011, pp. 1–5: IEEE. [DOI] [PubMed] [Google Scholar]
- [7].Collins S, Wiggin MB, and Sawicki G, “An exoskeleton that uses no energy yet reduces the metabolic cost of human walking,” Nature, vol. 522, pp. 212–215, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Asbeck AT, Schmidt K, and Walsh CJ, “Soft exosuit for hip assistance,” Robotics and Autonomous Systems, vol. 73, pp. 102–110, 2015. [Google Scholar]
- [9].Lee J, Warren HR, Agarwal V, Huber ME, and Hogan N, “Modulating hip stiffness with a robotic exoskeleton immediately changes gait,” in 2020 IEEE International Conference on Robotics and Automation (ICRA), 2020, pp. 733–739: IEEE. [Google Scholar]
- [10].Kang I, Hsu H, and Young A, “The effect of hip assistance levels on human energetic cost using robotic hip exoskeletons,” IEEE Robotics and Automation Letters, vol. 4, no. 2, pp. 430–437, 2019. [Google Scholar]
- [11].Pinto-Fernandez D, Torricelli D, del Carmen Sanchez-Villamanan M, Aller F, Mombaur K, Conti R, … & Pons JL, “Performance evaluation of lower limb exoskeletons: a systematic review,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 28, no. 7, pp. 1573–1583, 2020. [DOI] [PubMed] [Google Scholar]
- [12].Cho YK, Kim K, Ma S, and Ueda J, “A robotic wearable exoskeleton for construction worker’s safety and health,” in ASCE construction research congress, 2018, pp. 19–28. [Google Scholar]
- [13].Tricomi E, Lotti N, Missiroli F, Zhang X, Xiloyannis M, Müller T, Crea S, Papp E, Krzywinski J, Vitiello N, and Masia L, “Underactuated Soft Hip Exosuit Based on Adaptive Oscillators to Assist Human Locomotion,” vol. 7, no. 2, pp. 936–943, 2021. [Google Scholar]
- [14].MacLean MK and Ferris DP, “Energetics of walking with a robotic knee exoskeleton,” Journal of applied biomechanics, vol. 35, no. 5, pp. 320–326, 2019. [DOI] [PubMed] [Google Scholar]
- [15].Shamaei K, Cenciarini M, Adams AA, Gregorczyk KN, Schiffman JM, and Dollar AM, “Biomechanical effects of stiffness in parallel with the knee joint during walking,” IEEE Transactions on Biomedical Engineering, vol. 62, no. 10, pp. 2389–2401, 2015. [DOI] [PubMed] [Google Scholar]
- [16].Sawicki GS, Lewis CL, and Ferris DP, “It pays to have a spring in your step,” Exercise and sport sciences reviews, vol. 37, no. 3, p. 130, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Yang X, Huang TH, Hu H, Yu S, Zhang S, Zhou X, Carriero A, Yue G, Su H, “Spine-inspired continuum soft exoskeleton for stoop lifting assistance,” IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 4547–4554, 2019. [Google Scholar]
- [18].Park EJ, Akbas T, Eckert-Erdheim A, Sloot LH, Nuckols RW, Orzel D, Schumm L, Ellis TD, Awad LN, and Walsh CJ, “A Hinge-Free, Non-Restrictive, Lightweight Tethered Exosuit for Knee Extension Assistance During Walking,” IEEE Transactions on Medical Robotics and Bionics, vol. 2, no. 2, pp. 165–175, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Karavas N, Ajoudani A, Tsagarakis N, Saglia J, Bicchi A, and Caldwell D, “Tele-impedance based assistive control for a compliant knee exoskeleton,” Robotics and Autonomous Systems, vol. 73, pp. 78–90, 2015. [Google Scholar]
- [20].Lee D, Kwak EC, McLain BJ, Kang I, and Young AJ, “Effects of Assistance During Early Stance Phase Using a Robotic Knee Orthosis on Energetics, Muscle Activity, and Joint Mechanics During Incline and Decline Walking,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 28, no. 4, pp. 914–923, 2020. [DOI] [PubMed] [Google Scholar]
- [21].Aguirre-Ollinger G and Yu H, “Lower-Limb Exoskeleton With Variable-Structure Series Elastic Actuators: Phase-Synchronized Force Control for Gait Asymmetry Correction,” IEEE Transactions on Robotics, 2020. [Google Scholar]
- [22].Braun DJ, Chalvet V, Chong T-H, Apte SS, and Hogan N, “Variable stiffness spring actuators for low-energy-cost human augmentation,” IEEE Transactions on Robotics, vol. 35, no. 6, pp. 1435–1449, 2019. [Google Scholar]
- [23].Yu S, Huang TH, Yang X, Jiao C, Yang J, Chen Y, Yi J, and Su H, “Quasi-Direct Drive Actuation for a Lightweight Hip Exoskeleton with High Backdrivability and High Bandwidth,” IEEE/ASME Transactions on Mechatronics, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Yu S, Huang TH, Wang D, Lynn B, Sayd D, Silivanov V, Park YS, Tian Y, and Su H, “Design and Control of a High-Torque and Highly Backdrivable Hybrid Soft Exoskeleton for Knee Injury Prevention During Squatting,” IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 4579–4586, 2019. [Google Scholar]
- [25].Maeda D, Tominaga K, Oku T, Pham HT, Saeki S, Uemura M, Hirai H, and Miyazaki F, “Muscle synergy analysis of human adaptation to a variable-stiffness exoskeleton: Human walk with a knee exoskeleton with pneumatic artificial muscles,” in 2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012), 2012, pp. 638–644: IEEE. [Google Scholar]
- [26].Sridar S, Qiao Z, Rascon A, Biemond A, Beltran A, Maruyama T, Kwasnica C, Polygerinos P, and Zhang W, “Evaluating Immediate Benefits of Assisting Knee Extension With a Soft Inflatable Exosuit,” IEEE Transactions on Medical Robotics and Bionics, vol. 2, no. 2, pp. 216–225, 2020. [Google Scholar]
- [27].Wensing PM, Wang A, Seok S, Otten D, Lang J, and Kim S, “Proprioceptive actuator design in the MIT Cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots,” Ieee transactions on robotics, vol. 33, no. 3, pp. 509–522, 2017. [Google Scholar]
- [28].Katz B, Di Carlo J, and Kim S, “Mini cheetah: A platform for pushing the limits of dynamic quadruped control,” in 2019 International Conference on Robotics and Automation (ICRA), 2019, pp. 6295–6301: IEEE. [Google Scholar]
- [29].Zhu H, Nesler C, Divekar N, Ahmad MT, and Gregg RD, “Design and Validation of a Partial-Assist Knee Orthosis with Compact, Backdrivable Actuation,” in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), 2019, pp. 917–924: IEEE. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Lee D, Mclain BJ, Kang I, and Young A, “Biomechanical comparison of assistance strategies using a bilateral robotic knee exoskeleton,” IEEE Transactions on Biomedical Engineering, 2021. [DOI] [PubMed] [Google Scholar]
- [31].Prasanth H, Caban M, Keller U, Courtine G, Ijspeert A, Vallery H, and Von Zitzewitz J, “Wearable sensor-based real-time gait detection: A systematic review,” vol. 21, no. 8, p. 2727, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Winter DA, Biomechanics and motor control of human gait: normal, elderly and pathological 1991. [Google Scholar]
- [33].Caputo JM and Collins SH, “A universal ankle–foot prosthesis emulator for human locomotion experiments,” Journal of biomechanical engineering, vol. 136, no. 3, 2014. [DOI] [PubMed] [Google Scholar]
- [34].Martinez A, Lawson B, and Goldfarb M, “A controller for guiding leg movement during overground walking with a lower limb exoskeleton,” IEEE Transactions on Robotics, vol. 34, no. 1, pp. 183–193, 2017. [DOI] [PubMed] [Google Scholar]
- [35].Lim B, Lee J, Jang J, Kim K, Park YJ, Seo K, and Shim Y, “Delayed output feedback control for gait assistance with a robotic hip exoskeleton,” IEEE Transactions on Robotics, vol. 35, no. 4, pp. 1055–1062, 2019. [Google Scholar]
- [36].Quintero D, Villarreal DJ, Lambert DJ, Kapp S, and Gregg RD, “Continuous-phase control of a powered knee–ankle prosthesis: Amputee experiments across speeds and inclines,” IEEE Transactions on Robotics, vol. 34, no. 3, pp. 686–701, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Thatte N, Shah T, and Geyer H, “Robust and adaptive lower limb prosthesis stance control via extended Kalman filter-based gait phase estimation,” IEEE Robotics and Automation Letters, vol. 4, no. 4, pp. 3129–3136, 2019. [Google Scholar]
- [38].Holt KG, Wagenaar RC, LaFiandra ME, Kubo M, and Obusek JP, “Increased musculoskeletal stiffness during load carriage at increasing walking speeds maintains constant vertical excursion of the body center of mass,” Journal of biomechanics, vol. 36, no. 4, pp. 465–471, 2003. [DOI] [PubMed] [Google Scholar]
- [39].Zhang J and Collins SH, “The passive series stiffness that optimizes torque tracking for a lower-limb exoskeleton in human walking,” Frontiers in neurorobotics, vol. 11, p. 68, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Chen J, Damiano DL, Lerner ZF, and Bulea TC, “Validating Model-Based Prediction Of Biological Knee Moment During Walking With An Exoskeleton in Crouch Gait: Potential Application for Exoskeleton Control,” in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), 2019, pp. 778–783: IEEE. [DOI] [PubMed] [Google Scholar]
- [41].Liu L, Leonhardt S, Ngo C, and Misgeld BJ, “Impedance-Controlled Variable Stiffness Actuator for Lower Limb Robot Applications,” IEEE Transactions on Automation Science and Engineering, vol. 17, no. 2, pp. 991–1004, 2019. [Google Scholar]
- [42].Shamaei K, Sawicki GS, and Dollar AM, “Estimation of quasi-stiffness of the human knee in the stance phase of walking,” PloS one, vol. 8, no. 3, p. e59993, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Fukuchi CA, Fukuchi RK, and Duarte M, “A public dataset of overground and treadmill walking kinematics and kinetics in healthy individuals,” PeerJ, vol. 6, p. e4640, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Farris DJ and Sawicki GS, “The mechanics and energetics of human walking and running: a joint level perspective,” Journal of The Royal Society Interface, vol. 9, no. 66, pp. 110–118, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Jacobs R, Bobbert MF, and van Ingen Schenau GJ, “Mechanical output from individual muscles during explosive leg extensions: the role of biarticular muscles,” Journal of biomechanics, vol. 29, no. 4, pp. 513–523, 1996. [DOI] [PubMed] [Google Scholar]
- [46].van Ingen Schenau G. v, Bobbert M, and Rozendal R, “The unique action of bi-articular muscles in complex movements,” Journal of anatomy, vol. 155, p. 1, 1987. [PMC free article] [PubMed] [Google Scholar]
- [47].Schenau GJVI, “From rotation to translation: Constraints on multi-joint movements and the unique action of bi-articular muscles,” Human Movement Science, vol. 8, no. 4, pp. 301–337, 1989. [Google Scholar]
- [48].Kim J, Lee G, Heimgartner R, Arumukhom Revi D, Karavas N, Nathanson D, Galiana I, Eckert-Erdheim A, Murphy P, Perry D, and Menard N, “Reducing the metabolic rate of walking and running with a versatile, portable exosuit,” Science, vol. 365, no. 6454, pp. 668–672, 2019. [DOI] [PubMed] [Google Scholar]
- [49].Mooney LM and Herr HM, “Biomechanical walking mechanisms underlying the metabolic reduction caused by an autonomous exoskeleton,” Journal of neuroengineering and rehabilitation, vol. 13, no. 1, pp. 1–12, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Zelik KE, Takahashi KZ, and Sawicki GS, “Six degree-of-freedom analysis of hip, knee, ankle and foot provides updated understanding of biomechanical work during human walking,” Journal of Experimental Biology, vol. 218, no. 6, pp. 876–886, 2015. [DOI] [PubMed] [Google Scholar]
- [51].Ergin MA and Patoglu V, “A self-adjusting knee exoskeleton for robot-assisted treatment of knee injuries,” in 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2011, pp. 4917–4922: IEEE. [Google Scholar]
- [52].Lerner ZF, Damiano DL, Park H-S, Gravunder AJ, and Bulea TC, “A robotic exoskeleton for treatment of crouch gait in children with cerebral palsy: Design and initial application,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 25, no. 6, pp. 650–659, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].McGibbon CA, Sexton A, Jayaraman A, Deems-Dluhy S, Gryfe P, Novak A, Dutta T, Fabara E, Adans-Dester C, and Bonato P, “Evaluation of the Keeogo exoskeleton for assisting ambulatory activities in people with multiple sclerosis: an open-label, randomized, cross-over trial,” Journal of neuroengineering and rehabilitation, vol. 15, no. 1, p. 117, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Mcleod JC, Ward SJ, and Hicks AL, “Evaluation of the Keeogo™ Dermoskeleton,” Disability and Rehabilitation: Assistive Technology, vol. 14, no. 5, pp. 503–512, 2019. [DOI] [PubMed] [Google Scholar]
- [55].Tamai K, Kawamoto H, and Sankai Y, “Weight-Supported Walking Assist Device for Knee Osteoarthritis Patients,” in 2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR), 2019, pp. 374–379: IEEE. [DOI] [PubMed] [Google Scholar]
- [56].Ding Y, Kim M, Kuindersma S, and Walsh CJ, “Human-in-the-loop optimization of hip assistance with a soft exosuit during walking,” Science Robotics, vol. 3, no. 15, p. eaar5438, 2018. [DOI] [PubMed] [Google Scholar]
- [57].Franks PW, Bryan GM, Martin RM, Reyes R, and Collins SH, “Comparing optimized exoskeleton assistance of the hip, knee, and ankle in single and multi-joint configurations,” bioRxiv, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Wang J, Li X, Huang TH, Yu S, Li Y, Chen T, Carriero A, Oh-Park M, and Su H, “Comfort-centered design of a lightweight and backdrivable knee exoskeleton,” IEEE Robotics and Automation Letters, vol. 3, no. 4, pp. 4265–4272, 2018. [Google Scholar]
- [59].Lee Y, Roh SG, Lee M, Choi B, Lee J, Kim J, Choi H, Shim Y, and Kim YJ, “A flexible exoskeleton for hip assistance,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017, pp. 1058–1063: IEEE. [Google Scholar]
- [60].Zhang T and Huang H, “A lower-back robotic exoskeleton: industrial handling augmentation used to provide spinal support,” IEEE Robotics & Automation Magazine, vol. 25, no. 2, pp. 95–106, 2018. [Google Scholar]
- [61].Huo W, Mohammed S, Amirat Y, and Kong K, “Fast gait mode detection and assistive torque control of an exoskeletal robotic orthosis for walking assistance,” IEEE Transactions on Robotics, vol. 34, no. 4, pp. 1035–1052, 2018. [Google Scholar]
- [62].Zhu H, Nesler C, Divekar N, Peddinti V, and Gregg R, “Design Principles for Compact, Backdrivable Actuation in Partial-Assist Powered Knee Orthoses,” IEEE/ASME Transactions on Mechatronics, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Dollar AM and Herr H, “Lower extremity exoskeletons and active orthoses: Challenges and state-of-the-art,” IEEE Transactions on robotics, vol. 24, no. 1, pp. 144–158, 2008. [Google Scholar]
- [64].Zanotto D, Akiyama Y, Stegall P, and Agrawal SK, “Knee joint misalignment in exoskeletons for the lower extremities: Effects on user’s gait,” IEEE Transactions on Robotics, vol. 31, no. 4, pp. 978–987, 2015. [Google Scholar]
- [65].Lora-Millán JS, Moreno JC, and Rocon E, “Assessment of gait symmetry, torque interaction and muscular response due to the unilateral assistance provided by an active knee orthosis in healthy subjects,” in 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), 2020, pp. 229–234: IEEE. [Google Scholar]
- [66].Zhang J, Fiers P, Witte KA, Jackson RW, Poggensee KL, Atkeson CG, and Collins SH, “Human-in-the-loop optimization of exoskeleton assistance during walking,” Science, vol. 356, no. 6344, pp. 1280–1284, 2017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


