Abstract
Phenotyping electronic health records (EHR) focuses on defining meaningful patient groups (e.g., heart failure group and diabetes group) and identifying the temporal evolution of patients in those groups. Tensor factorization has been an effective tool for phenotyping. Most of the existing works assume either a static patient representation with aggregate data or only model temporal data. However, real EHR data contain both temporal (e.g., longitudinal clinical visits) and static information (e.g., patient demographics), which are difficult to model simultaneously. In this paper, we propose Temporal And Static TEnsor factorization (TASTE) that jointly models both static and temporal information to extract phenotypes. TASTE combines the PARAFAC2 model with non-negative matrix factorization to model a temporal and a static tensor. To fit the proposed model, we transform the original problem into simpler ones which are optimally solved in an alternating fashion. For each of the sub-problems, our proposed mathematical re-formulations lead to efficient sub-problem solvers. Comprehensive experiments on large EHR data from a heart failure (HF) study confirmed that TASTE is up to 14× faster than several baselines and the resulting phenotypes were confirmed to be clinically meaningful by a cardiologist. Using 60 phenotypes extracted by TASTE, a simple logistic regression can achieve the same level of area under the curve (AUC) for HF prediction compared to a deep learning model using recurrent neural networks (RNN) with 345 features.
Keywords: Tensor Factorization, Computational Phenotyping, Predictive modeling
1. INTRODUCTION
Phenotyping is the process of identifying patient groups sharing similar clinically-meaningful characteristics and is essential for treatment development and management [1, 2]. However, the complexity and heterogeneity of the underlying patient information render manual (or hand-curated) phenotyping impractical for large populations or complex conditions. Unsupervised EHR-based phenotyping based on tensor factorization, e.g., [3–5], provides an effective alternative. However, existing unsupervised phenotyping methods are unable to handle both static and dynamically-evolving information, which is the focus of this work.
Traditional tensor factorization models [6–9] assume the same dimensionality along each tensor mode. However, in practice one mode such as time can be irregular. For example, different patients may vary by the number of clinical visits over time. To handle such longitudinal datasets, [10] and [11] propose algorithms to fit the PARAFAC2 model [12] which are faster and more scalable for handling irregular and sparse data. However, these PARAFAC2 approaches only focus on modeling the dynamically-evolving features for every patient (e.g., the structured codes recorded for every visit). Static features (such as race and gender) which do not evolve are completely neglected; yet, they are crucial factors for phenotyping analyses (e.g., some diseases have the higher prevalence in a certain race).
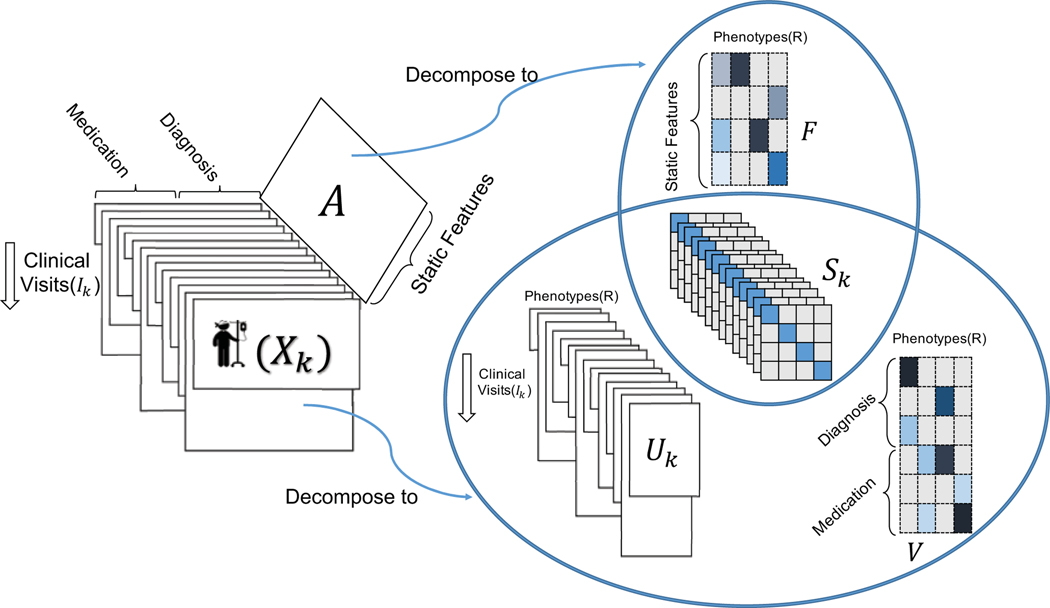
To address this problem, we propose a scalable method called TASTE which jointly models both temporal and static features by combining the non-negative PARAFAC2 model with non-negative matrix factorization as shown in Figure 1. We reformulate our new non-convex problem into simpler sub-problems (i.e., orthogonal Procrustes, least square and non-negativity constrained least square) and solve each of the sub-problems efficiently by avoiding unnecessary computations (e.g., expensive Khatri-Rao products).
Figure 1:
TASTE applied on dynamically-evolving structured EHR data and static patient information. Each Xk represents the medical features recorded for different clinical visits for patient k. Matrix A includes the static information (e.g., race, gender) of patients. TASTE decomposes {Xk} into three parts: {Uk}, {Sk}, and V. Static matrix A is decomposed into two parts: {Sk} and F. Note that {Sk} (personalized phenotype scores) is shared between static and dynamically-evolving features.
We summarize our contributions below:
Temporal and Static Tensor Factorization: We propose a new optimization problem to jointly model static and dynamic features from EHR data as non-negative factor matrices.
Fast and Accurate Algorithm: Our proposed fitting algorithm is up to 14 × faster than the state-of-the-art baseline. At the same time, TASTE preserves model constraints which promote model uniqueness better than baselines while maintaining interpretability.
Case Study on Heart Failure Phenotyping: We demonstrate the practical impact of TASTE through a case study on heart failure (HF) phenotyping. We identified clinically-meaningful phenotypes which are confirmed by a cardiologist. Using phenotypes extracted by TASTE, a simple logistic regression model can achieve comparable predictive accuracy with deep learning techniques such as RNNs.
2. BACKGROUND & RELATED WORK
Table 1 summarizes the notations used in this paper.
Table 1:
Notations
| Symbol | Definition |
|---|---|
| * | Element-wise Multiplication |
| Khatri Rao Product | |
| Y, y | matrix, vector |
| Y(i, :) | the i-th row of Y |
| Y(:, r) | the r-th column of Y |
| Y (i, r) | element (i,r) of Y |
| Xk | Feature matrix of patient k |
| diag(Y) | Extract the diagonal of matrix Y |
| vec(Y) | Vectorizing matrix Y |
| svd(Y) | Singular value decomposition on Y |
| Frobenius Norm | |
| max(0, Y) | max operator replaces negative values in Y with 0 |
| Y ≥ 0 | All elements in Y are non-negative |
2.1. PARAFAC2 Model
The PARAFAC2 model [13], has the following objective function:
| (1) |
where is the input matrix, factor matrix diagonal matrix , and factor matrix are output matrices. Factor matrix is an orthogonal matrix, and . SPARTan [10] introduces a scalable algorithm to fit this model for sparse datasets. COPA [11] extends this work and incorporates different constraints such as temporal smoothness and sparsity to the model factors to produce more meaningful results. However, none of these models (i.e., the original PARAFAC2 model, SPARTan [10], and COPA [11]) can incorporate a non-negativity constraint on the factor matrix Uk.
The uniqueness property ensures that a decomposition is pursuing the true latent factors, rather than an arbitrary rotation of them. The unconstrained version of PARAFAC2 in (1) without constraints is not unique. Assume B is an invertible R × R matrix and {ZK} are R × R diagonal matrices. Then, we can transform as:
which is another valid solution achieving the same approximation error [13]. This is problematic in terms of the interpretability of the result. To promote uniqueness, Harshman [12] introduced the cross-product invariance constraint, which dictates that should be constant . To achieve that, the following constraint is added:.
2.2. Non-Negativity constrained Least Squares (NNLS)
The Non-Negativity constrained Least Squares (NNLS) problem has the following form:
| (2) |
Here, NNLS is a convex problem and the optimal solution of 2 can be solved efficiently. For example, the block principal pivoting method [14] can be used to solve NNLS problems. Authors in [14] showed the block principal pivoting method achieves state-of-the-art performance.
2.3. Unsupervised Computational Phenotyping
A wide range of approaches applies tensor factorization techniques to extract phenotypes. [3, 4, 15–19] incorporate various constraints (e.g., sparsity, non-negativity, integer) into regular tensor factorization to produce more clinically-meaningful phenotypes. [10, 11] identify phenotypes and their temporal trends by using irregular tensor factorization based on PARAFAC2 [12]; yet, those approaches cannot model both dynamic and static features for meaningful phenotype extraction. As part of our experimental evaluation, we demonstrate that naively adjusting existing PARAFAC2-based approaches to incorporate static information results in biased and less interpretable phenotypes. The authors of [5] proposed a collective non-negative tensor factorization for phenotyping purposes. However, the method is not able to jointly incorporate static information such as demographics with temporal features. Also they do not employ the orthogonality constraint on the temporal dimension, a strategy that result in non-unique solutions [12, 13].
3. THE TASTE FRAMEWORK
3.1. Intuition
We first explain the intuition of TASTE in the context of the phenotyping application.
Input data include both temporal and static features for all K patients:
Temporal features (XK); For patient k, we record the medical features for different clinical visits in matrix where Ik is the number of clinical visits and J is the total number of medical features. Note that Ik can be different for different patients.
Static features (A): The static features like gender, race, body mass index (BMI), smoking status1 are recorded in where K is the total number of patients and P is the number of static features. In particular, each row A(k, :) contains the static features for patient k.
The phenotyping process maps input data into a set of phenotypes, which involves the definition of phenotypes and a patient’s temporal evolution. Figure 1 illustrates the following model interpretation. First, phenotype definitions are shared by factor matrices V and F for temporal and static features, respectively. In particular, V (:, r) or F (:, r) are the rth column of factor matrix V or F which indicates the participation of temporal or static features in the rth phenotype. Second, personalized phenotype scores for patient k are provided in the diagonal matrix Sk where its diagonal element Sk (r, r) indicates the overall importance of the rth phenotype for patient k. Finally, temporal phenotype evolution for patient k is specified in factor matrix Uk where its rth column UK (:, r) indicates the temporal evolution of phenotype r over all clinical visits of patient k.
3.2. Objective function and challenges
We introduce the following optimization problem:
| (3) |
Our objective function has three main parts as follows:
-
(1)
The first part is related to fitting a PARAFAC2 model that factorizes a set of temporal feature matrices diagonal matrix
-
(2)
The second part is for optimizing the static feature matrix A where also is the weight parameter. Common factor matrices {Sk} are shared between static and temporal features by setting .
-
(3)
The third part enforces both non-negativity of the Uk factor and also minimizes its difference to QkH. Due to the constraint , minimizing encourages be constant over K subjects, which is a desirable PARAFAC2 property that promotes uniqueness, and thus enhances interpretability [13].
λ and μk are weighting parameters which are set by the user. For simplicity, we set μ1 = μ2 = ··· = μk = μ. The challenge in solving the above optimization problem lies in: 1) addressing all the non-negative constraints especially on Uk, 2) trying to make constant over K subjects by making non-negative Uk as close as possible to QkH while QkH can contain negative values, 3) estimating all factor matrices in order to best approximate both temporal and static input matrices, and 4) developing a computationally efficient method to scale to large patient populations.
3.3. Algorithm
To optimize the objective function (3), we need to update {Qk}, H, {Uk}, V, {Sk}, and F iteratively. Although the original problem in Equation 3 is non-convex, our algorithm utilizes the Block Coordinate Descent framework [20] to mathematically reformulate the objective function (3) into simpler sub-problems. In each iteration, we update {Qk} based on the Orthogonal Procrustes problem [21] which ensures an orthogonal solution for each . Factor matrix H can be solved efficiently by least square solvers. For factor matrices and F, we reformulate the objective function (3) so that the factor matrices are instances of the non-negativity constrained least squares (NNLS) problem. Each NNLS sub-problem is a convex problem and the optimal solution can be found easily. We use block principal pivoting method [14] to solve each NNLS sub-problem, as it achieved state-of-the-art performance on NNLS problems compared to other optimization techniques [14] as discussed in section 2.2. We also exploit structure in the underlying computations (e.g., involving Khatri-Rao products) so that each one of the sub-problems is solved efficiently. Next, we summarize the solution for each factor matrix.
3.3.1. Solution for factor matrix Qk.
We can rewrite objective function (3) with respect to Qk based on trace properties [22] as:
| (4) |
Removing the constant terms and applying the trace property Trace(ABC) = Trace(CAB) yields the following new objective:
| (5) |
The optimal value of Qk can then be computed via the Orthogonal Procrustes problem [21] which has the closed form solution are the right and left singular vectors of . Note that each Qk can contain negative values.
3.3.2. Solution for factor matrix H.
The objective function with respect to H can be rewritten as an unconstrained problem:
| (6) |
Note that Equation 6 is different than the original formulation introduced in Equation 3, where the Frobenius norm contains the term Uk − QkH. Through this reformulation, TASTE can utilize the least square solver to efficiently update H.
To obtain the new objective function, we observe that is a rectangular orthogonal matrix . We introduce a new orthogonal matrix, . This can be used to produce a new square orthogonal matrix .
| (7) |
Since is a square orthogonal matrix (shown in Equation (7)), we can now demonstrate that Equation (6) and Equation (3) are equivalent objectives for H.
| (8) |
where is a constant and independent of the parameter under minimization. Therefore, the value of H that minimizes also minimizes and the update rule for factor matrix H is based on the least square solution and has the following form:
3.3.3. Solution for phenotype evolution matrix Uk.
After up-dating the factor matrices Qk, H, we focus on solving for Uk. In classic PARAFAC2 [12, 13], this factor is retrieved through the simple multiplication Uk = QkH. However, for improved interpretability, we prefer temporal factor matrix Uk to be non-negative because the temporal phenotype evolution for patient k (Uk) should not be negative. As shown in the empirical results, a naive enforcement of non-negativity (max (0, Qk H)) violates the important uniqueness property of PARAFAC2. Therefore, we consider Uk as an additional factor matrix, constrain it to be non-negative, and minimize its difference to Qk H.
The objective function with respect to Uk can be combined into the following NNLS form:
| (9) |
As mentioned earlier, factor matrix Uk is updated based on block principal pivoting method.
3.3.4. Solution for temporal phenotype definition V.
Factor matrix V defines the participation of temporal features in different phenotypes. In Equation (3), the factor matrix V participates in the PARAFAC2 part with the non-negativity constraint. Therefore, the objective function for factor matrix V has the following form:
| (10) |
To update V based on block principal pivoting, the algorithm calculates for all K samples which can be done in an embarrassingly parallel fashion.
3.3.5. Solution for factor matrix W or {Sk}.
The objective function with respect to W yields the following format:
| (11) |
Factor matrices {Sk} are shared between the PARAFAC2 input and matrix A where W(k,:)=diag(Sk). Since vec(UkSkVT) = (V ⊙ Uk)W (k, :)T, Equation (11) can be rewritten in the following NNLS form:
| (12) |
where denotes Khatri-Rao product. Each row of factor matrix W (W(k, :) or diag(Sk)) can be solved separately and in parallel. Unfortunately, the update for each factor matrix Sk involves computing two time-consuming operations: and . Instead of explicitly forming the Khatri-Rao product, both operations can be replaced with more efficient counterparts. The first operation can be replaced with where * denotes the element-wise (Hadamard) product [23]. The second operation also can be replaced with diag [23]. Thus, each row of W can be efficiently updated via block principal pivoting.
3.3.6. Solution for static phenotype definition F.
Finally, factor matrix F represents the participation of static features for the phenotypes. The objective function for factor matrix F has the following NNLS form:
| (13) |
which can be easily updated via block principal pivoting.
3.4. Phenotype inference on new data
Given the learned phenotype definition (V, F) and factor matrix H for some training set, TASTE can project data of new unseen patients into the existing low-rank space. This is useful because healthcare providers may want to fix the phenotype definition while score new patients with those existing definitions. Moreover, such a methodology enables using the low-rank representation of patients such as (Sk) as feature vectors for a predictive modeling task.
Suppose, represents the temporal information of unseen patients indicates their static information. TASTE projects the new patient’s information into the existing low-rank space (H, V, and F) by optimizing {Qn}, {Un} and {Sn} for the following objective function:
| (14) |
The updates for the factor matrices {Qn} are based on Equation (5). {Un} can be minimized based on Equation (9) Finally, W can be updated based on Equation (12) where diag .
4. EXPERIMENTAL RESULTS
We focus on answering the following questions:
Q1. Does TASTE preserve accuracy and the uniqueness-promoting constraint, while being fast to compute?
Q2. How does TASTE scale for increasing number of patients (K)?
Q3. Does TASTE recover the true factor matrices? How does promoting uniqueness correlate with recovery in the presence of noise?
Q4. Does the static information added in TASTE improve predictive performance for detecting heart failure?
Q5. Are the heart failure phenotypes produced by TASTE meaningful to an expert cardiologist?
4.1. Data Set Description
Table 2 summarizes the statistics of data sets.
Table 2:
Summary statistics of two real data sets.
| Dataset | # Patients | # Temporal Features | Mean(Ik) | # Static Features |
|---|---|---|---|---|
| Sutter | 64,912 | 1164 | 29 | 22 |
| CMS | 151,349 | 284 | 50 | 30 |
Sutter:
This dataset is from Sutter Palo Alto Medical Foundation, a large primary care and multispecialty group practice. The data set contains the EHRs for patients with new onset of heart failure and matched controls (matched by encounter time, and age). It includes 5912 cases and 59300 controls. For all patients, encounter features (e.g., medication orders, diagnoses) were extracted from the electronic health records. We use standard medical concept groupers to convert the available ICD-9 or ICD-10 diagnosis codes to Clinical Classification Software (CCS level 3) [24]. We also group the normalized drug names based on unique therapeutic sub-classes using the Anatomical Therapeutic Chemical (ATC) Classification System. Static patient information includes their gender, age, race, smoking status, alcohol status and BMI.
Centers for Medicare and Medicaid (CMS):2
The second data set is CMS 2008–2010 Data Entrepreneurs’ Synthetic Public Use File (DE-SynPUF). The goal of CMS data set is to provide a set of realistic data by protecting the privacy of Medicare beneficiaries by using 5% of real data to synthetically construct the whole dataset. We extract the ICD-9 diagnosis codes and convert them to CCS diagnostic categories as in the case of Sutter dataset.
4.2. Evaluation metrics:
RMSE:
Accuracy is evaluated as the Root Mean Square Error (RMSE) which is a standard measure used in coupled matrix-tensor factorization literature [25, 26]. Given an input collection of matrices and a static input matrix , we define
| (15) |
Xk (i, j) denotes the (i, j) element of input matrix Xk and its approximation through a model’s factors (the (i, j) element of the product UkSkVT in the case of TASTE). Similarly, A(i, j) is the (i, j) element of input matrix A and is its approximation (in TASTE, this is the (i, j) element of WFT).
Cross-Product Invariance (CPI):
We use CPI to assess the solution’s uniqueness, since this is the core constraint promoting it [13]. In particular we check whether is close to constant . The cross-product invariance measure is defined as:
The range of CPI is between [−∞, 1], with values close to 1 indicating unique solutions(i.e., is close to constant).
Area Under the ROC Curve (AUC):
We examine the classification model’s performance when the data is imbalanced by comparing the actual and estimated labels. We use AUC on the test set to evaluate predictive model performance.
4.3. Implementation details
TASTE is implemented in MATLAB. To facilitate reproducibility, we provide the source code repository on Github. All the approaches (including the baselines) are evaluated on MatlabR2017b. We utilize the capabilities of Parallel Computing Toolbox of Matlab by activating parallel pool for all methods. For both datasets, we used 12 workers. For the prediction task, we use the implementation of regularized logistic regression from Scikit-learn machine learning library in Python 3.6.
4.4. Q1. TASTE is fast, accurate and preserves uniqueness-promoting constraints
4.4.1. Baseline Approaches:
In this experiment, we compare TASTE with methods that incorporate non-negativity constraint on all factor matrices. Note that SPARTan [10] and COPA [11] are not able to incorporate non-negativity constraint on factor matrices {Uk}.
Cohen+ [27]:
Cohen et al. proposed a PARAFAC2 framework which imposes non-negativity constraints on all factor matrices based on non-negative least squares algorithm [20]. We modified this method to handle the situation where a static matrix A is coupled with PARAFAC2 input based on Figure 1. To do so, we add to their objective function and solve both factor matrices W and F in an Alternating Least Squares manner, similar to how the rest of the factors are updated in [27].
COPA+:
One simple and fast way to enforce non-negativity constraint on factor matrix Uk is to compute Uk as: Uk:= max(0, QkH), where max() is taken element-wise to ensure non-negative results. Therefore, we modify the implementation in [11] to handle both the PARAFAC2 input and the static matrix A and then apply the simple heuristic to make {Uk} non-negative. We will show in the experimental results section that this heuristic method no longer guarantees unique solutions (i.e., it violates model constraints).
4.4.2. Setting hyper-parameters:
We perform a grid search for for TASTE and Cohen+ for different target ranks (R = {5, 10, 20, 40}). Each method is run with the specific parameter for 5 random initializations and the best values of λ and μ are selected based on the lowest average RMSE value. For COPA+, we search for the best value of λ ∈ {0.1, 1, 10} since it does not have a μ parameter.
4.4.3. Results:
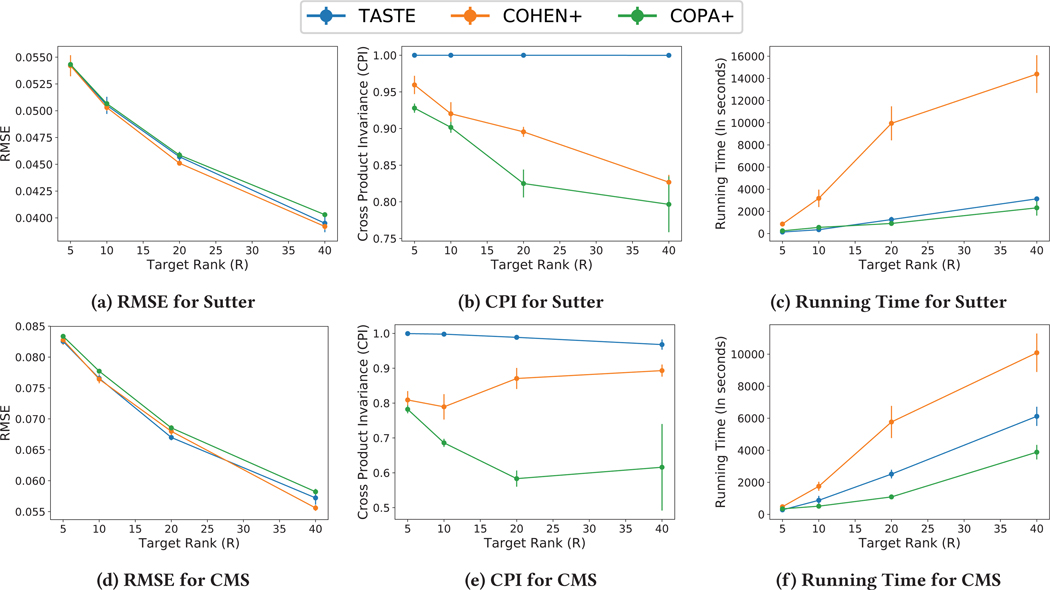
Apart from purely evaluating the RMSE and the computational time achieved, we assess to what extent the cross-product invariance constraint is satisfied [13]. Therefore, in Figure 2 we present the average and standard deviation of RMSE, CPI, and the computational time for both the Sutter and CMS data sets for four different target ranks (R ∈ {5, 10, 20, 40}). In Figures 2a, 2d, we compare the RMSE for all three methods. We observe that all methods achieve comparable RMSE values on the two different data sets. On the other hand, Figures 2b, 2e show the cross-product invariance (CPI) for Sutter and CMS respectively. COPA+ achieves poor values of CPI for both data sets. This indicates that the output factors violate model constraints and do not satisfy the uniqueness property [13]. Also TASTE significantly outperforms Cohen on CPI in Figures 2b and 2e. Finally, Figures 2c, 2f show the running time comparison for all three methods where TASTE is up to 4.5× and 2× faster than Cohen on Sutter and CMS data sets. Therefore, our approach is the only one that achieves a fast and accurate solution (in terms of RMSE) and preserves model uniqueness (in terms of CPI).
Figure 2:
The average and standard deviation of RMSE (lower is better), CPI (higher is better), and total running time (in seconds) (lower is better) for different approaches and for different target ranks (R = {5, 10, 20, 40}) related to 5 different random initialization for Sutter and CMS data sets.
4.5. Q2. TASTE is scalable
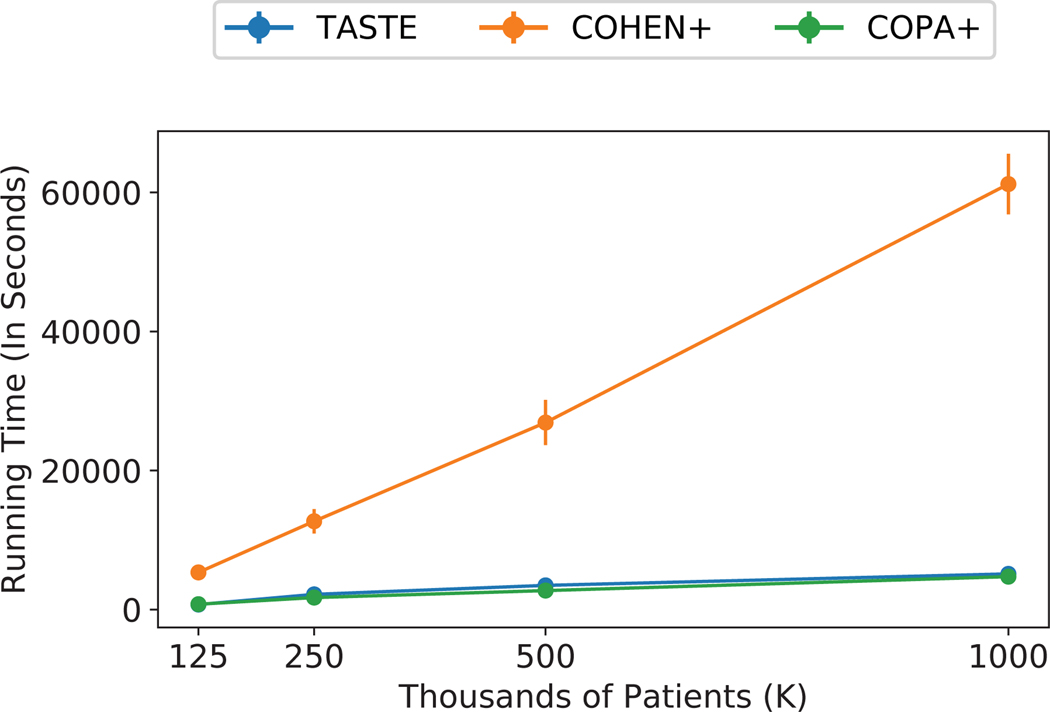
Apart from assessing the time needed for increasing values of target rank (i.e., number of phenotypes), we evaluate the same three approaches from section 4.4 in terms of computation time for an increasing amount of input patients. Each method is run 5 times and the convergence threshold is set to 1e − 4 for all of them. Figure 3 compares the average and standard deviation of total running time for 125K, 250K, 500K, and 1 Million patients for R = 40. TASTE is up to 14× faster than Cohen’s baseline for R = 40. While COPA+ is a fast approach, this baseline suffers from not satisfying model constraints which promote uniqueness as demonstrated in the previous experiment.
Figure 3:
The average and standard deviation of running time (in seconds) for R = 40 and for 5 random initialization by varying number of patients from 125K to 1 million for CMS data set. TASTE is upto 14× faster than Cohen.
4.6. Q3. Recovery of true factor matrices
In this section, we assess to what extent the original factor matrices can be recovered through synthetic data experiments 3. We demonstrate that: a) TASTE recovers the true latent factors more accurately than baselines for noisy data; and b) the baseline (COPA+) which does not preserve a high CPI measure fails to match TASTE in terms of latent factor recovery, despite achieving similar RMSE.
4.6.1. Evaluation Metric: Similarity between two factor matrices:
We define the cosine similarity between two vectors . Then the similarity between two factor matrices can be computed as (similar to [13]):
The range of Sim is between [0,1] and values near 1 indicate higher similarity.
4.6.2. Synthetic Data Construction:
We construct the ground-truth factor matrices by drawing a number uniformly at random between (0,1) to each element of each matrix. For each factor matrix , we create a binary non-negative matrix such that and then compute . After constructing all factor matrices, we compute the input based on . We set K = 100, J = 30, P = 20, Ik = 100, and R = 4. We then add Gaussian normal noise to varying percentages of randomly-drawn elements ({5%, 10%, 15%, 20%, 25%, 30%, 35%, 40%}) of Xk, ∀k = 1, …, K and A input matrices.
4.6.3. Results:
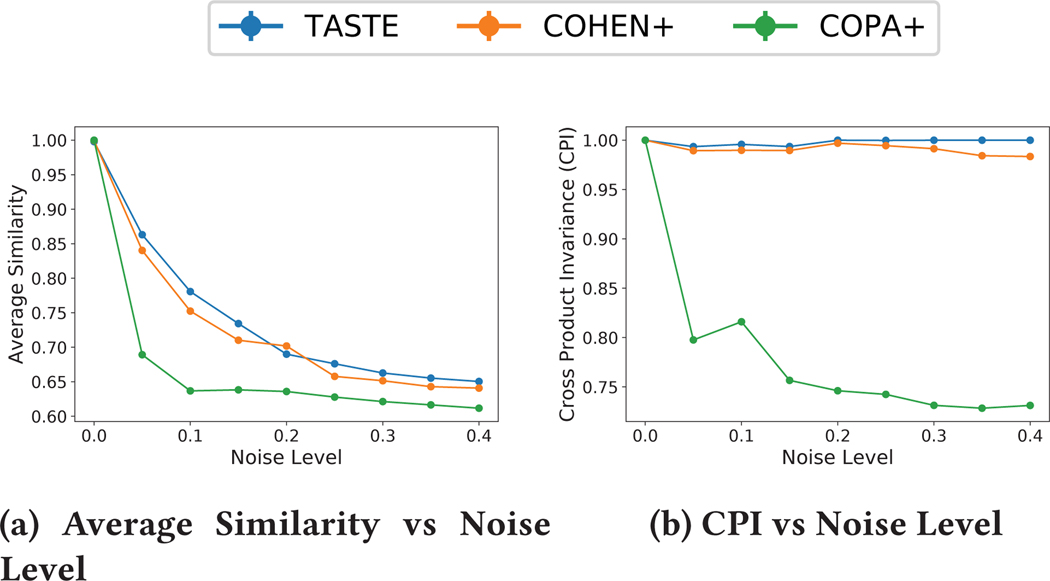
All three methods achieve the same value for RMSE, therefore, we omit the RMSE versus different noise levels plot. We assess the similarity measure between each ground truth latent factor and its corresponding estimated one (e.g., Sim ), and consider the average (·, ·) measure across all output factors as shown in Figure 4a. We also measure CPI and provide the results in 4b for different levels of noise. We observe that despite achieving comparable RMSE, COPA+ scores the lowest on the similarity between the true and the estimated factors. On the other hand, our model achieves the highest amount of recovery, in accordance to the fact that it achieves the highest CPI among all approaches. Overall, we demonstrate how promoting uniqueness (by enforcing the CPI measure to be preserved [13]) leads to more accurate parameter recovery, as suggested by prior work [13, 28].
Figure 4:
Figure 4a provides total average similarity between the estimated and the true factor matrices for different noise levels ({5%, 10%, 15%, 20%, 25%, 30%, 35%, 40%}) on synthetic data. Figure 4b provides the CPI of three methods for different levels of noise for a synthetic data with K = 100, J = 30, P = 20, Ik = 100, R = 4. All points in the figures is computed as an average of 5 random initialization. All three algorithms achieve similar values for RMSE.
4.7. Q4. Static features in TASTE improve predictive power
We measure the importance of static features in TASTE indirectly using classification performance. The task is to predict whether a patient will be diagnosed with heart failure (HF) or not. We assess whether static features handled by TASTE boost predictive performance by using personalized phenotype scores for all patients (W) as features.
4.7.1. Cohort Construction:
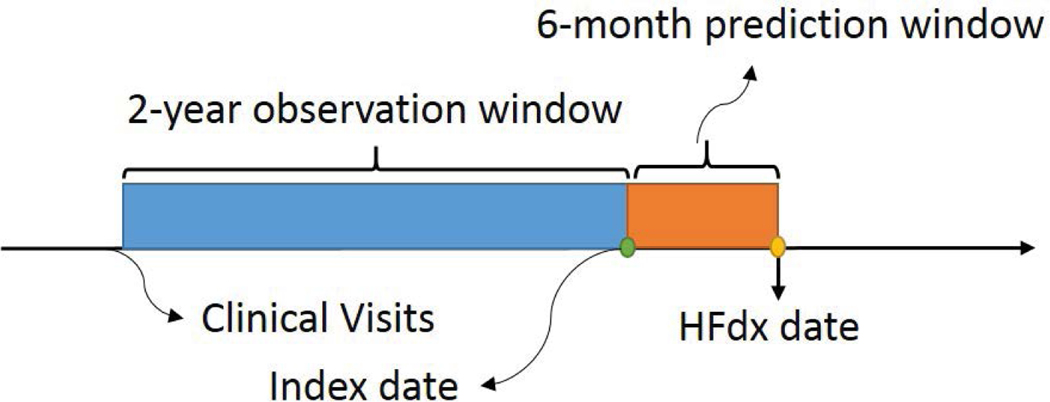
After applying the preprocessing steps (i.e. removing sparse features and eliminating patients with less than 5 clinical visits), we create a data set from Sutter with 35,113 patients where 3,244 of them are cases and 31,869 are controls (prevalence of 9.2 %). For case patients, we know the date that they are diagnosed with heart failure (HF dx). Control patients also have the same index dates as their corresponding cases. We extract 145 medications, 178 diagnosis codes, and 22 static features from a 2-year observation window and set the prediction window length to 6 months. Figure 5 depicts the observation and prediction windows in more detail.
Figure 5:
The arrow represents the encounter visits of a patient. We extract diagnosis and medications from a 2-year observation window by setting prediction window length to 6 months.
4.7.2. Baselines:
We assess the performance of TASTE with 6 different baselines.
RNN-regularized CNTF:
CNTF [5] feeds the temporal phenotype evolution matrices ({Uk}) into an LSTM model for HF prediction. This baseline only uses temporal medical features.
RNN Baseline:
We use the GRU model for HF prediction implemented in [29]. The one-hot vector format is used to represent all dynamic and static features for different clinical visits.
Logistic regression with raw dynamic:
We create a binary matrix where the rows are the number of patients and columns are the total number of medical features (323). Row k of this matrix is created by aggregating over all clinical visits of matrix Xk.
Logistic regression with raw static+dynamic:
Same as the previous approach, we create a binary matrix where the rows are number of patients and columns are the total number of temporal and static features (345) by appending matrix A to raw dynamic baseline matrix.
COPA Personalized Score Matrix:
We use the implementation of pure PARAFAC2 from [11] which learns the low-rank representation of phenotypes (Vcopa) from the training set and then projects all the new patients onto the learned phenotypic low-rank space.
COPA (+static) Personalized Score Matrix:
This is same as the previous baseline, however, we incorporate the static features into PARAFAC2 matrix by repeating the value of static features of a particular patient for all encounter visits.
4.7.3. TrainingDetails:
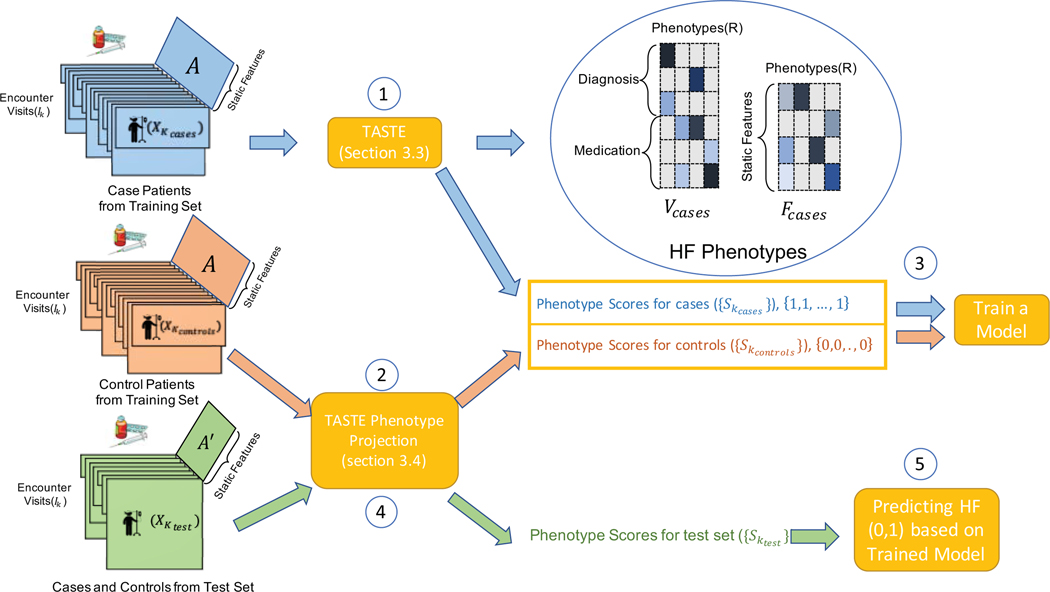
To calculate the AUC score for our model, we extended 5-fold cross-validation processes (described below) to access how to use phenotyping models to perform HF prediction, by calculating AUC score in the cross validation. At each fold, we take 80% percent of patients as the training set and the remaining 20% as the test set. Figure 6 depicts our heart failure prediction framework which contains 5 steps including:
Figure 6:
HF prediction Framework contains five steps.
First, we apply TASTE on case patients in the training set and extract the HF phenotypes (Vcases, Fcases) and calculate phenotype score values for them .
Second, we assign the existing HF phenotypes (Vcases, Fcases) to the control patient information from training set (based on section 3.4) and extract personalized phenotype scores for control patients .
We train a regularized logistic regression classifier on personalized phenotype scores for all patients in the training set .
We assign the existing HF phenotypes (Vcases, Fcases) to the patient information from test set (including cases and controls) and extract their personalized phenotype scores .
Finally, we predict HF (AUC score) for patients in the test set based on the classifier model trained in step 3. we pick the best parameters (C, λ, μ) based on the highest average AUC score on the test set.
All the other tensor baselines have the same training strategy as TASTE. For all the baselines under comparison, we apply 5-fold cross-validation processes and train a Lasso Logistic Regression 4. Lasso Logistic Regression has regularization parameter (C = [1e − 2, 1e − 1, 1, 10, 100, 1000, 10000]). For all 6 baselines, we just need to tune parameter C. However, for TASTE we need to perform a 3-D grid search over λ ∈ {0.01, 0.1, 1} and μ1 = μ2 = … = μk = μ = ∈ {0.01, 0.1, 1} and C.
Results:
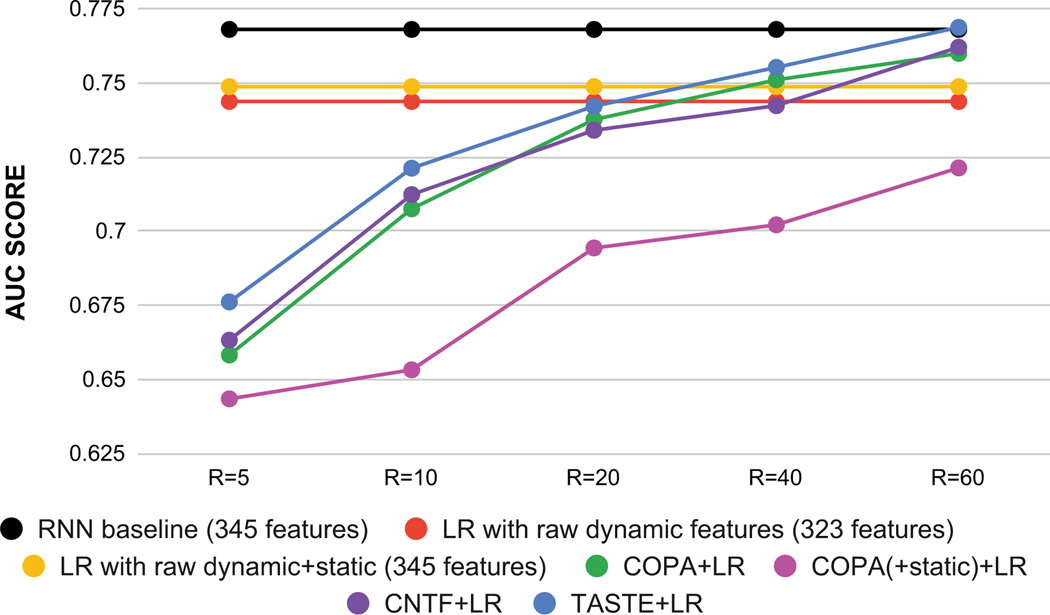
Figure 7 shows the average of AUC for all baselines and TASTE. For COPA, COPA(+static), CNTF and TASTE we report the AUC score for different values of R ({5, 10, 20, 40, 60}). TASTE improves the AUC score over a simple non-negative PARAFAC2 model (COPA and COPA(+static)) and CNTF which suggests: 1) incorporating static features with dynamic ones will increase the predictive power (comparison of TASTE with COPA and CNTF); and 2) incorporating static features using a coupled matrix improves predictive power (comparison of TASTE and COPA(+static)). We also observe that TASTE with R=60 (AUC=0.7687) performs slightly better than the RNN baseline model. Moreover, TASTE offers interpretability as the phenotype definitions can be readily extracted. RNNs require additional mechanisms to explain the model [30].
Figure 7:
The average of AUC score for varying number of phenotypes (R) for TASTE and 3 other tensor baselines on the test set. The AUC score for a baseline with raw dynamic features (323) is 0.7437, for the raw dynamic+static baseline (345) is 0.7487 and for RNN baseline is 0.7680.
4.8. Q5. Heart Failure Phenotype Discovery
Heart failure (HF) is a complex, heterogeneous disease and is the leading cause of hospitalization in people older than 65 5. However, there are no well-defined phenotypes other than the simple categorization of ejection fraction of the heart (i.e., preserved or reduced ejection fraction). With the comprehensive collection of available longitudinal EHR data, now we have the opportunity to computationally tackle the challenge of phenotyping HF patients.
4.8.1. Cohort Construction:
We select the patients diagnosed with HF from the EHRs in Sutter dataset. We extract 145 medications and 178 diagnosis codes from a 2-year observation window which ends 6 months before the heart failure diagnosis date (HFdx). 6 The total number of patients (K) is 3,244 (the HF case patients of Sutter dataset) same as section 4.7.
4.8.2. Pure PARAFAC2 cannot handle static feature integration.
In this experiment, we further analyze the results of the naive way of incorporating static feature information into a simpler PARAFAC2-based framework [11]. We posit that this results in less interpretable phenotypes. We incorporate the static features into PARAFAC2 input by repeating the value of static features on all clinical visits of the patients in the same fashion as COPA(+static). For instance, if the male feature of patient k has value 1, we repeat the value 1 for all the clinical visits of that patient. Then we compare the phenotype definitions discovered by TASTE (matrices V, F) and by COPA (matrix V). Table 3 contains two sample phenotypes discovered by this baseline, using the same truncation threshold that we use throughout this work (we only consider features with values greater than 0.1). We observe that the static features introduce a significant amount of bias into the resulting phenotypes: the phenotype definitions are essentially dominated by static features, while the values of weights corresponding to dynamic features are close to 0. This suggests that pure PARAFAC2-based models such as the work in [11] are unable to produce meaningful phenotypes that handle both static and dynamic features. Such a conclusion extends to other PARAFAC2-based work which does not explicitly model side information [10, 13, 27].
Table 3:
Two sample phenotypes discovered by COPA(+static) baseline by naively integrating static features into a simpler PARAFAC2-based model [11].
| Phenotype 1 | weight |
|---|---|
| Static_Alcohol_yes | 0.3860 |
| Static_White | 0.2160 |
| Static_Non_Hispanic | 0.2064 |
| Static_Smk_Quit | 0.1743 |
| Static_male | 0.1508 |
| Static_moderately_obese | 0.1025 |
| Phenotype 2 | weight |
| Static_age_between_70_79 | 1 |
| Static_Non_Hispanic | 0.8233 |
| Static_White | 0.7502 |
| Static_Alcohol_No | 0.6905 |
| Static_moderately_obese | 0.2098 |
| Static_male | 0.2026 |
| Static_Smk_No | 0.1614 |
4.8.3. TASTE Findings of HF Phenotypes.
Based on Figure 7, we present the top 5 phenotypes extracted from TASTE using R = 40 due to space limitations7. This rank is selected as outperforms all but the RNN baseline and is comparable to R = 60 in terms of performance. The 5 phenotypes are all confirmed and annotated by an expert cardiologist. Table 4 provides the details of these phenotypes. The clinical description of the 5 phenotypes as provided by the cardiologist are:
Table 4:
TASTE extracted 5 phenotypes from the HF dataset. Red indicates the static features; Dx_ indicates diagnoses; Rx_ indicates medication; The phenotype names are provided by the cardiologist.
| P1. Hypertensive Heart Failure: | Weight |
|---|---|
| dx_Essential hypertension [98.] | 0.804074 |
| Rx_Calcium Channel Blockers | 0.752547 |
| Rx_ACE Inhibitors | 0.648243 |
| Rx_Beta Blockers Cardio-Selective | 0.439681 |
| Rx_Angiotensin IIReceptorAntagonists | 0.230808 |
| Rx_Thiazides andThiazide-Like Diuretics | 0.221251 |
| Static_Non_Hispanic | 0.411001 |
| Static_female | 0.264393 |
| Static_white | 0.263096 |
| Static_Smk_NO | 0.25793 |
| Static_Alchohol_No | 0.239262 |
| P2. Atrial Fibrillation (AF): | Weight |
| dx_Cardiac dysrhythmias [106.] | 0.621756 |
| Rx_Coumarin Anticoagulants | 0.482428 |
| dx_Heart valve disorders [96.] | 0.428493 |
| Static_white | 0.216603 |
| Static_age_greater_80 | 0.20026 |
| Static_Non_Hispanic | 0.191727 |
| Static_male | 0.163882 |
| Static_Alchohol_yes | 0.157758 |
| Static_Smk_Quit | 0.132414 |
| P3. Obesity-induced Heart Failure: | Weight |
| dx_Other back problems | 0.439425 |
| Rx_Opioid Agonists | 0.36535 |
| dx_Intervertebral disc disorders | 0.33781 |
| Rx_Central Muscle Relaxants | 0.326111 |
| dx_Other nervous system symptoms and disorders | 0.22293 |
| Static_white | 0.133696 |
| Static_Static_Severely_obese | 0.110279 |
| Static_age_between_70_79 | 0.107631 |
| P4. Cardiometablic Driving Heart Failure: | Weight |
| dx_Diabetes mellitus without complication [49.] | 0.58191 |
| Rx_Biguanides | 0.075524 |
| Rx_Diagnostic Tests | 0.044592 |
| Rx_Sulfonylureas | 0.041006 |
| Rx_Insulin | 0.031447 |
| Rx_HMG CoA Reductase Inhibitors | 0.027469 |
| dx_Esophageal disorders [138.] | 0.022313 |
| Static_Severely_obese | 0.223931 |
| Static_Alchohol_No | 0.205342 |
| Static_Smk_NO | 0.149338 |
| Static_male | 0.128847 |
| Static_Non_Hispanic | 0.124907 |
| Static_age_between_60_69 | 0.119808 |
| P5. Severe Coronoary Heart Disease: | Weight |
| dx_Coronary atherosclerosis and other heart disease | 0.495272 |
| Rx_Platelet Aggregation Inhibitors | 0.434221 |
| Rx_Nitrates | 0.333018 |
| dx_Heart valve disorders [96.] | 0.230577 |
| Rx_Alpha-Beta Blockers | 0.225503 |
| dx_Peripheral andvisceral atherosclerosis [114.] | 0.124041 |
| Rx_Beta Blockers Cardio-Selective | 0.121939 |
| Static_male | 0.324708 |
| Static_Smk_Quit | 0.190111 |
| Static_white | 0.117237 |
| Static_Overweight | 0.116107 |
| Static_Non_Hispanic | 0.10634 |
[P1.] Hypertensive Heart Failure:
This is a classic and dominant heart failure phenotype, representing a subgroup of patients with long history of hypertension, and cardiac performance declines over time. Anti-hypertensive medications are spelled out as to indicate the treatment to hypertension.
[P2.] Atrial Fibrillation (AF):
This phenotype represents patients with irregular heartbeat and AF predisposes to HF. Medications are related to managing AF and preventing strokes. This phenotype is usually more prevalent in male and old patients (i.e. 80 years or older).
[P3.] Obesity-induced Heart Failure:
This phenotype captures patients with severe obesity (BMI>35) and obesity-induced orthopedic conditions.
[P4.] Cardiometablic Driving Heart Failure:
This phenotype is featured by diabetes and cardiometabolic conditions (i.e. hyperlipidemia, hypertension). Diabetes is a well known risk factor for cardiovascular complications (i.e. stroke, myocardial infaction, etc.), and increases the risk for heart failure.
[P5.] Severe Coronoary Heart Disease:
This phenotype is associated with a greater deterioration of left ventricle function and a worse prognosis. This phenotype is also more prevalent in the male and white population.
5. CONCLUSIONS
TASTE jointly models temporal and static information from electronic health records to extract clinically meaningful phenotypes. We demonstrate the computational efficiency of our model on extensive experiments that showcase its ability to preserve important properties underpinning the model’s uniqueness, while maintaining interpretability. TASTE not only identifies clinically meaningful heart failure phenotypes validated by a cardiologist but the phenotypes also retain predictive power for predicting heart failure.
To promote reproducibility, we make our implementation public at: https://github.com/aafshar/TASTE.
6. ACKNOWLEDGEMENTS
This work was in part supported by the National Science Foundation awards IIS-1418511, CCF-1533768, IIS-1838042, IIS-1838200 and the National Institute of Health awards 1R01MD011682-01, R56HL138415, 2R56HL116832-04, and 1K01LM012924-01.
Footnotes
Although BMI and smoking status can change over time, in our data set these values for each patient are constant over time.
The reason that we are working with synthetic data here is that we do not know the original factor matrices in real data sets.
Both CNTF [5] and RNN baseline [29] applied logistic regression model to the final state of the hidden layer to perform the binary classification.
Figure 5 presents the observation window in more detail.
The top 5 phenotypes are selected based on highest phenotype’s prevalence. Prevalence of a phenotype is the number of patients belong to that phenotype and is calculated based on applying hard clustering of patients on the maximum coordinate of the vector along the diagonal of Sk factor matrix.
ACM Reference Format:
Ardavan Afshar, Ioakeim Perros, Haesun Park, Christopher deFilippi, Xiaowei Yan, Walter Stewart, Joyce Ho, and Jimeng Sun. 2020. TASTE: Temporal and Static Tensor Factorization for Phenotyping Electronic Health Records. In ACM Conference on Health, Inference, and Learning (ACM CHIL ‘20), April 2–4, 2020, Toronto, ON, Canada. ACM, New York, NY, USA, 11 pages.
Contributor Information
Ardavan Afshar, Georgia Institute of Technology.
Ioakeim Perros, HEALTH[at]SCALE.
Haesun Park, Georgia Institute of Technology.
Christopher deFilippi, INOVA Heart and Vascular Institute.
Xiaowei Yan, Sutter Health.
Walter Stewart, Medcurio.
Joyce Ho, Emory University.
Jimeng Sun, Georgia Institute of Technology.
REFERENCES
- [1].Richesson Rachel L, Sun Jimeng, Pathak Jyotishman, Kho Abel N, and Denny Joshua C. Clinical phenotyping in selected national networks: demonstrating the need for high-throughput, portable, and computational methods. Artificial intelligence in medicine, 71:57–61, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Fu Tianfan, Gao Tian, Xiao Cao, Ma Tengfei, and Sun Jimeng. Pearl: Prototype learning via rule learning. In Proceedings of the 10th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, pages 223–232, 2019. [Google Scholar]
- [3].Ho Joyce C, Ghosh Joydeep, and Sun Jimeng. Marble: high-throughput phenotyping from electronic health records via sparse nonnegative tensor factorization. In KDD, pages 115–124. ACM, 2014. [Google Scholar]
- [4].Perros Ioakeim, Papalexakis Evangelos E., Park Haesun, Vuduc Richard, Yan Xiaowei, Defilippi Christopher, Stewart Walter F., and Sun Jimeng. Sustain: Scalable unsupervised scoring for tensors and its application to phenotyping. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD ‘18, pages 2080–2089, New York, NY, USA, 2018. ACM. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yin K, Qian D, Cheung WK, Fung BCM, and Poon J Learning phenotypes and dynamic patient representations via rnn regularized collective non-negative tensor factorization. In AAAI, Honolulu, HI, January 2019. [Google Scholar]
- [6].Carroll J Douglas and Chang Jih-Jie. Analysis of individual differences in multidimensional scaling via an n-way generalization of “eckart-young” decomposition. Psychometrika, 35(3):283–319, 1970. [Google Scholar]
- [7].Hitchcock Frank L. The expression of a tensor or a polyadic as a sum of products. Journal of Mathematics and Physics, 6(1–4):164–189, 1927. [Google Scholar]
- [8].Harshman Richard A. Foundations of the parafac procedure: Models and conditions for an” explanatory” multimodal factor analysis. 1970. [Google Scholar]
- [9].Afshar Ardavan, Ho Joyce C, Dilkina Bistra, Perros Ioakeim, Elias B Khalil Li Xiong, and Sunderam Vaidy. Cp-ortho: An orthogonal tensor factorization framework for spatio-temporal data. In Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, pages 1–4, 2017. [Google Scholar]
- [10].Perros Ioakeim, Papalexakis Evangelos E, Wang Fei, Vuduc Richard, Searles Elizabeth, Thompson Michael, and Sun Jimeng. SPARTan: Scalable PARAFAC2 for large & sparse data. In KDD, KDD ‘17, pages 375–384. ACM, 2017. [Google Scholar]
- [11].Afshar Ardavan, Perros Ioakeim, Papalexakis Evangelos E., Searles Elizabeth, Ho Joyce, and Sun Jimeng. COPA: Constrained parafac2 for sparse & large datasets. CIKM ‘18, pages 793–802, New York, NY, USA, 2018. ACM. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Harshman RA PARAFAC2: Mathematical and technical notes. UCLA Working Papers in Phonetics, 22:30–44, 1972. [Google Scholar]
- [13].Kiers Henk AL, Berge Jos MF Ten, and Bro Rasmus. Parafac2-part i. a direct fitting algorithm for the parafac2 model. Journal of Chemometrics, 13(3–4):275–294, 1999. [Google Scholar]
- [14].Kim Jingu and Park Haesun. Fast nonnegative matrix factorization: An active-setlike method and comparisons. SIAM Journal on Scientific Computing, 33(6):3261–3281, 2011. [Google Scholar]
- [15].Ho Joyce C, Ghosh Joydeep, Steinhubl Steve R, Stewart Walter F, Denny Joshua C, Malin Bradley A, and Sun Jimeng. Limestone: High-throughput candidate phenotype generation via tensor factorization. Journal of biomedical informatics, 52:199–211, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Henderson Jette, Ho Joyce C, Kho Abel N, Denny Joshua C, Malin Bradley A, Sun Jimeng, and Ghosh Joydeep. Granite: Diversified, sparse tensor factorization for electronic health record-based phenotyping. In (ICHI), 2017, pages 214–223. IEEE, 2017. [Google Scholar]
- [17].Zhao Juan, Zhang Yun, Schlueter David J, Wu Patrick, Kerchberger Vern Eric, Rosenbloom S Trent, Wells Quinn S, Feng QiPing, Denny Joshua C, and Wei Wei-Qi. Detecting time-evolving phenotypic topics via tensor factorization on electronic health records: Cardiovascular disease case study. Journal of biomedical informatics, 98:103270, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zhao Juan, Feng QiPing, Wu Patrick, Warner Jeremy L, Denny Joshua C, and Wei Wei-Qi. Using topic modeling via non-negative matrix factorization to identify relationships between genetic variants and disease phenotypes: A case study of lipoprotein (a)(lpa). PloS one, 14(2):e0212112, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Jiang Xiaoqian, Lhatoo Samden, Zhang Guo-Qiang, Chen Luyao, and Kim Yejin. Combining representation learning with tensor factorization for risk factor analysis-an application to epilepsy and alzheimer’s disease. arXiv preprint arXiv:1905.05830, 2019. [Google Scholar]
- [20].Kim Jingu, He Yunlong, and Park Haesun. Algorithms for nonnegative matrix and tensor factorizations: A unified view based on block coordinate descent framework. Journal of Global Optimization, 58(2):285–319, 2014. [Google Scholar]
- [21].Schönemann Peter H. A generalized solution of the orthogonal procrustes problem. Psychometrika, 31(1):1–10, 1966. [Google Scholar]
- [22].Petersen Kaare Brandt, Pedersen Michael Syskind, et al. The matrix cookbook. Technical University of Denmark, 7(15):510, 2008. [Google Scholar]
- [23].Van Loan Charles F. The ubiquitous kronecker product. Journal of computational and applied mathematics, 123(1–2):85–100, 2000. [Google Scholar]
- [24].Slee Vergil N. The international classification of diseases: ninth revision (icd-9). Annals of internal medicine, 88(3):424–426, 1978. [DOI] [PubMed] [Google Scholar]
- [25].Choi Dongjin, Jang Jun-Gi, and Kang U . Fast, accurate, and scalable method for sparse coupled matrix-tensor factorization. arXiv preprint arXiv:1708.08640, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Beutel Alex, Talukdar Partha Pratim, Kumar Abhimanu, Faloutsos Christos, Papalexakis Evangelos E, and Xing Eric P. Flexifact: Scalable flexible factorization of coupled tensors on hadoop. In Proceedings of the 2014 SIAM International Conference on Data Mining, pages 109–117. SIAM, 2014. [Google Scholar]
- [27].Cohen Jeremy E and Bro Rasmus. Nonnegative parafac2: a flexible coupling approach. In International Conference on Latent Variable Analysis and Signal Separation, pages 89–98. Springer, 2018. [Google Scholar]
- [28].Williams Alex H, Kim Tony Hyun, Wang Forea, Vyas Saurabh, Ryu Stephen I, Shenoy Krishna V, Schnitzer Mark, Kolda Tamara G, and Ganguli Surya. Unsupervised discovery of demixed, low-dimensional neural dynamics across multiple timescales through tensor component analysis. Neuron, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Choi Edward, Schuetz Andy, Stewart Walter F, and Sun Jimeng. Using recurrent neural network models for early detection of heart failure onset. Journal of the American Medical Informatics Association, 24(2):361–370, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Fu Tianfan, Hoang Trong Nghia, Xiao Cao, and Sun Jimeng. Ddl: Deep dictionary learning for predictive phenotyping. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]