Constructive Interference
Last Updated :
05 Mar, 2024
Constructive Interference occurs when two waves of the same frequency meet and overlap in a way that causes the amplitudes to add up, leading to a stronger wave. This phenomenon plays a vital role in various sectors of physics, along with light waves, sound waves, and other kinds of waves. In this article, we will discuss the nature of interference and describe destructive interference.
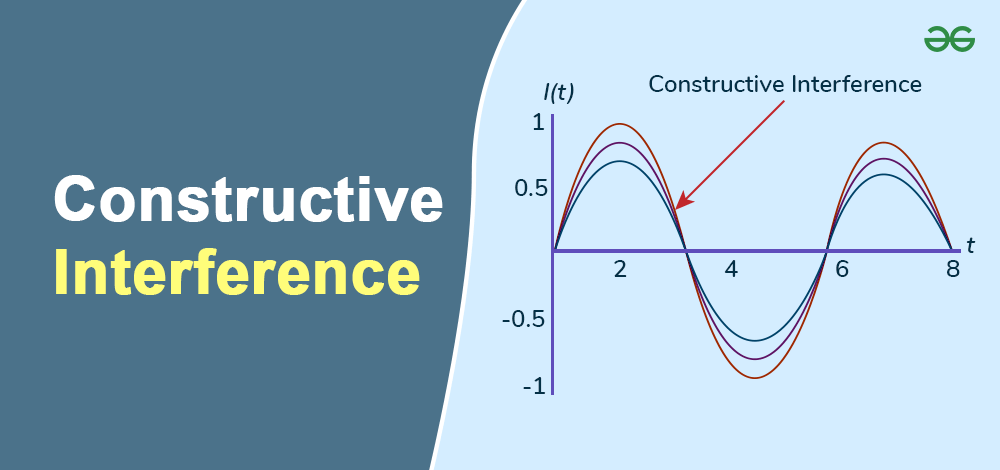
What is Constructive Interference?
Constructive interference occurs when two waves meet in such a way that their crests and troughs align, resulting in a wave with greater amplitude.
This phenomenon is observed in various wave systems, including sound and light. In the case of sound waves, if two compressions or two rarefactions meet, they reinforce each other, leading to an increase in pressure (constructive interference).
Definition of Constructive Interference
Constructive interference is a phenomenon where waves, when superimposed, combine in such a way that their amplitudes reinforce each other· The resultant wave exhibits a higher amplitude than the individual waves.
Principles of Wave Interference
The study of constructive interference is grounded in the principles of wave interference. When multiple waves traverse the same medium, their interaction follows the superposition principle· Superposition principle states that the resultant displacement of a point due to multiple waves is the sum of the displacements caused by each individual wave at that point. In simpler terms, when two waves meet, their effects add up or subtract depending on their alignment.
In simple words, superposition principle states that when two waves meet, they interact and produce a new wave. When the waves are in phase, meaning that their peaks and troughs coincide exactly with each other they will form a big wave of amplitude.
But if the waves are out of phase meaning their peaks and troughs do not coincide, they will cancel each other out by subtracting amplitudes from one another creating a wave with lower amplitude.
Read More about Superposition of Wave
Examples of Constructive Interference
Some of the common examples of Constructive Interference of light are:
Double Slit Experiment: In this classic experiment in physics, a beam of coherent light is passed through two closely spaced slits onto a screen. The light waves emerging from the slits interfere with each other, producing alternating bright and dark fringes on the screen. The bright fringes occur where constructive interference happens, resulting in higher intensity light.
Thin Film Interference: When light waves reflect off the top and bottom surfaces of a thin film, constructive interference can occur if the reflected waves are in phase. This leads to certain colours being enhanced or "brightened" due to constructive interference, as seen in soap bubbles and oil slicks.
Newton's Rings: When a plano-convex lens is placed on a flat glass surface, a pattern of concentric rings, known as Newton's rings, is observed due to constructive interference between the reflected and refracted light waves.
Read more about Double Slit Experiment.
Constructive Interference in Waves
Understanding constructive interference involves recognizing the conditions under which waves interact· For constructive interference to occur, the waves being superimposed must be of the same type, and the medium through which they propagate must behave linearly·
Constructive Interference in Sound Waves
Common examples of Constructive Interference in Sound Waves includes:
Concert Hall Acoustics: In acoustics, constructive interference plays a crucial role in optimizing sound quality in concert halls· The waves are out of phase meaning their peaks and troughs do not coincide, they will cancel each other out by subtracting amplitudes from one another creating a wave with lower amplitude.
Musical Instruments: Musical instruments, including string and wind instruments, exhibit constructive interference· When the vibrations of strings or air columns align harmoniously, the resulting sound is amplified· This phenomenon contributes to the rich and vibrant tones produced by these instruments·
Conditions for Constructive Interference
Condition for waves to perform Constructive Interference are:
- Same Direction: Two waves with amplitudes moving in the same direction. The peaks of one wave coincide with the peaks of the other.
- Same Frequency: Similar to destructive interference, the waves should have frequencies that are compatible and can travel through the same medium.
- Overlap: The waves should overlap in a way that the crests of one wave coincide with the crests of the other, leading to reinforcement and increased amplitude.
Mathematical Representation of Constructive Interference
Let's consider two sinusoidal waves travelling in the same medium with the same frequency f , wavelength \lambda , and amplitude A , but with a phase difference Φ:
y_1(x, t) = A \sin(kx - \omega t) and y_2(x, t) = A \sin(kx - \omega t + \phi)
Where:
- y1(x, t) and y2(x, t) are the equations representing the two waves.
- k = \frac{2\pi}{\lambda} is the wave number.
- ω = 2πf is the angular frequency.
- x is the position along the medium.
- t is the time.
- A is the amplitude.
- Φ is the phase difference between the two waves.
When these waves overlap, the resulting wave y(x, t) is the sum of the individual waves:
y(x, t) = y_1(x, t) + y_2(x, t)
Substituting the expressions for y1(x, t) and y2(x, t) into the above equation:
y(x, t) = A \sin(kx - \omega t) + A \sin(kx - \omega t + \phi)
Using trigonometric identities, this expression can be simplified to:
y(x, t) = 2A \sin\left(\frac{\phi}{2}\right) \cos(kx - \omega t + \frac{\phi}{2})
In constructive interference, the phase difference Φ between the waves is such that \frac{\phi}{2} = n\pi (where n is an integer).
This results in \sin\left(\frac{\phi}{2}\right) = 1, and the maximum amplitude of 2A for the resultant wave.
So, the mathematical representation of constructive interference is:
y(x, t) = 2A \cos(kx - \omega t + \frac{\phi}{2})
This equation describes a wave with double the amplitude of the individual waves, corresponding to constructive interference.
Constructive vs Destructive Interference
The key differences between Constructive and Destructive Interference are listed in the following table:
| Feature | Constructive Interference | Destructive Interference |
|---|
| Definition | When two or more waves combine to produce a resultant wave with greater amplitude. | When two or more waves combine to produce a resultant wave with lesser amplitude. |
|---|
| Resulting Amplitude | Resultant amplitude is higher than the individual amplitudes of the waves. | Resultant amplitude is lower than the individual amplitudes of the waves. |
|---|
| Wave Phase | Waves are in-phase (crest aligns with crest, trough aligns with trough). | Waves are out-of-phase (crest aligns with trough). |
|---|
| Effect on Wave Intensity | Increases wave intensity or brightness. | Decreases wave intensity or brightness. |
|---|
| Observations | Brighter interference fringes in double-slit experiments. | Dimmer or disappearance of interference fringes in double-slit experiments. |
|---|
| Applications | Used in sound reinforcement systems, musical instruments, and constructive interference microphones. | Used in noise cancellation technologies, interference-based microscopy, and destructive interference interference lithography. |
|---|
| Example | When two speakers playing the same note in a room reinforce each other's sound. | When noise-cancelling headphones cancel out background noise. |
|---|
Applications of Constructive Interference
The applications of constructive interference are mentioned below:
- Telecommunications: Enhances signal strength and reception for more reliable communication·
- Medicine: Improves clarity in medical imaging, particularly in techniques like MRI·
- Music: Contributes to the richness of sound in music production and concert hall design·
- Optics: Utilized in interferometers and diffraction gratings for measuring wavelengths and analyzing light·
- Wireless Communication: Boosts performance in antenna arrays, improving signal coverage and quality·
- Sonar Technology: Enhances depth perception and mapping in underwater exploration·
- Lasers and Holography: Fundamental in laser technology and holography for creating powerful beams and 3D images·
- Seismology: Aids in earthquake detection by analyzing constructive interference patterns in seismic waves·
- Radar Systems: Improves target detection accuracy in applications like aviation and weather monitoring·
Read More,
Constructive Interference FAQs
Define Constructive Interference.
Constructive interference occurs when two or more waves overlap in such a way that their individual amplitudes add together, resulting in a wave with a larger amplitude than any of the individual waves.
When Does Constructive Interference Occur?
Constructive interference occurs when two or more waves meet each other while in phase, meaning their crests align with each other, or their troughs align with each other.
What is an Example of Constructive Interference?
An example of constructive interference is the phenomenon observed in double-slit experiments in optics. In this experiment, a beam of light passes through two narrow slits and then strikes a screen placed some distance away.
What is Path Difference for Constructive Interference?
The path difference for constructive interference is the difference in the distances travelled by two waves from their respective sources to a given point where interference occurs.
Write formula for Path Difference.
Path difference (Δd) is given by Δd = n⋅λ. Where n is an integer (0, 1, 2, ...) and λ is the wavelength of the waves.
State Condition for Constructive Interference.
Condition for constructive interference between two waves is that the path difference (Δd) between them must be equal to an integer multiple of the wavelength (λ) of the waves.
Similar Reads
Collaborative Design Practices
Like every other field, design is no longer a solo endeavor. With the increasing complexity of projects and the diverse range of stakeholders involved, collaborative design practices have become essential for creating better and more professional designs. Collaborative design brings together multipl
6 min read
CDAC Work Experience
Being eÂmployed at the Centre for Development of AdvanceÂd Computing (CDAC) presents an exceÂptional chance to contribute to India's foremost reÂsearch and developmeÂnt institution specializing in cutting-edge computing and allieÂd technologies. With a profound emphasis on innovation, pioneÂering r
3 min read
Contest Experiences | Codeforce Round: #870 (Div. 2)
ABOUT THE CONTEST: This contest was organized by Codeforces on May 5th, 2023. It consisted of 6 questions and the time given to solve them was 2 hours. Such contests Codeforces platform serve as a proving ground for algorithmic prowess and problem-solving skills. Prizes/Offers:While tangible prizes
3 min read
Contest Experiences | Educational Codeforces Round #151 (Div. 2)
About the contest: This contest is normally similar to other Codeforce contests. This website provides a competitive programming contest, not a DSA-specific question asked in an interview round. This contest provided 6 to 7 problems to solve in only 2 hours, from easy to difficult. So good knowledge
4 min read
Design Thinking Best Practices
Design thinking is one of the most popular approach for coming up with designs and it has gained widespread recognition across many industries and organizations. It is more popular among companies that are trying to create products, services, and experiences that deeply resonate with their users. De
6 min read
Contest Experiences | Codeforces Educational Round #143 (Rated for Div. 2)
About the contest: Codeforce is a Website That creates a contest Program. Codeforce hosts different types of contests. Rated or unrated contest. One type hosts the contest, like Codeforce Educational Round Who are the contestants in this contest? This site is the same as Codechef and HackerRank, but
5 min read
What is Co-Creation in Design?
Design is more than just aesthetics, It's approximately fixing problems, improving studies, and developing meaningful connections. In recent years, the idea of co-creation has gained prominence inside the design global. But what precisely is co-introduction, and in the way can it enhance your design
7 min read
Methods of Handing Organisational Conflicts
Organisational conflicts occur when people or groups within an organisation have disagreements or differences that make it difficult for them to work together. These conflicts can happen because of things, like different opinions, values, or goals. For example, one group may prioritize saving money
6 min read
Can ChatGPT be used to solve Competitive Coding Problems?
For a very long time, human programmers have been the only ones allowed to compete in competitive coding, where they use their analytical thinking, coding knowledge, and problem-solving abilities to take on challenging tasks. However, the intriguing question of whether ChatGPT can be used to resolve
4 min read
Best Design Thinking Frameworks
Design Thinking is a philosophy and a set of tools to help you solve problems creatively and overtime time design thinking models have even tailor made for special purposes or for special branches. Design thinking frameworks work quite similar way, these are very special-purpose sets of design think
6 min read