Introduction to Max-Heap – Data Structure and Algorithm Tutorials
Last Updated :
18 Oct, 2024
A Max-Heap is defined as a type of Heap Data Structure in which each internal node is greater than or equal to its children. A max-heap is always a complete binary tree and typically represented as an array. Note that unlike a normal binary tree, a complete binary tree can be represented as an array without wasting any memory.
The heap data structure is a type of binary tree that is commonly used in computer science for various purposes, including sorting, searching, and organizing data.

Introduction to Max-Heap Data Structure
Purpose and Use Cases of Max-Heap:
- Priority Queue: One of the primary uses of the heap data structure is for implementing priority queues.
- Heap Sort: The heap data structure is also used in sorting algorithms.
- Graph Algorithms: The heap data structure is used in various graph algorithms. For example, Dijkstra’s shortest path algorithm uses a heap data structure to keep track of the vertices with the shortest path from the source vertex.
Max-Heap Data structure in Different languages:
A max heap can be implemented using the priority_queue container from the Standard Template Library (STL). The priority_queue container is a type of container adapter that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.
Syntax: priority_queue<int>maxH;
In Java, a max heap can be implemented using the PriorityQueue class from java.util package. The PriorityQueue class is a priority queue that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.
Syntax: PriorityQueue maxHeap= new PriorityQueue<>(Comparator.reverseOrder());
In Python, a max heap can be implemented using the heapq module, which provides functions for implementing heaps. Specifically, the heapq module provides a way to create and manipulate heap data structures.
Syntax: heap = []
heapify(heap)
4. Max-Heap in C#
In C#, a max heap can be implemented using the PriorityQueue<T> class from the System.Collections.Generic namespace. The PriorityQueue<T> class is a priority queue that provides a way to store elements in a queue-like data structure in which each element has a priority associated with it.
Syntax: var maxHeap = new PriorityQueue<int>((a, b) => b - a);
A max heap is a binary tree where every node has a value greater than or equal to its children. In JavaScript, you can implement a max heap using an array, where the first element represents the root node, and the children of a node at index i are located at indices 2i+1 and 2i+2.
Syntax: const miaxHeap = new MaxHeap();
| | Min Heap | Max Heap |
|---|
| 1. | In a Min-Heap the key present at the root node must be less than or equal to among the keys present at all of its children. | In a Max-Heap the key present at the root node must be greater than or equal to among the keys present at all of its children. |
|---|
| 2. | In a Min-Heap the minimum key element present at the root. | In a Max-Heap the maximum key element present at the root. |
|---|
| 3. | A Min-Heap uses the ascending priority. | A Max-Heap uses the descending priority. |
|---|
| 4. | In the construction of a Min-Heap, the smallest element has priority. | In the construction of a Max-Heap, the largest element has priority. |
|---|
| 5. | In a Min-Heap, the smallest element is the first to be popped from the heap. | In a Max-Heap, the largest element is the first to be popped from the heap. |
|---|
Internal Implementation of Max-Heap Data Structure:
A Max heap is typically represented as an array.
- The root element will be at Arr[0].
- For any ith node Arr[i].
- left child is stored at index 2i+1
- Right child is stored at index 2i+2
- Parent is stored at index floor((i-1)/2)
The Internal Implementation of the Max-Heap require 3 major steps:
- Insertion: To insert a new element into the heap, it is added to the end of the array and then “bubbled up” until it satisfies the heap property.
- Deletion: To delete the maximum element (the root of the heap), the last element in the array is swapped with the root, and the new root is “bubbled down” until it satisfies the heap property.
- Heapify: A heapify operation can be used to create a max heap from an unsorted array.
Operations on Max-heap Data Structure and their Implementation:
Here are some common operations that can be performed on a Heap Data Structure data structure,
Elements can be inserted to the heap following a similar approach as discussed above for deletion. The idea is to:
- First increase the heap size by 1, so that it can store the new element.
- Insert the new element at the end of the Heap.
- This newly inserted element may distort the properties of Heap for its parents. So, in order to keep the properties of Heap, heapify this newly inserted element following a bottom-up approach.
Illustration:
Suppose the Heap is a Max-Heap as:
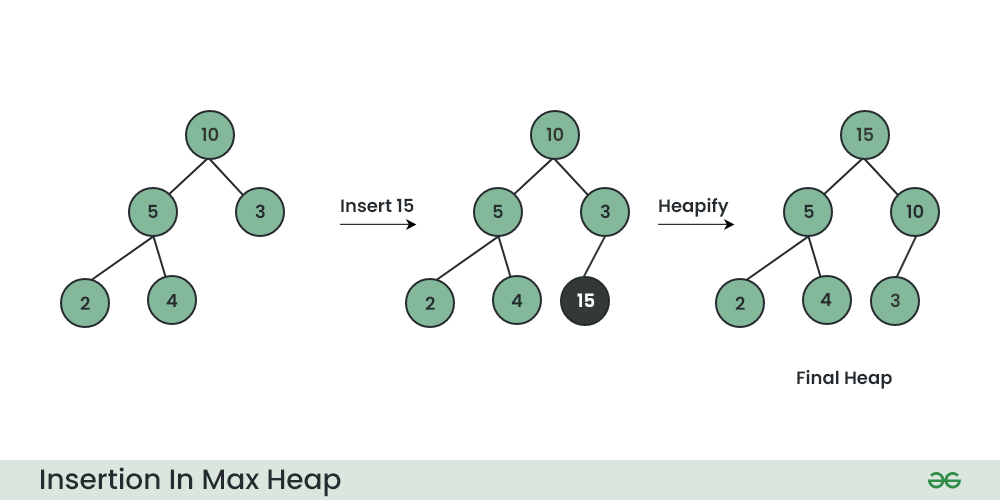
Insertion in Max heap
Implementation of insertion operation in Max-Heap:
C++
// C++ program to insert new element to Heap
#include <iostream>
using namespace std;
#define MAX 1000 // Max size of Heap
// Function to heapify ith node in a Heap
// of size n following a Bottom-up approach
void heapify(int arr[], int n, int i)
{
// Find parent
int parent = (i - 1) / 2;
if (arr[parent] > 0) {
// For Max-Heap
// If current node is greater than its parent
// Swap both of them and call heapify again
// for the parent
if (arr[i] > arr[parent]) {
swap(arr[i], arr[parent]);
// Recursively heapify the parent node
heapify(arr, n, parent);
}
}
}
// Function to insert a new node to the Heap
void insertNode(int arr[], int& n, int Key)
{
// Increase the size of Heap by 1
n = n + 1;
// Insert the element at end of Heap
arr[n - 1] = Key;
// Heapify the new node following a
// Bottom-up approach
heapify(arr, n, n - 1);
}
// A utility function to print array of size n
void printArray(int arr[], int n)
{
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "\n";
}
// Driver Code
int main()
{
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
int arr[MAX] = { 10, 5, 3, 2, 4 };
int n = 5;
int key = 15;
insertNode(arr, n, key);
printArray(arr, n);
// Final Heap will be:
// 15
// / \
// 5 10
// / \ /
// 2 4 3
return 0;
}
// Java program for implementing insertion in Heaps
public class insertionHeap {
// Function to heapify ith node in a Heap
// of size n following a Bottom-up approach
static void heapify(int[] arr, int n, int i)
{
// Find parent
int parent = (i - 1) / 2;
if (arr[parent] > 0) {
// For Max-Heap
// If current node is greater than its parent
// Swap both of them and call heapify again
// for the parent
if (arr[i] > arr[parent]) {
// swap arr[i] and arr[parent]
int temp = arr[i];
arr[i] = arr[parent];
arr[parent] = temp;
// Recursively heapify the parent node
heapify(arr, n, parent);
}
}
}
// Function to insert a new node to the heap.
static int insertNode(int[] arr, int n, int Key)
{
// Increase the size of Heap by 1
n = n + 1;
// Insert the element at end of Heap
arr[n - 1] = Key;
// Heapify the new node following a
// Bottom-up approach
heapify(arr, n, n - 1);
// return new size of Heap
return n;
}
/* A utility function to print array of size n */
static void printArray(int[] arr, int n)
{
for (int i = 0; i < n; ++i)
System.out.println(arr[i] + " ");
System.out.println();
}
// Driver Code
public static void main(String args[])
{
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
// maximum size of the array
int MAX = 1000;
int[] arr = new int[MAX];
// initializing some values
arr[0] = 10;
arr[1] = 5;
arr[2] = 3;
arr[3] = 2;
arr[4] = 4;
// Current size of the array
int n = 5;
// the element to be inserted
int Key = 15;
// The function inserts the new element to the heap and
// returns the new size of the array
n = insertNode(arr, n, Key);
printArray(arr, n);
// Final Heap will be:
// 15
// / \
// 5 10
// / \ /
// 2 4 3
}
}
// The code is contributed by Gautam goel
# program to insert new element to Heap
# Function to heapify ith node in a Heap
# of size n following a Bottom-up approach
def heapify(arr, n, i):
parent = int(((i-1)/2))
# For Max-Heap
# If current node is greater than its parent
# Swap both of them and call heapify again
# for the parent
if arr[parent] > 0:
if arr[i] > arr[parent]:
arr[i], arr[parent] = arr[parent], arr[i]
# Recursively heapify the parent node
heapify(arr, n, parent)
# Function to insert a new node to the Heap
def insertNode(arr, key):
global n
# Increase the size of Heap by 1
n += 1
# Insert the element at end of Heap
arr.append(key)
# Heapify the new node following a
# Bottom-up approach
heapify(arr, n, n-1)
# A utility function to print array of size n
def printArr(arr, n):
for i in range(n):
print(arr[i], end=" ")
# Driver Code
# Array representation of Max-Heap
'''
10
/ \
5 3
/ \
2 4
'''
arr = [10, 5, 3, 2, 4, 1, 7]
n = 7
key = 15
insertNode(arr, key)
printArr(arr, n)
# Final Heap will be:
'''
15
/ \
5 10
/ \ /
2 4 3
Code is written by Rajat Kumar....
'''
// C# program for implementing insertion in Heaps
using System;
public class insertionHeap {
// Function to heapify ith node in a Heap of size n following a Bottom-up approach
static void heapify(int[] arr, int n, int i) {
// Find parent
int parent = (i - 1) / 2;
if (arr[parent] > 0) {
// For Max-Heap
// If current node is greater than its parent
// Swap both of them and call heapify again
// for the parent
if (arr[i] > arr[parent]) {
// swap arr[i] and arr[parent]
int temp = arr[i];
arr[i] = arr[parent];
arr[parent] = temp;
// Recursively heapify the parent node
heapify(arr, n, parent);
}
}
}
// Function to insert a new node to the heap.
static int insertNode(int[] arr, int n, int Key) {
// Increase the size of Heap by 1
n = n + 1;
// Insert the element at end of Heap
arr[n - 1] = Key;
// Heapify the new node following a
// Bottom-up approach
heapify(arr, n, n - 1);
// return new size of Heap
return n;
}
/* A utility function to print array of size n */
static void printArray(int[] arr, int n) {
for (int i = 0; i < n; ++i)
Console.WriteLine(arr[i] + " ");
Console.WriteLine("");
}
public static void Main(string[] args) {
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
// maximum size of the array
int MAX = 1000;
int[] arr = new int[MAX];
// initializing some values
arr[0] = 10;
arr[1] = 5;
arr[2] = 3;
arr[3] = 2;
arr[4] = 4;
// Current size of the array
int n = 5;
// the element to be inserted
int Key = 15;
// The function inserts the new element to the heap and
// returns the new size of the array
n = insertNode(arr, n, Key);
printArray(arr, n);
// Final Heap will be:
// 15
// / \
// 5 10
// / \ /
// 2 4 3
}
}
// This code is contributed by ajaymakvana.
// Javascript program for implement insertion in Heaps
// To heapify a subtree rooted with node i which is
// an index in arr[].Nn is size of heap
let MAX = 1000;
// Function to heapify ith node in a Heap of size n following a Bottom-up approach
function heapify(arr, n, i)
{
// Find parent
let parent = Math.floor((i-1)/2);
if (arr[parent] >= 0) {
// For Max-Heap
// If current node is greater than its parent
// Swap both of them and call heapify again
// for the parent
if (arr[i] > arr[parent]) {
let temp = arr[i];
arr[i] = arr[parent];
arr[parent] = temp;
// Recursively heapify the parent node
heapify(arr, n, parent);
}
}
}
// Function to insert a new node to the Heap
function insertNode(arr, n, Key)
{
// Increase the size of Heap by 1
n = n + 1;
// Insert the element at end of Heap
arr[n - 1] = Key;
// Heapify the new node following a
// Bottom-up approach
heapify(arr, n, n - 1);
return n;
}
/* A utility function to print array of size N */
function printArray(arr, n)
{
for (let i = 0; i < n; ++i)
console.log(arr[i] + " ");
console.log("</br>");
}
let arr = [ 10, 5, 3, 2, 4 ];
let n = arr.length;
let key = 15;
n = insertNode(arr, n, key);
printArray(arr, n);
// This code is contributed by ajaymakvana
Time Complexity: O(log(n)) (where n is no of elements in the heap)
Auxiliary Space: O(n)
Deleting an element at any intermediary position in the heap can be costly, so we can simply replace the element to be deleted with the last element and delete the last element of the Heap.
- Replace the root or element to be deleted with the last element.
- Delete the last element from the Heap.
- Since the last element is now placed at the position of the root node. So, it may not follow the heap property. Therefore, heapify the last node placed at the position of the root.
Illustration:
Suppose the Heap is a Max-Heap as:
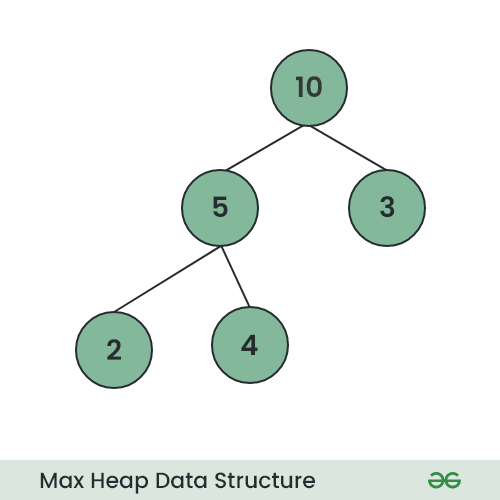
Max Heap Data Structure
The element to be deleted is root, i.e. 10.
Process:
The last element is 4.
Step 1: Replace the last element with root, and delete it.
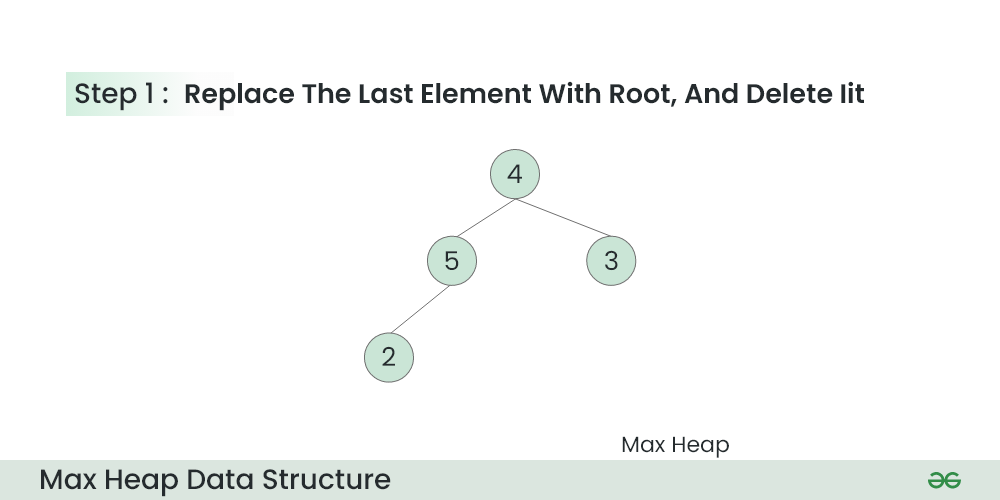
Max Heap
Step 2: Heapify root.
Final Heap:
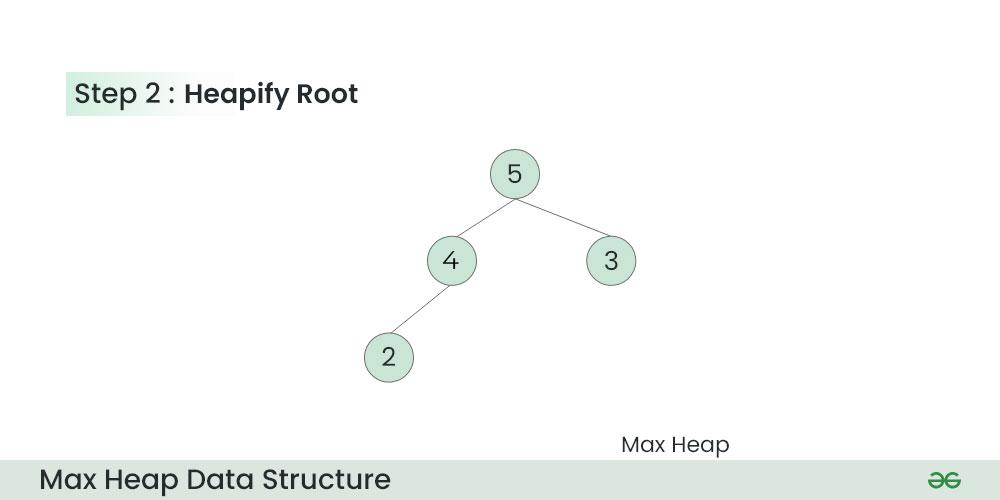
Max Heap
Implementation of Deletion operation in Max-Heap:
C++
// C++ program for implement deletion in Heaps
#include <iostream>
using namespace std;
// To heapify a subtree rooted with node i which is
// an index of arr[] and n is the size of heap
void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2 * i + 1; // left = 2*i + 1
int r = 2 * i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i) {
swap(arr[i], arr[largest]);
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
// Function to delete the root from Heap
void deleteRoot(int arr[], int& n)
{
// Get the last element
int lastElement = arr[n - 1];
// Replace root with last element
arr[0] = lastElement;
// Decrease size of heap by 1
n = n - 1;
// heapify the root node
heapify(arr, n, 0);
}
/* A utility function to print array of size n */
void printArray(int arr[], int n)
{
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
cout << "\n";
}
// Driver Code
int main()
{
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
int arr[] = { 10, 5, 3, 2, 4 };
int n = sizeof(arr) / sizeof(arr[0]);
deleteRoot(arr, n);
printArray(arr, n);
return 0;
}
// Java program for implement deletion in Heaps
public class deletionHeap {
// To heapify a subtree rooted with node i which is
// an index in arr[].Nn is size of heap
static void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2 * i + 1; // left = 2*i + 1
int r = 2 * i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
// Function to delete the root from Heap
static int deleteRoot(int arr[], int n)
{
// Get the last element
int lastElement = arr[n - 1];
// Replace root with first element
arr[0] = lastElement;
// Decrease size of heap by 1
n = n - 1;
// heapify the root node
heapify(arr, n, 0);
// return new size of Heap
return n;
}
/* A utility function to print array of size N */
static void printArray(int arr[], int n)
{
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver Code
public static void main(String args[])
{
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
int arr[] = { 10, 5, 3, 2, 4 };
int n = arr.length;
n = deleteRoot(arr, n);
printArray(arr, n);
}
}
# Python 3 program for implement deletion in Heaps
# To heapify a subtree rooted with node i which is
# an index of arr[] and n is the size of heap
def heapify(arr, n, i):
largest = i #Initialize largest as root
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
#If left child is larger than root
if (l < n and arr[l] > arr[largest]):
largest = l
#If right child is larger than largest so far
if (r < n and arr[r] > arr[largest]):
largest = r
# If largest is not root
if (largest != i):
arr[i],arr[largest]=arr[largest],arr[i]
#Recursively heapify the affected sub-tree
heapify(arr, n, largest)
#Function to delete the root from Heap
def deleteRoot(arr):
global n
# Get the last element
lastElement = arr[n - 1]
# Replace root with last element
arr[0] = lastElement
# Decrease size of heap by 1
n = n - 1
# heapify the root node
heapify(arr, n, 0)
# A utility function to print array of size n
def printArray(arr, n):
for i in range(n):
print(arr[i],end=" ")
print()
# Driver Code
if __name__ == '__main__':
# Array representation of Max-Heap
# 10
# / \
# 5 3
# / \
# 2 4
arr = [ 10, 5, 3, 2, 4 ]
n = len(arr)
deleteRoot(arr)
printArray(arr, n)
# This code is contributed by Rajat Kumar.
// C# program for implement deletion in Heaps
using System;
public class deletionHeap
{
// To heapify a subtree rooted with node i which is
// an index in arr[].Nn is size of heap
static void heapify(int []arr, int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2 * i + 1; // left = 2*i + 1
int r = 2 * i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i)
{
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
// Function to delete the root from Heap
static int deleteRoot(int []arr, int n)
{
// Get the last element
int lastElement = arr[n - 1];
// Replace root with first element
arr[0] = lastElement;
// Decrease size of heap by 1
n = n - 1;
// heapify the root node
heapify(arr, n, 0);
// return new size of Heap
return n;
}
/* A utility function to print array of size N */
static void printArray(int []arr, int n)
{
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
// Driver Code
public static void Main()
{
// Array representation of Max-Heap
// 10
// / \
// 5 3
// / \
// 2 4
int []arr = { 10, 5, 3, 2, 4 };
int n = arr.Length;
n = deleteRoot(arr, n);
printArray(arr, n);
}
}
// This code is contributed by Ryuga
<script>
// Javascript program for implement deletion in Heaps
// To heapify a subtree rooted with node i which is
// an index in arr[].Nn is size of heap
function heapify(arr, n, i)
{
let largest = i; // Initialize largest as root
let l = 2 * i + 1; // left = 2*i + 1
let r = 2 * i + 2; // right = 2*i + 2
// If left child is larger than root
if (l < n && arr[l] > arr[largest])
largest = l;
// If right child is larger than largest so far
if (r < n && arr[r] > arr[largest])
largest = r;
// If largest is not root
if (largest != i)
{
let swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(arr, n, largest);
}
}
// Function to delete the root from Heap
function deleteRoot(arr, n)
{
// Get the last element
let lastElement = arr[n - 1];
// Replace root with first element
arr[0] = lastElement;
// Decrease size of heap by 1
n = n - 1;
// heapify the root node
heapify(arr, n, 0);
// return new size of Heap
return n;
}
/* A utility function to print array of size N */
function printArray(arr, n)
{
for (let i = 0; i < n; ++i)
document.write(arr[i] + " ");
document.write("</br>");
}
let arr = [ 10, 5, 3, 2, 4 ];
let n = arr.length;
n = deleteRoot(arr, n);
printArray(arr, n);
// This code is contributed by divyeshrabdiya07.
</script>
Time complexity: O(log n) where n is no of elements in the heap
Auxiliary Space: O(n)
3. Peek operation on Max-heap Data Structure:
To access the maximum element (i.e., the root of the heap), the value of the root node is returned. The time complexity of peek in a max heap is O(1).

Peak Element Of Max- Heap
Implementation of Peek operation in Max-Heap:
C++
#include <iostream>
#include <queue>
int main() {
// Create a max heap with some elements using a priority_queue
std::priority_queue<int> maxHeap;
maxHeap.push(9);
maxHeap.push(8);
maxHeap.push(7);
maxHeap.push(6);
maxHeap.push(5);
maxHeap.push(4);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(1);
// Get the peak element (i.e., the largest element)
int peakElement = maxHeap.top();
// Print the peak element
std::cout << "Peak element: " << peakElement << std::endl;
return 0;
}
import java.util.PriorityQueue;
public class GFG {
public static void main(String[] args) {
// Create a max heap with some elements using a PriorityQueue
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
maxHeap.add(9);
maxHeap.add(8);
maxHeap.add(7);
maxHeap.add(6);
maxHeap.add(5);
maxHeap.add(4);
maxHeap.add(3);
maxHeap.add(2);
maxHeap.add(1);
// Get the peak element (i.e., the largest element)
int peakElement = maxHeap.peek();
// Print the peak element
System.out.println("Peak element: " + peakElement);
}
}
import heapq
# Create a max heap with some elements using a list
max_heap = [1,2,3,4,5,6,7,8,9]
heapq.heapify(max_heap)
# Get the peak element (i.e., the largest element)
peak_element = heapq.nlargest(1, max_heap)[0]
# Print the peak element
print("Peak element:", peak_element)
using System;
using System.Collections.Generic;
public class GFG {
public static void Main() {
// Create a min heap with some elements using a PriorityQueue
var maxHeap = new PriorityQueue<int>();
maxHeap.Enqueue(9);
maxHeap.Enqueue(8);
maxHeap.Enqueue(7);
maxHeap.Enqueue(6);
maxHeap.Enqueue(5);
maxHeap.Enqueue(4);
maxHeap.Enqueue(3);
maxHeap.Enqueue(2);
maxHeap.Enqueue(1);
// Get the peak element (i.e., the smallest element)
int peakElement = maxHeap.Peek();
// Print the peak element
Console.WriteLine("Peak element: " + peakElement);
}
}
// Define a PriorityQueue class that uses a max heap
class PriorityQueue<T> where T : IComparable<T> {
private List<T> heap;
public PriorityQueue() {
this.heap = new List<T>();
}
public int Count {
get { return this.heap.Count; }
}
public void Enqueue(T item) {
this.heap.Add(item);
this.BubbleUp(this.heap.Count - 1);
}
public T Dequeue() {
T item = this.heap[0];
int lastIndex = this.heap.Count - 1;
this.heap[0] = this.heap[lastIndex];
this.heap.RemoveAt(lastIndex);
this.BubbleDown(0);
return item;
}
public T Peek() {
return this.heap[0];
}
private void BubbleUp(int index) {
while (index > 0) {
int parentIndex = (index - 1) / 2;
if (this.heap[parentIndex].CompareTo(this.heap[index]) >= 0) {
break;
}
Swap(parentIndex, index);
index = parentIndex;
}
}
private void BubbleDown(int index) {
while (index < this.heap.Count) {
int leftChildIndex = index * 2 + 1;
int rightChildIndex = index * 2 + 2;
int largestChildIndex = index;
if (leftChildIndex < this.heap.Count && this.heap[leftChildIndex].CompareTo(this.heap[largestChildIndex]) > 0) {
largestChildIndex = leftChildIndex;
}
if (rightChildIndex < this.heap.Count && this.heap[rightChildIndex].CompareTo(this.heap[largestChildIndex]) > 0) {
largestChildIndex = rightChildIndex;
}
if (largestChildIndex == index) {
break;
}
Swap(largestChildIndex, index);
index = largestChildIndex;
}
}
private void Swap(int i, int j) {
T temp = this.heap[i];
this.heap[i] = this.heap[j];
this.heap[j] = temp;
}
}
// Define a MaxHeap class that uses an array
class MaxHeap {
constructor() {
this.heap = [];
}
push(item) {
this.heap.push(item);
this.bubbleUp(this.heap.length - 1);
}
pop() {
let item = this.heap[0];
let lastIndex = this.heap.length - 1;
this.heap[0] = this.heap[lastIndex];
this.heap.pop();
this.bubbleDown(0);
return item;
}
peak() {
return this.heap[0];
}
bubbleUp(index) {
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
if (this.heap[parentIndex] >= this.heap[index]) {
break;
}
this.swap(parentIndex, index);
index = parentIndex;
}
}
bubbleDown(index) {
while (index < this.heap.length) {
let leftChildIndex = index * 2 + 1;
let rightChildIndex = index * 2 + 2;
let largestChildIndex = index;
if (leftChildIndex < this.heap.length && this.heap[leftChildIndex] > this.heap[largestChildIndex]) {
largestChildIndex = leftChildIndex;
}
if (rightChildIndex < this.heap.length && this.heap[rightChildIndex] > this.heap[largestChildIndex]) {
largestChildIndex = rightChildIndex;
}
if (largestChildIndex === index) {
break;
}
this.swap(largestChildIndex, index);
index = largestChildIndex;
}
}
swap(i, j) {
let temp = this.heap[i];
this.heap[i] = this.heap[j];
this.heap[j] = temp;
}
}
// Create a max heap with some elements using an array
let maxHeap = new MaxHeap();
maxHeap.push(9);
maxHeap.push(8);
maxHeap.push(7);
maxHeap.push(6);
maxHeap.push(5);
maxHeap.push(4);
maxHeap.push(3);
maxHeap.push(2);
maxHeap.push(1);
// Get the peak element (i.e., the largest element)
let peakElement = maxHeap.peak();
// Print the peak element
console.log("Peak element: " + peakElement);
Time complexity:
- In a max heap implemented using an array or a list, the peak element can be accessed in constant time, O(1), as it is always located at the root of the heap.
- In a max heap implemented using a binary tree, the peak element can also be accessed in O(1) time, as it is always located at the root of the tree.
Auxiliary Space: O(n)
4. Heapify operation on Max-heap Data Structure:
A heapify operation can be used to create a max heap from an unsorted array. This is done by starting at the last non-leaf node and repeatedly performing the “bubble down” operation until all nodes satisfy the heap property. The time complexity of heapify in a max heap is O(n).
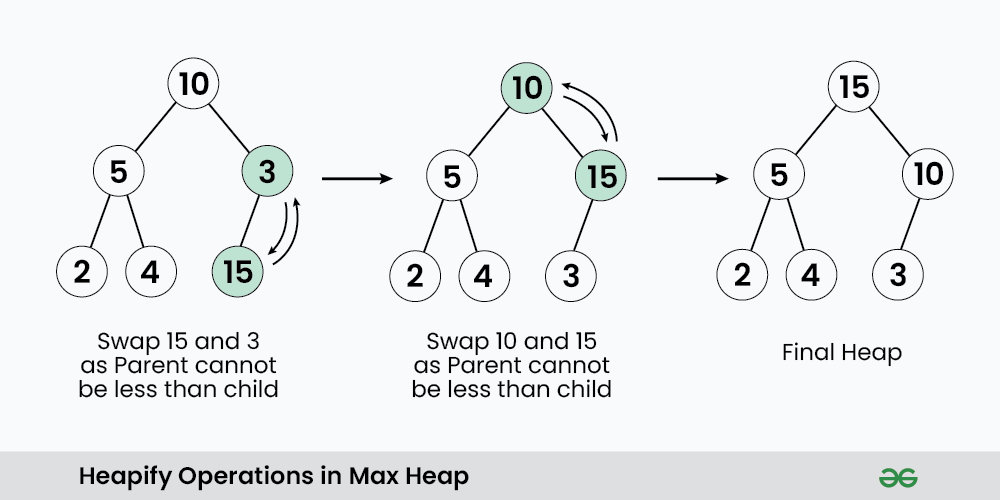
Heapify Operations in Max-Heap
5. Search operation on Max-heap Data Structure:
To search for an element in the max heap, a linear search can be performed over the array that represents the heap. However, the time complexity of a linear search is O(n), which is not efficient. Therefore, searching is not a commonly used operation in a max heap.
Here’s an example code that shows how to search for an element in a max heap using std::find():
C++
#include <iostream>
#include <queue> // for std::priority_queue
using namespace std;
int main() {
std::priority_queue<int> max_heap;
// example max heap
max_heap.push(10);
max_heap.push(9);
max_heap.push(8);
max_heap.push(6);
max_heap.push(4);
int element = 6; // element to search for
bool found = false;
// Copy the max heap to a temporary queue and search for the element
std::priority_queue<int> temp = max_heap;
while (!temp.empty()) {
if (temp.top() == element) {
found = true;
break;
}
temp.pop();
}
if (found) {
std::cout << "Element found in the max heap." << std::endl;
} else {
std::cout << "Element not found in the max heap." << std::endl;
}
return 0;
}
import java.util.PriorityQueue;
public class GFG {
public static void main(String[] args) {
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
maxHeap.add(3); // insert elements into the priority queue
maxHeap.offer(1);
maxHeap.offer(4);
maxHeap.offer(1);
maxHeap.offer(6);
int element = 6; // element to search for
boolean found = false;
// Copy the max heap to a temporary queue and search for the element
PriorityQueue<Integer> temp = new PriorityQueue<>(maxHeap);
while (!temp.isEmpty()) {
if (temp.poll() == element) {
found = true;
break;
}
}
if (found) {
System.out.println("Element found in the max heap.");
} else {
System.out.println("Element not found in the max heap.");
}
}
}
import heapq
max_heap = [10, 8, 7, 6, 5, 3, 2, 1] # example max heap
heapq._heapify_max(max_heap)
element = 6 # element to search for
found = False
# Copy the max heap to a temporary list and search for the element
temp = list(max_heap)
while temp:
if heapq._heappop_max(temp) == element:
found = True
break
if found:
print("Element found in the max heap.")
else:
print("Element not found in the max heap.")
using System;
using System.Collections.Generic;
class Program {
static void Main(string[] args) {
// Create a max heap with some elements using a PriorityQueue
PriorityQueue<int> maxHeap = new PriorityQueue<int>();
maxHeap.Enqueue(10);
maxHeap.Enqueue(9);
maxHeap.Enqueue(8);
maxHeap.Enqueue(6);
maxHeap.Enqueue(4);
int element = 6; // element to search for
bool found = false;
// Copy the max heap to a temporary queue and search for the element
PriorityQueue<int> temp = new PriorityQueue<int>(maxHeap);
while (temp.Count > 0) {
if (temp.Peek() == element) {
found = true;
break;
}
temp.Dequeue();
}
if (found) {
Console.WriteLine("Element found in the max heap.");
} else {
Console.WriteLine("Element not found in the max heap.");
}
}
}
// PriorityQueue class
class PriorityQueue<T> where T : IComparable<T> {
private List<T> heap = new List<T>();
public void Enqueue(T item) {
heap.Add(item);
int child = heap.Count - 1;
while (child > 0) {
int parent = (child - 1) / 2;
if (heap[child].CompareTo(heap[parent]) > 0) {
T tmp = heap[child];
heap[child] = heap[parent];
heap[parent] = tmp;
child = parent;
} else {
break;
}
}
}
public T Dequeue() {
int last = heap.Count - 1;
T frontItem = heap[0];
heap[0] = heap[last];
heap.RemoveAt(last);
last--;
int parent = 0;
while (true) {
int leftChild = parent * 2 + 1;
if (leftChild > last) {
break;
}
int rightChild = leftChild + 1;
if (rightChild <= last && heap[leftChild].CompareTo(heap[rightChild]) < 0) {
leftChild = rightChild;
}
if (heap[parent].CompareTo(heap[leftChild]) < 0) {
T tmp = heap[parent];
heap[parent] = heap[leftChild];
heap[leftChild] = tmp;
parent = leftChild;
} else {
break;
}
}
return frontItem;
}
public T Peek() {
return heap[0];
}
public int Count {
get {
return heap.Count;
}
}
}
const maxHeap = new PriorityQueue((a, b) => b - a);
maxHeap.add(3); // insert elements into the priority queue
maxHeap.add(1);
maxHeap.add(4);
maxHeap.add(1);
maxHeap.add(6);
const element = 6; // element to search for
let found = false;
// Copy the max heap to a temporary queue and search for the element
const temp = new PriorityQueue(maxHeap);
while (!temp.isEmpty()) {
if (temp.poll() === element) {
found = true;
break;
}
}
if (found) {
console.log("Element found in the max heap.");
} else {
console.log("Element not found in the max heap.");
}
OutputElement found in the max heap.
Time complexity: O(n), where n is the size of the heap.
Auxiliary Space: O(n),
Applications of Max-Heap Data Structure:
- Heapsort algorithm: The heap data structure is the basis for the heapsort algorithm, which is an efficient sorting algorithm with a worst-case time complexity of O(n log n). The heapsort algorithm is used in various applications, including database indexing and numerical analysis.
- Memory management: The heap data structure is used in memory management systems to allocate and deallocate memory dynamically. The heap is used to store the memory blocks, and the heap data structure is used to efficiently manage the memory blocks and allocate them to programs as needed.
- Graph algorithms: The heap data structure is used in various graph algorithms, including Dijkstra’s algorithm, Prim’s algorithm, and Kruskal’s algorithm. These algorithms require efficient priority queue implementation, which can be achieved using the heap data structure.
- Job scheduling: The heap data structure is used in job scheduling algorithms, where tasks are scheduled based on their priority or deadline. The heap data structure allows efficient access to the highest-priority task, making it a useful data structure for job scheduling applications.
- Efficiently maintain the maximum value: A max heap allows constant-time access to the maximum element in the heap, which makes it useful in applications where the maximum element needs to be found quickly.
- Efficient insert and delete operations: The insert and delete operations in a max heap have a time complexity of O(log n), which makes them efficient for large collections of elements.
- Priority Queues: A max heap can be used to implement a priority queue, which is useful in many applications such as job scheduling, task prioritization, and event-driven simulation.
- Sorting: A max heap can be used to implement heapsort, which is an efficient sorting algorithm that has a worst-case time complexity of O(n log n).
- Space efficiency: A max heap can be implemented as an array, which requires less memory compared to other data structures such as a binary search tree or a linked list.
Max heap data structure is a useful and efficient tool for maintaining and manipulating collections of elements, particularly when the maximum element needs to be accessed quickly or when elements need to be sorted or prioritized.
Unlock your potential with our DSA Self-Paced course, designed to help you master Data Structures and Algorithms at your own pace. In 90 days, you’ll learn the core concepts of DSA, tackle real-world problems, and boost your problem-solving skills, all at a speed that fits your schedule. With comprehensive lessons and practical exercises, this course will set you up for success in technical interviews and beyond.
And here's the challenge – join the Three 90 Challenge! Complete 90% of the course in 90 days, and you’ll earn a 90% refund. It's a great way to stay motivated, track your progress, and reward yourself for your dedication. Start the challenge today, and push your limits to achieve mastery in DSA!
Similar Reads
Introduction to Max-Heap – Data Structure and Algorithm Tutorials
A Max-Heap is defined as a type of Heap Data Structure in which each internal node is greater than or equal to its children. A max-heap is always a complete binary tree and typically represented as an array. Note that unlike a normal binary tree, a complete binary tree can be represented as an array
15+ min read
Introduction to Heap - Data Structure and Algorithm Tutorials
A Heap is a special Tree-based Data Structure that has the following properties. It is a Complete Binary Tree.It either follows max heap or min heap property.Max-Heap: The value of the root node must be the greatest among all its descendant nodes and the same thing must be done for its left and righ
15+ min read
Introduction to Min-Heap – Data Structure and Algorithm Tutorials
A Min-Heap is a Data Structure with the following properties. It is a complete Complete Binary Tree.The value of the root node must be the smallest among all its descendant nodes and the same thing must be done for its left and right sub-tree also.Use Cases of Min-Heap:Implementing Priority Queue: O
15+ min read
Introduction to Segment Trees - Data Structure and Algorithm Tutorials
A Segment Tree is used to stores information about array intervals in its nodes. It allows efficient range queries over array intervals.Along with queries, it allows efficient updates of array items.For example, we can perform a range summation of an array between the range L to R in O(Log n) while
15+ min read
Heap Sort - Data Structures and Algorithms Tutorials
Heap sort is a comparison-based sorting technique based on Binary Heap Data Structure. It can be seen as an optimization over selection sort where we first find the max (or min) element and swap it with the last (or first). We repeat the same process for the remaining elements. In Heap Sort, we use
14 min read
Introduction to Hierarchical Data Structure
We have discussed Overview of Array, Linked List, Queue and Stack. In this article following Data Structures are discussed. 5. Binary Tree 6. Binary Search Tree 7. Binary Heap 8. Hashing Binary Tree Unlike Arrays, Linked Lists, Stack, and queues, which are linear data structures, trees are hierarchi
13 min read
Top 50 Problems on Heap Data Structure asked in SDE Interviews
A Heap is a special Tree-based Data Structure in which the tree is a complete binary tree. Generally, heaps are of two types: Max-Heap and Min-Heap. To know more about this Data Structure in-depth refer to the Tutorial on Heap Data-Structure. Given below are the most frequently asked interview quest
2 min read
Heap data structure implementation in swift
A heap is a complete binary tree where each node satisfies the heap property. The heap property is different for different types of heaps but, in general, it means that each node has a value that is greater than or equal to (or less than or equal to) the values of its children nodes. Heaps are commo
3 min read
How to Recognize which Data Structure to use in a question?
Data structures are fundamental components in computer science that help organize and store data effectively. Choosing the right data structure is crucial for solving problems efficiently. Different data structures have unique properties that make them suitable for specific types of problems. Unders
4 min read
Applications of Heap Data Structure
Heap Data Structure is generally taught with Heapsort. Heapsort algorithm has limited uses because Quicksort is better in practice. Nevertheless, the Heap data structure itself is enormously used. Priority Queues: Heaps are commonly used to implement priority queues, where elements with higher prior
2 min read
Common operations on various Data Structures
Data Structure is the way of storing data in computer's memory so that it can be used easily and efficiently. There are different data-structures used for the storage of data. It can also be defined as a mathematical or logical model of a particular organization of data items. The representation of
15+ min read
How Data Structures can be used to achieve Efficient Memory Utilization
In the world of computer programming, using memory effectively is like fuelling a car efficiently. Similarly, in programming, memory is like the fuel that powers our software. Using memory wisely means making sure we don't waste it and use it for a purpose. To achieve efficient memory use, we use sp
12 min read
Leaf starting point in a Binary Heap data structure
Binary Heap is a complete tree (All levels are completely filled except possibly the last level and the last level has all keys as left as possible). In other words, we can say that it's an almost complete binary tree. A Binary heap is typically represented as array. If we take a closer look, we can
2 min read
Stack Vs Heap Data Structure
What is Stack? A stack is a linear data structure where the last element entered exits first. The order of stack data structure might be LIFO, FILO: According to this technique, the piece that is in last will come out first. As an example, consider a stack of dishes stacked on top of each other. The
3 min read
Types of Heap Data Structure
Different types of heap data structures include fundamental types like min heap and max heap, binary heap and many more. In this post, we will look into their characteristics, and their use cases. Understanding the characteristics and use cases of these heap data structures helps in choosing the mos
8 min read
Fibonacci Heap | Set 1 (Introduction)
INTRODUCTION:A Fibonacci heap is a data structure used for implementing priority queues. It is a type of heap data structure, but with several improvements over the traditional binary heap and binomial heap data structures.The key advantage of a Fibonacci heap over other heap data structures is its
5 min read
Heap Data Structure for Competitive Programming
Competitive programming needs smart tools to solve problems quickly. One key tool is the Heap Data Structure, which helps organize data in a way that's super fast. In this article, we'll break down the Heap, looking at its types, basic moves, and how it's a big deal in competitive programming. We'll
15+ min read
Explain an alternative Sorting approach for MO's Algorithm
MO's Algorithm is an algorithm designed to efficiently answer range queries in an array in linear time. It is a divide-and-conquer approach that involves pre-processing the array, partitioning it into blocks, and then solving the queries in each of the blocks. Alternate Approach for Sorting: An alte
15+ min read
Top 50 Problems on Queue Data Structure asked in SDE Interviews
A Queue is defined as a linear data structure that is open at both ends and the operations are performed in First In First Out (FIFO) order. We define a queue to be a list in which all additions to the list are made at one end, and all deletions from the list are made at the other end. The element w
3 min read