Given a weighted, undirected, and connected graph with V vertices and E edges, your task is to find the sum of the weights of the edges in the Minimum Spanning Tree (MST) of the graph. The graph is represented by an adjacency list, where each element adj[i] is a vector containing vector of integers. Each vector represents an edge, with the first integer denoting the endpoint of the edge and the second integer denoting the weight of the edge.

Input:
3 3
0 1 5
1 2 3
0 2 1

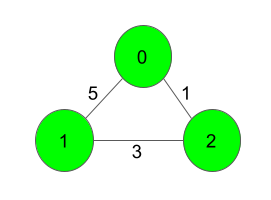Output: 4
Explanation:

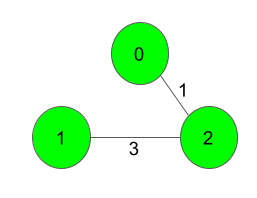The Spanning Tree resulting in a weight
of 4 is shown above.

Input: 
2 1 
0 1 5

  

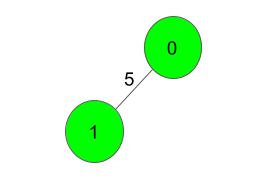
Output: 5 

Explanation: Only one Spanning Tree is possible which has a weight of 5.

Constraints:
2 ≤ V ≤ 1000
V-1 ≤ E ≤ (V*(V-1))/2
1 ≤ w ≤ 1000
The graph is connected and doesn't contain self-loops & multiple edges.