Quadrant is defined as a region in space that is divided into four equal parts by two axes namely the X-axis and the Y-axis in the Cartesian Plane. These two axes intersect each other at 90 degrees and the four regions so formed are called four quadrants, namely I quadrant, II quadrant, III quadrant, and IV quadrant.
In this article, we will explore essential quadrant concepts, including what a quadrant is, its area, quadrant graph, Cartesian Plane, sign conventions within the quadrant, abscissa, and coordinate, as well as the plotting of points on a quadrant.
What are Quadrants of Graph?
A quadrant is a designated area on a Cartesian plane, created by the intersection of the X and Y axes. In this plane, four quadrants are formed, each with its unique traits. The first quadrant, in the upper right, has positive x and y coordinates. The second quadrant, in the upper left, has negative x and positive y coordinates, and so on. Understanding these quadrants is essential for locating and interpreting points on the graph, providing a systematic way to navigate and analyze Cartesian coordinates.
4 Quadrants on Coordinate Plane
The Cartesian plane, formed by the X and Y axes, is split into four quadrants, each with distinct characteristics:
- First Quadrant: Located in the upper right, both x and y-coordinates are positive. This quadrant represents points in the top-right portion of the plane.
- Second Quadrant: Situated in the upper left, the x-coordinate is negative, and the y-coordinate is positive. This quadrant covers points in the top-left part of the plane.
- Third Quadrant: Positioned in the lower left, both x and y-coordinates are negative. Points in the bottom-left area of the plane fall into this quadrant.
- Fourth Quadrant: Found in the lower right, the x-coordinate is positive, and the y-coordinate is negative. This quadrant includes points in the bottom-right portion of the plane.
-min.png)
The quadrants are numbered in an anti-clockwise direction, starting from the upper right. The point where the X and Y axes intersect is called the origin, with coordinates (0,0), indicating zero values for both x and y. Understanding these quadrants helps locate points within the Cartesian plane.
What is Origin?
Starting point on a graph, known as the origin and shown as (0, 0), is where the horizontal x-axis and the vertical y-axis intersect. This means that at the origin, the values for both x and y are zero. It serves as a reference point for locating other points on the graph. In the image added above point O shows the origin.
Abscissa and Ordinate in Quadrants
In the four quadrants, numbers are represented as pairs (a, b), where 'a' stands for the x-coordinate, and 'b' for the y-coordinate. To figure out where a point is without plotting, pay attention to the signs of the x-coordinate (abscissa) and y-coordinate (ordinate). For example, if you have a point like Q (3, -5), the signs (+ve, -ve) indicate it's in quadrant IV.
The abscissa shows the horizontal distance from the Y-axis. A positive abscissa means to the right, and in our example, abscissa = 3 means go right from the origin along the x-axis by 3 units.
The ordinate indicates the vertical distance from the origin. A negative ordinate means to go down from the origin along the y-axis. In the example, ordinate = -5 means go down by 5 units.
Sign Convention in Quadrants
Sign conventions in the quadrants can be easily understood using the image added below,
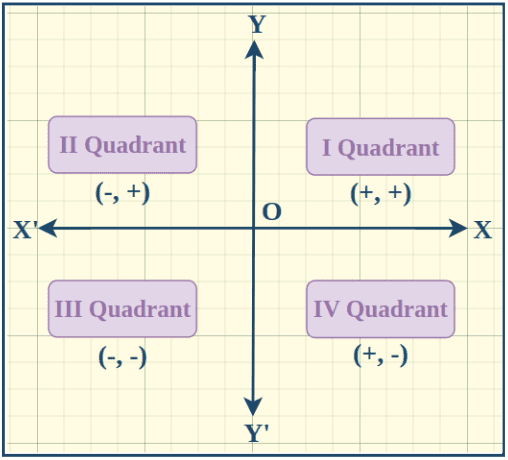
In the XY plane, as we move from left to right along the x-axis, the x-coordinate increases. Similarly, along the y-axis, moving from bottom to top results in an increase in the y-coordinate. The XY plane is divided into four quadrants, each with specific sign conventions for x and y coordinates:
|
Positive (+)
| Positive (+)
|
Negative (-)
| Positive (+)
|
Negative (-)
| Negative (-)
|
Positive (+)
| Negative (-)
|
Therefore, points in the 1st quadrant have positive values for both x and y, those in the 2nd quadrant have a negative x and a positive y, the 3rd quadrant has both negative x and y values, and the 4th quadrant has a positive x and a negative y.
Plotting Points on Quadrants
In a Cartesian plane, points are identified by the x-axis and y-axis. These points are denoted as (a, b), where 'a' is the x-coordinate (abscissa), and 'b' is the y-coordinate (ordinate). To position a point in a quadrant, we consider the signs of these coordinates. The values of x and y represent how far the point is from the x-axis and y-axis, respectively.
For example, plot the point (2, -5) on the Cartesian plane. Analyzing the sign of the coordinates reveals that the point is in the 4th quadrant. It will be 2 units away from the x-axis (to the right) and 5 units away from the y-axis (down), using the origin as a reference point.
.PNG)
Trigonometric Values in Different Quadrants
The values of various trigonometric functions in different quadrants can be learn by studying the table added below as,
|
+
| +
| +
| +
| +
| +
|
+
| -
| +
| +
| -
| -
|
-
| -
| -
| -
| -
| +
|
-
| -
| -
| -
| +
| -
|
In the 1st quadrant, all trigonometric ratios are positive. In the 2nd quadrant, Sine and Cosecant are positive (+), while Cosine and Secant are negative (-). In the 3rd quadrant, Tangent and Cotangent are positive (+), while Cosine and Secant are negative (-). In the 4th quadrant, Sine and Cosecant are negative (-), while Cosine and Secant are positive (+).
Read More,
Solved Examples on Quadrant
Example 1: Plot the point A (3, -4) and identify its Quadrant.
Solution:
Point A is located at coordinates (3, -4). Since the x-coordinate is positive (3) and the y-coordinate is negative (-4), Point A lies in Quadrant IV.
Example 2: Plot the point P (-5, 2) and determine its quadrant
Solution:
Coordinates of point P are (-5, 2). To determine the quadrant, we examine the signs of the x and y coordinates.
X-coordinate is -5, indicating a position to the left of the origin.
Y-coordinate is 2, indicating a position above the origin.
Therefore, since the x-coordinate is negative and the y-coordinate is positive, point P is located in Quadrant II.
Point P (-5, 2) is situated in Quadrant II of the Cartesian plane.
Practice Problems on Quadrants
Problem 1: Plot the point (1, -1) and identify its quadrant.
Problem 2: Find three points on the x-axis and determine their quadrants.
Problem 3: If a point lies on the y-axis with coordinates (0, -3), which quadrant is it in?
Problem 4: Locate the points Q (2, 2), R (-2, -2), and S (0, 0) and check for collinearity.
Problem 5: Plot the point (-4, -3) and explain in which quadrant it is situated.
FAQs on Quadrants
1. What is a Quadrant in Maths?
In mathematics, a quadrant is one of the four sections created by the intersection of two perpendicular lines or axes. These axes are typically labeled as the x-axis and y-axis in a Cartesian coordinate system.
2. What is the Intersection of Two Axes Called?
The intersection of two axes in a Cartesian coordinate system is called the origin. It is represented by the point where the x-axis and y-axis meet, usually denoted as (0,0).
3. What are 4 Quadrants?
The four quadrants are the sections formed by dividing a Cartesian coordinate plane into four equal parts. They are labeled as the first quadrant (Q1), second quadrant (Q2), third quadrant (Q3), and fourth quadrant (Q4).
4. Which Quadrant is Positive?
The positive quadrant in a Cartesian coordinate system is the first quadrant (Q1). In this quadrant, both the x and y coordinates are positive.
5. What is the Use of Quadrants in Graphs?
Quadrants in graphs provide a systematic way to organize and locate points based on their coordinates. They help in visualizing relationships between variables and analyzing patterns in data sets, making it easier to interpret graphical representations.
6. Which Quadrant has both the values of Coordinates Positive?
The first quadrant (Q1) is the quadrant where both the x and y coordinates of points are positive. It is the only quadrant with both positive values.
7. What are the 4 Quadrants of a Circle?
The concept of quadrants is not directly applicable to circles. Instead, circles are divided into angles measured in degrees. However, if referring to circular sectors, one might use terms like first sector, second sector, third sector, and fourth sector, corresponding to different angular regions.
Similar Reads
Quadrants in Geometry
Quadrant is defined as a region in space that is divided into four equal parts by two axes namely the X-axis and the Y-axis in the Cartesian Plane. These two axes intersect each other at 90 degrees and the four regions so formed are called four quadrants, namely I quadrant, II quadrant, III quadrant
8 min read
Ray in Geometry
Rays in mathematics are part of Geometry that has one side fixed and the other can be infinitely extended. In geometry, a ray is a line that starts at a single point, known as the endpoint and stretches infinitely in one direction. A real-world example of a ray is a beam of sunlight; the sun serves
9 min read
Triangles in Geometry
A triangle is a polygon with three sides (edges), three vertices (corners), and three angles. It is the simplest polygon in geometry, and the sum of its interior angles is always 180°. A triangle is formed by three line segments (edges) that intersect at three vertices, creating a two-dimensional re
13 min read
Uses of Co-Ordinate Geometry
Coordinate geometry is a branch of mathematics, which is used to represent various geometric figures in a 2-D plane. Coordinate geometry is used to describe various curves such as circles, parabolas, etc that can be can be plotted on the coordinate plane using coordinate geometry formulas. Coordinat
8 min read
Area of a Quadrant
Area of a Quadrant is defined as the one-fourth space of a circle as a Quadrant is the one-fourth part of a circle. A circle is defined as the locus of a considerable number of focuses that are equidistant from the inside of the circle. When a circle is partitioned equally by drawing two perpendicul
10 min read
Geometry
Geometry is a branch of mathematics that studies the properties, measurement, and relationships of points, lines, angles, surfaces, and solids. From basic lines and angles to complex structures, it helps us understand the world around us. Geometry for Students and BeginnersBranches of Geometry Algeb
2 min read
Perimeter of Quadrilateral
Perimeter of a Quadrilateral is the sum of all the sides of a perimeter. Suppose we are given a quadrilateral ABCD with sides AB, BC, CD, and DA then its perimeter is AB + BC + CD + DA. In this article, we will learn about the Perimeter of Quadrilateral Definition and Formulas for Perimeter of vario
9 min read
Geometry Symbols
Geometry Symbols: Various symbols are used in Geometry. Geometry is a branch of mathematics that explores the properties, relationships, and measurements of shapes, sizes, positions, and dimensions of objects in space. It delves into the study of points, lines, angles, surfaces, and solids, investig
6 min read
Angle Sum Property of a Quadrilateral
Angle Sum Property of a Quadrilateral: Quadrilaterals are encountered everywhere in life, every square rectangle, any shape with four sides is a quadrilateral. We know, three non-collinear points make a triangle. Similarly, four non-collinear points take up a shape that is called a quadrilateral. It
9 min read
What is Adjacent Angle in Geometry?
Adjacent Angles are the angles that have a common vertex, a common arm, and the rest two arms lie on either side of the common arm. Angles are particularly important in geometry as they help define and understand different geometric figures and their characteristics. Geometry is a branch of mathe
10 min read
Construction of a Quadrilateral
It is famously said that Geometry is the knowledge that appears to be produced by human beings, yet whose meaning is totally independent of them. Practical geometry is an important branch of geometry that helps us to study the size, positions, shapes as well as dimensions of objects and draw them wi
7 min read
GRE Geometry | Lines and Angles
Lines: A Line is a one-dimensional geometrical figure having negligible breadth extending infinitely in both directions. A line may be straight or curved. A straight line has same direction throughout its whole length from point to point. A curved line changes it's direction continuously from point
4 min read
Practice Questions on Coordinate Geometry
Coordinate geometry is essential for anyone who wants to study mathematics, physics, engineering, or computer science. Coordinate geometry is a branch of mathematics that uses algebraic equations to describe and analyze geometric shapes and their properties on a coordinate plane. In this article, we
8 min read
Area of Quadrilateral
A quadrilateral is a polygon with four sides, four angles, and four vertices. It is a two-dimensional figure, formed by joining four points (vertices) with straight lines (sides). The side of a quadrilateral may or may not be equal. Various types of quadrilaterals can be defined based on the propert
9 min read
Geometric Proofs for Polygons
Geometric Proofs for Polygons are 2D shapes with straight edges, and they have the same number of sides as they do corners (vertices). Because there are so many different kinds of polygons, there aren’t many features that apply to all of them. However, when we need to prove something about polygons,
10 min read
Practice Question on Non-Euclidean Geometry
Non-Euclidean geometry is a type of geometry that differs from the standard Euclidean geometry formulated by Euclid. It arises when Euclid's fifth postulate, the parallel postulate, is replaced with an alternative. Non-Euclidean Geometry FormulasHyperbolic GeometryDistance Formula: The distance d be
6 min read
Quadrilateral Formulas
A quadrilateral is a closed figure and a type of polygon which has four sides or edges, four angles, and four corners or vertices. The word quadrilateral is derived from the Latin words "quad", a variant of four, and "latus", meaning side. It is also called a tetragon, derived from the Greek word "t
7 min read
Geometry Aptitude Questions & Answers
Geometry is the study of different varieties of shapes, figures, and sizes. It gives us knowledge about distances, angles, patterns, areas, and volumes of shapes. In this article, we have provided aptitude questions with solutions on geometry along with unsolved questions as well. Prerequisites: Geo
5 min read
Quadrilaterals
Quadrilateral is a two-dimensional figure characterized by having four sides, four vertices, and four angles. It can be broadly classified into two categories: concave and convex. Within the convex category, there are several specific types of quadrilaterals, including trapezoids, parallelograms, re
12 min read