Surface Area of a Rectangular Prism
Last Updated :
24 Jan, 2024
Surface Area of a Rectangular Prism is the area covered by all the surfaces of the rectangular prism. A rectangular prism is a 3-D geometrical figure with four lateral faces with two congruent and parallel faces. A rectangular prism has a total of six faces where the opposite faces are identical, i.e., a rectangular prism has three pairs of identical faces. The dimensions of a rectangular prism are length, width, and height. It has a total of six faces, twelve edges, and eight vertices.
In this article, we will learn about the Surface Area of a Rectangular Prism (Right Rectangular Prism), the Lateral Surface Area of a (Right) Rectangular Prism, the Total Surface Area of a (Right) Rectangular Prism, and others in detail.
What is Surface Area of a Rectangular Prism?
A rectangular prism is similar to a cuboid and its surface area is the sum of areas of all the faces of the rectangular prism. In a rectangular prism, we have two types of areas Curved Surface Or Lateral Surface Area or Total Surface Area. Both of them are explained in the article below. The image added below shows the rectangular prism.
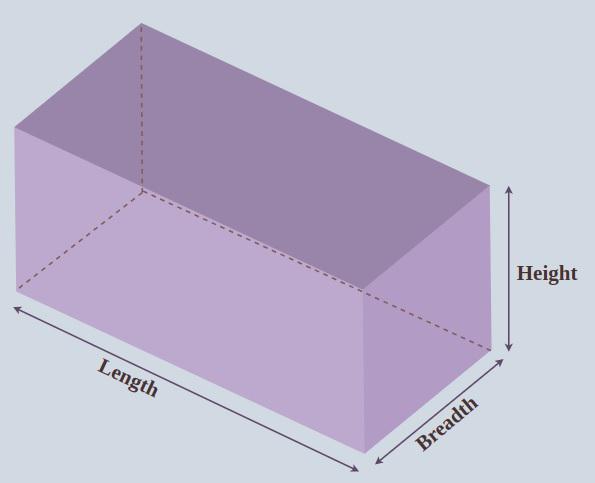
Surface Area of a Rectangular Prism Definition
Total area occupied by all the three-dimensional surfaces of a three-dimensional geometric structure is called its surface area. The surface area of the prism is equal to the area of its net. So, to find the surface area of a right rectangular prism, we have to calculate the areas of each of its faces, then add the resulting areas.
There are two formulas that are used to calculate the area of a rectangular prism that are,
- Lateral Surface Area
- Total Surface Area
The image added below shows the rectangular prism and its net. Now let’s learn about both the surface area of the rectangular prism.

Lateral Surface Area of a Rectangular Prism
The lateral surface area of a right prism (LSA) is equal to the sum of the areas of its four lateral faces.
Lateral Surface Area of a Prism (LSA) = Sum of areas of four lateral faces.
So, the formula for calculating the lateral surface area of a right rectangular prism is given as follows:
Lateral Surface Area of a Rectangular Prism = 2h (l + b) square units
where,
- “l” is the length of the side of a base
- “b” is the breadth of the side of a base
- “h” is the height of the prism
Total Surface Area of a Rectangular Prism
The total surface area of a right rectangular prism is equal to the sum of the total areas of all its faces.
Total Surface Area of a Prism (TSA) = LSA + 2 × Base Area
So, the formula for calculating the total surface area of a right rectangular prism is given as below,
TSA = 2(lb + bh + lh) square units
where,
- “l” is the length of the side of a base
- “b” is the breadth of the side of a base
- “h” is the height of the prism
How to Find Surface Area of a Rectangular Prism?
Let us go through an example to understand the concept of calculating the surface area of a rectangular prism.
Example: Calculate the surface area of a rectangular prism if its height is 15 units and the length and breadth of the base are 10 units and 6 units, respectively.
Step 1: Note the dimensions of the given rectangular prism. In the given example, the length and breadth of the rectangular prism’s base are 10 units and 6 units, respectively, and its height is 15 units.
Step 2: We know that the surface area of a rectangular prism is equal to 2(lb + bh + lh) square units. Now, substitute the given values of length, breadth, and height in the formula.
Step 3: So, the surface area of the rectangular prism is calculated as, A = 2× (10 × 6 + 6 × 15 + 10 × 15) = 600 sq. units.
Using the above steps Surface Area of a Rectangular Prism is found.
Read More,
Surface Area of Rectangular Prism Examples
Example 1: Determine the total surface area of a rectangular prism if its lateral surface area is 560 sq. cm and the length and breadth of the base are 12 cm and 8 cm, respectively.
Solution:
Given,
- Length of the rectangular base (l) = 12 cm
- Breadth of the rectangular base (b) = 8 cm
- Lateral surface area of the prism (LSA) = 560 sq. cm
We have,
Total surface area of a prism (TSA) = LSA + 2 × Base area
Base Area = 2(l + b)
= 2 × (12 + 8) = 2 × 20 = 40 sq. cm
TSA = 560 + 2 × 40
= 560 + 80 = 640 sq. cm
Hence, the rectangular prism’s total surface area is 640 sq. cm.
Example 2: Calculate the length of the base of a rectangular prism if its height is 9 inches and the breadth of the base is 4 inches, and the lateral surface area is 198 sq. in.
Solution:
Given,
- Lateral surface area = 198 sq. in
- Breadth of Rectangular base (b) = 4 inches
- Height = 9 inches
Length of Rectangular base (l) = ?
We have,
Lateral Surface Area of a Rectangular Prism = 2h (l + b) square units
⇒ 2 × 9 × (l + 4) = 198
⇒ 18 × (l + 4) = 198
⇒ l + 4 = 198/18 = 11
⇒ l = 11 − 4 = 7 in
Thus, length of the rectangular prism is 7 inches.
Example 3: Find the lateral surface area of a rectangular prism if its height is 18 cm and the length and breadth of the base are 14 cm and 10 cm, respectively.
Solution:
Given,
- Length of Rectangular base (l) = 14 cm
- Breadth of Rectangular base (b) = 10 cm
- Height = 18 cm
We know that,
Lateral Surface Area of a Rectangular Prism = 2h (l + b) square units
= 2 × 18 × (14 + 10)
= 36 × 24 = 864 sq. cm
Hence, the lateral surface of the given prism is 864 sq. cm.
Example 4: Determine the surface area of a rectangular prism if its height is 12 cm and the length and breadth of the base are 8 cm and 5 cm, respectively.
Solution:
Given,
- Length of Rectangular base (l) = 8 cm
- Breadth of Rectangular base (b) = 5 cm
- Height = 12 cm
We have,
Total Surface Area of a Rectangular Prism = 2(lb + bh + lh) square units
= 2 × (8 × 5 + 5 × 12 + 8 × 12)
= 2 × (40 + 60 + 96)
= 2 × 196 = 392 square units
Hence, the rectangular prism’s surface area is 392 square units.
Example 5: Determine the surface area of a rectangular prism if its height is 14 units and the length and breadth of the base are 10 units and 7 units, respectively.
Solution:
Given,
- Length of Rectangular base (l) = 10 units
- Breadth of Rectangular base (b) = 7 units
- Height = 14 units
We have,
Total Surface Area of a Rectangular Prism = 2(lb + bh + lh) square units
= 2 × (10 × 7 + 7 × 14 + 10 × 14)
= 2 × (70 + 98 + 140)
= 2 × 308 = 616 square units
Hence, the rectangular prism’s total surface area is 616 square units.
Practice Questions on Surface Area of Rectangular Prism
Q1. Find surface area of a right rectangular prism if its height is 10 units and the length and breadth of the base are 18 units and 9 units, respectively.
Q2. If the lateral surface area of the right Rectangualr Prism is 120 sq units and its height is 10 units find the Total surface area of rectangular prism
Q3. Find lateral surface area of a right rectangular prism if the length and breadth of the base are 8 units and 7 units, respectively.
Q4. Determine the surface area of a right rectangular prism if its height is 20 units and the length and breadth of the base are 10 units and 15 units, respectively.
FAQs on Rectangular Prism
1. What is a Rectangular Prism?
In mathematics, a rectangular prism is a three-dimensional geometric figure that has four lateral faces with two congruent and parallel bases. The dimensions of a rectangular prism are length, width, and height. It has a total of six faces, twelve edges, and eight vertices.
2. What are Some Examples of a Rectangular Prism?
Some examples of rectangular prisms that we see in our everyday lives are fish tanks, notebooks, diaries, cargo containers, rooms, etc.
3. What is Total Surface Area of a Rectangular Prism?
The total surface area of a rectangular prism is equal to the sum of the total areas of all its faces. TSA = 2(lb + lh + bh) square units
4. What is Lateral Surface Area of a Rectangular Prism?
The lateral surface area of a prism (LSA) is equal to the sum of the areas of its four lateral faces. So, the formula for calculating the lateral surface area of a rectangular prism is, LSA = 2h (l + b) square units
5. What is Formula for Surface Area?
Surface Area Formulas related to Right Rectangular Prism are,
- Lateral Surface Area of Right Rectangular Prism: 2h (l + b) sq units
- Total Surface Area of Right Rectangular Prism: 2(lb + bh + lh) sq units
6. What is the Formula for the Surface Area of a Rectangle?
The formula for the area of rectangle is l.b sq units. Where l and b are length and breadth of rectangle respectively.
7. How to Find Surface Area of Rectangular Prism?
Surface Area of a Rectangular Prsim is calculated using the formula, Lateral Surface Area of Right Rectangular Prism: 2h (l + b) sq units and Total Surface Area of Right Rectangular Prism: 2(lb + bh + lh) sq units.
8. What is Surface Area of a Rectangular Prism?
The Surface Area of a Rectangular Prsim is the total area occupied by all the surfaces of the rectangular prsim.
Similar Reads
Surface Area of a Rectangular Prism
Surface Area of a Rectangular Prism is the area covered by all the surfaces of the rectangular prism. A rectangular prism is a 3-D geometrical figure with four lateral faces with two congruent and parallel faces. A rectangular prism has a total of six faces where the opposite faces are identical, i.
9 min read
Surface Area of a Prism
Surface Area of a Prism: In mathematics, a prism is an essential member of the polyhedron family and is defined as a three-dimensional shape having two identical polygons facing each other that are connected by rectangular or parallelogram faces laterally. The identical polygons can be triangles, sq
14 min read
Volume of a Rectangular Prism Formula
A rectangular prism is a three-dimensional geometric shape with two congruent and parallel rectangular bases and four rectangular faces connecting them. This type of prism is also known as a cuboid. It is a member of the polyhedron family and is characterized by its six rectangular faces, twelve edg
6 min read
Area of a Rectangular Pyramid
Understanding the area of a rectangular pyramid is essential for students, educators, and professionals alike. A rectangular pyramid, also known as a rectangular-based pyramid, is a three-dimensional geometric shape with a rectangular base and four triangular faces that meet at a common point called
9 min read
Surface Area of a Rectangle Formula
Geometry includes the study of a plethora of shapes in mathematics. Not only that, their dimensions and numerous calculations pertaining to their dimensions are also done under geometry. A quadrilateral whose opposite sides are of equal lengths and all the four angles are right angles is called a r
2 min read
Surface Area of a Square Pyramid
Pyramid is a three-dimensional geometric structure with a polygonal base and triangular faces equal to the number of sides in the base. The triangular faces or lateral surfaces of a pyramid meet at a single point known as the apex or the vertex. In a pyramid, the base is connected to all the faces o
8 min read
Volume of a Triangular Prism Formula
A prism is a three-dimensional solid figure with two identical ends. It is made up of flat sides, similar bases, and equal cross-sections. Its faces are parallelograms or rectangles without bases. Such a prism that has three rectangular faces and two parallel triangle bases is called a triangular pr
3 min read
Volume of a Triangular Prism
A triangular prism is a 3-D prism made up of a triangular base. It is defined as a three-dimensional solid shape with flat sides and equal bases. It has no bases and faces that are either parallelograms or rectangles. Three rectangular planes and two parallel triangle bases make up a triangular pris
7 min read
Volume of a Rectangular Pyramid
Rectangular pyramid is a three-dimensional object that has a rectangular base upon which are erected four triangular faces that meet at a common point called the apex. It has a total of five faces, i.e., a rectangular base, four triangular faces, five vertices, and eight edges. In a rectangular pyra
6 min read
Surface Area of a Triangular Prism Formula
A prism is a three-dimensional solid shape with two ends that are identical. It has flat sides, identical bases, and equal cross-sections. It has faces that are either parallelograms or rectangles with no bases. A triangular prism is one with three rectangular sides and two parallel triangle bases.
3 min read