Abstract
Purpose: The objective of the study was to demonstrate that, in x-ray computed tomography (CT), more than two types of materials can be effectively separated with the use of an energy resolved photon-counting detector and classification methodology. Specifically, this applies to the case when contrast agents that contain K-absorption edges in the energy range of interest are present in the object. This separation is enabled via the use of recently developed energy resolved photon-counting detectors with multiple thresholds, which allow simultaneous measurements of the x-ray attenuation at multiple energies.
Methods: To demonstrate this capability, we performed simulations and physical experiments using a six-threshold energy resolved photon-counting detector. We imaged mouse-sized cylindrical phantoms filled with several soft-tissue-like and bone-like materials and with iodine-based and gadolinium-based contrast agents. The linear attenuation coefficients were reconstructed for each material in each energy window and were visualized as scatter plots between pairs of energy windows. For comparison, a dual-kVp CT was also simulated using the same phantom materials. In this case, the linear attenuation coefficients at the lower kVp were plotted against those at the higher kVp.
Results: In both the simulations and the physical experiments, the contrast agents were easily separable from other soft-tissue-like and bone-like materials, thanks to the availability of the attenuation coefficient measurements at more than two energies provided by the energy resolved photon-counting detector. In the simulations, the amount of separation was observed to be proportional to the concentration of the contrast agents; however, this was not observed in the physical experiments due to limitations of the real detector system. We used the angle between pairs of attenuation coefficient vectors in either the 5-D space (for non-contrast-agent materials using energy resolved photon-counting acquisition) or a 2-D space (for contrast agents using energy resolved photon-counting acquisition and all materials using dual-kVp acquisition) as a measure of the degree of separation. Compared to dual-kVp techniques, an energy resolved detector provided a larger separation and the ability to separate different target materials using measurements acquired in different energy window pairs with a single x-ray exposure.
Conclusions: We concluded that x-ray CT with an energy resolved photon-counting detector with more than two energy windows allows the separation of more than two types of materials, e.g., soft-tissue-like, bone-like, and one or more materials with K-edges in the energy range of interest. Separating material types using energy resolved photon-counting detectors has a number of advantages over dual-kVp CT in terms of the degree of separation and the number of materials that can be separated simultaneously.
Keywords: photon-counting detectors, CT, material separation, K-edge, spectral CT
INTRODUCTION
Spectral computed tomography (CT) uses measurements of the x-ray attenuation by an object at multiple energies to extract additional information about the object. Therefore, it is also often referred to as multi-energy CT. The spectral measurements contain information about the energy dependence of the x-ray attenuation coefficients of materials in the object, which is useful in quantitatively determining composition and in discriminating between materials based on differences in their energy dependences.
Spectral CT can be performed by irradiating the object using more than one x-ray spectrum, e.g., by operating the tube at two or more different voltages, by using different source filtrations, or both.1, 2, 3 When two spectra are used, the current standard method for clinical spectral CT procedures, this method is called dual-energy CT. Dual-energy CT can be performed using dual-source synchronous acquisition,4 single-source sequential acquisition, and single-source fast-kVp-switching acquisition.5
Alternatively, spectral CT acquisition is possible via the use of novel x-ray detectors. For instance, a two-layer detector6, 7, 8, 9 is capable of measuring the intensity of the (relatively) low-energy and (relatively) high-energy photons, respectively.
One common drawback of the previously mentioned implementations of spectral CT is the overlap of the energy spectra in the different measurements. Ideally, the incident spectra should not overlap in energy and should have mean energies that are sufficiently far apart. However, generating nonoverlapping spectra using conventional x-ray tubes (by far the most widely used and practical x-ray sources) with fluxes high enough for in vivo CT is not currently feasible. The multilayer detector scheme is also unable to provide measurements that are sufficiently separated in energy, i.e., where the energies of the relatively low-energy and relatively high-energy photons detected in the two layers do not overlap.
Clinical dual-energy CT is performed using two x-ray spectra obtained at different tube voltages. To address the limitation of overlapping spectra, preobject shaping filters are almost always used to improve the spectral separation and the overall imaging performance.10, 11, 12
An alternative solution to obtaining spectral measurements at different and relatively independent energies is through the use of energy resolved detectors,13, 14 which provide simultaneous measurements of the x-ray attenuation at multiple energies using standard polychromatic x-ray sources. These energy resolved detectors use high speed, typically solid-state, radiation sensors combined with very fast readout application specific integrated circuits (ASICs) that process individual photons.15, 16, 17 These ASICs have an electronics chain for each pixel in the detector. The current signal from the detector is integrated, amplified, and shaped. The resulting pulses are processed by a set (typically two to six) of independent comparator circuits. One input to each comparator is attached to a voltage corresponding to an energy threshold and the other is attached to the output of the shaping amplifier. The output of each comparator is counted in a counting circuit. The values of the counter for each threshold and each pixel can be read out rapidly to provide the number of photons detected during the acquisition period that have energies greater than each of the energy thresholds. As a result, photon count measurements in several nonoverlapping energy windows can be obtained by subtracting the detected counts acquired from adjacent energy thresholds.
As previously mentioned, data from multi-energy CT can be used to separate various materials in the image, as has been widely done in dual-energy imaging.18, 19, 20, 21 In the energy range of interest for CT, the energy dependence of the x-ray linear attenuation coefficients, which are functions of elemental composition and density, is determined by the energy dependent probability of Compton and photoelectric interactions (i.e., two basis functions). With dual-energy measurements, theoretically, two (or more than two, if additional constraints are imposed, e.g., Ref. 20) types of materials can be separated simultaneously (e.g., soft tissue and bone).
Under the same principle, the multiple energy windows of an energy resolved detector also provide sufficient data to separate materials. Different types of material can be defined by different densities (e.g., muscle and fat), compositions (e.g., water and iodine solution), or both (e.g., soft tissue and bone). The focus of this work was to use energy resolved detectors to separate materials that differ in composition. In particular, we focus on the case when absorption edges are present in the energy range of interest and, consequently, more than two basis functions are needed to fully describe the attenuation coefficients. Absorption edge energies are characteristic of the chemical elements in a material and result in discontinuities in the energy dependence of the attenuation coefficients. These discontinuities provide the potential to separate materials containing elements that contribute to the absorption edges. Typically, elements having such edges (e.g., iodine, gadolinium, bismuth, barium, and gold) are used as imaging contrast agents.
One way to identify materials in an object using an energy resolved photon-counting detector is via the use of rigorous basis decomposition methods.13, 22, 23 However, this method requires careful calibration of the basis functions and energy response of the imaging system. Alternatively, one can use reconstructed images from each of the energy windows combined with a classification method to separate the object into various materials or regions. In this paper, the second approach was taken. The aim of this work was to demonstrate that images acquired from energy resolved photon-counting detectors contain the requisite information to allow separation of materials with absorption edges in the energy range of interest from other materials (e.g., soft tissue and bone) that do not have a K-edge in the energy range of interest.
THEORY
Energy-dependent x-ray attenuation
In x-ray CT, the linear attenuation coefficient μ(E) is determined by Compton scattering and photoelectric absorption cross sections. As a result, μ(E) can be approximated by a weighted combination of two basis functions24
| (1) |
where ρ is the material’s mass density, fCompton(E) approximates the energy dependence of Compton scattering, and gPE(E) approximates the energy dependence of photoelectric absorption. Both interactions have been extensively studied and tabulated data or empirical formulas are available.24, 25
The constants a1 and a2 only depend on the composition of the material.24 Together with ρ, they describe the dependence of μ(E) on fCompton(E) and gPE(E) and thus, the dependence of μ(E) on photon energy, E.
The photoelectric basis function has element-specific discontinuities at atomic energy levels. As a result, materials containing elements with atomic edges in the energy range of interest exhibit energy dependence different from those without edges (Fig. 1). In diagnostic imaging applications, the most significant discontinuities occur at the K-shell binding energies. For a material having a K-edge in the energy range of interest, Eq. 1 needs to be modified to
| (2) |
where the additional basis function gPE-Kshell(E) describes the element-specific photoelectric absorption that results due to its K energy level. When multiple K-edges are present, each adds a unique corresponding basis function.
Figure 1.
Linear attenuation coefficients of water, bone, Omnipaque™350 iodine-based (K-edge at 33.2 keV) contrast agent solution, and Magnevist™ gadolinium-based (K-edge at 50.2 keV) contrast agent solution (attenuation data obtained from Ref. 26).
The contrast between the attenuation coefficients of two materials results from differences in density, composition, or both. For example, muscle and fat have very similar chemical compositions, while muscle has a higher density (1.06 g∕cm3 vs 0.9 g∕cm3). Thus, the observed linear attenuation coefficient of muscle is higher, due largely to its greater density. On the other hand, the contrast between water and iodine solution is due primarily to the differences in their compositions. Given their similar composition, the linear attenuation of muscle and fat at two different energies is expected to change by a similar ratio. That is, similarity in material composition results in similarity in energy dependence of the attenuation coefficient. However, this energy dependence will be different for materials with different compositions (e.g., water and iodine solution).
In single-energy CT, the linear attenuation coefficient is measured using a single-energy spectrum and the energy information is not retained in the detector. Thus, it is not possible to obtain information about the energy dependence of the attenuation coefficient. However, with spectral CT techniques, such as dual-energy or multi-threshold energy resolved detectors, the attenuation of the object can be measured at multiple energies, allowing the use of this energy dependence information to separate different materials based on their chemical compositions.
Material separation using energy resolved detectors
In the absence of K-edges, a1 and a2 can be uniquely determined by measuring the x-ray absorption at two different energies, e.g., using two different energy spectra.27 The measurements for the different spectra contain information about the spectral dependence of the x-ray absorption in the object and can be used to extract information about the object’s composition. For example, in dual-energy CT, a dual-energy index4 (DEI) is calculated to quantify the degree of spectral differentiation of different materials provided by images acquired at two tube voltages
| (3) |
where xlow is the CT number measured (in Hounsfield units or HU) at the lower voltage and xhigh is that measured at the higher voltage. However, with the inclusion of one or more K-edges in the energy range of interest, the attenuation is a combination of three or more basis components (Eq. 2), and dual-energy CT does not directly provide the requisite number of measurements to fully exploit the energy dependence of the attenuation coefficients (e.g., simultaneously separate soft tissue, bone, and iodine).
One solution is the use of energy resolved photon-counting detectors. For such a detector with n energy thresholds (and therefore n energy windows), this is equivalent to obtaining n nonoverlapping measurements simultaneously with a single x-ray exposure. When n≥3 and properly chosen energy windows are used, there is potentially enough information to allow separation of materials with K-edges (e.g., contrast agents) in the energy range of interest. For example, Refs. 13, 23 used an energy resolved detector to investigate iodine-based and gadolinium-based contrast agents and, iodine-based and gold nanoparticle contrast agents, respectively, by basis decomposition analysis.
Alternatively, in this study we applied classification methodology to distinguish soft-tissue-like, bone-like materials, and contrast agents in reconstructed images. The method can be viewed as an extension of the low-vs-high-kVp plots used in dual-energy CT (e.g., Fig. 3 in Ref. 28) to multi-energy CT.
Theoretically, in the absence of K-edge absorption, materials with similar compositions (e.g., various soft-tissue-like materials) are expected to exhibit a similar dependence on Compton and photoelectric components of their attenuation coefficients (i.e., similar a1 and a2), with differences resulting mainly from differences in density. Consider a graph where the axes are the attenuation coefficient values measured at two energies; for a voxel containing a particular material, the slope of the line from the origin to the point defined by the attenuation coefficient in the voxel obtained at two energies is given by a density-independent constant
| (4) |
Thus, plotting attenuation coefficients in this space results in clusters of points lying along lines that define their material type (i.e., one line for soft-tissue-like materials, one line for bone-like materials, etc.). The same argument can be applied for two energy spectra or two energy windows, as long as no K-edge is present in the energy range investigated.
Using measurements from two energies, two pieces of spectral information are obtained, based on which two types of materials (e.g., soft-tissue-like and bone-like) can be separated. However, materials with K-edges in the energy range of interest demonstrate a different energy dependence from those without, especially around their K-shell binding energies. This is illustrated in Fig. 2, which shows the average linear attenuation coefficients for several materials in different energy ranges. In both plots, the soft-tissue-like materials (i.e., water, polymethyl methacrylate (PMMA), polytetrafluoroethylene (PTFE), and polyoxymethylene (POM)) tend to cluster along a line that passes through the origin. In Fig. 2a, the iodine solution lies far from the line, as the two energy ranges were chosen such that one was above (33–38 keV) and one was below (27–33 keV) the iodine K-edge (33.2 keV). Also from Fig. 2a, we can make the following observations: (1) Bone cannot be separated from soft-tissue-like materials due to their similar energy dependence in the two energy windows plotted in that figure (Fig. 1) and (2) since both ranges are below the gadolinium K-edge (50.2 keV), the attenuation of gadolinium behaves very similar to non-contrast-agent materials (Fig. 1) and, as a result, the gadolinium solution is collinear with and cannot be separated from the other soft-tissue-like materials.
Figure 2.
Theoretically calculated linear attenuations of different materials for different energy ranges (attenuation data obtained from Ref. 26). Two dotted lines label the soft-tissue-like and bone-like materials, which overlap in (a).
In Fig. 2b, if one range was chosen below (in this case 44–50 keV) the gadolinium K-edge (50.2 keV) and one above (in this case 50–80 keV), a similar significant separation can be observed for gadolinium as for iodine in Fig. 2a. Note that: (1) Bone is separated from soft-tissue-like materials, due to their different energy dependence in the two energy windows plotted (Fig. 1) and (2) unlike gadolinium in Fig. 2a, the attenuation coefficient of the iodine solution is not collinear with the attenuation coefficients of the soft-tissue-like materials, possibly because the iodine K-edge at 33.2 keV results in a different slope at this energy range, as indicated by Eq. 4.
The goal of this paper was to demonstrate, via simulations and physical experiments, that the above behavior can indeed be observed using a microCT system based on an energy resolved photon-counting detector.
METHODS
Physical experiments
We constructed a table-top microCT system29 based on an energy resolved photon-counting detector, designed and manufactured by Gamma Medica-Ideas (AS), Norway. The detector consisted of a cadmium telluride (CdTe) radiation sensor bonded to readout electronics implemented as a set of ASICs. It had one row of 512 pixels with an effective pixel pitch of 0.4 mm. The readout electronics had six adjustable energy thresholds for each pixel, each with an associated independent 16-bit counter. The useful operating energy range was 25–122 keV. In this study, the energy thresholds were set to 27, 29, 33, 40, 50, and 60 keV to straddle the iodine and gadolinium K-edges and to ensure comparable count levels in other energy windows.
The system used a SourceRay (Bohemia, NY) SB-120-350 x-ray generator system capable of up to 350 μA and 120 kVp with a 75 μm focal spot. The x-rays were collimated by a 1.6 mm wide lead slit to provide fan-beam x-ray irradiation. The x-ray tube had a beryllium exit window and was further filtered using a 0.79-mm thick aluminum filter to virtually eliminate x-rays with energies below the noise floor of the detector.
The detector was positioned 88.8 cm from the x-ray tube focal spot, while the phantom rotational stage was 20.3 cm from the tube focal spot (Figs. 3a, 4). Hence, magnification was 4.3 and the expected spatial resolution at isocenter was approximately 0.09 mm.
Figure 3.
(a) The microCT system used in this work. (b) The PMMA cylindrical phantom with holes for various inserts.
Figure 4.
A schematic drawing of the microCT system setup (the same geometry was modeled in the simulation experiments).
To investigate the imaging properties, we used a 2.54-cm diameter cylindrical phantom made from PMMA (or acrylic). The phantom (Fig. 3b) had five 4.8-mm diameter holes with centers at equiangular increments on a circle with a radius of 6.25 mm and centered on the axis of the cylinder. These holes could be filled with different solutions or solid rod inserts. We investigated materials including PMMA (or acrylic), PTFE (or Teflon™), POM (or Delrin™), polycarbonate, glycol-modified polyethylene terephthalate (PET), bone-equivalent plastic, water, and aqueous solutions with various concentrations of iodine-based (Omnipaque™350) or gadolinium-based (Magnevist™) contrast agents. The iodine and gadolinium K-edges are at 33.2 and 50.2 keV, respectively. The compositions of the materials imaged are listed in Table 1.
Table 1.
Summary of the materials investigated.
| Material name | Formula | Mass density (g∕cm3) |
|---|---|---|
| Water | H2O | 1.00 |
| PMMA | (C5H2O8)n | 1.19 |
| POM | (CH2O)n | 1.40–1.50 |
| PTFE | CnF2n+2 | 2.20 |
| PET | (C10H8O4)n | 1.45 |
| Polycarbonate | (C16H14O3)n | 1.20 |
| Bone-equivalent plastic | N∕A | 1.42 |
| Omnipaque™350 | C19H26I3N3O9 | N∕A |
| Magnevist™ | C28H54GdN5O20 | N∕A |
We used a 60 kV tube voltage and a 100 μA tube current. A low tube current was used in this study to minimize the effect of pulse pileup. Projection data were acquired over 360° with 1° increments. Bad pixels were identified as ones having either anomalously low or high count rates in the projection data. The pixel values in bad pixels were replaced with the average pixel values in the nearest properly operating neighboring pixels. We reconstructed the projections using a standard fan-beam filtered backprojection algorithm.
To exclude pulse pileup, the highest energy threshold was set to an energy equal to the tube voltage. Thus, data from five energy windows were available to perform material separation. A rectangular region of interest (ROI) was drawn over each material in the reconstructed images in each energy window to measure their respective linear attenuation coefficients.
To demonstrate the principles outlined in Sec. 2, we generated scatter plots of the linear attenuation coefficients of materials in various pairs of energy windows, similar to those presented in Fig. 2. Specifically, each axis of the plot represented the attenuation coefficient in one of the five energy windows. The goal was to investigate whether attenuation coefficients for the contrast agents fell along different lines than the other materials, indicating the capability to separate them in the object.
Simulation experiments
To provide a benchmark for performance of the physical experiments in the absence of degrading factors present in the real detector, we simulated an energy resolved photon-counting detector with an analytical CT projector (modified from Ref. 30). The detector specifications and system configurations were identical to those used in the physical experiments.
We measured the 60 kVp spectrum from the x-ray tube on the previously introduced microCT system with a commercial spectrometer (XR-100T-CdTe, Amptek Inc., Bedford, MA) and used it in the simulation. Quantum noise was modeled as a Poisson random variable. Other degrading effects including finite energy resolution, charge sharing, and pulse pileup were not modeled.
For comparison, dual-kVp acquisition with integrating detectors was also simulated using x-ray beams corresponding to tube voltages of 60 and 120 kV. Both the 60 and 120 kVp spectra were measured from the x-ray tube with the spectrometer. Preobject filtration identical to that in Ref. 10 was used to improve the spectral separation. The resulting postfiltering spectra are plotted in Fig. 5. The two spectra were scaled such that they had equal flux and the sum of their total flux equaled that of the 60 kVp spectrum used with the energy resolved photon-counting detector.
Figure 5.
The 60 and 120 kVp spectra used in the dual-energy simulation. The 60 kVp spectrum was filtered by 0.6 mm of titanium and the 120 kVp spectrum was filtered by 1.2 mm of titanium (as in Ref. 10) to improve the spectral separation between the two.
The simulated cylindrical phantom (Fig. 6) was 2.54 cm in diameter, with eight 4-mm diameter holes at equiangular increments on a circle with a radius of 6.35 mm and centered on the axis of the cylinder. Its dimension was comparable with the phantom used in the physical experiments except that there were more holes for inserts so that a greater number of materials could be imaged at the same time.
Figure 6.
The computer phantom used in the simulation experiments.
We investigated all of the materials used in the physical experiments, but with more combinations of volume concentrations of the two contrast agent solutions. Similarly, ROIs were drawn for each material and scatter plots were generated for the linear attenuation coefficients between various pairs of energy windows. For dual-kVp acquisition, the linear attenuation coefficients for the lower and higher kVp measurements were plotted (as in a standard low-vs-high-kVp plot used in dual-energy CT).
RESULTS
Simulation experiments
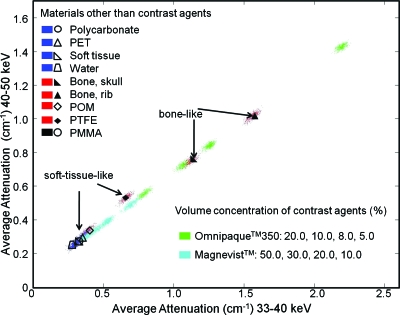
Figure 7 demonstrates the case for an energy resolved photon-counting detector when the choice of energy windows resulted in little or no separation of the materials. For display convenience, only the Omnipaque™350 and Magnevist™ solutions (no mixtures) are shown. The energy windows used in this plot were on the same side of the iodine and gadolinium K-edges. Thus, both the Compton and photoelectric dependences were continuous in the energy range considered and the approximation in Eq. 4 held. Note that almost all materials fell on a common line except for PTFE, which lay moderately above the line. This is possibly due to the different composition of PTFE, which contains a relatively large amount of fluorine compared to the other compounds, which contain mainly carbon, hydrogen, and oxygen.
Figure 7.
Linear attenuation coefficients measured for energy windows 33–40 (horizontal axis) and 40–50 keV (vertical axis) from the simulation experiments. The soft-tissue-like and bone-like materials are labeled by the color and marker combinations described in the legend. Also, since all the contrast agent solutions are collinear with the non-contrast-agent materials, their mixtures (not shown in this figure) will be collinear as well.
However, with one energy window below and the other above the iodine K-edge (33.2 keV), mixtures containing iodine (e.g., Omnipaque™350) significantly deviated from the soft tissue common line, as shown in Fig. 8. The concentrations of the two contrast agents in the mixture solutions are indicated by the lines that intersect at the point cluster (the legend is in the right bottom corner). For iodine-containing solutions, the distance to the noniodine-containing line (i.e., soft-tissue-like, bone-like, and gadolinium-only solutions) was approximately proportional to the concentration of iodine present in the sample, while variations in the gadolinium concentration resulted in almost parallel shifts of the clusters. Furthermore, consistent with theoretical prediction (Fig. 2a), this particular energy window combination could not separate bone from soft tissue.
Figure 8.
Linear attenuation coefficients measured for 29–33 (horizontal axis) and 33–40 keV (vertical axis).
An example of separating gadolinium-containing mixtures is shown in Fig. 9. The two energy windows were above and below the gadolinium K-edge (50.2 keV). The results are largely consistent with those from Fig. 8, with the concentration of gadolinium being proportional to the extent of deviation from the soft tissue common line. The results are also consistent with Fig. 2b, in which bone separated from soft-tissue-like materials in this energy window combination. These simulation experiments demonstrate the potential for using multiple energy windows to simultaneously separate soft tissue, bone, and materials with multiple K-edges.
Figure 9.
Linear attenuation coefficients measured for 40–50 (horizontal axis) and 50–60 keV (vertical axis).
One way to simultaneously visualize data from more than two (e.g., three) energy windows is to use 3-D “wall plots.” These show the projection of the data on three planes defined by three different energy window axes. With simultaneous data acquisition in multiple (e.g., five in this study) energy windows, it is theoretically feasible to generate 5-D plots including all the spectral information from the acquisitions. However, displaying and understanding scatter plots in a high dimensional space is difficult. The wall plots are a compromise, representing a 3-D scatter plot with projections in three 2-D planes. As suggested by the previous 2-D scatter plots, in some planes the projections were not separable, while in others, significant separation was observed due to the K-edge discontinuity, as shown in Fig. 10 (iodine) and Fig. 11 (gadolinium).
Figure 10.
Linear attenuation coefficients measured for 29–33, 33–40, and 40–50 keV.
Figure 11.
Linear attenuation coefficients measured for 33–40, 40–50, and 50–60 keV.
For comparison, a low-vs-high-kVp scatter plot (Fig. 12) was generated using the dual-kVp data. The separation among the contrast agents was smaller compared to Figs. 89. Also, to specify various target materials (e.g., iodine in Fig. 8 and gadolinium in Fig. 9), dual-kVp techniques require choosing suitable filtering materials and multiple acquisitions∕exposures. On the other hand, energy resolved photon-counting only requires the use of appropriate energy threshold settings, which does not require knowledge of the energy spectra and is relatively easy to implement using current detector technology.
Figure 12.
Linear attenuation coefficients measured for 60 (horizontal axis) and 120 kVp (vertical axis).
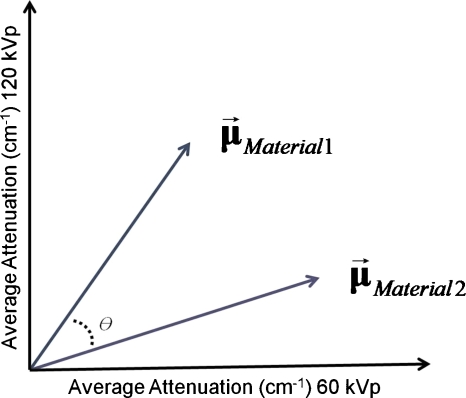
For other non-contrast-agent materials, the additional information provided by the multiple energy windows also helped to separate them. To partially quantify the difference in separation, we used the separation angle θ between the vectors of attenuation coefficients. θ is defined as the angle between the vector of linear attenuations coefficients for two materials. For instance, for dual-kVp CT, θ is defined as in Fig. 13, where and . Thus, . Note that the vectors involved can be of arbitrary dimension.
Figure 13.
The separation angle θ between two materials was defined to quantify the amount of separation achieved.
For acquisition from energy resolved photon-counting detectors, θ can be similarly computed from the dot product of the attenuation vector . Here, consists of measurements from all of the energy windows (five in this study) or any subset of them.
Since the attenuation vectors in this study were measured at multiple pixels in a ROI, an average vector was computed for each material and each energy window∕kVp over multiple pixels. The error bars in the separation angle calculations therefore result directly from noise (and artifacts, if they exist) in the reconstructed images.
The separation angle θ between other non-contrast-agent targets and the PMMA background was computed. For the dual-kVp approach, measurements with both kVps were used, while in the energy resolved photon-counting approach, measurements from all five windows were used. The result is plotted in Fig. 14. For non-contrast-agent materials, energy resolved photon-counting provided improved separation from the background compared to the dual-kVp approach.
Figure 14.
The separation angles (in radians) were computed for all non-contrast-agent materials using both the dual-kVp acquisition (“dual-kVp-integrating”) and the energy resolved photon-counting (“five-window-counting”) acquisition approaches.
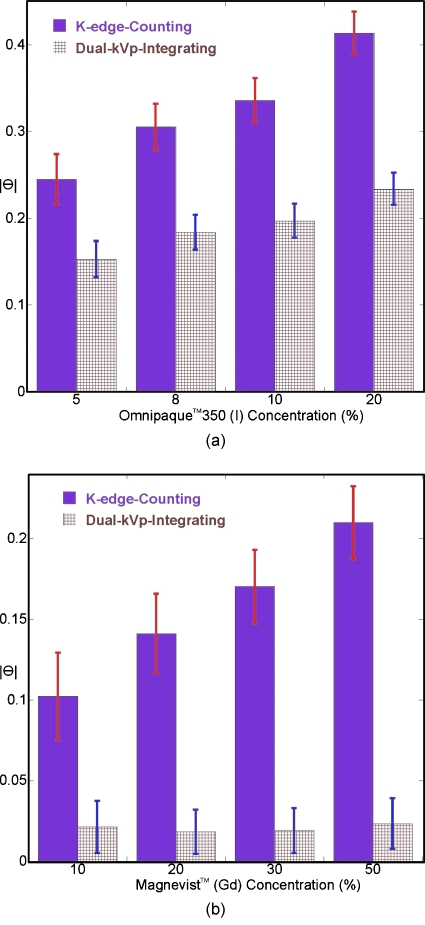
For contrast agents, as described previously, energy resolved photon-counting provided an easy way to choose different energy window pairs to specify various target material with a single acquisition. Figure 15a plots the separation angles (with respect to PMMA background) for different concentrations of Omnipaque™350 solutions. Here, for energy resolved photon-counting, only measurements from 29–33 to 33–40 keV were used (“K-edge-counting”) to separate iodine.
Figure 15.
The separation angles (in radians) were computed for contrast agent solutions using both the dual-kVp acquisition approach and the energy resolved photon-counting acquisition approach. The latter only utilized energy windows immediately below and above the respective K-edge. Plots are shown for (a) the iodine-based contrast agent Omnipaque™350 and (b) the gadolinium-based contrast agent Magnevist™.
Figure 15b shows similar results for Magnevist™ solutions: Measurements from 40–50 and 50–60 keV were used to separate gadolinium using energy resolved photon-counting. Consistent with Figs. 8912, as well as theoretical predictions, comparing attenuation coefficients below and above a K-edge for contrast agents provided improved separation with respect to the background and the separation angle θ monotonically increased with increasing contrast agent concentrations.
Physical experiments
We simultaneously imaged three cylindrical phantoms with the microCT system described in Sec. 3A. Two of the cylinders were filled with mixtures of different volume concentrations of the two contrast agents and the other cylinder contained solid inserts of bone-equivalent plastic and the soft-tissue-like materials PTFE, POM, polycarbonate, and water.
In Fig. 16, when one energy window was below the iodine K-edge (33.2 keV) and the other above it, the attenuation coefficient values from voxels in the soft-tissue-like materials (PMMA, PTFE, POM, polycarbonate, and water), bone-equivalent plastic, and gadolinium-only solutions clustered along a common line (dotted), consistent with theoretical calculations (e.g., see Fig. 2a). As the simulation experiments predicted, solutions with high iodine concentrations, both those with and without gadolinium, lay above the soft tissue common line, although they displayed less separation compared to the simulation results (Fig. 19, to be discussed in Sec. 5).
Figure 16.
Linear attenuation coefficient scatter plot for 29–33 (horizontal axis) and 33–40 keV (vertical axis) windows from the physical experiments. The distributions of the attenuation coefficients for soft-tissue-like and bone-like materials are labeled by a dotted line, as they are collinear (consistent with Figs. 2a, 8).
Figure 19.
The separation angles (in radians) were computed for contrast agent solutions (no mixtures). For both types of contrast agent, a pair of windows straddling its respective K-edge was used (e.g., 29–33 and 33–40 keV for iodine and 40–50 and 50–60 keV for gadolinium).
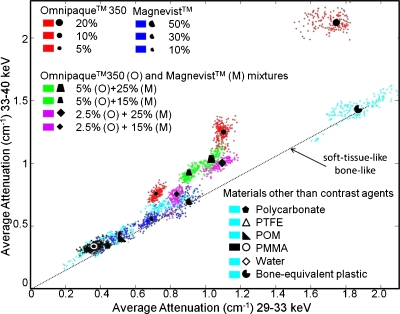
A similar phenomenon was observed (Fig. 17) with one energy window below and the other above the gadolinium K-edge (50.2 keV). There was strong separation for solutions with high gadolinium concentrations, which again confirms that the discontinuity in the attenuation coefficient curve causes this separation. Also, in contrast with iodine (Fig. 16), the result for gadolinium was in very good agreement with the previous simulation experiments (Fig. 19). Bone-equivalent plastic and iodine-only solutions fell below the soft tissue common line, also consistent with the theoretical calculations (Fig. 2b).
Figure 17.
Linear attenuation scatter plots for 40–50 (horizontal axis) and 50–60 keV (vertical axis) windows. The distributions of the attenuation coefficients for soft-tissue-like and bone-like materials are labeled by two dotted lines (which overlap in Fig. 16).
These data suggest that the contrast agent and bone could be separated from soft tissue and each other by scatter plots from multi-energy-window measurements and classification methods. We observed that the energy window combination that provided the best separation from soft-tissue-like materials was different for each material. For the two contrast agents used in this study, the largest separation was obtained with one window above and one window below the K-edge of the contrast agent.
Similar to Figs. 1415, the separation angles with respect to the PMMA background were computed. Figure 18 compares the results for the non-contrast-agent materials, while Fig. 19 compares the results for the nonmixture contrast agent solutions. Figure 18 demonstrates consistency between the simulations and physical experiments, although, as would be expected, due to degrading factors such as ring artifacts, finite energy resolution, charge sharing, and pulse pileup, the separation angles are smaller with the real detector than with the simulation for all materials except POM. Figure 19 further supports the previous observation that the degree of separation provided by the K-edge is proportional to the contrast agent concentration. While dual-kVp physical experiments were not available for comparison in this study, the consistency between the observed degree of angular separation between the simulations and physical experiments is indirect evidence of the superior material separation provided by the energy resolved photon-counting device.
Figure 18.
The separation angles (in radians) were computed for all non-contrast-agent materials and compared to the previous simulations. Measurements from all five windows were used for non-contrast-agent materials.
DISCUSSION
In the simulations and physical experiments, the separation angles of soft-tissue-like and bone-like materials were measured using their attenuation coefficients from all five energy windows. If these were to be measured from two windows (as was done with the contrast agent solutions), we could expect them to be also dependent on the choices of energy window pairs. For instance, bone is collinear with soft-tissue-like materials in the energy window combination in Fig. 16 but is not in Fig. 17.
The above phenomenon, as well as other information (e.g., density, prior knowledge, etc), can aid the separation of three or more biological tissue types that do not have a K-edge in the energy range of interest (e.g., bone, fat, and muscle). Without K-edges, chemical compositions and densities are the keys to distinguishing these tissues. Biological tissues can be generally categorized into three categories: Bone (high Z), fat (low density), and others (close to water). Distinguishing tissues between categories is relatively simple based on their respective category properties. For instance, despite falling along a common line, water (low density) and PTFE (high density) can be separated by their different vector norms (e.g., as shown in Figs. 1617). On the other hand, water (low Z) and bone (high Z) can be separated by their different energy dependence (e.g., different separation angles shown in Figs. 917). Note that the separation angle used in this paper is largely determined by the chemical composition. In future works, it may be desirable to incorporate the vector norm information to help distinguish different densities.
Separating biological tissues in the same category can be challenging due to their similar compositions (Z) and densities. The ability to distinguish these tissues depends on image noise (which is related to dose), the properties of these tissues, and variations within the same tissue type (e.g., different types of soft tissue, skull bone vs rib bone, etc., as shown in Figs. 789). This task is highly complicated, calling for a systematic evaluation of both the imaging system and the separation methodology. A complete evaluation of this problem is beyond the scope of the current paper and thus is not included here.
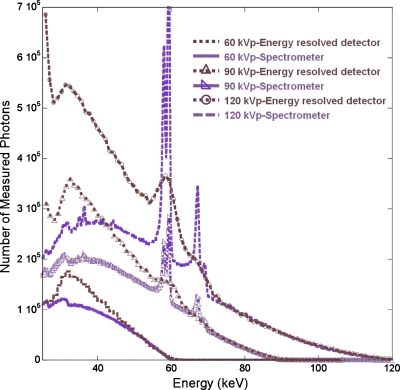
One observation from the physical experiments that differs strongly from the simulation experiments is that, compared to gadolinium, iodine separation was more difficult than was theoretically predicted (Figs. 1619). We hypothesized that various degrading factors present in the physical system resulted in larger spectral distortions around the iodine K-edge (33.2 keV) than at higher energies. To validate this assumption, we measured polychromatic spectra from the x-ray tube used in the microCT system with the investigated energy resolved detector and compared the results to measurements from the spectrometer. The results (Fig. 20) show a significant excess of detected events at low energies near those of the iodine K-edge.
Figure 20.
60, 90, and 120 kVp tube spectra measured by the energy resolved photon-counting detector and the spectrometer.
These measurements were performed with low tube currents (50 μA) so pulse pileup was modest and would largely affect higher energies. Energy resolution does contribute to the widening and blurring of the features (e.g., the tungsten characteristic x-rays), but cannot account for these large discrepancies at low energies. We suspect that a combination of charge sharing and electronic noise (the noise floor of the photon-counting detector used in this work was ∼23–24 keV) contribute to this effect. Since the proposed separation method relies on accurate measurements of the attenuation coefficients, such spectral distortions can significantly reduce its effectiveness.
Previous authors have shown that charge sharing resulted in significant spectral distortion in x-ray and gamma ray detection. For example, Refs. 31, 32 reported significant charge sharing in CdZnTe detectors at 662 and 122 keV gamma ray energies. The energy resolved photon-counting detector investigated in this study had a similar pixel pitch and crystal thickness and was operated under a comparable bias voltage to those employed in Refs. 31, 32. The carrier properties in CdTe are also similar to those in CdZnTe. Thus, we expected that charge sharing would be a major contributing effect to the observed spectral distortions and the resulting difficulty in separating iodine. However, due to the different energies of the gamma rays and x-rays used, the magnitudes of distortion would vary. In addition to charge sharing, there are other effects (e.g., pulse pileup and characteristic x-ray) that also result in distortions to the spectral measurements. We are currently working to identify the sources of the observed spectral distortions and eventually model and compensate for these distortions in energy resolved photon-counting detectors.33
The current study focused on the imaging of mouse-sized objects. Both the system configuration and phantom dimensions were chosen to realistically demonstrate the separation concept for a small animal imaging application. There are additional challenges in extending this concept and quantitative analysis to human imaging applications. For example, although scatter contamination is not a major issue in imaging mouse-sized objects,34 it is much more severe in human imaging due to larger object sizes. For the same reason, beam hardening can be significant even within relatively narrow energy windows,35 resulting in inaccurate measurements of the linear attenuation coefficients and difficulties in accurately quantifying contrast agents based on the proposed principle. Human imaging also requires larger x-ray fluxes, which will contribute to pulse pileup, spectral distortions, and count rate losses in counting detectors.36
CONCLUSIONS
We have demonstrated that an energy resolved photon-counting detector with more than two energy windows can allow the discrimination of more than two types of materials (e.g., soft tissue, bone, and one or more contrast agents) having K-edges in the energy range of interest.
The simulation experiments not only validated this principle, but also showed the potential to provide quantitative estimates of the concentration of the contrast agents present in the sample. In the physical experiments, despite imperfect detector behavior due to finite energy resolution, ring artifacts, pulse pileup, and charge sharing, it was still possible to separate four materials using energy windows straddling K-edge discontinuities in the attenuation coefficients. Furthermore, and consistent with the simulations, the concentrations of the contrast agents determined the amount of separation from the non-contrast-agent materials. These results indicate that quantitative separation is possible in practice, but that advances in hardware and software corrections are needed to fully exploit this capability.
ACKNOWLEDGMENTS
This work was supported by NIH NCRR Grant No. 2R44021794. The authors also thank the careful and constructive suggestions made by the anonymous Associate Editor and reviewers that helped improve the quality of this manuscript.
References
- Kalender W. A., Perman W. H., Vetter J. R., and Klotz E., “Evaluation of a prototype dual-energy computed tomographic apparatus. I. Phantom studies,” Med. Phys. 13, 334–339 (1986). 10.1118/1.595958 [DOI] [PubMed] [Google Scholar]
- Marshall W., Hall E., Doost-Hoseini A., Alvarez R., Macovski A., and Cassel D., “An implementation of dual energy CT scanning,” J. Comput. Assist. Tomogr. 8, 745–749 (1984). 10.1097/00004728-198408000-00029 [DOI] [PubMed] [Google Scholar]
- W. H.Marshall, Jr., Alvarez R. E., and Macovski A., “Initial results with prereconstruction dual-energy computed tomography (PREDECT),” Radiology 140, 421–430 (1981). [DOI] [PubMed] [Google Scholar]
- Flohr T. G., McCollough C. H., Bruder H., Petersilka M., Gruber K., Suss C., Grasruck M., Stierstorfer K., Krauss B., Raupach R., Primak A. N., Kuttner A., Achenbach S., Becker C., Kopp A., and Ohnesorge B. M., “First performance evaluation of a dual-source CT (DSCT) system,” Eur. Radiol. 16, 256–268 (2006). 10.1007/s00330-005-2919-2 [DOI] [PubMed] [Google Scholar]
- Pavlicek W., Panse P., Hara A., Boltz T., Paden R., Yamak D., Licato P., Chandra N., Okerlund D., Dutta S., Bhotika R., and Langan D., “Initial use of fast switched dual energy CT for coronary artery disease,” Proc. SPIE 7662, 76221V (2010). 10.1117/12.844859 [DOI] [Google Scholar]
- Alvarez R. E., Seibert J. A., and Thompson S. K., “Comparison of dual energy detector system performance,” Med. Phys. 31, 556–565 (2004). 10.1118/1.1645679 [DOI] [PubMed] [Google Scholar]
- Brooks R. A. and Di Chiro G., “Split-detector computed tomography: A preliminary report,” Radiology 126, 255–257 (1978). [DOI] [PubMed] [Google Scholar]
- Drost D. J. and Fenster A., “Experimental dual xenon detectors for quantitative CT and spectral artifact correction,” Med. Phys. 7, 101–107 (1980). 10.1118/1.594672 [DOI] [PubMed] [Google Scholar]
- Stevens G. M. and Pelc N. J., “Depth-segmented detector for x-ray absorptiometry,” Med. Phys. 27, 1174–1184 (2000). 10.1118/1.598982 [DOI] [PubMed] [Google Scholar]
- Mahnken A. H., Stanzel S., and Heismann B., “Spectral rhoZ-projection method for characterization of body fluids in computed tomography: Ex vivo experiments,” Acad. Radiol. 16, 763–769 (2009). 10.1016/j.acra.2009.01.002 [DOI] [PubMed] [Google Scholar]
- Primak A. N., Ramirez Giraldo J. C., Liu X., Yu L., and McCollough C. H., “Improved dual-energy material discrimination for dual-source CT by means of additional spectral filtration,” Med. Phys. 36, 1359–1369 (2009). 10.1118/1.3083567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito M., “Spectral optimization for measuring electron density by the dual-energy computed tomography coupled with balanced filter method,” Med. Phys. 36, 3631–3642 (2009). 10.1118/1.3157098 [DOI] [PubMed] [Google Scholar]
- Schlomka J. P., Roessl E., Dorscheid R., Dill S., Martens G., Istel T., Baumer C., Herrmann C., Steadman R., Zeitler G., Livne A., and Proksa R., “Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography,” Phys. Med. Biol. 53, 4031–4047 (2008). 10.1088/0031-9155/53/15/002 [DOI] [PubMed] [Google Scholar]
- Shikhaliev P. M., “Tilted angle CZT detector for photon counting/energy weighting x-ray and CT imaging,” Phys. Med. Biol. 51, 4267–4287 (2006). 10.1088/0031-9155/51/17/010 [DOI] [PubMed] [Google Scholar]
- Arfelli F., Bonvicini V., Bravin A., Cantatore G., Castelli E., Dalla Palma L., Di Michiel M., Longo R., Olivo A., Pani S., Pontoni D., Poropat P., Prest M., Rashevsky A., Tromba G., Vacchi A., and Vallazza E., “At the frontiers of digital mammography: SYRMEP,” Nucl. Instrum. Methods Phys. Res. A 409, 529–533 (1998). 10.1016/S0168-9002(97)01309-0 [DOI] [Google Scholar]
- Beuville E., Cahn R., Cederstrom B., Danielsson M., Hall A. L., Hasegawa B., Luo L., Lundqvist M., Nygren D., Oltman E., and Walton J., “High resolution x-ray imaging using a silicon strip detector,” IEEE Trans. Nucl. Sci. 45, 3059–3063 (1998). 10.1109/23.737664 [DOI] [Google Scholar]
- Tumer T. O., Clajus M., Visser G. I., Yin S., Willson P. D., D’Aries L., Parnham K. B., Glick B., Perry J. L., Gamble T., Creede G., Worthington E., Sparling J., Maeding D., and Gorzen D., “Preliminary results obtained from a novel CdZnTe pad detector and readout ASIC developed for an automatic baggage inspection system,” in IEEE Nuclear Science Symposium and Medical Imaging Conference Record, 2000. (unpublished).
- Kruger R. A., Armstrong J. D., Sorenson J. A., and Niklason L. T., “Dual energy film subtraction technique for detecting calcification in solitary pulmonary nodules,” Radiology 140, 213–219 (1981). [DOI] [PubMed] [Google Scholar]
- Goodsitt M. M., Rosenthal D. I., Reinus W. R., and Coumas J., “Two postprocessing CT techniques for determining the composition of trabecular bone,” Invest. Radiol. 22, 209–215 (1987). 10.1097/00004424-198703000-00005 [DOI] [PubMed] [Google Scholar]
- Liu X., Yu L., Primak A. N., and McCollough C. H., “Quantitative imaging of element composition and mass fraction using dual-energy CT: Three-material decomposition,” Med. Phys. 36, 1602–1609 (2009). 10.1118/1.3097632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michael G. J., “Tissue analysis using dual energy CT,” Australas. Phys. Eng. Sci. Med. 15, 75–87 (1992). [PubMed] [Google Scholar]
- Roessl E. and Proksa R., “K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors,” Phys. Med. Biol. 52, 4679–4696 (2007). 10.1088/0031-9155/52/15/020 [DOI] [PubMed] [Google Scholar]
- Cormode D. P., Roessl E., Thran A., Skajaa T., Gordon R. E., Schlomka J. P., Fuster V., Fisher E. A., Mulder W. J., Proksa R., and Fayad Z. A., “Atherosclerotic plaque composition: Analysis with multicolor CT and targeted gold nanoparticles,” Radiology 256, 774–782 (2010). 10.1148/radiol.10092473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez R. E. and Macovski A., “Energy-selective reconstructions in x-ray computerized tomography,” Phys. Med. Biol. 21, 733–744 (1976). 10.1088/0031-9155/21/5/002 [DOI] [PubMed] [Google Scholar]
- Victoreen J. A., “The absorption of incident quanta by atoms as defined by the mass photoelectric absorption coefficient and the mass scattering coefficient,” J. Appl. Phys. 19, 855–860 (1948). 10.1063/1.1698220 [DOI] [Google Scholar]
- Berger M. J., Hubbell J. H., Seltzer S. M., Chang J., Coursey J. S., Sukumar R., and Zucker D. S., XCOM: Photon cross section database.
- Lehmann L. A., Alvarez R. E., Macovski A., Brody W. R., Pelc N. J., Riederer S. J., and Hall A. L., “Generalized image combinations in dual KVP digital radiography,” Med. Phys. 8, 659–667 (1981). 10.1118/1.595025 [DOI] [PubMed] [Google Scholar]
- Johnson T. R., Krauss B., Sedlmair M., Grasruck M., Bruder H., Morhard D., Fink C., Weckbach S., Lenhard M., Schmidt B., Flohr T., Reiser M. F., and Becker C. R., “Material differentiation by dual energy CT: Initial experience,” Eur. Radiol. 17, 1510–1517 (2007). 10.1007/s00330-006-0517-6 [DOI] [PubMed] [Google Scholar]
- Wang X., Meier D., Sundal B. M., Øya P., Maehlum G. E., Wagenaar D. J., Tsui B. M. W., Patt B. E., and Frey E. C., “A digital line-camera for energy resolved x-ray photon counting,” in IEEE Nuclear Science Symposium and Medical Imaging Conference Record, Vol. M09-383, 2009. (unpublished).
- Segars W. P., Mahesh M., Beck T. J., Frey E. C., and Tsui B. M., “Realistic CT simulation using the 4D XCAT phantom,” Med. Phys. 35, 3800–3808 (2008). 10.1118/1.2955743 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Z., Li W., Knoll G. F., Wehe D. K., and Du Y. F., “Effects of charge sharing in 3-D position sensitive CdZnTe gamma-ray spectrometers,” Nucl. Instrum. Methods Phys. Res. A 439, 619–624 (2000). 10.1016/S0168-9002(99)00841-4 [DOI] [Google Scholar]
- Kalemci E. and Matteson J. L., “Investigation of charge sharing among electrode strips for a CdZnTe detector,” Nucl. Instrum. Methods Phys. Res. A 478, 527–537 (2002). 10.1016/S0168-9002(01)00892-0 [DOI] [Google Scholar]
- Wang X., Dirk M., Hugg J., Chowdhury S., Wagenaar D. J., Patt B. E., and Frey E. C., “Modeling spectral distortions in energy resolved photon-counting x-ray detectors,” in Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference, Knoxville, TN, 2010. (unpublished).
- Frey E. C., Wang X., Du Y., Taguchi K., Xu J., and Tsui B. M. W., “Investigation of the use of photon counting x-ray detectors with energy discrimination capability for material decomposition in micro-computed tomography,” Proc. SPIE 6510, 65100A (2007). 10.1117/12.711711 [DOI] [Google Scholar]
- Shikhaliev P. M., “Beam hardening artefacts in computed tomography with photon counting, charge integrating and energy weighting detectors: A simulation study,” Phys. Med. Biol. 50, 5813–5827 (2005). 10.1088/0031-9155/50/24/004 [DOI] [PubMed] [Google Scholar]
- Taguchi K., Frey E. C., Wang X., Iwanczyk J. S., and Barber W. C., “An analytical model of the effects of pulse pileup on the energy spectrum recorded by energy resolved photon counting x-ray detectors,” Med. Phys. 37, 3957–3969 (2010). 10.1118/1.3429056 [DOI] [PMC free article] [PubMed] [Google Scholar]