Geodesic image regression with a sparse parameterization of diffeomorphisms

James Fishbaugh; Marcel Prastawa; Guido Gerig; Stanley Durrleman

doi:10.1007/978-3-642-40020-9_9

. Author manuscript; available in PMC: 2015 Feb 4.

Published in final edited form as: Geom Sci Inf (2013). 2013;8085:95–102. doi: 10.1007/978-3-642-40020-9_9

Geodesic image regression with a sparse parameterization of diffeomorphisms

James Fishbaugh ¹, Marcel Prastawa ¹, Guido Gerig ¹, Stanley Durrleman ²

PMCID: PMC4316381 NIHMSID: NIHMS626565 PMID: 25664349

Abstract

Image regression allows for time-discrete imaging data to be modeled continuously, and is a crucial tool for conducting statistical analysis on longitudinal images. Geodesic models are particularly well suited for statistical analysis, as image evolution is fully characterized by a baseline image and initial momenta. However, existing geodesic image regression models are parameterized by a large number of initial momenta, equal to the number of image voxels. In this paper, we present a sparse geodesic image regression framework which greatly reduces the number of model parameters. We combine a control point formulation of deformations with a L¹ penalty to select the most relevant subset of momenta. This way, the number of model parameters reflects the complexity of anatomical changes in time rather than the sampling of the image. We apply our method to both synthetic and real data and show that we can decrease the number of model parameters (from the number of voxels down to hundreds) with only minimal decrease in model accuracy. The reduction in model parameters has the potential to improve the power of ensuing statistical analysis, which faces the challenging problem of high dimensionality.

1 Introduction

A prominent tool for longitudinal analysis in medicine is regression of imaging data. Regression allows data from different subjects to be brought into temporal alignment, including images acquired at different time points and with different number of observations. Furthermore, regression is a necessary tool to align imaging data with cognitive assessments not necessarily acquired at the same time. Many longitudinal analysis frameworks require to compare such individual trajectories across populations [4,6,8,9,12]. Several methods for regression have been proposed, including the extension of piecewise linear regression to shapes represented as currents [4]. In [5,14] second-order models have been proposed which ensure that trajectories of shape change are smooth in time. Kernel regression was extended to image time series in [2]. These models require to store model parameters over time in order to characterize the evolution. This makes their use for statistical analysis cumbersome, as statistics are most naturally performed when model parameters can be compared in a common space.

This problem is addressed in the work of [7,11,13] where geodesic regression is proposed for image time series as well as in the Riemannian setting. The geodesic regression model is generative, being fully characterized by the baseline image (the intercept) and the momenta vectors defining the geodesic at the baseline image (the slope). While these models cannot match the observed data as closely as the class of non-generative models discussed above (in general), the power of such models lies in the simplification of the statistical analysis. To compare two trajectories of change, one only needs to compare the initial conditions [10].

Although model parameters are located only at a baseline time point, the geodesic regression models of [11,13] still require to store a large number of parameters. In fact, the number of parameters for these geodesic regression models is equal to the number of image voxels, which can quickly become unwieldy, particularly for 3D medical images. However, the dynamics of image evolution are likely characterized by considerably fewer parameters. Intuitively, momenta should be concentrated in areas where the most dynamic changes are occurring.

In this paper, we present a new geodesic image regression framework which decouples the parameterization of the time-varying deformations from the specific representation of the images. This allows the number of model parameters to reflect the complexity of anatomical changes in time rather than the sampling of the images. An upper bound on the dimensionality of the deformation is chosen by the user, and a L¹ penalty selects the most relevant subset of initial momenta, those that describe the most salient changes over time. We apply our sparse geodesic regression model to both synthetic and real data and show that we can decrease the number of model parameters (from the number of voxels down to hundreds) with only minimal decrease in model accuracy.

2 Methods

The goal of image regression is to infer the continuous image evolution which best describes a discrete set of observed images O_{t_i} at time t_i within the time interval [t₀, T]. The dynamics of image evolution are modeled as the geodesic flow of diffeomorphisms applied to a baseline image I₀, defined as $I (t) = I_{0} \circ ϕ_{t}^{- 1}$ .

Let y = (y₁, …, y_M) be the physical coordinates of the pixel locations of the observed image furthest in time. The trajectory of the image points can be written as $Y (t, y) = ϕ_{t}^{- 1} (y)$ where Y(0, y) = y The trajectory Y(t, y) can then be used to interpolate the gray values of the neighboring voxels in the baseline image, allowing image evolution to be written as I(t, y) = I₀(Y(t, y)). The variational framework for image regression can be expressed by the criterion

E (I_{0}, ϕ_{t})) = \sum_{i = 1}^{N_{obs}} {‖ I_{0} (Y (t_{i})) - O_{t_{i}}) ‖}_{L^{2}}^{2} + Reg (ϕ) = \sum_{i = 1}^{N_{obs}} D (I_{0} (Y (t_{i})), O_{t_{i}}) + L (ϕ)

(1)

where D represents the squared distance between images and L is a measure of the regularity of the entire time-varying deformation ϕ_t for all times t.

2.1 Discrete parameterization of deformations

The dense flow of diffeomorphisms ϕ_t is constructed by interpolating a discrete set of momenta located at self-interacting control points [3]. Let c₀ = {c₁, …, c_N_c} be a finite set of control points and corresponding initial momenta vectors α₀ = {α₁, …, α_{N_c}}, which together form the initial state of the system S₀ = {c₀,α₀}.

The set of particles act as initial conditions for the geodesic equations of motion, which define the trajectory of the control points and momenta forward in time:

{\begin{matrix} ċ_{i} (t) = \sum_{p = 1}^{N_{c}} K (c_{i} (t), c_{p} (t)) α_{p} (t) \\ {α̇}_{i} (t) = - \sum_{p = 1}^{N_{c}} α_{i} {(t)}^{t} α_{p} (t) \nabla_{1} K (c_{i} (t), c_{p} (t)) \end{matrix}

(2)

such that the energy of the system is conserved over time and K is the interpolating kernel governing the interaction between control points. The state of the system S(t) = {c_i(t), α_i(t)} evolves according to these equations, which will be written in short as S(t) = F(S(t)).

The trajectories of control points c_i(t) and α_i(t) parameterize a time-varying velocity field

υ (x, t) = \sum_{p = 1}^{N_{c}} K (x, c_{p} (t)) α_{p} (t) .

(3)

which is defined at any point in space x and time t. The starting pixel locations y follow the trajectory $Y (t, y) = ϕ_{t}^{- 1} (y)$ , which evolves in time by the ODE

Ẏ (t, y) = - [d_{y} Y (t, y)] υ (y, t) with Y (0, y) = y .

(4)

which is written in short as Ẏ (t, ․) = G(Y(t, ․), S(t)).

Using the pixel locations y as final conditions at time T, integrating this ODE backwards in time computes the inverse deformation of the pixel coordinates from time T to t₀. The deformed pixel locations Y(t) are used to interpolate the gray values of the neighboring voxels in the baseline image. Therefore the flow of diffeomorphisms is fully determined by the initial state of the system S₀.

2.2 Regression criterion and minimization

The initial state of the system S₀ = {c₀, α₀} consists of N_c control points and momenta vectors which fully parameterize the geodesic flow of diffeomorphisms ϕ_t in the criterion (2), acting as initial conditions for the flow equations (2). The deformation can then be applied to the pixel coordinates y according to this flow by solving equation (4) and deformed images can be constructed by interpolating the baseline image I(t) = I₀(Y(t)). Geodesic image regression is now described by the specific regression criterion

E (I_{0}, S_{0}) = \sum_{i = 1}^{N_{obs}} \frac{1}{2 λ^{2}} D (Y (t_{i})) + L (S_{0})

(5)

subject to

{\begin{matrix} Ṡ (t) = F (S (t)) & with S (0) = {c_{0}, α_{0}} \\ Ẏ (t) = G (Y (t), S (t) & with Y (0, y) = y \end{matrix}

(6)

where λ² is the tradeoff parameter and $L (S_{0}) = \sum_{p, q} α_{0, p}^{t} K (c_{0, p}, c_{0, q}) α_{0, q}$ is the kinetic energy of the particles. The first part of (6) governs the time evolution of the control points and momenta as in (2). The second equation of (6) represents flowing the pixel coordinates along the deformation defined by S(t) as in (4).

Gradient with respect to control points and initial momenta

The gradient of the criterion (5) with respect to the initial state of the system is

\nabla_{S_{0}} E = ξ (0) + \nabla_{S_{0}} L

(7)

where the auxiliary variables θ(t) and ξ(t) = {ξ^c, ξ^α} satisfy the ODEs:

\begin{matrix} θ̇ (t) = - \partial_{1} G {(t)}^{t} θ (t) + \sum_{i = 1}^{N_{Obs}} \nabla_{Y (t_{i})} D (t_{i}) δ (t - t_{i}) & θ (T) = 0 \\ ξ̇ (t) = - (\partial_{2} G {(t)}^{t} θ (t) + d_{S (t)} F {(t)}^{t} ξ (t)) & ξ (T) = 0 \end{matrix}

(8)

The gradient is computed by first integrating equations (2) forward in time to construct the flow of diffeomorphisms. The deformations are then applied by integrating equation (4) backward in time. With the full trajectory of the deformed pixel coordinates, one can compute the gradient of the data term ∇_{Y(t_i)}D(t_i), corresponding to each observation. The ODEs (8) are then integrated backwards in time, with the gradients of the data term added at observation time points. The final values of the auxiliary ξ(t₀) is then used to update the location of the control points and initial momenta.

Gradient with respect to baseline image

The gradient with respect to the baseline image I₀ can be computed as the sum of gradients ∇_I₀D(Y(t_i),O_{t_i}) for each observed image O_{t_i}. Recall that the intensity of the baseline image I₀(Y_k(t)) for some voxel k and time t is computed by interpolating gray values, written as ∑_p∈𝒩(Y_k(t)) ρ_p(Y_k(t))I₀(π_p(Y_k(t))) in a neighborhood 𝒩 of voxels π around Y_k(t) with weights ρ from bilinear (2D) or trilinear (3D) interpolation. Let R_{t_i} be the residual image I₀(Y(t_i)) − O_{t_i}. Then a variation I₀ leads to

δ D (Y (t_{i})) = \sum_{i = 1}^{N_{obs}} \sum_{k = 1}^{N_{vox}} R_{t_{i}} (Y_{k} (t_{i})) \sum_{p \in 𝒩 (Y_{k} (t))} ρ_{p} (Y_{k} (t)) δ I_{0} (π_{p} (Y_{k} (t)))

(9)

= \sum_{i = 1}^{N_{obs}} [\sum_{k = 1}^{N_{vox}} ρ_{p} (Y_{k} (t_{i})) R_{t_{i}} (Y_{k} (t_{i}))] δ I_{0} (π_{p} (Y_{i} (t_{i}))) .

(10)

The gradient of D is computed by flowing a voxel Y_k(t) to time t and computing the residual. The gray value in the residual image at voxel k is then distributed to its neighboring voxels with weights defined by bilinear or trilinear interpolation. The summation over observations shows that the gray values are accumulated for every observed image.

2.3 Sparsity on initial momenta

To determine the optimal number of control points/momenta, we introduce a L¹ penalty used in the context of atlas building [3] to the regression criterion:

E (I_{0}, S_{0}) = \sum_{i = 1}^{N_{obs}} \frac{1}{2 λ^{2}} D (Y (t_{i})) + L (S_{0}) + γ_{s p} \sum_{i = 1}^{N_{c}} ‖ α_{i} (t_{0}) ‖

(11)

where N_c denotes the total number of control points and $α_{k}^{i}$ is the kth initial momentum. We use the Fast Iterative Shrinkage and Thresholding Algorithm [1] to optimize the regression criterion (11) which now contains non-differentiable terms. The update equations for the baseline image, control points, and initial momenta are not affected by the L¹ term. The update equation for momenta can be found in [3], which involves a soft thresholding function to eliminate momenta with small magnitude.

3 Experiments

Synthetic Evolution

We first explore a synthetic image time series. The synthetic data, shown in Fig. 1, was generated by shooting the baseline image along predefined initial momenta. The resulting evolution is therefore geodesic, which serves as a best case scenario for our model. We explore the impact of the sparsity parameter by estimating several geodesic models with a range of values of γ_sp. Each model was initialized with control points distributed on a regular grid with 20 pixel spacing, deformation kernel σ_V = 20 pixels, and λ = 0.5.

The estimated baseline shape and initial momenta for increasing values of sparsity parameter γ_sp are shown in Fig. 2. Increasing the sparsity parameter results in a decrease in the number of control points, leading to a more compact representation of the dynamics of shape change over time. The momenta which remain for high values of γ_sp represent the areas that undergo the most dynamic changes. In that sense, these momenta hold the most important information about the trajectory of image evolution. The left panel of Fig. 3 shows the impact the sparsity parameter has on the number of control points as well as the accuracy in which the estimated evolution matches observed data. We can obtain a 43% decrease in the number of control points for less than a 2% relative increase in data matching error, or a 70% decrease in control points for a 10% cost. We obtain a reasonable model of shape change with as few as 67 momenta, compared to 79804 momenta (one for every pixel) for dense deformation models.

Fig. 3 — Impact of the sparsity parameter for the synthetic experiment (left) and for the developing brain (right). There is a range of values of the sparsity parameter which result in a considerable decrease in the number of control points for only minimal increase in the relative error of the data matching term.

Pediatric Brain Development

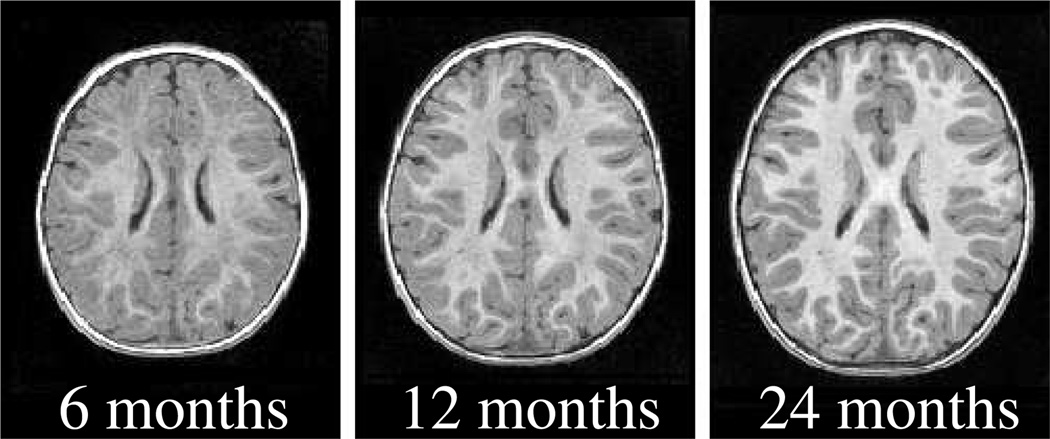
Next we investigate the application of sparse geodesic regression to model pediatric brain development. The data considered here, shown in Fig. 4, consists of T1W images acquired from the same child at 6, 12, and 24 months old. Due to the limited contrast in the image at 6 months, we estimate geodesic models with baseline image at 24 months, and follow the evolution backwards in time. We estimate several models by varying the sparsity parameter γ_sp, with control points initialized on a regular grid with 14 mm spacing, deformation kernel σ_V = 14 mm, and λ = 0.1.

Fig. 4 — Observed data acquired from the same child at 6, 12, and 24 months of age.

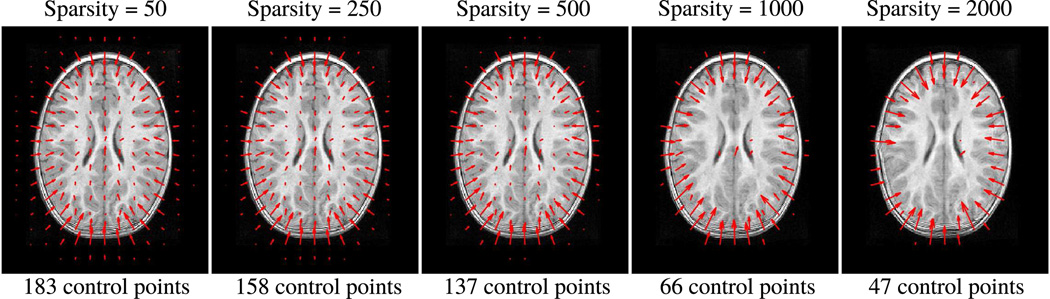
Fig. 5 shows the estimated baseline images at 24 months and initial momenta which characterize evolution backwards in time. For high values of γ_sp, the momenta cluster around the outside of the brain and around the the lateral ventricles. This can be interpreted to mean that the change in brain and ventricle size are the most notable descriptors of this child’s trajectory of growth. The right panel of Fig. 3 summarizes the impact of the sparsity parameter in terms of control points and accuracy. We can decrease the number of control points by 80% for just over 2% relative increase in data matching error. This has the potential to improve the power of ensuing statistical analysis, as the discarded momenta can be considered as noise in the description of image evolution.

4 Conclusions

We have presented a sparse geodesic image regression framework that decouples deformation parameters from the specific representation of input images, allowing the dimensionality of the model to be controlled by the user. We further add a L¹ penalty which selects an optimal subset of initial momenta which reflects the complexity of anatomical changes in time instead of the sampling of the image. This reduces the amount of model parameters from the number of image voxels down to tens or hundreds. The reduction of momenta has the potential to improve statistical power, as additional momenta can be considered noise in the description of image change over time. We showed on synthetic and real data that we can greatly reduce the number of momenta, incurring only a minimal cost in terms of matching the target images. Future work will focus on incorporating our sparse geodesic regression model into a framework for longitudinal analysis. Such an integration would require a way to compare sparse sets of momenta across subjects and populations.

References

1.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Img. Sci. 2009;2(1):183–202. [Google Scholar]
2.Davis B, Fletcher P, Bullitt E, Joshi S. ICCV. IEEE; 2007. Population shape regression from random design data; pp. 1–7. [Google Scholar]
3.Durrleman S, Allassonnière S, Joshi S. Sparse adaptive parameterization of variability in image ensembles. IJCV. 2012:1–23. [Google Scholar]
4.Durrleman S, Pennec X, Trouvé A, Braga J, Gerig G, Ayache N. Toward a comprehensive framework for the spatiotemporal statistical analysis of longitudinal shape data. IJCV. 2012:1–38. doi: 10.1007/s11263-012-0592-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Fishbaugh J, Durrleman S, Gerig G. Estimation of smooth growth trajectories with controlled acceleration from time series shape data. In: Fichtinger G, Peters T, editors. MICCAI. LNCS. Vol. 6892. Springer; 2011. pp. 401–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Fishbaugh J, Prastawa M, Durrleman S, Piven J, Gerig G. Analysis of longitudinal shape variability via subject specific growth modeling. In: Ayache N, Delingette H, Golland P, Mori K, editors. MICCAI. LNCS. Vol. 7510. Springer; 2012. pp. 731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Fletcher P. Geodesic Regression on Riemannian Manifolds. In: Pennec X, Joshi S, Nielsen M, editors. MICCAI MFCA. 2011. pp. 75–86. [Google Scholar]
8.Hart G, Shi Y, Zhu H, Sanchez M, Styner M, Niethammer M. DTI longitudinal atlas construction as an average of growth models. In: Gerig G, Fletcher P, Pennec X, editors. MICCAI STIA. 2010. [Google Scholar]
9.Liao S, Jia H, Wu G, Shen D. A novel longitudinal atlas construction framework by groupwise registration of subject image sequences. NeuroImage. 2012;59(2):1275–1289. doi: 10.1016/j.neuroimage.2011.07.095. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Lorenzi M, Ayache N, Pennec X. Schilds ladder for the parallel transport of deformations in time series of images. In: Szekely G, Hahn H, editors. IPMI. LNCS. Vol. 6801. 2011. pp. 463–474. [DOI] [PubMed] [Google Scholar]
11.Niethammer M, Huang Y, Vialard FX. Geodesic regression for image time-series. In: Fichtinger G, Peters T, editors. MICCAI. LNCS. Vol. 6982. Springer; 2011. pp. 655–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Singh N, Hinkle J, Joshi S, Fletcher P. A hierarchical geodesic model for diffeomorphic longitudinal shape analysis. IPMI. 2013 doi: 10.1007/978-3-642-38868-2_47. p. (to appear) [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Singh N, Hinkle J, Joshi S, Fletcher P. A vector momenta formulation of diffeomorphisms for improved geodesic regression and atlas construction. ISBI. 2013 doi: 10.1109/ISBI.2013.6556700. p. (to appear) [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Vialard F, Trouvé A. Shape splines and stochastic shape evolutions: A secondorder point of view. Quarterly of Applied Mathematics. 2012;70:219–251. [Google Scholar]

[R1] 1.Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Img. Sci. 2009;2(1):183–202. [Google Scholar]

[R2] 2.Davis B, Fletcher P, Bullitt E, Joshi S. ICCV. IEEE; 2007. Population shape regression from random design data; pp. 1–7. [Google Scholar]

[R3] 3.Durrleman S, Allassonnière S, Joshi S. Sparse adaptive parameterization of variability in image ensembles. IJCV. 2012:1–23. [Google Scholar]

[R4] 4.Durrleman S, Pennec X, Trouvé A, Braga J, Gerig G, Ayache N. Toward a comprehensive framework for the spatiotemporal statistical analysis of longitudinal shape data. IJCV. 2012:1–38. doi: 10.1007/s11263-012-0592-x. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.Fishbaugh J, Durrleman S, Gerig G. Estimation of smooth growth trajectories with controlled acceleration from time series shape data. In: Fichtinger G, Peters T, editors. MICCAI. LNCS. Vol. 6892. Springer; 2011. pp. 401–408. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] 6.Fishbaugh J, Prastawa M, Durrleman S, Piven J, Gerig G. Analysis of longitudinal shape variability via subject specific growth modeling. In: Ayache N, Delingette H, Golland P, Mori K, editors. MICCAI. LNCS. Vol. 7510. Springer; 2012. pp. 731–738. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.Fletcher P. Geodesic Regression on Riemannian Manifolds. In: Pennec X, Joshi S, Nielsen M, editors. MICCAI MFCA. 2011. pp. 75–86. [Google Scholar]

[R8] 8.Hart G, Shi Y, Zhu H, Sanchez M, Styner M, Niethammer M. DTI longitudinal atlas construction as an average of growth models. In: Gerig G, Fletcher P, Pennec X, editors. MICCAI STIA. 2010. [Google Scholar]

[R9] 9.Liao S, Jia H, Wu G, Shen D. A novel longitudinal atlas construction framework by groupwise registration of subject image sequences. NeuroImage. 2012;59(2):1275–1289. doi: 10.1016/j.neuroimage.2011.07.095. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Lorenzi M, Ayache N, Pennec X. Schilds ladder for the parallel transport of deformations in time series of images. In: Szekely G, Hahn H, editors. IPMI. LNCS. Vol. 6801. 2011. pp. 463–474. [DOI] [PubMed] [Google Scholar]

[R11] 11.Niethammer M, Huang Y, Vialard FX. Geodesic regression for image time-series. In: Fichtinger G, Peters T, editors. MICCAI. LNCS. Vol. 6982. Springer; 2011. pp. 655–662. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] 12.Singh N, Hinkle J, Joshi S, Fletcher P. A hierarchical geodesic model for diffeomorphic longitudinal shape analysis. IPMI. 2013 doi: 10.1007/978-3-642-38868-2_47. p. (to appear) [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.Singh N, Hinkle J, Joshi S, Fletcher P. A vector momenta formulation of diffeomorphisms for improved geodesic regression and atlas construction. ISBI. 2013 doi: 10.1109/ISBI.2013.6556700. p. (to appear) [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.Vialard F, Trouvé A. Shape splines and stochastic shape evolutions: A secondorder point of view. Quarterly of Applied Mathematics. 2012;70:219–251. [Google Scholar]

PERMALINK

Geodesic image regression with a sparse parameterization of diffeomorphisms

James Fishbaugh

Marcel Prastawa

Guido Gerig

Stanley Durrleman

Abstract

1 Introduction

2 Methods

2.1 Discrete parameterization of deformations