A Two-Phase Algorithm for Differentially Private Frequent Subgraph Mining

Xiang Cheng; Sen Su; Shengzhi Xu; Li Xiong; Ke Xiao; Mingxing Zhao

doi:10.1109/tkde.2018.2793862

. Author manuscript; available in PMC: 2020 Nov 20.

Published in final edited form as: IEEE Trans Knowl Data Eng. 2018 Jan 15;30(8):1411–1425. doi: 10.1109/tkde.2018.2793862

A Two-Phase Algorithm for Differentially Private Frequent Subgraph Mining

Xiang Cheng ¹, Sen Su ², Shengzhi Xu ³, Li Xiong ⁴, Ke Xiao ⁵, Mingxing Zhao ⁶

PMCID: PMC7678507 NIHMSID: NIHMS980354 PMID: 33223776

Abstract

Mining frequent subgraphs from a collection of input graphs is an important task for exploratory data analysis on graph data. However, if the input graphs contain sensitive information, releasing discovered frequent subgraphs may pose considerable threats to individual privacy. In this paper, we study the problem of frequent subgraph mining (FSM) under the rigorous differential privacy model. We present a two-phase differentially private FSM algorithm, which is referred to as DFG. In DFG, frequent subgraphs are privately identified in the first phase, and the noisy support of each identified frequent subgraph is calculated in the second phase. In particular, to privately identity frequent subgraphs, we propose a frequent subgraph identification approach, which can improve the accuracy of discovered frequent subgraphs through candidate pruning. Moreover, to compute the noisy support of each identified frequent subgraph, we devise a lattice-based noisy support computation approach, which leverages the inclusion relations between the discovered frequent subgraphs to improve the accuracy of the noisy supports. Through formal privacy analysis, we prove that DFG satisfies ϵ-differential privacy. Extensive experimental results on real datasets show that DFG can privately find frequent subgraphs while achieving high data utility.

Keywords: Differential Privacy, Data Privacy, Frequent Subgraph Mining, Frequent Pattern Mining

1. Introduction

FREQUENT subgraph mining (FSM) is a fundamental and essential problem in data mining research. Given a collection of input graphs, FSM aims to find all subgraphs that occur in input graphs more frequently than a given threshold. FSM has practical importance in a number of applications, ranging from bioinformatics to social network analysis. For example, discovering frequent subgraphs in social networks can be vital to understand the mechanics of social interactions. Despite valuable information the discovery of frequent subgraphs can potentially provide, if the data is sensitive (e.g., mobile phone call graphs, trajectory graphs and web-click graphs), directly releasing the frequent subgraphs will pose considerable concerns on the privacy of the users participating in the data [1]

Differential privacy [2] has been proposed as a way to address such problem. Unlike the anonymization-based privacy models (e.g., k-anonymity [3], l-diversity [4]), differential privacy offers strong privacy guarantees and robustness against adversaries with prior knowledge. In general, by randomization mechanisms, such as adding a carefully chosen amount of perturbation noise, differential privacy assures that the output of a computation is insensitive to the change of any individual record, and thus restricting privacy breaches through the results.

In this paper, we study the problem of mining frequent subgraphs under differential privacy. The work most related to ours is proposed by Shen et al. [5]. They employ the Markov Chain Monte Carlo (MCMC) sampling to extend the exponential mechanism [6], and use the extended exponential mechanism to directly select frequent subgraphs from all possible graphs which may or may not exist in the input graphs. However, since verifying the convergence of MCMC remains an open problem when the distribution of samples is not observable, the algorithm proposed in [5] guarantees only the weaker (ϵ, δ)-differential privacy. Moreover, as the output space contains all possible graphs, it results in a very large output space, which makes the selections of frequent subgraphs inaccurate. A growing number of studies have recently been proposed for mining frequent itemsets and frequent sequences under differential privacy [7], [8], [9]. However, since these studies are designed specifically for the type of pattern being mined, they cannot be applied to mining frequent subgraphs. To our best knowledge, we are not aware of any existing studies which can find frequent subgraphs with high data utility while satisfying ϵ-differential privacy.

To this end, we present a novel differentially private frequent subgraph mining algorithm, which is referred to as DFG. DFG consists of two phases, where frequent subgraphs are privately identified in the first phase, and the noisy support of the identified frequent subgraphs is calculated in the second phase. In the first phase of DFG, to privately identify frequent subgraphs, we propose a level-wise frequent subgraph identification approach. In this approach, given the candidate subgraphs at a certain level, by leveraging the idea of binary search, we first put forward a binary estimation method to estimate the number of frequent subgraphs at this level. We then develop a conditional exponential method, which utilizes the noisy support of candidate subgraphs to prune the obviously infrequent candidate subgraphs, and privately selects frequent subgraphs from the remaining candidate subgraphs. The rationale behind this conditional exponential method can be explained as follows. In practice, the number of frequent subgraphs is usually much smaller than the number of candidate subgraphs. If we can effectively prune unpromising candidate subgraphs, the number of candidate subgraphs can be considerably reduced and thus the probabilities of selecting the true frequent subgraphs can be significantly improved. Notice that, our frequent subgraph identification approach outputs only the identified frequent subgraphs without any support information.

In the second phase of DFG, to calculate the noisy support of the identified frequent subgraphs, we propose a lattice-based noisy support computation approach. In this approach, we first build a lattice for the identified frequent subgraphs based on their inclusion relations, where each node represents an identified frequent subgraph. To compute the noisy support of the graphs represented by the nodes in a given path in the lattice, we then devise a count accumulation method, where the noisy support of the graphs is obtained by accumulating the counts of the graphs in mutually disjoint subdatabases. We show that, compared with directly perturbing the support of the graphs, our count accumulation method can significantly improve the accuracy of the noisy supports. Therefore, given a lattice of the identified frequent subgraphs, we can construct a set of paths to cover all the nodes in the lattice, and use the count accumulation method to compute the noisy support of the graphs represented by the nodes in each path. Moreover, we found different sets of paths might result in different data utilities. To further improve the accuracy of the noisy supports, we also introduce an error-aware path construction method for constructing the set of paths which are taken as input by the count accumulation method.

The key contributions of this paper are summarized as follows.

We present a novel two-phase algorithm for mining frequent subgraphs under differential privacy called DFG, which consists of a frequent subgraph identification phase and a noisy support computation phase. To our best knowledge, it is the first algorithm which can find frequent subgraphs from a collection of input graphs with high data utility while satisfying ϵ-differential privacy. In addition, it can be easily extended for mining other frequent patterns (e.g., frequent itemsets and frequent sequences).
To privately identify frequent subgraphs from the input graphs, we propose a frequent subgraph identification approach, which includes a binary estimation method and a conditional exponential method.
To calculate the noisy support of each identified frequent subgraph, we propose a lattice-based noisy support computation approach, which includes a count accumulation method and an error-aware path construction method.
Through formal privacy analysis, we prove that our DFG algorithm guarantees ϵ-differential privacy. We conduct extensive experiments to evaluate the performance of our algorithm. Experimental results show that our DFG algorithm can privately find frequent subgraphs with high data utility.
To demonstrate the generality of our DFG algorithm, we also extend it for mining frequent itemsets and sequences, and conduct experiments to evaluate the performance of the extended algorithms. Experimental results show that the extended algorithms can also obtain good performance on differentially private itemset mining and differentially private sequence mining.

The rest of our paper is organized as follows. We provide a literature review in Section 2. Section 3 presents the necessary background on differential privacy and frequent subgraph mining. We identify the technical challenges in designing a differentially private FSM algorithm in Section 4. Sections 5, 6, 7 and 8 show the details of our DFG algorithm. The experimental results are reported in Section 9. Finally, in Section 10, we conclude the paper.

2. Related Work

There are two broad settings for privacy-preserving data analysis. The non-interactive setting aims at developing privacy-preserving algorithms that can publish a synthetic dataset, which can then be used to support various data analysis tasks. The interactive setting aims at developing customized privacy-preserving algorithms for various data analysis tasks. For the non-interactive setting, Li et al. [10] analyze and systematize the state-of-the-art graph data privacy and utility techniques. In particular, they propose and develop a uniform and open-source graph data sharing/publishing system called SeGraph. SeGraph is the first system that enables data owners to anonymize data by existing anonymization techniques, measure the data’s utility, and evaluate the data’s vulnerability against modern De-Anonymization attacks. Different from the work [10], in this paper, we focus on the interactive setting. We broadly categorize existing studies on differentially private frequent pattern mining into three groups based on the type of pattern being mined, and review each group of studies as follows.

A number of studies have been proposed to address the frequent itemset mining (FIM) problem under differential privacy. Bhaskar et al. [1] utilize the exponential mechanism [6] and Laplace mechanism [11] to develop two differentially private FIM algorithms. To meet the challenge of high dimensionality in transaction databases, Li et al. [7] introduce an algorithm which projects the high-dimensional database onto lower dimensions. Zeng et al. [8] find the utility and privacy tradeoff in differentially private FIM can be improved by limiting the length of transactions. They propose a transaction truncating method to limit the length of transactions. Different from [8], Cheng et al. [12] propose a transaction splitting method to limit the length of transactions. Based on the FP-growth algorithm [13], Su et al. [14] present an efficient algorithm called PFP-growth for mining frequent itemsets under differential privacy. Since all these differentially private FIM algorithms [1], [7], [8], [12], [14], [15] are designed specifically for FIM, they cannot be applied for mining frequent subgraphs. Recently, Lee et al. [16] introduce a differentially private top-k FIM algorithm. They propose a generalized sparse vector technique to identify frequent itemsets, which perturbs the threshold and the support of each candidate itemset. However, Machanavajjhala et al. [17] found such technique does not satisfy differential privacy. The main reason lies in that this technique ignores the consistency of the noisy threshold in each comparison between the noisy support and the noisy threshold.

There are several studies on frequent sequence mining with differential privacy. Bonomi et al. [18] propose a two-phase differentially private algorithm for mining both prefixes and substring patterns. Xu et al. [9] utilize a sampling-based candidate pruning technique to discover frequent sub-sequences under differential privacy. In [19], Cheng et al. introduce a differentially private algorithm for finding maximal frequent sequences. Unfortunately, the algorithms proposed by these studies are also designed specifically for mining sequential patterns, and thus cannot be applied to solving our problem.

For frequent subgraph mining (FSM) under differential privacy, Shen et al. [5] propose a Markov Chain Monte Carlo (MCMC) sampling based algorithm for privately mining frequent subgraphs from a set of input graphs. However, their algorithm only achieves (ϵ, δ)-differential privacy, which is a relaxed version of ϵ-differential privacy. In addition, their algorithm directly selects frequent subgraphs from the space which contains the subgraphs of all possible sizes, and leads to a large amount of added noise.

Besides finding frequent subgraphs from a set of input graphs, another variant of the FSM problem is to find frequent subgraphs in different regions of a single graph. In this variant, it needs to count the number of occurrences of subgraphs in a single graph. Recently, several studies have been proposed to address the problem of subgraph counting in a single graph under differential privacy. Karwa et al. [20] propose algorithms to privately count the occurrences of two families of subgraphs (k-stars and k-triangles). Chen et al. [21] present a new recursive mechanism which can privately release the occurrences of multiple kinds of subgraphs. Proserpio et al. [22] develop a private data analysis platform wPINQ over weighted datasets, which can be used to answer subgraph-counting queries. Very recently, Zhang et al. [23] propose a ladder framework to privately count the number of occurrences of subgraphs. Different from the above studies which answer subgraph-counting queries in a single graph, our work aims to find frequent subgraphs from a collection of input graphs.

This paper is extended from our previous work [24]. The significant additions in this extended manuscript can be summarized as follows. First, we propose a simple and effective method, namely error-aware path construction, for constructing the set of paths which are taken as input in the count accumulation method. Compared to our previous work, which has to employ two methods (i.e., the path construction and path extension methods) to get the final set of paths, we use only this new method to construct the set of paths (See Sec. 7.2). Since the error-aware path construction method can directly reduce the errors of noisy supports during computation, it results in better data utility than the two methods proposed in our previous work, especially when the threshold is relatively low (See Sec. 9.5). Second, to illustrate the generality of our DFG algorithm, we extend it for mining both frequent itemsets and frequent sequences. In particular, based on the unique characteristics of FIM, we also propose an optimized approach for computing the noisy support of frequent itemsets (See Sec. 8.4). Experimental results on real datasets show that the extended algorithms can also obtain good performance (See Sec. 9.6 and 9.7). Third, to evaluate the efficiency of our DFG algorithm, we compare it against the non-private FSM algorithm FSG [25]. Experimental results show that our DFG algorithm can obtain comparable efficiency to the FSG algorithm (See Sec. 9.3).

3. Preliminaries

3.1. Differential Privacy

Differential privacy [2] has become a de facto principle for privacy-preserving data analysis. In general, it requires an algorithm to be insensitive to the changes in any individual’s record. Two databases D₁, D₂ are considered as neighboring databases iff they differ by at most one input record (by adding or removing an individual record). Formally, differential privacy is defined as follows.

Definition 1. (ϵ-differential privacy). A randomized algorithm $A$ satisfies ϵ-differential privacy iff for any neighboring databases D₁ and D₂, and for any possible output S ∈ Range( $A$ ),

\Pr [A (D_{1}) = S] \leq e^{ϵ} \times \Pr [A (D_{2}) = S] .

A fundamental concept for achieving differential privacy is sensitivity [11]. It is used to measure the largest difference in the outputs over any two neighboring databases.

Definition 2. (Sensitivity). For any function $f : D \to R^{n}$ , and any neighboring databases D₁ and D₂, the sensitivity of f is:

Δ f = \max_{D_{1}, D_{2}} ‖ f (D_{1}) - f (D_{2}) ‖ .

Laplace mechanism [11] is a widely used approach for designing algorithms to achieve differential privacy. It adds random noise drawn from the Laplace distribution to the true outputs of a function. The Laplace distribution with magnitude λ, i.e., Lap(λ), follows the probability density function as $Pr [x ∣ λ] = \frac{1}{2 λ} e^{- ∣ x ∣ ∕ λ}$ , where $λ = \frac{Δ f}{ϵ}$ is determined by the sensitivity Δf and the privacy budget ϵ.

Theorem 1. For any function $f : D \to R^{n}$ with sensitivity Δf, the algorithm $A$

A (D) = f (D) + L a p (Δ f / ϵ)

achieves ϵ-differential privacy.

Another widely adopted mechanism for designing algorithms to achieve differential privacy is exponential mechanism [6]. Given the whole output space, the exponential mechanism assigns each possible output a utility score, and draw a sample from the output space based on the assigned utility scores.

Theorem 2. For a database D, output space $R$ and a utility score function $u : D \times R \to R$ , the algorithm $A$

\Pr [A (D) = r] \propto \exp (\frac{ϵ \times u (D, r)}{2 Δ u})

satisfies ϵ-differential privacy, where Δu is the sensitivity of the utility score function.

As proved in [11], a sequence of differentially private computations also satisfies differential privacy. This is called the composition property of differential privacy.

Theorem 3. (Sequential Composition). Let f₁, … f_t be t computations, each provides ϵ_i-differential privacy. A sequence of f_i(D) over database D provides (Σϵ_i)-differential privacy.

Theorem 4. (Parallel Composition). Let f₁, …, f_t be t computations, each provides ϵ_i-differential privacy. A sequence of f_i (D_i) over disjoint databases D₁, …, D_t provides max(ϵ_i)-differential privacy.

3.2. Frequent Subgraph Mining

A graph G = (V, E) consists of a set of vertices V and a set of edges E. Each vertex is associated with a label, which is drawn from a set of vertex labels. The label of each vertex is not required to be unique and multiple vertices can have the same label. The size of a graph is defined to be the number of edges in this graph. A graph is called an i-graph if its size is i. Take the graph G₁ in Fig. 1 as an example. Since G₁ has 5 edges, G₁ is a 5-graph. In this paper, we consider that each edge in a graph is undirected and not associated with a label. However, our solution can be extended to the case of graphs with directed and labeled edges.

Suppose there are two graphs G_x = (V_x, E_x) and G_y = (V_y, E_y). Let L(u) denote the label of vertex u. We say that G_x is contained in G_y if there exists a function f: V_x → V_y, such that, ∀ (u, v) ∈ E_x, we have (f(u), f(v)) ∈ E_y, L(u) = L(f(u)) and L(v) = L(f(v)). If G_x is contained in G_y, we say that G_x is a subgraph of G_y, and G_y is a supergraph of G_x, denoted by G_x ⊆ G_y. For the collection D of graphs in Fig. 1, it’s not hard to find that G₂ is a subgraph of G₁ and G₁ is a supergraph of G₂ (i.e., G₂ ⊆ G₁).

A graph database is a collection of graphs, where each graph represents an individual record. The support of a subgraph is the number of input graphs containing it. Given a threshold, a subgraph is called frequent if its support is no less than this threshold. Fig. 1 shows a frequent 3-subgraph in D for the given threshold 2. The problem of frequent subgraph mining (FSM) can be formalized as follows.

Definition 3. (Frequent Subgraph Mining). Given a graph database D and a threshold θ, frequent subgraph mining (FSM) aims to find all frequent subgraphs that have support no less than θ in D, and also report the support of each frequent subgraph.

In FSM, to count the support of graphs, a basic operation is to determine whether a graph is a subgraph (or supergraph) of another graph. The computational problem of determining whether a graph is a subgraph (or supergraph) of another graph is called the subgraph isomorphism problem. The subgraph isomorphism problem is known to be NP-complete [26]. Therefore, the FSM problem is also NP-complete.

FSM takes as input a graph database consisting of the records (e.g., trajectory graphs) contributed by a group of individuals, and produces as output the frequent subgraphs and their supports. However, releasing such results directly may pose considerable threat to individuals’ privacy. In this paper, we adopt differential privacy to solve this problem, and study the differentially private FSM problem. In the context of differentially private FSM, we consider two graph databases as neighboring databases iff they differ by at most one input record (i.e., graph). By applying differential privacy in FSM, adversaries cannot infer the presence or absence of any individual record from the results. Therefore, the privacy of individuals can be protected through the results.

3.3. Notations

We summarize the commonly used notations in this paper in Table 1.

TABLE 1.

Notations

Notation	Description
FSM	Frequent subgraph mining
FSG	The non-private frequent subgraph mining algorithm proposed in [25].
DFG	The differentially private frequent subgraph mining algorithm proposed in this paper.
FI₁	The frequent subgraph identification approach.
NC₂	The lattice-based noisy support computation approach.
θ	The threshold to determine whether a subgraph is a frequent subgraph.
ϵ	The privacy budget defined in differential privacy.
i-subgraph	A subgraph whose size is i.
F_i	A set of frequent i-subgraphs
C_i	A set of candidate i-subgraphs
s_g (D)	The true support of subgraph g in database D.
ns_g (D)	The noisy support of subgraph g in database D.
M_g	Given the threshold θ, M_g denotes the maximum size of the frequent subgraphs in the input database.
L_a	The lattice built based on all the identified frequent subgraphs.
V_{L_a}	The set of nodes in the lattice L_a.
p	A path in the lattice L_a.
P	A set of pathes which can cover all the nodes in the lattice L_a.
t	A tree in the lattice L_a.
T	A set of trees which can cover all the nodes in the lattice L_a.
ζ	ζ = {ζ₁, …, ζ_n}, where ζ_i is the maximum support of i-subgraphs.

Open in a new tab

4. A Straightforward Approach

In this section, based on the Laplace mechanism, we introduce a straightforward approach to make frequent subgraph mininig (FSM) satisfy ϵ-differential privacy. The main idea is to utilize the Laplace mechanism to perturb the support of all possible frequent subgraphs, and compare their noisy supports against the given threshold to determine which graphs are frequent. Given the threshold θ, suppose the maximum size of the frequent subgraphs in the input dataset D is M_g. Recall that the size of a graph (subgraph) is defined to be the number of edges in the graph (subgraph). We follow the level-wise algorithm Apriori [27] to discover frequent subgraphs in order of increasing size, i.e., from frequent 1-subgraph to frequent M_g-subgraph. For the mining of frequent (i+1)-subgraphs (1 ≤ i ≤ M_g), based on the candidate generation method in [25], we first use the frequent i-subgraphs to generate all possible frequent (i+1)-subgraphs. The generated (i+1)-subgraphs are called candidate (i+1)-subgraphs. Then, we perturb the support of these candidate (i+1)-subgraphs and compare their noisy supports against the threshold θ. We consider the candidate (i+1)-subgraphs whose noisy support exceeds θ as frequent (i+1)-subgraphs, and output these graphs together with their noisy supports. The above process continues until we discover all the frequent subgraphs with different sizes.

Privacy Analysis.

Let Q_i denote the support computations of the candidate i-subgraphs. The amount of noise added to the support of candidate i-subgraphs is determined by the allocated privacy budget and the sensitivity of Q_i. Here, we denote the sensitivity of Q_i by Δ_i. In particular, since the maximum size of frequent subgraphs is M_g, we uniformly assign Q_i a privacy budget $\frac{ϵ}{M_{g}}$ . Moreover, since a single input graph can affect the support of each candidate i-subgraph by at most one, the sensitivity of Q_i (i.e., Δ_i) is the number of candidate i-subgraphs. Thus, adding Laplace noise $L a p (\frac{M_{g} \times Δ_{i}}{ϵ})$ in Q_i achieves $\frac{ϵ}{M_{g}} - differential$ privacy. Overall, the mining process can be considered as a series of computations Q₁,Q₂, …, Q_{M_g}. Based on the sequential composition property [11], this approach satisfies ϵ-differential privacy.

Limitation.

The above approach, however, results in poor performance. The main reason can be explained as follows. In this approach, the amount of perturbation noise is proportional to the number of generated candidate subgraphs. During the mining process, a large number of candidate subgraphs are generated, which leads to a large amount of noise added to the support of each candidate subgraph. As a result, the utility of the results is drastically decreased.

To make FSM satisfy ϵ-differential privacy, another potential approach is to leverage the exponential mechanism. Specifically, for mining frequent i-subgraphs, we can first utilize the exponential mechanism to privately select subgraphs from the candidate i-subgraphs, and then compute the noisy support of each selected subgraph. In this way, the amount of perturbation noise is just proportional to the number of selected subgraphs. However, it is hard to know how many subgraphs we need to select from the candidate i-subgraphs (i.e., the number of frequent i-subgraphs). Moreover, in the mining process, a large number of candidate subgraphs are generated. It causes a large candidate set from which this approach has to select, making the selections inaccurate.

In the following four sections, we will introduce our DFG algorithm, which utilizes both the Laplace mechanism and the exponential mechanism to improve the utility of the results.

5. Overview of Our DFG Algorithm

To privately find frequent subgraphs while providing a high level of data utility, we present a two-phase differentially private frequent subgraph mining algorithm, which is referred to as DFG. DFG consists of a frequent subgraph identification phase and a noisy support computation phase.

In the first phase of DFG, we put forward a frequent subgraph identification approach (referred to as FI₁) to privately identify frequent subgraphs in order of increasing size. In this approach, a binary estimation method is proposed to estimate the number of frequent subgraphs for a certain size, and a conditional exponential method is proposed to improve the accuracy of identified frequent subgraphs. In the second phase of DFG, we devise a lattice-based noisy support computation approach (referred to as NC₂) to compute the noisy support of identified frequent subgraphs. In this approach, two methods, namely count accumulation and error-aware path construction, are proposed to improve the accuracy of the noisy supports. For the privacy budget ϵ, we divide it into three parts: ϵ₁, ϵ₂ and ϵ₃. In particular, ϵ₁ is used to estimate the maximum size M_g of frequent subgraphs, ϵ₂ is used in the FI₁ approach, and ϵ₃ is used in the NC₂ approach. An overview of this algorithm is shown in Fig. 2.

Fig. 2. — An Overview of Our *DFG* Algorithm

In the following two sections, we will show the details of our FI₁ and NC₂ approaches, respectively.

6. Frequent Subgraph Identification

In this section, we introduce our frequent subgraph identification (FI₁) approach, which identifies frequent subgraphs in order of increasing size. In particular, given the candidate i-subgraphs, based on the idea of binary search, we propose a binary estimation method to estimate the number of frequent i-subgraphs (See Sec. 6.1). Then, we privately select frequent i-subgraphs from the candidate i-subgraphs. To improve the accuracy of these selections, we propose a conditional exponential method, which uses the noisy support of the candidate subgraphs to prune those obviously infrequent candidate subgraphs (See Sec. 6.2).

Alg. 1 shows the main steps of our FI₁ approach. Specifically, for the identification of frequent i-subgraphs, we first generate the candidate i-subgraphs (line 3). If i = 1, we

Algorithm 1.

Frequent Subgraph Identification

Input:
	Graph database D; Threshold θ; Privacy budget ϵ₂; Maximum size of frequent subgraphs M_g;
Output:
	Frequent subgraphs F;
1:	F ← ∅; $ϵ_{b} = \frac{α ϵ_{2}}{M_{g}}$ ; $ϵ_{c} = \frac{(1 - α) ϵ_{2}}{M_{g}}$ ;
2:	for i from 1 to M_g do
3:	C_i ← generate the set of candidate i-subgraphs;
4:	count the support of each candidate i-subgraph;
5:	n_i = binary_estimation(C_i, ϵ_b, θ);\\see Sec. 6.1
6:	F_i = conditional_exponential(C_i, ϵ_c, θ, n_i);\\see Sec. 6.2
7:	F += F_i;
8:	end for
9:	return F;

Open in a new tab

enumerate all possible single-edge graphs as candidate 1-subgraphs. The number of enumerated candidate 1-subgraphs is |L|², where |L| is the number of vertex labels. If i > 1, based on the candidate generation method in [25], we use frequent (i−1)-subgraphs to generate candidate i-subgraphs. We then count the support of each candidate i-subgraph (line 4). Recall that counting the support of a graph involves dealing with the subgraph isomorphism problem, which is NP-complete. Here, we adopt the VF2 algorithm [28] to solve the this problem, which is an exact algorithm and has O(|V|!·|V|) time complexity, where |V| is the maximum number of vertices of the given two graphs. Next, we use our binary estimation method to estimate n_i, the number of frequent i-subgraphs (line 5). Finally, by leveraging our conditional exponential method, we privately select subgraphs from the candidate i-subgraphs, and output them as frequent i-subgraphs (line 6).

6.1. Binary Estimation Method

Given the candidate i-subgraphs, to estimate the number of frequent i-subgraphs, a simple method is to perturb the support of each candidate subgraph, and count the number of candidate subgraphs which have noisy support above the threshold. However, as shown in Sec. 4, it will cause a large perturbation noise.

Inspired by the method proposed in [8] for estimating the maximum size of frequent itemsets, we propose a binary estimation method to estimate the number of frequent i-subgraphs. Both of the binary estimation method and the method proposed in [8] use the idea of binary search to reduce the amount of added noise. Alg. 2 shows the details of our binary estimation method. It has O(|C_i| · ⌈log₂|C_i|⌉) time complexity, where |C_i| is the number of candidate i-subgraphs. In Alg. 2, we first obtain the noisy support of the candidate i-subgraph with the m-th largest support, where m = ⌊(|C_i|−1)/2⌋ (line 5). If this noisy support is larger than the threshold, it means the candidate i-subgraphs in the upper half are all above the threshold, and we only need to consider the candidate i-subgraphs in the lower half in the next iteration. Similarly, if this noisy support is smaller than the threshold, we only need to further search the candidate i-subgraphs in the upper half in the next iteration. This process continues until the number of candidate i-subgraphs that have noisy support above the threshold is determined.

Theorem 5. The binary estimation method (i.e., Algorithm 2) satisfies ϵ_b-differential privacy.

Proof. In our binary estimation method, we first obtain the noisy support of the candidate i-subgraph with the m-th

Algorithm 2.

Binary Estimation

Input:
	Candidate i-subgraphs C_i; Privacy budget ϵ_b; Threshold θ;
Output:
	The number of frequent i-subgraphs n_i;
1:	low ← 0; high ← \|C_i\| − 1;
2:	while low ≤ high do
3:	m ← ⌊(low + high) / 2⌋;
4:	s_m ← get support of the candidate i-subgraph with the m-th largest support;
5:	ns_m ← s_m + Lap(⌈log₂ \|C_i\|⌉ / ϵ_b);
6:	if ns_m == θ then
7:	return \|C_i\| − m;
8:	else if ns_m > θ then
9:	high = m − 1;
10:	else if ns_m < θ then
11:	low = m + 1;
12:	end if
13:	end while
14:	return \|C_i\| − 1 − high;

Open in a new tab

largest support, where m = ⌊(|C_i|−1)/2⌋ and |C_i| is the number of candidate i-subgraphs. Since adding (removing) an input graph can affect the result of such computation by at most one, the sensitivity of such computation is one. Thus, adding Laplace noise Lap(⌈log₂ |C_i|⌉/ϵ_b) in this computation satisfies (ϵ_b/⌈log₂ |C_i|⌉)-differential privacy.

In this method, like the binary search, we only need to obtain the support of at most ⌈log₂ |C_i| candidate i-subgraphs. Based on the sequential composition property [11], we can see our binary estimation method satisfies ϵ_b-differential privacy. ◻

6.2. Conditional Exponential Method

After getting the estimated number of frequent i-subgraphs, to identify frequent i-subgraphs from candidate i-subgraphs, a simple method is to directly use exponential mechanism to select frequent graphs from candidate subgraphs. However, this simple method might result in poor performance. The reason is explained as follows. For real-world datasets, the number of real frequent subgraphs is typically much smaller then that of candidate subgraphs generated by using the downward closure property, which makes the selections of real frequent subgraphs inaccurate. To solve this problem, we propose a conditional exponential method. The main idea of this method is to use the noisy support of candidate subgraphs to prune those obviously infrequent candidate subgraphs, such that the candidate set can be considerably reduced and the probabilities of selecting real frequent subgraphs can be significantly improved.

Alg. 3 shows the details of the conditional exponential method. It has O(n_i · |C_i|) time complexity, where n_i is the number of frequent i-subgraphs and |C_i| is the number of candidate i-subgraphs. In Alg. 3, we divide the privacy budget ϵ_c into two parts ϵ_c1 and ϵ_c2, which are used to perturb the support of candidate subgraphs and privately select frequent graphs, respectively. Given the candidate i-subgraphs, we first add Laplace noise $L a p (\frac{2 n_{i}}{ϵ_{c 1}})$ to the true support of each candidate i-subgraph (line 5). Then, we prune those candidate i-subgraphs that have noisy support below the threshold. Next, for each remaining candidate i-subgraph, we use its true support as its utility score. Based on the assigned scores, we

Algorithm 3.

Conditional Exponential Method

Input:
	Candidate i-subgraphs C_i; Privacy budget ϵ_c; Threshold θ; The number of frequent i-subgraphs n_i;
Output:
	Frequent i-subgraphs F_i;
1:	ϵ_c1 ← βϵ_c, ϵ_c2 ← (1-β)ϵ_c;
2:	for j from 1 to n_i do
3:	C_i’ ← ∅;
4:	for each subgraph g in C_i do
5:	$n s_{g} = s_{g} + L a p (\frac{2 n_{i}}{ϵ_{c 1}})$ ;
6:	if ns_g ≥ θ then
7:	add g into C_i’;
8:	end if
9:	end for
10:	if C_i’ is not empty then
11:	g_j ← select a subgraph from C_i’ such that $Pr [Selecting subgraph g] \propto exp (\frac{ϵ_{c 2} \times s_{g}}{2 n_{i}})$ ;
12:	remove g_j from C_i;
13:	add g_j into F_i;
14:	end if
15:	end for
16:	return F_i;

Open in a new tab

privately select a subgraph from the remaining candidate i-subgraphs, and output it as a frequent i-subgraph (line 11). The above steps iterate until we select n_i subgraphs from the candidate i-subgraphs. Notice that, in this method, we output only the selected i-subgraphs (i.e., the identified frequent i-subgraphs), and do not output their noisy supports.

Theorem 6. The conditional exponential method (i.e., Algorithm 3) satisfies ϵ_c-differential privacy.

Proof. In this method, we first use the noisy support of candidate subgraphs to prune the obviously infrequent candidate subgraphs. Then, we select a subgraph from the remaining candidate subgraphs. Overall, the utility score we assigned to each candidate subgraph can be considered as

u (g, D) = {\begin{array}{l} 0 & n s_{g} (D) < θ \\ \exp (\frac{ϵ_{c 2} \times s_{g} (D)}{2 n_{i}}) & n s_{g} (D) \geq θ \end{array},

where n_i is the number of frequent i-subgraphs, and s_g(D) and ns_g (D) are the true support and noisy support of subgraph g in database D, respectively.

Suppose D₁ and D₂ are two neighboring databases. For each candidate subgraph g, we have −1≤s_g(D₂)-s_g(D₁)≤1. Let $f (g, D) = exp (\frac{ϵ_{c 2} \times s_{g} (D)}{2 n_{i}})$ . Then, we can prove that

\exp (- \frac{ϵ_{c 2}}{2 n_{i}}) \leq \frac{f (g, D_{1})}{f (g, D_{2})} \leq \exp (\frac{ϵ_{c 2}}{2 n_{i}}) .

(1)

To prune candidate subgraphs, we add Laplace noise $L a p (\frac{2 n_{i}}{ϵ_{c 1}})$ to the support of each candidate subgraph. Let noise denote the amount of added noise. Based on the definition of Laplace mechanism, we have

\frac{\Pr [n o i s e = X]}{\Pr [n o i s e = X + 1]} = \frac{\exp (- \frac{ϵ_{c 1} | X |}{2 n_{i}})}{\exp (- \frac{ϵ_{c 1} | X + 1 |}{2 n_{i}})} = \exp (- \frac{ϵ_{c 1}}{2 n_{i}} (| X | - | X + 1 |)) \leq \exp (\frac{ϵ_{c 1}}{2 n_{i}}) .

(2)

Similarly, we also have

\frac{\Pr [n o i s e = X + 1]}{\Pr [n o i s e = X]} \leq \exp (\frac{ϵ_{c 1}}{2 n_{i}}) .

(3)

Based on equations (2) and (3), given any subgraph g, for its noisy support ns_g(D₁) = s_g(D₁) + noise in D₁ and its noisy support ns_g(D₂) = s_g(D₂) + noise in D₂, we can prove

\Pr [s_{g} (D_{1}) + n o i s e \geq θ] = \Pr [n o i s e \geq θ - s_{g} (D_{1})] = \int_{θ - s_{g} (D_{1})}^{\infty} \Pr [n o i s e = x] d x \leq \int_{θ - s_{g} (D_{2}) - 1}^{\infty} \Pr [n o i s e = x] d x = \int_{θ - s_{g} (D_{1})}^{\infty} \Pr [n o i s e = x - 1] d x \leq \int_{θ - s_{g} (D_{2})}^{\infty} e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n o i s e = x] d x = e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n o i s e \geq θ - s_{g} (D_{2})] = e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [s_{g} (D_{2}) + n o i s e \geq θ] .

That is, we have

\Pr [n s_{g} (D_{1}) \geq θ] \leq e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) \geq θ] .

(4)

Moreover, we can also prove

\Pr [n o i s e \geq θ - s_{g} (D_{1})] = \int_{θ - s_{g} (D_{1})}^{\infty} \Pr [n o i s e = x] d x \geq \int_{θ + 1 - s_{g} (D_{2})}^{\infty} \Pr [n o i s e = x] d x = \int_{θ - s_{g} (D_{2})}^{\infty} \Pr [n o i s e = x + 1] d x \geq e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \int_{θ - s_{g} (D_{2})}^{\infty} \Pr [n o i s e = x] d x = e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n o i s e \geq θ - s_{g} (D_{2})] .

That is, we also have

\Pr [n s_{g} (D_{1}) \geq θ] \geq e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) \geq θ] .

(5)

In a similar way, we can see that

\Pr [n s_{g} (D_{1}) < θ] \leq e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) < θ],

(6)

and

\Pr [n s_{g} (D_{1}) < θ] \geq e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) < θ] .

(7)

At last, based on equations (1), (4), (5), (6) and (7), we can prove that

\Pr [Selecting subgraph G from C_{i} in D_{1}] = \frac{0 \times \Pr [n s_{G} (D_{1}) < θ] + f (G, D_{1}) \times \Pr [n s_{G} (D_{1}) \geq θ]}{\sum_{g \in C_{i}} (0 \times \Pr [n s_{g} (D_{1}) < θ] + f (g, D_{1}) \times \Pr [n s_{g} (D_{1}) \geq θ])} = \frac{f (G, D_{1}) \times \Pr [n s_{G} (D_{1}) \geq θ]}{\sum_{g \in C_{i}} f (g, D_{1}) \times \Pr [n s_{g} (D_{1}) \geq θ]} \leq \frac{f (G, D_{1}) \times e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{G} (D_{2}) \geq θ]}{\sum_{g \in C_{i}} f (g, D_{1}) \times e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) \geq θ]} \leq \frac{e^{\frac{ϵ_{c 2}}{2 n_{i}}} f (G, D_{2}) \times e^{\frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{G} (D_{2}) \geq θ]}{\sum_{g \in C_{i}} e^{- \frac{ϵ_{c 2}}{2 n_{i}}} \times f (g, D_{2}) \times e^{- \frac{ϵ_{c 1}}{2 n_{i}}} \Pr [n s_{g} (D_{2}) \geq θ]} = e^{2 \times \frac{ϵ_{c 1}}{2 n_{i}} + 2 \times \frac{ϵ_{c 2}}{2 n_{i}}} \frac{f (G, D_{2}) \times \Pr [n s_{G} (D_{2}) \geq θ]}{\sum_{g \in C_{i}} f (g, D_{2}) \times \Pr [n s_{g} (D_{2}) \geq θ]} = e^{\frac{ϵ_{c}}{n_{i}}} \frac{0 \times \Pr [n s_{G} (D_{2}) < θ] + f (G, D_{2}) \times \Pr [n s_{G} (D_{2}) \geq θ]}{\sum_{g \in C_{i}} (0 \times \Pr [n s_{g} (D_{2}) < θ] + f (g, D_{2}) \times \Pr [n s_{g} (D_{2}) \geq θ])} = e^{\frac{ϵ_{c}}{n_{i}}} \Pr [Selecting subgraph G from C_{i} in D_{2}] .

Based on the above analysis, we can see that, in our conditional exponential method, selecting a frequent i-subgraph from the candidate i-subgraphs guarantees $\frac{ϵ_{c}}{n_{i}} - differential$ privacy. In this method, we iteratively select n_i frequent i-subgraphs from the candidate i-subgraphs without replacement. Based on the sequential composition property [11], this method overall satisfies ϵ_c-differential privacy. ◻

As shown in the proof of Thm. 6, in the conditional exponential method, selecting a frequent i-subgraph from the candidate i-subgraphs satisfies $\frac{ϵ_{c}}{n_{i}} - differential$ privacy. It indicates that, the overall amount of added noise in this method is proportional to the number of frequent i-subgraph (i.e., n_i). Notice that, in this method, before each selection of the frequent i-subgraphs, we add Laplace noise to the support of the candidate i-subgraphs for candidate pruning. In particular, the added noise to each candidate i-subgraph (i.e., $L a p (\frac{2 n_{i}}{ϵ_{c 1}})$ ) is proportional to n_i, although all the candidate i-subgraphs are involved. The rationale behind it is that, we do not output the noisy supports of the candidate i-subgraphs and use them only for candidate pruning. In addition, as shown in the proof of Thm. 6, adding such amount of noise to each candidate i-subgraph for candidate pruning can make each selection of the frequent i-subgraphs satisfies $\frac{ϵ_{c}}{n_{i}} - differential$ privacy.

7. Lattice-based Noisy Support Computation

After privately identifying frequent subgraphs, we now discuss how to compute their noisy supports. A simple method is to uniformly assign the privacy budget to the support computation of each frequent subgraph and directly perturb their supports. However, it causes the amount of added noise to be proportional to the number of frequent subgraphs.

To reduce the amount of added noise, we devise a lattice-based noisy support computation (NC₂) approach. In the NC₂ approach, we first build a directed lattice based on the identified frequent subgraphs. In the lattice, each node v_g is associated with a frequent subgraph g. A directed edge from node v_g₁ to node v_g₂ is introduced if graph g₂ can be expanded to graph g₁ by adding one edge. An example of a lattice formed by frequent subgraphs is shown in Fig. 3. In the lattice, there are several directed paths. For ease of presentation, we say a graph g is on a path p if g’s corresponding node v_g is contained in p, and the depth of g on p is the number of nodes from the first node in p to v_g. We then propose a count accumulation method to compute the noisy support of the graphs on a given path in the lattice (See Sec. 7.1). Moreover, to construct a set of paths that can cover all nodes in the lattice, we present an error-aware path construction method (See Sec. 7.2).

Fig. 3. — A Lattice Formed by Frequent Subgraphs

Algorithm 4.

Lattice-based Noisy Support Computation

Input:
	A set F of frequent subgraphs; Privacy budget ϵ₃;
Output:
	F together with noisy supports;
1:	L_a ← build a directed lattice based on F;
2:	P = error-aware_path_construction(L_a); \\ see Sec. 7.2
3:	for each path p in P do
4:	count_accumulation(p, ϵ₃/\|P\|); \\ see Sec. 7.1
5:	end for
6:	for each graph g having multiple noisy supports do
7:	combine its all noisy supports to get a more accurate result; \\ see Sec. 7.1
8:	end for
9:	return F with noisy supports;

Open in a new tab

Alg. 4 shows the main steps of our NC₂ approach. Specifically, given the identified frequent subgraphs, we first build a lattice L_a based on these frequent subgraphs (line 1). Then, by using the error-aware path construction method, we construct a set P of paths to cover all the nodes in the lattice (line 2). At last, for each path p in P, we utilize our count accumulation method to obtain the noisy support of the graphs on p (line 4). Since a node in L_a might be covered by more than one path, we might get multiple noisy supports of a graph. If a graph has multiple noisy supports, we will combine all its noisy supports to get a more accurate result (line 7).

7.1. Count Accumulation Method

For a path in a given lattice, we propose a count accumulation method to compute the noisy support of the graphs on this path. The main idea is to leverage the inclusion relations between the discovered frequent subgraphs and the parallel composition property of differential privacy to improve the accuracy of the results. Suppose a path p in the lattice contains |p| nodes, and these nodes represent |p| graphs g₁, g₂, …, g_|p|, where g₁ ⊆ g₂ … ⊆ g_|p|. For the input database D, we can utilize these |p| graphs to divide D into mutually disjoint subdatabases. Specifically, as shown in Fig. 4, we first divide D into two sub-databases based on graph g_|p|: the sub-database D_|p| that is consisted of all the input graphs containing g_|p| and the sub-database $\bar{D_{∣ p ∣}}$ that is consisted of the remaining input graphs. Then, we further divide $\bar{D_{∣ p ∣}}$ based on graph g_|p|−1. This process continues until D is partitioned into |p|+1 mutually disjoint sub-databases $\bar{D_{1}}$ , D₁, …, D_|p|.

Fig. 4. — The Sub-database Generation Process

For graphs g_j, g_i on p, where j>i, we have g_j⊇g_i. Obviously, if an input graph contains g_j, it also contains g_i. Thus, the input graphs containing g_i are distributed across subdatabases D_|p|, D_|p|−1, …, D_i. Let δ_x be the number of input graphs in D_x. Then, the support of g_i is equal to $Σ_{k = i}^{∣ p ∣} δ_{k}$ . Thus, based on δ_|p|, δ_|p|−1, …, δ₁, we can derive the support of each graph on p. Suppose the privacy budget allocated to p is ϵ_p. To satisfy differential privacy, we add Laplace noise Lap(1/ϵ_p) to each δ_x, where 1≤x≤|p|.

In the count accumulation method, we divide the input database D into mutually disjoint sub-databases based on the graphs on each path. Such process involves dealing the subgraph isomorphism problem. Therefore, the count accumulation method has exponential time complexity.

Theorem 7. Our count accumulation method guarantees ϵ_p-differential privacy.

Proof. In this method, we compute the noisy values of δ_|p|, δ_|p|−1, …, δ₁. For i from 1 to |p|, as an input graph can affect δ_i by at most one, the sensitivity of computing δ_i is one. Thus, adding Laplace noise Lap(1/ϵ_p) to δ_i satisfies ϵ_p-differential privacy. Moreover, as sub-databases D₁, D₂, …, D_|p| are mutually disjoint, by the parallel composition property [11], the privacy budgets used in computing δ₁, δ₂, …, δ_|p| do not need to accumulate. For the graphs on path p, as their noisy supports are obtained based on the noisy values of δ₁, δ₂, …, δ_|p|, we can safely use them without privacy implications. Therefore, our count accumulation method satisfies ϵ_p-differential privacy. ◻

We will now show that, compared with directly perturbing the support of each graph on a path, our count accumulation method can significantly improve the accuracy of the noisy supports. In particular, we use the noise variance to measure the accuracy of the noisy supports. Continue from the above example, if we directly perturb the support of the | p| graphs on path p, as an input graph can affect the support of a graph by at most one, the sensitivity of computing the support of a graph is one. For each graph on p, we uniformly assign it a privacy budget ϵ_p/|p|, and add noise Lap(|p|/ϵ_p) to its support, which has variance $2 ∣ p ∣^{2} ∕ ϵ_{p}^{2}$ . We can see the error of the noisy support of each graph is quadratic to the depth of path p. In contrast, in our count accumulation method, we add Laplace noise Lap(1/ϵ_p) to δ_x (1≤x≤|p|), which has variance $2 ∕ ϵ_{p}^{2}$ . For the i-th graph g_i on path p, its noisy support sup_i is equal to the sum of the noisy values of δ_i, δ_i+1, …, δ_|p|. Since the noise added to δ_i, δ_i+1, …, δ_|p| is generated independently, the noise variance of sup_i is the sum of the noise variances of δ_i, δ_i+1, …, δ_|p|, which is $2 (∣ p ∣ - i + 1) ∕ ϵ_{p}^{2}$ . We can see, in our count accumulation method, the error of the noisy support of a graph is proportional to the depth of this graph on path p. Thus, our count accumulation method can significantly improve the accuracy of the noisy supports.

Given a set of paths which cover all the nodes in the lattice, we can use our count accumulation method to calculate the noisy support of the graphs on each path. When a node in the lattice is covered by more than one path, we will get multiple noisy supports of the graph represented by this node. In this case, similar to [7], we combine the noisy supports of a graph to obtain a more accurate support. Specifically, if a node representing graph g is covered by two paths, we can get two noisy supports of g. Suppose ns_g with variance η and $n s_{g}^{'}$ with variance η′ are the two noisy supports of g, we can combine ns_g and $n s_{g}^{'}$ to get a more accurate support $\frac{η^{'} \times n s_{g} + η \times n s_{g}^{'}}{η + η^{'}}$ with variance $\frac{η \times η^{'}}{η + η^{'}}$ . If a node representing graph g is covered by more than two paths, we can iteratively combine the noisy supports of g in a similar way.

7.2. Error-aware Path Construction Method

Given a set of paths which cover all the nodes in the lattice, we can utilize the count accumulation method to obtain the noisy support of the graphs on each path. In addition, we can use the noise variance to measure the accuracy of the noisy supports. Assume the set of paths is P = {p₁, p₂, …, p_z} and

Algorithm 5.

Error-Aware Path Construction

Input:
	Lattice L_a ;
Output:
1:	P ← ∅;
2:	M_g ← the maximum size of frequent subgraph;
3:	for i from M_g to 1 do
4:	V_i ← find all the nodes that represent frequent i-subgraphs in L_a;
5:	for each node v in V_i do
6:	C_p ← ∅
7:	/** Case 1 **/
8:	P₀ ← P.copy();
9:	initialize v as a new path and add it into P₀;
10:	add P₀ into C_P;
11:	for each path p in P do
12:	P’ ← P.copy();
13:	if p.tail.size > v.size && v is reachable from p.tail in L_a then
14:	/** Case 2 **/
15:	append v at the end of p in P’;
16:	add P’ into C_P;
17:	else if p.tail.size == v.size && v is reachable from p.tail.parent in L_a then
18:	/** Case 3 **/
19:	p’ ← p.copy();
20:	replace p’.tail by v;
21:	add p’ into P’;
22:	add P’ into C_P;
23:	end if
24:	end for
25:	P ← find the candidate path set with minimal noise variance in C_P;
26:	end for
27:	end for
28:	return P;

Open in a new tab

the privacy budget is ϵ₃. We allocate each path in P a privacy budget ϵ₃/z. For the i-th graph g_i on a path p, based on the count accumulation method, the noise variance of its noisy support is $2 z^{2} (∣ p ∣ - i + 1) ∕ ϵ_{3}^{2}$ . If g_i is on more than one path, its noise variance can be also computed as we discussed in the previous section. Clearly, different sets of paths will result in different data utilities. Therefore, to improve the accuracy of the noisy supports, we should find the path set, where the sum of the noise variances of all the noisy supports derived from the path set is minimal. We formulate this problem as follows.

Problem 1. (Path Construction): Given a lattice L_a, where each node v represents a frequent subgraph, the set of nodes in L_a is V_{L_a} and the set of nodes in a path p is V_p. Find a path set P, such that U_p∈P V_p = V_{L_a}, and Σ_{v∈V_La} v.η is minimized, where v.η is the noise variance of node v’s noisy support.

Considering the complexity of the above problem, we propose a heuristic method, called error-aware path construction, to construct the set of paths which are taken as input by the count accumulation method. The main idea of this method is to iteratively use the nodes in the lattice to construct the path set while ensuring that the noise variance introduced by each node is minimal. Alg. 5 shows the details of this method. It has O(|V_La|²) time complexity, where |V_{L_a}| is the number of nodes in the lattice L_a.

Specifically, given the lattice L_a, we incrementally construct the set P of paths by using the nodes in La in descending

Algorithm 6.

DFG Algorithm

Input:
	Graph database D; Threshold θ; Privacy budgets ϵ₁, ϵ₂ and ϵ₃ (ϵ₁ + ϵ₂ + ϵ₃ = ϵ);
Output:
	A set F of frequent subgraphs together with their noisy supports;
1:	ζ ← get the maximum support of subgraphs with different sizes; \\ this step can be done offline
2:	M_g ← get the maximum frequent subgraph size based on ζ using ϵ₁;
3:	F ← frequent_subgraph_identification(D, θ, ϵ₂, M_g);
4:	lattice-based_noisy_support_computation(F, ϵ₃);
5:	return F;

Open in a new tab

order of their size (i.e., the size of the frequent subgraphs the nodes represent). Suppose the set of nodes that represent frequent i-subgraphs is V_i. We use each node in V_i to update P. For a node v in V_i, we first initialize v as a new path and add it into a copy of the current path set P (line 9). We denote the resulting path set by P₀, which is a candidate for the update of P. We add P₀ into a candidate set C_P (line 10). We then try to insert v into each path in P to get other candidates. For a path p in P, we make a copy of the current path set P (denoted by P′) (line 12). We consider the node with the smallest size in p as the tail node of p and denote it by p.tail. If v is reachable from p.tail and the size of p.tail is larger than the size of v, we first append v at the end of the path p in P′ and then add P′ into C_P (lines 13 - 16). Otherwise if v is reachable from the parent node of p.tail and the size of p.tail is equal to the size of v, we make a copy of p (denoted by p′) (line 19). Then, we replace the tail node of p′ by v and add p′ into P′ (lines 20 - 21). At last, we add P′ into C_P (line 22). After we get all the candidates for the update of P by using v, we take the candidate path set with minimal noise variance (i.e., the candidate path set where the sum of the noise variances of all the noisy supports derived from it is minimal) in C_P to update P (line 25). The path construction process is finished until all the nodes in L_a are considered.

8. DFG Algorithm

In this section, we will first describe our DFG algorithm, then show the DFG algorithm is ϵ-differentially private, and discuss the extensions of this algorithm for mining other frequent patterns at last.

8.1. Algorithm Description

Our DFG algorithm is shown in Alg. 6. In DFG, we first estimate the maximum size M_g of frequent subgraphs. We use the method proposed in [8] to estimate M_g. In particular, we first compute an array ζ = {ζ₁, …, ζ_n}, where ζ_i is the maximum support of i-subgraphs (line 1). We then compute the number of elements in ζ larger than θ by using binary search, and set M_g to this number (line 2). Notice that, since it is infeasible to exactly compute every element in ζ, in practice, we choose a very small threshold and run the non-private FSM algorithm FSG to get ζ. Moreover, the computation of ζ can be done in an offline manner, as it is irrelevant to the input threshold θ and needs to be performed only once for a database.

After that, we utilize our frequent subgraph identification approach to identify frequent subgraphs from the input database (line 3). At last, we adopt our lattice-based noisy support computation approach to calculate the noisy support of each identified frequent subgraph (line 4).

8.2. Privacy Analysis

Theorem 8. Our DFG algorithm is ϵ-differentially private.

Proof. In our DFG algorithm, based on the binary estimation method, we first estimate the maximum size M_g of frequent subgraphs by using ϵ₁. According to Thm. 5, we can see that estimating M_g satisfies ϵ₁-differential privacy.

Then, we utilize our frequent subgraph identification (FI₁) approach to privately identify frequent subgraphs in order of increasing size. In the FI₁ approach, to privately identify frequent i-subgraphs, we first use our binary estimation method to estimate the number of frequent i-subgraphs, which achieves ϵ_b-differential privacy. After that, we use our conditional exponential method to privately select frequent i-subgraphs. According to Thm. 6, it guarantees ϵ_c-differential privacy. Based on the sequential composition property [11], we can see that our FI₁ approach satisfies ϵ₂-differential privacy, where ϵ₂ = (ϵ_b+ϵ_c)×M_g.

At last, we use our lattice-based noisy support computation (NC₂) approach to calculate the noisy support of identified frequent subgraphs. In our NC₂ approach, we first build a lattice based on the identified frequent subgraphs. We only utilize the inclusion relations between identified frequent subgraphs without accessing the input database. Thus, we can safely use this lattice. Moreover, to construct a set of paths which can cover all the nodes in the lattice, we do not use any other information but only rely on the lattice. Thus, the constructed path set does not breach the privacy either. Suppose the resulting path set is P = {p₁, p₂, …, p_z}. We uniformly assign each path in P a privacy budget ϵ₃/z. Then, we use our count accumulation method to obtain the noisy support of the graphs on each path. As shown in Thm. 7, it achieves ϵ₃/z-differential privacy for each path. For each of the graphs which have multiple noisy supports, we combine all its noisy supports to get a more accurate result. Since this is done without reference to the input database, the results still satisfy differential privacy. Based on the sequential composition property [11], our NC₂ approach overall satisfies ϵ₃-differential privacy.

In summary, based on the sequential composition property [11], we can conclude our DFG algorithm achieves ϵ-differential privacy, where ϵ = ϵ₁+ϵ₂+ϵ₃. ◻

8.3. Generality of The DFG Algorithm

We will now discuss the generality of our DFG algorithm. The DFG algorithm consists of a frequent subgraph identification phase and a noisy support computation phase. In the frequent subgraph identification phase, we first estimate the number of frequent i-subgraphs, and then privately select frequent i-subgraphs. Two methods (i.e., the binary estimation and conditional exponential methods) are employed to achieve this task. Since these two methods utilize only the support (or noisy support) information of the pattern being mined, they can also be applied for privately mining other frequent patterns. In the noisy support computation phase, leveraging the inclusion relations of discovered frequent patterns (i.e., the downward closure property of frequent patterns), we first build a lattice for the discovered frequent subgraphs. Obviously, for other types of frequent patterns, we can build the corresponding lattices in a similar way. Then, the error-aware path construction and count accumulation methods are used to calculate the noisy support of frequent subgraphs. Since these two methods are designed based on the lattice and do not use any structural properties of graphs, they can be utilized to compute the noisy support of other frequent patterns.

Overall, since our DFG algorithm does not use any structural properties of graphs (except support counting) and relies only on the downward closure property of frequent patterns and the properties of differential privacy, it can be easily extended to mine other types of frequent patterns (e.g., frequent itemsets and frequent sequences).

8.4. Further Optimization of Noisy Support Computation for Frequent Itemset Mining

Observing that, in frequent itemset mining, both the discovered frequent patterns and records in the input database are sets of items, we propose an optimized approach for computing the noisy support of frequent itemsets. The main idea of this approach is to utilize a set of trees to cover all the nodes in the lattice L_a, and then use the idea of count accumulation to derive the noisy support of frequent itemsets. This approach consists of three main steps: 1) tree construction; 2) subdatabase generation; 3) noisy support computation.

Specifically, in the first step, we first find the set V₀ of nodes with zero in-degree in L_a. Then, considering each node in V₀ as the root of a tree, we can get the set T of trees which are used to cover all the nodes in L_a.

In the second step, for each tree t in T, we first perform a breadth-first traversal on t and record the node visiting order. According to such order, we then divide the input database D into mutually disjoint sub-databases in the following manner. Suppose the node visiting order is v₁, v₂, …, v_|t|, where |t| denotes the number of nodes in T, and the corresponding itemsets are X₁, X₂, …, X_|t|. We first divide D into two subdatabases based on X₁: the sub-database D₁ that is consisted of all the records containing X₁ and the sub-database $\bar{D_{1}}$ that is consisted of the remaining records. Then, we further divide $\bar{D_{1}}$ based on X₂. This process is terminated until D is partitioned into |t| + 1 mutually disjoint sub-databases, i.e., $D_{1}, D_{2}, \dots, \bar{D_{∣ t ∣}}$ .

In the third step, we compute the noisy support of the itemsets represented by the nodes in each tree t. Suppose v_i is a tree node of t, and the set of all its ancestors in t is A_i. We denote the itemset represented by v_i by X_i, and denote the the set of itemsets represented by A_i by I_i. Obviously, X_i is contained in each itemset in I_i, i.e., $X_{i} \subseteq X_{i}^{j} (X_{i}^{j} ϵ I_{i})$ . The support of X_i is equal to $∣ D_{i} ∣ + Σ_{j = 1}^{∣ A_{i} ∣} ∣ D_{i}^{j} ∣$ , where |D_i| denotes the number of records in the sub-database corresponding to X_i, and $∣ D_{i}^{j} ∣$ denotes the number of records in the subdatabase corresponding to $X_{i}^{j}$ . Suppose the privacy budget allocated to t is ϵ_t. To guarantee differential privacy, we add Laplace noise Lap(1/ϵ_t) to the number of records in each subdatabase. For the itemsets having multiple noisy supports, we use the method proposed in Sec. 7.1 to combine the noisy supports of each of them.

In this optimized approach, we use trees to cover the nodes in the lattice L_a instead of using paths. As the number of used trees is always less than the number of used paths, for a given privacy budget, we can allocate a larger portion of the privacy budget to each tree. Therefore, in this optimized approach, less noise is added to the support of each frequent itemset compared to the approach proposed previously.

Notice that this optimized approach cannot be used to compute the noisy support of frequent sequences (or frequent subgraphs). The following example explains this. Suppose “abc” is a frequent sequence, and there is a record “abbcdefg” in the input database. The frequent sequence “abc” is not contained in the record, but its subsequences “ab” and “bc”, which are also frequent, are both contained in the record. In this case, if the optimized approach is applied, we will get a wrong support of subsequence “ab” (or “bc”) before adding noise.

9. Experiments

In this section, we evaluate the performance of our DFG algorithm. We compare it with the following two algorithms. The first one is the straightforward algorithm we proposed in Sec. 4, which satisfies ϵ-differential privacy. The second one is the MCMC sampling based algorithm proposed in [5], which guarantees the weaker (ϵ, ϔ)-differential privacy. We denote these two algorithms by Naive and DFPM, respectively. We implement all these algorithms in Java. The source code of our DFG algorithm is publicly available at [29]. The experiments are conducted on a PC with Intel Core2 Duo E8400 CPU (3.0GHz) and 64GB RAM. Due to the randomness of the algorithms, we run every algorithm ten times and report the average results. In all these experiments, the relative threshold (i.e., the fraction of records that contain a pattern) is used. The absolute threshold can be obtained by multiplying the relative threshold by the number of input records. In DFG, we allocate the total privacy budget ϵ as follows: ϵ₁ = 0.1ϵ, ϵ₂ = 0.5ϵ and ϵ₃ = 0.4ϵ. We set the default value of ϵ to 0.2. In Sec. 9.2, we also present the experimental results when ϵ is varied.

Datasets.

Three publicly available real datasets are used in our experiments. Specifically, dataset Cancer includes structures of human tumor cell lines [30], dataset HIV contains molecules tested against HIV virus [30], and dataset SPL contains structures of FDA-approved clinical drugs [31]. Their characteristics are summarized in Tab. 2.

TABLE 2.

Data Characteristics

Dataset	#Graphs	Avg.size	Max.size	#Vertex Labels
Cancer	32557	28.3	236	67
HIV	42689	27.5	247	65
SPL	53804	47.5	831	104

Open in a new tab

Utility Measures.

In the experiments, we employ two widely used metrics to evaluate the performance of the algorithms. The first is F-score [8], which is used to measure the utility of discovered frequent subgraphs. The second is Relative Error (RE) [7], which is used to measure the error with respect to the true supports.

9.1. Frequent Subgraph Mining

Fig. 5(a) – 5(f) show the performance of DFG, DFPM and Naive for different values of threshold on the three datasets. For DFPM, it only guarantees the weaker (ϵ, δ)-differential privacy. Moreover, DFPM is designed for top-k FSM. In this experiment, we consider the scenario where DFPM sets k to be the number of frequent subgraphs for the given threshold. Notice that, such setting might violate the privacy. However, even with these privacy relaxations, we observe DFG significantly outperforms DFPM. In DFPM, to find a frequent subgraph, it first randomly generates a graph and then performs random walk in the output space. The transition is determined based on the support of the current graph and its neighboring graphs. However, if the first generated graph is in a region where the support of all neighboring graphs is very low, the random walk will seldom move and an infrequent subgraph will be output, which negatively affects the utility of the results.

For the algorithm Naive, as its results for RE are always orders of magnitudes larger than the other comparison algorithms, we omit it to ensure the readability of the figures. Fig. 5(a) – 5(f) show DFG significantly outperforms Naive. In Naive, it perturbs the support of all candidate subgraphs. However, as discussed in Sec. 4, a large number of candidate subgraphs are generated in the mining process, causing a large amount of perturbation noise. For example, in dataset SPL, the number of vertex labels is 104 and the number of candidate 1-subgraphs (i.e., all possible single-edge graphs) is $C_{104}^{2} = 5356$ . Thus, Naive gets poor performance in terms of both F-score and RE.

We also compare the performance of these algorithms for top-k FSM. To extend DFG and Naive to discover the k most frequent subgraphs, we adapt them by setting the threshold to be the support of the k-th frequent subgraph. To avoid privacy breach, we add Laplace noise to that computation as the sensitivity of such computation is one. Fig. 5(g) – 5(l) show the results by varying the parameter k from 20 to 100. We can see our DFG algorithm achieves the best performance.

9.2. Effect of Privacy Budget

Fig. 6 shows the performance of the three algorithms for mining top-50 frequent subgraphs under varying privacy budget ϵ on datasets Cancer and HIV. We can see DFG consistently achieves the best performance at the same level of privacy. All these algorithms perform in a similar way: the utility of the results is improved when e increases. This is because, when e increases, a smaller amount of noise is required and a lower degree of privacy is guaranteed.

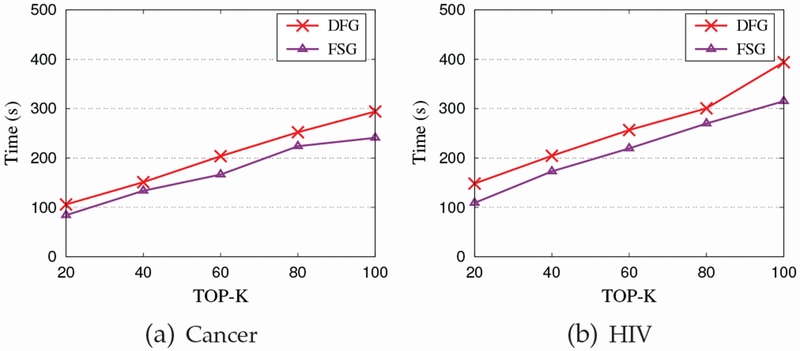
9.3. Efficiency of DFG

Fig. 7 shows the running time of our DFG algorithm and the non-private FSM algorithm FSG [25] for finding top-k frequent subgraphs in datasets Cancer and HIV by varying k from 20 to 100. For DFG, the running time does not include computing the array ζ (i.e., the step of Alg. 6), as the computation of ζ can be done offline. We can see that, although DFG runs slower than FSG, it achieves comparable performance to FSG. In both FSG and DFG, computing the support of graphs is the most time-consuming part, which has exponential time complexity. For DFG, it needs an extra phase (i.e., the noisy support computation phase) to compute the noisy support of the frequent subgraphs. This is the main reason that DFG is slower than DFG. However, as the number of frequent subgraphs is typically much smaller than that of candidate subgraphs, such phase does not introduce too much computation cost. In addition, as shown earlier, most of the key components in DFG have polynomial time complexity, and thus they also do not introduce too much computation cost. These are the reasons that DFG can obtain comparable performance to FSG.

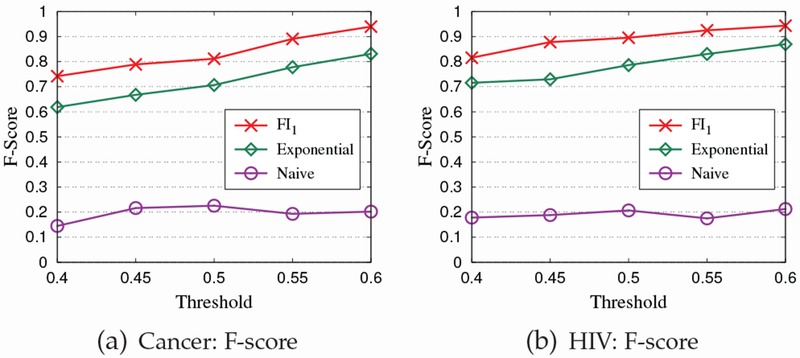
9.4. Effect of FI₁ Approach

In this experiment, we study the effectiveness of our frequent subgraph identification approach (denoted by FI₁) on datasets Cancer and HIV. We compare FI₁ with two algorithms. Specifically, the first one is the straightforward algorithm proposed in Sec. 4 (denoted by Naive), which first perturbs the support of candidate subgraphs by using the Laplace mechanism, and then outputs the candidate subgraphs which have support above the threshold. The second one first utilizes our binary estimation method to estimate the number of frequent subgraphs, and then uses the exponential mechanism to select frequent subgraphs from candidate subgraphs. Here, we denote the second algorithm by Exponential. From Fig. 8, we can see, our FI₁ approach gets the best performance in terms of F-score. This is because FI₁ uses the conditional exponential method to identify frequent subgraphs, which can improve the accuracy of the private selections of frequent subgraphs by candidate pruning.

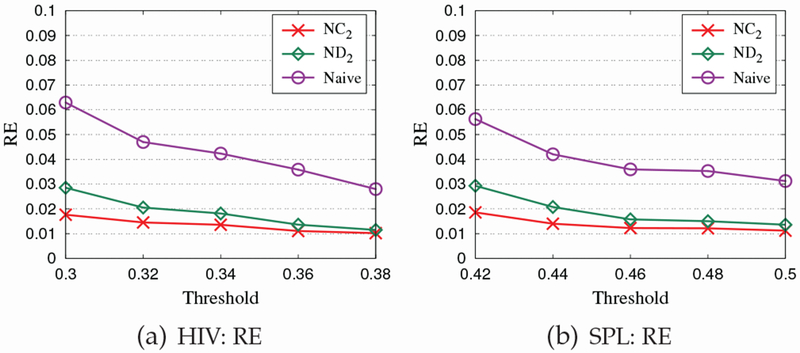
9.5. Effect of NC₂ Approach

We also evaluate the effectiveness of our lattice-based noisy support computation approach (denoted by NC₂) on datasets HIV and SPL. We compare NC₂ with two algorithms. The first one is the straightforward algorithm proposed in Sec. 4 (denoted by Naive), where the noisy supports of identified frequent subgraphs are obtained by directly perturbing their true supports. The second one calculates the noisy support of identified frequent subgraphs by using the noisy support derivation approach (denoted by ND₂) proposed in our conference paper [24]. The difference between NC₂ and ND₂ is that NC₂ utilizes the error-aware path construction method to construct the set of paths, while ND2 uses the path construction and path extension methods to construct that set of paths. Fig. 9 shows that our NC₂ approach achieves the best performance in terms of RE. In particular, we observe that NC₂ obtains better results than ND₂, especially when the threshold is relatively low. The reasons can be explained as follows. First, while the path construction and extension methods used in ND₂ attempt to minimize the number of paths which is correlated with the overall error, the error-aware path construction method used in NC₂ can directly reduce the errors of noisy supports. Second, to extend a constructed path, the path extension method used in ND₂ inserts nodes only at the start and end positions of the path without considering the positions in the middle of the path.

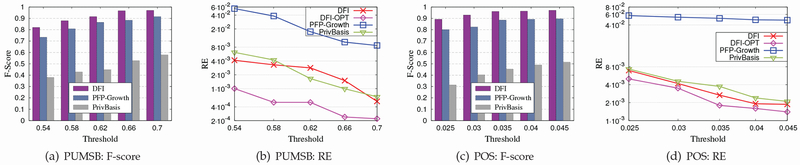
9.6. Extending DFG for Mining Frequent Itemsets

To demonstrate the generality of our DFG algorithm, we extend it to mine frequent itemsets under ϵ-differential privacy. In particular, we denote the extended algorithm which adopts the general approach (i.e., NC₂) to compute the noisy support of frequent itemsets by DFI, and denote the extended algorithm which adopts the optimized approach proposed in Sec. 8.4 to compute the noisy support of frequent itemsets by DFI-OPT. We compare DFI and DFI-OPT with the following two algorithms: 1) the PFP-Growth algorithm proposed in [14], which privately finds the itemsets based on FP-growth; 2) the PrivBasis algorithm proposed in [7], which privately finds the k most frequent itemsets by constructing the basis set. In the experiments, we use two real datasets. A summary of the characteristics of the datasets is illustrated in Tab. 3.

TABLE 3.

Data Characteristics

Dataset	#Transactions	#Items	Max.length	Avg.length
PUMSB	49046	2088	63	50.5
POS	515597	1657	164	6.5

Open in a new tab

Fig. 10 shows the performance of DFI, DFI-OPT, PFP-Growth and PrivBasis for different values of threshold on the two datasets. For the top-k FIM algorithm PrivBasis, we consider the scenario where PrivBasis sets k to be the number of frequent itemsets for a given threshold. We want to emphasize that this setting might create privacy concerns. As DFI and DFI-OPT use the same approach to find frequent itemsets (i.e., FI₁), for the metric F-score, we only report the experimental results of DFI. From Fig. 10, we can observe that DFI outperforms PFP-Growth and PrivBasis in terms of F-score. In addition, we can also observe that both DFI and DFI-OPT gets the good performance in terms of RE. In particular, DFI-OPT gets better results than DFI, as it injects less noise into the support of frequent itemsets than DFI.

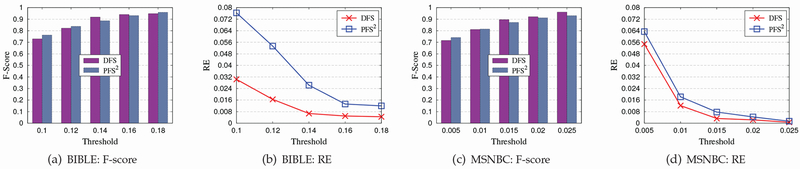
9.7. Extending DFG for Mining Frequent Sequences

We also extend our DFG algorithm to mine frequent sequences under ϵ-differential privacy. We denote this extended algorithm by DFS. We compare DFS against a state-of-the-art algorithm called PFS² [9], which privately finds the sequences whose support exceeds a given threshold via sampling-based candidate pruning. In the experiments, we also use two real datasets. A summary of the characteristics of the datasets is illustrated in Tab. 4.

TABLE 4.

Data Characteristics

Dataset	#Sequences	#Items	Max.length	Avg.length
BIBLE	36369	13905	100	21.64
MSNBC	989818	17	14795	4.75

Open in a new tab

Fig. 11 shows the performance of DFS and PFS² for different values of threshold on the two datasets. From Fig. 11, we can observe that DFS achieves comparable performance to PFS² in terms of F-score. However, for the metric RE, DFS obtains much better results than PFS².

10. Conclusion

In this paper, we study the problem of designing a frequent subgraph mining (FSM) algorithm, which can satisfy ϵ-differential privacy and achieve high data utility. We present a differentially private FSM algorithm called DFG, which consists of a frequent subgraph identification phase and a noisy support computation phase. DFG can be easily extended for mining other frequent patterns, such as frequent itemsets and frequent sequences. Through privacy analysis, we prove that our DFG algorithm satisfies ϵ-differential privacy. Extensive experiments on real datasets show that the proposed DFG algorithm can privately find frequent subgraphs with good data utility.

Acknowledgments

We thank the reviewers for their valuable comments which significantly improved this paper. The work was supported by National Natural Science Foundation of China under grant 61502047. LX was supported in part by the Patient-Centered Outcomes Research Institute (PCORI) under contract ME-1310-07058, the National Institute of Health (NIH) under award number R01GM114612 and R01GM118609.

Biographies

Xiang Cheng received his PhD degree in computer science from the Beijing University of Posts and Telecommunications, China, in 2013. He is currently an associate professor at the Beijing University of Posts and Telecommunications. His research interests include data mining and data privacy.

Sen Su received his PhD degree in computer science from the University of Electronic Science and Technology, China, in 1998. He is currently a professor at the Beijing University of Posts and Telecommunications. His research interests include service computing, cloud computing and data privacy.

Shengzhi Xu received his PhD degree in computer science from the Beijing University of Posts and Telecommunications, China, in 2016. He is currently a specialist of general management in State Grid International Development Co., Ltd., and his research interests include data mining and data privacy.

Li Xiong received her PhD degree in computer science from the Georgia Institute of Technology, Atlanta, GA, USA. She is currently a professor at the Emory University, Atlanta, GA, USA. Her current research interests include spatiotemporal data management, and health informatics.

Ke Xiao received his Master degree in computer science from the Beijing University of Posts and Telecommunications, China. He is working as a full-time software engineer at Baidu Company now. His research interests include data mining, data privacy, deep learning and distributed system.

Mingxing Zhao is working toward his master at the Beijing University of Posts and Telecommunications in China. His major is computer science. His research interests include data mining and machine learning.

Footnotes

The preliminary version of this paper has been published in the proceedings of the 2016 IEEE International Conference on Data Engineering (ICDE 2016), Helsinki, Finland, May 16-20, 2016.

Contributor Information

Xiang Cheng, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing China.

Sen Su, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing China.

Shengzhi Xu, State Grid International Development Co., Ltd., Beijing China.

Li Xiong, Emory University, Atlanta, GA USA.

Ke Xiao, Institute of Vision Search Technology, Baidu, Beijing China.

Mingxing Zhao, State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing China.

References

[1].Bhaskar R, Laxman S, Smith A, and Thakurta A, “Discovering frequent patterns in sensitive data,” in KDD, 2010. [Google Scholar]
[2].Dwork C, “Differential privacy,” in ICALP, 2006. [Google Scholar]
[3].Sweeney L, “k-anonymity: A model for protecting privacy,” Int. J. Uncertain. Fuzziness Knowl.-Base Syst, 2002. [Google Scholar]
[4].Machanavajjhala A, Gehrke J, Kifer D, and Venkitasubramaniam M, “l-diversity: Privacy beyond k-anonymity,” in ICDE, 2006. [Google Scholar]
[5].Shen E and Yu T, “Mining frequent graph patterns with differential privacy,” in KDD, 2013. [Google Scholar]
[6].McSherry F and Talwar K, “Mechanism design via differential privacy,” in FOCS, 2007. [Google Scholar]
[7].Li N, Qardaji W, Su D, and Cao J, “Privbasis: frequent itemset mining with differential privacy,” in VLDB, 2012, pp. 305–316. [Google Scholar]
[8].Zeng C, Naughton JF, and Cai J-Y, “On differentially private frequent itemset mining,” in VLDB, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
[9].Xu S, Su S, Cheng X, Li Z, and Xiong L, “Differentially private frequent sequence mining via sampling-based candidate pruning,” in ICDE, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
[10].Ji S, Li W, Mittal P, Hu X, and Beyah RA, “Secgraph: A uniform and open-source evaluation system for graph data anonymization and de-anonymization.” in USENIX Security Symposium, 2015, pp. 303–318. [Google Scholar]
[11].Dwork C, McSherry F, Nissim K, and Smith A, “Calibrating noise to sensitivity in private data analysis,” in TCC, 2006. [Google Scholar]
[12].Cheng X, Su S, Xu S, and Li Z, “Dp-apriori: A differentially private frequent itemset mining algorithm based on transaction splitting,” Computers & Security, 2015. [Google Scholar]
[13].Han J, Pei J, and Yin Y, “Mining frequent patterns without candidate generation,” in SIGMOD, 2000. [Google Scholar]
[14].Su S, Xu S, Cheng X, Li Z, and Yang F, “Differentially private frequent itemset mining via transaction splitting,” TKDE, 2015. [Google Scholar]
[15].Li H, Xiong L, and Jiang X, “Differentially private synthesization of multi-dimensional data using copula functions,” in EDBT, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
[16].Lee J and Clifton C, “Top-k frequent itemsets via differentially private fp-trees,” in kDd, 2014. [Google Scholar]
[17].Chen Y and Machanavajjhala A, “On the privacy properties of variants on the sparse vector technique,” CoRR, 2015. [Online]. Available: http://arxiv.org/abs/1508.07306 [Google Scholar]
[18].Bonomi L and Xiong L, “A two-phase algorithm for mining sequential patterns with differential privacy,” in CIKM, 2013. [Google Scholar]
[19].Xiang C, Su S, Xu S, Tang P, and Li Z, “Differentially private maximal frequent sequence mining,” Computers & Security, 2015. [Google Scholar]
[20].Karwa V, Raskhodnikova S, Smith A, and Yaroslavtsev G, “Private analysis of graph structure,” in VLDB, 2011. [Google Scholar]
[21].Chen S and Zhou S, “Recursive mechanism: towards node differential privacy and unrestricted joins,” in SIGMOD, 2013. [Google Scholar]
[22].Proserpio D, Goldberg S, and McSherry F, “Calibrating data to sensitivity in private data analysis: A platform for differentially-private analysis of weighted datasets,” in VLDB, 2014. [Google Scholar]
[23].Zhang J, Cormode G, Procopiuc C, Srivastava D, and Xiao X, “Private release of graph statistics using ladder functions,” in SIGMOD, 2015. [Google Scholar]
[24].Xu S, Su S, Xiong L, Cheng X, and Xiao K, “Differentially private frequent subgraph mining,” in ICDE, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
[25].Kuramochi M and Karypis G, “An efficient algorithm for discovering frequent subgraphs,” TKDE, 2004. [Google Scholar]
[26].Gary MR and Johnson DS, “Computers and intractability: A guide to the theory of np-completeness,” 1979. [Google Scholar]
[27].Agrawal R and Srikant R, “Fast algorithms for mining association rules,” in VLDB, 1994. [Google Scholar]
[28].Cordella LP, Foggia P, Sansone C, and Vento M, “A (sub) graph isomorphism algorithm for matching large graphs,” TPAMI, 2004. [DOI] [PubMed] [Google Scholar]
[29].“A publicly available implementation of DFG,” http://github.com/igoingdown/DFG.
[30].“Nci,” http://cactus.nci.nih.gov/download/nci.
[31].“Fda,” http://cactus.nci.nih.gov/download/fda.

[R1] [1].Bhaskar R, Laxman S, Smith A, and Thakurta A, “Discovering frequent patterns in sensitive data,” in KDD, 2010. [Google Scholar]

[R2] [2].Dwork C, “Differential privacy,” in ICALP, 2006. [Google Scholar]

[R3] [3].Sweeney L, “k-anonymity: A model for protecting privacy,” Int. J. Uncertain. Fuzziness Knowl.-Base Syst, 2002. [Google Scholar]

[R4] [4].Machanavajjhala A, Gehrke J, Kifer D, and Venkitasubramaniam M, “l-diversity: Privacy beyond k-anonymity,” in ICDE, 2006. [Google Scholar]

[R5] [5].Shen E and Yu T, “Mining frequent graph patterns with differential privacy,” in KDD, 2013. [Google Scholar]

[R6] [6].McSherry F and Talwar K, “Mechanism design via differential privacy,” in FOCS, 2007. [Google Scholar]

[R7] [7].Li N, Qardaji W, Su D, and Cao J, “Privbasis: frequent itemset mining with differential privacy,” in VLDB, 2012, pp. 305–316. [Google Scholar]

[R8] [8].Zeng C, Naughton JF, and Cai J-Y, “On differentially private frequent itemset mining,” in VLDB, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] [9].Xu S, Su S, Cheng X, Li Z, and Xiong L, “Differentially private frequent sequence mining via sampling-based candidate pruning,” in ICDE, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] [10].Ji S, Li W, Mittal P, Hu X, and Beyah RA, “Secgraph: A uniform and open-source evaluation system for graph data anonymization and de-anonymization.” in USENIX Security Symposium, 2015, pp. 303–318. [Google Scholar]

[R11] [11].Dwork C, McSherry F, Nissim K, and Smith A, “Calibrating noise to sensitivity in private data analysis,” in TCC, 2006. [Google Scholar]

[R12] [12].Cheng X, Su S, Xu S, and Li Z, “Dp-apriori: A differentially private frequent itemset mining algorithm based on transaction splitting,” Computers & Security, 2015. [Google Scholar]

[R13] [13].Han J, Pei J, and Yin Y, “Mining frequent patterns without candidate generation,” in SIGMOD, 2000. [Google Scholar]

[R14] [14].Su S, Xu S, Cheng X, Li Z, and Yang F, “Differentially private frequent itemset mining via transaction splitting,” TKDE, 2015. [Google Scholar]

[R15] [15].Li H, Xiong L, and Jiang X, “Differentially private synthesization of multi-dimensional data using copula functions,” in EDBT, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] [16].Lee J and Clifton C, “Top-k frequent itemsets via differentially private fp-trees,” in kDd, 2014. [Google Scholar]

[R17] [17].Chen Y and Machanavajjhala A, “On the privacy properties of variants on the sparse vector technique,” CoRR, 2015. [Online]. Available: http://arxiv.org/abs/1508.07306 [Google Scholar]

[R18] [18].Bonomi L and Xiong L, “A two-phase algorithm for mining sequential patterns with differential privacy,” in CIKM, 2013. [Google Scholar]

[R19] [19].Xiang C, Su S, Xu S, Tang P, and Li Z, “Differentially private maximal frequent sequence mining,” Computers & Security, 2015. [Google Scholar]

[R20] [20].Karwa V, Raskhodnikova S, Smith A, and Yaroslavtsev G, “Private analysis of graph structure,” in VLDB, 2011. [Google Scholar]

[R21] [21].Chen S and Zhou S, “Recursive mechanism: towards node differential privacy and unrestricted joins,” in SIGMOD, 2013. [Google Scholar]

[R22] [22].Proserpio D, Goldberg S, and McSherry F, “Calibrating data to sensitivity in private data analysis: A platform for differentially-private analysis of weighted datasets,” in VLDB, 2014. [Google Scholar]

[R23] [23].Zhang J, Cormode G, Procopiuc C, Srivastava D, and Xiao X, “Private release of graph statistics using ladder functions,” in SIGMOD, 2015. [Google Scholar]

[R24] [24].Xu S, Su S, Xiong L, Cheng X, and Xiao K, “Differentially private frequent subgraph mining,” in ICDE, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] [25].Kuramochi M and Karypis G, “An efficient algorithm for discovering frequent subgraphs,” TKDE, 2004. [Google Scholar]

[R26] [26].Gary MR and Johnson DS, “Computers and intractability: A guide to the theory of np-completeness,” 1979. [Google Scholar]

[R27] [27].Agrawal R and Srikant R, “Fast algorithms for mining association rules,” in VLDB, 1994. [Google Scholar]

[R28] [28].Cordella LP, Foggia P, Sansone C, and Vento M, “A (sub) graph isomorphism algorithm for matching large graphs,” TPAMI, 2004. [DOI] [PubMed] [Google Scholar]

[R29] [29].“A publicly available implementation of DFG,” http://github.com/igoingdown/DFG.

[R30] [30].“Nci,” http://cactus.nci.nih.gov/download/nci.

[R31] [31].“Fda,” http://cactus.nci.nih.gov/download/fda.

PERMALINK

A Two-Phase Algorithm for Differentially Private Frequent Subgraph Mining

Xiang Cheng

Sen Su

Shengzhi Xu

Li Xiong

Ke Xiao

Mingxing Zhao

Abstract

1. Introduction

2. Related Work

3. Preliminaries

3.1. Differential Privacy

3.2. Frequent Subgraph Mining

Fig. 1.

3.3. Notations

TABLE 1.

4. A Straightforward Approach

Privacy Analysis.

Limitation.

5. Overview of Our DFG Algorithm

Fig. 2.

6. Frequent Subgraph Identification

Algorithm 1.

6.1. Binary Estimation Method

Algorithm 2.

6.2. Conditional Exponential Method

Algorithm 3.

7. Lattice-based Noisy Support Computation

Fig. 3.

Algorithm 4.

7.1. Count Accumulation Method

Fig. 4.

7.2. Error-aware Path Construction Method

Algorithm 5.

Algorithm 6.

8. DFG Algorithm

8.1. Algorithm Description

8.2. Privacy Analysis

8.3. Generality of The DFG Algorithm

8.4. Further Optimization of Noisy Support Computation for Frequent Itemset Mining

9. Experiments

Datasets.

TABLE 2.

Utility Measures.

9.1. Frequent Subgraph Mining

Fig. 5.

9.2. Effect of Privacy Budget

Fig. 6.

9.3. Efficiency of DFG

Fig. 7.

9.4. Effect of FI1 Approach

Fig. 8.

9.5. Effect of NC2 Approach

Fig. 9.

9.6. Extending DFG for Mining Frequent Itemsets

TABLE 3.

Fig. 10.

9.7. Extending DFG for Mining Frequent Sequences

TABLE 4.

Fig. 11.

10. Conclusion

Acknowledgments

Biographies

Footnotes

Contributor Information

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

9.4. Effect of FI₁ Approach

9.5. Effect of NC₂ Approach