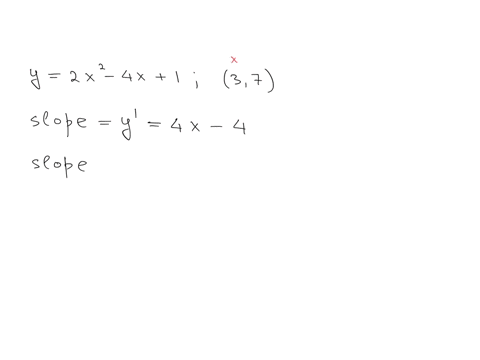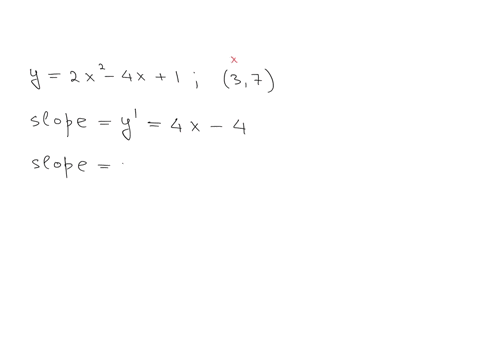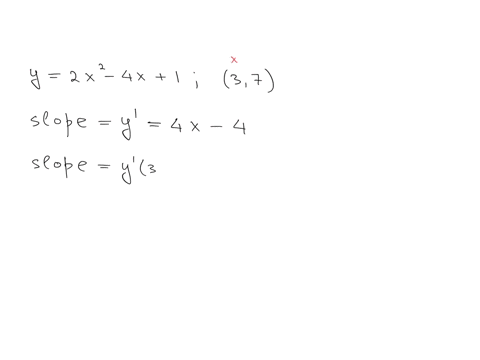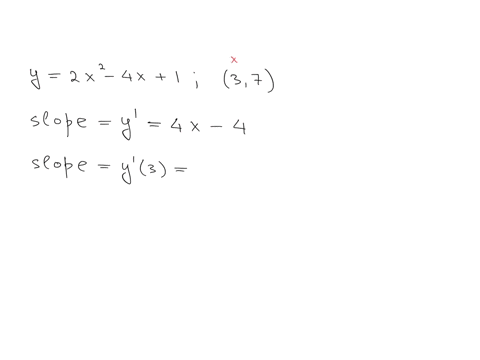00:01
The third derivative of the function is given as the third derivative, which is equal to 2x quib.
00:08
So first of all, let's try to get the second derivative.
00:11
So the second derivative is the integral, the third derivative of this function here, which is the x.
00:17
So that would be 2x cubed the x.
00:21
If i take the integral 2x to the power 4 over 4 and plus the constant c, so the second derivative of the function is equal to x to the power of 4.
00:30
4 over 2 plus c.
00:33
And also an additional information is given the slope of the inflection on tangent at negative 1.
00:39
So that means this function has the inflection point at x is equal to negative 1.
00:45
That means the second derivative of the function is equal to 0 at x is equal to negative 1.
00:50
Let's plug in negative 1 here.
00:53
Second derivative at x is equal to 1, which is 1 over 2 plus c, which is 0.
00:57
So from here, c would be negative 1 over 2.
01:01
So we got the second derivative as x to the power 4 over 2 and minus 1 half.
01:08
Let's find the first derivative, which is the integral of the second derivative, x to the power 2 minus 1 over x, the x.
01:16
So from here, x to the power 5 over 10 and minus x over 2 plus another constant.
01:23
Let's say this is c1.
01:24
So the tangent, the inflectional tangent, has the value of 2 over 3.
01:32
That means the first derivative of this function, when x is equal to 1, which is equal to 2 over 3...