At a glance
Powered by AI
The document derives the work-energy theorem from first principles and shows that it relates the net work done on an object to the change in its kinetic energy. Kinetic energy can be understood as the amount of work required to accelerate an object from rest.
10/18/2019Chapter 06 Homework Assignmenthttps://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=74882171/15
Chapter 06 Homework Assignment
Due: 11:59pm on Thursday, October 17, 2019
You will receive no credit for items you complete after the assignment is due. Grading Policy
The Work-Energy Theorem
Learning Goal:
To understand the meaning and possible applications of the work-energy theorem.In this problem, you will use your prior knowledge to derive one of the most important relationships in mechanics: the work-energy theorem. We will start with a special case: a particle of mass moving in the
x
direction at constant acceleration .During a certain interval of time, the particle accelerates from to , undergoing displacement given by .
Part A
Find the acceleration of the particle.
Express the acceleration in terms of , , and .Hint 1.
Some helpful relationships from kinematicsBy definition for constant acceleration,.Furthermore, the average speed is,and the displacement is.Combine these relationships to eliminate . ANSWER:
CorrectPart B
Find the net force acting on the particle.
Express your answer in terms of and .Hint 1.
Using Newton's lawsWhich of Newton's laws may be helpful here? ANSWER:
i
f
=−
f
i
i
f
=
−
f
i
=
avg +
i
f 2
=
avg
=
−
2
2 2
10/18/2019Chapter 06 Homework Assignmenthttps://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=74882172/15
CorrectPart C
Find the net work done on the particle by the external forces during the particle's motion.
Express your answer in terms of and .
ANSWER:
CorrectPart D
Substitute for from Part B in the expression for work from Part C. Then substitute for from the relation in Part A. Thiswill yield an expression for the net work done on the particle by the external forces during the particle's motion in termsof mass and the initial and final velocities. Give an expression for the work in terms of those quantities.
Express your answer in terms of , , and .
ANSWER:
Correct
The expression that you obtained can be rearranged asThe quantity has the same units as work. It is called the
kinetic energy
of the moving particle and isdenoted by . Therefore, we can write and .Note that like momentum, kinetic energy depends on both the mass and the velocity of the moving object.However, the mathematical expressions for momentum and kinetic energy are different. Also, unlike momentum,kinetic energy is a scalar. That is, it does not depend on the sign (therefore direction) of the velocities.
Part E
Find the net work done on the particle by the external forces during the motion of the particle in terms of the initial andfinal kinetic energies.
Express your answer in terms of and .
ANSWER: =
=
i
f
=
−
2
2
2
2
=
−
.
1 2
f 2 1 2
i 2
1 2
2
=
i 1 2
i 2
=
f 1 2
f 2
i
f
10/18/2019Chapter 06 Homework Assignmenthttps://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=74882173/15
Correct
This result is called the work-energy theorem. It states that the net work done on a particle equals the change inkinetic energy of that particle. Also notice that if is zero, then the work-energy theorem reduces to.In other words, kinetic energy can be understood as the amount of work that is done to accelerate the particlefrom rest to its final velocity.The work-energy theorem can be most easily used if the object is moving in one dimension and is being actedupon by a constant net force directed along the direction of motion. However, the theorem is valid for more generalcases as well.Let us now consider a situation in which the particle is still moving along the
x
axis, but the net force, which is still directed alongthe
x
axis, is no longer constant. Let's see how our earlier definition of work,needs to be modified by being replaced by an integral. If the path of the particle is divided into very small displacements , wecan assume that over each of these small displacement intervals, the net force remains essentially constant and the work done to move the particle from to is,where is the
x
component of the net force (which remains virtually constant for the small displacement from to ). Thenet work done on the particle is then given by.Now, usingand,it can be shown that.
Part F
Evaluate the integral .
Express your answer in terms of , , and .Hint 1.
An integration formulaThe formula for is . =
−
i
=
f
=⋅,
⃗
⃗
+
=
+
=
=
∫
f
i
∫
f
i
=
===
=
∫
f
i
=
∫
f
i
i
f
∫
=
∫
−
2
2 2
10/18/2019Chapter 06 Homework Assignmenthttps://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=74882174/15
ANSWER:
Correct
The expression that you havejust obtained is equivalent to . Not surprisingly, we are back to thesame expression of the work-energy theorem! Let us see how the theorem can be applied to problem solving.
Part G
A particle moving in the
x
direction is being acted upon by a net force , for some constant . The particlemoves from to . What is , the change in kinetic energy of the particle during that time?
Express your answer in terms of and .Hint 1.
Finding the workIntegrate to calculate the work done on the particle.
Hint 2.
An integration formulaThe formula for is . ANSWER:
Correct
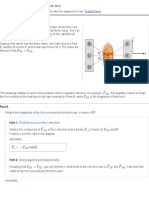
It can also be shown that the work-energy theorem is valid for two- and three-dimensional motion and for a varyingnet force that is not necessarily directed along the instantaneous direction of motion of the particle. In that case,the work done by the net force is given by the line integralwhere and are the initial and the final positions of the particle, is the vector representing a smalldisplacement, and is the net force acting on the particle.
Work from a Constant Force
Learning Goal:
To understand how to compute the work done by a constant force acting on a particle that moves in a straight line.In this problem, you will calculate the work done by a constant force. A force is considered constant if is independent of .This is the most frequently encountered situation in elementary Newtonian mechanics. =
−
2
2
2
2
=−
f
i
(
)=
2
=
i
=3
f
Δ
(
)
∫
2
=
∫
2 −
3
3 3
=
Δ
26
3 3
=⋅,
∫
f
i
⃗
→
i
f
→
⃗()
⃗
⃗
⃗