Moments in statistics
- 1. MOMENTS Subject: SMDM Submitted to: Prof. S.C.Singh To be presented by Sanjay Saw Roll No-36 FMS-BHU
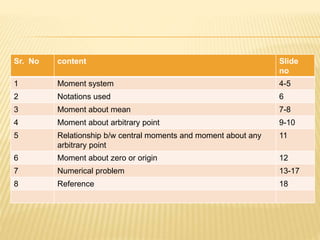
- 2. Sr. No content Slide no 1 Moment system 4-5 2 Notations used 6 3 Moment about mean 7-8 4 Moment about arbitrary point 9-10 5 Relationship b/w central moments and moment about any arbitrary point 11 6 Moment about zero or origin 12 7 Numerical problem 13-17 8 Reference 18
- 3. A quantity of data which by its mere bulk may be incapable of entering the mind is to be replaced by relatively few quantities which shall adequately represent the whole or which in other words, shall contain as much as possible ,ideally the whole ,of the relevant information contained in the original data. R.A.Fisher
- 4. MOMENT SYSTEM Sub group of measurement of central tendency i.e variability and skewness. Includes measurement like mean ,average deviation ,std. deviation and so on. It is analogous to the term “moment”used in physics. Size of class intervals represent the force and deviation of mid value of each class from the observation represent the distance.
- 5. CONTD.. Moments basically represents a convenient and unifying method for summarizing certain descriptive statistical measures.
- 6. Notation of moments Greek letter (mu) if deviation are taken from the actual mean. Greek letter (nu) or ’. if deviation are taken from some assumed mean (or arbitrary value other than zero).
- 7. MOMENTS ABOUT MEAN let x1,x2,x3………,xn n observations with mean x̅. Then the rth moment about the actual mean of a variable both for ungrouped and grouped data is given by: For ungrouped data: r= 1/n*(x- x̅)^r r=1,2,3,4….
- 8. CONTD…. When r=1, 1=1/n* x ;A.M r=2, 2= 1/n*(x- x̅ )^2 ;σ2(variance) r=3, 3= 1/n*(x- x̅ )^3 ;indicates symmetry or asymmetry r=4, 4= 1/n*(x- x̅ )^4 ;kurtosis(flatness) of the frequency curve For grouped data: r= 1/N*f(x- x̅ )^r r=1,2,3,4; N= fi
- 9. MOMENTS ABOUT ARBITRARY POINTS When from the data it is being feel that the actual mean is bit difficult to find out or in fractions.the moments are first calculated about an assumed mean say A and then converted about the actual mean For grouped data ’r=1/ n* f(x-A)^r ;r=1,2,3,4
- 10. CONTD…… For ungrouped data ’r=1/ n* (x-A)^r ;r=1,2,3,4 For r=1,we have ’r=1/ n* (x-A) =1/n* (x)-A = x̅ -A
- 11. RELATION BETWEEN CENTRAL MOMENTS AND MOMENTS ABOUT ANY ARBITRARY POINTS 1=’1 2=’2-(’1)^2 3=’3-3’2’1+2(’1)^3 4=’4-4’3’1+6’2(’1)^2- 3(’1)4
- 12. MOMENT ABOUT ZERO OR ORIGIN The moments about zero or origin are obtained as follows: Vr=1/n*fx^r ;r=1,2,3,4 The first moment about origin gives the mean V1=1/n* fx ; A.M
- 13. EXAMPLE Following is the data on early earning(in rs)of employees in a company: Earnin g 50-70 70-90 90-110 110-130 130-150 150-170 170-190 No of workers 4 8 12 20 6 7 3 Calculate the first four moments about the point 120 .convert the results into moments about the mean also find out the first moment about origin.
- 14. SOLUTION class Mid value( m=x) Solution:- Frequency( f) f*x d=(m- A)/20 fd Fd^2 Fd^ 3 Fd^4 50-70 60 4 240 -3 -12 36 -108 324 70-90 80 8 640 -2 -16 32 -64 128 90-110 100 12 1200 -1 -12 12 -12 12 110-130 120=A 20 2400 0 0 0 0 0 130-150 140 6 840 1 6 6 6 6 150-170 160 7 1120 2 14 28 56 112 170-190 180 3 540 3 9 27 81 243 60 6980 -11 141 -41 825
- 15. The moments about some arbitrary origin or point(A=120)is given by ’r=1/ n* f(x-A)^r ;for grouped data =1/n*(fd^r)h^r ;d=(m-A)/h or (m-A)=hd here (x=mid value i.e=m) For A=120 and x=m,we get ’1=1/n* fd*h=1/60*(-11)*20= -3.66 ’2=1/n* fd^2*h^2=1/60*(141)*20^2=940 ’3=1/n* fd^3*h^3=1/60*(-41)*20^3=-5466.66 ’4=1/n* fd^4*h^4=1/60*(825)*20^4=2200000
- 16. CONTD.. The moments about actual mean (’2=940)is given by 1=’1=-3.66 2=’2-(’1)^2=940-(-3.66)^2=926.55 3=’3-3’2’1+2(’1)^3=4774.83 4=’4-4’3’1+6’2(’1)^2- 3(’1)4 =2195107.20
- 17. CONTD… Since 3 is positive ,therefore the given distribution is positively skewed. The moment about origin is Vr=1/n*fx^r ; (x=mid value i.e=m) When r=1; v1=1/60*6980=116.33334
- 18. REFERENCE Business statistics 2nd edition by J.K.SHARMA
- 19. THANK YOU ALL