Euclids postulates
- 2. EUCLIDEUCLID Euclid (300 BC), also known as Euclid of Alexandria,Euclid (300 BC), also known as Euclid of Alexandria, was a Greek mathematician, often referred to as thewas a Greek mathematician, often referred to as the "Father of Geometry". He was active in the Greek"Father of Geometry". He was active in the Greek colony of Alexandria. during the reign of Ptolemy Icolony of Alexandria. during the reign of Ptolemy I (323–283 BC). His(323–283 BC). His ElementsElements is one of the mostis one of the most influential works in the history of mathematics,influential works in the history of mathematics, serving as the main textbook for teachingserving as the main textbook for teaching mathematics (especially geometry) from the time ofmathematics (especially geometry) from the time of its publication until the late 19th or early 20thits publication until the late 19th or early 20th century. In thecentury. In the ElementsElements, Euclid deduced the, Euclid deduced the principles of what is now called Euclidean geometryprinciples of what is now called Euclidean geometry from a small set of axioms. Euclid also wrote worksfrom a small set of axioms. Euclid also wrote works on perspective, conic sections, spherical geometry,on perspective, conic sections, spherical geometry, number theory and rigor. Euclid's contributions werenumber theory and rigor. Euclid's contributions were built on the Greek culture of philosophicalbuilt on the Greek culture of philosophical investigation into which he was born, relying on theinvestigation into which he was born, relying on the works of thinkers such as Plato, Aristotle, Eudoxus,works of thinkers such as Plato, Aristotle, Eudoxus, and Theaetetus.and Theaetetus. EUCLIDEUCLID
- 7. AXIOMSAXIOMS In mathematics, the termIn mathematics, the term axiomaxiom is used in twois used in two related but distinguishable senses: "logical axioms“related but distinguishable senses: "logical axioms“ and "non-logical axioms". In both senses, an axiom isand "non-logical axioms". In both senses, an axiom is any mathematical statement that serves as aany mathematical statement that serves as a starting point from which other statements arestarting point from which other statements are logically derived. Unlike theorems, axioms (unlesslogically derived. Unlike theorems, axioms (unless redundant) cannot be derived by principles ofredundant) cannot be derived by principles of deduction, nor are they demonstrable by mathematicaldeduction, nor are they demonstrable by mathematical proofs, simply because they are starting points; thereproofs, simply because they are starting points; there is nothing else from which they logically followis nothing else from which they logically follow (otherwise they would be classified as theorems).(otherwise they would be classified as theorems).
- 8. POSTULATESPOSTULATES Euclidean geometry is an axiomatic system, in which allEuclidean geometry is an axiomatic system, in which all theorems ("true statements") are derived from a smalltheorems ("true statements") are derived from a small number of axioms. Near the beginning of the first book ofnumber of axioms. Near the beginning of the first book of the Elements, Euclid gives fivethe Elements, Euclid gives five postulatespostulates(axioms) for plane(axioms) for plane geometry,stated in terms of constructions:geometry,stated in terms of constructions: 11stst POSTULATEPOSTULATE :: A straight line may be drawn from any one point to any other point.Same may be stated as axiom .Given two distinct points, there is a unique line that passes through them.
- 9. This postulates simple says that if you have any twoThis postulates simple says that if you have any two points--A and B, say--then you can always connectpoints--A and B, say--then you can always connect them with a straight line.them with a straight line. 22NDND POSTULATE:POSTULATE: A terminated line can be produced indefinitely. It tells us that we can always make a line segment longer. That means that we never run out of space; that is, space is infinite.
- 10. 3RD POSTULATE: A circle can be drawn with any centre and any radius. It allows for the existence of circles of any size and center--say center A and radius AB.
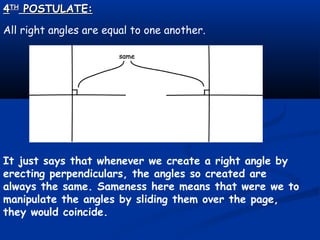
- 11. 44THTH POSTULATE:POSTULATE: All right angles are equal to one another. It just says that whenever we create a right angle by erecting perpendiculars, the angles so created are always the same. Sameness here means that were we to manipulate the angles by sliding them over the page, they would coincide.
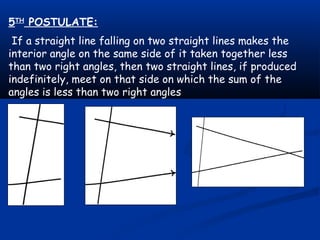
- 12. 5TH POSTULATE: If a straight line falling on two straight lines makes the interior angle on the same side of it taken together less than two right angles, then two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles
- 13. The two different version of fifth postulate a) For every line l and for every point P not lying on l, there exist a unique line m passing through P and parallel to l. b) Two distinct intersecting lines can not be parallel to the same line Equivalent Versions of Euclid's Fifth Postulate Although Euclid's statement of the postulates only explicitly asserts the existence of the constructions, they are also taken to be unique. The Elements also include the following five "common notions :
- 14. 1. Things that equal the same thing also equal one another. 2.If equals are added to equals, then the wholes are equal. 3.If equals are subtracted from equals, then the remainders are equal. 4.Things that coincide with one another equal one another. 5.The whole is greater than the part
- 15. Methods of Proof Euclidean geometry is constructive. Postulates 1, 2, 3, and 5 assert the existence and uniqueness of certain geometric figures, and these assertions are of a constructive nature: that is, we are not only told that certain things exist, but are also given methods for creating them with no more than a compass and an unmarked straightedge.
- 16. THANK YOU